Abstract
We provide foundations for a characteristic free study of foliated varieties in terms of infinitesimal actions of formal groupoids. The ultimate goal is the bi-rational geometry of the same, and to this end we prove a cone theorem for foliations in curves, together with structure theorems for extremal rays, and, of course, a minimal model theorem for surfaces. All possible wild ramification effects of Deligne–Mumford champ are built in, along with the occasional use of Artin champ to address the \(\mathbb Q\)-Gorenstein condition.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Formal groups have been crucial to the development of arithmetic for over half a century. There is, however, here a question of whether the chicken or the egg comes first, since the natural definition of a group is a groupoid with one object. Thus, for example, on identifying discrete groupoids with 1-homotopy types, groups are the 1-homotopy types of connected spaces. In any case, in characteristic zero, the only 1-dimensional formal group is \(\widehat{\mathbb G}_a\) and in any characteristic an action, A, by it on a space X may be written as a power series,
and from additivity of the action, cf. Notation/Revision 1.6, resp. \(A^*\) multiplicative, we conclude, cf. (1.8), resp. (1.11),

In particular, therefore, the latter implies that \(\Delta _1\) is a vector field, \(\partial \), while, if we’re in characteristic zero, the former gives \(\Delta _{n}= \frac{\partial ^n}{n!}\), and conversely. As such a \(\widehat{\mathbb G}_a\)-action in characteristic zero is, locally, identical with a foliation by curves, and it’s plain that once we find ourselves in positive, \(p>0\), characteristic with \(p\,{|}\,n\) in (0.1) that the situation will be very different. Indeed, already the formal group \(\widehat{\mathbb G}_m\) acts on \(\mathbb A^1_k\) by,
which, if it were given by a vector field, then, from (0.2), it would be \(\Delta _1=X\frac{\partial }{\partial X}\), but then \(\Delta _1^p\) would be \(\Delta _1\) in characteristic p rather than 0 as required of \(\widehat{\mathbb G}_a\)-actions in op. cit., and, quite generally, there are infinitely many 1-dimensional formal groups in positive characteristic, with corresponding possibilities for their infinitesimal actions. All of which, in turn, may be globalised to a formal groupoid,

acting on an algebraic space, or Deligne–Mumford champFootnote 1X such that the source s, equivalently the sink t, is a representable smooth map \({\mathfrak {F}}\rightarrow X\) of relative dimension 1. The generality of Deligne–Mumford champ is only relevant to the global questions of minimal model theory since the representability condition ensures, as the local model (0.1) suggests, that, most of the time, X might as well be an affine variety, while the condition of smooth source and sink is the strict analogue of the characteristic zero condition of being defined by a global vector field, so, it is actually a regularity condition that we call absolutely Gorenstein, or absolutely regular in the higher rank case, Definition 1.5. Irrespectively, over a field k of positive characteristic, or, indeed ring of mixed characteristic, Definition 1.1 of a foliation is subtly different from its immediate predecessors, namely [17, 3.6] & [4, §1]. Specifically, the former supposes some liftability to characteristic zero, so, locally the emphasis remains on vector fields and the algebra of operators it generates, whereas the latter concentrates on positive characteristic and prefers not just to replace the resulting exhaustion \({\mathfrak {F}}_n\rightrightarrows X\), Remark 3.3, of (0.4) by infinitesimal schematic relations, but, usually, even to fix \(n=1\), i.e. vector fields, \(\partial \), such that \(\partial ^p\), which by Leibniz’s rule is again a vector field, is parallel to \(\partial \). However, once one pays less attention to the 1st order data, the critical new phenomenon emerges, to wit: for an absolutely regular foliation in characteristic 0 if, Fact 2.5, at a point x,  is finite, then it’s an embedding, and in the complete local ring at x, the foliation is a smooth fibration, whereas, Remark 2.8, this fails in positive characteristic. Consequently, we distinguish absolutely singular points where
is finite, then it’s an embedding, and in the complete local ring at x, the foliation is a smooth fibration, whereas, Remark 2.8, this fails in positive characteristic. Consequently, we distinguish absolutely singular points where  isn’t finite, Definition 2.3, from those where it simply fails to be an embedding, where, in fact, the behaviour is closer to that of smooth points than absolutely singular ones. In particular, these simple observations tend to explain a wealth of pathology which may occur even under our blanket,
isn’t finite, Definition 2.3, from those where it simply fails to be an embedding, where, in fact, the behaviour is closer to that of smooth points than absolutely singular ones. In particular, these simple observations tend to explain a wealth of pathology which may occur even under our blanket,
Convention 0.1
For ease of exposition, and even though many things are true more generally, throughout the article: all champs, algebraic spaces etc., are “geometric”, i.e. separated and of finite type (or, formally so if that is our context) over a base ring k, further properties of which (e.g. being a field) may be specified, but it is always quasi-excellent.
With these standing hypothesis in mind, we may proceed to a summary of §1–§4, via:
§1 An important technical point is to replace  by the infinitesimalisation, \({\mathfrak {J}}_{X/k}\rightrightarrows X\), of the relation all points are equivalent, i.e. Grothendieck jets, Definition 1.1, which cleanly skips technical issues like the diagonal is an embedding iff X is a separated algebraic space. Otherwise, the principal point is to observe that seemingly characteristic 0 specific theorems such as the components of an invariant sub-scheme are themselves invariant are actually true, Lemma 1.9, in the presence of absolute regularity. Hence, it’s important to guarantee it, and the main theorem of this section is Fact/Definition 1.12 which, for foliations by curves, glues together index 1-covers associated to the canonical bundle of \({\mathfrak {F}}/X\) to the Gorenstein covering champ. In characteristic p this will only be Artin rather than Deligne–Mumford. Nevertheless, we have an explicit presentation of it as the quotient of a \(\mathbb G_m\)-action on a punctured cone, and the resulting theory is highly satisfactory.
by the infinitesimalisation, \({\mathfrak {J}}_{X/k}\rightrightarrows X\), of the relation all points are equivalent, i.e. Grothendieck jets, Definition 1.1, which cleanly skips technical issues like the diagonal is an embedding iff X is a separated algebraic space. Otherwise, the principal point is to observe that seemingly characteristic 0 specific theorems such as the components of an invariant sub-scheme are themselves invariant are actually true, Lemma 1.9, in the presence of absolute regularity. Hence, it’s important to guarantee it, and the main theorem of this section is Fact/Definition 1.12 which, for foliations by curves, glues together index 1-covers associated to the canonical bundle of \({\mathfrak {F}}/X\) to the Gorenstein covering champ. In characteristic p this will only be Artin rather than Deligne–Mumford. Nevertheless, we have an explicit presentation of it as the quotient of a \(\mathbb G_m\)-action on a punctured cone, and the resulting theory is highly satisfactory.
§2 Contains the aforesaid distinctions about singularities, and examples thereof.
§3 Having recalled the relation of the definitions of §1 to the inseparable scheme quotients of [4, §3], we come to the elephant in the room which op. cit. didn’t address, namely: can we have the absolutely Gorenstein condition and avoid absolute singularities, or more generally absolute log singularities, in codimension 1. In characteristic zero this just amounts to working with saturated sub-sheaves of the tangent, or more generally log tangent, bundle, and whence we call what we’re after absolutely saturated, Fact/Definition 3.5. Irrespectively, in positive characteristic there are multiple issues. The first is that  might even fail to be coherent in codimension 1, Fact 3.4. Such issues already occur in characteristic zero at the singular points of foliated surfaces because, codimension 2 notwithstanding, punctured formal schemes can have large Picard groups, whereas here coherence in codimension 1 is equivalent to finiteness of the transverse ramification, (3.15) et seq., of Ekedahl’s inseparable scheme quotients. Further, even once things are coherent, it may still be necessary, Scholion 3.6, to make an inseparable covering to obtain an absolutely saturated foliation. Equally, the coherence condition is trivial for foliations arising from algebraic families of curves, and we prove, Scholion 3.6, that if the fibres have multiplicity \(p\ell \), \((\ell ,p)=1\), or even \(p^2\ell \), then there is an absolute saturation. This is ample evidence that all algebraic examples of foliations in curves admit an absolute saturation, and once one has an absolute saturation on every bi-rational model it would make sense to talk about canonical singularities, and whence a motivating future goal that semi-stable reduction of curves should follow from the existence of an absolutely saturated model with canonical singularities.
might even fail to be coherent in codimension 1, Fact 3.4. Such issues already occur in characteristic zero at the singular points of foliated surfaces because, codimension 2 notwithstanding, punctured formal schemes can have large Picard groups, whereas here coherence in codimension 1 is equivalent to finiteness of the transverse ramification, (3.15) et seq., of Ekedahl’s inseparable scheme quotients. Further, even once things are coherent, it may still be necessary, Scholion 3.6, to make an inseparable covering to obtain an absolutely saturated foliation. Equally, the coherence condition is trivial for foliations arising from algebraic families of curves, and we prove, Scholion 3.6, that if the fibres have multiplicity \(p\ell \), \((\ell ,p)=1\), or even \(p^2\ell \), then there is an absolute saturation. This is ample evidence that all algebraic examples of foliations in curves admit an absolute saturation, and once one has an absolute saturation on every bi-rational model it would make sense to talk about canonical singularities, and whence a motivating future goal that semi-stable reduction of curves should follow from the existence of an absolutely saturated model with canonical singularities.
§4 Proves, over a perfect field, a series of adjunction formulae relating the canonical bundle, \(K_{{\mathcal {F}}}\), of a foliation by curves, \({\mathfrak {F}}\rightrightarrows X\), i.e. the restriction to the diagonal of the relative canonical bundle of \({\mathfrak {F}}/X\) and not some random (as it would be in positive characteristic) rank 1 quotient of the cotangent bundle, and the canonical bundle of the normalisation \(f:{{\mathscr {L}}}\rightarrow X\) of invariant curves on X. The only hypotheses are that the foliation should be absolutely \(\mathbb Q\)-Gorenstein, Definition/Revision 1.11, and not absolutely singular along the curve. The final statement, Fact 4.5, taking account of all p-effects is a bit of a mouthful, whereas the essential new feature that such formulae hold along singular curves which aren’t absolutely singular is evidenced by the cleaner formula, Fact 4.4, in the absolutely Gorenstein (as opposed to absolutely \(\mathbb Q\)-Gorenstein) case.
The final two sections apply these considerations to the study of the canonical bundle \(K_{{\mathcal {F}}}\) of \({\mathfrak {F}}\rightrightarrows X\) of an absolutely \(\mathbb Q\)-Gorenstein foliation in curves. In this context all of [3] works out of the box in a characteristic free way for absolutely regular foliations of any rank, i.e. the main theorem of op. cit. on the existence of invariant rationally connected varieties through points of a curve \(f:C\rightarrow X\) with \(f^*N_{\Delta /{\mathfrak {F}}}\) ample is valid mutatis mutandis. However if X is a Deligne–Mumford champ then, a priori, such rationally connected varieties would be sub-varieties of the moduli, rather than the champ itself, which, inter alia, we allow to be wildly ramified over the moduli, and this is without even addressing what is equally necessary for minimal model theory, i.e. whether they lift to rational objects on the Gorenstein covering champ whenever the index of \(K_{{\mathcal {F}}}\) is divisible by p. As such, we not only concentrate on foliations by curves, but employ a novel work around to obtain best possible rationality results. Specifically, we use the algebraisation technique of [3, 2.1.1] to prove the following cone theorem,
Proposition 0.2
(Fact 5.7) Let \({\mathfrak {F}}{\rightrightarrows }X\) be an absolutely \({\mathbb {Q}}\)-Gorenstein foliation by curves, Definition/Revision 1.11, of a (possibly wild) Deligne–Mumford champ over a field k with projective moduli and \(Z\hookrightarrow X\) the absolutely singular locus, Definition 2.3, then there are countably many invariant champs \({{\mathcal {L}}}_i\hookrightarrow X\) not factoring through Z with  such that,
such that,
wherein the rays \({\mathbb {R}}_+{{\mathcal {L}}}_i\) are locally discrete in the open complement of \({\overline{\mathrm {NE}}}_1(X)_{K_{{{\mathcal {F}}}}\geqslant 0}\) \({}+{\overline{\mathrm {NE}}}_1(Z)_{K_{{{\mathcal {F}}}}<0}\) and every extremal ray therein is of this form.
which, a priori, doesn’t even attempt to address whether the \(K_{{\mathcal {F}}}\)-negative extremal rays, which aren’t absolutely singular, are rational. We are, however, studying foliations by curves, so we can employ the adjunction formulae of §4 to conclude,
Proposition 0.3
(Fact 6.5–Fact 6.6) Let everything be as in Proposition 0.2 with \([E/\mathbb G_m]\) \(\rightarrow X\) the Gorenstein covering champ, and suppose further that k is algebraically closed, then for any 1-dimensional sub-champ \({{\mathcal {L}}}\rightarrow X\) which isn’t absolutely singular with  there is a rational curve
there is a rational curve  dominating \({{\mathcal {L}}}\).
dominating \({{\mathcal {L}}}\).
wherein, it should be borne in mind that the formula (6.20) for the degree of the canonical bundle of an inseparable twist of the normalisation of  is more precise still. Specifically, Frobenius can kill many \(\mu _p\) effects in characteristic p, so, a priori Proposition 0.3 doesn’t exclude many points where the non-generic relative monodromy of
is more precise still. Specifically, Frobenius can kill many \(\mu _p\) effects in characteristic p, so, a priori Proposition 0.3 doesn’t exclude many points where the non-generic relative monodromy of  is \(\mu _{p^r}\). However, Fact 6.6, there is at most one point where this, or, indeed wild ramification of \({{\mathcal {L}}}\) over its moduli can occur. Irrespectively, if our plan is to prove 0.3 by adjunction then we a priori need to know the case where X (which may have both a generic stabiliser and wild ramification over its moduli) has dimension 1, which is almost the main theorem of [10] but not quite, so we have an appendix, §A, devoted to the Mori theory of 1-dimensional champ.
is \(\mu _{p^r}\). However, Fact 6.6, there is at most one point where this, or, indeed wild ramification of \({{\mathcal {L}}}\) over its moduli can occur. Irrespectively, if our plan is to prove 0.3 by adjunction then we a priori need to know the case where X (which may have both a generic stabiliser and wild ramification over its moduli) has dimension 1, which is almost the main theorem of [10] but not quite, so we have an appendix, §A, devoted to the Mori theory of 1-dimensional champ.
Finally we apply all of this to the Mori theory of foliations in curves \({\mathfrak {F}}\rightrightarrows X\) of bi-dimensional normal champ over a field k, Corollary 6.3, while continuing to allow the possibility of absolute singularities in codimension 1. Of course the Hodge index theorem alone will ensure a model with \(K_{{\mathcal {F}}}\) nef., as soon as it is pseudo effective, but it doesn’t ensure that a contraction of a curve which isn’t absolutely singular enjoys the rationality properties of Proposition 0.3 nor does it ensure,
Proposition 0.4
(Corollary 6.8) If the minimal model programme for a proper normal champ of dimension 2 with an absolutely Gorenstein in codimension 2 foliation in curves, \({\mathfrak {F}}\rightrightarrows X\), over an algebraically closed field k does not terminate in a model with \(K_{{\mathcal {F}}}\) nef. in Mumford intersection theory, then it terminates in a Mori fibre space, the induced foliation is algebraic, and, off any absolutely singular curves, there is an invariant map from \(\mathbb P^1_k\).
Of course one already knows, [15, III.2.1], the theorem in characteristic zero, so we only prove it in positive characteristic p which permits the pleasing subterfuge of reducing the question to one over finite fields where the \(\mathbb Q\)-Gorenstein condition is free by [1, 2.11], albeit that by Proposition 0.3 the only necessity for doing this is a poor understanding of absolute singularities in codimension 1.
This circle of ideas was employed by Matteo Stacone in his N.Y.U. doctoral thesis, where, inter alia, there is a particularly useful elaboration of the example (2.17), and the limits it places on which characteristic zero phenomenon will extend to all characteristics. It is a pleasure to thank him for the initial typesetting of the manuscript.
2 Foliations and relations
This section is an extension of [4, §2–3]. Specifically the focus of op. cit. is infinitesimal relations, but even just to blow up necessitates the more general setting of infinitesimal groupoids, to wit:
Definition 1.1
Let X/k be an algebraic space, or Deligne–Mumford champ, of essentially finite type over a ring k. As such there is a well defined sheaf of adic algebras \({{\mathscr {P}}}_{X/k}^{\infty }={\varprojlim _{\,n}{{{\mathscr {P}}}_{X/k}^{\,n}}}\) [6, 16.3.1] affording the trivial infinitesimal relation (all points are equivalent) defined by,
and we define a foliation to be a representable infinitesimal groupoid \((s,t):{\mathfrak {F}}\rightrightarrows X\), i.e. s, t are representable maps from the formal spectrum of an adic algebra satisfying the groupoid axioms in the formal category, such that,
-
(1)
At every generic point of X, s (equivalently t) is smooth.
-
(2)
At every generic point of X the induced map,
$$\begin{aligned} {\mathfrak {F}}\xrightarrow {s\times t} {\mathfrak {J}}_{X/k} \end{aligned}$$(1.2)is an embedding.
Furthermore by way of notation we will write \({{\mathscr {P}}}_{{{\mathcal {F}}}}^{\infty }= {\varprojlim _{\,n}{{{\mathscr {P}}}_{{{\mathcal {F}}}}^{\,n}}}\) for the adic \({\mathcal {O}}_X\) algebra which defines \({\mathfrak {F}}\).
Before progressing let us observe some technically pleasing aspects of the definition by way of,
Remark 1.2
In the first place, and by definition of a groupoid, there is an identity,
which, again by definition of an infinitesimal groupoid, is the trace of the formal space, or champ \({\mathfrak {F}}\). Better still there is, [6, 16.8.9.1], a unique coproduct on \({{\mathscr {P}}}_{X/k}^{\infty }\), which under the functor \(\text {Spf}\) is opposite to the groupoid composition,

and whence by item (2) of Definition 1.1 composition in \({\mathfrak {F}}\) is unique at every generic point. In particular \({\mathfrak {F}}\) is, even for X/k only a champ, an actual groupoid, and not some sort of 2-groupoid where composition etc. is only defined up to equivalence of functors.
Related to this we have the dual notion,
Definition 1.3
Let everything be as in Definition 1.1 and view \({{\mathscr {P}}}_{X/k}^{\infty }\) as an \({\mathcal {O}}_X\)-module via \(s^*\) then we define,
which by 1.2 affords maps,
To which we may adjoin some pertinent observations by way of,
Remark 1.4
Let everything be as in Definition 1.3, then:
-
(1)
If X is reduced or, more generally the 0 ideal in \({{\mathcal {O}}}_X\) is unmixed, the maps of (1.6) are injections of sheaves.
-
(2)
Composition in \({\mathfrak {F}}\) (equivalently coproduct in \({{\mathscr {P}}}_{{\mathcal {F}}}\), cf. (1.4) et seq.) affords operator composition in \({{\mathscr {D}}}_{{\mathcal {F}}}\).
-
(3)
The product in \({{\mathscr {P}}}_{{\mathcal {F}}}\) is opposite to the coproduct in \({{\mathscr {D}}}_{{{\mathcal {F}}}}\).
Proof
The only item that might require proof is (1). Plainly the discussion is local, i.e. we have maps of \({{\mathcal {O}}}_X\)-modules,
which are surjective after localising at the set of nonzero divisors by item (2) of Definition 1.1, so if \(D\in {{\mathscr {D}}}_{{{\mathcal {F}}}}^{-n}\) goes to zero under (1.6) it’s because \(fD=0\) where f is not a zero divisor, so, in fact, \(D=0\). \(\square \)
To this we need to add a series of regularity properties beginning with,
Definition 1.5
Following standard usage we denote by \(T_{{{\mathcal {F}}}}\) the first order operators, i.e. \(n=1\) in (1.5), modulo \({{\mathcal {O}}}_X\), and we say that \({{\mathcal {F}}}\) is 1-regular if \(T_{{{\mathcal {F}}}}\) is a bundle. If, however, \(s:{\mathfrak {F}}\xrightarrow []{}X\) (equivalently t) is smooth, then, we say that \({{\mathcal {F}}}\) is absolutely regular. In the case of foliations in curves, i.e. when volume coincides with length, we will say 1-Gorenstein, resp. absolutely Gorenstein, instead of 1-regular, resp. absolutely regular. Irrespectively, regardless of the leaf dimension, 1-regular and absolutely regular coincide in characteristic zero, Warning 1.7.
With a view to describing absolutely regular foliations let us recall,
Notation/Revision 1.6
For any \({{\mathcal {O}}}_X\)-module, \({{\mathcal {M}}}\), we write \(\Gamma ({{\mathcal {M}}})\) for its module of divided symmetric powers. In particular if \({{\mathcal {F}}}\) is absolutely regular, Definition 1.5, then, [6, 16.11.2] (mutatis mutandis) there is a natural isomorphism
Similarly, and following the notation of op. cit. for \(s:F\xrightarrow []{}X\) smooth, we can choose, locally, \(z_1,\dots ,z_n\in {{\mathcal {O}}}_{{\mathfrak {F}}}\) such that,
so that for \(I=(i_1,\dots ,i_n)\), \(i_a\in {\mathbb {Z}}_{\geqslant 0}\), \(1\leqslant a \leqslant n\), a multi-index we get operators \(D_I\) dual to \(z^I\), [6, 16.11.2.3], i.e.

together with Leibniz’s formula for the coproduct, i.e.

In particular, by the definition of the left hand side of (1.8) if k has characteristic p the \(D_I\) for any non-zero \(i_a\) a pth power, e.g. \(1=0^0\) if \(p=0\), generate the algebra \({{\mathscr {D}}}_{{\mathcal {F}}}^{-\infty }\).
To avoid confusion about the notion of absolute regularity let us make,
Warning 1.7
It is important not to read too much into the conditions of Definition 1.5, and, already in characteristic zero, not to confuse it with Definition 2.1 of a smooth foliation. Indeed for a Gorenstein foliation by curves in characteristic zero, defined locally by a vector field \(\partial \), the algebra of \({\mathfrak {F}}\) is given by,

Indeed this is the clean way, [16, II.a], to define [3, 2.1]’s graphic neighbourhood, and it is wholly indifferent to whether the vector field is singular, even in codimension 1, or not. Similarly even in positive characteristic absolutely regularity is reasonably easy to guarantee. It is, however, much less trivial than in characteristic zero. For example, if over \(k={\mathbb {F}}_2\) we start from,
\({\mathfrak {F}}=\text {Spf}\,{{\mathscr {P}}}_{X/S}^{\infty }\) and \(\partial \) the field \(x\frac{\partial }{\partial x}+ y\frac{\partial }{\partial y}\) then \({{\mathcal {F}}}\) is absolutely regular and described by a somewhat more complicated variant of (0.2), i.e. an infinitesimal \(\mathbb G_m\), rather than \(\mathbb G_a\)-action. If, however, \(\nu :{\widetilde{X}}\rightarrow X\) is the blow-up in the origin then \(\partial \) lifts to a field which vanishes everywhere along the exceptional divisor. In particular, although, Fact/Definition 2.9, there is a lifting,
it is not saturated, and if we saturate it to a co-algebra \({{\mathscr {D}}}_{\tilde{{\mathcal {F}}}}^{-\infty }\) then the resulting foliation \({\widetilde{{\mathcal {F}}}}\) is 1-Gorenstein but not absolutely Gorenstein. Indeed the saturated tangent bundle \(T_{\tilde{{\mathcal {F}}}}\) is given by a non-zero vector field at every point of the exceptional divisor, and quite generally, Fact 2.2, such a foliation, cf. (2.4), is everywhere locally a smooth fibration iff it’s absolutely Gorenstein, which is plainly not the case here since not only does (1.13) have multiplicity 2 along the exceptional divisor, there are also nodes where the proper transforms of the x, resp. y, axis cross it.
As such the good way to transform this, and many other examples, is logarithmically, to wit:
Notation/Revision 1.8
Say X/k is smooth and \(x_1\cdots x_n=0\) étale locally a simple normal crossing boundary B in some (subsystem of) coordinates \(x_i\), then we can define a smooth infinitesimal groupoid,
by the following procedure,
-
(1)
Blow up \({\mathfrak {J}}_{X/k}\) in the ideal \((s^*x_1,t^*x_1)\) to get \({\mathfrak {J}}_{X/k}^1\xrightarrow []{}{\mathfrak {J}}_{X/k}\).
-
(2)
By hypothesis \((s^*x_1,t^*x_1)\) restricts to a Cartier divisor on the trace of X, so this lifts to an embedding \(X\hookrightarrow {\mathfrak {J}}_{X/k}^1\), and we define \({\mathfrak {J}}_1\) to be the completion of \({\mathfrak {J}}_{X/k}^1\) in X.
-
(3)
Repeat the above but start from blowing up \({\mathfrak {J}}_1\) in \((s^*x_2,t^*x_2)\), etc.
The finale result is (1.15) which as the notation suggests is independent of the order \(1,\dots ,n\). In particular, therefore, we get an adic algebra,
opposite to (1.15) which we can dualise to obtain,
More generally if X/k is only a geometrically normal variety over a field, so that a priori this discussion only has sense in codimension 2 we will use the notation (1.17) for meromorphic differential operators which belong to the dual of (1.16) outside a closed subset of codimension 2. In any case we say that a foliation \({{\mathcal {F}}}\) is 1-log-saturated along B, or just 1-log-saturated if B is clear from the context, or indeed just saturated if B is empty, if for each n the maps of (1.6) factorise as,
with torsion free quotient, i.e. (1.18) is saturated.
In any case absolute regularity allows many trivialities from characteristic zero which fail for 1-regular foliations to generalise, for example,
Lemma 1.9
Let \({{\mathcal {F}}}\) be an absolutely regular foliation in the sense of Definition 1.5, then every irreducible component of an \({{\mathcal {F}}}\)-invariant subspace \(Z\hookrightarrow X\), or champ, is also \({{\mathcal {F}}}\)-invariant.
Proof
The algebraic definition of invariance,
for \(I_Z\) the ideal of Z, is equivalent to an identity of the fibres,
By hypothesis, however, \({\mathfrak {F}}/X\) is smooth so the irreducible components of \(s^*Z\), resp. \(t^*Z\), are the pullbacks of the irreducible components of Z under  , resp.
, resp.  , which, in turn, cannot be permuted by an infinitesimal groupoid, so \(s^*Y=t^*Y\) for every component Y of Z. \(\square \)
, which, in turn, cannot be permuted by an infinitesimal groupoid, so \(s^*Y=t^*Y\) for every component Y of Z. \(\square \)
Needless to say, therefore, criteria for absolute regularity are important, and a particularly practical one is,
Fact 1.10
Let everything be as in Definition 1.1 and suppose moreover that \({{\mathcal {F}}}\) is everywhere 1-regular, and absolutely regular in codimension 2, then if X is \(\mathrm {S}_2\) for every \(m\geqslant 1\) the double dual \(\widetilde{{\mathcal {P}}}^{\,m}_{{\mathcal {F}}}\) of \({{\mathscr {P}}}^{\,m}_{{\mathcal {F}}}\) is a vector bundle, and we have an exact sequence of bundles,
In particular, therefore, there is an absolutely regular foliation,

Proof
The in particular is clear since the product and co-product are given by limits of maps between vector bundles which are already defined in codimension 2. As such we proceed to prove that the \(\widetilde{{\mathcal {P}}}^{\,m}_{{\mathcal {F}}}\) are vector bundles and that (1.21) holds by induction on m, which for \(m=1\) is just the definition of 1-regular, and the fact that the groupoid identity splits (1.21). Otherwise, for \(m\geqslant 1\), and for I the ideal of the trace we have a split exact sequence

so double dualising is still split exact. However, by the inductive hypothesis, for \(\Omega \) the dual of \(T_{{\mathcal {F}}}\), the double dual of the kernel in (1.23) is, for a foliation of rank r, resolved by the Koszul complex,

wherein any \(\widetilde{{\mathcal {P}}}\) with a negative suffix is understood to be zero. Similarly, one gets the exactness in (1.21) by way of a 9-diagram using (1.24). \(\square \)
However, rather than 1-regular what one can guarantee in practice is,
Definition/Revision 1.11
Suppose X is \(\mathrm {S}_2\) and \(T_{{\mathcal {F}}}\) of Definition 1.5 has rank r at every generic point, then we say that \({{\mathcal {F}}}\) is \(\mathbb Q\)-Gorenstein at a geometric point x of X if there is a positive integer n(x) such that,
is a line bundle in an étale neighbourhood of x. In addition we call the smallest integer such that this holds the index of \(K_{{\mathcal {F}}}\) at x, and we say that \({{\mathcal {F}}}\) is \(\mathbb Q\)-Gorenstein if this holds everywhere. Arguably, therefore, we should, cf. Definition 1.5, call this 1 \(\mathbb Q\)-Gorenstein, but that’s a bit of a mouthful, nor will there be any danger for confusion. We will, however, say that \({{\mathcal {F}}}\) is absolutely \(\mathbb Q\)-Gorenstein if it is everywhere \(\mathbb Q\)-Gorenstein, and absolutely Gorenstein in codimension 2.
Putting all of this together we arrive to a key,
Fact/Definition 1.12
Let \({{\mathcal {F}}}\) be a \(\mathbb Q\)-Gorenstein foliation by curves on a normal Deligne–Mumford champ X over a ring k and E/X the punctured cone,

then there is a well defined Artin champ, \(Y:=[E/\mathbb G_m]\), the Gorenstein covering champ, which is Deligne–Mumford wherever the index of \(K_{{\mathcal {F}}}\) is invertible in k, and otherwise admits a fpqf-presentation such that,
-
(1)
The double dual, written slightly abusively as \(K_{{\mathcal {F}}}|_E\), of the pullback of \(K_{{\mathcal {F}}}\) to E, and whence, by definition to Y, is a line bundle.
-
(2)
If, moreover, \({{\mathcal {F}}}\) is absolutely \(\mathbb Q\)-Gorenstein with
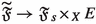 the normalisation of the irreducible component containing
the normalisation of the irreducible component containing 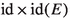 then \({{\widetilde{{\mathfrak {F}}}}}/E\) is a representable \(\mathbb G_m\)-equivariant smooth map, equivalently, \([{{\widetilde{{\mathfrak {F}}}}}/\mathbb G_m]/Y\) is a representable smooth map.
then \({{\widetilde{{\mathfrak {F}}}}}/E\) is a representable \(\mathbb G_m\)-equivariant smooth map, equivalently, \([{{\widetilde{{\mathfrak {F}}}}}/\mathbb G_m]/Y\) is a representable smooth map. -
(3)
Again supposing \({{\mathcal {F}}}\) absolutely \(\mathbb Q\)-Gorenstein, double dualising the pullback of \({{\mathcal {F}}}\) to E, cf. (1.22), yields, in the notation of (1), an absolutely regular \({\mathbb {G}}_m\)-equivariant foliation \({\mathfrak {F}}_E\rightrightarrows E\) with cotangent bundle,
$$\begin{aligned} 0\xrightarrow []{}K_{{{\mathcal {F}}}}|_E\xrightarrow []{}\Omega _{{{\mathcal {F}}}_E}\xrightarrow []{}\Omega _{{\mathbb {G}}_m}\xrightarrow []{}0. \end{aligned}$$(1.27)
Proof
The meaning of the classifier \([E/\mathbb G_m]\) when X is itself a champ will be addressed separately in Scholion 1.13, while the rest of the proposition is étale local on X, i.e. without loss of generality we may suppose that X is an affine scheme. In any case, E/X is smooth where the latter is \(\mathrm {R}_1\) and each \({{\mathcal {A}}}_n\) in (1.26) has depth at least 2 so E is certainly normal, while the tautological maps,

furnish a section of \(K_{{\mathcal {F}}}|_E\), which proves (1). Similarly (2) is just a variation of the proof of Fact 1.10, i.e. by induction on \(m\geqslant 1\) with (1) being the initial case, the double dual \(\widetilde{{\mathcal {P}}}^{\,m}_{{\mathcal {F}}}\) of  is a vector bundle, fitting into an exact sequence,
is a vector bundle, fitting into an exact sequence,
of bundles. As such we have (2), i.e. a smooth fibration,

which in turn we base change via the sink,

to get what is the base change of the groupoid \({\mathfrak {F}}\rightrightarrows X\) to E. Now observe that the pullback of \({{\mathcal {F}}}\) via t to \({\widetilde{{\mathfrak {F}}}}\) is the smooth fibration of (1.30), and, so, in particular, the double dual of \(t^*K_{{{\mathcal {F}}}}\) is a bundle. On the other hand the left hand side of (1.31) is obtained from pulling back, along t, the algebra 1.26. As such the normalisation of the left hand side of (1.31) is the \({\mathbb {G}}_m\)-torsor,

Now complete (1.32) in the section afforded by the diagonal of E to get \({\mathfrak {F}}_E\rightrightarrows E\). Its source is the composition of the smooth maps (1.30) and (1.32) so \({\mathfrak {F}}_E/E\) is smooth. As such it is the normalisation of the base change of \({{\mathcal {F}}}\), so it is also an infinitesimal groupoid. Finally its cotangent bundle is plainly (1.27) in codimension 2, and this is indeed an exact sequence of bundles everywhere by (1.30) and (1.32).
Now \(\mathbb G_m\) acts on \({{\mathcal {A}}}\) with weight n on \({{\mathcal {A}}}_n\), so, irrespectively of Scholion 1.13, for X affine we can certainly define,
and it remains to investigate the finiteness of Y/X. To this end let \(U=U_x\) be a sufficiently small étale neighbourhood of a closed point x of X. Thus, by hypothesis, \(K_{{\mathcal {F}}}\) is an index \(n=n(x)\) \(\mathbb Q\)-Cartier divisor, and we can form an index n cover, i.e. if \(U'\hookrightarrow U\) is the locus where U is regular, then after a choice of trivialisation \(\tau \) we have a fibre square,

wherein [0] is the zero section, so the index n-cover (up to normalisation) is the closure V of \(V'\) in  . However, the \(\mathbb G_m\)-orbit of every point in \(E_U\) meets V, so \(Y_U/U\) is equivalent to \([V/\mu _{n}]\), i.e. Y has an fpqf presentation which is Deligne–Mumford whenever n is invertible in k. \(\square \)
. However, the \(\mathbb G_m\)-orbit of every point in \(E_U\) meets V, so \(Y_U/U\) is equivalent to \([V/\mu _{n}]\), i.e. Y has an fpqf presentation which is Deligne–Mumford whenever n is invertible in k. \(\square \)
The remaining issue to address is, therefore,
Scholion 1.13
The meaning of the classifier \([E/\mathbb G_m]\) whenever X is a champ. Given a presentation [U/R] of X as an étale groupoid we get a presentation of E,
by restricting the punctured cone of 1.26 to R, resp. U. As such for every \(e\in E^0\) and arrow f with source \(s(f)=\pi (e)\) there is a unique arrow,
and in turn every element of \(E^1\) has this form. Further the arrows in (1.36) commute with the action of \({\mathbb {G}}_m\) on the fibres of \(\pi \), so we get a groupoid,

and by definition \([E/\mathbb G_m]\) is the classifier of (1.37). In particular, therefore, there is a subgroup scheme \(G\xrightarrow []{}U\) of the stabiliser given by arrows in (1.37) in which \(\epsilon _f\) is the identity, which is a normal sub-groupoid in the sense of [12, 7.1] because the \({\mathbb {G}}_m\)-action commutes with (1.36). On the other hand G/U is finite by (1.34) et seq. so, for any prime, the p-torsion subgroup scheme \(P\hookrightarrow G\) is well defined, and, of course it’s a normal sub-groupoid of (1.37). Consequently as in [12, 7.4] we get a groupoid,

which over a ring of characteristic p can be sliced to a Deligne–Mumford champ,
factoring the Gorenstein covering champ. We did, however, suppose X normal, so \(Y/P\xrightarrow []{}X\) is an isomorphism in codimension 2, and whence,
Remark 1.14
Since we will be working with Deligne–Mumford champ it will be possible, without loss of generality in characteristic p, to replace X by the almost étale cover Y/P of (1.39), and thus suppose that all the stabilisers of the action (1.37) are \(\mu _q\)’s for, possibly varying, powers q of the characteristic p.
3 Singularities
In the first place there is an unambiguous definition of smooth, to wit:
Definition 2.1
Let \({{\mathcal {F}}}\) be an absolutely regular foliation, Definition 1.5, of an algebraic space or Deligne–Mumford champ over a ring k, then we say that \({{\mathcal {F}}}\) is smooth at a point x of X if \({\mathfrak {F}}\xrightarrow {s\times t}{\mathfrak {J}}_{X/k}\) is an embedding in a neighbourhood of  .
.
This definition does exactly what it says it should on the packet, i.e.
Fact 2.2
Let everything be as in Definition 2.1 with \({\widehat{X}}\) the formal spectrum of the completion of the local ring of X in x and \({\widehat{{\mathfrak {F}}}}\) the induced groupoid

wherein the fibre products are taken in the formal category, then \({{\mathcal {F}}}\) is smooth at x iff there is a smooth fibration \(\pi :{\widehat{X}}\xrightarrow []{}{\widehat{X}}/{\widehat{{\mathfrak {F}}}}\) such that,

Proof
Plainly the discussion is local at x, so we may as well say X/k is an affine scheme and identify \({\mathfrak {F}}\) with the formal spectrum of,
As such \({\mathfrak {F}}\xrightarrow []{s\times t}{\mathfrak {J}}_{X/k}\) is an embedding at  iff there is a surjection,
iff there is a surjection,
which is certainly independent of replacing X by \({\widehat{X}}\), so the if direction in Fact 2.2 is clear. Conversely if \({\widehat{{\mathfrak {F}}}}\) is smooth at \({\widehat{X}}\) in the sense of Definition 2.1 then there are functions \(x_1,\dots ,x_n\in {{\mathcal {O}}}_{{\widehat{X}}}\) such that,

wherein we confuse \(dx_i\in \Omega _{X/k}\) with its image in \(\Omega _{{{\mathcal {F}}}}\) under (2.4). Now consider the transversal Y cut out by the \(x_1,\dots ,x_n\), i.e.
then the fibre  is the formal spectrum of,
is the formal spectrum of,
so the pullback of this along t of I is just the ideal \((dx_1,\dots ,dx_n)\) and whence there is a fibre square,

while  is the formal spectrum of (2.7) by symmetry in s and t so the top horizontal is essentially surjective, i.e. \({\widehat{X}}/{\widehat{{\mathfrak {F}}}}\xrightarrow []{\sim }Y\) as required. \(\square \)
is the formal spectrum of (2.7) by symmetry in s and t so the top horizontal is essentially surjective, i.e. \({\widehat{X}}/{\widehat{{\mathfrak {F}}}}\xrightarrow []{\sim }Y\) as required. \(\square \)
Despite this reassuring start there are competing definitions for a foliation to be singular which we clarify by way of,
Definition 2.3
Let everything be as in Definition 2.1, then we say that \({{\mathcal {F}}}\) is singular at a point x if it is not smooth. We say, however, that \({{\mathcal {F}}}\) is absolutely singular at x if, \({\mathfrak {F}}\xrightarrow []{s\times t}{\mathfrak {J}}_{X/k}\) is not finite at  . Similarly if X is geometrically normal with k a field, and B a Weil divisor such that
. Similarly if X is geometrically normal with k a field, and B a Weil divisor such that  factors through \({\mathfrak {J}}_{X/k}(\log B)\), Definition 1.8, then we say that \({{\mathcal {F}}}\) is log smooth, resp. log singular, resp. absolutely log singular if \({\mathfrak {F}}\xrightarrow {s\times t}{\mathfrak {J}}_{X/k}(\log B)\) is an embedding, resp. not an embedding, resp. not finite. Notice, in particular,
factors through \({\mathfrak {J}}_{X/k}(\log B)\), Definition 1.8, then we say that \({{\mathcal {F}}}\) is log smooth, resp. log singular, resp. absolutely log singular if \({\mathfrak {F}}\xrightarrow {s\times t}{\mathfrak {J}}_{X/k}(\log B)\) is an embedding, resp. not an embedding, resp. not finite. Notice, in particular,
Remark 2.4
If a Weil divisor, B, is absolutely singular, a lifting \({\mathfrak {F}}\xrightarrow {s\times t} {\mathfrak {J}}_{X/k}(\log B)\) necessarily exists by Notation/Revision 1.8 so, under such hypothesis, absolutely log singular is a strictly stronger condition.
Now to fix ideas, the difference between singular and absolutely singular is a positive characteristic phenomenon, as is evident from,
Fact 2.5
Again let everything be as in Definition 2.1 then, plainly, and irrespective of the characteristic, an absolutely singular point is singular, while the converse holds iff k is a field of characteristic zero.
Proof
The initial assertion is trivial while an example showing the necessity of characteristic zero is provided by the Whitney umbrella of (2.15). Otherwise, for sufficiency, everything is local, so for X affine suppose (2.4) is not a surjection then since \({{\mathcal {F}}}\) is absolutely regular,

Equally \(\partial \) generates a sub-algebra \(k[\partial ]\) of \({{\mathscr {D}}}^{\,-\infty }_{{{\mathcal {F}}}}\) dual to a foliation by curves,
which in turn is embedded because operators of degree at least \(-n\) in \(k[\partial ]\) are in a sub-vector bundle of \({{\mathscr {D}}}_{{{\mathcal {F}}}}^{\geqslant -n}\). As such, if \({{\mathcal {F}}}\) is not absolutely singular at x then neither is \({{\mathcal {F}}}_{\partial }\). However at the level of adic rings \({\mathfrak {F}}_{\partial }\xrightarrow []{s\times t}{\mathfrak {J}}_{X/k}\) is,

which by (2.9) is the zero map mod \({\mathfrak {m}}(x)\), so \(\partial ^{\vee }\) cannot be integral over \({{\mathscr {P}}}_{X/k}\). \(\square \)
In a sense, however, the difference is not so dramatic since the appropriate generalisation of Fact 2.2 is,
Fact 2.6
Let everything be as in Fact 2.2 then \({{\mathcal {F}}}\) is not absolutely singular at x iff there is a transversal \(Y\hookrightarrow {\widehat{X}}\) such that for \({\widehat{\times }}\) the complete tensor product the induced groupoid,

is proper and fpqf. In particular the coarse moduli \(\pi :{\widehat{X}}\xrightarrow []{}{\widehat{X}}/{\widehat{{\mathfrak {F}}}}\) (i.e. Y/R by (2.12)) exists.
Proof
Once we know the existence of the coarse moduli Y/R the converse is clear. The existence, however, is a question in complete local rings so [12, 5.1] works just as well in our formal context as it does in the scheme context of op. cit. As such it remains to produce the transversal Y, or, more accurately check that op. cit. 3.3 continues to hold which it does since \({\mathfrak {F}}/X\) is smooth, whence, a fortiori Cohen–Macaulay, so we don’t need step 1 of op. cit. while step 2 works as stated. \(\square \)
Consequently the easier situation in characteristic zero is simply a manifestation of the fact that in characteristic zero any zero-dimensional infinitesimal group is a point since as soon as \(R\rightrightarrows Y\) in (2.12) has no stabiliser the coarse moduli \(\pi \) in Fact 2.6 is also fine. Irrespectively observe a useful characteristic-free description of the absolutely singular points, to wit:
Fact 2.7
Let everything be as in Definition 2.1 and suppose in addition that \({\mathfrak {F}}\rightrightarrows X\) is a foliation in curves over a field k then a closed point x is absolutely singular iff the maximal ideal is invariant.
Proof
By the definition of invariant, (1.20),

so, irrespective of the rank of \({{\mathcal {F}}}\), such points are always absolutely singular. Conversely, \(s^{-1}(x)\) is isomorphic to,

So either  is too, or
is too, or  is finite at
is finite at  . \(\square \)
. \(\square \)
We may also usefully observe,
Remark 2.8
Even for an absolutely Gorenstein foliation by curves, it is perfectly possible that Fact 2.6 holds, but the foliation is not smooth. For example, over a field of characteristic \(p>0\) there is an infinitesimal action of \(\mathbb G_a\ni T\) given by,
of which the map to the coarse moduli is,
Similarly in dimension 2, one can start with a perfectly smooth example such as a product of curves  such that \(\mathbb Z/p\) acts on C, then take X to be the quotient by the diagonal action with \({{\mathcal {F}}}\) the first projection. It’s plain that such an example isn’t smooth in the sense of Definition 2.1, but this is equally true of a tame diagonal \(\mu _\ell \) action, \((p,\ell )=1\), however, the difference between the two is that the \(\mathbb Z/p\) quotient can be made absolutely Gorenstein. For example, following [2] for \(p=2\) and e even, we can take C to be,
such that \(\mathbb Z/p\) acts on C, then take X to be the quotient by the diagonal action with \({{\mathcal {F}}}\) the first projection. It’s plain that such an example isn’t smooth in the sense of Definition 2.1, but this is equally true of a tame diagonal \(\mu _\ell \) action, \((p,\ell )=1\), however, the difference between the two is that the \(\mathbb Z/p\) quotient can be made absolutely Gorenstein. For example, following [2] for \(p=2\) and e even, we can take C to be,

then by op. cit. if we take the foliation to be projection to u, with v a coordinate in the other direction, X is given by,

so the foliation is certainly 1-Gorenstein with generator,
and whence absolutely Gorenstein by Fact 1.10.
Closely related to these considerations are how a foliation transforms under bi-rational modifications, for example,
Fact/Definition 2.9
Let \((s,t):{\mathfrak {F}}\rightrightarrows X\) be an absolutely regular foliation, Definition 1.5, of a Deligne–Mumford champ over a ring k, and M an invariant ideal with \(\nu :{\widetilde{X}}\xrightarrow []{}X\) the blow-up in the same, then, we have a fibre square,

thus by the universal property of fibre products we get a map,

to the induced groupoid  , and \(\nu ^*{\mathfrak {F}}\) is a sub-groupoid, independent of the choice of the first projection in (2.20), which by construction defines an absolutely regular foliation. In particular, operators lift, i.e. we have a map,
, and \(\nu ^*{\mathfrak {F}}\) is a sub-groupoid, independent of the choice of the first projection in (2.20), which by construction defines an absolutely regular foliation. In particular, operators lift, i.e. we have a map,
Proof
The only thing that isn’t wholly automatic from the definitions is that \(\nu ^*{\mathfrak {F}}\) is closed under groupoid composition. Observe, however, that if we start from,

then no matter what choices of projections to X we make, we always get the same ideal on the top left, resp. right, entry of (2.23), so,

and composition lifts. \(\square \)
Contractions, even on surfaces in characteristic zero, are less satisfactory, to wit:
Fact/Definition 2.10
Let \({\mathfrak {F}}\rightrightarrows X\) be a foliation of a normal algebraic space or Deligne–Mumford champ over a ring k; \(c:X\rightarrow X_0\) a contraction with \(X_0\) normal; and \(j:U\hookrightarrow X_0\) the locus where c is an isomorphism, then we define,

which although a well defined formal scheme mapping to \({\mathfrak {J}}_{X_0/k}\), may very well fail, even if \({\mathfrak {F}}\) is absolutely regular, to be a groupoid. As such, in an abus de language, by the contracted foliation we a priori only mean its restriction to U and we extend this to a foliation on \(X_0\), or its Gorenstein covering champ, when we can by Fact 1.10, or, much more likely in practice Fact/Definition 1.12. Consequently if these latter conditions aren’t verified then \(K_{{\mathcal {F}}}\), \(T_{{{\mathcal {F}}}}\) etc. may only mean \(j_*(K_{{{\mathcal {F}}}|U})\), \(j_*(T_{{{\mathcal {F}}}|U})\) etc.
4 Inseparable quotients
In positive characteristic, foliations determine inseparable scheme quotients,
Notation/Revision 3.1
([4, §3]) Let \((s,t):{\mathfrak {F}}\rightrightarrows X\) be a foliation as in Definition 1.1 but over an algebraically closed field k of positive characteristic p. As such base change by r fold iteration, \(r\in {\mathbb {Z}}_{\geqslant 0}\), of the inverse Frobenius of k determines a conjugate variety \(X^{(-r)}\) to which the r-fold geometric Frobenius,
maps. Better still the relation,

together with \({\mathfrak {F}}\) generates a relation,
which following [4, 3.1] we refer to as the height r foliation (or just r-foliation) associated to \({\mathfrak {F}}\). In particular the coarse moduli of (3.3) determines a factorisation,

of the geometric Frobenius.
For differential operators, the situation is as follows: the pullback of jets,
takes the ideal of the trace on the left to a sub-ideal of the qth power of the trace on the right, so:
In particular therefore the non-constant operators, \({{\mathscr {D}}}_{{{\mathcal {F}}}}^{>-q}\,\, \mathrm {mod}\,{{\mathcal {O}}}_X,\) of Definition 1.3 of order greater than \(-q\) operate trivially on \(X^{(-r)}\) while,
where, because of the saturation issues of (1.18) et seq., the correspondence,
only determines \({\mathfrak {F}}\) generically. If however X were irreducible and \({\mathfrak {F}}\) were saturated along a Weil divisor, (1.18), then the correspondence implied by (3.8) is, on fixing B, 1-1. Similarly if X is normal then \(X/{\mathfrak {F}}^r\) is too since, from (3.7),
We also have from (3.7) a chain,
factorising \(\rho _r\), so many questions can be reduced to the study of \(\rho _1\), of which a particularly pertinent invariant is,
Definition 3.2
Let everything be as in Notation/Revision 3.1 but with X normal, and B a reduced Weil divisor. In particular [4, 3.2] holds in codimension 2, so, off a closed subset of the said codimension, we have an exact sequence of bundles,
where \(\Omega _{{{\mathcal {F}}}}\) is the dual of \(T_{{\mathcal {F}}}\) of Definition 1.5 provided the latter is saturated along the divisor, B is confused with its image in \(X/{\mathfrak {F}}^{1}\), and everything else is defined by the exact sequence (3.11). Equally, for any r there is an exact sequence,
which, also, serves as the definition of the kernel in (3.12), and whence there is a natural map,
It does not however follow from the definition of Notation/Revision 3.1, unlike that of [4, 3.1], of height r-foliation that (3.13) is an isomorphism, and indeed it may not be, e.g. the blow-up post (1.13) in characteristic 2 with B empty (rather than the exceptional divisor) is a counter-example. Nevertheless we can take the first Chern class of everything in (3.11)–(3.12) as a Weil divisor, i.e.
So that (3.13) defines a (transverse) ramification divisor R by way of,
which in turn by (3.11) equally satisfies,
while for the avoidance of confusion we observe,
where \( K_{X/{{\mathcal {F}}}}\) is defined via (3.14) with B empty.
All of which provides a rather convenient way to do calculations, i.e.
Remark/Definition 3.3
Let \(I_{{\mathfrak {F}}}\) be the ideal of the trace for a foliation \({\mathfrak {F}}\rightrightarrows X\), then for  , \(r\geqslant 1\), we have an inclusion,
, \(r\geqslant 1\), we have an inclusion,
Conversely if \(q'\) is the largest pth power less than  then,
then,
so as \(q\rightarrow \infty \) they define the same topology and we have the convenient formula,
together with an alternative filtration on differential operators,
As such, in the particular case of the trivial foliation \({\mathfrak {J}}_{X/k}\rightrightarrows X\),
and so in the presence of a divisor we extend Notation/Revision 1.8 by way of,
Finally to tie this up with the inseparable quotients of Notation/Revision 3.1 observe that the operators of (3.6) generate those of (3.21) with as ever  , so we get a factorisation,
, so we get a factorisation,
Indeed, a priori the rightmost arrow in (3.24) may not be injective, its image is, however, some infinitesimal algebra \({{\mathcal {O}}}_R\) which is flat over \({{\mathcal {O}}}_X\) in codimension 2. As such, its spectrum defines a groupoid \(R\rightrightarrows X\) with flat source and sink over an open whose complement has codimension 2. On the other hand, étale locally,  is a generic isomorphism, thus there is a bi-rational map \(X_r\rightarrow X/R\) between \(\mathrm {R}_1\) varieties, so an isomorphism in codimension 2, and whence the the middle term in (3.24) is torsion free, so the rightmost arrow in op. cit. is injective because it is so generically. Similarly, if \({\mathfrak {F}}\) factors through \({\mathfrak {J}}_{X/k}(\log B)\) we take,
is a generic isomorphism, thus there is a bi-rational map \(X_r\rightarrow X/R\) between \(\mathrm {R}_1\) varieties, so an isomorphism in codimension 2, and whence the the middle term in (3.24) is torsion free, so the rightmost arrow in op. cit. is injective because it is so generically. Similarly, if \({\mathfrak {F}}\) factors through \({\mathfrak {J}}_{X/k}(\log B)\) we take,
as the definition of the middle term. As such,
also defines a groupoid flat in codimension 2, and we define \({\mathscr {D}}{} \textit{iff}_{X/X_r}(-\log B)\) to be the dual of (3.26).
With this in mind we come to the key intervention of the ramification,
Fact 3.4
Let everything be as in Definition 3.2 and Remark 3.3 (so, inter alia X normal) then there exists \( r_0\in {\mathbb {Z}}_{\geqslant 0}\) such that for all \(r\geqslant r_0\) the map \(X_r\xrightarrow []{} X_{r+1}\) has no ramification, in the sense of (3.15)–(3.16), iff there is a Zariski \(U\hookrightarrow X\) with codimension 2 complement such that the restriction to U of the inverse system (3.25) is defined by a coherent sheaf of ideals on \({\mathfrak {J}}_{X/k}(\log B)\).
Proof
The proposition is local, and k is algebraically closed, so we may suppose X is a smooth affine k-scheme with B simple normal crossing. Now consider first sufficiency in the case that \(r_0=0\), then, for \(I_\Delta \) the ideal of the trace of \({{\mathscr {P}}}_{X/k}^{\infty }(\log B)\) and \(I_r\) the kernel of the rightmost arrow in (3.25) we have, by hypothesis,
so that for \(J_r\) the ideal of the diagonal of the middle term in (3.25)
Consequently if we further restrict attention to the locus where \(J_1/J_1^2\) is locally free then for any r the graded algebra of the middle term in (3.25) is the algebra,
Indeed the map from (3.29) to the graded is always surjective, while it’s injective because it’s so generically, and thus we get,
which is what we required to prove. Now, say \(r_0\) is arbitrary, and consider
then the map of the latter, resp. the former, to (3.20), defines a sheaf of ideals, \({{\mathcal {I}}}\), resp. \({{\mathcal {J}}}\), on \({\mathfrak {J}}_X(\log B)\), resp. \({\mathfrak {J}}_{X^{(-r)}}(\log B)\). Now, we’ve proved \({{\mathcal {J}}}\) is coherent over \(U\hookrightarrow X\) with codimension 2 complement, i.e. for \(W\subseteq V\) affines in U,

On the other hand (3.31) is a finite inseparable map, so \(\Gamma (W, {{\mathcal {I}}}) \) is the unique prime of the rightmost term in (3.31) lying over the leftmost term in (3.32) after restricting to W, and since we may argue similarly on V,  also lies over the same prime, so these are equal and \({{\mathcal {I}}}\) is coherent. Necessity is easier, since,
also lies over the same prime, so these are equal and \({{\mathcal {I}}}\) is coherent. Necessity is easier, since,
in the above notations, so, around every codimension 1 point, the sequence on the left of (3.33) is a decreasing sequence in the Artinian module \(I_1+ I_\Delta ^2/{{\mathcal {I}}}+I_\Delta ^2\). \(\square \)
This motivates the following,
Fact/Definition 3.5
Let \({\mathfrak {F}}\rightrightarrows X\) be an absolutely Gorenstein foliation in curves satisfying the equivalent conditions of Fact 3.4 and observe by Definition 2.3, of an absolutely singular divisor D, \({\mathfrak {F}}\) factors through \({\mathfrak {J}}_X(\log D)\), so without loss of generality, we insist that B contains all codimension one points where \({\mathfrak {F}}\) is absolutely singular. Furthermore by (3.29) then there is a smallest \(0\leqslant r\leqslant r_0\) such that there exists an open \(U\hookrightarrow X\) with codimension 2 complement over which the normalisation, \(\widetilde{{\mathfrak {F}}}_r\), of the image of \({\mathfrak {F}}_{U}\) in \({\mathfrak {J}}_{U_r}(\log B)\) defines an absolutely Gorenstein foliation \(\widetilde{{\mathfrak {F}}}_r\rightrightarrows U_r\), the  of \({{\mathcal {F}}}\), which is not absolutely log singular, Definition 2.3. In particular if the tangent bundle of the resulting foliation on \(U_r\) satisfies the \(\mathbb Q\)-Gorenstein condition of Definition/Revision 1.11, then \(\widetilde{{\mathfrak {F}}}_r\rightrightarrows U_r\) may be completed to an absolutely regular foliation on the Gorenstein covering champ \(Y_r\rightarrow X_r\) of Fact/Definition 1.12 which is not absolutely log-singular, and, irrespectively, we say that \({\mathfrak {F}}\rightrightarrows X\) is absolutely
of \({{\mathcal {F}}}\), which is not absolutely log singular, Definition 2.3. In particular if the tangent bundle of the resulting foliation on \(U_r\) satisfies the \(\mathbb Q\)-Gorenstein condition of Definition/Revision 1.11, then \(\widetilde{{\mathfrak {F}}}_r\rightrightarrows U_r\) may be completed to an absolutely regular foliation on the Gorenstein covering champ \(Y_r\rightarrow X_r\) of Fact/Definition 1.12 which is not absolutely log-singular, and, irrespectively, we say that \({\mathfrak {F}}\rightrightarrows X\) is absolutely  if \(r=0\) and \({\mathfrak {F}}\) equals \(\widetilde{{\mathfrak {F}}}\) in codimension 2.
if \(r=0\) and \({\mathfrak {F}}\) equals \(\widetilde{{\mathfrak {F}}}\) in codimension 2.
Proof
\({\mathfrak {F}}_r\rightarrow {\mathfrak {J}}_{X_r}(\log B)\) embeds at every generic and \({\mathfrak {F}}\) is normal, so we always have a map \({\mathfrak {F}}_r\rightarrow \widetilde{{\mathfrak {F}}}_r\). Similarly \(\widetilde{{\mathfrak {F}}}_r\) is equally the normalisation of the base change to \(U_r\) of \(\widetilde{{\mathfrak {F}}}_{r_0}\rightrightarrows U_{r_0}\), so the only issue is whether \(\widetilde{{\mathfrak {F}}}_r\rightrightarrows U_r\) inherits a groupoid structure. We can, of course, shrink U as necessary, and since \(\widetilde{{\mathfrak {F}}}_r\) is finite over its image in \({\mathfrak {J}}_{X_r}(\log B)\) and equal to it at every generic point of \(X_r\), the diagonal lifts to \(\widetilde{{\mathfrak {F}}}_r\) in codimension 2, while, even without shrinking U, transposition lifts to \(\widetilde{{\mathfrak {F}}}_r\) so the latter is a groupoid whenever composition lifts which is automatic as soon as  is normal, which in turn follows from absolutely Gorenstein. \(\square \)
is normal, which in turn follows from absolutely Gorenstein. \(\square \)
This raises the question to whether every foliation is absolutely saturated in the sense of Fact/Definition 3.5, which we address by way of,
Scholion 3.6
In general a foliation will not be equal to its debugging. Proceeding by decreasing induction from \(r_0\), the problem occurs when one tries to go from an absolutely saturated example \({\mathfrak {F}}_1\rightrightarrows X_1\) by normalisation of the base change groupoid along the quotient \(\rho :X\rightarrow X_1\) of (3.10), and what has to be verified is that at every codimension one point \(\beta \hookrightarrow X\) where \({\mathfrak {F}}\) is absolutely singular the fibre  of the normalisation is smooth and equal to
of the normalisation is smooth and equal to  . Now, for \(\beta _1=\rho (\beta )\), if \(\beta =\rho ^* \beta _1\) this is already true for the base change groupoid, which must, therefore, equal the normalisation. If, however,
. Now, for \(\beta _1=\rho (\beta )\), if \(\beta =\rho ^* \beta _1\) this is already true for the base change groupoid, which must, therefore, equal the normalisation. If, however,  then there is an issue. To describe the normalisation in this case, we have, away from a closed set of codimension 2, for \({{\mathcal {G}}}\) the 1-foliation corresponding to \(X_1^{(1)}\rightarrow X\), an exact diagram,
then there is an issue. To describe the normalisation in this case, we have, away from a closed set of codimension 2, for \({{\mathcal {G}}}\) the 1-foliation corresponding to \(X_1^{(1)}\rightarrow X\), an exact diagram,

so the saturation of the middle vertical defines a 1-foliation, \({{\mathcal {E}}}\), on \({\mathfrak {F}}_1^{(1)}\) such that \(\widetilde{{\mathfrak {F}}}\) is the quotient \({\mathfrak {F}}_1^{(1)}/{{\mathcal {E}}}\). As such the original foliation on X admits an absolute saturation iff \({{\mathcal {E}}}\) isn’t singular at \(\Delta (\beta )\), i.e. around \(\beta \), the saturation of the middle vertical in (3.34) surjects onto the saturation of the rightmost vertical around \(\beta _1^{(1)}\). There is, however, no restriction on \(X\rightarrow X_1\) except that it’s purely inseparable of degree p. Indeed starting from an absolutely saturated foliation \({\mathfrak {F}}_1\rightrightarrows X_1\), the base change to any such \(X\rightarrow X_1\) affords a foliation by curves \({\mathfrak {F}}\rightrightarrows X\) such that, in the notation of (3.10),  , so the failure of \({{\mathcal {E}}}\) to be smooth at codimension 1-points where we have the generic behaviour
, so the failure of \({{\mathcal {E}}}\) to be smooth at codimension 1-points where we have the generic behaviour  is rather common.
is rather common.
As such, further hypothesis is required to deduce an absolutely Gorenstein foliation in codimension 2 on X from one on \(X_1\). An example is provided by fibrations in curves which plainly satisfy the second of the equivalent conditions of Fact 3.4, and once there is no ramification all fibres have multiplicity one, so, say, over an algebraically closed field, \(\pi :X_1\rightarrow S\) a map from a normal surface to a smooth curve with all fibres reduced. Now if the restriction of \(X\xrightarrow {\rho } X_1\) to a curve \(B={\bar{\beta }}\hookrightarrow X\) in a fibre of \(\pi \) is not inseparable, there is \(x=0\), resp. \(z=0\), a local equation for B, resp. \(\pi (B)_{{\mathrm {red}}}\), with y a coordinate along B, such that, around B, \(\rho \) is given by,
wherein u is a unit, and the resulting 1-foliation, \(dy=0\), is the saturation of du, so all of z, y and \(\xi =x^p\) are coordinate functions on \(X_1\), whence \(\Omega _{{\mathcal {G}}}\) of (3.34) is \(d\xi =0\). As such the 1-foliation defined by the middle arrow in (3.34) is given by,

with divided power operators understood in the coordinate system z, y. Now, the order of vanishing at  along the rightmost vertical in (3.34) is,
along the rightmost vertical in (3.34) is,

so to calculate \(t^*d\xi \) modulo \(s^*d\xi \) and terms of order (3.37) is already modulo \(s^*dz\). Thus, modulo \(s^*d\xi \) the order of vanishing of \(t^*d\xi \) is the min of (3.37) and

which is at least (3.37). Consequently the middle and rightmost verticals in (3.34) saturate to the same order along B, so the saturation of the middle vertical is a smooth 1-foliation at every point of the fibre of \({\mathfrak {F}}_1^{(1)}\) over  . Thus, \(\widetilde{{\mathfrak {F}}}\) is regular at \(\Delta (\beta )\), so the diagonal is a Cartier divisor there, and s is smooth over \(\beta \).
. Thus, \(\widetilde{{\mathfrak {F}}}\) is regular at \(\Delta (\beta )\), so the diagonal is a Cartier divisor there, and s is smooth over \(\beta \).
5 Adjunction formulae
The presence of singular points which aren’t absolutely singular gives rise to new relations between the canonical bundle of the foliation and that of invariant sub-varieties which we investigate by way of,
Set Up 4.1
Let \({\mathfrak {F}}\rightrightarrows X\) be an absolutely regular foliation, Definition 2.1, of a Deligne–Mumford champ, X, over a filed k, with \(\lambda :L\xrightarrow []{}X\) a map from a connected k-smooth Deligne–Mumford champ such that:
-
(1)
\(\lambda \) is an embedding at its generic point.
-
(2)
\({{\mathcal {F}}}\) is not absolutely singular at the generic point of L.
-
(3)
The image of the generic point is invariant by \({{\mathcal {F}}}\).
In such circumstances we have,
Fact 4.2
Let everything be according to Set Up 4.1 then there is a unique map  rendering commutative
rendering commutative

Proof
Let \({\overline{L}}\hookrightarrow X\) be the image of L with I its ideal, then, by item (3) of Set Up 4.1, \(t^*I\) is zero over the generic point of  . The latter is however smooth over \({\overline{L}}\), which in turn is irreducible, thus \(t^*I\) is, in fact, zero everywhere, i.e. I is invariant in the sense of (1.20), and so we have a fibre square,
. The latter is however smooth over \({\overline{L}}\), which in turn is irreducible, thus \(t^*I\) is, in fact, zero everywhere, i.e. I is invariant in the sense of (1.20), and so we have a fibre square,

Now étale locally \({\mathfrak {J}}_{{\overline{L}}/k}\), resp. \({\mathfrak {J}}_{L/k}\), is  , resp.
, resp.  , completed in the diagonal, so \({\mathfrak {J}}_{L/k}\) is the normalisation of the irreducible component of the trace of the top right corner in (4.2), and
, completed in the diagonal, so \({\mathfrak {J}}_{L/k}\) is the normalisation of the irreducible component of the trace of the top right corner in (4.2), and  is smooth, whence (4.1). \(\square \)
is smooth, whence (4.1). \(\square \)
This allows us to relate the geometry of L to that of \({{\mathcal {F}}}\), for example,
Fact 4.3
Again let everything be as in Set Up 4.1 and suppose moreover that \({{\mathcal {F}}}\) is smooth at the generic point of L then the horizontal arrow in (4.1) at the level of the ideal of the trace modulo its square furnishes a generic isomorphism,
Proof
Let \(\Delta \), resp. \({\widetilde{\Delta }}\), be the trace in \({\mathfrak {J}}_L\), resp.  with ideal \(I_{\Delta }\), resp. \(I_{{\tilde{\Delta }}}\), then \(\Lambda ^{-1}I_{\Delta }\subset I_{{\tilde{\Delta }}}\) which gives (4.3). \(\square \)
with ideal \(I_{\Delta }\), resp. \(I_{{\tilde{\Delta }}}\), then \(\Lambda ^{-1}I_{\Delta }\subset I_{{\tilde{\Delta }}}\) which gives (4.3). \(\square \)
In general, however, there is no more reason for (4.3) to be a generic isomorphism than there is for a dominant equidimensional map to be separable, and since in dimension 1 any inseparable map is generically a power of Frobenius we can, for foliations in curves, be rather precise about the problem, to wit:
Fact 4.4
Let everything be as in Set Up 4.1 and suppose moreover that \({{\mathcal {F}}}\) is a foliation in curves, with \(\rho _r:{\mathfrak {F}}\rightarrow {\mathfrak {F}}_r\) the inseparable scheme quotient defined by r-iterations of Frobenius along the fibres of the first projection, i.e. the factorisation of r iterates of the geometric Frobenius \(\mathrm {Fr}_{{\mathfrak {F}}/k}\), (3.1), in which each square is fibred,

then there is a maximal r such that (4.1) factors as

and for  , r aforesaid maximal, there is a generic isomorphism,
, r aforesaid maximal, there is a generic isomorphism,
which vanishes at every point \(x\in L\) such that \(\lambda (x)\) is absolutely singular. Furthermore at any other point \(x\in L\) where (4.6) vanishes, the map of fibres
is generically étale with wild ramification at \(\Delta (x)\) to order the vanishing of (4.6).
Proof
By item (2) of Set Up 4.1, \(\Lambda \) of (4.1) is finite, so there is a maximal r such that (4.5) holds, and (4.6) is a generic isomorphism iff it is so after completing in the image \(\lambda (x)\) of a generic closed point x. After completion, however, we can appeal to Fact 2.6 and identify \({\overline{L}}\) with a fibre of the coarse moduli, and r with the maximal power of Frobenius such that we have a factorisation,
Consequently, for r maximal, the rightmost arrow in (4.8) is generically étale, and whence (4.6) is generically an isomorphism. Similarly, \(\Lambda ^{-1}\Delta \) contains all the fibres over absolutely singular points by (2.13), while all maps in (4.5) are finite, so this is equally true of \(\Lambda _r^{-1}\Delta \), and thus (4.6) vanishes at such points. As to the final item we complete around such a point and retake the notations of Fact 2.6, so that we have a diagram of fibre squares,

wherein the moduli map \(\mu \) cannot be an isomorphism since otherwise \({{\mathcal {F}}}\) would be smooth at x. It is, however, the case that \({\mathfrak {F}}_{\lambda (x)}\) is given by (2.14) thus the fibre of \({\widehat{X}}\) over the coarse moduli has at most one branch, so it must be exactly \({\overline{L}}_x\). Now, irrespectively of whether its reduced or not there must be an embedding
where the infinitesimal stabiliser group scheme G is non-zero since \(\mu \) isn’t an isomorphism by [12, 6.5]. Equally  is a formal sub-scheme of an irreducible with the same reduced structure so they’re the same. As such,
is a formal sub-scheme of an irreducible with the same reduced structure so they’re the same. As such,

which has degree over \({\overline{L}}_x\) the degree of G, thus \({\mathfrak {F}}_{\lambda (x)}\xrightarrow []{}L_x\) has degree a power of the necessarily positive characteristic p, while both \({\mathfrak {F}}_{\lambda (x)}\) and \(L_x\) are isomorphic to (2.14) so after we’ve eliminated the inseparable part by way of the factorisation (4.8) what we’re left with is the rightmost map in (4.8) wildly ramifying at \(\Delta (x)\) which, in turn, is the order of vanishing of \(d\lambda \) in (4.3). \(\square \)
Observe that post (4.2) we used Set Up 4.1’s standing hypothesis of absolute regularity in a fairly essential way in the proof of Fact 4.2. We will, however, need such a result for absolutely \(\mathbb Q\)-Gorenstein foliations by curves. Consequently, with such a hypothesis, for \(\gamma :Y=[E/\mathbb G_m]\rightarrow X\) the Gorenstein covering champ of Fact/Definition 1.12, let \(f:{{\mathcal {L}}}\xrightarrow []{}X\) be the normalisation of a curve on X and form the fibre squares,

then take the normalisation, L, of the component of the generic point. This gives us a curve \([L/{\mathbb {G}}_m]\) on \([E/{\mathbb {G}}_m]\). On the other hand, and quite generally, whenever we have a \(\mathbb G_m\)-action, completion in the identity afford an action of the formal group \(\widehat{\mathbb G}_m\), which, in turn, is a foliation by curves, and whence, the sequence of infinitesimal scheme quotients of Notation/Revision 3.1, or, equivalently, the quotients by the action of \(\mu _{p^r}\hookrightarrow \mathbb G_m\), \(r>0\). In particular, the action of \(\mu _{p^r}\) on L, resp. on the fibres of \(s:{\mathfrak {J}}_{L/k}\rightarrow L\), resp. \(s:{\mathfrak {F}}_E\rightarrow E\), affords sequences of infinitesimal scheme quotients,
and we have the following generalisation of Fact 4.3,
Fact 4.5
Let \({\mathfrak {F}}\rightrightarrows X\) be an absolutely \({\mathbb {Q}}\)-Gorenstein foliation by curves of a normal Deligne–Mumford champ over a perfect field k with \(f:{{\mathcal {L}}}\xrightarrow []{}X\) as above satisfying items (1)–(3) of Set Up 4.1 then the \(\mathbb G_m\)-equivariant map \(\lambda :L\xrightarrow []{}E\), from the necessarily smooth k-champ L, of (4.12) with generic stabiliser \(\mu _Q\),  , in the presence of the simplifying Remark 1.14, also satisfies items (1)–(3) of Set Up 4.1 but for the absolutely regular foliation \({\mathfrak {F}}_E\rightrightarrows E\). Further, there is a maximal r such that étale locally the coarse moduli of (4.1) factors, cf. Scholion 1.13, as
, in the presence of the simplifying Remark 1.14, also satisfies items (1)–(3) of Set Up 4.1 but for the absolutely regular foliation \({\mathfrak {F}}_E\rightrightarrows E\). Further, there is a maximal r such that étale locally the coarse moduli of (4.1) factors, cf. Scholion 1.13, as

wherein \(\rho _r\) is exactly as per (4.4), albeit for \({\mathfrak {F}}_E\), while for  , should \(q\leqslant Q\), resp. \(Q\leqslant q\), there is a generic isomorphism,
, should \(q\leqslant Q\), resp. \(Q\leqslant q\), there is a generic isomorphism,
In particular (4.15) furnishes nonzero maps of line bundles over \([L(r)/{\mathbb {G}}_m]\),
which vanishes along the absolutely singular points (whether of \({{\mathcal {F}}}\) or \({{\mathcal {F}}}_E\) since these loci coincide) while at any other point \(x\in L\) where (4.16) vanishes, the map of fibres
is generically étale wildly ramifying at \(\Delta (x)\) to order that of the vanishing of (4.16).
Proof
We put ourselves in the situation of Fact 4.3 but for the foliation \({\mathfrak {F}}_E\rightrightarrows E\) of Fact/Definition 1.12, and of course invariant map \(\lambda :L\xrightarrow []{}E\). Now k is perfect and L is normal with a transitive \(\mathbb G_m\)-action, thus L/k is smooth, so the hypotheses of Fact 4.2 are verified, and whence we have the map (4.1), while, again by item (2) of our Set Up 4.1, (4.14) is a factorisation of a finite map so, once more r exists. Now, exactly as in Fact 4.3, take a generic closed point x, identify \(L_x\) with fibre of the coarse moduli, and, observe that by item (3) of Fact/Definition 1.12 there are coordinates s, t with the former in the \(\mathbb G_m\)-direction such that,

so, for \(Q\geqslant q\), resp. \(q\geqslant Q\) the maps in (4.17) are generically étale, which gives us the generic isomorphisms (4.15) & (4.16). It is, however, clear that (4.16) isn’t an isomorphism at absolutely singular points since (4.1) isn’t even finite there. As to any other singular points the top line of (4.9) becomes,
wherein everything admits an infinitesimal \({\mathbb {G}}_m\)-action, and for exactly the same reason, (4.11) et seq., the rightmost map in (4.19) is a covering of order a power of the characteristic, so, as soon as we eliminate the inseparable effects via the twists of (4.17), any ramification that remains is wild. \(\square \)
Notice, en passant, a not inconsiderable bonus,
Fact 4.6
Let everything be as in Fact 4.5 with \(x\in L\) a point where (4.15) is an isomorphism, then, supposing the simplification of Remark 1.14, for \(q\leqslant Q\), resp. \(Q\leqslant q\), \([L/\mathbb G_m]\), resp. \([L(r-R)/\mathbb G_m]\) is isomorphic to \({{\mathcal {L}}}\) in a neighbourhood of x.
Proof
By [8, Exposé VII, 4.1], for \(q\leqslant Q\), resp. \(Q\leqslant q\) there are coordinates s, t on L, resp. \(L(r-R)\) such that modulo generic stabilisers \(\lambda \in {\mathbb {G}}_m\) acts by,
where \(s\ne 0\) and \(t=0\) is the orbit of x. As such the stabiliser of our point is that of \(t=0\), i.e. \(\mu _a\), so if a is prime to p we’re done by the simplifying Remark 1.14, while otherwise, for \(F_x\) equal to \(\bigl ({\mathfrak {F}}_E^{(-r)}(R-r)\bigr )_{\lambda (x)}\), resp. \(\bigl ({\mathfrak {F}}_E^{(-r)}\bigr )_{\lambda (x)}\),
and \(a=0\) modulo p implies this is zero at s, so (4.15) cannot be an isomorphism. \(\square \)
6 The cone theorem
With Definition 1.5 in place, the algebraisation theorem of [3, 2.1–2.2] works, cf. Warning 1.7, in a characteristic free way, beginning with,
Basic Construction 5.1
(cf. [3, 2.1]) Let \((s,t):{\mathfrak {F}}\rightrightarrows X\) be an absolutely Gorenstein, Definition 1.5, foliation by curves of an algebraic space, or Deligne–Mumford champ, over a field k, then for \(f:C\xrightarrow []{}X\) a projective curve, the complete fibre product,

is a formal scheme with trace, \(C=\mathrm {id}(C)\), and,
More generally for an absolutely \(\mathbb Q\)-Gorenstein foliation on a normal algebraic space or Deligne–Mumford champ X over k with \(\gamma :Y=[E/\mathbb G_m]\rightarrow X\) the Gorenstein covering champ of Fact/Definition 1.12 and \(f:C\rightarrow Y\) a map from a curve, the complete fibre product,

where \({\mathfrak {F}}_E\rightrightarrows E\) is the absolutely regular foliation in item (3) of Fact/Definition 1.12, is a formal scheme with regularly embedded trace,  , such that,
, such that,

Proof
The normality assumption in the second part is only to guarantee that the Gorenstein covering champ has sense, whence, it is, an otherwise more general assertion, and we confine our attention to it. As such, in the first place, given the map f we have, in the notation of (1.26), a punctured cone,

and a section of \([(\gamma f)^*E/\mathbb G_m]\), so, a fortiori, a series of local sections of (5.5). A priori such sections are in the smooth topology of C, but every smooth map has étale local sections, so on an étale cover \(C_\alpha \) of C we have a quotient,
of \({{\mathcal {O}}}_C\) algebras, which can equally be identified with a \(\mathbb G_m\)-equivariant map,

in some indeterminate \(T_\alpha \). Now, by hypothesis, these maps must patch up to the action of \(\mathbb G_m\), i.e. there is a multiplicative co-cycle \(g^{\alpha }_{\beta }\) such that,
so for L the bundle defined by \(T_\beta =g^{\alpha }_{\beta }T_\alpha \), we can rewrite (5.7) as the graded map,
Now since both positive and negative integers occur in (5.9), this is an isomorphism in sufficiently divisible degree’s, so L certainly has the same degree as the pullback of the \(\mathbb Q\)-Cartier divisor \(K_{{\mathcal {F}}}\). However we even have a bundle \(f^*(K_{{\mathcal {F}}}|_E)\) obtained by pulling back (1) of Fact/Definition 1.12, and for every n a natural map,
while if \(w_n (x)=0\) then for d sufficiently divisible \(w_{nd}(x^{d})=0\) so \(x^{d}=0\), which is iff \(\nu _{d}(x^{d})=0\), and whence \(\nu _1(x)=0\). Consequently, the image of (5.9) factors through (5.10), and since L has the same degree as \(f^* (K_{{\mathcal {F}}}|_E)\) these are the same mod torsion. Finally, by Definition 1.1, the source and sink of \({\mathfrak {F}}_E\) are representable, and curve means curve, not orbifold, so \(f^* {\mathfrak {F}}_E\) is a \(\mathbb G_m\)-equivariant formal scheme over the punctured cone,
Better, this action is free, so taking the quotient we get (5.3)–(5.4) by (1.27). \(\square \)
At this point we have the fundamental observation of [3],
Fact 5.2
([3, 2.1.1]) If \({\mathfrak {F}}\rightrightarrows X\) is absolutely \(\mathbb Q\)-Gorenestien and \(K_{{\mathcal {F}}}\cdot _f C<0\), then for any line bundle L on \({\mathfrak {F}}\) there is a constant \(C=C(L)\) such that,
Proof
For I the ideal of the trace  in (5.3), and \(F_m\) the mth thickening of \({\mathfrak {F}}\) we have an exact sequence,
in (5.3), and \(F_m\) the mth thickening of \({\mathfrak {F}}\) we have an exact sequence,

wherein the leftmost bundle is dual to \(\mathrm {Sym}^m(N_{C/{\mathfrak {F}}_C})\) of (5.4), so,

since \(-K_{{\mathcal {F}}}\cdot _f C\) was supposed positive, and whence,
from which (5.12) by taking, as per op. cit., \(\mathrm {H}^0\) of (5.13) for \(m\leqslant M\). \(\square \)
Continuing to follow op. cit. we apply this in the obvious way, i.e.
Fact 5.3
Let \(\mu :X\xrightarrow []{}|X|\) be the Keel–Mori moduli space, [12, 1.3], of X (so \(X=|X|\) if X is just an algebraic space and not a champ) and otherwise everything as in the general \(\mathbb Q\)-Gorenstein case of the Basic Construction 5.1, then if,  and,
and,
-
(a)
A Zariski open neighbourhood of \((\mu f)(C)\) embeds into a projective space \({\mathbb {P}}_k^N\),
-
(b)
The foliation is not absolutely singular at the generic point of f(C),
there is an algebraic surface,
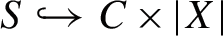 (5.16)
(5.16)such that every fibre is invariant by the induced action of \({\mathfrak {F}}\) on |X|.
Proof
Define S to be the Zariski closure of the image of \({\mathfrak {F}}_C\) in  . Applying Fact 5.2 with L the pullback of the tautological bundle on \({\mathbb {P}}_k^N\), it’s clear that the dimension of S is at most 2, while by hypothesis (b) at a generic point,
. Applying Fact 5.2 with L the pullback of the tautological bundle on \({\mathbb {P}}_k^N\), it’s clear that the dimension of S is at most 2, while by hypothesis (b) at a generic point,  is finite onto its (a priori formal) image, so, in fact, the dimension of S is exactly 2, while, by construction, every fibre is invariant. \(\square \)
is finite onto its (a priori formal) image, so, in fact, the dimension of S is exactly 2, while, by construction, every fibre is invariant. \(\square \)
This leads to a variant of Miyaoka–Mori’s bend and break estimate, cf. [18, Theorem 5], to wit:
Fact 5.4
([16, II.c.2–5]) Let \({\mathfrak {F}}\rightrightarrows X\) be an absolutely \(\mathbb Q\)-Gorenstein foliation by curves on a Deligne–Mumford champ over a field k then for a map \(f:C\xrightarrow []{}X\) from a curve satisfying (a), (b) of Fact 5.3, and  through every closed point \(c\in C\) there is a 1-dimensional \({\mathfrak {F}}\)-invariant champ \({{\mathcal {L}}}_c\), such that if M is any nef \({\mathbb {R}}\) divisor on X,
through every closed point \(c\in C\) there is a 1-dimensional \({\mathfrak {F}}\)-invariant champ \({{\mathcal {L}}}_c\), such that if M is any nef \({\mathbb {R}}\) divisor on X,

In light of the Basic Construction 5.1 and Fact 5.3, the remaining issues are the degree estimate (5.17), which is the wholly general Sub-Fact 5.6 below, and the applicability of Basic Construction 5.1 which merits,
Warning 5.5
Large chunks of the theory of the Gorenstein covering champ \([E/\mathbb G_m]\rightarrow X\) are valid without supposing that \(K_{{\mathcal {F}}}\) is a \(\mathbb Q\)-divisor, e.g. if we just defined  to be the degree of the bundle L of (5.8) et seq. then the Basic Construction 5.1 would remain valid. However, cf. (1.33) et seq., by definition, \(K_{{\mathcal {F}}}\) is a \(\mathbb Q\)-divisor iff \([E/\mathbb G_m]\) admits an fpqf presentation, and this is exactly what guarantees, cf. [14, 16.6], that starting from a curve \(f:C\rightarrow X\) there is at worst a finite cover \(C'\xrightarrow {g} C\xrightarrow {f} X\) such that the composition, fg, lifts to \([E/\mathbb G_m]\), i.e. we can always apply the Basic Construction 5.1.
to be the degree of the bundle L of (5.8) et seq. then the Basic Construction 5.1 would remain valid. However, cf. (1.33) et seq., by definition, \(K_{{\mathcal {F}}}\) is a \(\mathbb Q\)-divisor iff \([E/\mathbb G_m]\) admits an fpqf presentation, and this is exactly what guarantees, cf. [14, 16.6], that starting from a curve \(f:C\rightarrow X\) there is at worst a finite cover \(C'\xrightarrow {g} C\xrightarrow {f} X\) such that the composition, fg, lifts to \([E/\mathbb G_m]\), i.e. we can always apply the Basic Construction 5.1.
Consequently we can conclude to Fact 5.4 by way of,
Sub-Fact 5.6
([16, II.c.7]) Let \(S\xrightarrow []{}C \) be a normal surface fibred over a curve with a section \(\sigma \) such that \(\sigma (C)^2>0\), then for M a nef \({\mathbb {R}}\)-divisor on S a generic fibre \(L_c\) satisfies,

Proof of Sub-Fact 5.6
Say \(x\in {\mathbb {R}}_{>0}\) to be chosen, then the Hodge index theorem, affords the inequality,

so choosing  yields (5.18). \(\square \)
yields (5.18). \(\square \)
Putting everything together we therefore obtain,
Fact 5.7
Let \({\mathfrak {F}}\rightrightarrows X\) be an absolutely \({\mathbb {Q}}\)-Gorenstein foliation by curves of a Deligne–Mumford champ over a field k with projective moduli and \(Z\hookrightarrow X\) the absolutely singular locus of Definition 2.3, then there are countably many invariant champs \({{\mathcal {L}}}_i\hookrightarrow X\) not factoring through Z with \(K_{{{\mathcal {F}}}}\cdot {{\mathcal {L}}}_i<0\) such that,
wherein the rays \({\mathbb {R}}_+{{\mathcal {L}}}_i\) are locally discrete in the open complement of \({\overline{\mathrm {NE}}}_1(X)_{K_{{{\mathcal {F}}}}\geqslant 0}\) \({}+{\overline{\mathrm {NE}}}_1(Z)_{K_{{{\mathcal {F}}}}<0}\) and every extremal ray therein is of this form.
Proof
This is purely formal consequence of Fact 5.4, i.e. [13, III.1.2] goes through mutatis mutandis. \(\square \)
7 Fine structure of extremal rays and minimal models of surfaces
In the particular case of surfaces we can do better, to wit:
Fact 6.1
Let \({\mathfrak {F}}\rightrightarrows X\) be a foliation by curves of a proper bi-dimensional normal Deligne–Mumford champ over a field k of positive characteristic which is absolutely Gorenstein in codimension 2, with \(Z\hookrightarrow X\) the possibly empty (but certainly finite) set of curves where the foliation is absolutely log singular, Definition 2.3, then understanding \(K_{{\mathcal {F}}}\) in the worst case scenario of Fact/Definition 2.10 and the Néron–Severi group in the sense of Mumford intersection theory, [19, II.b], there are countably many invariant champs \({{\mathcal {L}}}_i\hookrightarrow X\) not in Z with  such that,
such that,

wherein the rays \({\mathbb {R}}_+[{{\mathcal {L}}}_i]\) are locally discrete in the open half space \(\mathrm {NE}(X)_{K_{{{\mathcal {F}}}}<0}\) and every extremal ray therein is of this form or belongs to Z.
Proof
We first do the case of k a finite field, so by [11, 0.3] or [1, 2.11] X is \({\mathbb {Q}}\)-factorial with projective moduli. Consequently (6.1) will follow from (5.20) if we prove that the negative curves in Z must be absolutely log singular, or equivalently,
Claim 6.2
Let \({\mathfrak {F}}\rightrightarrows X\) be an absolutely \(\mathbb {Q}\)-Gorenstein foliation by curves of a proper normal bi-dimensional Deligne–Mumford champ over a field k of characteristic \(p>0\) which is absolutely singular but not absolutely log singular along an irreducible \(\mathbb Q\)-Cartier divisor C then,

Proof of Claim 6.2
Let \(\gamma :[E/\mathbb G_m]\rightarrow X\) be the Gorenstein covering champ of Fact/Definition 1.12, with \(E_C\) the fibre over C then for \({{\mathcal {F}}}_E\) as in item (3) of op. cit., absolutely singular around C is the same thing as,
while not absolutely log singular means, Notation/Revision 1.6 post (1.11), there exists \(q=p^r\) such that generically along C,

To profit from this, observe that for any positive integer n, we have a pairing,

Indeed for the nth power of \({{\mathcal {O}}}_E(-C)\), rather than it’s double dual, we just apply the co-product formula (1.11) and (5.20), and then one does the double dual case by induction on the order of the operator by way of (1.11) again. Similarly the co-product formula and (6.3) imply that (6.5) is linear mod \({{\mathcal {O}}}_E(-C)\), so we get an \({{\mathcal {O}}}_E\) linear map,
As such fix a sufficiently divisible n, so that by (6.4) there is a biggest \(-1\geqslant -m>-\infty \) such that (6.6) is non-zero on non-constant operators of order \(-m\), and whence we get a non-zero map,
The left hand side of (6.7) is, however, filtered by the dual of the exact sequence (1.27), while operators in the \(\mathbb G_m\)-direction act trivially on functions pulled back from the base, so that, finally, we get a non-zero map,
which is plainly \(\mathbb G_m\)-equivariant, and we conclude. \(\square \)
Returning to the proof of 6.1, it remains to address the case of an arbitrary field of positive characteristic. To this end we make a model \({\mathfrak {F}}_S\rightrightarrows X_S\) of our foliated champ over an affine scheme S of finite type over \({\mathbb {F}}_p\) and proceed as follows,
(1) First prove (6.2) in Mumford intersection theory at the generic point \(\sigma \) of S. Indeed for closed points \(s\in S\) outside of a closed set Mumford intersection numbers of any two Weil divisors are constant and equal to their value at \(\sigma \), so 6.2 over a finite field implies the same in general.
(2) Prove Fact 5.4, but, again, with intersection numbers understood in the Mumford sense. As such the only subtly is that the moduli, |X|, may only be an algebraic space. It does, however, admit classes h in Mumford’s Néron–Severi group which are strictly positive on \({\overline{\mathrm {NE}}}_1\), and every component of the Hilbert scheme of curves on |X| with bounded h degree is of finite type because bounded h degree implies bounded degree on a projective resolution.
Consequently one concludes formally to (5.20), understood in the Mumford sense, from (2), after which we can use (1) to replace absolutely singular by absolutely log-singular , and whence arrive to (6.1). \(\square \)
Unsurprisingly, therefore, we may apply Fact 6.1 to obtain
Corollary 6.3
Let \({\mathfrak {F}}\rightrightarrows X\) be an absolutely Gorenstein in codimension 2 foliation by curves of a proper bi-dimensional normal Deligne–Mumford champ over a field k of positive characteristic, then there is a contraction,
of an invariant Weil divisor \(E\hookrightarrow X\) such that for \({\mathfrak {F}}_0\rightrightarrows X_0\) the resulting foliation, understood in the sense of Fact/Definition 2.10, exactly one of the following occurs,
-
(1)
\(K_{{{\mathcal {F}}}_0}\) is nef in Mumford intersection theory.
-
(2)
There exists a map \(\pi :X_0\xrightarrow []{}X_0/{{\mathcal {F}}}_0\) to a curve such that every fibre of \(\pi \) is supported on an invariant irreducible champs \({{\mathcal {L}}}_x\), \(x\in X_0/{{\mathcal {F}}}_0\), with
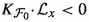 . In particular \(\pi \) is a Mori fibre space.
. In particular \(\pi \) is a Mori fibre space. -
(3)
The rank of Néron–Severi of \(X_0\), in the Mumford sense, is 1, and \(X_0\) is covered by an invariant family of champs \({{\mathcal {L}}}_x\), with
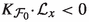 . In particular \(X_0\xrightarrow []{}\mathrm{pt}\) is itself a Mori fibre space.
. In particular \(X_0\xrightarrow []{}\mathrm{pt}\) is itself a Mori fibre space.
Proof
By hypothesis X satisfies (6.1). As such either there is an extremal ray represented by an invariant Weil divisor in the half space \({\overline{\mathrm {NE}}}_1(X)_{K_{{\mathcal {F}}}<0}\) with negative square, or there isn’t. If there is such a ray we contract it. The resulting normal champ still satisfies (6.1), so without loss of generality there are no extremal rays in \({\overline{\mathrm {NE}}}_1(X)_{K_{{\mathcal {F}}}<0}\) with negative square, and exactly one of the following occurs,
-
(1)
There are no extremal rays in \({\overline{\mathrm {NE}}}_1(X)_{K_{{\mathcal {F}}}<0}\) so, by (6.1), \(K_{{\mathcal {F}}}\) is nef.
-
(2)
There is such an extremal ray R, and \(R^2=0\).
-
(3)
Again there is an extremal ray but \(R^2>0\).
Now observe that it’s formal that the rank of Néron–Severi in (3) is 1. Indeed for any class \(\alpha \), there is some large m, depending on \(\alpha \), such that,

thus \(mR-\alpha \in {\overline{\mathrm {NE}}}_1(X)\), and R is extremal so \(\alpha \) is parallel to R. In case (2), however, although R is effective by (6.1), it may not even move. We may, however, find a sequence of maps \(f_n:C_n\xrightarrow []{}X\) from smooth projective curves whose cycles are ample such that the rays, but not the cycles, \({\mathbb {R}}_+[C_n]\), converge to R. In particular for \(n\gg 0\),  and Fact 5.4 applies to produce for every \(x\in C_n\) an invariant sub-champ \({{\mathcal {L}}}^n_x\) satisfying (5.18), the right hand side of which limits on,
and Fact 5.4 applies to produce for every \(x\in C_n\) an invariant sub-champ \({{\mathcal {L}}}^n_x\) satisfying (5.18), the right hand side of which limits on,

As such the families \({{\mathcal {L}}}^n_x\) are bounded independently of n, and there is at most one invariant curve through the generic point, so, altogether, they cut out a curve H in the Hilbert scheme independently of n. Now drop the suffix n and apply (6.11) with \(M=R\), to get for \(x\in H\) generic,

and since both R and \(L_x\) are nef they’re parallel by Hodge. To conclude, therefore, observe that for \(x\ne y\) any 2-closed points in H,

so H is indeed the coarse moduli \(X/{{\mathcal {F}}}\) and since R is extremal every fibre is irreducible. The outstanding item of covering X by invariant curves in (3) is similar, and strictly easier, since we can take the above sequence \(C_n\) to be constant. \(\square \)
To address the fine structure of the extremal rays in Fact 5.7, so, a fortiori, of those in Fact 6.1 and those contracted in Corollary 6.3, we require,
Fact 6.4
Let \(L\rightarrow {{\mathcal {L}}}\) be a representable map between normal champ over a perfect field k with \({{\mathcal {L}}}\) one-dimensional and L admitting a \(\mathbb G_m\)-action with finite stabilisers such that étale locally, \({{\mathcal {L}}}\) is the coarse moduli \(L/\mathbb G_m\), cf. Scholion 1.13, then the canonical bundle \(K_L\) of L is a line bundle on \([L/{\mathbb {G}}_m]\) whose degree is given by,

wherein Q is the cardinality of the stabiliser of the generic point, and  is understood to be the, possibly fractional, degree of the point x in \({{\mathcal {L}}}\) over which the stabiliser of the \({\mathbb {G}}_m\)-orbit is \(\mu _{Qq_x}\).
is understood to be the, possibly fractional, degree of the point x in \({{\mathcal {L}}}\) over which the stabiliser of the \({\mathbb {G}}_m\)-orbit is \(\mu _{Qq_x}\).
Proof
By hypothesis k is perfect, thus regular coincides with smooth and the action of \({\mathbb {G}}_m\) is transitive so L/k is smooth as soon as \({{\mathcal {L}}}\) is normal. Plainly \({\mathbb {G}}_m\) acts on the canonical bundle \(K_L\) thus it is a bundle on the 1-dimensional champ \([L/{\mathbb {G}}_m]\), so it only remains to compute its degree. To this end observe that the effect of the generic stabiliser is built into the left hand side of (6.14), so without loss of generality the action is generically free, while by Remark 1.14 we’re reduced to \(q_x\) a power of the characteristic. Irrespectively, the \({\mathbb {G}}_m\)-action affords an exact sequence,
wherein the \({\mathbb {G}}_m\)-equivariant divisor D is defined via the image of \(\Omega _L\) in (6.15). Now the formula (6.14) is unchanged by passing to the algebraic closure so we may as well do this so that the function field of a component \(D_x\) of D is rational. Moreover \({\mathbb {G}}_m\) is a diagonalisable group, so on completing in \(D_x\) we can, [8, Exposé VIII, 4.1], linearise the action in the ring of formal functions, \({\widehat{{{\mathcal {O}}}}}\), at the generic point of \(D_x\) by way of,
for some positive integer \(\ell _x\) prime to p. In addition, \({{\mathcal {L}}}\) is étale locally the coarse moduli of the action of \({\mathbb {G}}_m\) on L so from (6.15) we have a map,
whose \({\mathbb {G}}_m\)-equivariant image we may perfectly well calculate in an étale neighbourhood of \(D_x\). Thus we may take an \(\ell _x\)th root of s in (6.16) to conclude that a coordinate in the complete local ring of \({{\mathcal {O}}}_{{{\mathcal {L}}}}\) at x is given by,
Putting all of this together, by (6.15) and (6.16), \(K_L(D)\) is generated by ds and \(D=D_x\) is reduced while from (6.18), the order of vanishing of (6.17) along \(D_x\) is \(q_x\) so altogether, the local additive form of (6.17) around x is,
Finally \(L_x=q_xD_x\) by (6.18) and off D (6.17) is an isomorphism, whence (6.14). \(\square \)
Putting this together with Fact 4.5 we have therefore,
Fact 6.5
Let \({\mathfrak {F}}\rightrightarrows X\) be an absolutely \({\mathbb {Q}}\)-Gorenstein foliation by curves of a Deligne–Mumford champ over a perfect field k, with \(f:{{\mathcal {L}}}\xrightarrow []{}X\) an invariant map from a connected smooth 1-dimensional k-champ which is bi-rational at its generic point and does not factor through the absolutely singular locus \(Z\hookrightarrow X\), with \(f:[L/{\mathbb {G}}_m]\xrightarrow []{}Y=[E/{\mathbb {G}}_m]\) the lifting of (4.12) to the Gorenstein covering champ \(\gamma :Y\rightarrow X\), for \(Q=p^R\), \(q=p^r\), as encountered in Fact 4.5, and \(r_+:=\max \{0,r-R\}\),
with degrees understood in \([L(r_+)/{\mathbb {G}}_m]\) after correction for the generic stabiliser, so if \(Qq_x\) is the cardinality of the stabiliser at x in L relative to \({{\mathcal {L}}}\), then the corresponding point in \([L(r_+)/{\mathbb {G}}_m]\) has a stabiliser of cardinality  .
.
Proof
This is just a recapitulation of Fact 4.5 and Fact 6.4. \(\square \)
Finally we can, therefore, deduce
Fact 6.6
Let everything be as in Fact 5.7 with X normal over a prefect field k. As such we may apply the simplifying Remark 1.14 to suppose that the relative stabilisers of the Gorenstein covering champ \(Y=[E/{\mathbb {G}}_m]\xrightarrow []{}X\) are all powers of the characteristic (so \(Y=X\) in characteristic zero) then the normalisation, \(f:{{\mathcal {L}}}\xrightarrow []{}X\), of a \(K_{{\mathcal {F}}}\) negative 1-dimensional champ which is not absolutely singular lifts, in the notation of (6.20), to a curve,
such that  . Moreover there is at most one point, \(\infty \in L\) where any of the following might occur,
. Moreover there is at most one point, \(\infty \in L\) where any of the following might occur,
-
(a)
(4.15) is not an isomorphism;
-
(b)
The ramification of \({{\mathcal {L}}}\) over its moduli \(|{{\mathcal {L}}}|\) is wild;
-
(c)
Supposing the simplification of Remark 1.14, modulo the generic stabaliser, \([L(r_+)/{\mathbb {G}}_m]\) \(\ne {{\mathcal {L}}}\) in a neighbourhood of \(\infty \).
Thus if one of these occurs, then any other that occurs happens at the same unique point. Further continuing to suppose the simplification of Remark 1.14, let  , then we have a (possibly non-trivial) fibration,
, then we have a (possibly non-trivial) fibration,

and if none of (a), (b) or (c) occur, resp. one such does occur, modulo its generic stabiliser \({{\mathcal {L}}}\), resp. \({{\mathcal {L}}}\backslash \infty \) is a prime to p-orbifold of positive Euler characteristic, resp. \([{\mathbb {A}}^1/\mu _{\ell }]\) for some integer \(\ell \) prime to the characteristic, and, in either case, \([L(r_+)/\mathbb G_m]\) is covered by \(\mathbb P^1_k\) if k is algebraically closed.
Proof
By way of notation let m be the cardinality of the generic stabiliser of \({{\mathcal {L}}}\), \(G_x\) the stabiliser of a point x of \({{\mathcal {L}}}\) modulo the generic one, \(q_x\) the order of the relative stabiliser of \([L(r_+)/{\mathbb {G}}_m]\) over \({{\mathcal {L}}}\), with \(Z_x\), respectively \(W_x\), the contribution, if any at x, of the absolute, resp. wild ramification of (4.17), and \(w_x\) any excess ramification should \({{\mathcal {L}}}\) over \(|{{\mathcal {L}}}|\) be wild there; then by (6.20),

wherein \(-2\) is the degree of the canonical bundle of the necessarily rational moduli. As such if either (a) or (b) occur at x then they contribute at least one to the right hand side of (6.23), so they can happen at most once and in the same point. Similarly by Fact 4.6 if (c) occurs at x, then so does (a), which proves the first part. As to the second part, the diagram (6.22) is automatic since everything is normal, while should neither (b) nor (c) occur then modulo the generic stabiliser \({{\mathcal {L}}}\) is certainly a prime to p orbifold. Consequently, without loss of generality there is a point \(\infty \) where at least one of (a), (b), (c) has occurred, so \(|{{\mathcal {L}}}|\xrightarrow {\sim } \mathbb P^1_k\), while for \(x\ne \infty \), \(q_x=1\), \(|G_x|\) is prime to p, and,

so either every \(G_x\) has cardinality 1, or there is a unique point \(x\ne \infty \) where \(|G_x|>1\), thus modulo its generic stabiliser \({{\mathcal {L}}}\backslash \infty \) is \([{\mathbb {A}}_k^1/\mu _{\ell }]\) with \(\mu _{\ell }=G_x\). Finally if k is algebraically closed, we can apply Corollary A.4 in the former case, and Corollary A.6 to find a map from \(\mathbb P^1_k\) to \([L(r_+)/\mathbb G_m]\). \(\square \)
A priori this doesn’t apply to normal surfaces since in the proof of Fact 6.1 we took refuge in the subterfuge of working over finite fields, nevertheless,
Fact 6.7
Again, let \({\mathfrak {F}}\rightrightarrows X\) be a foliation by curves of a normal bi-dimensional proper champ over a perfect field k of positive characteristic which is absolutely \(\mathbb Q\)-Gorenstein in codimension 2, with \(f:{{\mathcal {L}}}\rightarrow X\) the normalisation of a \(K_{{\mathcal {F}}}\)-negative invariant sub-champ which is not absolutely singular, then either \({{\mathcal {F}}}\) is \(\mathbb Q\)-Gorenstein in a neighbourhood of \({{\mathcal {L}}}\), and Fact 6.6 applies as stated, or there is a unique point \(\infty \) whose image under f does not admit a \(\mathbb Q\)-Gorenstein neighbourhood, and the description of (6.22) et seq. outwith \(\infty \) applies.
Proof
Let \(X_S/S\) be a model over a finite type affine scheme over the prime field, then at a closed point \(s\in S\) with k(s) of finite cardinality the right hand side of (6.23) is at least \(-2\), which bounds the generic stabiliser independently of s. Thus if none of (a), (b), (c) occur we have,

with bounded left hand side, which in turn bounds the cardinalities \(|G_x|\) independently of s. Otherwise, (6.24) applies to bound \(|G_x|\) independently of s for \(x\ne \infty _s\), which, a priori depends on s, but any normal surface has at most finitely many points which aren’t Gorenstein, so, in fact, \(\infty _s\) is the specialisation to k(s) of a unique point \(\infty \) independent of s. \(\square \)
This in turn has some attractive corollaries, to wit:
Corollary 6.8
Let everything be as in Fact 6.7 with \(X'\) the \(\mathbb Q\)-Gorenstein locus, and \(Y'\xrightarrow {\gamma } X'\) the Gorenstein covering champ in the presence of the simplification of Remark 1.14, and suppose moreover that X is a Mori fibre space, i.e. either (b) or (c) of Corollary 6.3, occur with Z the absolutely singular locus then if,
-
(a)
\(\mathrm {NS}_1(X)\) has rank 1, all invariant curves which aren’t absolutely singular meet Z in a unique point \(\infty \), which, in turn is the only point where irreducible invariant curves (even the absolutely singular ones) can meet, \(X'\) coincides with X off Z, and the foliation defines a map \(Y\backslash {\infty }\rightarrow Y/{\mathfrak {F}}\) to a curve, every non-absolutely singular fibre of which is described by Fact 6.6–Fact 6.7 so, in particular, covered by \(\mathbb A^1_k\).
-
(b)
\(\mathrm {NS}_1(X)\) has rank 2, so the \(K_{{{\mathcal {F}}}}\)-invariant curves are the fibres of \(\pi :X\xrightarrow []{}X/{\mathfrak {F}}\), while there is a finite (possibly empty) subset \(F\subseteq Z\) of absolutely singular fibres, and we denote by \(\zeta \) the closure of the locus where any of (a), (b), or (c) occur at a fibre of \(\pi \) in \(Y'\) which is not absolutely singular, with \(\zeta '\) the locus (of dimension at most 0) where \(X'\ne X\), then off \(\zeta '\) every closed geometric fibre is covered by
 , while if the dimension of \(\zeta \) is,
, while if the dimension of \(\zeta \) is, -
(1)
One, it is a section, of \(\pi \), and
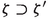 . Furthermore, if it is singular, then it is absolutely singular, and the fibres of \(\pi \,{|}\, Y\backslash \zeta \cup F\) are described by Fact 6.6–Fact 6.7 so, again, are covered by \(\mathbb A^1_k\).
. Furthermore, if it is singular, then it is absolutely singular, and the fibres of \(\pi \,{|}\, Y\backslash \zeta \cup F\) are described by Fact 6.6–Fact 6.7 so, again, are covered by \(\mathbb A^1_k\). -
(2)
At most 0, then \(\pi \,{|}\, Y\backslash \pi ^{-1}\pi (\zeta \cup \zeta ')\cup F\) is (modulo the generic stabiliser) a fibration in prime to p orbifolds while \(\mathbb A^1_k\) covers
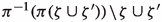 .
.
-
(1)
Proof
In case (a) all the invariant curves must meet which is already a singularity if any two meet, and since, by Fact 6.6, there is at most one singularity on any given not absolutely singular curve, all other such curves must meet a given one in the same point, which, in turn, must be an absolutely singular point, \(\infty \), by Fact 2.6 as well as being the only point where an invariant curve which isn’t absolutely singular might, by Fact 6.7, not lie in \(\mathbb Q\)-Gorenstein locus. Equally, the restriction of the groupoid to \(X\backslash Z\) has a quasi projective normal coarse moduli space, S, say, which by [9, Theorem 2] we can complete in the Hilbert scheme of Y (i.e. extend \(Y'\) over \(\infty \) by identifying it there with X) and normalise to a family \({\overline{Y}}/{\overline{S}}\) such that \({\overline{Y}}\rightarrow Y\) only contracts the points, C, over \(\infty \), so by Zariski’s main theorem \({\overline{Y}}\backslash C\xrightarrow {\sim } Y\backslash \{\infty \}\), and \({\overline{S}}=Y/{\mathfrak {F}}\).
As to case (b), Fact 6.6 applies as stated at the generic fibre of \(\pi \), so if \(\zeta \) meets a generic fibre, it’s certainly a section, while on taking a model X/S with, again, S of finite type over the prime field; at the specialisation to a finite field k(s) the criteria (a), (b), (c) of Fact 6.6 are upper semi-continuous in \(X_{k(s)}\) so  by Fact 6.7. In item (1) it remains, therefore to check what happens if \(\zeta \) is singular. Should this happen, and it weren’t absolutely singular then Fact 2.6 would apply so \(\pi \) of op. cit. would be the current \(\pi \) of Corollary 6.8.(b), with \(\zeta \) a fibre and transverse to the fibres at the same time, which is nonsense. Finally (2) is just a restatement of Fact 6.6 for fibres missing
by Fact 6.7. In item (1) it remains, therefore to check what happens if \(\zeta \) is singular. Should this happen, and it weren’t absolutely singular then Fact 2.6 would apply so \(\pi \) of op. cit. would be the current \(\pi \) of Corollary 6.8.(b), with \(\zeta \) a fibre and transverse to the fibres at the same time, which is nonsense. Finally (2) is just a restatement of Fact 6.6 for fibres missing  , and Fact 6.7 otherwise. \(\square \)
, and Fact 6.7 otherwise. \(\square \)
Notes
The mistranslation stack will be eschewed.
References
Artin, M.: Some numerical criteria for contractability of curves on algebraic surfaces. Amer. J. Math. 84(3), 485–496 (1962)
Artin, M.: Wildly ramified \(Z/2\) actions in dimension two. Proc. Amer. Math. Soc. 52(1), 60–64 (1975)
Bogomolov, F., McQuillan, M.: Rational curves on foliated varieties. In: Cascini, P. et al. (eds.) Foliation Theory in Algebraic Geometry. Simons Symposia, pp. 21–51. Springer, Cham (2016)
Ekedahl, T.: Foliations and inseparable morphisms. In: Bloch, S.J. (ed.) Algebraic Geometry, Bowdoin, 1985 (Brunswick, Maine, 1985). Proceedings of Symposia in Pure Mathematics, vol. 46, pp. 139–149. American Mathematical Society, Providence (1987)
Giraud, J.: Cohomologie non Abélienne. Die Grundlehren der Mathematischen Wissenschaften, Band 179. Springer, Berlin (1971)
Grothendieck, A.: Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. Inst. Hautes Études Sci. Publ. Math. (1964–1967), no. 20 (§ 0–1), 24 (§ 2–7), 28 (§ 8–15), 32 (§ 16–21). Rédigés avec la collaboration de Jean Dieudonné
Grothendieck, A.: Revetêments étales et groupe fondamental (SGA 1). In: Séminaire de Géométrie Algébrique du Bois Marie 1960–1961. Augmenté de deux exposés de M. Raynaud. Lecture Notes in Mathematics, vol. 224. Springer, Berlin (1971)
Grothendieck, A., Demazure, M.: Schémas en groupes. In: Séminaire de Géométrie Algébrique du Bois Marie 1962/64 (SGA 3). Lecture Notes in Mathematics, vol. 151 (§ I–VIIB), 152 (§ VIII–XVIII), 153 (§ IXX–XXVI). Springer, Berlin (1970)
Hall, J., Rydh, D.: The Hilbert stack. Adv. Math. 253, 194–233 (2014)
Katz, N.M.: Local-to-global extensions of representations of fundamental groups. Ann. Inst. Fourier (Grenoble) 36(4), 69–106 (1986)
Keel, S.: Basepoint freeness for nef and big line bundles in positive characteristic. Ann. Math. 149(1), 253–286 (1999)
Keel, S., Mori, S.: Quotients by groupoids. Ann. Math. 145(1), 193–213 (1997)
Kollár, J.: Rational Curves on Algebraic Varieties. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, vol. 32. Springer, Berlin (1996)
Laumon, G., Moret-Bailly, L.: Champs Algébriques. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, vol. 39. Springer, Berlin (2000)
McQuillan, M.: Canonical models of foliations. Pure Appl. Math. Q. 4(3), part 2, 877–1012 (2008)
McQuillan, M.: Semi-stable reduction of foliations (2017). Revised version of IHÉS pre-print. http://www.matmat.uniroma2.it/mcquilla/files/newss.pdf
Miyaoka, Y.: Deformations of a morphism along a foliation and applications. In: Bloch, S.J. (ed.) Algebraic Geometry, Bowdoin, 1985 (Brunswick, Maine, 1985). Proceedings of Symposia in Pure Mathematics, vol. 46, pp. 245–268. American Mathematical Society, Providence (1987)
Miyaoka, Y., Mori, S.: A numerical criterion for uniruledness. Ann. Math. 124(1), 65–69 (1986)
Mumford, D.: The topology of normal singularities of an algebraic surface and a criterion for simplicity. Inst. Hautes Études Sci. Publ. Math. 9, 5–22 (1961)
Funding
Open access funding provided by Universit degli Studi di Roma Tor Vergata within the CRUI CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The research was partly supported by the grant “Beyond Borders" of the Università degli studi “Tor Vergata”, together with the PRIN Real and Complex Manifolds: Topology, Geometry and holomorphic dynamics n. 2017JZ2SW5.
A Appendix: One-dimensional Mori theory
A Appendix: One-dimensional Mori theory
To avoid some technicalities we’ll confine ourselves to the following,
Set Up A.1
We denote by \({{\mathscr {L}}}/k\) a connected proper 1-dimensional Deligne–Mumford champ smooth over an algebraically closed field k. As such there exists a finite group \(\Gamma \), the generic stabiliser, such that \({{\mathscr {L}}}\) is a fibration,

where \({{\mathcal {L}}}/k\) is again a proper 1-dimensional Deligne–Mumford champ smooth over k, but without generic monodromy. Similarly by [12, 1.3], there is a moduli map, which is a generic isomorphism, to a smooth k-curve
and we write \(G_x\) for the stabilisers of (A.2). Consequently, we have the formulae,

where \(w_x\) is any excess ramification occasioned by wild effects in positive characteristic, and we say that \({{\mathcal {L}}}\) is tame if all the \(w_x\) are zero, or, equivalently every \(|G_x|\) is prime to the characteristic.
To set the scene let us recall,
Revision A.2
If  and \({{\mathcal {L}}}\) is tame, then \({{\mathcal {L}}}\) has finite fundamental group with universal cover a weighted projective champ, i.e. the classifier of the action,
and \({{\mathcal {L}}}\) is tame, then \({{\mathcal {L}}}\) has finite fundamental group with universal cover a weighted projective champ, i.e. the classifier of the action,

for m, n relatively prime to themselves and the characteristic. Furthermore there is a non-trivial map \(\mathbb P^1_k\rightarrow {{\mathscr {L}}}\).
Proof
From (A.3), \(|{{\mathcal {L}}}|\xrightarrow {\sim }\mathbb P^1_k\) and at most 3 points have \(|G_x|\ne 1\), while everything is tame so by [7, Exposé XIII, 5.1] the fundamental group of \({{\mathcal {L}}}\) is the same as the characteristic zero orbifold fundamental group. As such, if there is at most one such point then \({{\mathcal {L}}}\) is simply connected, while if there are two, \(|G_0|\), \(|G_\infty |\) then the universal cover is the fibre of (A.2) over multiplication in \(|{{\mathcal {L}}}|\) by their greatest common divisor, and otherwise \({{\mathcal {L}}}\) has \(\mathbb P^1\) as its universal cover. Thus, without loss of generality, we may suppose that \({{\mathcal {L}}}\) is the classifier of (A.4). In particular, it’s simply connected, and whence for  the decomposition of the centre of G into its prime to, resp. divisible by, the characteristic parts the isomorphism classes of gerbes satisfying (A.1) are, by [5, 3.3.3],
the decomposition of the centre of G into its prime to, resp. divisible by, the characteristic parts the isomorphism classes of gerbes satisfying (A.1) are, by [5, 3.3.3],
Now for characteristic \(p>0\), we can address the p-divisible part inductively via the Artin–Schreier sequence,
and since \(\mu \) is tame, it’s acyclic, so,
thus the only possibility for a non-trivial gerbe is the prime to p part which we put in its proper context, to wit:
Claim A.3
Let d be an integer, not necessarily prime to the characteristic, and \({{\mathcal {L}}}\) the weighted projective champ of (A.4), then, there is a canonical isomorphism,
and the isomorphism class of a gerbe \({{\mathscr {L}}}\rightarrow {{\mathcal {L}}}\) in the left hand side of (A.8) trivialises after pulling back along the endomorphism of (A.4) defined by,

Proof of Claim A.3
Instead of (A.6) we use the Kummer sequence,
and since \({{\mathcal {L}}}\) is generically \(|{{\mathcal {L}}}|\) there is no Brauer group by Tsen’s theorem, whence there is an exact sequence,

On the other hand a line bundle on \({{\mathcal {L}}}\) is, by (A.4), a line bundle on \(\mathbb A^2\) with \(\mathbb G_m\)-action. The former, however, must be trivial, so we have a canonical isomorphism,

which proves (A.8), while \(d^*\) of (A.9) is multiplication by d on the Picard group, so the gerbe trivialises after pulling back along the same. \(\blacksquare \)
Consequently our original gerbe, (A.1), restricted to the universal cover trivialises after pulling back along (A.9) with \(d=|Z'|\). \(\square \)
Notice en passant a bonus that we used in Fact 6.6 whenever the Gorenstein covering champ has non-trivial \(\mu _p\) monodromy at the generic point of our curve, to wit:
Corollary A.4
Suppose in addition that \(L\rightarrow {{\mathscr {L}}}\) is as in Fact 6.4, with  and \({{\mathcal {L}}}\) tame, then there is a non-trivial map \(\mathbb P^1_k\rightarrow [L/\mathbb G_m]\).
and \({{\mathcal {L}}}\) tame, then there is a non-trivial map \(\mathbb P^1_k\rightarrow [L/\mathbb G_m]\).
Proof
As usual we suppose the simplification of Remark 1.14 so that all relative stabilisers of the \(\mathbb G_m\)-action on L are powers of the necessarily positive characteristic, p. In any case, by (6.14),  so, Revision A.2 applies to yield a map \(\mathbb P^1_k\rightarrow {{\mathscr {L}}}\) along which we can pull back \([L/\mathbb G_m]\), so, without loss of generality \({{\mathscr {L}}}\) is \(\mathbb P^1_k\). Equally for Q as in Fact 6.4 we can factor \([L/\mathbb G_m]\rightarrow {{\mathscr {L}}}\) as a fibration in \(\mathrm{B}_{\mu _Q}\)’s over a gerbe
so, Revision A.2 applies to yield a map \(\mathbb P^1_k\rightarrow {{\mathscr {L}}}\) along which we can pull back \([L/\mathbb G_m]\), so, without loss of generality \({{\mathscr {L}}}\) is \(\mathbb P^1_k\). Equally for Q as in Fact 6.4 we can factor \([L/\mathbb G_m]\rightarrow {{\mathscr {L}}}\) as a fibration in \(\mathrm{B}_{\mu _Q}\)’s over a gerbe  which is a generic isomorphism with relative stabilisers the \(\mu _{q_x}\) of (6.14), and quite generally for \(p^r\geqslant \max _x q_x\), the rth iterate of Frobenius \({{\mathscr {L}}}^{(r)}\rightarrow {{\mathscr {L}}}\) factors through
which is a generic isomorphism with relative stabilisers the \(\mu _{q_x}\) of (6.14), and quite generally for \(p^r\geqslant \max _x q_x\), the rth iterate of Frobenius \({{\mathscr {L}}}^{(r)}\rightarrow {{\mathscr {L}}}\) factors through  . Thus, without loss of generality
. Thus, without loss of generality  too, and there are no twisted forms of \(\mu _Q\) over \(\mathbb P^1_k\) so Claim A.3 applies with \(d=Q\). \(\square \)
too, and there are no twisted forms of \(\mu _Q\) over \(\mathbb P^1_k\) so Claim A.3 applies with \(d=Q\). \(\square \)
Now we have to do the same in the wild case, starting with,
Fact A.5
Suppose the characteristic is \(p>0\), and let K be the fraction field of \(k[[T^{-1}]]\), then there is a pro p-group, P, such that:

Better still on identifying \(k[[T^{-1}]]\) with the completion at \(\infty \) of \(\mathbb P^1_k\) any étale covering of \(\mathrm {Spec}(K)\) extends to an étale cover of \(\mathbb A^1_k\xrightarrow {\sim }\mathbb P^1_k\backslash \{\infty \}\).
Proof
Most of this is in [10], including the better still which is the key case of the main theorem 1.4.1 of op. cit.. However, op. cit. 1.4.12 only asserts that (A.13) is a semi direct product, which is a priori weaker if \(\ell \,{|}\, p-1\). In any case, since p-groups are soluble, and the smallest Galois covering of a covering with fibre of cardinality n has group a sub-group of \(S_n\) it will suffice to start with a Galois extension L whose group, G, is a semi-direct product  for n prime to p and to show that it’s actually a product. To this end, apply the main theorem of op. cit. to extend this to a G-covering \(g:C\rightarrow \mathbb P^1\) which is étale over \(\mathbb G_m\) and factors as an étale cover of \(T\mapsto T^n\) at the origin, 0. As such \(g^{-1}(0)\), counted without multiplicity, has cardinality p. Now choose a point c in the fibre over zero, then its stabiliser in G is a copy of \(\mu _n\) whose orbit under conjugation is either itself or p copies of it. In the first case we’re done, and should the latter case occur no two stabilisers of points over 0 are the same, so we get a cover \(g':C':=C/\mu _n\rightarrow \mathbb P^1\) with \(1+ (p-1)/n\) points over the origin where, apart from the image of c, \(g'\) is ramified to order n everywhere else. If, however, we appeal again to Katz’s main theorem, \(g'\) must be the extension over \(\mathbb P^1\) of the not a priori Galois, p-extension \(K\hookrightarrow L^{\mu _n}\), whence the absurdity, op. cit. 1.4.2, that this is un-ramified at 0. \(\square \)
for n prime to p and to show that it’s actually a product. To this end, apply the main theorem of op. cit. to extend this to a G-covering \(g:C\rightarrow \mathbb P^1\) which is étale over \(\mathbb G_m\) and factors as an étale cover of \(T\mapsto T^n\) at the origin, 0. As such \(g^{-1}(0)\), counted without multiplicity, has cardinality p. Now choose a point c in the fibre over zero, then its stabiliser in G is a copy of \(\mu _n\) whose orbit under conjugation is either itself or p copies of it. In the first case we’re done, and should the latter case occur no two stabilisers of points over 0 are the same, so we get a cover \(g':C':=C/\mu _n\rightarrow \mathbb P^1\) with \(1+ (p-1)/n\) points over the origin where, apart from the image of c, \(g'\) is ramified to order n everywhere else. If, however, we appeal again to Katz’s main theorem, \(g'\) must be the extension over \(\mathbb P^1\) of the not a priori Galois, p-extension \(K\hookrightarrow L^{\mu _n}\), whence the absurdity, op. cit. 1.4.2, that this is un-ramified at 0. \(\square \)
At which juncture we can conclude,
Corollary A.6
Let everything be as in Set Up A.1, and suppose that  , then even if \({{\mathcal {L}}}\rightarrow |{{\mathcal {L}}}|\) is wild, then it still has finite fundamental group with universal cover (A.4) for some m, n prime to p. In particular Corollary A.4 holds without the tameness assumption.
, then even if \({{\mathcal {L}}}\rightarrow |{{\mathcal {L}}}|\) is wild, then it still has finite fundamental group with universal cover (A.4) for some m, n prime to p. In particular Corollary A.4 holds without the tameness assumption.
Proof
The in particular is clear since all we used in the proof of Corollary A.4 was that (A.4) defined the universal cover. Irrespectively, on identifying \(|{{\mathcal {L}}}|\) with \(\mathbb P^1_k\), by (A.3) there can be at most one non-tame point, \(\infty \), say, and at most one other with non-trivial monodromy, say, 0 with monodromy \(\mu _m\), \((m,p)=1\), where, for obvious notational reasons \(m=1\) is allowed. Now, by Fact A.5 the monodromy, G, splits as a product of \(\mu _n\), \((n,p)=1\) with a p-group, P, and the latter extends to a Galois P cover \(g:C\rightarrow \mathbb P^1\) ramified only in \(\infty \). As such if we replace a neighbourhood of every point in \(g^{-1}(0)\), resp. the point in \(g^{-1}(\infty )\), by the classifier of the action of \(\mu _m\), resp. \(\mu _n\), on a sufficiently small étale neighbourhood of 0, resp. \(\infty \), then we get an étale P-covering \({{\mathcal {C}}}\rightarrow {{\mathcal {L}}}\). In particular  while, by construction, \({{\mathcal {C}}}\rightarrow |{{\mathcal {C}}}|\) is tame so we conclude by Revision A.2. \(\square \)
while, by construction, \({{\mathcal {C}}}\rightarrow |{{\mathcal {C}}}|\) is tame so we conclude by Revision A.2. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
McQuillan, M. Formal groupoids. European Journal of Mathematics 8 (Suppl 2), 629–673 (2022). https://doi.org/10.1007/s40879-022-00565-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-022-00565-1




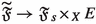 the normalisation of the irreducible component containing
the normalisation of the irreducible component containing 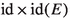 then
then 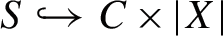
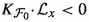 . In particular
. In particular 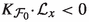 . In particular
. In particular 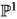 , while if the dimension of
, while if the dimension of 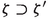 . Furthermore, if it is singular, then it is absolutely singular, and the fibres of
. Furthermore, if it is singular, then it is absolutely singular, and the fibres of 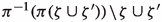 .
.