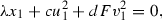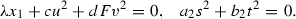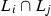Abstract
We study the stable rationality problem for quadric and cubic surface bundles over surfaces from the point of view of the specialization method for the Chow group of 0-cycles. Our main result is that a very general hypersurface X of bidegree (2, 3) in  is not stably rational. Via projections onto the two factors,
is not stably rational. Via projections onto the two factors,  is a cubic surface bundle and
is a cubic surface bundle and  is a conic bundle, and we analyze the stable rationality problem from both these points of view. Also, we introduce, for any \(n\geqslant 4\), new quadric surface bundle fourfolds
is a conic bundle, and we analyze the stable rationality problem from both these points of view. Also, we introduce, for any \(n\geqslant 4\), new quadric surface bundle fourfolds  with discriminant curve
with discriminant curve  of degree 2n, such that \(X_n\) has nontrivial unramified Brauer group and admits a universally \(\mathrm {CH}_0\)-trivial resolution.
of degree 2n, such that \(X_n\) has nontrivial unramified Brauer group and admits a universally \(\mathrm {CH}_0\)-trivial resolution.
Similar content being viewed by others
References
Ahmadinezhad, H., Okada, T.: Stable rationality of higher dimensional conic bundles (2016). arXiv:1612.04206
Auel, A., Colliot-Thélène, J.L., Parimala, R.: Universal unramified cohomology of cubic fourfolds containing a plane. In: Auel, A., Hassett, B., Várilly-Alvarado, A., Viray, B. (eds.) Brauer Groups and Obstruction Problems. Progress in Mathematics, vol. 320, pp. 29–56. Birkhäuser, Basel (2017)
Auel, A., Böhning, Chr., Graf von Bothmer, H.-Chr., Pirutka, A.: Conic bundles with nontrivial unramified Brauer group over threefolds (2016). arXiv:1610.04995
Beauville, A.: A very general sextic double solid is not stably rational. Bull. London Math. Soc 48(2), 321–324 (2016)
Beklemishev, N.D.: Invariants of cubic forms of four variables. Moscow Univ. Math. Bull. 37, 54–62 (1982)
Bloch, S., Ogus, A.: Gersten’s conjecture and the homology of schemes. Ann. Sci. Éc. Norm. Supér. 7, 181–201 (1974)
Böhning, Chr., Graf von Bothmer, H.-Chr.: On stable rationality of some conic bundles and moduli spaces of Prym curves. Comment. Math. Helv. 93(1), 133–155 (2018)
Bosma, W., Cannon, J., Playoust, C.: The Magma algebra system. I. The user language. J. Symbolic Comput. 24(3–4), 235–265 (1997)
Chatzistamatiou, A., Levine, M.: Torsion orders of complete intersections. Algebra Number Theory 11(8), 1779–1835 (2017)
Clebsch, A.: Ueber eine Transformation der homogenen Functionen dritter Ordnung mit vier Veränderlichen. J. Reine Angew. Math. 58, 109–126 (1861)
Clebsch, A.: Zur Theorie der algebraischer Flächen. J. Reine Angew. Math. 58, 93–108 (1861)
Colliot-Thélène, J.-L.: Birational invariants, purity and the Gersten conjecture. In: Jacob, W., Rosenberg, A. (eds.) \(K\)-Theory and Algebraic Geometry. Proceedings of Symposia in Pure Mathematics, vol. 58.1, pp. 1–64. American Mathematical Society, Providence (1995)
Colliot-Thélène, J.-L.: Un théorème de finitude pour le groupe de Chow des zéro-cycles d’un groupe algébrique linéaire sur un corps \(p\)-adique. Invent. Math. 159(3), 589–606 (2005)
Colliot-Thélène, J.-L., Ojanguren, M.: Variétés unirationnelles non rationnelles: au-delà de l’exemple d’Artin et Mumford. Invent. Math. 97(1), 141–158 (1989)
Colliot-Thélène, J.-L., Pirutka, A.: Cyclic covers that are not stably rational. Izv. Math. 80(4), 665–677 (2016) (in Russian)
Colliot-Thélène, J.-L., Pirutka, A.: Hypersurfaces quartiques de dimension 3: non-rationalité stable. Ann. Sci. Éc. Norm. Supér. 49(2), 371–397 (2016)
Coombes, K.R.: Every rational surface is separably split. Comment. Math. Helv. 63(2), 305–311 (1988)
Dolgachev, I.: Lectures on Invariant Theory. London Mathematical Society Lecture Note Series, vol. 296. Cambridge University Press, Cambridge (2003)
Edge, W.L.: The discriminant of a cubic surface. Proc. R. Irish Acad. Sect. A 80(1), 75–78 (1980)
Elsenhans, A.-S., Jahnel, J.: The discriminant of a cubic surface. Geom. Dedicata 159, 29–40 (2012)
Gabber, O., Liu, Q., Lorenzini, D.: The index of an algebraic variety. Invent. Math. 192(3), 567–626 (2013)
Goursat, É.: Étude des surfaces qui admettent tous les plans de symétrie d’un polyèdre régulier. Ann. Sci. Éc. Norm. Supér. 4, 159–200 (1887)
Hassett, B., Kresch, A., Tschinkel, Yu.: Stable rationality and conic bundles. Math. Ann. 365(3–4), 1201–1217 (2016)
Hassett, B., Pirutka, A., Tschinkel, Yu.: Stable rationality of quadric surface bundles over surfaces (2016). arXiv:1603.09262
Hassett, B., Pirutka, A., Tschinkel, Yu.: A very general quartic double fourfold is not stably rational (2016). arXiv:1605.03220
Hassett, B., Pirutka, A., Tschinkel, Yu.: Intersections of three quadrics in \(\mathbb{P}^7\) (2017). arXiv:1706.01371
Hassett, B., Tschinkel, Yu.: On stable rationality of Fano threefolds and del Pezzo fibrations. J. Reine Angew. Math. https://doi.org/10.1515/crelle-2016-0058
Kollár, J.: Nonrational hypersurfaces. J. Amer. Math. Soc. 8(1), 241–249 (1995)
Krylov, I., Okada, T.: Stable rationality of del Pezzo fibrations of low degree over projective spaces (2017). arXiv:1701.08372
Liu, Q.: Algebraic Geometry and Arithmetic Curves. Oxford Graduate Texts in Mathematics, vol. 6. Oxford University Press, Oxford (2002). Translated from the French by Reinie Erné
Okada, T.: Stable rationality of cyclic covers of projective spaces (2016). arXiv:1604.08417
Okada, T.: Smooth weighted hypersurfaces that are not stably rational (2017). arXiv:1709.07748
Okada, T.: Stable rationality of index one Fano hypersurfaces containing a linear space (2017). arXiv:1709.07757
Pirutka, A.: Varieties that are not stably rational, zero-cycles and unramified cohomology (2016). arXiv:1603.09261
Salmon, G.: On quaternary cubics. Philos. Trans. R. Soc. Lond. 150, 229–239 (1860)
Schreieder, S.: Quadric surface bundles over surfaces and stable rationality (2017). arXiv:1706.01358 (to appear in Algebra Number Theory)
Schreieder, S.: On the rationality problem for quadric bundles (2017). arXiv:1706.01356
Sir Swinnerton-Dyer, P.: The Brauer group of cubic surfaces. Math. Proc. Cambridge Philos. Soc. 113(3), 449–460 (1993)
Totaro, B.: Hypersurfaces that are not stably rational. J. Amer. Math. Soc. 29(3), 883–891 (2016)
Voisin, C.: Unirational threefolds with no universal codimension \(2\) cycle. Invent. Math. 201(1), 207–237 (2015)
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors would like to thank the organizers of the Simons Foundation conference on Birational Geometry held in New York City, August 21–25, 2017, as well as the Laboratory of Mirror Symmetry and Automorphic Forms, HSE, Moscow, where some of this work was accomplished. The first author was partially supported by NSA Young Investigator Grant H98230-16-1-0321. The third author was partially supported by ANR Grant ANR-15-CE40-0002-01, NSF Grant DMS-1601680 and by the Laboratory of Mirror Symmetry and Automorphic Forms NRU HSE, RF Government grant, Ag. No. 14.641.31.0001. The authors would like to thank Jean-Louis Colliot-Thélène, Bjorn Poonen, Stefan Schreieder, Yuri Tschinkel, and the anonymous referee for helpful comments.
Appendix: Analysis of singularities
Appendix: Analysis of singularities
The main goal of this section is to prove the following result.
Theorem 6.1
Let \(X_n\) be as defined in (7). Then \(X_n\) admits a universally \(\mathrm {CH}_0\)-trivial resolution  .
.
The following lemma is known:
Lemma 6.2
Let X be a proper variety over a field k of characteristic zero. If X admits a universally \(\mathrm {CH}_0\)-trivial resolution \(\widetilde{X}\rightarrow X\), then any resolution  is universally \(\mathrm {CH}_0\)-trivial.
is universally \(\mathrm {CH}_0\)-trivial.
Proof
We note that by resolution of singularities, there is a smooth projective variety \(\widetilde{X}'\) together with birational morphisms  and
and  . Then, it is enough to observe that any birational morphism of smooth projective varieties over k is universally \(\mathrm {CH}_0\)-trivial. For this, we use weak factorization, the fact that a blow-up with smooth center is a universally \(\mathrm {CH}_0\)-trivial morphism, and the fact that, by definition, a composition of two universally \(\mathrm {CH}_0\)-trivial maps is universally \(\mathrm {CH}_0\)-trivial. \(\square \)
. Then, it is enough to observe that any birational morphism of smooth projective varieties over k is universally \(\mathrm {CH}_0\)-trivial. For this, we use weak factorization, the fact that a blow-up with smooth center is a universally \(\mathrm {CH}_0\)-trivial morphism, and the fact that, by definition, a composition of two universally \(\mathrm {CH}_0\)-trivial maps is universally \(\mathrm {CH}_0\)-trivial. \(\square \)
By [16, Proposition 1.8] we have the following criterion: a proper morphism \(\widetilde{X}\rightarrow X\) is universally \(\mathrm {CH}_0\)-trivial if for any scheme-theoretic point \(P \in X\), the fiber \(\widetilde{X}_{\!P}\) is a universally \(\mathrm {CH}_0\)-trivial variety over the residue field \(\kappa (P)\). Using this criterion, in order to prove that a sequence of blow-ups of a variety X provides a universally \(\mathrm {CH}_0\)-trivial resolution \(f:\widetilde{X}\rightarrow X\), it is enough to work formally locally on X. Indeed, if \(\widehat{\mathcal {O}}_{X,P}\) is the completion of the local ring \({\mathcal {O}}_{X,P}\), then the fiber of the induced morphism  at the closed point of \(\mathrm {Spec}\,\widehat{\mathcal {O}}_{X,P}\) is
at the closed point of \(\mathrm {Spec}\,\widehat{\mathcal {O}}_{X,P}\) is  .
.
We now analyze different types of singularities that could appear for \(X_n\).
1.1 Equations defining singular locus
By symmetry, we may work over an open chart \(z\ne 0\) of  . Then we have the following equations defining the singular locus:
. Then we have the following equations defining the singular locus:

Note that if  satisfies the condition that (x, y) is not contained in
satisfies the condition that (x, y) is not contained in  , then P is a smooth point. Indeed, we then have \(abcdF(P)\ne 0\) and the conditions above imply that \(s=t=u=v=0,\) which is not possible since s, t, u, v are projective coordinates.
, then P is a smooth point. Indeed, we then have \(abcdF(P)\ne 0\) and the conditions above imply that \(s=t=u=v=0,\) which is not possible since s, t, u, v are projective coordinates.
Also, if \(P\in C\), but not on any line \(L_1, \dots , L_m\), conditions (15) imply that

which is impossible since the conic C is smooth.
Hence we need to analyze the following four types of singularities:
-
over the generic point of lines \(L_i\);
-
over the intersection points
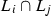 ;
; -
over the tangency point of C and \(L_i\);
-
over closed points of lines \(L_i\), that are not on other lines or on the conic C.
Note that by [24, 25], a universally \(\mathrm {CH}_0\)-trivial resolution exists in the following cases:
In the arguments below, up to a linear change of variables x and y, we may assume that  and
and  .
.
The analysis below provides the following global description of singularities:
-
(a)
the curves \(C_i\) (18), (20) over the lines \(L_i\), some of these curves are singular at a point \(P_i\) (23) over the tangency point of C and \(L_i\);
-
(b)
singular lines (21) and (22), over the intersection points of \(L_i\) and
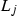 ;
; -
(c)
the curves \(D_i\) (24) over the tangency points of C and \(L_i\).
We consider the map
given by successive blow-ups of the singular locus in the following order:
-
we blow up lines (21);
-
we blow up the points \(P_i\) and then we blow up the exceptional divisors over \(P_i\),
-
we blow up the proper transform of \(C_1\), the proper transform of \(C_2, \dots \), and then proper transform of \(C_m\),
-
we blow up successively the proper transforms of lines (22),
-
finally, we blow up the proper transforms of the curves \(D_i\).
We claim that the only singularities of the variety \(X_n'\) are over some intersection points of \(L_i\) and  , the blow-up \(\widetilde{X}_n\) of these singularities is smooth, and the resulting map
, the blow-up \(\widetilde{X}_n\) of these singularities is smooth, and the resulting map  is a universally \(\mathrm {CH}_0\)-trivial resolution.
is a universally \(\mathrm {CH}_0\)-trivial resolution.
1.2 Singularities over lines \(L_i\)
We have two cases to consider:
-
(a)
\(\ell _i=x\) divides precisely two among the coefficients a, b, c, by symmetry we may assume that \(x {|} a,b\), we then write \(a=xa_1\), \(b=xb_1\);
-
(b)
x divides d, by symmetry, we may assume that
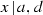 and we write \(d=xd_1\), \(a=xa_1\).
and we write \(d=xd_1\), \(a=xa_1\).
Then the analysis of the singular locus in each case is as follows:
(a) The equations (15) imply \(u=v=0\), \(a_1s^2+b_1t^2=0\). Let \(\lambda \) be the common factor of \(a_1\) and \(b_1\): \(\lambda \) is the product of (some of) lines \(\ell _1, \cdots , \ell _m\) and \(a_1=\lambda a_2\), \(b_1=\lambda b_2\). We obtain a curve  in the singular locus \(X_n^{\mathrm {sing}}\) of \(X_n\):
in the singular locus \(X_n^{\mathrm {sing}}\) of \(X_n\):

We claim that the blow-up of the curve \(C_i\) is smooth at any point of the exceptional divisor that is not over a point of C or a point on another line, and that the corresponding fibers are universally \(\mathrm {CH}_0\)-trivial.
For the fibers over a point \(P\in X_n\) lying over a closed point \(Q\in L_i\), we work over the local ring \(\widehat{\mathcal {O}}_{X_n, P}\). Since the residue field of Q is the field of complex numbers, any element of  , which does not vanish at Q, is a square in
, which does not vanish at Q, is a square in  , and hence in \(\widehat{\mathcal {O}}_{X_n, P}\). We then obtain the following formal equation:
, and hence in \(\widehat{\mathcal {O}}_{X_n, P}\). We then obtain the following formal equation:

the singularity is defined by \(u=v=0\), \(x=0\), \(s^2+t^2=0\). This type of singularity has been already treated in [24] (compare with equations (16)), it is resolved with one blow-up, and the corresponding fiber is universally \(\mathrm {CH}_0\)-trivial.
For the fiber over the generic point of \(C_i\), it is enough to consider the following charts of the blow-up:
-
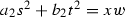 , \(u=x u_1\), \(v=xv_1\). The blow-up is given by the conditions
, \(u=x u_1\), \(v=xv_1\). The blow-up is given by the conditions 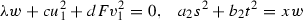
and the exceptional divisor is defined by
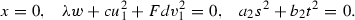
This variety is smooth and rational over the generic point of \(C_i\) since \(b_2/a_2\) is a square at the generic point of \(C_i\).
-
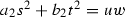 , \(x=ux_1\), \(v=uv_1\). The blow-up is given by the conditions
, \(x=ux_1\), \(v=uv_1\). The blow-up is given by the conditions 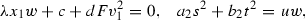
it is smooth since \(a_2, b_2, \lambda \) and c do not vanish at the generic point of \(L_i\) and \(s\ne 0\) or \(t\ne 0\). The exceptional divisor is also smooth and rational, defined by \(u=0\). The chart with the exceptional divisor defined by \(v=0\) is similar.
-
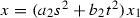 ,
, 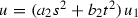 ,
, 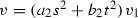 . The blow-up is given by the condition
. The blow-up is given by the condition 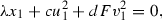
it is smooth. The exceptional divisor is smooth and rational, defined by
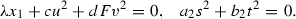
(b) Similarly as in the previous case, let \(\lambda \) be the common factor of \(a_1\) and \(d_1\) and \(a_1=\lambda a_2\), \(d_1=\lambda d_2\). We obtain the equation of the singular locus:

The formal equation at closed points are the same as the equations in the previous case (19). For the generic fiber, we consider the following chart of the blow-up:

The blow-up is given by the conditions

and the exceptional divisor is defined by

This variety is smooth and rational over the generic point of \(C_i\) since \(d_2F/a_2\) is a square at the generic point of \(C_i\).
The analysis of the other charts is similar to the previous case.
1.3 Singularities over intersection points 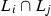
Let Q be the intersection point of \(L_i\) and  and let P be a singular point of \(X_n\) over Q. We have the following cases to consider:
and let P be a singular point of \(X_n\) over Q. We have the following cases to consider:
(a) Only two coefficients among a, b, c, d vanish at Q. We then have the following possibilities (up to a symmetry):  or
or  and the corresponding singular lines are given by the (global) conditions
and the corresponding singular lines are given by the (global) conditions
Again, working formally locally, we may assume that any function that does not vanish at Q is a square. Hence, in all cases, up to a symmetry, we have the following type of local equation:

and the singularity is given by \(x=y=u=v=0\). Also we can change variables \(s^2+t^2=s_1t_1\) and consider the chart \(t_1=1\), so that we have the following local equation:

The map \(X_n'\rightarrow X_n\), restricted to \(\widehat{\mathcal {O}}_{X_n, P}\), is the following composition:
-
blow-up of the line \(x=y=u=v=0\);
-
blow-up of the proper transform of \(x=s_1=u=v=0\);
-
blow-up of the proper transform of \(y=s_1=u=v=0\).
By symmetry between u and v we consider the following charts of the first blow-up:
-
\(x=yx_1\), \(u=yu_1\), \(v=yv_1\); the equation of the blow-up is \(x_1s_1+u_1^2+v_1^2=0\) and the exceptional divisor is given by \(y=0\). This blow-up map is universally \(\mathrm {CH}_0\)-trivial over this chart. Next, we blow up the locus \(x_1=s_1=u_1=v_1=0\), which is the product of a line and an ordinary double point singularity, hence this second blow-up has smooth total space with universally \(\mathrm {CH}_0\)-trivial fibers. By smoothness, the third blow-up is universally \(\mathrm {CH}_0\)-trivial over this chart.
-
\(y=xy_1\), \(u=xu_1\), \(v=xv_1\); the equation of the blow-up is \(y_1s_1+u_1^2+v_1^2=0\) and the exceptional divisor is given by \(x=0\). Next we blow up the locus \(x=s_1=u_1=v_1=0\). We consider the following charts (again, using symmetry between \(u_1\) and \(v_1\)):
-
(i)
\(s_1=xs_2\), \(u_1=xu_2\), \(v_2=xv_2\), where the equation of the blow-up is \({y_1s_2+x(u_2^2+v_2^2)=0}\), the exceptional divisor is \(x=0\). The fibers of the second blow-up are universally \(\mathrm {CH}_0\)-trivial. Next we blow up the locus \(y_1=s_2=u_2=v_2=0\). The charts corresponding to the exceptional divisors \(y_1=0\) and \(s_2=0\) are smooth, and the fibers are universally \(\mathrm {CH}_0\)-trivial:
- \(\bullet \) :
-
\(s_2=y_1s_3\), \(u_2=y_1u_3\), \(v_2=y_1v_3\), where the equation of the blow-up is given by \({s_3+x(u_3^2+v_3^2)=0}\);
- \(\bullet \) :
-
\(y_1=s_2y_3\), \(u_2=s_2u_3\), \(v_2=s_2v_3\), where the equation of the blow-up is given by \({y_3+x(u_3^2+v_3^2)=0}\);
In the chart \(y_1=u_2y_3\), \(s_2=u_2y_3\), \(v_2=u_2v_3\) we have the following equation: \(y_3s_3+x(1+v_3^2)=0\), the ordinary double singularities \(v_3=\pm i, x=y_3=s_3=0\) are resolved after one blow-up, and the exceptional divisor is rational.
-
(ii)
\(x=s_1x_2\), \(u_1=s_1u_2\), \(v_2=s_1v_2\), where the equation of the blow-up is \(y_1+s_1(u_2^2+v_2^2)=0\), \(x=s_1x_2\), the exceptional divisor is \(s_1=0\), the fibers are universally \(\mathrm {CH}_0\)-trivial. The blow-up is smooth, hence the third blow-up is universally \(\mathrm {CH}_0\)-trivial over this chart.
-
(iii)
\(x=u_1x_2\), \(s=u_1s_2\), \(v_2=u_1v_2\); the equation of the blow-up is \(y_1s_2+u_1+u_1v_2^2=0\), \(x=u_1x_2\), the exceptional divisor is given by \(u_1=0\). Next we blow up \(y_1=s_2=u_1=v_2=0\). Note that this chart is smooth along this locus, hence the third blow-up is universally \(\mathrm {CH}_0\)-trivial in this chart. The remaining singularity \(y_1=s_2=u_1=0\), \(v_2=\pm i\) is resolved as at the end of case (i) above.
-
\(x=ux_1\), \(y=uy_1\), \(v=uv_1\); the equation of the blow-up is \(x_1y_1s_1+1+v_1^2=0\); it is smooth and the exceptional divisor is given by \(u=0\). This blow-up map is universally \(\mathrm {CH}_0\)-trivial in this chart. Since the first blow-up is smooth over this chart, the second and third blow-ups are universally \(\mathrm {CH}_0\)-trivial.
(b) Only three coefficients among a, b, c, d vanish at Q. Then, we may assume that  , that
, that  , and that
, and that  . The case when x or y divides d is similar. The singular locus over \(x=y=0\) is given by \(t=u=v=0\), hence, it is the point of the intersection of the curves \(C_i\) and
. The case when x or y divides d is similar. The singular locus over \(x=y=0\) is given by \(t=u=v=0\), hence, it is the point of the intersection of the curves \(C_i\) and  . The restriction of the map \(X_n'\rightarrow X_n\) to \(\widehat{\mathcal {O}}_{X_n, P}\) is the composition of the blow-up of \(C_i\) and the proper transform of
. The restriction of the map \(X_n'\rightarrow X_n\) to \(\widehat{\mathcal {O}}_{X_n, P}\) is the composition of the blow-up of \(C_i\) and the proper transform of  . Note that over the point P we have the following formal equation:
. Note that over the point P we have the following formal equation:

The same type of formal equation corresponds to the case considered in [24] (compare with equations (16)), where it is showed that the two blow-ups as above provide a universally \(\mathrm {CH}_0\)-trivial resolution.
(c) All coefficients a, b, c, d vanish at Q. We then assume \(a=xa_1\), \(b=xb_1\), \(c=yc_1\), \(d=yd_1\) and we have the following equation for \(X_n\):
and the expression of the singular locus

Since \(a_1, b_1, c_1, d_1F\) evaluated at Q are nontrivial constants, this singular locus is the union of four lines, and the points with coordinates \(s=t=0\) or \(u=v=0\) correspond to the intersection points of these lines with the curves \(C_i\) and  .
.
We now describe the the formal equation. Changing variables, we may replace  by
by  and \(c_1u^2+d_1Ft^2\) by \(u_1v_1\), and, by symmetry, we may consider the affine chart \(t_1=1\). We then have the following formal equation:
and \(c_1u^2+d_1Ft^2\) by \(u_1v_1\), and, by symmetry, we may consider the affine chart \(t_1=1\). We then have the following formal equation:

The singular locus is the union of the two lines defined by \(x=y=s_1=u_1=0\) and \(x=y=s_1=v_1=0\). The restriction of the map \(\widetilde{X}_n\rightarrow X_n\) is as follows:
-
blow-up of the locus \(x=s_1=u_1=v_1=0\) (we separate two lines);
-
blow-up of the strict transform of the lines defined by \(x=y=s_1=u_1=0\) and \(x=y=s_1=v_1=0\).
(Note that only one of the blow-ups of \(C_i\) and  is not an isomorphism for the case \(t_1=1\) we consider). By symmetry, we have the following charts of the first blow-up to consider:
is not an isomorphism for the case \(t_1=1\) we consider). By symmetry, we have the following charts of the first blow-up to consider:
-
\(s=xs_2\), \(u=xu_2\), \(v=xv_2\), where the equation of the blow-up is \(s_2+yu_2v_2=0\); it is smooth and the exceptional divisor, defined by \(x=0\), is smooth and rational. By smoothness, the second blow-up is universally \(\mathrm {CH}_0\)-trivial over this chart.
-
\(s=u_1s_2\), \(x=u_1x_2\), \(v=u_1v_2\); the equation of the blow-up is \(x_2s_2+yv_2=0\), and the exceptional divisor is rational, given by \(u_1=0\); the singular locus \(x_2=s_2=y=v_2=0\) is resolved by the second blow-up, and the exceptional divisor is rational.
From the equations above, the fibers of the map \(X_n'\rightarrow X_n\) at P are universally \(\mathrm {CH}_0\)-trivial over this chart.
1.4 Singularities over the tangency point of C and \(L_i\)
Assume C is tangent to \(L_i\) at the point Q. We have the following cases:
(a) d vanishes at Q. By symmetry, we assume  and write \(a=xa_1\), \(d=xd_1\). Then conditions (15) imply
and write \(a=xa_1\), \(d=xd_1\). Then conditions (15) imply

hence we obtain a point
on the curve \(C_i\) in case (20). The local form is as follows:

This is the same type of formal equation as for the quadric bundle we considered in [25] (see equations (16)), by loc. cit., the map (17) provides a universally \(\mathrm {CH}_0\)-trivial resolution: we blow up successively the point \(P_i\), then the exceptional divisor of the blow-up and the proper transform of \(C_i\).
(b) d does not vanish at Q. We may then assume \(a=xa_1\), \(b=xb_1\), so that conditions (15) imply

Arguing as in the previous cases, we obtain the following formal local form of the singular locus:

This is the same type of formal equation as for the quadric bundle we considered in [24] [see equations (16)], by loc. cit., the map (17) provides a universally \(\mathrm {CH}_0\)-trivial resolution. This finishes the proof of Theorem 6.1.
Rights and permissions
About this article
Cite this article
Auel, A., Böhning, C. & Pirutka, A. Stable rationality of quadric and cubic surface bundle fourfolds. European Journal of Mathematics 4, 732–760 (2018). https://doi.org/10.1007/s40879-018-0233-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-018-0233-1




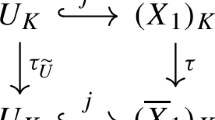
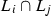 ;
;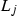 ;
;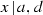 and we write
and we write 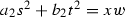 ,
, 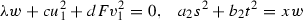
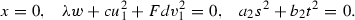
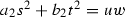 ,
, 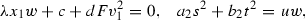
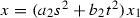 ,
, 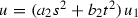 ,
, 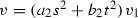 . The blow-up is given by the condition
. The blow-up is given by the condition