Abstract
We introduce and study smooth compactifications of the moduli space of n labeled points with weights in projective space, which have normal crossings boundary and are defined as GIT quotients of the weighted Fulton–MacPherson compactification. We show that the GIT quotient of a wonderful compactification is also a wonderful compactification under certain hypotheses. We also study a weighted version of the configuration spaces parametrizing n points in affine space up to translation and homothety. In dimension one, the above compactifications are isomorphic to Hassett’s moduli space of rational weighted stable curves.






Similar content being viewed by others
References
Alexeev, V.: Moduli of Weighted Hyperplane Arrangements, with Applications (2013). http://alpha.math.uga.edu/~valery/preprints/BarcelonaNotes11-26-13.pdf
Chen, L., Gibney, A., Krashen, D.: Pointed trees of projective spaces. J. Algebraic Geom. 18(3), 477–509 (2009)
Dolgachev, I.: Lectures on Invariant Theory. London Mathematical Society Lecture Note Series, vol. 296. Cambridge University Press, Cambridge (2003)
Fulton, W., MacPherson, R.: A compactification of configuration spaces. Ann. Math. 139(1), 183–225 (1994)
Gallardo, P., Giansiracusa, N.: The Chen–Gibney–Krashen moduli space as a Chow quotient (2015). arXiv:1509.03608
Gallardo, P., Giansiracusa, N., McFaddin, P.K., Wu, X.: The Chen–Gibney–Krashen moduli spaces revisited (2016) (in preparation)
Giansiracusa, N., Gillam, W.D.: On Kapranov’s description of \(\overline{M}_{0, n}\) as a Chow quotient. Turkish J. Math. 38(4), 625–648 (2014)
Hacking, P., Keel, S., Tevelev, J.: Compactification of the moduli space of hyperplane arrangements. J. Algebraic Geom. 15(4), 657–680 (2006)
Hassett, B.: Moduli spaces of weighted pointed stable curves. Adv. Math. 173(2), 316–352 (2003)
Hu, Y.: Relative geometric invariant theory and universal moduli spaces. Internat. J. Math. 7(2), 151–181 (1996)
Hu, Y.: A compactification of open varieties. Trans. Amer. Math. Soc. 355(12), 4737–4753 (2003)
Hu, Y., Keel, S.: Mori dream spaces and GIT. Michigan Math. J. 48, 331–348 (2000)
Ishii, S.: Moduli space of polarized del Pezzo surfaces and its compactification. Tokyo J. Math. 5(2), 289–297 (1982)
Kapranov, M.M.: Chow quotients of Grassmannians. I. In: Gelfand, S., Gindikin, S. (eds.) I.M. Gelfand Seminar. Advances in Soviet Mathematics, vol. 16, part 2, pp. 29–110. American Mathematical Society, Providence (1993)
Keel, S.: Intersection theory of moduli space of stable \(n\)-pointed curves of genus zero. Trans. Amer. Math. Soc. 330(2), 545–574 (1992)
Keel, S., Tevelev, J.: Geometry of Chow quotients of Grassmannians. Duke Math. J. 134(2), 259–311 (2006)
Kirwan, F.C.: Partial desingularisations of quotients of nonsingular varieties and their Betti numbers. Ann. Math. 122(1), 41–85 (1985)
Li, L.: Wonderful compactification of an arrangement of subvarieties. Michigan Math. J. 58(2), 535–563 (2009)
Losev, A., Manin, Yu.: New moduli spaces of pointed curves and pencils of flat connections. Michigan Math. J. 48, 443–472 (2000)
Pandharipande, R.: A geometric invariant theory compactification of \(M_{g,n}\) via the Fulton–MacPherson configuration space (1995). arXiv:alg-geom/9505022
Reichstein, Z.: Stability and equivariant maps. Invent. Math. 96(2), 349–383 (1989)
Routis, E.: Weighted compactifications of configuration spaces and relative stable degenerations (2014). arXiv:1411.2955
Routis, E.: The Chow ring of the moduli space of genus 0 weighted stable curves (2015). http://www.math.brown.edu/~r0utis/chow_ring_hassett.pdf
Ulyanov, A.P.: Polydiagonal compactification of configuration spaces. J. Algebraic Geom. 11(1), 129–159 (2002)
Acknowledgements
We thank Valery Alexeev, Kenny Ascher, Angela Gibney, Noah Giansiracusa for helpful discussions. We especially thank Danny Krashen for carefully reading an earlier draft of this article and for providing valuable feedback. The first author was supported by the NSF Grant DMS-1344994 of the RTG in Algebra, Algebraic Geometry, and Number Theory, at the University of Georgia. The second author is supported by the World Premier International Research Center Initiative (WPI), MEXT, Japan.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Lemma 6.1
Let \(Z\hookrightarrow X\) be an embedding of smooth varieties, both flat over a variety Y. For any geometric point \(y\in Y\) let \(Z_y\) and \(X_y\) be the fibers of \(Z\rightarrow Y\) and \(X\rightarrow Y\) over y. Then the blowup \(\mathrm{Bl}_Z X\) of X at Z is flat over Y and we have an isomorphism

Proof
Let \(\mathscr {I}\) be the ideal sheaf corresponding to the embedding \(Z\hookrightarrow X\). Since Z and X are smooth, that embedding is regular. Consequenlty,  is a locally free, hence flat, sheaf of -modules for all \(n\geqslant 0\). By the hypothesis is flat over \(\mathscr {O}_Y\), consequently
is a locally free, hence flat, sheaf of -modules for all \(n\geqslant 0\). By the hypothesis is flat over \(\mathscr {O}_Y\), consequently  is also flat over \(\mathscr {O}_Y\). Then, by the exact sequence
is also flat over \(\mathscr {O}_Y\). Then, by the exact sequence

we deduce by induction that  is also flat over \( \mathscr {O}_Y\) for all \(n\geqslant 0\). Now, the lemma follows by [13, Lemma 1]. \(\square \)
is also flat over \( \mathscr {O}_Y\) for all \(n\geqslant 0\). Now, the lemma follows by [13, Lemma 1]. \(\square \)
Lemma 6.2
Let Z be a smooth subvariety of a smooth variety Y and let \(\pi :\mathrm{Bl}_Z Y\rightarrow Y\) be the blowup, with exceptional divisor \(E=\pi ^{-1}(Z)\).
-
(i)
Let V be a smooth subvariety of Y, not contained in Z, and let \(\widetilde{V}\subset \mathrm{Bl}_Z Y\) be its strict transform. Then:
- (i\(_1\)):
-
If V meets Z transversally (or is disjoint from Z), then \(\widetilde{V}=\pi ^{-1}(V)\) and \(\mathscr {I}_{\pi ^{-1}(V)}=\mathscr {I}_{\widetilde{V}}\). Moreover,
$$\begin{aligned} N_{\widetilde{V}/\mathrm{Bl}_Z Y}\cong \pi ^*\!N_{V/Y}. \end{aligned}$$ - (i\(_2\)):
-
If \(V\supset Z\), then \(\mathscr {I}_{\pi ^{-1}(V)}=\mathscr {I}_{\widetilde{V}}\cdot \mathscr {I}_E\). Moreover,
$$\begin{aligned} N_{\widetilde{V}/\mathrm{Bl}_Z Y}\cong \pi ^*\!N_{V/Y}\otimes \mathscr {O}(E). \end{aligned}$$Also, if Z has codimension 1 in V, the projection from \(\widetilde{V}\) to V is an isomorphism.
-
(ii)
Let \(Z_1, Z_2\) be smooth subvarieties of Y intersecting transversally.
- (ii\(_1\)):
-
Assume \(Z_1\cap Z_2 \supseteq Z\). Then their strict transforms \(\widetilde{Z_1}\) and \(\widetilde{Z_2}\) intersect transversally and \(\widetilde{Z_1}\cap \widetilde{Z_2}= \widetilde{Z_1\cap Z_2}\); in particular, if \(Z_1\cap Z_2 = Z\), then \(\widetilde{Z_1}\cap \widetilde{Z_2}= \varnothing \).
- (ii\(_2\)):
-
Assume Z intersects transversally with \(Z_1\) and \(Z_2\), as well as with their intersection \(Z_1\cap Z_2\). Then their strict transforms \(\widetilde{Z_1}\) and \(\widetilde{Z_2}\) intersect transversally and \(\widetilde{Z_1}\cap \widetilde{Z_2}= \widetilde{Z_1\cap Z_2}\).
- (ii\(_3\)):
-
If \(Z_1\supseteq Z\) and \(Z_2\) intersects transversally with Z, then the intersections
$$\begin{aligned} \widetilde{Z_1}\cap \widetilde{Z_2}\quad \text {and}\quad (E\cap \widetilde{Z_1})\cap \widetilde{Z_2} \end{aligned}$$are transversal. Moreover, \(\widetilde{Z_1}\cap \widetilde{Z_2}=\widetilde{Z_1\cap Z_2}\).
Proof
(i) is standard; the proof of (ii) follows from [18, Lemma 2.9]. \(\square \)
1.1 Proofs of Lemmas 4.24 and 4.25
In order to prove Lemma 4.24, we consider the intersections of the iterated strict transforms of \(\delta _I\) with the centers of each of the blowups in the sequence  . In addition, we distinguish two types of subvarieties
\(\delta _J\cap \delta _I\) of \(\delta _I\) under the identification (5) of \(\delta _I\) with
. In addition, we distinguish two types of subvarieties
\(\delta _J\cap \delta _I\) of \(\delta _I\) under the identification (5) of \(\delta _I\) with

as follows:
-
(a)
Let \(\delta _J \in \mathscr {H}^I_1\) (i.e. J contains I). In this case
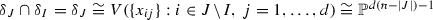 .
. -
(b)
Let \(\delta _J \in \mathscr {H}^I_2\) (i.e. J is disjoint from I). In this case
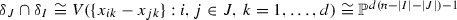 .
.
Clearly, we have an equality of sets

where \(\mathscr {H}_{\mathscr {A}_+(I^\mathrm{c})}\) is defined in Definition 4.15 for input data \((d,n-|I|+1, \mathscr {A}_+(I^\mathrm{c}))\). We give \(\mathscr {H}_{\mathscr {A}_+(I^\mathrm{c})}\) an order \((\lessdot )\) compatible with the order \((\prec )\) of Definition 4.20, that is:
-
for any \(\delta _J \in \mathscr {H}^I_1\cup \mathscr {H}^I_2\), \(\delta _J\cap \delta _I \lessdot \delta _{J'}\cap \delta _I\) if and only if
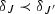 .
.
Lemma 6.3
The ordered set \((\mathscr {H}_{\mathscr {A}_+(I^\mathrm{c})},\lessdot )\) satisfies the second condition of Theorem 3.9.
Proof
The proof is very similar to the Proof of Lemma 4.16, so we omit it. \(\square \)
For any  let \(M_i\) be the cardinality of the set \(\mathscr {H}^I_1\!\cup \cdots \cup \mathscr {H}^I_i\). For any \(k\in \mathbb {Z}\) such that \(0<k\leqslant M_4\), we define \(P_{I,k}\) to be k-th step in the sequence of blowups with respect to the order \((\prec )\). Moreover, for any
let \(M_i\) be the cardinality of the set \(\mathscr {H}^I_1\!\cup \cdots \cup \mathscr {H}^I_i\). For any \(k\in \mathbb {Z}\) such that \(0<k\leqslant M_4\), we define \(P_{I,k}\) to be k-th step in the sequence of blowups with respect to the order \((\prec )\). Moreover, for any  , we denote by \(V^{(k)}\) the iterated dominant transform of
, we denote by \(V^{(k)}\) the iterated dominant transform of  in \(P_{I,k}\). In particular \(\delta _J^{(M_i)}\!=\delta _J^{[i]}\) for any \(\delta _J\in \mathscr {H}_{\mathscr {A}}\).
in \(P_{I,k}\). In particular \(\delta _J^{(M_i)}\!=\delta _J^{[i]}\) for any \(\delta _J\in \mathscr {H}_{\mathscr {A}}\).
Lemma 6.4
-
(i)
Let \(\delta _J \in \mathscr {H}^I_1\cup \mathscr {H}^I_2\). For each k such that \(0\leqslant k\leqslant M_2\) the subvariety \({\delta _J}^{(k)}\) of \(P_{I,k}\) either contains or intersects transversally with the center of the blowup \(P_{I,k+1}\rightarrow P_{I,k}\).
-
(ii)
\(({\delta _I\cap \delta _J})^{(k)}= {\delta _I}^{(k)}\cap {\delta _J}^{(k)}\) for any \(\delta _J\in \mathscr {H}_2^I\) and \(0\leqslant k\leqslant M_1\). Moreover, each intersection \({\delta _I}^{(k)}\cap {\delta _J}^{(k)}\) is transversal.
-
(iii)
\({\delta _I}^{(M_1)}\cap {\delta _J}^{(M_1)}=\varnothing \) for any \(\delta _J\in \mathscr {H}_3^I\). Therefore \({\delta _I}^{(k)}\cap {\delta _J}^{(k)}=\varnothing \) for all \(k>M_1\) as well.
-
(iv)
\(({\delta _I\cap \delta _J})^{(k)}= {\delta _I}^{(k)}\cap {\delta _J}^{(k)}\) for any \(\delta _J\in \mathscr {H}_2^I\) and \(M_1< k\leqslant M_2\). Moreover, each intersection \({\delta _I}^{(k)}\cap {\delta _J}^{(k)}\) is transversal.
Proof
(i) By Lemma 4.21, \(\mathscr {H}^I_1\cup \mathscr {H}^I_2\) is a building set. Also, observe that the order \((\prec )\) on \(\mathscr {H}^I_1\cup \mathscr {H}^I_2\) is inclusion preserving. Therefore, the claim follows from Proposition 3.8 (ii).
(ii) Let k be such that \(0\leqslant k\leqslant M_1\). By part (i), the iterated strict transform of each  in \(P_{I,k}\) must either intersect the blowup center inside \(P_{I,k}\) transversally or it must contain that center. Also, observe that for
in \(P_{I,k}\) must either intersect the blowup center inside \(P_{I,k}\) transversally or it must contain that center. Also, observe that for  we have that the intersection \(\delta _I\cap \delta _J\) is transversal. Moreover, the iterated strict transform of \(\delta _I\) in \(P_{I,k}\) contains the corresponding center for all the above k. Therefore, by a repeated use of Lemma 6.2 (ii\(_1\)) and (ii\(_3\)) we deduce (ii).
we have that the intersection \(\delta _I\cap \delta _J\) is transversal. Moreover, the iterated strict transform of \(\delta _I\) in \(P_{I,k}\) contains the corresponding center for all the above k. Therefore, by a repeated use of Lemma 6.2 (ii\(_1\)) and (ii\(_3\)) we deduce (ii).
(iii) For any \(\delta _J\in \mathscr {H}_3^I\), by definition, the set J overlaps with I. Consider an element \(j\in J\cap I\) and set  . Since \({\delta _{J'}}^{(M_1)}\supseteq {\delta _J}^{(M_1)}\), it is enough to show that \({\delta _I}^{(M_1)}\cap {\delta _{J'}}^{(M_1)}=\varnothing \). While \(\delta _{J'}\) is not necessarily an element of \(\mathscr {H}_{\mathscr {A}}\), the same argument as in Lemma 4.16 shows that the set
. Since \({\delta _{J'}}^{(M_1)}\supseteq {\delta _J}^{(M_1)}\), it is enough to show that \({\delta _I}^{(M_1)}\cap {\delta _{J'}}^{(M_1)}=\varnothing \). While \(\delta _{J'}\) is not necessarily an element of \(\mathscr {H}_{\mathscr {A}}\), the same argument as in Lemma 4.16 shows that the set  , with \(\mathscr {H}_1^I\) given an ascending dimension order and \(\delta _J\) listed last, is a building set. Now the intersection \(\delta _I\cap \delta _J'=\delta _{I\cup J'}\) belongs to \(\mathscr {H}_1^I\); assume it is the m-th element of that set with respect to \((\prec )\) for some m with \(0<m\leqslant M_1\). Consider the iterated strict transforms \(\delta _I^{(m-1)}\) and \(\delta _{J'}^{(m-1)}\) of \(\delta _I\) and \(\delta _{J'}\) respectively under
, with \(\mathscr {H}_1^I\) given an ascending dimension order and \(\delta _J\) listed last, is a building set. Now the intersection \(\delta _I\cap \delta _J'=\delta _{I\cup J'}\) belongs to \(\mathscr {H}_1^I\); assume it is the m-th element of that set with respect to \((\prec )\) for some m with \(0<m\leqslant M_1\). Consider the iterated strict transforms \(\delta _I^{(m-1)}\) and \(\delta _{J'}^{(m-1)}\) of \(\delta _I\) and \(\delta _{J'}\) respectively under  . Since the intersection \(\delta _I\cap \delta _{J'}\) is transversal, by using the argument of the previous paragraph we see that \(\delta _I^{(m-1)}\cap \delta _{J'}^{(m-1)}=\delta _{I\cup J'}^{(m-1)}\). Now consider the m-th blowup \(P_{I,m}\rightarrow P_{I,m-1}\). By Lemma 6.2 (ii), we deduce that \(\delta _I^{(m)}\cap \delta _{J'}^{(m)}=\varnothing \), so \({\delta _I}^{(M_1)}\cap {\delta _{J'}^{(M_1)}}=\varnothing \).
. Since the intersection \(\delta _I\cap \delta _{J'}\) is transversal, by using the argument of the previous paragraph we see that \(\delta _I^{(m-1)}\cap \delta _{J'}^{(m-1)}=\delta _{I\cup J'}^{(m-1)}\). Now consider the m-th blowup \(P_{I,m}\rightarrow P_{I,m-1}\). By Lemma 6.2 (ii), we deduce that \(\delta _I^{(m)}\cap \delta _{J'}^{(m)}=\varnothing \), so \({\delta _I}^{(M_1)}\cap {\delta _{J'}^{(M_1)}}=\varnothing \).
(iv) By Lemma 4.21, \(\mathscr {H}^I_1\cup \mathscr {H}^I_2\) is a building set and it is straightforward to see that the set \(\mathscr {H}^I_1\cup \mathscr {H}^I_2\cup \{\delta _I\}\) is a building set as well. Since the latter is a subset of \(\mathscr {H}_{\mathscr {A}}\) we can consider it ordered with order (\(\prec \)). Now, observe that the order \((\prec )\) on \(\mathscr {H}^I_1\cup \mathscr {H}^I_2 \cup \{\delta _I\}\) is inclusion preserving. Therefore, by Proposition 3.8 (ii), \(\delta _I^{(k)}\) intersects transversally with the center of the k-th blowup for all k as in the statement and so does \(\delta _J^{(k)}\) where \(\delta _J\in \mathscr {H}_2^I\). The proof is then very similar to the proof of (ii). \(\square \)
Proof of Lemma 4.24
By Lemma 6.4 (iii), we see that the iterated dominant transform \(\delta _I^{[3]}\subset \mathbf P _I^{[3]}\) is isomorphic to the iterated dominant transform \(\delta _I^{[2]}\subset \mathbf P _I^{[2]}\). By Lemma 6.4 (ii) and (iv), the latter is, in turn, equal to the iterated blowup of \(\delta _I\) at the ordered building set \((\mathscr {H}_{\mathscr {A}_+(I^\mathrm{c})},\lessdot )\). The lemma now follows by Lemma 6.3 and Theorem 3.9 (ii). \(\square \)
Proof of Lemma 4.25
(i) First, note that the normal bundle of  in
in  is isomorphic to
is isomorphic to

Clearly \(\mathscr {O}_{\mathbb {P}^{d(n-1)-1}}(-1)\) pulls back to \(\mathscr {O}_\mathbf{P ^{[1]}}(-1)\) on \(\mathbf P ^{[1]}\), so \(\mathscr {O}_{\mathbb {P}^{d(n-|I|)-1}}(-1)\) pulls back to \(\mathscr {O}_{{\delta _I}^{[1]}}(-1)\) on \({\delta _I}^{[1]}\). Therefore, by a repeated application of Lemma 6.2 (i\(_2\)) we see that the normal bundle of the iterated strict transform of \(\delta _I\) in \(\mathbf P ^{[1]}\) is isomorphic to

Now, by Lemma 6.4 (iii) and (iv), the intersection of each iterated strict transform of \(\delta _I\) in the sequence of blowups \(\mathbf P ^{[3]}\rightarrow \mathbf P ^{[1]}\) with every blowup center (corresponding to \(\mathscr {H}_2^I \cup \mathscr {H}_3^I\)) is transversal (even empty). Therefore, by applying Lemma 6.2 (i\(_1\)) we complete the proof.
The proof of part (ii) is identical to the proof of (i) and is therefore omitted. \(\square \)
Rights and permissions
About this article
Cite this article
Gallardo, P., Routis, E. Wonderful compactifications of the moduli space of points in affine and projective space. European Journal of Mathematics 3, 520–564 (2017). https://doi.org/10.1007/s40879-017-0170-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-017-0170-4
Keywords
- Wonderful compactifications
- Geometric invariant theory
- Hyperplane arrangements
- Fulton–MacPherson compactification
- Weighted stable curves



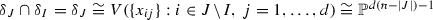 .
.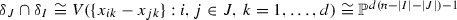 .
.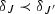 .
.