Introduction

Granular materials like sand and soils are widely used in several engineering applications, ranging from construction techniques such as pile driving to water treatment systems, and are of great interest in civil, geotechnical, petroleum and mechanical engineering.

Particulate media exhibit remarkable stress wave attenuation and kinetic energy dissipation properties when subjected to highly dynamic events such as blast loading [1, 2], earthquakes [3] and projectile penetration [4, 5] and are, consequently, of particular relevance also to defense and mining industry. A comprehensive conspectus on the experimental and numerical techniques relevant to the study of rapid projectile penetration into granular media was presented in [6].

The extensively increasing adoption of granular materials in impulsive loading applications requires the characterisation of their mechanical response at high strain rate. The dynamic behaviour of granular materials is dependent on their particle morphology, initial density, confinement, water content, and strain rate [7,8,9,10] and is commonly measured by means of experiments conducted on the Split Hopkinson Pressure bar apparatus (SHPB) [11, 12]. These present, for particulate media, additional complexities related to the representative volume of the samples, their relatively low stress wave propagation velocity [13] and the maximum compressive strains achievable during the tests.

Several researchers have previously conducted investigations into the mechanical behaviour of different types of dry sand and soils [14,15,16,17]. The effects of the lateral confinement on the dynamic behaviour of dry sand were investigated in [8, 18]. An empirical model based on the concept of strain energy density was used in [19] to predict the response of particulate materials at different strain rates. More recently, the effect of particle size on the dynamic behaviour of calcareous sand was presented in [20].

The presence of the liquid phase significantly affects the dynamic response of wet sand, as water does not have sufficient time to dissipate through the pores during high rate compression [7]. The effects of moisture content and strain rate on the mechanical response of sand were investigated in [21,22,23,24,25]. Hendron et al. [21] investigated the effect of the degree of saturation on the quasi static response of silty clay and sandy silt and reported a stiffer response, dominated by the presence of water, at high strains. Felice et al. [22] assessed the effect of water saturation on the high strain rate compressive response of Clayey silty sand. It was found that the specimen response stiffened as the moisture content increased. Veyera et al. [23] studied the dynamic behaviour of Eglin Sand, Tyndall sand and Ottawa 20-20 samples characterised by different moisture, observing lock-up behaviour at high saturation degrees. Martin et al. [24] investigated the effects of water content on the dynamic behaviour of poorly graded fine quartz and found that the presence of the liquid phase results in a lower resistance to compression for low degrees of saturation while higher water contents result in lock-up behaviour. The influence of strain rate and moisture content on the behaviour of a quartz sand was assessed in [25] by means of high pressure quasi static and high strain rate experiments under uniaxial strain. Barr et al. [26] studied the effect of water content on the dynamic compressibility and particle breakage of loose sand. The dynamic response of partially saturated Stockton Beach sand was examined in [27].

Volcanic Sand has recently attracted the attention of several researchers due to its importance in geotechnical, petroleum and aerospace engineering. The determination of its dynamic properties is of interest to defense, quarrying and oil and gas industries.

The intense heat transmitted to source rocks during volcanic activity accelerates the thermal evolution of organic matter and promotes the generation of hydrocarbons [28,29,30]. As a result these can be present in volcanic soils, often in significant quantities [31]. The determination of the mechanical properties of volcanic sand provides information on the percussive and rotary drillability of igneous materials and on the subsequent wear and damage of drilling tools [32,33,34].

Additionally, ash clouds from eruptions are regarded by international aviation authorities as a dangerous environment for aircraft engines and an immediate safety concern [35].

The ingestion of volcanic particulate into jet engines erodes the surface of stators and rotors modifying their profiles. Moreover the deposition of melted [36] volcanic sand on blades and vanes alters their geometry, thus affecting the overall performance, efficiency and operating life of gas turbine jet engines [37, 38].

The dynamic behaviour of dry Etnean volcanic sand and the effect of its impingement on titanium alloys was investigated in [39]. It was found that loose dry sand from Mount Etna exhibits a noticeable rate sensitivity while the effect of strain rate is negligible in dense Etnean sand. However the effect of the water content on the high rate compressive response of this inherently porous and partially vitreous granular material has not been previously investigated in the open literature.

The research presented in this manuscript aims to extend the work conducted in [39] by systematically investigating the influence of moisture content, initial void ratio and strain rate on the mechanical response of Etnean Sand compressed in near-uniaxial strain conditions.

Uniaxial compression experiments were carried out using an electromechanical screw-driven testing machine and a bespoke Split Hopkinson Bar apparatus, enabling the achievement of compressive strains substantially larger than those achievable by a conventional SHPB setup. The dimensions of the specimens were chosen as an optimal compromise between minimizing the effect of the lateral confinement and facilitating the attainment of dynamic equilibrium conditions during high rate experiments [40]

The particle size distribution and morphology of uncompressed and compressed samples were analysed by means of contrast edge detection techniques and microscopic imaging. The obtained results provide an insight into the dominant mechanisms of deformation and breakage of the sand grains during compression.

Parent Material and Wet Samples Preparation

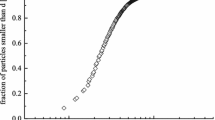
The material under investigation was collected from the south east flank of Mount Etna following the explosive activity of the volcano in December 2014. The granular material was separated from impurities and sieved to obtain an approximately homogeneous size distribution of grains, representative of the average dimensions of the volcanic debris that reaches the neighbouring airport and cities during the eruptive activity. Figure 1 illustrates the cumulative distribution of the raw Etnean sand grains, determined using the contrast detection technique detailed in ‘Particle Analysis’ section. The particles present a mean diameter equal to 0.531 mm with a standard deviation of 0.257 mm.

Fig. 1
figure 1

Grain size distribution of the raw Etnean volcanic sand utilised during the experiments

Full size image

Volcanic sand from Mount Etna is mainly composed of two minerals: cristobalite, a silica polymorph present in SiO2-rich volcanic and sedimentary environments, and anorthite (CaAl2Si2O8), a mineral common in young soils and ubiquitous in all rocks of Mount Etna [41,42,43]. The granular structure of the volcanic sand was examined by means of a Carl Zeiss Evo LS15 Environmental Scanning Electron Microscope, equipped with a range of imaging detectors. The micrographs in Fig. 2 confirm a discretely wide distribution of sizes and illustrate the morphology of the material, characterised by a sub-angular shape and middle-low sphericity [41]. Etnean volcanic ashes are characterised by the presence of abundant vesicles (Fig. 2a, b) providing the grains with inherent porosity. These are small, generally spherical cavities generated in the magmatic material by the expansion of gases and steam prior to its complete solidification. Their shape can occasionally assume a more complex geometry due to coalescence of multiple vesicles. The materials present in the volcanic ashes are representative of the lava melt as quenched right after the eruptive burst. Figure 2c, d shows the partially vitreous nature of volcanic sand. This is caused by the very rapid cooling lava undergoes preventing its minerals to rearrange in a crystalline structure.

Fig. 2
figure 2

ESEM images illustrating the morphology and microstructure of Etnean volcanic sand grains. The microstructure of Etnean volcanic ashes is characterised by the presence of numerous vesicles (arrowed in b) and by a partially vitreous nature (arrowed in c and d)

Full size image

The dynamic mechanical response of a granular material is highly sensitive to its initial compaction. This is usually quantified using one of the two equivalent parameters, void ratio \(e\) and porosity \(\eta\) [39, 44] (Table 1).

Table 1 List of symbols
Full size table

Granular assemblies are, in their natural occurring state, three phase materials composed of particles, void and water. Therefore, the dynamic response of a volcanic sand is also strongly dependent on the quantity of water contained in it. The moisture content of a sand sample can be expressed as volumetric or gravimetric water content [44].

Gravimetric water content \({\theta }_{G}\) is defined as the mass of water \({m}_{w}\) per mass of dry soil \({m}_{s}\).

$${\theta }_{G}= \frac{{m}_{w}}{{m}_{s}}$$
(1)

Volumetric water content \({\theta }_{V}\) is defined as the volume of water \({V}_{w}\) per total volume of the sample \({V}_{tot}\).

$${\theta }_{v}= \frac{{V}_{w}}{{V}_{tot}}$$
(2)

The two above parameters are linked by the following equation

$${\theta }_{V}=\frac{{\theta }_{G} \cdot { \rho }_{bulk}}{{\rho }_{w}}$$
(3)

where \({\rho }_{w}\) is the density of water and \({\rho }_{bulk}\) is the bulk density, defined as the mass of the dry specimen \({m}_{s}\) per total volume of the sample \({V}_{tot}\). The initial porosity \(\eta\) of a dry sample defines the maximum possible volumetric water content that can be added to the sample before reaching full saturation. In other words, once the initial porosity \(\eta\) of a dry sample is determined, the maximum volume of water \({V}_{w\_max}\) that can added to the sample before all available voids are replaced by water is equal to:

$${V}_{w\_max}=\eta \cdot {V}_{tot}$$
(4)

It is therefore possible to define the parameter degree of saturation \(S\), as the ratio between the volume of water \({V}_{w}\) and the volume of voids \({V}_{v}\) initially available within the sample:

$$S= \frac{{V}_{w}}{{V}_{v}}.$$
(5)

It is worth mentioning that samples characterised by same saturation \(S\) contain similar volumes of water only when their initial porosity is comparable. Hence, the mechanical response of samples characterised by same degree of saturation but different porosities cannot be correlated directly.

Two procedures for the preparation of initially loose and dense volcanic sand specimens were developed in order to obtain dry specimens of consistent void ratio \(e\). The total volume of the samples \({V}_{tot}\) was determined a priori via numerical simulations determining the representative volume element for the granular material under investigation [39, 40]. Different initial void ratios were then obtained by keeping the volume \({V}_{tot}\) constant and varying the mass of sand to be poured into the sample.

Each of the experiments conducted in this study were carried out in near-uniaxial strain conditions. This was ensured by employing stainless steel confinements of thickness equal to 5 mm, therefore exerting a considerable confining pressures on the volcanic sand samples throughout compression. The inner diameter and length of the confinement were 20 mm and 120 mm respectively. The inner diameter of the confinement was produced with a maxim manufacturing tolerance on the internal diameter of + 0.04 mm in order to guarantee near-uniaxial strain conditions and one dimensional wave propagation. A schematic of the confinements used for SHPB and quasi static experiments is shown in Fig. 3. The friction between the sand specimen and the steel confinement and anvils introduces shear stresses along the specimen [45]. However these effects are extremely difficult to quantify during a dynamic event and are often neglected [24]. The magnitude of the shear stresses between sample and confinement has not been determined in this study.

Fig. 3
figure 3

Geometry and dimensions of the particles confinement used in this study

Full size image

All sand specimens were prepared by weighing the required mass of sand \({m}_{s}\) using a precision scale.Footnote 1 Loose samples (Table 2) were prepared by pouring the weighed sand slowly into the confinement using a small funnel, avoiding any contact between the funnel and the container. The confinement was then gently tapped twice on four diametrical points, to give the sample a flat finish for the top anvil to rest. The void ratio of loose samples corresponds to the void ratio of the Etnean sand in its loosest state.

Table 2 Summary of the experiments conducted in this study
Full size table

Dense samples (Table 2) were prepared by pouring the weighed sand into the confinement a third at a time. After each third, the confinement was tapped five times on four diametrical points, and a weight of 380 g was dropped onto the specimen 20 times from a height of approximately 10 mm, facilitating the rearrangement of the grains into a more compact state. The void ratio of dense samples corresponds to the void ratio of the Etnean sand in its densest state. Denser samples could be produced only through particle breakage.

Once dry samples of consistent porosity were prepared, the volume of water needed to obtain a desired degree of saturation \(S\) was determined as:

$${V}_{w}=\eta \cdot {V}_{tot}\cdot S= {\theta }_{V}\cdot {V}_{tot}$$
(6)

water was then added to the sample using a 1 ml syringe. It was injected into several positions in the sample and then mixed thoroughly to ensure homogeneous conditions. The tapping procedure was repeated to recreate the flat finish on the top of the sample. For dense samples, the compaction procedure was also repeated.

A small amount of petroleum jelly was spread exclusively around the external perimeter of the anvils faces in contact with the sand particles to prevent any leakage of water during the preparation of samples characterised by high degrees of saturation. A number of trial tests on dry sand were conducted to assess that the amount of petroleum jelly added had no influence on the measured mechanical response.

It is worth stressing that consistency in the preparation of the samples is crucial to the accuracy and repeatability of the obtained experimental results. Variations in the void ratio considerably affect the mechanical response of the specimens and the required water content (Eq. 6).

Mixing the sample can introduce air, increasing the sample height slightly, and thus decreasing the degree of saturation. The specimen height was hence re-measured after the water was added to get a more accurate picture of the specimen properties. A significant number of samples were discarded due to discrepancies in the final void ratio. Table 2 summarises the sample properties and testing conditions of the experiments reported in this study. It is noted that the parameters \(e\) and \(\eta\) refer to the initial void ratio (\(e\)) and porosity (\(\eta\)) in dry conditions, defining the volume of water to be injected in the samples to obtain the desired saturation level. Variation in the order of small percent (± 1–2%) with respect to this nominal values were considered acceptable.

It is observed that the values of porosity obtained for Etnean sand are noticeably higher than the usual porosities achievable for silica sand samples [46]. This is due to the inherent porosity determined by the presence of numerous cavities in the material.

Experimental Methods

Quasi Static Experiments

Low strain rate compression experiments on Etnean sand were conducted using a screw-driven universal testing machine.Footnote 2 The granular samples were confined as depicted in Fig. 3. The applied load was recorded by a resistive load cellFootnote 3 while a non-contact laser extensometer was employed to record the displacement of the anvils, thereby removing any displacement associated with the compliance of the machine and fixtures during loading from the calculated strain.

High Strain Rate Experiments

The dynamic response of Etnean volcanic sand samples of different water content was characterised by means of a series of laboratory experiments on the Split Hopkinson Pressure Bar apparatus (Fig. 4). In this apparatus the sample, enclosed in its confinement, is interposed between two instrumented collinear rods, named the input and output bars. A striker, propelled by means of a compressed air piston system, impacts the input bar generating a stress pulse of duration and magnitude proportional to its length and initial velocity respectively [11]. The generated stress pulse propagates along the input bar and, once it reaches the bar-specimen interface, is partially reflected back to the input bar and partially transmitted to the output bar.

Fig. 4
figure 4

Schematic representation of the Split Pressure Hopkinson Bar apparatus used for the determination of the mechanical response of wet Etnean sand at high strain rate

Full size image

The particle velocity histories \({v}_{inp}\) and \({v}_{out}\) at the cross sections between the bars and the specimen can be determined from the recorded strain gauges signals by using one dimensional stress wave propagation theory as follows:

$${v}_{inp}(t)=\frac{{\varepsilon }_{r}\left(t\right)-{\varepsilon }_{i}\left(t\right)}{\rho {c}_{0}}$$
(7)
$${v}_{out}\left(t\right)=\frac{-{\varepsilon }_{t}(t)}{\rho {c}_{0}}$$
(8)

where \({\varepsilon }_{i}\left(t\right)\) and \({\varepsilon }_{r}\left(t\right)\) are the histories of incident and reflected waves at the interface between input bar and specimen, \({\varepsilon }_{t}\left(t\right)\) is the history of the transmitted wave at the interface between output bar and specimen, \(\rho\) and \({c}_{0}\) are the density and the longitudinal elastic stress wave propagation velocity of the material of the bars.

Dynamic strain rate \(\dot{\varepsilon }\left(t\right)\), strain \(\varepsilon (t)\) and stress \(\sigma \left(t\right)\) in the specimen can therefore be determined as:

$$\dot{\varepsilon }\left(t\right)=\frac{{v}_{inp}-{v}_{out} }{l}=\frac{1}{l} \left(\frac{{\varepsilon }_{r}\left(t\right)-{\varepsilon }_{i}\left(t\right)}{\rho {c}_{0}}+\frac{{\varepsilon }_{t}(t)}{\rho {c}_{0}}\right)$$
(9)
$$\varepsilon (t)={\int }_{0}^{T}\dot{\varepsilon }(t)dt$$
(10)
$$\sigma \left(t\right)=\frac{{A}_{0}}{2{A}_{s}}{E}_{0}[{\varepsilon }_{i}\left(t\right)+{\varepsilon }_{r}\left(t\right)+{\varepsilon }_{t}(t)]$$
(11)

where \(l\) is the length of the sample, \({A}_{0}\) and \({A}_{s}\) are the cross-sectional areas of bars and specimen and \({E}_{0}\) is the elasticity modulus of the material of the bars.

Measuring the high strain rate compressive response of granular materials presents additional technical difficulties. Unlike solid materials, where the specimen can be of smaller diameter, the cross section of compression specimens of granular material is defined by the diameter of the loading bars. Consequently, the magnitude and duration of the stress pulse required to compress these relatively large samples to high compressive strains is increased substantially, particularly in the case of wet samples.

This difficulty was addressed by employing a SHPB setup comprising of striker, input and output bars of length equal to 2.7 m. All bars were made of Ti-6AL-4V and had diameter equal to 20 mm. The anvils illustrated in Figs. 3 and 4 were manufactured using the same material to ensure mechanical impedance matching. The considerable length of the striker bar allowed for the generation of stress pulses of duration exceeding 1.1 ms and, therefore, the achievement of compressive strains substantially larger than those achievable by a conventional SHPB setup [47]. Both input and output bars were supported by low-friction polymeric circular bearings, positioned at a pitch of approximately 300 mm in order to avoid sagging, buckling and any undesired lateral movement.

A length of the projectile equal to the length of the input bar inevitably leads to the superimposition of incident and reflected elastic stress waves into the input bar at the gauge location. It was not therefore possible to distinguish the incident and the reflected waves directly from the strain measurements on the input bar. A data analysis procedure, based on the method of characteristics and D’Alambert’s solution of wave equations was employed to determine the magnitude of forward and backward travelling waves at the interfaces between bars and specimen as functions of time. Detail on the procedure can be found in [8].

Furthermore, the relatively slow stress wave propagation velocity of granular materials causes difficulty in the achievement of dynamic equilibrium conditions, in particular for granular materials characterised by intrinsic porosity. Satisfactory equilibrium conditions and approximately constant strain rates were obtained by reducing the specimen length. It is noted that this reduction is limited by the minimum representative volume element for the material [40]. The length of all specimens utilised in this study was 6.8 mm (Table 2). This length was determined a priori using the procedure illustrated in [40] ensuring the optimal distribution of the void ratio within the sample for the chosen sample diameter (20 mm). Additionally, all experiments presented in this manuscript were conducted by interposing 1 mm thick cardboard shims (436 g/m2) between the striker and the input bar, thus slightly lengthening the rise time of the loading pulse and reducing the transmitted Pochhammer-Chree oscillations [48].

Particle Analysis

The grain size distribution of the samples was evaluated using contrast edge detection techniques on binary images. Wet specimens were dried in in a Binder® FED series oven, at 50 °C for 500 h to remove any moisture. The Etnean sand grains, black in colour, were scattered onto a white surface with a calibration object. A representative number of images per sample (30) were taken using an AF MICRO NIKKOR 60 mm lens and a Nikon camera with an APS-C image sensor. A field of view of 27 mm × 17 mm was selected as an appropriate compromise between particle definition and quantity of grains in a single image.

The images were analysed using a bespoke MATLAB script. Within the script, the images were first subdivided into quarters to reduce the influence of any light gradient and then converted to greyscale and binary images by selecting an appropriate threshold. The area of individual particles was evaluated and the diameter of circular particles with equivalent area was calculated. The minimum particle size diameter that was possible to measure accurately was equal to 0.055 mm.

The morphology of the grains was described by means of the two parameters: aspect ratio and sphericity. The aspect ratio is herein the ratio of the minor axis length to the major axis length of the ellipse circumscribing the grain. The sphericity is calculated as the ratio between the perimeter of the equivalent circle and the perimeter of the grain. In both cases a result close to unity suggests that the particles of a sample are well rounded and spherical.

Experimental Results

Quasi Static Results

Previous studies [24] have indicated, for granular materials of different nature and morphology, that water content affects the quasi static response of partially saturated samples making it more compliant than the response of dry sand. A series of quasi static experiments were conducted on Etnean sand to assess the effect of water content on its response at low rates of strain.

Figure 5 shows that the stress strain response of loose (Fig. 5a) and dense (Fig. 5b) sand (Table 2) in quasi-static conditions has negligible dependence on water content. At low loading rates the liquid phase can flow through the grains without getting trapped. Lock up conditions [24] do not occur. There is sufficient time for the pore water to drain out of the specimen under the applied load, hence the behaviour of initially wet Etnean sand is reduced to that of dry specimens of the same initial void ratio. It is evident that the water content does not affect the quasi static response of wet samples. The mechanical response appears to be affected solely from the initial density of the samples.

Fig. 5
figure 5

Mechanical response of Etnean volcanic ashes at quasi static strain rate. Effect of water content on the behaviour of a loose samples and b dense samples

Full size image

High Strain Rate Results

This section presents the stress–strain relationships measured during high rate experiments on wet volcanic sand samples to assess the effect of water content on their dynamic response. Experiments conducted at each saturation level and initial density were repeated a number of times to evaluate the variability in the material behaviour (Table 2). All tests were conducted in near-uniaxial strain conditions, enclosing the specimens in a steel confinement (Fig. 3).

The validity of the measured stress–strain responses was verified by checking the achievement of dynamic equilibrium conditions during all SHPB tests. Figure 6 presents the time histories of the forces acting on the sample at its interfaces with input and output bars for a set of representative experiments. The same charts display the time history of the strain rate.

Fig. 6
figure 6

Dynamic equilibrium conditions during SHPB experiments on a 15% water saturated loose volcanic sand sample, b 65% water saturated dense volcanic sand sample and c 90% water saturated dense volcanic sand sample

Full size image

Figure 6a illustrates the achievement of dynamic equilibrium conditions for an experiment conducted on a loose sand sample of water saturation equal to 15%. Input and output forces approximately matched at a test time of 225 μs, corresponding to a compressive engineering strain in the region of 0.1. Figure 6b presents the test validity conditions for an experiment conducted on a wet dense sample of water saturation equal to 65%. The dynamic loads at the two sides of the specimen equalized at a test time of 75 μs, corresponding to a nominal compressive strain of about 0.04. Similarly, Fig. 6c illustrates the time histories of the input and output forces acting on a 90% water saturated dense sample. Dynamic equilibrium conditions were achieved at a time of 103 μs, when the specimen under consideration was compressed to an engineering strain of approximately 0.06.

The loading histories shown in Fig. 6 are representative of the wide range of water contents investigated in the present study. All experimental results reported in this section were measured during experiments in which dynamic equilibrium conditions were achieved during the early stages of deformation.

Figure 7 illustrates how water content and strain rate affected the compressive response of Etnean volcanic sand. Figure 7a provides a summary of the stress strain relationships measured during high rate experiments on dense samples characterised by four different water contents (\(S\) = 20%, \(S\) = 45%, \(S\) = 65% and \(S\) = 90%). The high rate response of the wet samples is compared to the responses measured on dry samples of equal initial void ratio at both quasi static and high rates of strain.

Fig. 7
figure 7

Effects of water saturation and strain rate on the mechanical response of a dense and b loose wet volcanic sand samples

Full size image

It is evident that dense Etnean sand does not display any significant rate dependence when tested in dry conditions, indicating that the rate sensitivity of the materials is not attributable to the particle breakage process, plausibly due to the small dimensions of the grains.

Wet Etnean sand in its dense state exhibits a more compliant response compared to its dry counterpart for water contents equal to \(S\) = 20% and \(S\) = 45% when tested at high strain rate. It is also observable that the maximum compressive strain measured during high rate experiments on 20% water saturated samples is larger than in dry conditions.

This effect, for relatively low values of water content, can be explained by the lubrication of inter-granular contacts and grains-confinement contacts induced by the presence of liquid. In these conditions it is reasonable to assume that water occupies only the contact areas between grains, reducing the friction while enabling the pore air to displace within the sample. A similar trend was observed in [24] on Quikrete #1961 dense sand samples characterized by different water content.

For higher degrees of saturation, the amount of water occupying the volume available between the grains increases. During high strain rate loading there is not sufficient time for the liquid phase to flow through the grains. Water is trapped between the particles. If the water content is such that the strains produced during high rate loading are enough to displace all the air voids, the dynamic compressive response becomes dominated by the response of the nearly incompressible water. Lock up conditions occur and the mechanical response of wet sand exhibits an abrupt increase in stiffness [7, 23, 49].

Lock up behaviour was observed on dense Etnean sand samples of degree of saturation \(S\) equal to 65% and 90% at strains in the region of 0.17 and 0.1 respectively, and was already noticeable, for strains larger than approximately 0.3, on specimens of degree of saturation equal to 45% (Fig. 7a). It is evident that the dominance of the liquid phase on the mechanical response takes place at smaller strains for higher water contents. This is explained by the fact that for a larger saturation \(S\), the volume occupied by air voids is smaller, hence a smaller compressive strain is needed to displace the gaseous phase [27].

Figure 7b illustrates the dynamic behaviour of loose wet Etnean sand. The high rate response of loose wet samples is compared to the responses measured on dry samples of equal initial void ratio at both quasi static and high rates of strain.

It is clear that loose volcanic sand from Mount Etna exhibits a noticeable strain rate sensitivity when tested in dry conditions, indicating that the rate dependency of the material is mainly associated with particle sliding and grains rearrangement within the sample volume.

It can also be observed that the dynamic response of 15% saturated loose volcanic sand is more compliant than its dry counterpart tested at high strain rate. This is believed to be due to the intergranular lubrication induced by the presence of water between the contact areas. Conversely, samples of degree of saturation \(S\) = 65% exhibited lock up behaviour starting at strains in the region of 0.27. Nearly fully saturated specimens (\(S\) = 95–100%) presented a very stiff response dominated by the response of water, with lock up occurring during the early phase of loading, at compressive strains of approximately 0.03. A qualitatively similar trend was observed in [26] on loose quartz sand samples characterised by different moisture content.

It is noted that the reduction in stiffness induced by intergranular lubrication at low moisture contents is observed during dynamic experiments but not during quasi static loading. This can be explained by the different deformation mechanisms dominating at the two deformation rates. At quasi static strain rate the complex shaped volcanic particles have sufficient time to rearrange, increasing the number of contacts and locking in a new in a denser configuration. At high strain rate the particles do not have time to rearrange and deformation occurs mainly via sliding and rolling. The lubrication of particle-to-particle contacts induced by the presence of water promotes intergranular slippage and a more compliant response of the samples.

It is worth mentioning that it is not possible to compare directly the stress strain relationships obtained on loose and dense samples of same degree of saturation. Different samples can be compared using the parameter \(S\) only if they are characterised by similar void ratios. This is because a greater volume of water is required to obtain the same degree of saturation in loose relative to dense specimens (Table 2).

Particle Analysis

This section outlines the effects of compaction, loading rate and water content on particle size distribution and morphology of the sand under investigation. A summary of mean particle diameter, aspect ratio and sphericity for different specimens and loading rates is given in Table 3.

Table 3 Summary of particle analysis results
Full size table

It is evident that volcanic particles comminute noticeably during compression, regardless of the initial compaction and water content. It is also clear, as indicated by the mean values of aspect ratio and sphericity in Table 3, that tested samples comprise of particles significantly more rounded and spherical compared to their raw counterpart. This suggests that the deformation and breakage are accompanied by extensive chipping and abrasion of the several irregularities present in Etnean sand grains. The micrographs in Fig. 8, where grains appear more rounded and with smoother surface in comparison to the raw grains in Fig. 2, confirm this hypothesis. Table 3 also suggest that particle breakage may be a rate dependent process [7] as the average particles diameters increase with increasing strain rate.

Fig. 8
figure 8

ESEM micrographs illustrating the dimensions and morphology of Etnean sand grains after mechanical testing: a grains of fully saturated dense sample after quasi static compression b grains of 45% water saturated dense sample after compression at high strain rate, c grains of 65% water saturated loose sample after compression at high strain rate

Full size image

Figure 9 provides a more detailed comparison between the grain size distribution of dry, loose and dense samples tested at high strain rate. The cumulative distribution shows that, although the average particle diameter is similar in the two cases, the scatter in the distribution of grain sizes is more pronounced in the case of loose sand, with a larger number of smaller particles in the region between 0.1 and 0.3 mm. This can be explained by the fact that there are fewer intergranular contacts in loose samples. This causes greater internal stresses at the contact areas, hence promoting particle chipping and breakage [7]. It is reasonable to assume that the failure mechanism is different during quasi static loading as the grains have time to rearrange into the voids during compression.

Fig. 9
figure 9

Comparison between the grain size distributions of dry loose and dry dense volcanic sand samples after Split Hopkinson Pressure Bar experiments. The distribution of the raw volcanic sand utilised is also reported for comparison

Full size image

Figure 10 illustrates the effect of water content on the grains size distribution. It is visible that water content reduces particle breakage during quasi static compression of dense samples (Fig. 10a), presumptively due to the reduction in intergranular friction induced by the liquid phase. This effect is less evident during quasi static compression of loose samples (Fig. 10b).

Fig. 10
figure 10

Effect of water content on the particle size distribution of volcanic sand samples tested at quasi static (a, b) and high strain rate (c, d). The distribution of the raw volcanic sand utilised is reported in all charts for comparison

Full size image

Water content appears to have no effect on the particle distribution of dense samples compressed at high strain rate (Fig. 10c) whereas it is not possible to identify an univocal trend for loose samples (Fig. 10d). This is believed to be the result of two competing actions: while the liquid phase reduces intergranular friction, high levels of water content cause lock up to take place. The higher the water content the lower the strain at which lock up occur and, hence, the more the time for particles to comminute under the larger stresses.

The distributions obtained at high strain rate on volcanic sand appear to identify a different trend when compared to granular materials of different morphology and mineralogy. Previous studies on quartz and Eglin dense samples [26, 49] have indicated a slight increase in particle breakage for low water content, due to the higher strains achieved [26], and a reduction of particle breakage for higher water content, due to the increase in pore pressure and consequent reduction of particle-to-particle contact [26, 49].

Table 4 summarises the particle size distribution parameters (Table 1) of the distributions reported in Figs. 1, 9 and 10.

Table 4 Summary of particle distributions parameters
Full size table

Conclusions

An experimental campaign was undertaken in order to characterise the effect of water content on the high strain rate mechanical response of wet volcanic sand from Mount Etna. The dynamic compressive response of the granular material was assessed on samples characterised by different initial compaction and water saturation. The specimens were loaded in near-uniaxial strain conditions enclosing them in a steel confinement of appropriate thickness. Additional quasi static experiments were conducted to verify that the presence of water has negligible effect on the mechanical behaviour at low strain rate.

No similar set of data had been previously published, mainly due to the difficulties associated with the dynamic experiments, which were overcome by using a bespoke Long Split Hopkinson Pressure Bar setup, by relying on load pulse shaping techniques and a priori determination of specimen dimensions by means of numerical analysis of the representative volume element.

The grain size distribution and morphology of raw and compressed samples was analysed by means of contrast edge detection techniques to evaluate the effects of initial compaction, strain rate and water content on particles fragmentation.

The main conclusions of this study are:

  • Dense Etnean sand does not display any significant rate dependence when tested in dry conditions, indicating that the rate sensitivity of the materials is not attributable to the particle breakage process, plausibly due to the small dimensions of the grains.

  • Loose volcanic sand from Mount Etna exhibits a noticeable strain rate sensitivity when tested in dry conditions, indicating that the rate dependency of the material is mainly associated with particle sliding and grains rearrangement within the sample volume.

  • The high strain rate mechanical response of wet volcanic sand from Mount Etna is more compliant than its dry counterpart for limited amounts of water content. Specifically both wet dense and wet loose samples display a softer response than in dry conditions for saturation degrees \(S\) = 20% and \(S\) = 15% respectively. This is believed to be due to the intergranular lubrication induced by the presence of water between the particles contact areas.

  • The dynamic response of wet volcanic sand samples of high water content exhibit a steep increase in stiffness when the compressive strains produced during loading are sufficient to displace all air in the specimen and the mechanical behaviour is dominated by the response of the water. This behaviour was observed on both dense and loose samples of water saturation higher than 65% and was already visible on dense specimens of degree of saturation equal to 45%.

  • Particle analysis and micrographs of the tested samples show that during compression, deformation and breakage are accompanied by extensive chipping and abrasion of the several irregularities present in Etnean sand grains.

  • Grain size distributions show that the presence of water reduces particle fragmentation during quasi static compression of dense samples. This effect is less evident for quasi static compression of loose samples. The grain size distributions of specimens tested at high strain rate show that water content has no effect on the particle distribution of dense samples while it is not possible to identify a univocal trend for loose samples.