Numerical Simulation of Dynamic Tensile Extrusion Test of OFHC Copper

Abstract

The dynamic tensile extrusion (DTE) test offers unique possibility to probe material response under very large plastic strain, high strain rate and temperature to support constitutive modelling development. From the computational point of view, the DTE test is particularly challenging and a number of issues need to be assessed before proceeding with material modelling verification. In this work, an extensive and detailed computational work was carried out in order to provide the guidelines for accurate simulation of DTE test. Two constitutive models, the first phenomenological the latter physically-based, were used to simulated the behavior of fully annealed OFHC copper in dynamic extrusion at different velocities. Material models parameters were calibrated using uniaxial test data at different strain rates and temperatures. The number, size and shape of the ejected fragments at different velocity were used as validation metrics for the selected constitutive models. Results indicate that material behavior under dynamic extrusion can be accurately predicted limiting the influence of numerical parameters not related to the constitutive model under investigation. The physically based modelling allows a more accurate prediction of the material response and the possibility to incorporate microstructure evolution processes, such as dynamic recrystallization, which seems to control the response of OFHC copper in DTE tests at higher velocity.

Introduction

In a number of industrial applications, materials are requested to perform at extreme operating conditions involving large plastic deformation, high strain rates, elevated temperature and severe dynamic pressure. In defense engineering applications, such as armor and anti-armor technology, materials subjected to high velocity impact experience deformations in excess of 500 %, strain rates up to 10⁶/s, temperature up to melting temperature, and pressure of the order of several GPa [1]. Similarly, in more traditional field of applications, such as hot metal working (i.e. forging, rolling, extrusion, wire drawing and sheet metal forming), metals and alloys undergo considerably large plastic deformation (10–100 %) at elevated temperature (500–800 °C) with moderate to high strain rate (1.0–100/s) and pressure varying from few MPa up to several hundreds of MPa [2]. Other engineering fields of applications are aerospace engineering (debris and foreign object impact), oil and gas industry (chemical reactor, pipeline, pressure valve and perforating gun design) [3], naval engineering (ship collision), safe and handling of energetic materials (protection against blast), etc. [4].

Under such operating conditions, the material is also subjected to significant modification at the microstructure level with direct consequence on the response measured at the continuum scale. Understanding the mechanisms governing the deformation process and response under such extreme conditions is fundamental for the development of material modelling and for the improvement of design assessment routes [5].

In general, it is impossible to characterize material response under arbitrary combinations of plastic deformation, strain rate, temperature and pressure levels. Traditional testing techniques (such as traction and compression tests) allows for investigating material response under limited ranges of such controlling variables Extreme conditions, such as those mentioned above, are often obtained with dynamic transient loading in which plastic strain, strain rate, temperature and pressure varies with time making extremely difficult to separate mutual effects [6, 7].

An alternative approach consists in probing the material response using both characterization and “validation” tests [8]. These latter ones are tests in which the material is subjected to deformation, strain rate, temperature, and pressure similar to those expected in the applications but without the possibility to control their evolution path. In these type of tests, most of the information about the material response are obtained post mortem and used in a reverse engineering process as objective functions to validate the selected constitutive model and to identify its material characteristic parameters. In this perspective, numerical simulation becomes a fundamental tool to probe material response under such extreme conditions.

In high strain rate processes, examples of validation tests are the Taylor anvil impact and the symmetric Taylor, or rod on rod, impact test [9]. In such types of test, a cylinder, made of the material of interest, is subjected to an impact at prescribed velocity. Different quantities (such as the deformed shape, the length of the elastic region, the final length/diameter/bulge diameter, time resolved velocity profile of the rear section, etc.) can be used as metric of validation for computational analysis [10].

Los Alamos National Lab (LANL) introduced the dynamic tensile extrusion test (DTE) [11]. In such test, a projectile made of the material of interest is launched into a conical die with an exit opening smaller than the projectile diameter. During the travel into the die, the material deforms subjected to pressure and shear waves. If the impact velocity is high enough, the material is dynamically extruded producing a material jet travelling up to two times faster than the initial speed. During the dynamic extrusion, the material is subjected to very large deformation and high strain rate (10⁵–10⁶/s). The deformation process is quasi adiabatic and the heat generated by the plastic work increases considerably the temperature, which softens the material and promotes further plastic strain accumulation, microstructure transformation and damage development. Because of the velocity difference between the tip and the tail, the jet of extruded material is subjected to stretching and fragments similarly to a shaped charge jet [12].

A procedure for modelling assessment, based on validation tests, requires an extensive use of numerical simulation, which has to be qualified in order to limit the uncertainty and variability in the results due to computational aspects and to put in evidence on the role and performances of the selected constitutive model [13].

Numerical simulation of validation tests, such as Taylor impact or DTE, is particularly challenging because, beside the material model, it involves a number of computational features (contact between deformable bodies, coupled thermo-mechanical analysis, thermal softening, friction, etc.) which strongly affect the results [14, 15].

In this work, an extensive computational analysis work was performed to evaluate the modelling performance of two material models under very large strain-high strain rate conditions and to provide general guidelines for robust numerical simulation of DTE test.

Material and Experimental Testing

Material

The oxygen-free high conductivity (OFHC) copper was obtained in the form of half-hardened (H02) bars. The material commercial purity was 99.98 %, although quantitative chemical analysis revealed a purity of at least 99.99 %. After machining of DTE test samples, the material was annealed for 30 min at 400 °C in an inert Argon atmosphere and allowed to cool in the oven after it was turned off. The microstructure was characterized by electron backscatter diffraction (EBSD) after final electrochemical polishing. Figure 1a shows an inverse pole figure (IPF) map of the extrusion direction in the initial microstructure. The IPF in Fig. 1b indicates a random starting texture. The grain size, based on linear intercept method, was estimated to 14 μm, if the twin boundaries (which make up close to 70 % of the boundaries in the annealed state) were included. Neglecting twin boundaries results in a grain size of 47 μm.

Fig. 1

a Inverse pole figure map and b pole figures for the annealed material. The inverse pole figure map shows orientations aligned with the DTE extrusion direction, which is horizontal in the figure. The pole figures show a random initial texture

Material Characterization

The material was fully characterized at low and high strain rates. Quasi static traction tests at the nominal strain rate of 5.0 × 10⁻³/s were performed for the identification of the material flow curve. Dynamic traction experiments were performed across a range of strain rates from 10⁻³ to 10⁴/s, at room temperature. These tests were conducted using the direct tension split Hopkinson pressure bar (SHPB) [16–18] located at the University of Cassino and Southern Lazio which is comprised of a 3.50 m long input bar, 2.50 m output bar, 14 mm diameter 7075-T6 aluminum alloy (Ergal). The tensile impulse is obtained pre-straining a portion (1.0 m) of the input bar by means of a rigid clamp which is released by fracture of a brittle joint. This configuration allows accurate full control of the stress pulse intensity and shape and high repeatability as well as visual access to the sample during the test.

DTE Testing

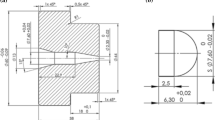
DTE test was implemented and performed with the single stage light gas-gun facility at the University of Cassino and Southern Lazio. The gun is 3.50 m long with a 7.62 mm bore operating with 300 bar reservoir maximum pressure. The gun is fired bursting a Mylar^® rupture disk by means of a thermo-resistance. This solution allows full control on the firing pressure increasing testing repeatability. In the DTE test initially introduced by Gray III et al. [11], the projectile shape was a sphere. In this study, a bullet shape sample geometry, as proposed by Iannitti et al. [19], was used. This geometry is easier to be machined and allows, verifying ex-post that the rear section of the fragment in the die remains perpendicular to the symmetry axis, the correct alignment of the projectile at the impact. Similar geometry was also used to perform DTE test on zirconium by Escobedo et al. [20]. The dimension of the DTE test sample are shown in Fig. 2. In particular, the projectile was designed to have same mass and diameter of the spherical bullet used in [11]. The geometry of the hollow die is the same used in Gray III et al. [11]. The nominal dimensions are given in Fig. 3. Quality control revealed that the entrance diameter was 7.55 mm instead of the nominal 7.60 ± 0.02 mm. This causes a pre-compression of the projectile before entering in the hollow die where extrusion will occur. The height of die block is almost twice longer than that used in [11] and this may have an effect on the dynamics of the stress waves generated at the impact, travelling in the die and reflecting back at the free surfaces. In order to avoid propelling gas overpressure after the impact of the sample and during its extrusion, a recoil compensator, located before the hollow die at the end of the gun, was used. All samples were launched using a cork sabot, which minimizes pressure losses. Tests were performed in vacuum and extruded fragments were soft recovered with a ballistic gel block. The sample extrusion was recorded using high-speed video camera at 70,000 frames per second providing a mean to estimate the muzzle velocity and to obtain time resolved shape of the jet to be used for later comparisons.

Fig. 2

DTE bullet: dimensions in mm and 3D sketch

Fig. 3

DTE die dimensions in mm

A series of DTE tests were performed at 350, 380, 400 and 420 m/s respectively. In each test, the overall number of fragments and their size were measured. The test at 400 m/s was used to compare with test results reported by Gray III et al. [11] on same material grade with different grain sizes (65, 118, and 185 μm). In particular, for this test, a detailed microscopy investigation of microstructure and texture evolution in the fragment that remain in the die was performed [21]. Results indicates that, because of large plastic deformation and temperature rise due to quasi-adiabatic condition, dynamic recrystallization (DRX) can occur. As discussed later in the paper, the occurrence of DRX would have a considerable effect on the extruded jet elongation since it permits abnormally rapid local stress-relief that suppress void nucleation and growth mechanism [22] allowing large reduction of area and consequently an increase in the overall ductility. In the following, the result of the DTE test performed at 400 m/s will be used as a reference case for model validation and material parameters calibration.

Material Modelling

As mentioned, in the DTE test the material is subjected to complex stress–strain histories involving large plastic deformation, very high strain rate, elevated temperature and relevant dynamic compression. These conditions are particularly challenging from the modeling and numerical simulation point of view. Therefore, the DTE test results can be used to validate the effective capability of a selected constitutive model to predict the material response under such extreme conditions.

At continuum scale, constitutive formulations proposed over the years may be divided into two main groups: phenomenological constitutive relationships and physical-based constitutive models. The first provides a definition of the material flow stress based on empirical observations. These models consist of mathematical expressions—in general not supported by any physical background—that fit experimental observations. A general characteristic of phenomenological models is the reduced number of material constants and their relatively easy identification. Examples of such model can be found in [23–25]. Because of their empirical nature, their use if often restricted to applications with limited ranges of strain rate and temperature. In addition, they exhibit limited flexibility and lack of transferability from one material to another. Physical-based constitutive relations are derived accounting for deformation mechanisms and related effects. Some examples can be found in [26–29]. With respect to phenomenological models, these models require a larger number of material constants and their identification procedure follows physical assumptions. In contrast, they allow for an accurate definition of material behaviors under wide ranges of loading conditions.

In this work, a phenomenological and a physical-based model were selected to investigate the possibility to reproduce OFHC copper extruded jet in DTE test at different velocity. The first is the Johnson–Cook model [25] and the latter is the Rusinek–Klepaczko [30, 31] model. Both model formulations were modified to account for several features and improvements as discussed below.

Modified Johnson–Cook (MJC) Model

The Johnson–Cook (JC) original model gives the following relation for the flow stress,

$$ \sigma_{\text{y}} \left( {\varepsilon_{\text{p}} ,\dot{\upvarepsilon }_{\text{p}} ,{\text{T}}} \right) = \left( {A + B\varepsilon_{\text{p}}^{n} } \right)\left( {1 + C\ln \dot{\upvarepsilon }_{\text{p}}^{*} } \right)\left( {1-{\text{T}}^{*m} } \right) $$

(1)

where ɛ _p is the plastic strain, $\dot{\upvarepsilon }_{\text{p}}$ is the plastic strain rate, and A, B, C, n, m are material constants. The normalized strain rate and temperature are defined as,

$$ \dot{\upvarepsilon }_{\text{p}}^{*} = \dot{\upvarepsilon }_{\text{p}} /\dot{\upvarepsilon }_{\text{p0}} $$

(2)

$$ {\text{T}}^{*} = \frac{{{\text{T}}-{\text{T}}_{ 0} }}{{{\text{T}}_{\text{m}} -{\text{T}}_{ 0} }} $$

(3)

where $\dot{\upvarepsilon }_{\text{p0}}$ is a user defined plastic strain-rate (usually taken equal to 1.0/s), T₀ is the reference temperature and T_m is the melting temperature. For the condition where T^* < 0, m = 1 is assumed. The first bracketed term on the right hand side represents the reference material flow curve at T = T₀ and for $\dot{\upvarepsilon }_{\text{p}} = \dot{\upvarepsilon }_{\text{p0}}$, the second and third terms account for the strain rate and temperature effect respectively.

The JC model describes fairly well strain rate and temperature effects on the material yield stress, at least in the thermally activated deformation regime where a linear dependence of the flow stress on the $\log \dot{\upvarepsilon }_{\text{p}}$ is observed. However, it suffers the following major limitations: (a) the strain rate effect, as formulated, predicts an increase of the work-hardening rate (∂σ/∂ɛ_p) at fixed strain, which is not observed in all materials although it is true for copper [32]; (b) the assumption of a power law expression for the material flow curve is unphysical since the stress has to reach a limiting value at very large strain; (c) at very high strain rate the model does not account for the further increase of the flow stress due to viscous drag.

In this work, the original JC expression was modified to account for the latter two considerations. In particular, the power law term was replaced with a Voce type law. Hereafter, this modified model formulation is indicated as MJC model. This is particularly relevant for annealed copper since the flow curve at large strain cannot be fitted accurately with a simple power law. The strain rate effect was reformulated introducing a linear term dominating in the viscous drag regime,

$$ \sigma_{\text{y}} \left( {\varepsilon_{\text{p}} ,\dot{\upvarepsilon }_{\text{p}} ,{\text{T}}} \right) = \left[ {\sigma_{\text{y0}} + \sum\limits_{\text{i}}^{\text{n}} {R_{\text{i}} } \left( {1-\exp (-\varepsilon_{\text{p}} /b_{\text{i}} )} \right)} \right]\left( {1 + D_{1} \ln \dot{\upvarepsilon }_{\text{p}}^{*} + D_{2} \dot{\upvarepsilon }_{\text{p}}^{*} } \right)\left( {1-{\text{T}}^{*m} } \right) $$

(4)

where σ_y0 is the reference yield stress, n is the total number of saturating terms (n = 1 reduces to the typical Voce law), R _i, b _i D ₁ and D ₂ are material constants.

Modified Rusinek–Klepaczko Model (MRK2)

Rusinek et al. [30] modified the original model formulation proposed in [31] for face-centered cubic (FCC) metals. In such model, the Huber–Mises stress is assumed as the sum of three terms accounting for different deformation mechanisms:

$$ \bar{\sigma } = \frac{\text{E(T)}}{{{\text{E}}_{0} }}\left[ {\bar{\sigma }_{\text{ath}} + \bar{\sigma }_{\text{th}} } \right] + \bar{\sigma }_{\text{vd}} $$

(5)

Here, E(T)/E₀ defines the elasticity modulus dependence on temperature and it is defined as,

$$ \frac{\text{E(T)}}{{{\text{E}}_{0} }} = 1-\frac{\text{T}}{{{\text{T}}_{\text{m}} }}\exp \left[ {\uptheta^{*} \left( {1-\frac{{{\text{T}}_{\text{m}} }}{\text{T}}} \right)} \right]T > 0 $$

(6)

where E₀ is the elasticity modulus at 0 K, T_m is the melting temperature in K, and θ* is the characteristic homologous temperature that for FCC metals is ~0.9.

In this work, a series of modifications to the model version given in [30] have been introduced and hereafter, the current version of the model has been indicated as MRK2.

In Eq. (5), $\bar{\sigma }_{\text{ath}}$ is the athermal stress component independent on the plastic strain [28, 33]. In agreement with [34], $\bar{\sigma }_{\text{ath}}$ is related to the flow stress Y of the undeformed material and does not describe the strain hardening. However, the flow stress depends on the material grain size which can be accounted for by the Hall–Petch effect,

$$ \bar{\sigma }_{\text{ath}} = Y + \frac{\text{k}}{{\sqrt {{\text{d}}_{ 0} } }} $$

(7)

where k is a constant and d₀ is the reference grain size.

$\bar{\upsigma }_{\text{ath}}$ is the flow stress component defining rate-dependent interactions with short-range obstacles. It represents the rate-controlling deformation mechanism from thermal activation. At temperatures greater than 0 K, thermal activation assists the applied stress. It reduces the stress level required to force dislocations past obstacles [30]. Based on the theory of the thermodynamics and kinetics of slip [35], Rusinek and Klepaczko [31] proposed the following expression,

$$ \bar{\upsigma }_{\text{th}} = \upsigma_{0}^{*} \left\langle 1-\xi_{1} \left( {\frac{\text{T}}{{{\text{T}}_{\text{m}} }}} \right)\log \left( {\frac{{\dot{\upvarepsilon }_{\hbox{max} } }}{{\dot{\upvarepsilon }_{\text{p}} }}} \right)\right\rangle^{{1/\xi_{2} }} $$

(8)

where ξ₁ and ξ₂ are material constants defining the temperature and rate sensitivities of the material, respectively. $\dot{\upvarepsilon }_{\hbox{max} }$ is the maximum strain rate at which the strain rate effect becomes zero [35, 36]. In FCC metals, the thermal activation processes show strain dependence. Zerilli and Armstrong [27] and Voyiadjis and Abed [33] proposed, for the thermal activated stress, a power law expression function of the plastic strain. Rusinek et al. [30] modified the power law expression introducing a temperature and strain rate dependence. However, the term σ ^*₀ accounts for the strain hardening at 0 K, and should be temperature and strain rate independent since it represents the athermal material hardening. In this work, following the same considerations discussed above, a Voce type law was used to describe material hardening at 0 K,

$$ \sigma_{0}^{*} = {\bar{\text{R}}}_{ 0} \left[ {1-\exp \left( {-\varepsilon_{\text{p}} /\varepsilon_{\text{p}}^{0} } \right)} \right] $$

(9)

where ${\bar{\text{R}}}_{ 0}$ and ɛ ⁰_p are material parameters assumed independent of strain, strain rate and temperature.

At very high strain rates or dislocation velocities, a viscous drag is known to exist on the glide dislocations [37]. At low temperature, this viscous drag is mainly due to electron damping while at high temperature it is dominated by phonon damping, phonon scattering, forest dislocations and solute atoms. Kumar and Kumble [38] proposed a simple law for the viscous drag stress,

$$ \upsigma_{\text{vd}} = \upalpha \frac{B}{{\uprho_{\text{m}} b^{2} }}\dot{\upvarepsilon }_{\text{p}} $$

(10)

where B is the drag coefficient, ρ_m is the mobile dislocation density, and b is the magnitude of the Burgers vector and α is a constant. As the dislocation velocity approaches that of sound, the stress required to move it increases more rapidly. This is in part caused by the relativistic constraint of the strain field, which causes the elastic energy to rise steeply, imposing a limiting velocity on the moving dislocation. There is evidence [37] that also mobile dislocation density rises towards a limiting value, so that an upper limiting strain-rate, and therefore a limit to viscous drag, exists. Nemat-Nasser et al. [39] proposed an exponential function for the viscous drag that saturates at very large strain rate. In this work, a Weibull distribution function was used to describe the viscous drag evolution as a function of the strain rate,

$$ \upsigma_{\text{vd}} = \chi_{\lim } \left[ {1-\exp \left( {-\dot{\upvarepsilon }_{\text{p}} /\dot{\upvarepsilon }_{\lim } } \right)^{v} } \right] $$

(11)

here, χ_lim, $\dot{\upvarepsilon }_{\lim}$ and ν are material parameters. The parameter χ_lim represents the limiting stress. Kocks et al. [35] estimated this value to be of the order of,

$$ \upchi_{\lim } \sim \frac{\text{G}}{200} $$

(12)

where G is the shear modulus. Although drag mechanisms are not thermally activated, this expression implies an indirect temperature dependence of the limiting stress as a consequence of the temperature dependence of the shear modulus. Therefore, Eq. (11) was reformulated as follows,

$$ \upsigma_{\text{vd}} = \chi_{\lim }^{0} \Bigg\{ {1-\frac{\text{T}}{{{\text{T}}_{\text{m}} }}\exp \left[ {\theta^{*} \left( {1-\frac{{{\text{T}}_{\text{m}} }}{\text{T}}} \right)} \right]} \Bigg\}\left[ {1-\exp \left( {-\dot{\upvarepsilon }_{\text{p}} /\dot{\upvarepsilon }_{\lim } } \right)^{v} } \right] $$

(13)

where $\chi_{\lim }^{0}$ is the limiting stress at 0 K. Here, the same temperature variation for the shear modulus, as given in Eq. (6), was assumed.

In model applications, most of the time, the material melting temperature is assumed constant. However, this parameter is influenced by pressure and since pressure can be significantly high in DTE test, it should be considered in the simulation process. Several authors investigated the pressure effect on melting temperature of copper by means of dedicated experiments and simulation. Gonikberg et al. [40] were the first to report melting temperatures of copper up to 1.7 GPa using differential thermal analysis (DTA). Later Cohen et al. [41] used DTA to determine the melting point up to 4 GPa. Mitra et al. [42] extended the pressure range up to 6 GPa while, more recently, Japel et al. [43] reported laser heated diamond anvil cell measurement from 17 to 97 GPa showing a reasonable agreement with ab initio simulated curves calculated by Vočadlo et al. [44]. More recently, Brand et al. [45] measured the melting curve of copper up to 16 GPa using a multi-anvil press which provided better accuracy with respect to DTA, fitting the data with following second order polynomial,

$$ {\text{T}}_{\text{m}} - 1355( \pm 5) + 44.3( \pm 31){\text{P}} - 0.61( \pm 21){\text{P}}^{2} $$

(14)

where the temperature is in Kelvin and the pressure in GPa. Hieu and Ha [46], based on the Lindemann’s formula of melting and the pressure-dependent Grüneisen parameter, derived the following expression for the melting temperature as a function of pressure,

$$ {\text{T}}_{\text{m}} = {\text{T}}_{0} \left( {\frac{\text{V}}{{{\text{V}}_{0} }}} \right)\exp \Bigg\{ {\frac{{2\gamma_{0} }}{\text{q}}\left[ {1-\left( {\frac{\text{V}}{{{\text{V}}_{0} }}} \right)^{\text{q}} } \right]} \Bigg\} $$

(15)

where T₀ is the reference melting temperature at 0 pressure, γ₀ and q are material parameters. Therefore, using an equation of state (EOS), an explicit expression for pressure dependence of T_m can then be obtained. Here, recalling Murnaghan EOS we can write,

$$ {\text{P(V) = }}\frac{{{\text{K}}_{0} }}{{{\text{K}}^{\prime}_{0} }}\left[ {\left( {\frac{\text{V}}{{{\text{V}}_{0} }}} \right)^{{-{\text{K}}^{\prime}_{0} }} -1} \right] $$

(16)

where K ₀ and $K^{\prime}_{0}$ are the isothermal bulk modulus and its pressure derivative at ambient pressure. Substituting Eq. (16) in Eq. (15) we finally get,

$$ {\text{T}}_{\text{m}} = {\text{T}}_{0} \left[ {1 + {\text{P}}\frac{{{\text{K}}^{\prime}_{0} }}{{{\text{K}}_{0} }}} \right]^{{-\frac{2}{{3{\text{K}}^{\prime}_{0} }}}} \exp \left\{ {\frac{{2\upgamma_{0} }}{\text{q}}\left[ {1-\left( {1 + {\text{P}}\frac{{{\text{K}}^{\prime}_{0} }}{{{\text{K}}_{0} }}} \right)^{{-\frac{\text{q}}{{{\text{K}}^{\prime}_{0} }}}} } \right]} \right\} $$

(17)

This expression was found to describe well the pressure effect on the melting temperature of copper. In this work, T₀, K ₀ and $K^{\prime}_{0}$ were taken from reported data [46], while γ₀ and q where fitted using the experimental data provided in [45] and [43] over a pressure range up to 100 GPa with different experimental techniques. The comparison of the fitted curve with experimental data is given in Fig. 4.

Fig. 4

Comparison of experimental data and Hieu and Ha model integrated with Murnaghan EOS for melting temperature function of pressure in copper

Model Parameters Identification

Both selected material models require the determination of a number of material parameters. These have been identified using data coming from different sources and characterization tests. For the MJC model, the Voce type law parameters were determined by means of a FEM based inverse calibration procedure having as objective function the applied load versus elongation response measured in tensile test at RT for a reference strain rate of 5.0 E–03 s [47]. This procedure ensures the determination of the “true” material flow curve for plastic deformation up-to and beyond the necking. For annealed OFHC copper, a two-term Voce type equation was found to fit well experimental data,

$$ \upsigma_{\text{y}} (\upvarepsilon_{\text{p}} ) = \left[ {\upsigma_{\text{y0}} + R_{1} \left( {1-\exp (-\upvarepsilon_{\text{p}} /b_{1} )} \right) + R_{2} \left( {1-\exp (-\upvarepsilon_{\text{p}} /b_{2} )} \right)} \right] $$

(18)

In Fig. 5a, the comparison between the measured and calculated applied load vs elongation response after calibration, is shown. Here, the predicted response that would be obtained using a simple power law, calibrated using experimental data up to the occurrence of necking, is also reported. Then, in Fig. 5b, the calibrated flow curve is shown and compared with the power law fit.

Fig. 5

MJC model parameters identification. Identification of the flow curve: a comparison of the calculated and measured applied load versus elongation response in smooth uniaxial bar in tension; b estimated flow curve at RT and $\dot{\upvarepsilon }$ = 5.0 E–03 s

Strain rate sensitivity parameters D₁ and D₂ were determined fitting the flow stress, at 0.15 plastic strain, as a function of the $\log \dot{\upvarepsilon }_{\text{p}}$ using the data reported by Follansbee et al. [48] as shown in Fig. 6. Finally, the temperature sensitivity parameter m was taken from [25].

Fig. 6

MJC model parameters identification. Identification of the strain rate sensitivity parameters

Model predictive capability at different strain rates, Fig. 7, and temperature, Fig. 8, was verified comparing the predicted flow curve with available experimental data coming from different sources [32, 36, 49]. In both case, the MJC solution seems to be in a general good agreement with experimental data. Data at high strain rate are usually obtained SHPB were the material is tested in compression while the hardening curve in the MJC model is identified using tensile test data. The MRK2 model requires the determination of several parameters. The grain size effect on the athermal component of stress was determined fitting available experimental data with Hall–Petch relationship.

$$ \upsigma_{\text{y}} = \upsigma^{\prime}\left( {\upvarepsilon_{\text{p}} } \right) + \upsigma ({\text{d}}_{0} ) $$

(19)

where the first right hand-side term is only function of the plastic deformation level, for a reference temperature and strain rate, and the latter is only function of the grain size d ₀. Hansen and Ralph [50] measured the variation of the yield stress, as a function of the grain size, for different values of the plastic strain finding a general confirmation of the Hall–Petch relationship with a grain size exponent equal to −½. By data manipulation, they identified the theoretical flow curve for a single crystal (${\text{d}}_{0} \to \infty$, no grain size effect), σ′(ɛ_p) which can be used to scale experimental data, relative to a specific level of plastic strain, at the condition of nominal yield stress (ɛ_y = σ_y/E). These data were consistent with the data reported in [47] and with that presented in this work. By fitting, we found: k = 5.78 MPa (mm)^{^0.5} and σ′(ɛ_y) = 14.89 MPa. In Fig. 9, the comparison between the experimental data and the proposed fit is given. To be noted that, current fit is very close to that proposed in [50].

Fig. 7

MJC model parameters verification: comparison of true stress versus true strain curve at different strain rates at RT

Fig. 8

MJC model parameters verification: comparison of true stress versus true strain curve at different temperature for the reference strain rate 4000 and 2000/s

Fig. 9

Grain size effect (Hall–Petch) for OFHC copper

For what concerns the thermally activated part of the yield stress, Eq. (8), σ ^*₀ can be determined in accordance to the procedure given in [30], fitting the stress values as function of temperature, at fixed strain levels, and extrapolating to 0 K. Here, the data reported in [30] were fitted using Eq. (9). In Fig. 10, the comparison of the proposed fit with the power-law interpolation given in [30], is also shown. Other parameters in Eq. (8) were taken as given in [30]. It is interesting to note that, the flow curve at 0 K determined in this work, if scaled by the grain size effect, is found to be in a very good agreement with the σ′(ɛ_y) data reported by Hansen and Ralph [50] for copper at T = 80 K, as shown in Fig. 11. As for the MJC model, in Figs. 12 and 13, the comparison with the experimental data of the flow curves predicted with MRK2 model, at different strain rates and temperature, is shown. Finally, the parameters for viscous drag term, Eq. (11), were calibrated fitting the flow stress, at ~0.15 plastic strain, as a function of the $\log \dot{\upvarepsilon }_{\text{p}}$ using the data reported by Follansbee et al. [48] and verified comparing with flow stress data at high rates for ~0.10 of plastic deformation, at 290, 450 and 600 K [51] respectively, as shown in Fig. 14.

Fig. 10

Flow curve at 0 K for OFHC copper

Fig. 11

Comparison of MRK2 model parameters identification. Identification of the viscous drag term parameters. Comparison of flow stress prediction as a function of strain rate at different temperatures

Fig. 12

MRK2 model parameters verification: comparison of true stress versus true strain curve at different strain rates at RT

Fig. 13

MRK2 model parameters verification: comparison of true stress versus true strain curve at different strain rates at RT

Fig. 14

MRK2 model parameters identification. Identification of the viscous drag term parameters. Comparison of flow stress prediction as a function of strain rate at different temperatures

Numerical Simulation

Numerical simulations of DTE tests of OFHC copper at different impact velocity were simulated with finite element method. All numerical simulations have been performed with the commercial implicit finite element method (FEM) code MSC MARC r2014. Since the geometry of the test is axisymmetric and no loss of symmetry occurs during the extrusion of the material, only half of the entire geometry was simulated using axisymmetric elements. Both the projectile and the die were modelled as deformable bodies eventually coming into contact (with friction) during the extrusion process. Dynamic transient analysis was simulated using a Single Step Houbolt procedure, which is unconditionally stable, second order accurate and asymptotically annihilating. This algorithm is computationally more convenient compared to the standard Houbolt method and it is recommended for implicit dynamic contact analyses. The deformation of the projectile occurs under quasi-adiabatic condition, therefore coupled thermo-mechanical analysis was performed to account for temperature changes due to the conversion of the plastic work into heat. Simulations were carried out using large displacement, finite strain formulation and lagrangian updating procedure. Both the projectile and the die were meshed using four node, isoparametric, arbitrary quadrilateral written for axisymmetric applications with bilinear interpolation functions. This element is preferred over higher-order elements when used in a contact analysis. The stiffness of this element is formed using four-point Gaussian integration. For nearly incompressible behavior, including plasticity or creep, it is advantageous to use a constant dilatation method, which eliminates potential element locking.

During the dynamic extrusion, the projectile undergoes large deformation. As a consequence of this, extreme element distortion is expected to take place. In order to avoid convergence problems and loss of accuracy, global remeshing was used.

For 2-D analysis, the remeshing techniques include outline extraction, repair, and mesh generation. After the outline is extracted and repaired, the mesh generators is called to create a mesh. Among various mesh generator available, the advancing front mesher (AFM) was used. This 2-D mesher creates a quadrilateral mesh. For a given outline boundary, it starts by creating the elements along the boundary. The new boundary front is then formed when the layer of elements is created. This front advances inward until the complete region is meshed. Some smoothing technique is used to improve the quality of the elements. In general, this mesher works with any enclosed geometry and for geometry that has holes inside. The element size can be changed gradually from the boundary to the interior allowing smaller elements near the boundary. However, in this work, parameters have been set in order to keep the average element size constant during the entire analysis. Remeshing was performed at the beginning of the analysis and, during the analysis according to the penetration remeshing criteria, which is based upon examining the distance between the edge of an element and the contacted body. The initial reference mesh (before remeshing) is shown in Fig. 15.

Fig. 15

Initial mesh for the DTE test configuration. The horizontal line is the axis along which symmetry condition is enforced

Numerical simulations were carried out using both MJC and MRK2 models. Material model parameters for OFHC copper, determined as described in the previous section, are summarized in Tables 1 and 2. The extrusion die, which is made of stainless steel, was simulated as deformable body using standard Johnson and Cook material model, Table 3. In DTE test, the material jet stretches as a result of the velocity difference between the tip and the tail, eventually breaking in fragments. Simulating fragmentation requires a failure model. The literature on failure models for ductile materials such as OFHC copper is extensive. Gray III et al. [11] found evidence of void nucleation and growth close to the DTE fragments tips. Iannitti et al. [19] showed the possibility to simulate ductile damage development in DTE using a continuum damage mechanics based model [52]. Recently, Hörnqvist et al. [21] found evidence of dynamic recrystallization (DRX) in the DTE fragments near tip regions which seems to indicative of the fact that fragments separation occurs by dynamic recovery where deformation becomes localized in a neck or shear band and continues until the cross sectional area has gone to zero [22]. Most of the damage models available in the literature are derived from nucleation and growth of cavities. Consequently, they are not appropriate to describe such type of ductile failure. In this work, a simple abrupt criterion was used. Based on numerical simulation, the maximum plastic strain at the complete reduction of the cross sectional area of the necked fragment, was estimated. This condition occurs when, as a result of the remeshing, only one element is generated in the cross sectional area of the neck. For the analyses presented here, material failure occurs when the total equivalent plastic strain exceeds 7.0. At failure, the element is removed.

Table 1 Summary of MRK2 model parameters for OFHC copper

Table 2 Summary of MJC model parameters for OFHC copper

Table 3 Summary of JC model parameters for the steel used to simulate the behavior of the extrusion die

The fraction of the rate of plastic work dissipated as heat is often assumed to be a constant parameter of 0.9, for most metals. However, Ravichandran et al. [53] showed that at high strain rate and plastic deformation larger than 0.3, the entire plastic work is dissipated as heat. Hereafter, the conversion factor was assumed equal to 1.0.

In a transient dynamic analysis, damping represents the dissipation of energy in the structural system. It also retards the response of the structural system. In the present simulation work, numerical damping was used to damp out unwanted high-frequency chatter in the structure. This type of damping is particularly useful in problems where the characteristics of the model and/or the response change strongly during analysis. Element damping uses coefficients on the element matrices and is represented by the equation:

$$ {\text{C}}=\sum\limits_{\text{i = 1}}^{\text{n}} {\left\{ {\alpha_{\text{i}} {\text{M}}_{\text{i}} + \left({\beta_{\text{i}} + \gamma_{\text{i}} \frac{{\Delta {\text{t}}}}{\pi}} \right){\text{K}}_{\text{i}} }\right\}} $$

(20)

where Δt is the time increment, M_i and K_i are the mass and the stiffness matrices of the ith element, and α_i, β_i, and γ_i are the damping coefficients.

Because of the complexity of the problem, several numerical factors can influence the solutions. Among all, the role of damping and friction have been investigated performing a parametric analysis for the reference condition of dynamic extrusion at 400 m/s.

Damping

Preliminary investigation revealed that the damping in the die can affect the shape and length of the extruded jet as a result of the stress waves dynamics. Based on this, no damping was used for the projectile because energy dissipation is controlled by plastic deformation. For the extrusion die, numerical damping coefficient, γ, was varied to investigate the effect and influence on the calculated material jet.

Friction

During the extrusion, frictional contact occurs between the projectile and the die. Unfortunately, it represents an unknown that can significantly affect the computational results. For the present case, it cannot be measured experimentally, and this presents an unresolved disconnection between the numerical simulation and experiment. Friction models available in FEM codes not necessarily are suitable to reproduce the effective conditions occurring in dynamic impacts. In order to have indication about the role of friction on the shape and number of fragments, a parametric investigation was performed. Here, the bilinear shear based friction model was used. It states that the shear (friction) stress in a node is proportional to the applied shear (friction) force, which is limited by:

$$ \sigma_{\text{t}} = \text{min} \left({m\sigma_{\text{n}}, m\frac{{\sigma_{\text{eq}}}}{\sqrt 3}} \right) $$

(21)

where m is the friction coefficient and σ_eq is the equivalent von Mises stress.

Results and Discussion

The reference test configuration for the numerical assessment work is the DTE test on OFHC copper at 400 m/s. For this impact velocity, parametric investigations aimed to understand the role of computational parameters such as damping and friction were carried out. As validation metric, the number, size and shape of the fragments was used. Time resolved shape of the jet at the exit of the die, as well as the velocity of the fragments at a specific time, would eventually help in the model validation process. Trujillo et al. [54] showed the possibility to measure the velocity of the lead fragment with planar doppler velocimetry (PDV). Unfortunately, such technique was not available and reliable velocity measures from high-speed recording could not be extracted during our tests. Therefore, it was decided not to use fragment velocity as validation metric at this stage.

The DTE test at 400 m/s resulted in four fragments: the one that remains in the die and three dynamically extruded. Hörnqvist et al. [21] showed that information about the strain-temperature history of the material during the deformation in the extrusion die can be extracted post mortem looking at the microstructure evolution of the material point along the symmetry axis. The extruded fragments showed evidence of shear band development while fragmentation did occur by reduction to zero of the cross section area of the necks that develops by plastic instability. In Fig. 16, the soft recovered fragments for all tests are shown.

Fig. 16

DTE test on OFHC copper at 350, 380, 400 and 420 m/s: shear band development and reduction to zero of the cross section at the necks is clearly visible in the second and third fragments in all the tests

Numerical simulation with the MRK2 model, varying the friction coefficient and the numerical damping, were performed. Results were reported in terms of error on the estimated fragments length. In Fig. 17, the error varying the friction coefficient is shown. Here, for a damping coefficient equal to 1.2, the solution obtained with the friction coefficient equal to 0.0, 0.08 and 0.16 is shown. In addition, the error obtained with no friction and no damping is shown for reference. Results indicate that friction has a major effect in controlling the size of the second fragment, which shows the largest variation. Similar results have been found for the damping coefficient used for the extrusion die. In Fig. 18, the results for a friction coefficient equal to 0.08 and a numerical damping equal to 1.2, 10 and 100 respectively, are shown. Also in this plot the reference solution for no friction and 0.0 damping is given (open symbols). Again, damping has a major effect in determining the size of the second extruded fragment. For all friction and damping values examined here, the error in the estimated length of other fragments is bounded within ±10 %. This seems to indicate that, the length of the second extruded fragment should be used as validation metric for the selection of the numerical parameters. Based on this, hereafter, results were obtained taking the friction coefficient and the numerical damping equal to 0.08 and 1.2 respectively.

Fig. 17

Friction effect on calculated fragments length with MRK2 model

Fig. 18

Damping effect on calculated fragments length with MRK2 model

The results, for all impact velocities, obtained with MRK2 model are summarized in Fig. 19. Here, the contours of equivalent plastic strain are shown. The results have been extracted at the time instant when fragments are no longer elongating although some of them still have considerable residual velocity. For presentation purposes, fragments have been moved closer as for the experiments.

Fig. 19

Summary of predicted fragments for DTE test of OFHC copper at different impact velocities with MRK2 model. Colors indicates total equivalent plastic strain contours (Color figure online)

In Fig. 20, for 400 m/s test velocity, calculated fragment size and shape, predicted with MRK2 model, are qualitatively compared with soft recovered fragments. In Fig. 21, quantitative measurements of the fragments size and shape are reported and compared with experimental data. For such experiment, model sensitivity analysis was performed. Numerical results were computed with: (a) the MRK2 model not considering the Hall–Petch effect and the pressure dependence of the melting temperature; (b) the MRK2 model with the grain size dependence only; (c) with the full model. Although, for all the cases the agreement with the experimental data is good, accounting for the pressure effect on the melting temperature provides a better agreement. In particular, the increase of the melting temperature with pressure hardens the computed flow curve. Because of this, fragment sizes are slightly shorter than that observed experimentally, although the shape of the fragments is predicted more accurately. As a confirmation of this, the fragment in the die, which is probably more affected by the pressure effect, is now predicted with increased accuracy.

Fig. 20

Qualitative comparison of predicted and experimental soft recovered fragments for 400 m/s impact

Fig. 21

Quantitative comparison of measured fragment shapes and lengths and prediction using three model options: the MRK2 model (no grain size effect and pressure effect on the melting temperature), MRK2 with grain size effect and complete MRK2 model

In Fig. 22, the extruded jet for 400 m/s predicted with the MJC model is shown. Here, is interesting to note that, with the MJC model, a continuous material jet without break-up into fragments is predicted. This result is the consequence of the unlimited increase of the material flow curve with the strain rate as shown in Fig. 6. The continuous increase of the flow stress causes the material to harden delaying indefinitely the occurrence of strain localization and necking development, which controls the fragments formation. The disagreement between the computed behavior and the experimental evidence can be taken as an indirect confirmation that the flow stress has to show a limit value (viscous drag controlled) at high strain rates. Based on this, for the MJC model, a cut-off value was introduced. Since the flow stress depends on the temperature, strain rate, and plastic strain level, introducing a saturation value is not immediate. Here, during the calculation of the flow stress as in Eq. (4), it was imposed that the strain rate has to be limited to 2.5 E+04 s. This returns a saturation of the flow stress independently on the current plastic strain and temperature. The results are presented in Fig. 23 where the formation of fragments is now obtained, in a general agreement with experimental data.

Fig. 22

Predicted extruded jet for MJC model at 400 m/s. Colors indicates total equivalent plastic strain contours (Color figure online)

Fig. 23

Summary of predicted fragments for DTE test of OFHC copper at different impact velocities with MJC model (with strain rate cut-off). Colors indicates total equivalent plastic strain contours (Color figure online)

Finally, in Fig. 24, a quantitative comparison of fragments length, predicted with MRK2 model, as a function of the impact velocity is shown. Similar comparison is given in Fig. 25 for the MJC model with strain rate cut-off. Data are summarized in Table 4. These plots indicates that MRK2 model perform better in predicting material behavior under different test conditions with an accuracy that can be estimated within [+5, −10 %] error band. Although, for the MJC model the error is limited within a ±20 % band, at low velocity, where the error is apparently smaller, the model fails to predict the correct number of fragments. Both models fail in predicting the size of the second and third fragment at 420 m/s. A possible explanation can be found in the fact that during dynamic extrusion of copper, there are the conditions for dynamic recrystallization (DRX) to occur. Evidence of DRX at 400 m/s was reported in [21]. Therefore, it is expected that DRX could occur more extensively at higher velocity and this will affect the constitutive response of the material, which is not accounted for in the modelling used in this work.

Fig. 24

Model transferability at different velocity: error in estimated fragment size with MRK2 model

Fig. 25

Model transferability at different velocity: error in estimated fragment size with MJC, with strain rate cut-off, model

Table 4 Summary of calculated length and diameter of fragments for 400 m/s DTE test and relative errors

Conclusions

In this work, the results of an extensive numerical simulation work of DTE test of OFHC copper are presented. The performances of Johnson–Cook type model (JC) and physically-based Rusinek-Klepaczko model (MRK), have been investigated. Both the models were updated in order to overcome some limitations and to extend their range of applicability. In particular, the JC was modified to account for viscous drag at very high strain rates, while the MRK model was simplified in its original formulation, reducing the number of parameters to be determined, and improved for the viscous drag regime. Material model parameters were identified using uniaxial stress data at different strain rate and temperature and used to predict the material response in DTE test at different impact velocities. Since the results of the numerical simulations of DTE test can be affected by computational parameters independently of the constitutive model, a parametric investigation was performed in order to assess the role of numerical damping and friction coefficient in the simulation. Results showed that the MRK2 model provides more accurate results than the MJC model. In spite of the larger number of material parameters that need to be determined, the physically-based model provides a more flexible framework that can be further improved to account for mechanisms associated with microstructure evolution. In this perspective, the DTE test would also offer a unique possibility to probe material microstructure and texture evolution to support such modelling [21]. In fact, quantitative information, such as the grain size variation along the extrusion direction and the fragment extent possibly interested by DRX, can be used as validation metric for microstructure evolution models.