1 Introduction

Since urban traffic conditions become heavier, monorail transportation system has been introduced in many cities in China, which has the advantages of low costs, short construction period, little influence on the surrounding environment and strong adaptability to the complex terrain and line type. The first monorail transportation line in China has been put into operation in Chongqing City, which is imported from Japanese technology. The mechanism of this monorail transportation system should be explored in depth; however, the publications of studies on the monorail transportation system are scarce. Lee [1], Kim [2, 3] and Naeimi et al. [4] investigated the dynamic responses of the straddle monorail train and the degree of riding comfort based on the multi-rigid-body principle, respectively. Trahair [5] proposed a calculation method which takes the beneficial lateral load into account in the analysis of the lateral buckling of the monorail steel beam. Kim and Kawatani [6] analyzed the dynamic responses of the improved monorail steel track beam with a transverse support system under seismic activities. Ren et al. [7, 8], Zhao [9], Du and Wang [10], Ma [13], Liu [11, 12] and Shan [14] also studied the responses of the straddle monorail vehicle from different aspects. All the studies above studied the mechanism of the straddle-type monorail train, but there were no publications that recorded the mechanism of the monorail track beam under different factors.

The influence of the various factors on dynamic responses of the straddle-type monorail track beam is investigated in this paper. The mechanism obtained in the analytical procedure provides the necessary theoretical accumulation for the development of the straddle-type monorail traffic technology.

2 Straddle-Type Monorail Track Beam System

The straddle-type monorail track beam is not only the load-bearing structure but also the guild way for the straddle-type monorail train. At present, in the monorail system constructed in Chongqing, track beams are mostly built with prestressed concrete or reinforced concrete, which are simply supported. The longest span of the track beams in Chongqing monorail transportation system is 24 m which has been developed with a length longer than the longest one used in Japan. All the track beams of the whole line are 0.85 m wide and 1.5 m high which are limited by the structure of the vehicle and the weight of the material. The straddle-type monorail track beam in Chongqing is shown in Fig. 1.

Fig. 1
figure 1

Track beam used in monorail transportation in Chongqing

Full size image

To simulate dynamic responses of the straddle-type monorail track beam system, the mathematical model is deduced first and a finite element model of track beam is set up (see Fig. 2). Equations of the track beam are derived in a curved local coordinate system (XYZ).

Fig. 2
figure 2

FEM model of track beam

Full size image

According to the principle of the finite element method, the vertical displacement (∆y), lateral displacement (∆x), angle with respect to axis X (\(\Delta \theta\)) and angle with respect to axis Y (\(\Delta \phi\)) of the beam element can be expressed by Eqs. (1)–(4), respectively. Axial displacement (∆z) and angle with respect to axis Z (\(\Delta \psi\)) of the track beam are expressed by Eqs. (5) and (6), respectively.

$$\Delta y = a_{0} + a_{1} \xi + a_{2} \xi^{2} + a_{3} \xi^{3} + a_{4} \xi^{4} + a_{5} \xi^{5}$$
(1)
$$\Delta x = b_{0} + b_{1} \xi + b_{2} \xi^{2} + b_{3} \xi^{3} + b_{4} \xi^{4} + b_{5} \xi^{5}$$
(2)
$$\Delta \theta = c_{0} + c_{1} \xi + c_{2} \xi^{2} + c_{3} \xi^{3} + c_{4} \xi^{4} + c_{5} \xi^{5}$$
(3)
$$\Delta \phi = d_{0} + d_{1} \xi + d_{2} \xi^{2} + d_{3} \xi^{3} + d_{4} \xi^{4} + d_{5} \xi^{5}$$
(4)
$$\Delta z = e_{0} + e_{1} \xi + e_{2} \xi^{2} + e_{3} \xi^{3}$$
(5)
$$\Delta \psi = f_{0} + f_{1} \xi + f_{2} \xi^{2} + f_{3} \xi^{3}$$
(6)

In Eqs. (1)–(6), \(a_{0} \sim a_{ 5} ,\;b_{0} \sim b_{5} ,\;c_{0} \sim c_{ 5} ,\;d_{0} \sim d_{5} ,\;e_{0} \sim e_{3} \;{\text{and}}\;f_{0} \sim f_{ 3}\) are coefficients, and ξ can be represents as:

$$\xi = \frac{2z}{{l_{\text{e}} }}$$
(7)

where l e is the length of the track beam element.

The mass matrix can be expressed by Eq. (8) based on the energy method.

$$M = \int\limits_{\varOmega } {\rho N^{T} } N{\text{d}}\varOmega$$
(8)

In Eq. (8), ρ denotes the linear density of the beam; N denotes the shape function of the element which is derived from Eqs. (1) to (6).

According to the principle of virtual displacement, the expression of the element stiffness matrix can be expressed by Eq. (9) where [B] denotes the matrix of strain, [D] indicates the matrix of beam modulus.

$$\left[ K \right] = \int {\left[ B \right]}^{T} \left[ D \right]\left[ B \right]{\text{d}}z = \frac{{l_{\text{e}} }}{2}\int_{ - 1}^{1} {\left[ B \right]^{T} \left[ D \right]\left[ B \right]} {\text{d}}\xi$$
(9)

The damping matrix of the track beam is given based on Rayleigh damping principle. It is expressed by Eq. (10) where a 0 and a 1 are the constants expressed by Eqs. (11) and (12), respectively.

$$\left[ C \right] = a_{0} \left[ M \right] + a_{1} \left[ K \right]$$
(10)
$$a_{0} = \frac{{2\omega_{m} \omega_{n} \left( {\omega_{n} \xi_{\text{m}} - \omega_{m} \xi_{n} } \right)}}{{\omega_{n}^{2} - \omega_{m}^{2} }}$$
(11)
$$a_{1} = \frac{{2\omega_{m} \omega_{n} \left( { - \frac{{\xi_{\text{m}} }}{{\omega_{n} }} + \frac{{\xi_{n} }}{{\omega_{m} }}} \right)}}{{\omega_{n}^{2} - \omega_{m}^{2} }}$$
(12)

In Eqs. (11) and (12), \(\omega_{m}\) and \(\omega_{n}\) are the first-order and the second-order frequencies, respectively; \(\xi_{\text{m}}\) and \(\xi_{n}\) are the first-order and the second-order damping ratios of the track beam, respectively.

The governing vibration equations of the monorail track beam can be expressed by Eq. (13), where M indicates the mass matrix expressed by Eq. (8); C indicates the damping matrix expressed by Eq. (10); K indicates the stiffness matrix of the track beam expressed by Eq. (9); w is the deformation vector of the track beam; f b is the external force on the track beam caused by the moving straddle-type monorail vehicle; (·) indicates the derivative with respect to time.

$$M\ddot{w} + C\dot{w} + Kw = f_{b}$$
(13)

3 Monorail Vehicle System

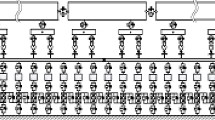
The straddle-type monorail train is different from all the railway and highway vehicles, as it has a special bogie which consists of four steering wheels, four driving wheels and two stabilizing wheels, as shown in Fig. 3. Based on these characteristics, the running mechanism of straddle-type monorail train is also different from any other vehicles on the railway and roads. In order to analyze the dynamic responses of the monorail vehicle, each straddle-type monorail vehicle is simplified as a system which consists of three rigid bodies, i.e., vehicle body, the front bogie and the rear bogie, as shown in Fig. 3, according to the principle of multi-rigid-body dynamics. In this multi-rigid-body system, the rigid bodies are connected by the spring–damping device. The calculation model of the straddle-type monorail train is shown in Fig. 4.

Fig. 3
figure 3

Multi-rigid-body system

Full size image
Fig. 4
figure 4

Diagram of monorail vehicle simplified dynamics model

Full size image

In the system, each rigid body has the six degrees of freedom: axial displacement (Z), vertical displacement (Y), radial displacement (X) and angular displacement about the axis X, axis Y and axis Z (φ, ψ and θ) (see Fig. 4). As each vehicle consists of three rigid bodies, one vehicle calculation model has 18 degrees of freedom. All the parameters of the straddle-type monorail vehicle model are summarized in Table 1.

Table 1 Notations of monorail vehicle dynamics model
Full size table

Based on Lagrange’s formulation, the equations of motion of the vehicle can be obtained. The Lagrange’s formulation can be expressed by Eq. (14).

$$\frac{\text{d}}{\text{d}t}\left(\frac{\partial T_{v}}{\partial \dot{q_{k}}}\right)-\frac{\partial T_{v}}{\partial q_{k}}+\frac{\partial U_v^e}{\partial q_{k}}+\frac{\partial U_v^q}{\partial \dot{q_{k}}}=0$$
(14)

In Eq. (14) \(T_{v}\) indicates the kinetic energy which is expressed by Eq. (15); \(U_{v}^{e}\) indicates the elastic potential energy which is expressed by Eq. (16); \(U_{v}^{q}\) indicates the damping potential energy which is expressed by Eq. (17); \(q_{k}\) denotes the generalized coordinates.

$$\begin{aligned} T_{v} & = \frac{1}{2}\left\{ {\sum\limits_{{{\text{i}} = 1}}^{nv} {\left[ {M_{ci} \left( {\dot{X}_{ci}^{2} + \dot{Y}_{ci}^{2} + \dot{Z}_{ci}^{2} } \right) + J_{c\theta i} \dot{\theta }_{ci}^{2} + J_{c\psi i} \dot{\psi }_{ci}^{2} + J_{c\phi i} \dot{\phi }_{ci}^{2} } \right]} } \right. \\ & \quad + \,\left. {\sum\limits_{j = 1}^{2} {\left[ {M_{tij} \left( {\dot{X}_{tij}^{2} + \dot{Y}_{tij}^{2} + \dot{Z}_{tij}^{2} } \right) + J_{t\theta ij} \dot{\theta }_{tij}^{2} + J_{t\psi ji} \dot{\psi }_{tij}^{2} + J_{t\phi ij} \dot{\phi }_{tij}^{2} } \right]} } \right\} \\ \end{aligned}$$
(15)

In Eq. (15), \(nv\) is the number of vehicle which is running on the track beam; notation “·” denotes the derivative with respect to time; all the other parameters are obtained from Table 1.

The elastic potential energy and damping potential energy of the straddle-type monorail vehicle can be expressed by Eqs. (16) and (17), respectively.

$$\begin{aligned} U_{v}^{e} & = \frac{1}{2}\left\{ {\sum\limits_{i = 1}^{nv} {\sum\limits_{j = 1}^{2} {\sum\limits_{m = 1}^{2} {\left( {K_{kijm}^{l} \mathop {\Delta_{kijm}^{l} }\nolimits^{2} + K_{kijm}^{h} \mathop {\Delta_{kijm}^{h} }\nolimits^{2} + K_{kijm}^{v} \mathop {\Delta_{kijm}^{v} }\nolimits^{2} } \right)} } } } \right. \\ & \left. {\quad + \,\sum\limits_{i = 1}^{nv} {\sum\limits_{j = 1}^{2} {\sum\limits_{m = 1}^{4} {\left( {K_{zijm}^{v} \Delta_{zijm}^{2} + K_{dijm} \Delta_{dijm}^{2} } \right)} } } + \sum\limits_{i = 1}^{nv} {\sum\limits_{j = 1}^{2} {\sum\limits_{m = 1}^{2} {K_{wijm} \Delta_{wijm}^{2} } } } } \right\} \\ \end{aligned}$$
(16)
$$\begin{aligned} U_{v}^{q} & = \frac{1}{2}\left\{ {\sum\limits_{i = 1}^{nv} {\sum\limits_{j = 1}^{2} {\sum\limits_{m = 1}^{2} {\left( {C_{kijm}^{l} \mathop {\mathop {\Delta_{kijm}^{l} }\limits^{ \cdot } }\nolimits^{2} +\, C_{kijm}^{h} \mathop {\mathop {\Delta_{kijm}^{h} }\limits^{ \cdot } }\nolimits^{2} +\, C_{kijm}^{v} \mathop {\mathop {\Delta_{kijm}^{v} }\limits^{ \cdot } }\nolimits^{2} } \right)} } } } \right. \\ & \left. {\quad + \,\sum\limits_{i = 1}^{nv} {\sum\limits_{j = 1}^{2} {\sum\limits_{m = 1}^{4} {\left( {C_{zijm}^{v} \mathop {\mathop {\Delta_{zijm}^{v} }\limits^{ \cdot } }\nolimits^{2} +\,C_{dijm} \mathop {\mathop {\Delta_{dijm} }\limits^{ \cdot } }\nolimits^{2} } \right)} } } + \sum\limits_{i = 1}^{nv} {\sum\limits_{j = 1}^{2} {\sum\limits_{m = 1}^{2} {C_{wijm} \mathop {\mathop {\Delta_{wijm} }\limits^{ \cdot } }\nolimits^{2} } } } } \right\} \\ \end{aligned}$$
(17)

In Eqs. (16) and (17), \(nv\) is the number of the vehicles which is running on the beams; subscripts(\(j\) and \(m\)) are the indexes of the position (shown in Fig. 4). The parameters (\(\Delta_{kijm}^{l}\), \(\Delta_{kijm}^{h}\) and \(\Delta_{kijm}^{v}\)) indicate deformation of the air suspension in longitudinal, lateral and vertical direction, respectively. The parameters (\(\Delta_{zijm}\), \(\Delta_{dijm}\) and \(\Delta_{wijm}\)) denote the displacement of the track beam at the position which contacts with the driving wheel, steering wheel and stabilizing wheel, respectively.

4 Case Study

The bridge–vehicle coupling system is a complex time-varying system which makes it impossible to obtain the solutions of motion equations by theoretical calculation. In order to obtain the solutions, numerical simulation is an effective way for the analysis of the bridge–vehicle coupling system. A numerical simulating software was developed on VB programming platform, based on the energy method and the FEM. Then a simply supported monorail track beam in Chongqing monorail transportation line is taken to serve as the dynamic response simulation example (shown in Fig. 5), and the influence of the curve radius, driving speed and vehicle load on the dynamic response of the straddle monorail track beam is studied by using the self-developed dynamics simulation software.

Fig. 5
figure 5

Monorail track beam (unit: mm)

Full size image

4.1 Influence of Radius of Curvature on Dynamic Responses of Track Beam

The time span in simulation is between the in and out locomotions of the vehicle on the track beam. Through the calculation, the record of vibration displacement and vibration amplitude of the mid-span was obtained, as shown in Figs. 6 and 7. When the track beam has different radius of the curvature, the vibration displacement and the amplitude in the lateral direction are different from those in the vertical direction. It is shown in Figs. 6 and 7 that the vertical vibration displacement and the vibration amplitude of the beam decrease with the increase in the radius of curvature, and the lateral vibration displacement and amplitude increase with the increase in the radius of the curvature. The maximum lateral vibration amplitude is 0.075 mm when the radius of the curvature is fixed at 1000 m, while the maximum vertical vibration amplitude is 0.43 mm when the radius of the curvature is fixed at 100 m.

Fig. 6
figure 6

Record of vibration displacement at middle span (unit: mm). a Lateral, b vertical

Full size image
Fig. 7
figure 7

Record of vibration amplitude at middle span (unit: mm). a Lateral, b vertical

Full size image

The observations of acceleration at the middle span with respect to radius of curves is shown in Fig. 8. The valuable information is that the lateral acceleration increases with the increase in radius, and the maximum lateral acceleration is 0.11 m/s2 in accordance with a radius of 1000 m. But the radius does not influence the vertical acceleration significantly. No significant difference is shown between the curves of acceleration according to different radius is shown in Fig. 8.

Fig. 8
figure 8

Observations of acceleration at middle span (unit: m/s2). a Lateral, b vertical

Full size image

4.2 Influence of Vehicle Speed on Dynamic Responses of Track Beam

Vehicle speed is another important factor that influences dynamic responses of the track beam. Through the calculations, dynamic responses of the track beam according to different speeds (20, 40, 60 and 80 km/h) are obtained. It is shown in Fig. 9 that the trends of the maximum amplitude in lateral and vertical direction are similar to each other and the maximum deflection in lateral and vertical direction increases as the driving speed increases. The maximum vertical deflection is 0.69 mm at the speed of 80 km/h, while the maximum lateral amplitude is 0.046 mm at the speed of 80 km/h.

Fig. 9
figure 9

Maximum of amplitude at middle span (unit: mm). a Lateral, b vertical

Full size image

The record of acceleration at the middle span with respect to different speeds (20, 40, 60 and 80 km/h) is shown in Fig. 10. The valuable information is that the lateral and vertical acceleration increases as the speed increases, and the maximum values are 0.15 and 0.62 m/s2, respectively. The rules investigated in this chapter denote that speed is a very important factor which affects dynamic responses of the track beam; how to control the speed of the straddle-type monorail train will be an important task for the managers.

Fig. 10
figure 10

History of acceleration at middle span (unit: m/s2). a Lateral, b vertical

Full size image

4.3 Influence of Vehicle Load on Dynamic Responses of Track Beam

As the weights of straddle-type monorail vehicle and track beam are approximately equal to each other, the influence of vehicle load on dynamic responses of track beam should be studied in depth. Figures 11 and 12 show the variation displacement and the vibration amplitude of monorail track beam in three load cases: passenger-free, normal load and full load. The results show that the vibration amplitude and the displacement in lateral and vertical direction increase with the increasing load. When the vehicle is full load, the maximum vibration amplitudes in lateral direction and vertical direction are 0.041 and 0.43 mm, respectively. This calculation denotes that the vehicle load can significantly affect the dynamic response of the track beam.

Fig. 11
figure 11

Record of vibration displacement at middle span (unit: mm). a Lateral, b vertical

Full size image
Fig. 12
figure 12

Record of vibration amplitude at middle span (unit: mm). a Lateral, b vertical

Full size image

The record of acceleration at the middle span with respect to different load conditions (no passengers, normal load and full load) is shown in Fig. 13. The valuable information is that the vertical acceleration increases with the increasing load and the maximum value is 0.44 m/s2. But the lateral acceleration is not sensitive to the variation of load as shown in Fig. 13.

Fig. 13
figure 13

Record of acceleration at middle span (unit: m/s2). a Lateral, b vertical

Full size image

The calculations denote that all the factors (curve radius, driving speed and vehicle load) have important effect on the dynamic responses of the straddle-type monorail track beam under a moving train. These rules with respect to different conditions should be very useful in the procedures of the design or operation of the straddle-type transportation system.

5 Conclusions

A theoretical and mathematical bridge–vehicle interaction dynamics model was set up and analyzed first, and then based on the energy principle and FEM, a bridge–vehicle dynamics numerical simulation software was developed. A time span between the in and out locomotions of the vehicle on the track beam is calculated with the self-developed FEM software. Through the dynamic response analysis of the straddle-type monorail vehicle–bridge coupling system, some valuable conclusions can be obtained.

  1. 1.

    The vertical vibration amplitude of the track beam decreases with the increasing radius of curvature, while the lateral amplitude increases with the increasing radius of the curvature. The maximum lateral vibration amplitude is 0.075 mm with respect to the radius of 1000 m, while the maximum vertical vibration amplitude is 0.43 mm with respect to the radius of 100 m; the lateral acceleration increases with the increasing radius, and the maximum lateral acceleration is 0.11 m/s2 in accordance with a radius of 1000 m. But the vertical acceleration is not easily affected by the variation of radius.

  2. 2.

    The maximum amplitude in the lateral and vertical direction increases as the driving speed increases, and the maximum vertical deflection is 0.69 mm, while the maximum lateral amplitude is 0.046 mm, at the speed of 80 km/h; the lateral and vertical acceleration increases as the speed increases, and the maximum values are 0.15 and 0.62 m/s2, respectively.

  3. 3.

    The vibration amplitude (lateral and vertical) increases with the increase in the load, and the maximum vibration amplitudes in lateral and vertical direction are 0.041 and 0.43 mm, respectively; the vertical acceleration increases with the increase in load, and the maximum value is 0.44 m/s2. But the lateral acceleration is not easily affected by the variation of load.

  4. 4.

    The proposed method for the analysis of straddle-type monorail vehicle–bridge coupling system in this paper can be used to simulate the dynamic responses of the bridge–vehicle interaction system, and the self-developed calculation software is efficient in the analysis of dynamic responses of the complex bridge–train coupling system.