Introduction

The elastocaloric effect (eCE) is associated with superelasticity of shape memory alloys (SMAs). When an SMA in its austenitic phase is uniaxially strained/stressed, an exothermic austenitic–martensitic transformation occurs, which causes a release of heat into the surroundings (in the isothermal process) or temperature increase of the material (in the adiabatic process). A reverse process, namely, the endothermic martensitic–austenitic transformation occurs when the stress is released, which causes heat to be absorbed from the surroundings (for an isothermal process) or a temperature decrease of the material (for an adiabatic process). These thermal effects are related to the martensitic transformation and were detected already in the 1980s in single-crystal Cu-based alloys (Cu–Al–Ni and Cu–Zn–Sn) [1–3] and in 1990s in the poly-crystal Ni–Ti alloys [4]. However, it was not until very recently that the eCE was recognized as a potential cooling or heat-pumping mechanism near room temperature [5]. In general, SMAs can be divided into two main groups: non-magnetic (Ni–Ti-based, Cu-based and Fe-based alloys), and magnetic SMAs. The most widely analysed elastocaloric material is near-equiatomic poly-crystal Ni–Ti alloy. For example, Cui et al. [6] measured an adiabatic temperature change of 25.5 K when they applied a tension stress of 650 MPa to a Ni–Ti wire and 17 K when the stress was removed. Similarly, Tušek et al. [7] evaluated well-stabilized Ni–Ti wires loaded in tension and measured a maximum adiabatic temperature change of 25 K during loading and 21 K during unloading. Ossmer et al. [8] analysed the eCE in Ni–Ti thin film and measured an adiabatic temperature change of 17 K during loading and 16 K upon unloading. They further compared the directly measured adiabatic temperature changes with the ones calculated by a phenomenological Tanaka-type model (with included term of a latent heat) combined with a heat transfer model. Very good agreement between measured and modelled values was obtained when a latent heat used as an input to the model was calculated based on measured adiabatic temperature changes. Pataky et al. [13] compared the eCE of Ni–Ti, Ni–Fe–Ga and Co–Ni–Al alloys measured directly and indirectly by mechanical (tensile) tests as well as calorimetry measurements and further calculated through the Clausius–Clapeyron equation. They measured (directly) adiabatic temperature changes of up to 14.2, 8.4 and 3.1 K for Ni–Ti, Ni–Fe–Ga and Co–Ni–Al alloy, respectively; while indirectly they estimated it to be nearly double the values of the directly measured adiabatic temperature change. With the goal of improving structural stability and fatigue life of Ni–Ti alloys, which is crucial for its application in practical cooling or heat-pumping devices, in recent years several studies on the eCE of Ni–Ti alloys doped with Cu, Co, Fe and V were made [9–12]. For example, it was shown that a Ni–Ti–Cu–Co thin film made by sputtering can withstand 10 million loading cycles up to a strain of 2.5% with adiabatic temperature changes up 10 K [10, 12]. Among Cu-based SMAs, the eCE was reported for a single-crystal Cu–Zn–Al alloy [5, 14, 15]. By indirect measurements Bonnot et al. [5] estimated the adiabatic temperature change of Cu–Zn–Al alloy to be 15 K when they applied a mechanical stress of 28.5 MPa (through the Clausius–Clapeyron equation). In the next years, the eCE of this alloy was further analysed by Vives et al. [14] and Mañosa et al. [15], who measured a negative adiabatic temperature change of about 6 K in a temperature range between 200 and 350 K under the removal of the applied stress up to 275 MPa. Among the Fe-based alloys, the eCE was reported for the Fe–Rh and Fe–Pd alloys. For the Fe–Rh alloy, Nikitin et al. [16] measured a negative adiabatic temperature change of 5.2 K, while indirectly by mechanical tensile testing and the Clausius–Clapeyron equation, they estimated it to be 8.7 K under the stress removal of 529 MPa. Xiao et al. [17, 18] reported the eCE of single-crystal Fe–Pd alloy and measured an adiabatic temperature change of about 2 K in the temperature range between 240 and 280 K. In addition to the SMAs, in recent years the eCE of magnetic SMAs, such as Ni–Mn–Sb–Co [19] and Ni–Fe–Ga alloy [20], and shape memory polymers, such as natural rubber [21] and poly(vinylidene fluoride–trifluoroethylene–chlorotrifluoroethylene) terpolymer [22], was reported as well, but those will not be considered here. For additional information on these and other elastocaloric materials the readers are to refer to [23–25].

Together with the research on elastocaloric materials in recent years, a significant progress was made also in development of elastocaloric cooling and heat-pumping devices. In several works, an evaluation of different elastocaloric thermodynamic cycles [26], numerical simulations of different types of devices and their performance [27–29] and also the first experimental prototypes [30–34] were reported.

It should be noted that the eCE is in many ways analogue to other so-called (ferro-)caloric effects such as magnetocaloric, electrocaloric and barocaloric effect [35–39]. Among them, to this point the most widely studied is the magnetocaloric effect, so research and experimental methods on other ferro-caloric effects can benefit from much of the existing magnetocaloric literature.

This paper presents experimental and theoretical techniques applied for studying the elastocaloric properties in SMAs. In recent years, different direct and indirect experimental (as well as modelling) methods for the evaluation of different elastocaloric properties have been applied. The aim of this work is to give an overview of those techniques and to present basic thermodynamic relations and elastocaloric properties, such as adiabatic temperature change, isothermal entropy change and total entropy of typical elastocaloric materials such as Ni–Ti and Cu–Zn–Al alloys. In the last part of the paper, the basic definition of the efficiency of the elastocaloric thermodynamic cycle [coefficient of performance (COP)] is presented and discussed.

Measuring of the Elastocaloric Effect

In general, one can distinguish between direct and indirect experimental methods applied for characterization of the eCE. Direct methods refers to the direct (adiabatic) temperature change measurements, while indirect methods are usually based on measuring mechanical (stress–strain and/or strain–temperature) properties, from which the elastocaloric properties can be further calculated.

Direct Methods

The most straightforward and in many cases the easiest way to evaluate the eCE is to directly measure the (adiabatic) temperature changes during loading and unloading of the material (between initial and final stress/strain). However, this method may lead to substantial error if not properly done. A precondition for accurate measurement of adiabatic temperature changes is to assure adiabatic conditions, which in reality may be difficult to achieve. Since the elastocaloric material needs to be physically connected to an actuator or similar system to load/unload it, there will always be a certain amount of heat leakage to the ambience through these connections. In order to minimize these losses, well-isolated, longer samples loaded/unloaded at high strain rates should be applied. For example, it was shown in [8, 14, 40, 41] for the case of non-isolated samples that the adiabatic conditions in air are relatively well approached at strain rates above 0.2 s−1. However, this strongly depends on the intensity of the heat transfer between the material and its surroundings, which is influenced by the sample’s geometry and fluid/ambient dynamics around the sample.

Figure 1 shows an example of direct eCE property measurements. Figure 1a shows the stress–strain characteristics of elastocaloric material at well-approximated adiabatic conditions (compared to the stress–strain characteristics measured at isothermal conditions), while Fig. 1b shows an example of the adiabatic temperature changes during adiabatic loading and unloading measured with a thermocouple placed on the sample surface.

Fig. 1
figure 1

a An example of stress–strain characteristics at well-approached adiabatic conditions (compared to the stress–strain characteristics measured at isothermal conditions) measured on a Ni0.56Ti0.44 dog-bone shaped sample (gauge length of 50 mm, width of 10 mm and thickness of 0.2 mm) with a uniaxial applied stress in the rolling direction. b An example of the corresponding adiabatic temperature changes during loading and unloading measured with a thermocouple

Full size image

Special attention should be paid to the temperature sensor used for the adiabatic temperature change measurements. One should distinguish between contact and non-contact type of temperature sensors. Contact temperature sensors, such as thermocouples, are mounted on the sample and the temperature in a single or a multiple discrete points is measured. It is known that the adiabatic temperature changes over the sample can be highly non-homogeneous, in particular when strains corresponding to the middle of the transformation plateau are applied as shown in the literature for Ni–Ti alloy [8, 11, 40–43] as well as for Cu–Zn–Al alloy [14]. In such case, the martensitic transformation is not fully completed and the transformation occurs only in certain regions in the sample (see Fig. 2). The martensitic transformation propagates with Lüders bands, rising from different parts of the sample (at high strain rate) and usually occurs at an angle between 45° and 55° [43–45]. As shown in [8, 14, 42], the location and growth of the temperature profiles measured with thermography fit well with the transformation regions (Lüders bands) simultaneously observed with digital image correlation or similar techniques. Therefore, single-point temperature measurements in such cases can lead to misleading results if the objective is to measure the average adiabatic temperature change over the sample. If thermocouples should be applied, several thermocouples should be situated over the sample to achieve more representative results of the temperature changes distribution. However, a more representative temperature distribution can be obtained by non-contact temperature measurement using thermography (IR camera), where spatially distributed adiabatic temperature changes can be measured at all times (see Fig. 2). In addition, due to certain contact resistivity and thermal capacity of the contact-type temperature sensors, the adiabatic temperature changes measured with thermocouples are generally to a certain extent smaller than measured with IR camera as shown in [14, 40]. In any case, a good thermal contact, as small thermal mass of the temperature sensor as possible and high sampling frequency (high enough to capture fast temperature changes), should be applied when using contact-type temperature sensors. On the other hand, a disadvantage of applying thermography is the inability to apply insulation to the sample, which limits the adiabatic conditions (which can be compensated with higher strain rate) and the need to coat the samples with a medium with a known emissivity.

Fig. 2
figure 2

An example adiabatic temperature change during loading and unloading at two applied stresses (one corresponds to the middle and another to the end of the transformation plateau) measured with IR camera. The experiments were performed on a Ni0.56Ti0.44 dog-bone shaped sample (gauge length of 50 mm, width of 10 mm and thickness of 0.2 mm) with a uniaxial applied stress in the rolling direction

Full size image

Indirect Methods

As an alternative to direct methods, indirect methods are often applied. These are usually based on mechanical measurements of the material’s superelastic response, such as stress–strain characteristics at different temperatures during loading and unloading (see Fig. 3a) or strain–temperature characterization at different applied stresses during heating and cooling (see Fig. 3b). In general, the elastocaloric properties can be obtained also from calorimetry measurements for different constant stresses (or strains), as demonstrated for evaluation of magnetocaloric effect for different magnetic fields [46, 47]. Designing a calorimetry test grid equipped with a mechanical tester for providing constant stress (strain) is very challenging due to heat leakage through the grips and mounting of Peltier elements on the straining material and has not yet been demonstrated in the literature. Therefore, in this paper we will focus on the method for calculation of elastocaloric properties based on mechanical (superelastic) behaviour. Figure 3a shows a stress–strain response of poly-crystal Ni–Ti wire at four different temperatures (above its austenitic finish temperature which is around 305 K) during tensile (un)loading [7]. The wire was mechanically trained (subjected to 400 loading–unloading cycles) at 342 K to stabilize its superelastic behaviour prior to testing. Figure 3b shows the strain–temperature response of single-crystal Cu–Zn–Al block at four different applied stresses in compression mode. A precondition for correct application of indirect methods and further correct evaluation of the elastocaloric properties are the existence of isothermal conditions. In order to assure those, stress–strain characteristics should be measured at very small strain rates (up to 4 × 10−4 s−1 [7, 48]) and strain–temperature characteristics should be measured at very small heating/cooling rates (up to 0.02 K/s [29]) in order to allow the latent heat generated during the martensitic transformation to be transmitted to the surrounding and not to heat up or cool down the material. It is suggested that forced convection over the sample should be applied to enhance isothermal conditions.

Fig. 3
figure 3

a An example of experimentally obtained stress–strain superelastic responses at four different temperatures of Ni–Ti alloy (full lines) and its comparison with the phenomenological model (dotted lines) shown for different temperatures (from 292 to 382 K with a step of 10 K). b An example of experimentally obtained strain–temperature superelastic response at four different stresses of Cu–Zn–Al alloy (full lines) and its comparison with phenomenological model (dotted lines) shown for different stresses (0, 14, 28, 53, 77, 100, 115 and 130 MPa)

Full size image

From the measured superelastic responses, one can apply basic thermodynamic relations, such as Maxwell relation [Eq. (1)] or the Clausius–Clapeyron equation [Eq. (4)] to calculate the isothermal entropy change (average over the sample) and other related elastocaloric properties. Since a great majority of the elastocaloric materials have a first-order phase transition with some degree of hysteresis in the transformation region, the elastocaloric properties in general differ for loading and unloading (or cooling and heating) paths. Namely, isothermal entropy changes and adiabatic temperature changes for loading and unloading differ for an irreversible entropy generation and temperature irreversibilities, which are analogue to the enclosed area of the hysteresis loop (for an isothermal response). The hysteresis-related temperature irreversibilities can be calculated as follows: \(\Updelta T_{\text{irr}} = (1/\rho c)\mathop {\oint }\nolimits \sigma {\text{d}}\varepsilon\) and can exceed several Kelvins as shown in [7]. It can be assumed that half of the entropy generation associated with hysteresis occurs during loading, while the other half during unloading. The equations shown further in the text can be applied for separate calculation of the eCE during loading and unloading. Alternatively, the eCE can be calculated based on the superelastic response with neglected hysteresis (based on average stress–strain response at each temperature or average strain–temperature response at each stress), while the entropy generation and temperature irreversibilities associated with hysteresis (calculated based on the enclosed area of the hysteresis loop) can be additionally included to the elastocaloric properties. The latter was applied for evaluation of hysteresis behaviour of magnetocaloric materials as shown in [49]. It should be noted that both methods are thermodynamically consistent only if the loading and unloading paths are independent on the applied stress/strain.

In the case of elastocaloric materials, the Maxwell relation has the following form:

$$\rho \left( {\frac{\partial s}{\partial \sigma }} \right)_{T} = \left( {\frac{\partial \varepsilon }{\partial T}} \right)_{\sigma } .$$
(1)

Using Eq. (1), the isothermal entropy change between initial and final stress can be calculated as follows (as a function of temperature and applied stress):

$$\Updelta s_{\text{iso}} = \frac{1}{\rho }\int_{{\sigma_{1} }}^{{\sigma_{2} }} {\left( {\frac{\partial \varepsilon }{\partial T}} \right)_{\sigma } } {\text{d}}\sigma ,$$
(2)

where ε is strain; σ is stress; T is temperature and ρ is the material’s density.

As reported for magnetocaloric effect in a first-order phase transition, where coexistence of two phases occurs during the transition, which is usually also the case in eCE in SMA, the application of the Maxwell relation can lead to unrealistic values of the isothermal entropy change if an experiment is not performed appropriately [50]. In the case of an ideal first-order transition with discontinuous transformation, the derivative ∂ɛ/∂T becomes infinite. However, the infinite ∂ɛ/∂T can arise only in an ideal first-order phase transition, and in real materials it is usually finite (especially for stabilized elastocaloric materials where the transformation plateau usually has a positive slope [7]), but the method is very sensitive to any experimental noise and sampling frequency. Furthermore, superelastic responses are usually measured only for a limited number of temperatures and applied stresses which make a correct application of the Maxwell relation based on experimental data more challenging. To reduce experimental errors (which can lead to infinite derivative ∂ɛ/∂T) and to increase the number of data points in the stress–strain–temperature space, we proposed a phenomenological model which can predict the superelastic response at any applied stress/strain and temperature [29]. It is in general analogous to the well-known Tanaka-type phenomenological model of SMAs, where certain experimentally obtained superelastic properties are used as the input data [8, 51, 52]. The model can be written using the following relations [29]:

$$\varepsilon (\sigma ,\;T) = \frac{{\varepsilon_{\text{tran}} }}{2}\tanh \left( {a \cdot \left( {\sigma - \sigma_{0} (T)} \right)} \right) + \frac{\sigma }{E} + \frac{{\varepsilon_{\text{tran}} }}{2},$$
(3)
$$a_{\text{AM}} = \frac{K}{{C_{\text{AM}} (M_{\text{s}} - M_{\text{f}} )}},$$
(3a)
$$a_{\text{MA}} = \frac{K}{{C_{\text{MA}} (A_{\text{f}} - A_{\text{s}} )}},$$
(3b)
$$\sigma_{{0,{\text{AM}}}} (T) = C_{\text{AM}} \left( {T - M_{\text{p}} } \right),$$
(3c)
$$\sigma_{{0,{\text{MA}}}} (T) = C_{\text{MA}} \left( {T - A_{\text{p}} } \right),$$
(3d)

where ε tran is the transformation strain, E is the elastic Young’s moduli of the austenitic and martensitic phases (here it is assumed that both moduli are the same, which fits well for the evaluated materials in this work), while a represents the slope of the transformation plateau [see Eqs. (3a) and (3b)] and σ 0 is the critical stress as a function of the temperature in the phase diagram [see Eqs. (3c) and (3d) and Fig. 4]. M s, M p, M f, A s, A p, A f are six transition temperatures, namely martensitic start, martensitic peak, martensitic finish, austenitic start, austenitic peak and austenitic finish temperature, respectively. The coefficient (K) in Eqs. (3a) and (3b) is K = 2·tanh−1(0.9) and is justified from the usual assumption that the start and the finish transition temperatures are defined at the temperatures at which the transition has advanced for 5 and 95%, respectively, spanning 90% of the total transformation (therefore factor 0.9 in coefficient K). The two coefficients, C AM and C MA, represent the Clausius–Clapeyron coefficients for forward and reverse transformation defined as the derivative of the critical transformation stress (stress at the middle of the transformation plateau at the particular temperature) over the temperature [C = (dσ/dT)cr], which are usually constant values. These eight properties, together with the elastic moduli (E) and the transformation strain (ε tran), are the experimentally obtained inputs parameters for the model and are given in Table 1 for Ni–Ti and Cu–Zn–Al alloys. A comparison of the measured and modelled superelastic responses for Ni–Ti and Cu–Zn–Al alloys is shown in Fig. 3. Good agreement was obtained between these two.

Fig. 4
figure 4

An example of the phase diagram based on experimentally obtained superelastic behaviour (full lines represent forward, while dotted lines represent reverse transformation)

Full size image
Table 1 Superelastic (and other) properties of the evaluated materials used as the model input data [15, 29, 56, 57]
Full size table

Alternatively to the Maxwell relation, the isothermal entropy change can be calculated using the Clausius–Clapeyron equation, which essentially leads to the same results as also shown for the magnetocaloric effect [53]. The Clausius–Clapeyron equation for elastocaloric material can be written as follows:

$$\left( {\frac{{{\text{d}}\sigma }}{{{\text{d}}T}}} \right)_{\text{cr}} = \rho \frac{\partial s}{\partial \varepsilon } \to \Updelta s_{\text{iso}} = \frac{1}{\rho }\varepsilon_{\text{tran}} \left( {\frac{{{\text{d}}\sigma }}{{{\text{d}}T}}} \right)_{\text{cr}} ,$$
(4)

where ε tran is the transformation strain and (dσ/dT)cr presents the Clausius–Clapeyron coefficient.

To calculate the adiabatic temperature change of the eCE from indirect measurements, the following equation is usually applied in the literature, e.g. [5, 13, 15]:

$$\Updelta T_{\text{ad}} \approx {-} \frac{1}{\rho }\frac{T}{c}\Updelta s_{\text{iso}} .$$
(5)

It should be noted that this equation can be used only for estimating the adiabatic temperature changes, since the specific heat (c) is taken as a constant value and the temperature at which adiabatic temperature change is calculated does not take into account self-heating and self-cooling of the sample which occurs under adiabatic conditions. More precise and correct way of calculating the adiabatic temperature changes is using the following equation (see Fig. 5):

$$\Updelta T_{\text{ad}} = T_{2} \left( {S_{\text{tot}} ,\;\sigma } \right) - T_{1} \left( {S_{\text{tot}} ,\;\sigma = 0} \right).$$
(6)
Fig. 5
figure 5

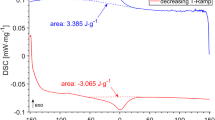
a A comparison of the total entropy as a function of temperature obtained based on calorimetry [and calculated with Eq. (8)] and modelled with Eq. (9) during cooling and heating for Ni–Ti alloy. b Calorimetry results of the stabilized Ni–Ti wire (measured in Netzsch DSC 200 F3 with heating/cooling rate of 5 K/min)

Full size image

Therefore, a precondition to calculate exact adiabatic temperature changes is a construction of a total entropy–temperature diagram at different applied stresses. This can be done by calculating the total entropy at zero applied stress and adding isothermal entropy changes at different temperatures and stresses:

$$S_{\text{tot}} = S_{{{\text{tot}}, \sigma = 0}} + \Updelta s_{\text{iso}} .$$
(7)

The total entropy at zero applied stress is in general defined as

$$S_{{{\text{tot}},\sigma = 0}} = \int_{{T_{1} }}^{{T_{2} }} {\frac{c}{T}} {\text{d}}T.$$
(8)

The specific heat (c) at zero stress (and at different temperatures) is often obtained with calorimetry measurements as shown in Fig. 5. However, as discussed later in the text it might be more suitable that the total entropy at zero stress is modelled using the following equation:

$$S_{{{\text{tot}},\sigma = 0}} = \left( {\int_{{T_{1} }}^{{T_{2} }} {\frac{{c(T_{1} )}}{T}{\text{d}}T} } \right) + \Updelta s_{\text{iso}} \left( {\sigma = \sigma_{\text{final}} } \right).$$
(9)

Here c presents the baseline specific heat (at the reference temperature T 1), which can be taken as a constant value. This value can either be obtained by calorimetry measurements or taken from the literature. The Δs iso(σ = σ final) is the isothermal entropy change at the final stress (and as function of temperature). Temperature T 1 is a reference temperature at which the total entropy is assumed to be zero. The reference temperature should be well below transformation temperatures at which the total entropy is stress independent and eCE equals to zero.

It is important to emphasize that the total entropy is a state function determined only by its initial and final states and is therefore path (hysteresis) independent. However, the method for calculation of elastocaloric properties applied in this work (which includes hysteresis irreversibilities) assumes different total entropies for loading and unloading (or cooling and heating) processes obtained by using different isothermal entropy changes for loading and unloading in Eqs. (7) and (9). By using Eq. (6) this further results in different adiabatic temperature changes for loading and unloading, which occurs due to hysteresis-related irreversibilities. Therefore, the total entropy shown in Figs. 5a and 6 should be considered as effective total entropy (used only with a purpose to calculate adiabatic temperature changes).

Fig. 6
figure 6

Isothermal entropy changes [calculated based on Eq. (2)], adiabatic temperature changes [calculated based on Eq. (6)] and the total entropy–temperature diagrams [calculated based on Eqs. (7) and (9)] for Ni–Ti alloy at applied stresses up to 800 MPa with a step of 200 MPa (left -hand side) and Cu–Zn–Al alloy at applied stresses up to 320 MPa with a step of 80 MPa (right-hand side). For comparison, isothermal entropy changes are shown also for applied strain rate at strains up to 5.71% with a step of 1.27% (for Ni–Ti alloy) and up to 6% with a step of 1.5% (for Cu–Zn–Al alloy). Arrows show increase of applied stress (strain)

Full size image

A comparison between the total entropy as function of temperature obtained from the calorimetry measurement (Fig. 5b) and modelled with Eq. (9) during cooling and heating for a Ni–Ti alloy is depicted in Figure 5a. The total entropy well below transformation temperatures was modelled using a baseline specific heat [c(T 1)] obtained using calorimetry measurements that was found to be 430 J/kg K. It is evident that the total entropy (as function of temperature) obtained from calorimetry measurements during heating has a similar trend as the modelled total entropy values (with a single transformation peak), while the total entropy during cooling measured by calorimetry shows two separated transformations (A–R–M) over a wider temperature range as is also shown in Fig. 5b. It is evident from Fig. 5a that the latent heat of the transformation, which results in a shift of the total entropy at the transformation temperatures, obtained with calorimetry, is larger compared to the modelling values. Similar results were recently also noted by Ossmer et al. [8] for a Ni–Ti film, who showed that latent heat accessible with tensile mechanical tests (based on superelastic behaviour) is less than half of the latent heat obtained with calorimetry. This is most probably due to the different nature of the transformation. During the calorimetry measurements, a two-stage temperature-induced transformation between austenite and twinned martensite with intermediate R-phase transformation occurs as shown in Fig. 5b, while during mechanical testing a stress-induced transformation between austenite and de-twinned martensite is observed [54]. As also indicated by Ossmer et al. [8], the material undergoes only a part of the two-stage transformation during mechanical (un)loading. Therefore, in this case it might be misleading to calculate the eCE based on calorimetry measurements, and it is recommended to measure the elastocaloric properties in the same manner as applied in potential elastocaloric device (through superelastic behaviour). On the other hand, Pataky et al. [13] generally obtained better agreement with direct measurements when the eCE was estimated based on calorimetry compared to mechanical testing. Further research, for example, by calorimetry measurements under applied stress (strain), is required to fully understand the reasons for these deviations. Furthermore, it is also evident from Fig. 5b that the transformation temperatures obtained with calorimetry are significantly lower compared to the transformation temperatures used for modelling (Table 1). As shown, for example, in [55], the presence of the R-phase usually changes the slope of the transformation lines at lower stresses. Especially the martensite transformation temperature is shifted towards lower temperatures due to the R-phase transformation, but since this occurs in the temperature region which is out of our interest it was not considered in the model. For modelling purposes the transformation temperatures were taken to fit the transformation lines in the analysed temperature range (see Fig. 4) with linear extrapolation, since our goal is to model the superelastic and further eCE at the temperature range where the superelastic measurements were performed.

Thermodynamic Properties of Some Elastocaloric Materials

In this section, the basic thermodynamic properties of two elastocaloric materials, i.e. Ni–Ti and Cu–Zn–Al alloys, calculated based on the above described phenomenological model are presented. The material’s properties used as the input for the model were obtained through tensile mechanical testing and are shown in Table 1. All the properties reported here are calculated separately for loading/unloading and cooling/heating paths. Figure 6 shows the isothermal entropy changes [calculations based on Eq. (2)], adiabatic temperature changes [calculations based on Eq. (6)] and the (effective) total entropy–temperature diagrams [calculations based on Eqs. (7) and (9)]. For Ni–Ti alloy, the elastocaloric properties are shown for the applied stress up to 800 MPa (with the step of 200 MPa), while up to 320 MPa (with the step of 80 MPa) for Cu–Zn–Al alloy.

It is important to emphasize that the phenomenological model presented in the previous section is based on an applied stress rate. In reality, the superelastic behaviour is often measured for a specific strain rate. If one needs to calculate elastocaloric properties as a function of applied strain, an interpolation process for constant strain rate can be applied as shown, for example, in Fig. 6a, b where the isothermal entropy changes at different stresses and strains are presented. The same can be done also for other elastocaloric properties. It is evident that the isothermal entropy change at the final stress and final corresponding strain is the same for constant stress rate and strain rate modes. However, due to non-linear mechanical responses, the values of elastocaloric properties at the stresses and strains below the final stress (strain) differ significantly if strain rate is applied instead of stress rate. For Ni–Ti alloy the isothermal entropy changes are shown for the strain up to 5.71% (with the step of 1.27%), while up to 6% (with the step of 1.5%) for Cu–Zn–Al alloy.

Comparing the eCE of the Ni–Ti alloy with the Cu–Zn–Al alloy, we can see that the Ni–Ti alloy has a larger eCE, i.e. larger isothermal entropy and adiabatic temperature changes. These results are also directly from the Clausius–Clapeyron equation [Eq. (4)] due to a larger product of transformation strain (ε tran) and Clausius–Clapeyron coefficient [(dσ/dT)cr]. It is further evident that due to the smoother transformation knees and smaller slope of the transformation plateau, the eCE for the Cu–Zn–Al alloy occurs in a narrower temperature region, i.e. is less spread out over temperature. We can further conclude that due to a smaller Clausius–Clapeyron coefficient of the Cu–Zn–Al alloy, the applied stress required to generate the eCE at a certain temperature range is significantly lower compared to the Ni–Ti alloy. On the other hand, a smaller (transformation) strain change is needed in the case of Ni–Ti alloy. Furthermore, due to smaller hysteresis of the Cu–Zn–Al alloy, the temperature irreversibilities, which are the difference in adiabatic temperature change during loading compared to unloading, are smaller compared to Ni–Ti. It should be noted that similar trends of the elastocaloric properties shown here (Fig. 6) are typically found also for first-order magnetocaloric materials [58, 59].

A comparison of modelled and measured (using thermocouples) adiabatic temperature changes for the Ni–Ti alloy is shown in Fig. 6c. The details of the measurements of the adiabatic temperature change can be found in [7]. We can see that the calculated adiabatic temperature changes are higher than the measured values by approximately 25%, but with the same trend of dependency. There are two reasons for the observed over predictions: (1) the measuring conditions were not fully adiabatic and the thermal resistance between the wire and the thermocouple results in some heat losses and (2) the experiments were performed only up to the strains slightly above the transformation plateau. Since there are some additional minor transformations even beyond the quite well-defined transformation plateau, the performed transformation in the experiment was not fully completed and the adiabatic temperature change was limited. The model, on the other hand, assumes complete transformation at the end of the transformation plateau, i.e. at a point where loading and unloading or cooling and heating curves come together at each temperature or stress.

Data Correction for Cyclic Elastocaloric Effect

Since it is often required to analyse the eCE under cyclic conditions, in particular when the final goal is to evaluate an elastocaloric material in a cooling (heat-pumping) device, a special attention must be paid in addressing the above presented elastocaloric properties. It should be noted that when an elastocaloric material is cyclically (un)loaded up to the stress at which the transformation is not fully completed (at a particular temperature), a correction of the elastocaloric properties shown in Fig. 6 is required. This situation is presented in Fig. 7. Figure 7a shows the stress–strain behaviour at three different temperatures. At the temperature T 2, both forward and reverse transformations are fully completed and at this temperature the model correctly predicts the elastocaloric properties, and no data correction is required. On the other hand, at the temperature T 3, the predicted unloading curve (dotted line) is unrealistic at the applied conditions, since the material can be unloaded only from the strain up to the point which it has been loaded. The dotted line would occur if the material would be fully transformed during loading, which would at this temperature occur at the stress above 800 MPa. Therefore, if the transformation is not completed, a correction needs to be applied into the model to correctly predict the unloading curve. This is done by calculating a martensite phase fraction, i.e. the ratio of martensite and austenite phase at each temperature and stress, in order to start the unloading from the same phase fraction as it occurs during loading. As shown in Fig. 7b, this further results in a smaller negative adiabatic temperature change at this temperature than initially predicted by the model. An analogue situation occurs also in first-order magnetocaloric materials as described in [60]. However, the situation is different at the temperature T 1, which is slightly below the austenitic finish temperature of the evaluated material. As noted in Fig. 7a with the dotted circle, a reverse transformation is not fully completed, and therefore the material remains slightly deformed (with some residual strain) even when the material is completely unloaded. This results in a larger eCE during loading than unloading at the temperature range between the austenitic start and austenitic finish temperature as displayed in Fig. 7b. This effect is already included in the model and no further corrections are required. However, if the material would be cyclically (un)loaded at that temperature the residual strain would gradually increase until the full sample would be martensitic after unloading, and the superelastic response and the eCE would disappear. Therefore, a precondition for a reproducible eCE is that the operating temperature is above the material’s austenitic finish temperature in order to avoid this situation. Furthermore, if adiabatic (un)loading is applied, which results in higher slope of the transformation plateau as it is usually the case during the exploitation of the eCE in an elastocaloric device, the operating temperature needs to be higher than material’s austenitic finish temperature (at least for a value of adiabatic temperature change higher). If the operating temperature is lower (but higher than austenitic finish temperature) this might result in a slight bending of the material (if loaded in tension) immediately after unloading and reduced negative adiabatic temperature change since the martensite is not fully transformed back to austenite as explained in detail in [7].

Fig. 7
figure 7

a Stress–strain behaviour of the Ni–Ti alloy at three different temperatures that correspond to three different cases (at T 1 reverse transformation is incomplete, at T 2 both transformations are complete, at T 3 both transformations are incomplete). b An example of corrected adiabatic temperature changes for unloading (the applied stress is 800 MPa)

Full size image

Efficiency of the Elastocaloric Effect

Another important property of the eCE is its efficiency. The most commonly used metric of efficiency of the cooling/heat-pumping cycle is the COP. It is defined as the ratio of the cooling (heating) power with the input work required to perform a thermodynamic cycle:

$${\text{COP}} = \frac{{\dot{Q}}}{{\dot{W}}}.$$
(10)

It is important to distinguish between COP of a material and COP of a system (device). The material’s COP can be calculated as follows(written with energies):

$${\text{COP}}_{m} = \frac{Q}{W} = \frac{{m \cdot c \cdot \Updelta T_{\text{ad}} }}{{\frac{1}{\rho }\oint {\sigma \cdot {\text{d}}\varepsilon } }}.$$
(11)

It should be noted that material’s COP calculated with Eq. (11) is the estimated value of the maximal COP that can be generated by elastocaloric material. The actual energy that can be transmitted from the material to the heat sink/source of the elastocaloric device and further its COP strongly depends on the efficiency of the heat transfer and operating frequency (number of performed cycles per time unit). If infinite frequency and ideal heat transfer between material and ambient are assumed, the device’s COP would essentially lead to the material’s COP calculated using Eq. (11). Therefore, the COP calculated with Eq. (11) is an upper limit of the COP value of the elastocaloric device at zero temperature span between heat sink and heat source. In reality, the device’s COP is often significantly lower due to additional losses, mostly irreversible heat transfer losses, i.e. in dependence on device configuration and its operating conditions, and enlargement of temperature span between heat sink and heat source (e.g. in regenerative device [29]), which is usually required in practical cooling or heat-pumping devices.

For example, applying isothermal (un)loading instead of adiabatic and assuming that the energy generated by the eCE is the same, even though adiabatic temperature change would be close to zero, can lead to an increase in the COP value, as the input work would be reduced (smaller hysteresis: see Fig. 1a). However, in this case irreversible heat transfer losses between the material and ambient would in reality significantly decrease the COP values of a device [61]. As shown in [27, 61], a combination of isothermal and adiabatic loading, namely, a combination of Ericsson and Brayton thermodynamic cycle, usually leads to the most efficient thermodynamic cycle for utilization of caloric effects.

An alternative and thermodynamically more consistent approach to calculate the COP values of the elastocaloric material is based on performed cycle in the total entropy–temperature diagram. Here, the COP is defined as (see Fig. 8)

$${\text{COP}}_{m} = \frac{Q}{W} = \frac{{Q_{\text{c}} }}{{Q_{\text{h}} - Q_{\text{c}} }} = \frac{{\mathop \smallint \nolimits_{4}^{1} T{\text{d}}S}}{{\mathop \smallint \nolimits_{3}^{2} T{\text{d}}S - \mathop \smallint \nolimits_{4}^{1} T{\text{d}}S}}.$$
(12)
Fig. 8
figure 8

An example of single-stage Brayton thermodynamic cycle (for zero temperature span between heat sink and heat source)

Full size image

It should be noted that the total entropy shown in Fig. 8 is calculated based on average isothermal entropy (for loading and unloading) at each temperature and applied stress, which is in accordance with equilibrium thermodynamics (entropy is a state function and therefore path and hysteresis independent). The entropy generated during loading and unloading process due to hysteresis is evident in Fig. 8 (noted with Δs hy).

The material’s COPs calculated using Eqs. (11) and (12) agree quite well as also shown in [26]. For the evaluated elastocaloric materials in this work, the material’s cooling COP values [calculated using Eq. (12)] at 350 K (and zero temperature span) and at applied stress at which both materials performed complete forward and reverse transformation are 8.8 and 14.2 for Ni–Ti and Cu–Zn–Al alloy, respectively. As shown in [20], COP values are increasing with decreased strain. As expected, Cu–Zn–Al alloy exhibit a larger COP value due to the significantly smaller hysteresis and related irreversibility losses. Comparing the material’s COP values reported here with the COP values of regenerative elastocaloric cooling device with the same elastocaloric materials operating at a temperature span of 30 K evaluated numerically [29] reveals that the device’s COP values are less than half of the material’s COP due to heat transfer losses and thermodynamic work required to increase the temperature span as already discussed.

Conclusions and Future Prospective

The eCE of SMAs has recently attracted significant attention for application in cooling and heat-pumping devices in different scales (electronic cooling, domestic appliances, cooling in transport applications, etc.). In general, the devices utilizing the eCE can be characterized as potentially highly efficient, environmentally friendly, solid-state devices with significant future potential. In the initial stages of the development of an elastocaloric device, a theoretical approach with numerical modelling is often required. In addition to characterization and comparison of the eCE of different elastocaloric materials, direct and indirect experimental methods combined with modelling approaches presented in this work can be applied for generating the required thermodynamic properties to be used as the basis for the numerical evaluation elastocaloric devices. The proposed methods can be potentially applied also for other materials to be discovered in the future. However, it was shown that indirect methods result in larger and generally more representative values of the adiabatic temperature changes of the eCE, as the adiabatic conditions are difficult to assure in reality. In a combination with proposed phenomenological model, indirect methods also enable more accurate description of elastocaloric properties (at any applied stress/strain and temperature), which is especially important if those are further applied for the modelling of an elastocaloric device.

Currently, the main drawback of elastocaloric technology is the limited fatigue life of most elastocaloric materials. It is estimated that in the lifetime of 10 years an elastocaloric material in a cooling or heat-pumping device has to perform up to 108 loading cycles. It was recently demonstrated that thin film Ni–Ti–Cu–Co alloy made by sputtering can withstand up to 107 loading cycles with no structural and functional fatigue and significant eCE [10]. This is an important step forward in the development of the applicable elastocaloric materials and further progress in that field is expected in the next years.