Skip to main content
SpringerLink
Log in

Exploring the dynamics of Bitcoin’s price: a Bayesian structural time series approach

  • Original Paper
  • Published:
Eurasian Economic Review Aims and scope Submit manuscript

Abstract

Currently, there is no consensus on the real properties of Bitcoin. The discussion comprises its use as a speculative or safe haven asset, while other authors argue that the augmented attractiveness could end up accomplishing money’s properties that economic theory demands. This paper explores the association between Bitcoin’s market price and a set of internal and external factors by employing the Bayesian structural time series approach (BSTS). The idea behind BSTS is to create a superposition of layers such as cycles, trend, and explanatory variables that are allowed to vary stochastically over time, additionally, it is possible to perform a variable selection through the application of the Spike and Slab method. This study aims to contribute to the discussion of Bitcoin price determinants by differentiating among several attractiveness sources and employing a method that provides a more flexible analytic framework that decomposes each of the components of the time series, applies variable selection, includes information on previous studies, and dynamically examines the behavior of the explanatory variables, all in a transparent and tractable setting. The results show that the Bitcoin’s price is negatively associated with the price of gold as well as the exchange rate between Yuan and US Dollar, while positively correlated to stock market index, USD to Euro exchange rate and diverse signs among the different countries’ search trends.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

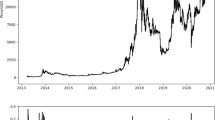
Source: Blockchain’s official website

Fig. 3

Source: Google trends

Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Notes

  1. The People’s Bank of China.

  2. Another debate around bitcoin’s digital currency and its appropriateness as money can be found in Böhme et al. (2015), Glaser et al. (2014), Rogojanu and Badea (2014), Simser (2015) and Wisniewska (2015).

  3. These variables will be explained in detail in the data section.

  4. Increasing risks in financial markets have established the need to invest in another type of assets, precious metals being the most frequent ones.

  5. For a broader discussion on gold’s and other assets application see Baur and Lucey (2010), Baur and McDermott (2010) and Ciner et al. (2013).

  6. Dynamic Time Warping (DTW) is a technique to find optimal alignment between time-dependent sequences. This method is particularly useful to measure similarity and, by extension in classification problems. For a broader explanation and application of this method read the reviews of Kate (2016) and Vaughan (2016).

  7. See Parmigiani et al. (2009) and West and Harrison (1996) for a further discussion.

  8. MCMC samplers must be checked in order to prove the distributional assumptions about the simulation, and it has to be stable over several draws. In most cases reduce by thinning (eliminating the burn-in iterations in compliance with parameter stability).

  9. Among the discrete version, we have the forward/backward stepwise selection that filters through all possible subsets, nevertheless is computationally costly when the number of predictors becomes large. On the other side, penalized shrinkage methods such as LASSO (Tibshirani 1996) or Ridge (Hoerl and Kennard 1970) are more generally recommended, especially in high-dimensional settings.

  10. The symmetric mean absolute percentage error (sMAPE) is an accuracy measure based on relative errors, it is evaluated as: \(\frac{100}{n}\mathop \sum \nolimits_{t = 1}^{n} \frac{{|\widehat{{Y_{t} }} - Y_{t} |}}{{(|Y_{t} | - |\widehat{{Y_{t} }}|)}}\).

  11. The mean absolute error (MAE) is as its name describes \(\frac{{\mathop \sum \nolimits_{t = 1}^{n} |\varepsilon_{i} |}}{n}\).

  12. The mean squared error (MSE) is represented as \(\frac{{\mathop \sum \nolimits_{t = 1}^{n} \varepsilon_{i}^{2} }}{n}\).

  13. Stability of the further simulation was proved given the update of the priors (Fig. 13).

  14. Extension of the process is described in detail in Xi et al. (2016).

References

Download references

Author information

Authors and Affiliations

  1. Universitat Autònoma de Barcelona, 08193, Barcelona, Spain

    Obryan Poyser

Authors
  1. Obryan Poyser
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Obryan Poyser.

Additional information

This paper has won the “Best Paper Award” in the 23rd EBES Conference held in Madrid on September 27–29, 2017.

Appendices

Appendix 1: Standardized coefficients effects on interpretation

Standardization of both sets of regressors and independent variables leads to several changes in interpretation and results. Here we present some of the very common:

  1. 1.

    The coefficient between \(x\) and \(y\) standardized variables will be equal to the covariance of them.

    $$\beta_{yx}^{*} = \frac{{cov(z_{y} ,z_{x} )}}{{var(z_{x} )}} = \frac{{cov(z_{y} ,z_{x} )}}{1} = cov(z_{y} ,z_{x} )$$
  2. 2.

    As expected, the covariance of \(x\) on \(y\) is equal to the covariance of \(y\) and \(x\)

    $$\beta_{xy}^{*} = \beta_{yx}^{*}$$
  3. 3.

    The covariance between two standardized variables is equal to the correlation between them

    $$\rho_{xy} = \frac{{cov(z_{y} ,z_{x} )}}{{\sigma (z_{x} )\sigma (z_{y} )}} = cov(z_{x} ,z_{y} )$$

Appendix 2: Gibbs sampling

Gibbs sampling generates posterior samples by smoothly moving through each variable to sample from its conditional distribution with the remaining variables fixed. The algorithm does not sample from the posterior directly, instead, it simulates samples from one random variable at a time. According to MCMC theory, the Gibbs sampler will converge to the target posterior (Yildirim 2012). For \(X_{D}\) random variables the algorithm works as:

$$\begin{array}{*{20}r} \hfill \begin{aligned} Initialize\:x^{0} \:q(x)\:for\:iteration\:i = 1, \ldots ,do \hfill \\ x_{1}^{1} \sim p(X_{1} = x_{1} |X_{2} = x_{2}^{i - 1} ,X_{3} = x_{3}^{i - 1} , \ldots ,X_{D} = x_{D}^{i - 1} ) \hfill \\ \end{aligned} \\ \hfill {x_{2}^{1} \sim p(X_{2} = x_{2} |X_{1} = x_{1}^{i - 1} ,X_{3} = x_{3}^{i - 1} , \ldots ,X_{D} = x_{D}^{i - 1} )} \\ \hfill \vdots \\ \hfill {x_{3}^{1} \sim p(X_{3} = x_{3} |X_{1} = x_{1}^{i - 1} ,X_{2} = x_{2}^{i - 1} , \ldots ,X_{D} = x_{D}^{i - 1} )} \\ \end{array}$$

Appendix 3: Extra graphics

See Figs. 10, 11, 12 and 13.

Fig. 10
figure 10

Periodogram of Bitcoin’s price

Full size image
Fig. 11
figure 11

Average search trend values by cluster

Full size image
Fig. 12
figure 12

Markov chain and Monte Carlo Simulations for time-invariant \(\beta\) coefficients

Full size image
Fig. 13
figure 13

Marginal posterior distributions employed to generate priors

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Poyser, O. Exploring the dynamics of Bitcoin’s price: a Bayesian structural time series approach. Eurasian Econ Rev 9, 29–60 (2019). https://doi.org/10.1007/s40822-018-0108-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40822-018-0108-2

Keywords

Search

Navigation