1 Introduction

With the rapid development of electronic information technology, electromagnetic wave exists everywhere in our environment that not only interferes with the electromagnetic control system and negates the effects of equipment, but also harms the physical and mental health of human beings. Therefore, it is of great significance to develop absorbing materials with electromagnetic wave absorbing ability that can both mind the requirements of “wide, thin, light and strong” [1,2,3,4]. Moreover, the miniaturization and integration of electronic circuits and components put forward the request of flexible portable microwave absorption electronic devices [5, 6].

Two-dimension (2D) materials, such as reduced graphene oxide (RGO) [7,8,9,10], MoS2 [11,12,13,14,15], and new member Mxene [16,17,18,19], are usually applied as microwave absorber owing to their high specific surface area and abundant functional groups as well as defects, which will enhance the propagation paths of incident electromagnetic wave (EMW) inside absorbers by scattering effect and increase the loss through polarization relaxation loss. As one of the 2D material, MoS2 has adjustable electrical property and can change between insulators and semiconductor metals. It has important applications in many fields such as optoelectronics [20, 21], secondary batteries [22, 23], and catalysis [24, 25]. In addition, MoS2 also has been proved to be an effective dielectric-type EMW absorbing material. As we know, MoS2 exists in various phase forms, such as 2H, 1T, and 3R. The natural MoS2 usually exists in the form of 2H (hexagonal) phase that the stacking sequence is AbA, BaB (the capital and lower case letters denote chalcogen and metal atoms, respectively), showing an adjustable band gap of 1.3–1.9 eV and presenting semiconductor properties. However, the inherent low conductivity loss would limit its further practical application in microwave absorption to some extent. The octahedral coordination of 1T (triangle)-MoS2 structure has metallic property that the stacking sequence is AbC, AbC, and belongs to metastable structure, but it shows a high electrical conductivity [26]. Therefore, combined with above advantages, the mixed phase MoS2 (1T@2H-MoS2) would have the great application potential in the field of microwave absorption [27].

Up to now, many researches about 2H-MoS2 applied for EMW absorbing field have been reported [28]. Cao et al. [29] investigated the EMW absorption properties of few-layered pure MoS2 nanosheets that prepared by a top-down exfoliation method. The optimum electromagnetic absorbing performance parameters of MoS2-NS/wax with 60% loading are −38.42 dB, 2.4 mm. Though the single 2H MoS2 exhibited good EMW absorption performance, the sample in sample-paraffin needs to fill in a high proportion, this will undoubtedly limit their practical application. There already have a few advances about 1T@2H-MoS2 as one of the components to EMW absorbing. Liu et al. [30] designed a 3D carbon foam/1T@2H-MoS2 composites, which had the maximum reflection loss of −45.88 dB. Moreover, Che et al. [31] planted the 1T@2H-MoS2 into RGO via ammonia insert and high-temperature annealing of 2H-MoS2/RGO, and this composite exhibited the excellent EMW absorption ability with the sample mass ratio of 30% in sample-paraffin. These researches mainly focus on the 1T@2H-MoS2-based composites, not involve pure 1T@2H-MoS2, let alone profound explore the influence of different MoS2 phase for electromagnetic absorbing properties.

In this work, we try to prepare two type phases of MoS2 via a simple synthesis method and compare the electromagnetic parameters corresponding to different phases of MoS2, thus obtain the excellent EMW absorber by analyzing the EMW absorbing mechanism. Normally, the transformation of MoS2 from 2H to 1T can be achieved by chemical exfoliation or substitutional doping [32, 33], which are complex and low yield. Herein, we developed a facile one-step hydrothermal method for producing gram-scale 1T@2H-MoS2 by imbedding the guest molecules and ions. The 2H-MoS2 is obtained by annealing treatment of 1T@2H-MoS2. The results show that 2H MoS2 and 1T@2H-MoS2 both can effectively EMW absorbing. The synergistic effect between 1T phase and 2H phase of 1T@2H-MoS2 in EMW absorbing can further improve the dielectric loss, which makes single 1T@2H-MoS2 has a great application prospect in the field of EMW absorbing. In addition, a flexible EMW absorbers that ultrathin 1T/2H MoS2 grown on the carbon fiber (CF) by using the same method except the adding of CF, which performs outstanding performance only with the matrix loading of 5%, again prove the significance of this work.

2 Experimental Section

2.1 Synthesis of 1T/2H MoS2

The (NH4)6Mo7O24·H2O (0.88 g) and CH3CSNH2 (0.9 g) were ultrasonic dissolved in 50 mL water, and then 1.98 g NH4HCO3 was added and stirred for 30 min to form a uniform liquid. The above solution was transferred into the 100-mL hydrothermal synthesis reactor and heated to 200 °C for 13 h. After cooling to room temperature, the black sediments were collected and washed with deionized water and ethanol for further use. The final product was obtained by drying in the vacuum oven for 12 h.

2.2 Synthesis of 2H MoS2

The above 1T/2H MoS2 was placed in an argon tube furnace and heated to 400 °C with a heating rate of 10 °C min−1 for 2 h to obtain 2H MoS2.

2.3 Synthesis of CF@1T/2H MoS2 and CF@2H MoS2

The CF is obtained via a simple electrospinning method, and the detailed process is in the supporting information [34]. The synthesis process of CF@1T/2H MoS2 and CF@2H MoS2 is the same as 1T/2H MoS2 and 2H MoS2 except adding the 0.5 g CF after the solution is transferred to hydrothermal synthesis reactor.

3 Results and Discussion

3.1 Composition and Structure

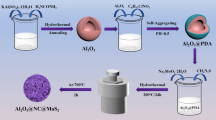
The schematic diagram of single MoS2 is shown in Scheme 1a. The 1T/2H MoS2 is successfully fabricated by hydrothermal method. As a guest, the ammonium bicarbonate decomposes into small molecules and ions such as NH4+, H2O, and CO2, which are inserted into the layered structure of MoS2 to form 1T/2H phase polyphase MoS2, consisting of 1T phase and 2H phase. The electrical conductivity of 1T/2H phase is greatly improved owning to the existence of the 1T phase. Furthermore, the combination with 2H phase helps to stabilize the metastable 1T phase and avoids the re-accumulation and transition to 2H phase. The transition from 1T/2H MoS2 to 2H MoS2 is by annealing treatment. The synthesis principle of CF@1T/2H MoS2 is similar to that of 1T/2H MoS2, as shown in Scheme 1b. Considering the advantages of 1T/2H MoS2, the carbon fiber is chosen as a flexible substrate to obtain high-performance flexible EMW absorbing film.

Scheme 1
scheme 1

Schematic drawings illustrating the fabrication process of single MoS2 (1T/2H MoS2 and 2H MoS2) and flexible CF/MoS2 film (CF@1T/2H MoS2 and CF@2H MoS2)

Full size image

The X-ray diffraction (XRD) patterns of MoS2 samples with different phases are shown in Fig. 1a. Obviously, the 1T/2H MoS2 and 2H MoS2 have different XRD patterns. The (002) crystal-peaks value of 2H MoS2 located at 14.4°, corresponds to the standard 2H phase bulk MoS2 (PDF card #75-1539) [35, 36]. As for 1T/2H MoS2, the corresponding (002) crystal peaks are situated at 2theta = 9.5° and 15.9°, and the d spacing difference between two (002) peaks proves the interlayer expansion. To further analyze the sample structure, Raman spectroscopy is introduced between 100 and 600 cm−1, as shown in Fig. 1b. The intensity ratio of peak E1g, E2g1, and A1g is situated at 284.7, 381.7, and 403.3, respectively. However, the intensity of E2g1 and A1g peaks over 1T/2H MoS2 is greatly decreased because of less 2H phase and worse crystallinity. As for 1T/2H MoS2, the additional strong peaks at 150.3 (J1), 215.6 (J2), and 336.8 (J3) cm−1 are observed, suggesting the formation of 1T phase MoS2. After annealing, the J1, J2, and J3 peaks of the 1T phase become very weak, and E1g, E2g1, and A1g peaks of the 2H phase become more significant, indicating that the 1T phase is successfully converted to the stable 2H phase. X-ray photoelectron spectrometer (XPS) displays the element content on the material surface. In Fig. 1c, the two peaks located at around 229 and 232 eV correspond to the spectra of Mo 3d5/2 and Mo 3d3/2, clarifying the existence of 2H phase [37]. The peak at 226 eV corresponds to the spectra of S 2 s. Moreover, as for 1T/2H MoS2, two other peaks around 228 and 231 eV are observed, which have the 1 eV shift compared to that of 2H MoS2, proving the presence of the metallic 1T phase [38, 39]. Similarly, the two peaks can be observed at around 162.7 and 161.6 eV corresponding to the spectra of S 2p1/2 and S 2p3/2 (Fig. 1d). However, two additional peaks are found to shift to lower binding energies at around 161 and 160.5 eV, which once again suggests the presence of metallic 1T phase [39]. The content of 1T phase is estimated to be 61% by calculating the peak area. In Fig. 1e, the N 1 s in the Mo 3p spectra of 1T/2H MoS2 demonstrates the presence of the N element in 1T/2H MoS2. But no N element can be detected after annealing in 2H MoS2. The peak at around 402 eV corresponding to the spectra of the N 1 s in Fig. 1f should be attributed to the intercalation of NH4+.

Fig. 1
figure 1

a XRD patterns, b XPS spectra, c Mo 3d spectra, d S 2p spectra, e Mo 3p spectra of 1T/2H MoS2 and 2H MoS2. f N 1s spectra of 1T/2H MoS2

Full size image

Figure 2 shows the SEM and TEM images of synthesized 1T/2H MoS2. The SEM image (Fig. 2a) demonstrates that the 1T/2H MoS2 is made up of an infinite number of tiny nanosheets, which is more clearly revealed by the TEM image in Fig. 2b, c. The crosswise dimension of each lamellar is approximately 80 nm. The high-resolution TEM image (Fig. 2d) confirms the co-existence of the trigonal prismatic 2H phase and the octahedral 1T phase in 1T/2H MoS2. Furthermore, the lateral heterostructures of 1T (Fig. 2e) and 2H (Fig. 2f) phases could also be clearly visualized by zooming in the selected area of Fig. 2d. The element mapping images and EDX (Fig. S1) of 1T/2H MoS2 demonstrate the uniform distribution of Mo and S elements. The N in the mapping of 1T/2H MoS2 also demonstrates the presence of the N element in 1T/2H MoS2, which is consistent with the XPS results. After annealing, the absence of N of the annealed 2H MoS2 as revealed by Fig. S2, the morphology and microstructure of 2H MoS2 are observed as shown in Fig. S3. On macroscopic view, the 2H MoS2 remains the same morphology of 1T/2H MoS2, but only the 2H phase can be find in the zoom HRTEM Fig. S3d, which demonstrates 1T phase is transformed into 2H phase under annealing condition completely.

Fig. 2
figure 2

a SEM image, b, c TEM image, d HRTEM images of 1T/2H MoS2. e, f Enlarged images of the selected yellow area

Full size image

To meet the demand of portable microwave absorption electronic devices, high-performance flexible film absorbers are urgently needed to be developed. Inspired by the synthetic methods of single 1T/2H MoS2 and 2H MoS2, the CF is added to the experiment as a substrate to obtain the flexible CF@1T/2H MoS2 and CF@2H MoS2 films. The XRD pattern and Raman spectrum of sample are shown in Fig. 3. In Fig. 3a, the CF@1T/2H MoS2 and CF@2H MoS2 have the same peaks as previous 1T/2H MoS2 and CF@2H MoS2 except the peak of carbon. As for Fig. 3b, the intensity ratio of peak D and G, situated at 1350 and 1580 cm−1, respectively, the characteristic peak of carbon material, can reflect the presence of carbon fiber. In this figure, the peaks of MoS2 are not obvious because the intensity of D peak and G peak is too high. After zooming the area of 150–600 cm−1, the E1g, E2g1, A1g in both CF@1T/2H MoS2 and CF@2H MoS2, the J1, J2, J3 peaks in CF@1T/2H MoS2 are the same as those in Fig. 1b.

Fig. 3
figure 3

a XRD patterns, b Raman spectroscopy of CF@1T/2H MoS2 and CF@2H MoS2

Full size image

To prove the microstructure and morphology of the obtained materials even further, SEM and TEM are also used to study the specific information of pure CF, CF@1T/2H MoS2, and CF@2H MoS2. The bare carbon fibers are made up of countless 400-nm-thin fibers, as shown in Fig. S4. The CF cloth has good flexibility and can be easily bent. After in situ growth of the CF@1T/2H MoS2 and CF@2H MoS2, it is easily seen that many sheets are coated on the surface of carbon fibers from Figs. 4 and S5, which turns out the same way that we did before to synthesize 1T/2H MoS2 and CF@2H MoS2 can also be used to synthesize flexible CF-based material. The presence of oxygen element in Fig. 4c comes from CF. Moreover, a large interlayer spacing of 9.3 Å is also observed in Fig. 4f, which should be attributed to the insertion of guest ions or molecules [24].

Fig. 4
figure 4

a, b SEM image, c element mapping of C, O, S, Mo, d, e TEM image, f HRTEM images of CF@1T/2H MoS2

Full size image

3.2 Electromagnetic Performance and Parameter

The coaxial transmission line method is adopted with aid of a vector network analyzer to obtain the EM parameters. First, the samples are mixed with paraffin with different mass ratio under 70 °C and then compressed into rings with natural cooling (diameter of the rings: φext = 7.00 mm, φint = 3.0 mm.) Normally, as for a absorber, the absorption strength mainly depends on the magnetic loss and dielectric loss, which are defined by the complex permeability (μr) and permittivity (εr) [40,41,42]:

$$\varepsilon_{r} = \varepsilon {^\prime} - j\varepsilon {^\prime }$$
(1)
$$\mu_{r} = \mu ^{\prime} - j\mu ^{\prime \prime}$$
(2)
$${\text{tan}}\delta_{\varepsilon } = \varepsilon ^{\prime \prime} /\varepsilon ^{\prime}$$
(3)
$${\text{tan}}\delta_{\mu } = \mu ^{\prime\prime}/\mu ^{\prime}$$
(4)

Generally speaking, the real and imaginary part indicate energy storage and energy loss, tanδε represents the ratio of energy loss capability to storage capability [43, 44]. In order to effectively explore the influence of different phase on the electromagnetic properties of MoS2, we measured the electromagnetic parameters of the 1T/2H MoS2 and 2H MoS2 with six kinds of proportion; the sample filling mass ratios in sample-paraffin mixture are 50%, 40%, 30%, 20%, 15%, and 10%. As shown in Fig. 5a, as for 1T/2H MoS2, the ε′ of six ratio 50%, 40%, 30%, 20%, 15%, and 10% are 12, 10.17, 9.16, 5.86, 4.31, and 3.59, respectively. As for 2H MoS2, the ε′ of six ratios 50%, 40%, 30%, 20%, 15%, and 10% are 4.2, 3.67, 3.13, 2.8, 2.7, and 2.6, respectively. More broadly, all the initial values of two samples both display the downward trend because MoS2 is a single dielectric loss type material. Thus, ε′ values naturally decrease as the sample proportion decreases. Moreover, the matrix loading percentage—initial ε″ curve of 1T/2H MoS2 and 2H MoS2, is shown in Fig. S6a. As matrix loading percentage goes down, so does initial ε″ values. The initial ε″ curve of 1T/2H MoS2 is still higher than 2H MoS2 at the same sample proportion. The all six ε′, ε″ and tanδε curves of 1T/2H MoS2 and 2H MoS2 are shown in Fig. S7. Overall, all ε′, ε″ and tanδε values of 1T/2H MoS2 are higher than the 2H MoS2 under the same sample ratio owing to the high electrical conductivity of 1T/2H MoS2. The conductivity of 1T/2H MoS2 and 2H MoS2 measured by four-point probe is 9 × 10–2 and 1.515 × 10–2, respectively, as shown in Fig. S9. The high conductivity of 1T/2H MoS2 not only can produce the more conduction loss, but also can improve the dielectric property compared with 2H MoS2. To be sure, the μ′ and μ″ values of single dielectric loss type material are the constant value 1 and 0, respectively.

Fig. 5
figure 5

a, b Matrix loading percentage–initial ε′ of 1T/2H MoS2 and 2H MoS2, CF@1T/2H MoS2 and CF@2H MoS2. c, d Calculated reflection loss of 1T/2H MoS2 and 2H MoS2 with the matrix loading of 15wt%. e, f CF@1T/2H MoS2 and CF@2H MoS2 with the matrix loading of 5wt%

Full size image

After adding CF, the study sample filling ratio is decreased because CF is also a high-dielectric loss type material. The final study ratios of CF@1T/2H MoS2 and CF@2H MoS2 are 10%, 7%, 5%. In Fig. 5b, the initial ε′ of 10%, 7%, 5% CF@1T/2H MoS2 are 12.2, 9.26, 6.1, respectively. Comparatively, the initial ε′ of 10%, 7%, 5% CF@2H MoS2 are 5.78, 4.97, 4.42, respectively. From Fig. S5b, we can also draw the same conclusion of the initial ε″ of CF@1T/2H MoS2 with 10%, 7%, and 5% ratios higher than the CF@2H MoS2 with 10%, 7%, and 5% ratios. The all three ε′, ε″, and tanδε curves of CF@1T/2H MoS2 and CF@2H MoS2 are shown in Fig. S8a-f. From the result, we can find even the initial ε′ value of 10% ratio CF@1T/2H MoS2 higher than 50% ratio single 1T/2H MoS2, which highlights the role of flexible CF. Furthermore, the conductivity of pure CF, CF@2H MoS2, and CF@1T/2H MoS2 measured by four-point probe are 1.5 × 10–1, 2.257 × 10–1, and 5.298 × 10–1, respectively, as shown in Fig. S9, consistent with the result of high initial ε′ value of 10 wt% CF@1T/2H MoS2.

The calculation of reflection loss can be based on the theory of electromagnetic wave transmission line, as shown in the following formula [45,46,47]:

$$R_{{\text{L}}} \left( {d{\text{B}}} \right) = 20\log_{10} \left| {\frac{{Z_{{{\text{in}}}} - Z_{0} }}{{Z_{{{\text{in}}}} + Z_{0} }}} \right|$$
(5)
$$Z_{{{\text{in}}}} = Z_{0} \sqrt {\mu_{{\text{r}}} /{\upvarepsilon }_{{\text{r}}} } {\text{tan}}h\left[ {j\left( {2\pi fd/c} \right)\sqrt {\mu_{{\text{r}}} \varepsilon_{{\text{r}}} } } \right]$$
(6)

Among them, Zin refers to the normalized input impedance of electromagnetic wave absorbing materials; Z0 refers to the impedance matching value in free space; f refers to the frequency of incident electromagnetic wave; d refers to the thickness of absorbing material; c refers to the propagation speed of electromagnetic wave. From Fig. 5c, d, as for the 15% filler loading of single MoS2, the more intuitive information can be obtained. As for 1T/2H MoS2, when the thickness is 2.6 mm, the minimum reflection loss (RLmin) value of 1T/2H MoS2 can reach −52.7 dB at 17.7 GHz. The EMW absorption performance of the sample 2H MoS2 is shown in Fig. 5d. The 2H MoS2 with 15% filler loading is almost impossible to achieve electromagnetic absorption because the low ε′ value. Herein, if RL = −10 dB at a certain frequency, the material can absorb 90% wave, which can be considered effective absorption. The region RL below −10 dB is called effective absorption bandwidth (EAB) [48, 49]. By contrast, the 2H MoS2 with high filler loading (50%) can exhibit a good EMW absorbing performance, as shown in Fig. S10. The RLmin is −60 dB when the thickness is 2.8 mm. Though 2H MoS2 also can behave effective EMW absorption, it is limited by big filler loading. In general, the 1T/2H MoS2 has a better electromagnetic absorption performance.

Figure 5e, f reflects the reflection loss of CF@1T/2H MoS2 and CF@2H MoS2 with the 5% filler loading. When the thickness is 2.7 mm, the RLmin value of CF@1T/2H MoS2 can reach −43 dB at 13.4 GHz only with 5% filler loading. Comparatively, the CF@2H MoS2 with 5% filler loading is almost impossible to achieve electromagnetic absorption. This result reasserts the superiority of 1T/2H MoS2.

In order to better reveal the EMW absorbing abilities of different phase, the 3D classical RL-f diagram (Fig. 6) can make a more intuitive comparison between the two kinds of materials. As shown in Fig. 6b, the corresponding EAB of 1T/2H MoS2 (15%) can reach 10.52 GHz when the thickness is from 1.5 to 4 mm, which is equivalent to a potential to absorb all waves in the X (8–12 GHz) and Ku (12–18 GHz) bands. As Fig. 6d shows, with the addition of CF, the EAB ranges from 9.25 to 18 GHz.

Fig. 6
figure 6

a, c 3D reflection loss, b, d corresponding contour maps of 1T/2H MoS2 (15%) and CF@1T/2H MoS2 (5%)

Full size image

3.3 EMW Absorption Mechanism

The next step is to explore the electromagnetic absorption mechanism of 1T/2H phase MoS2. As we know, good electromagnetic absorbing performance is closely related to the electromagnetic attenuation, more loss (here is dielectric loss) and good impedance matching. Firstly, the propagation paths of incident EMW inside MoS2-based absorbers can be enhanced by scattering effect because of the extreme thinness and high specific surface area of MoS2. Attenuation matching means the ability and speed to convert the energy of EM waves to other forms of energy. The higher the attenuation constant α is, the closer the material is to attenuation matching [50,51,52], and the specific formula is as follows:

$$\alpha = \frac{\sqrt 2 \pi f}{c} \times \sqrt {\left( {\mu {^{\prime \prime}} \varepsilon {^{\prime \prime}} - \mu {^\prime} \varepsilon {^\prime} } \right) + \sqrt {\left( {\mu {^{\prime \prime}} \varepsilon {^{\prime \prime}} - \mu {^\prime} \varepsilon {^\prime} } \right)^{2} + \left( {\mu {^\prime} \varepsilon {^{\prime \prime}} + \mu {^{\prime \prime}} \varepsilon {^\prime} } \right)^{2} } }$$
(7)

In Fig. 7a, four curves rise by frequency, and with the addition of CF, all the curves are in order of height: CF@1T/2H MoS2 (5%) ≥ 1T/2H MoS2 (15%) ≥ CF@2H MoS2 (5%) ≥ 2H MoS2 (15%). The maximum α value rises from 50 to 350. At their RLmin point, α of CF@1T/2H MoS2 (5%) is 236, larger than that of the CF@2H MoS2 (5%). The α of 1T/2H MoS2 (15%) is 73, still larger than that of the 2H MoS2 (15%). This proves that the 1T/2H MoS2 based material has good attenuation loss capacity.

Fig. 7
figure 7

a Attenuation constant of 1T/2H MoS2 and 2H MoS2 (15%), CF@1T/2H MoS2 and CF@2H MoS2 (5%). b Cole–Cole semicircle of 1T/2H MoS2 (15%) and CF@1T/2H MoS2 (5%)

Full size image

The dielectric loss in 2–18 GHz is chiefly dominated by polarization relaxation. Figure 7b shows the Cole–Cole semicircle analyzing how many relaxation processes each material own. According to the Debye theory,

$$\left( {\varepsilon {^\prime} - \frac{{\varepsilon_{{\text{s}}} + \varepsilon_{\infty } }}{2}} \right)^{2} + \left( {\varepsilon {^{\prime\prime}} } \right)^{2} = \left( {\frac{{\varepsilon_{{\text{s}}} - \varepsilon_{\infty } }}{2}} \right)^{2}$$
(8)

When ε″ varies with ε′, every semicircle represents a relaxation process [53,54,55]. The arc could be regarded as a similar process. For the 1T/2H MoS2, four processes are distinguished, while the CF@1T/2H MoS2 has five. More processes supply more dielectric loss; thus, the CF@1T/2H MoS2 has better dissipation ability.

To achieve an excellent absorption performance, the prerequisite is the less reflection, and zero reflection of the incident microwave is the best. Based on the transmission line theory, if the minimum RL could correspond to impedance matching ratio value (Z =|Zin/Z0|) equal 1 at the same frequency, the impedance of this material matches well. The calculation formula is as follows [56,57,58,59]:

$$Z_{{{\text{in}}}} = Z_{0} \sqrt {\mu_{{\text{r}}} /{\upvarepsilon }_{{\text{r}}} } {\text{tan}}h\left[ {j\left( {2\pi fd/c} \right)\sqrt {\mu_{{\text{r}}} \varepsilon_{{\text{r}}} } } \right]$$
(9)

The image in Fig. 8 displays the normalized input impedance of as-prepared samples. As we can see, the CF@1T/2H MoS2 (2.7 mm) and 1T/2H MoS2 (2.6 mm) meet this requirement, demonstrating the good impedance matching of 1T/2H MoS2-based absorber.

Fig. 8
figure 8

Dependence of the matching thickness (tm) on frequency (fm) under λ/4 and normalized input impedance of 1T/2H MoS2 (15%) and CF@1T/2H MoS2 (5%)

Full size image

When the thickness of the material is increasing, the frequency corresponding to minimum RL becomes smaller. This regularity is in line with the ¼ wave length model as follows [60,61,62]:

$$t_{{\text{m}}} = \frac{nc}{{4f_{{\text{m}}} \sqrt {\left| {\mu_{r} } \right|\left| {{\upvarepsilon }_{r} } \right|} }}$$
(10)

When the value of tmexp just falls on the curve tmfit, the electromagnetic wave is canceled because the two reflected waves formed by air-absorber and the metal-absorption interface form 180° out of phase. In the middle image of Fig. 8, all two curves of fit thickness decline with the increase in frequency. The circle marks correspond to the frequency that RL is reaching the minimum. The 1T/2H MoS2 (15%) and CF@1T/2H MoS2 (5%) perfectly fit the model by realizing the equality of two thicknesses of 2.6 and 2.7 mm, respectively. In total, considering the high dielectric loss result from better conductivity, big attenuation, good impedance matching and low filler loading, the as-prepared 1T/2H MoS2 is expected to exhibit excellent EMW absorbing abilities. Compared with the previous MoS2-based EMW absorbers, as shown in Table 1, the 1T/2H MoS2 and CF@1T/2H MoS2 can achieve the effective electromagnetic absorption only with low filler loading (15%) and (5%), respectively.

Table 1 Summary of MoS2-based EMW absorbers
Full size table

3.4 Radar Cross Section

When the geometrical shape of the absorbing material is stable, the radar cross section (RCS) is an important index to judge the absorbing ability of the absorbing material [63, 64]. The HFSS simulation is used to explore the RCS performance of CF@1T/2H MoS2 and 1T/2H MoS2. The aluminum (Al) plate is used as the substrate and set to a thin tube with 180 mm long and 5 mm thick [65]. The prepared samples are mixed with paraffin as the absorber coating; it has the same length as the Al plate but the thickness is chosen the above calculated thickness value corresponding to the optimum EMW absorbing performance. In this work, the thickness of 1T/2H MoS2 is 2.6 mm, the thickness of CF@1T/2H MoS2 is 2.7 mm, and the schematic diagram is shown in Fig. 9g. The incident direction of EM wave is oblique at 45°, the calculation can begin when the material is given an appropriate excitation boundary. After simulation calculations, the RCS values of Al plate and different absorbers are obtained. The 3D spherical coordinate diagrams in different directions and polar plots between −60°–60° are shown in Fig. 9a–f. It can be seen that when the EMW is incident on the Al plate coated with MoS2 absorber/paraffin mixture, the RCS values are smaller than that of single Al plate. In particular, the RCS values of 1T/2H MoS2 are smaller than 2H MoS2, which further proves the superiority of 1T/2H MoS2 as electromagnetic wave absorber. As for CF@1T/2H MoS2 and CF@2H MoS2, we can also draw a conclusion that the RCS values of CF@1T/2H MoS2 are smaller than CF@2H MoS2. In summary, the absorbers of 1T/2H MoS2 based material exhibit excellent EMW absorption performance.

Fig. 9
figure 9

a, b, d, e Three-dimensional spherical coordinate diagrams. c, f Polar coordinate diagram. g Schematic diagram of HFSS simulation analysis

Full size image

4 Conclusion

In this work, we successfully synthesize the 1T/2H MoS2 and 2H MoS2 through a facile hydrothermal route and profoundly explore the influence of different MoS2 phase for electromagnetic absorbing properties by analyzing electromagnetic parameters of 1T/2H MoS2 and 2H MoS2 with 50%, 40%, 30%, 20%, 15%, and 10% filler loading. As a result, the RLmin of 1T/2H MoS2 only with 15% filler loading can reach −52.7 dB at 17.7 GHz when the thickness is 2.6 mm. The excellent EMW absorption performance of 1T/2H MoS2 than 2H MoS2 is due to the high dielectric loss result from better conductivity, big attenuation and good impedance matching. In addition, taking the advantage of 1T/2H MoS2, the flexible CF@1T/2H MoS2 is also synthesized to mind the request of flexible portable microwave absorption electronic devices. When the thickness is 2.7 mm, the RLmin value of CF@1T/2H MoS2 can reach −43 dB at 13.4 GHz only with 5% filler loading.