Skip to main content

Advertisement

SpringerLink
Log in

Approximate Solution and Analysis of Smoking Epidemic Model with Caputo Fractional Derivatives

  • Original Paper
  • Published:
International Journal of Applied and Computational Mathematics Aims and scope Submit manuscript

Abstract

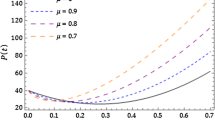
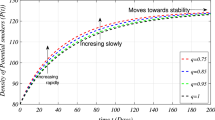
In this paper, an epidemic model is presented to describe the dynamics of drugs usage among the adults. The Caputo fractional derivative operator of order \(\phi \in (0, 1]\) is employed to obtain the system of fractional differential equations. Smoking is the large problem in the entire world. Despite the overwhelming facts about smoking, it is still a bad habit which is widely spread and socially accepted. A non-linear mathematical model is established to study and assess the dynamics of smoking and its impact on public health in a community. The analysis of two different states, disease free and endemic which means the disease dies out or persist in a population has been made by presenting sensitivity analysis. The stability of the model is provided by threshold or reproductive number. The Laplace Adomian decomposition method has been employed to solve smoking model which has five compartments, potential smoker P, occasional smokers O, smokers S, temporarily quit smokers Q and permanently quit smokers L. Finally, some numerical results are presented which shows the effect of fractional parameter \(\phi \) on our obtained solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Biazar, J.: Solution of the epidemic model by Adomian decomposition method. Appl. Math. Comput. 173, 1101–1106 (2006)

    MathSciNet  MATH  Google Scholar 

  2. Busenberg, S., Driessche, P.: Analysis of a disease transmission model in a population with varying size. J. Math. Bio. 28(1990), 65–82 (1990)

    MathSciNet  MATH  Google Scholar 

  3. El-Sayed, A.M.A., Rida, S.Z., Arafa, A.A.M.: On the solutions of time-fractional bacterial chemotaxis in a diffusion gradient chamber. Int. J. Nonlinear Sci. 7, 485–495 (2009)

    MathSciNet  MATH  Google Scholar 

  4. Makinde, O.D.: Adomian decomposition approach to a SIR epidemic model with constant vaccination strategy. Appl. Math. Comput. 184, 842–848 (2007)

    MathSciNet  MATH  Google Scholar 

  5. Arafa, A.A.M., Rida, S.Z., Khalil, M.: Fractional modeling dynamics of HIV and 4 T-cells during primary infection. Nonlinear Biomed. Phys. 6, 1–7 (2012)

    Article  Google Scholar 

  6. Kribs-Zaleta, C.M.: Structured models for heterosexual disease transmission. Math. Biosci. 160, 83–108 (1999)

    Article  MathSciNet  Google Scholar 

  7. Buonomo, B., Lacitignola, D.: On the dynamics of an SEIR epidemic model with a convex incidence rate. Ricerche Mat. 57, 261–281 (2008)

    Article  MathSciNet  Google Scholar 

  8. Liu, X., Wang, C.: Bifurcation of a predator–prey model with disease in the prey. Nonlinear Dyn. 62, 841–850 (2010)

    Article  MathSciNet  Google Scholar 

  9. Haq, F., Shah, K., Rahman, G., Shahzad, M.: Numerical solution of fractional order smoking model via Laplace Adomian decomposition method. Alex. Eng. J. (2017). https://doi.org/10.1016/j.aej.2017.02.015

    Article  MATH  Google Scholar 

  10. Erturk, V.S., Zaman, G., Momani, S.: A numeric analytic method for approximating a giving up smoking model containing fractional derivatives. Comput. Math. Appl. 64, 3068–3074 (2012)

    Article  MathSciNet  Google Scholar 

  11. Zaman, G.: Optimal campaign in the smoking dynamics. Comput. Math. Methods Med. Article ID 163834 (2011)

  12. Zaman, G.: Qualitative behavior of giving up smoking models. Bull. Malays. Math. Soc. 34, 403–415 (2011)

    MathSciNet  MATH  Google Scholar 

  13. Lubin, J.L., Caporaso, Z.E.: Cigarette smoking and lung cancer: modeling total exposure and intensity. Cancer Epidemiol. Biomark. Prev. 15, 517–523 (2006)

    Article  Google Scholar 

  14. Garsow, C.C., Salivia, G.J., Herrera, A.R.: Mathematical Models for the Dynamics of Tobacoo Use, Recovery and Relapse. Technical Report Series BU-1505-M, Cornell University, UK (2000)

  15. Sharomi, O., Gumel, A.B.: Curtailing smoking dynamics: a mathematical modeling approach. Appl. Math. Comput. 195, 475–499 (2008)

    MathSciNet  MATH  Google Scholar 

  16. Zeb, A., Chohan, I., Zaman, G.: The homotopy analysis method for approximating of giving up smoking model in fractional order. Appl. Math. 3, 914–919 (2012)

    Article  Google Scholar 

  17. Alkhudhari, Z, Al-Sheikh, S, Al-Tuwairqi, S: Global dynamics of a mathematical model on smoking. Appl. Math. Article ID 847075 (2014)

  18. Khalid, M., Khan, F.S., Iqbal, A.: Perturbation-iteration algorithm to solve fractional giving up smoking mathematical model. Int. J. Comput. Appl. 142, 1–6 (2016)

    Google Scholar 

  19. Agila, A., Baleanu, D., Eid, R., Irfanoglu, B.: Applications of the extended fractional Euler–Lagrange equations model to freely oscillating dynamical systems. Romanian J. Phys. 61, 350–359 (2016)

    Google Scholar 

  20. Abelman, S., Selvakumaran, K.A., Rashidi, M.M., Purohit, S.D.: Subordination conditions for a class of non-Bazilevivc type defined by using fractional q-calculus operators. Facta Universitatis Ser.: Math Info. 32, 255–267 (2017)

    Article  Google Scholar 

  21. Singh, J., Rashidi, M.M., Kumar, D., Swroop, R.: A fractional model of a dynamical Brusselator reaction–diffusion system arising in triple collision and enzymatic reactions. Nonlinear Eng. 5, 277–285 (2016)

    Google Scholar 

  22. Kumar, S., Kumar, D., Abbasbandy, S., Rashidi, M.M.: Analytical solution of fractional Navier–Stokes equation by using modified Laplace decomposition method. Ain Shams Eng. J. 5, 569–574 (2014)

    Article  Google Scholar 

  23. Yang, A., Zhang, Y.Z., Cattani, C., Xie, G., Rashidi, M.M., Zhou, Y.J., Yang, X.J.: Application of local fractional series expansion method to solve Klein–Gordon equations on cantor sets, Abst. Appl. Anal. Article ID 372741 (2014)

  24. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)

    MATH  Google Scholar 

  25. Bulut, H, Baskonus, H.M., Belgacem, F.B.M.: The analytical solutions of some fractional ordinary differential equations by Sumudu transform method. Abstr. Appl. Anal. Article ID 203875 (2013)

  26. Singh, J., Kumar, D., Qurashi, M., Baleanu, D.: A new fractional model for giving up smoking dynamics. Adv. Differ. Equ. (2017). https://doi.org/10.1186/s13662-017-1139-9

    Article  MathSciNet  Google Scholar 

  27. Area, I., Batarfi, H., Losada, J., Nieto, J.J., Shamma, W., Torres, A.: On a fractional order Ebola epidemic model. Adv. Differ. Equ. (2015). https://doi.org/10.1186/s13662-015-0613-5

    Article  MathSciNet  MATH  Google Scholar 

  28. Atangana, A., Nieto, J.J.: Numerical solution for the model of RLC circuit via the fractional derivative without singular kernel. Adv. Mech. Eng. 7, 1–7 (2015)

    Google Scholar 

  29. Shahed, M.E., Nieto, J.J., Ahmed, J.J., Abdelstar, I.: Fractional-order model for biocontrol of the lesser date moth in palm trees and its discretization. Adv. Differ. Equ. (2017). https://doi.org/10.1186/s13662-017-1349-1

    Article  MathSciNet  Google Scholar 

  30. Jafari, H., Khalique, C.M., Nazari, M.: Application of the Laplace decomposition method for solving linear and nonlinear fractional diffusion-wave equations. Appl. Math. Lett. 24, 1799–1805 (2011)

    Article  MathSciNet  Google Scholar 

  31. Jafari, H., Khalique, C.M., Khan, C.M., Ghasemi, M.: A two-step Laplace decomposition method for solving nonlinear partial differential equations. Int. J. Phys. Sci. 6, 4102–4109 (2011)

    Google Scholar 

  32. Johnston, S.J., Jafari, H., Moshokoa, H., Ariyan, H., Baleanu, D.: Laplace homotopy perturbation method for Burgers equation with space and time-fractional order. Open Phys. 14, 247–252 (2016)

    Article  Google Scholar 

  33. Ullah, R., Khan, M., Zaman, G.: Dynamical features of a mathematical model on smoking. J. Appl. Environ. Biol. Sci. 6, 92–96 (2016)

    Google Scholar 

  34. Hassan, H.N., El-Tawil, H.N.: A new technique of using homotopy analysis method for solving high-order nonlinear differential equations. Math. Methods Appl. Sci. 34, 728–742 (2011)

    Article  MathSciNet  Google Scholar 

  35. Liao, S.J.: A kind of approximate solution technique which does not depend upon small parameters: a special example. Int. J. Non-Linear Mech. 30, 371–380 (1995)

    Article  Google Scholar 

  36. Magin, R.: Fractional Calculus in Bioengineering. Begell House Publishers, Danbury (2004)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Engineering and Technology, Lahore, Pakistan

    M. Abdullah

  2. Department of Mathematics and Statistics, The University of Lahore, Lahore, Pakistan

    Aqeel Ahmad, M. Farman & M. O. Ahmad

  3. Department of Mathematics, University of the Punjab, Lahore, Pakistan

    Nauman Raza

Authors
  1. M. Abdullah
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Aqeel Ahmad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nauman Raza
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. M. Farman
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. M. O. Ahmad
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Abdullah.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Abdullah, M., Ahmad, A., Raza, N. et al. Approximate Solution and Analysis of Smoking Epidemic Model with Caputo Fractional Derivatives. Int. J. Appl. Comput. Math 4, 112 (2018). https://doi.org/10.1007/s40819-018-0543-5

Download citation

  • Published:

  • DOI: https://doi.org/10.1007/s40819-018-0543-5

Keywords

Search

Navigation