Nonlinear Pseudo State-Feedback Controller Design for Affine Fuzzy Large-Scale Systems with ${{\varvec{H}}}_{\boldsymbol{\infty }}$ Performance

Abstract

This paper treats robust controller design for Affine Fuzzy Large-Scale Systems (AFLSS) composed of Takagi–Sugeno-Kang type fuzzy subsystems with offset terms, disturbances, uncertainties, and interconnections. Instead of fuzzy parallel distributed compensation, a decentralized nonlinear pseudo state-feedback is developed for each subsystem to stabilize the overall AFLSS. Using Lyapunov stability, sufficient conditions with low codemputational effort and free gains are derived in terms of matrix inequalities. The proposed controller guarantees asymptotic stability, robust stabilization, and ${H}_{\infty }$ control performance of the AFLSS. A numerical example is given to illustrate the feasibility and effectiveness of the proposed approach.

1 Introduction

Large-scale systems (LSS) have been widely used to describe real-world problems, including the internet, economic systems, mobile networks, chemical processes, and electronic power grids [1, 2]. Because of the complexity of dynamical behaviors in these systems, it is necessary to seek techniques that reduce the complexity of the mathematical models and computational effort. Hence, there have been considerable efforts in modeling, analysis, optimization and control of LSS [2, 3], adaptive decentralized stabilization [4, 5], decentralized ${H}_{\infty }$ filtering [6], observer-based output feedback control [7], state estimation [8, 9], and many approaches have also been presented to investigate their stability, stabilization, and optimization [10,11,12,13].

Using fuzzy systems, qualitative knowledge can be represented in nonlinear functional forms. Among fuzzy models, the Takagi–Sugeno-Kang (TSK) model can provide a fuzzy representation of complex nonlinear systems. Stability analysis and controller design of fuzzy systems have also been extensively treated [14,15,16,17,18,19]. Some approaches based on the parallel distributed compensation (PDC) design have been reported [19, 20]. In addition, nonlinear state feedback controllers for fuzzy systems [16,17,18,19,20,21,22], and strategies based on fuzzy Lyapunov functions have been developed [13,14,15,16]. Moreover, stability analysis and stabilization of fuzzy large-scale systems (FLSS) have been studied for the discrete and continuous time [23,24,25,26,27,28]. One can also study the stabilization of the FLSS based on adaptive and observer design methods [29,30,31,32]. One of the most important strategies for controller design is to stabilize the system robustly while satisfying ${H}_{\infty }$-norm bounded constraints for fuzzy large-scale systems [33,34,35]. For continuous-time FLSS with parametric uncertainties, only a few results are available for stability analysis and robust stabilization. This could be a result of the complexity of such systems. However, robust stabilization and ${H}_{\infty }$ controller design for FLSS with affine terms have not yet been fully investigated, due to the difficulty of extending existing stability results.

In this paper, we will concentrate our efforts on asymptotic stability, robust stabilization, and ${H}_{\infty }$ controller design of an affine fuzzy large-scale system (AFLSS) consisting of $J$ interconnected subsystems. To investigate the stabilization of the overall system, each subsystem is decomposed into a set of fuzzy regions, for which a Takagi–Sugeno fuzzy model expresses the dynamical behavior of the subsystem. The whole large-scale system model is obtained by smoothly connecting all subsystems. Sufficient conditions for asymptotic stability of the overall system are derived using a new decentralized nonlinear pseudo state-feedback controller. A positive definite matrix $\left({P}_{i}\right)$ is shown to satisfy linear matrix inequalities corresponding to each sub-system.

Motivated from the previous work and their shortages in fuzzy large scale systems analysis as stated before, a new approach has been given for affine fuzzy large-scale systems with H_∞ performance in this paper. In comparison with the previous works which all gains for subsystems must be computed exactly according to all states of the system, here it is not required to have all gains and some of them can be selected optionally. In addition, the proposed method in this paper is applicable with much less computation and does not include restrictive conditions such as bounded norm. In contrast to the PDC method in which the control law is based on Lyapunov stability, the approach presented in this paper is simpler. There are some other merits for the proposed method will stated in the continuation.

The structure of this paper is as follows. Preliminaries and the problem formulation are presented in Sect. 2. In Sect. 3, decentralized nonlinear pseudo state-feedback controller is introduced, and the main results are obtained. Robust stabilization and ${H}_{\infty }$ controller design are investigated in Sect. 4. A numerical example is presented in Sect. 5. Finally, concluding remarks are presented in Section 6.

2 Preliminaries

Consider the AFLSS consisting of $J$ interconnected subsystems ${S}_{i} (i=\mathrm{1,2},\cdots ,J)$, each described as follows:

$$S_{i}^{l} = \left\{ \begin{gathered} {\mathbf{IF}}{ }\xi_{i1} \left( t \right) \,{\mathbf{is}}\, M_{i1}^{l} \,{\mathbf{and}} \cdots \xi_{{in_{i} }} \left( t \right)\,\, {\mathbf{is}} \,M_{{in_{i} }}^{l} \hfill \\ {\mathbf{THEN}}\,{ }\dot{x}_{i} \left( t \right) = A_{i}^{l} x_{i} \left( t \right) + B_{i}^{l} u_{i} \left( t \right) + D_{i}^{l} d_{i} \left( t \right) + \alpha_{i}^{l} + \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{J} C_{ij}^{l} x_{j} \left( t \right) \hfill \\ \end{gathered} \right.$$

(1)

where ${S}_{i}^{l}$ is $l$ th rule of ${S}_{i}$, ${u}_{i}(t)\in {\mathbb{R}}^{{m}_{i}}$ is control input of ${S}_{i}$ at time $t$, ${x}_{i}\left(t\right)\in {\mathbb{R}}^{{n}_{i}}$ is state vector of the $i$ th subsystem; ${x}_{i}\left(t\right)={\left[{x}_{i1}\left(t\right),{x}_{i2}\left(t\right),\cdots ,{x}_{i{n}_{i}}(t)\right]}^{T}$, ${C}_{ij}^{l}$ is interconnection matrix between the $i$ th and $j$ th subsystem of the $l$ th rule of ${S}_{i}$, ${r}_{i}$ is number of rules in subsystem ${S}_{i}$, ${n}_{i}$ is number of states in subsystem ${S}_{i}$, $\left({A}_{i}^{l},{B}_{i}^{l}\right)$ is controllable system matrices of rule $l$ in subsystem ${S}_{i}$, ${M}_{ik}^{l}$ is grade of membership of $\xi _{{ik}} \left( t \right);k = 1,2, \cdots ,n_{i}$, ${\xi }_{ik}\left(t\right)$ is known premise variable. ${\xi }_{i}\left(t\right)$ is used to denote the vector containing all individual elements ${\xi }_{i1}\left(t\right)\sim {\xi }_{i{n}_{i}}\left(t\right)$; $k = 1,2, \cdots ,n_{i}$, ${\alpha }_{i}^{l}$ is constant and deterministic offset term, $\left({d}_{i}\left(t\right),{D}_{i}^{l}\right)$ is disturbance and its coefficient matrix of rule $l$ in subsystem ${S}_{i}$, where $\Vert {d}_{i}\left(t\right)\Vert \le {{\beta }_{i}}^{2}$ and ${\beta }_{i}$ is scalar. The counters varying as $i=\mathrm{1,2},\cdots ,J, j=\mathrm{1,2},\cdots ,J, l=\mathrm{1,2},\cdots ,{r}_{i}$. Using a standard fuzzy inference method (product fuzzy inference) and also a central-average deffuzzifier, Eq. (1) can be obtained as

$$\dot{x}_{i} \left( t \right) = \mathop \sum \limits_{l = 1}^{{r_{i} }} \mu_{i}^{l} \left( {\xi_{i} \left( t \right)} \right)\left( {A_{i}^{l} x_{i} \left( t \right) + B_{i}^{l} u_{i} \left( t \right) + D_{i}^{l} d_{i} \left( t \right) + \alpha_{i}^{l} } \right) + \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{J} \mathop \sum \limits_{l = 1}^{{r_{i} }} \mu_{i}^{l} \left( {\xi_{i} \left( t \right)} \right)C_{ij}^{l} x_{j} \left( t \right)$$

(2)

where ${{w}_{i}}^{l}\left({\xi }_{i}\left(t\right)\right)=\prod_{k=1}^{{n}_{i}}{M}_{ik}^{l}\left({\xi }_{i}\left(t\right)\right)\ge 0$ and $\mu _{i} ^{l} \left( {\xi _{i} \left( t \right)} \right) = {\raise0.7ex\hbox{${w_{i} ^{l} \left( {\xi _{i} \left( t \right)} \right)}$} \!\mathord{\left/ {\vphantom {{w_{i} ^{l} \left( {\xi _{i} \left( t \right)} \right)} {\sum\limits_{{l = 1}}^{{r_{i} }} {w_{i} ^{l} } \left( {\xi _{i} \left( t \right)} \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sum\nolimits_{{l = 1}}^{{r_{i} }} {w_{i} ^{l} } \left( {\xi _{i} \left( t \right)} \right)}$}}$ represents the firing strength of the $l$ th rule of the $i$ th subsystem. In this paper, we assume that $\sum_{l=1}^{{r}_{i}}{{w}_{i}}^{l}\left({\xi }_{i}\left(t\right)\right)>0, \forall t$. Therefore, we have ${{\mu }_{i}}^{l}\left({\xi }_{i}\left(t\right)\right)\ge 0$ and $\sum_{l=1}^{{r}_{i}}{{\mu }_{i}}^{l}\left({\xi }_{i}\left(t\right)\right)=1, \forall t$. For stability purposes, decentralized nonlinear pseudo state-feedback controller [17, 26] is represented for each subsystem as follows:

$$u_{i} \left( t \right) = - \mathop \sum \limits_{k = 1}^{{c_{i} }} m_{i}^{k} \left( t \right)K_{i}^{k} x_{i} \left( t \right)$$

(3)

where $\sum_{k=1}^{{c}_{i}}{m}_{i}^{k}\left(t\right)=1, 0\le {m}_{i}^{k}\left(t\right)\le 1 \left(i=\mathrm{1,2},\cdots ,J, k=\mathrm{1,2},\cdots ,{c}_{i}\right)$ and ${K}_{i}^{k}$’s are state feedback gains with appropriate dimensions. The ${m}_{i}^{k}\left(t\right)$’s are also nonlinear functions defined as follows;

IF ${\sum }_{l=1}^{{r}_{i}}\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}\left({\mu }_{i}^{l}\left({\xi }_{i}\left(t\right)\right){H}_{ij}^{lk}\right)\ge 0,$ Then

$$m_{i}^{k} \left( t \right)\left( {2 \le k \le c_{i} } \right) = \left\{ \begin{gathered} \frac{{\mathop \sum \nolimits_{l = 1}^{{r_{i} }} \mathop \sum \nolimits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{J} \left( {\mu_{i}^{l} \left( {\xi_{i} \left( t \right)} \right)H_{ij}^{lk} } \right)}}{{\mathop \sum \nolimits_{h = 1}^{{c_{i} }} \mathop \sum \nolimits_{l = 1}^{{r_{i} }} \mathop \sum \nolimits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{J} \left| {\left. {\mu_{i}^{l} \left( {\xi_{i} \left( t \right)} \right)H_{ij}^{lh} } \right|} \right.}}\, {\mathbf{IF}}\mathop \sum \limits_{h = 1}^{{c_{i} }} \mathop \sum \limits_{l = 1}^{{r_{i} }} \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{J} \left| {\left. {\mu_{i}^{l} \left( {\xi_{i} \left( t \right)} \right)H_{ij}^{lh} } \right|} \right. \ne 0 \hfill \\ \frac{1}{{c_{i} }} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,{\mathbf{IF}} \mathop \sum \limits_{h = 1}^{{c_{i} }} \mathop \sum \limits_{l = 1}^{{r_{i} }} \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{J} \left| {\left. {\mu_{i}^{l} \left( {\xi_{i} \left( t \right)} \right)H_{ij}^{lh} } \right|} \right. = 0 \hfill \\ \end{gathered} \right.$$

(4)

and ${m}_{i}^{1}\left(t\right)=1-\sum_{k=2}^{{c}_{i}}{m}_{i}^{k}\left(t\right)$.

IF ${\sum }_{l=1}^{{r}_{i}}\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}\left({\mu }_{i}^{l}\left({\xi }_{i}\left(t\right)\right){H}_{ij}^{lk}\right)<0$, ${m}_{i}^{k}\left(t\right)(k\ne 1)=0$ and ${m}_{i}^{1}(t)=1$.

Note that ${H}_{ij}^{lh}=\frac{1}{J-1}{{x}_{i}\left(t\right)}^{T}{Q}_{i,cont}^{lh}{x}_{i}\left(t\right)-{F}_{ij}^{l}\left(t\right)$. Also, ${Q}_{i,cont}^{lh}$ is defined in the next sections according to Theorems 1 and 2, and ${F}_{ij}^{l}(t)={x}_{j}^{T}\left(t\right){{C}_{ij}^{l}}^{T}{P}_{i}{x}_{i}\left(t\right)+{{x}_{i}(t)}^{T}{P}_{i}{C}_{ij}^{l}{x}_{j}\left(t\right)$. In here, the ${c}_{i}$’s are parameters for designing the controller of each subsystem.

For readability, arguments “$t$” and ${\xi }_{i}\left(t\right)$ are omitted from $x\left(t\right),{m}_{i}^{k}\left(t\right), {F}_{ij}^{l}\left(t\right), {\mu }_{i}^{l}\left({\xi }_{i}\left(t\right)\right)$, and ${u}_{i}\left(t\right)$. Consequently, these terms are abbreviated as $x,{m}_{i}^{k}, {F}_{ij}^{l}, {\mu }_{i}^{l}$, and ${u}_{i}$, respectively. Using Eqs. (2)-(4), the closed-loop fuzzy subsystem now becomes

$$\dot{x}_{i} = \mathop \sum \limits_{l = 1}^{{r_{i} }} \mu_{i}^{l} \left( {A_{i}^{l} x_{i} - B_{i}^{l} \mathop \sum \limits_{k = 1}^{{c_{i} }} m_{i}^{k} K_{i}^{k} x_{i} + D_{i}^{l} d_{i} \left( t \right) + \alpha_{i}^{l} + \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{J} C_{ij}^{l} x_{j} } \right)$$

(5)

where, by considering ${Y}_{i}^{lk}={A}_{i}^{l}-{B}_{i}^{l}{K}_{i}^{k}$, we obtain

$$\dot{x}_{i} = \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{J} \mathop \sum \limits_{l = 1}^{{r_{i} }} \mathop \sum \limits_{k = 1}^{{c_{i} }} \mu_{i}^{l} m_{i}^{k} \left( {\left( {\frac{{Y_{i}^{lk} x_{i} + D_{i}^{l} d_{i} \left( t \right) + \alpha_{i}^{l} }}{J - 1}} \right) + C_{ij}^{l} x_{j} } \right)$$

(6)

Our task is to design the ${K}_{i}^{k}$’s such that the overall AFLSS is asymptotically stable. The stability conditions for the AFLSS described by Eq. (6) can be summarized by theorems stated in the following sections.

3 Stability Problem

In this section, we consider decentralized controllers for the AFLSS described in Eq. (6). For stabilization, the following description is required.

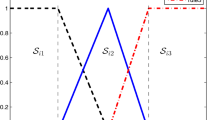
The rule set of the $i$ th subsystem is divided into ${I}_{i0}$ and ${I}_{i1}$. ${I}_{i0}$ represents rules that contain the origin and ${I}_{i1}$ are the remaining rules that do not contain the origin. As a result, if $l\in {I}_{i0}$, then ${D}_{i}^{l}{d}_{i}\left(t\right)=0, {\alpha }_{i}^{l}=0$ which guarantees the trivial solution ${\dot{x}}_{i}\equiv 0$ is the origin (i.e. ${x}_{i}\equiv 0$). In this paper, we assume that there is no perturbation for the rule $l\in {I}_{i0}$. We remark due to the problem formulation, ${D}_{i}^{l}$ might be scalar or considered to be a matrix. Now, assume that ${Z}_{i}^{l}$ is a bounded region in ${\mathbb{R}}^{\mathrm{n}}$, where the $l$ th rule of the $i$ th subsystem fires. For ${I}_{i1}$, one can obtain a hyper-ellipsoid containing ${Z}_{i}^{l}$ with definition $1-{{\overline{x} }_{i}^{l}}^{T}{\Theta }_{c}{\overline{x} }_{i}^{l}+{x}^{T}{\Theta }_{c}{\overline{x} }_{i}^{l}+{{\overline{x} }_{i}^{l}}^{T}{\Theta }_{c}x-{x}^{T}{\Theta }_{c}x\ge 0$ such that its parameters $\left({\overline{x} }_{i}^{l}, {\Theta }_{i}^{l}\right)$ satisfy $"1-{{\overline{x} }_{i}^{l}}^{T}{\Theta }_{i}^{l}{\overline{x} }_{i}^{l}<0"$, ${\overline{x} }_{i}^{l}$ represents its center and ${\Theta }_{i}^{l}$ is a positive definite matrix that characterizes the hyper-ellipsoid [15].

Definition 1

A Euclidean hyper-ellipsoid with center ${\overline{x} }_{c}$ and radius $r$ can be defined as $E\left({\overline{x} }_{c},{P}_{c}^{-1}\right)=\left\{\left.x\right|{\left(x-{\overline{x} }_{c}\right)}^{T}{P}_{c}^{-1}\left(x-{\overline{x} }_{c}\right)\le 1\right\}=\left\{\left.x\right|1-{\overline{x} }_{c}^{T}{\Theta }_{c}{\overline{x} }_{c}+{x}^{T}{\Theta }_{c}{\overline{x} }_{c}+{{\overline{x} }_{c}}^{T}{\Theta }_{c}x-{x}^{T}{\Theta }_{c}x\ge 0\right\}$ where ${P}_{c}^{-1}\left(={\Theta }_{c}\right)$ is a positive definite matrix. So, we can define ${I}_{i0}$ and ${I}_{i1}$ as ${I}_{i1}=\left\{l :1-{{\overline{x} }_{i}^{l}}^{T}{\Theta }_{i}^{l}{\overline{x} }_{i}^{l}<0, 1<l<{r}_{i}\right\}$ and ${I}_{i0} = \left\{1, 2, ..., {r}_{i}\right\} \backslash {I}_{i1}$. The term "$1-{{\overline{x} }_{i}^{l}}^{T}{\Theta }_{i}^{l}{\overline{x} }_{i}^{l}$" has been used to analyze the stability of an affine fuzzy model as stated later in the proof of the theorems in this paper.

Example a:

In Fig. 1, it is assumed that ${Z}_{i}^{3}$ (the region that rule ${A}_{3}\times {B}_{3}$ fires) does not contain the origin $\left(\left(X,Y\right)=\left(\mathrm{0,0}\right)\right)$. As a result, for a typical hyper-ellipsoid that contains ${Z}_{i}^{3}$, $"1-{{\overline{x} }_{i}^{l}}^{T}{\Theta }_{i}^{l}{\overline{x} }_{i}^{l}<0"$. For example, a typical hyper-ellipsoid can be described as $\left( {\bar{x}_{i}^{3} = \left( {\begin{array}{*{20}c} 5 \\ {0.5} \\ \end{array} } \right),\Theta _{i}^{3} = \left( {\begin{array}{*{20}c} {{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 {81}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${81}$}}} & 0 \\ 0 & 2 \\ \end{array} } \right)} \right)$.

Fig. 1

Fuzzy rules and hyper-ellipsoids

In summary, the stability conditions for AFLSS (6) can be presented as follows.

Theorem 1

AFLSS (2) can be made asymptotically stable by nonlinear pseudo state-feedback controllers in (3) if there exist symmetric positive definite matrices’s, Pi's positive scalars and $\left\{{\eta }_{i}^{l},{\rho }_{i}^{l},{\tau }_{i}^{l}\right\}$ state feedback gains, such that the following conditions are met:

$$- M < 0,\quad \quad \quad i = 1,2, \cdots ,J\quad J > 1$$

(7a)

$$\eta _{i}^{l} I_{i} \le Q_{i}^{{l1}} ,{\mkern 1mu} \quad \quad \quad {\mkern 1mu} l = 1,2, \cdots ,r_{i} ,i = 1,2, \cdots ,J$$

(7b)

For $l\in {I}_{i1}$;

$$\left[ {\begin{array}{*{20}c} { - P_{i} } & * \\ {\alpha _{i}^{{lT}} P_{i} + \rho _{i}^{l} \bar{x}_{i}^{{lT}} \Theta _{i}^{l} } & {\tau _{i}^{l} \beta _{i}^{2} D_{i}^{{lT}} P_{i} D_{i}^{l} + \rho _{i}^{l} {\text{O}}_{i}^{l} } \\ \end{array} } \right] \le 0,\quad i = 1,2, \cdots ,J$$

(7c)

where ${I}_{i}$ is the identity matrix in ${\mathbb{R}}^{{n}_{i}}\times {\mathbb{R}}^{{n}_{i}}$. Also

$$\left\{ \begin{gathered} - Q_{i}^{{lk}} = Y_{i}^{{lkT}} P_{i} + P_{i} Y_{i}^{{lk}} + \left( {\tau _{i}^{{l - 1}} + 1} \right)P_{i} - \rho _{i}^{l} \Theta _{i}^{l} ,\quad l \in I_{{i1}} \hfill \\ - Q_{i}^{{lk}} = Y_{i}^{{lkT}} P_{i} + P_{i} Y_{i}^{{lk}} ,\quad \quad \quad \quad \quad \quad \quad \quad \quad l \in I_{{i0}} \hfill \\ \end{gathered} \right.$$

$$M = \left[ {m_{ij} } \right] = \left\{ \begin{gathered} m_{i}^{1} \eta_{i} ,\quad \quad \quad \quad \quad \quad i = j \hfill \\ - m_{i}^{1} r_{i} \lambda_{max} \left( {P_{i} } \right)\delta_{ij} ,\quad \quad i \ne j \hfill \\ \end{gathered} \right.$$

where for $l\in {I}_{i1}$, ${\Theta }_{i}^{l}$ is a positive definite matrix of the hyper-ellipsoid that encircles the $l$ th rule region. Moreover, ${\rm O}_{i}^{l}=1-{{\overline{x} }_{i}^{l}}^{T}{\Theta }_{i}^{l}{\overline{x} }_{i}^{l}$, which is negative for $l\in {I}_{i1}$, ${\eta }_{i}=\underset{l}{\mathit{min}}\left({\eta }_{i}^{l}\right)$, ${\delta }_{ij}=\underset{l}{\mathit{max}}\left(\Vert {C}_{ij}^{l}\Vert \right)\left({n}_{i}+{n}_{j}\right)$ and ${Q}_{i,cont}^{lk}={Q}_{i}^{lk}$. We remark that ${Q}_{i,cont}^{lk}$ is used to define the parameters of the controllers in Eq. (4). In here, ‘‘$*$’’ denotes the matrix entries implied by symmetry, and ${\lambda }_{max}\left(P\right)$ denote the maximum eigen values of matrix $P$.

Proof:

See Appendix.

Remark 1:

Conditions (7b) and (7c) represent bilinear matrix inequalities (BMIs) that are. By pre-defining scalar variables, (7b) and (7c) can be rewritten in terms of LMIs as ${{Y}_{i}^{l1}}^{T}{P}_{i}+{P}_{i}{Y}_{i}^{l1}+{\varpi }_{i}^{l}\left({{\tau }_{i}^{l}}^{-1}+1\right){P}_{i}-{\varpi }_{i}^{l}{\rho }_{i}^{l}{\Theta }_{i}^{l}=-{Q}_{i}^{l1}\le -{\eta }_{i}^{l}{I}_{i}$, consequently.

$$\left( {A_{i}^{l} - B_{i}^{l} K_{i}^{1} } \right)^{T} P_{i} + P_{i} \left( {A_{i}^{l} - B_{i}^{l} K_{i}^{1} } \right) + \varpi_{i}^{l} \left( {\tau_{i}^{l - 1} + 1} \right)P_{i} - \varpi_{i}^{l} \rho_{i}^{l} \Theta_{i}^{l} \le - \eta_{i}^{l} I_{i}$$

(8)

where ${\varpi }_{i}^{l}=\left\{\begin{array}{c}1 \,\,for\,\, l\in {I}_{i1}\\ 0 \,\,for\,\, l\in {I}_{i0}\end{array}\right.$. Then, by pre-multiplying and post-multiplying both sides of Eq. (8) by ${P}_{i}^{-1}$, letting ${T}_{i}={P}_{i}^{-1}$ and ${v}_{i}^{1}={K}_{i}^{1}{T}_{i}$, we have ${\Phi }_{i}^{l1}+{T}_{i}\left(-{\varpi }_{i}^{l}{\rho }_{i}^{l}{\Theta }_{i}^{l}+{\eta }_{i}^{l}{I}_{i}\right){T}_{i}\le 0$ in which ${\Phi }_{i}^{l1}={{T}_{i}{A}_{i}^{l}}^{T}-{{v}_{i}^{1}}^{T}{{B}_{i}^{l}}^{T}+{A}_{i}^{l}{T}_{i}-{B}_{i}^{l}{v}_{i}^{1}+{\varpi }_{i}^{l}\left({{\tau }_{i}^{l}}^{-1}+1\right){T}_{i}$. Now, using the Schur complement we obtain the following

$$\left[ {\begin{array}{*{20}c} { - \left( { - \varpi_{i}^{l} \rho_{i}^{l} \Theta_{i}^{l} + \eta_{i}^{l} I_{i} } \right)^{ - 1} } & {*} \\ {T_{i} } & {\Phi_{i}^{l1} } \\ \end{array} } \right] \le 0$$

(9)

then ${K}_{i}^{1}={v}_{i}^{1}{T}_{i}^{-1}$. Equation (7c) can also be simplified. By pre-multiplying and post-multiplying both sides of (7c) by $diag\left({P}_{i}^{-1},{I}_{i}\right)$, and using the Schur complement, we obtain

$$\left[ {\begin{array}{*{20}c} { - T_{i} } & {*} & {*} \\ {\alpha_{i}^{lT} + \rho_{i}^{l} T_{i} \overline{x}_{i}^{l} \Theta_{i}^{l} } & {\rho_{i}^{l} {\rm O}_{i}^{l} } & {*} \\ 0 & {\tau_{i}^{l} \beta_{i} D_{i}^{l} } & { - \tau_{i}^{l} T_{i} } \\ \end{array} } \right] \le 0$$

(10)

where ${T}_{i}={P}_{i}^{-1}$. Because the above inequality is now in terms of ${T}_{i}$ and ${v}_{i}^{1}$, we can rewrite Theorem 1 as follows,

Corollary 1

AFLSS (2) can be stabilized asymptotically by nonlinear pseudo state-feedback controllers (3), if there are symmetric positive definite matrices ${T}_{i}$ ’s, a positive scalar set $\left\{{\eta }_{i}^{l},{\rho }_{i}^{l},{\tau }_{i}^{l}\right\}$ and vectors ${{v}_{i}^{1}}^{T}$ ’s such that (7a), (9), and for $l\in {I}_{i1}$ (10) are satisfied. We remark that the notations used here are similar to Theorem 1.

Due to Corollary 1, the control synthesis procedure can be summarized as the following algorithm.

3.1 ${{\varvec{H}}}_{\infty }$ Controller Design for the AFLSS

The ${H}_{\infty }$ problem is concerned with the design of a controller that stabilizes a system for which an ${H}_{\infty }$-norm bounded constraint on the disturbance attenuation is satisfied. Consider the subsystems ${S}_{i}$ described by the following rule-based equations.

$$S_{i}^{l} = \left\{ \begin{gathered} {\mathbf{IF}}\,\,\xi _{{i1}} \left( t \right){\mkern 1mu} {\mathbf{is}}\,\,{\mkern 1mu} M_{{i1}}^{l} {\mkern 1mu}\,\, {\mathbf{and}} \cdots \xi _{{in_{i} }} \left( t \right){\mkern 1mu} {\mkern 1mu} {\mathbf{is}}\,\,{\mkern 1mu} M_{{in_{i} }}^{l} \hfill \\ {\mathbf{THEN}}\left\{ \begin{gathered} \dot{x}_{i} = \hat{A}_{i}^{l} x_{i} + \hat{B}_{i}^{l} u_{i} + D_{i}^{l} d_{i} \left( t \right) + \hat{\alpha }_{i}^{l} + \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{J} C_{{ij}}^{l} x_{j} \hfill \\ y_{i} \left( t \right) = C_{i}^{l} x_{i} + E_{i}^{l} u_{i} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right.$$

(11)

where ${d}_{i}\left(t\right)$ is the square integrable disturbance, ${{\varvec{d}}}^{T}\left(t\right)={\left[{d}_{1}^{T}\left(t\right),{d}_{2}^{T}\left(t\right),\dots ,{d}_{J}^{T}\left(t\right)\right]}^{T}$, ${y}_{i}(t)$ is the controlled output and ${{\varvec{y}}}^{T}\left(t\right)={\left[{y}_{1}^{T}\left(t\right),{y}_{2}^{T}\left(t\right),\dots ,{y}_{J}^{T}\left(t\right)\right]}^{T}$, and ${\widehat{A}}_{i}^{l}={A}_{i}^{l}+\Delta {A}_{i}^{l}\left(t\right), \Delta {A}_{i}^{l}\left(t\right)={H}_{{a}_{i}}^{l}{F}_{{a}_{i}}^{l}\left(t\right){L}_{{a}_{i}}^{l}, {{F}_{{a}_{i}}^{l}}^{T}\left(t\right){F}_{{a}_{i}}^{l}\left(t\right)\le {R}_{{a}_{i}}^{l}$, ${\widehat{B}}_{i}^{l}={B}_{i}^{l}+\Delta {B}_{i}^{l}\left(t\right), \Delta {B}_{i}^{l}\left(t\right)={H}_{{b}_{i}}^{l}{F}_{{b}_{i}}^{l}\left(t\right){L}_{{b}_{i}}^{l}, {{F}_{{b}_{i}}^{l}}^{T}\left(t\right){F}_{{b}_{i}}^{l}\left(t\right)\le {R}_{{b}_{i}}^{l}$,${\widehat{\alpha }}_{i}^{l}={\alpha }_{i}^{l}+\Delta {\alpha }_{i}^{l}\left(t\right),\Delta {\alpha }_{i}^{l}\left(t\right)={H}_{{\alpha }_{i}}^{l}{F}_{{\alpha }_{i}}^{l}\left(t\right){L}_{{\alpha }_{i}}^{l},{{F}_{{\alpha }_{i}}^{l}}^{T}\left(t\right){F}_{{\alpha }_{i}}^{l}\left(t\right)\le {R}_{{\alpha }_{i}}^{l}$ in which $\left\{{R}_{{a}_{i}}^{l}, {R}_{{b}_{i}}^{l}, {R}_{{\alpha }_{i}}^{l}\right\}$ are symmetric positive matices, $\left\{\Delta {A}_{i}^{l}\left(t\right),\Delta {B}_{i}^{l}\left(t\right),\Delta {\alpha }_{i}^{l}\left(t\right)\right\}$ represents the system uncertainties satisfying the norm bounded condition. $H_{i}^{l} = [H_{{a_{i} }}^{l} ,H_{{b_{i} }}^{l} ,H_{{\alpha _{i} }}^{l} ]$ and $L_{i}^{l} = [L_{{a_{i} }}^{l} ,L_{{b_{i} }}^{l} ,L_{{\alpha _{i} }}^{l} ]$ are known constant matrices, ${\mathrm{and} F}_{{a}_{i}}^{l}\left(t\right)$, ${F}_{{b}_{i}}^{l}\left(t\right)$, and ${F}_{{\alpha }_{i}}^{l}\left(t\right)$ belong to ${\Omega }_{i}$ set as $\Omega _{i} = \left\{ {F_{i} \left( t \right)|F_{i}^{T} \left( t \right)F_{i} \left( t \right) \le I_{i} ,{\text{where}}\;{\text{elements}}\;{\text{of}}\;F_{i} \left( t \right){\text{are}}\;{\text{Lebesgue}}\;{\text{measurable}}} \right\}$. $\left({C}_{i}^{l}, {E}_{i}^{l}\right)$ are output matrices. Using nonlinear pseudo state-feedback controllers (3), the closed-loop system can be described as follows:

$$\dot{x}_{i} = \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{J} \mathop \sum \limits_{l = 1}^{{r_{i} }} \mathop \sum \limits_{k = 1}^{{c_{i} }} \mu_{i}^{l} m_{i}^{k} \left( {\left( {\frac{{\hat{Y}_{i}^{lk} x_{i} + D_{i}^{l} d_{i} \left( t \right) + \hat{\alpha }_{i}^{l} }}{J - 1}} \right) + C_{ij}^{l} x_{j} } \right)$$

(12)

where ${\widehat{Y}}_{i}^{lk}={\widehat{A}}_{i}^{l}-{\widehat{B}}_{i}^{l}{K}_{i}^{k}$. In this section, we consider ${H}_{\infty }$ controller design for the AFLSS (11), with nonlinear controllers presented in (3). The objective is to design suitable controllers for the AFLSS (11) that guarantee the performance in the ${H}_{\infty }$ sense. By specifying a prescribed level of disturbance attenuation, we determine the decentralized fuzzy control law ${u}_{i}(t)$ such that the induced ${L}_{2}$-norm of the operator from ${\varvec{d}}(t)$ to the controlled output ${\varvec{y}}(t)$ is less than $\gamma$, under zero initial conditions, i.e., ${\int }_{0}^{\infty }{\left|{\varvec{y}}(t)\right|}^{2}dt\le {\int }_{0}^{\infty }{\gamma }^{2}{\left|{\varvec{d}}\left(t\right)\right|}^{2}dt.$ We remark that the closed-loop system must be asymptotically stable when ${\varvec{d}}(t)=0$. If such a control law exists, then the system is said to be stabilizable with ${H}_{\infty }$-norm bound $\gamma$. Now, by removing the argument “$t$” from ${y}_{i}(t)$, and employing the proposed controllers, we obtain

$$y_{i} = \mathop \sum \limits_{l = 1}^{{r_{i} }} \mu_{i}^{l} \left( {C_{i}^{l} x_{i} - E_{i}^{l} \mathop \sum \limits_{k = 1}^{{c_{i} }} m_{i}^{k} K_{i}^{k} x_{i} } \right) = \mathop \sum \limits_{k = 1}^{{c_{i} }} \mathop \sum \limits_{l = 1}^{{r_{i} }} \mu_{i}^{l} \left( {\left( {C_{i}^{l} - E_{i}^{l} K_{i}^{k} } \right)x_{i} } \right)$$

(13)

The block diagram in Fig. 2 shows the details of the control procedure:

$$\left\{ \begin{gathered} S_{1} : \dot{x}_{i} \left( t \right) = \mathop \sum \limits_{l = 1}^{{r_{i} }} \mu_{i}^{l} \left( {\xi_{i} \left( t \right)} \right)\left( {A_{i}^{l} x_{i} \left( t \right) + B_{i}^{l} u_{i} \left( t \right) + D_{i}^{l} d_{i} \left( t \right) + \alpha_{i}^{l} } \right) + \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{J} \mathop \sum \limits_{l = 1}^{{r_{i} }} \mu_{i}^{l} \left( {\xi_{i} \left( t \right)} \right)C_{ij}^{l} x_{j} \left( t \right) \hfill \\ u_{1} : u_{i} \left( t \right) = - \mathop \sum \limits_{k = 1}^{{c_{i} }} m_{i}^{k} \left( t \right)K_{i}^{k} x_{i} \left( t \right) \hfill \\ \end{gathered} \right.$$

(14a)

Fig. 2

Block diagram of the controller

Theorem 2

The AFLSS defined in (12) and (13), is stabilizable with ${H}_{\infty }-$ norm bound $\gamma$ , using nonlinear pseudo state-feedback controllers (3), if there exist symmetric positive definite matrices ${P}_{i}$ , positive scalars $\left\{{\eta }_{i}^{l},{\epsilon }_{{\alpha }_{i}}^{l}, {\epsilon }_{{a}_{i}}^{l},{\epsilon }_{{b}_{i}}^{l},{\rho }_{i}^{l}\right\}$ , non-negative scalars ${\tau }_{i}^{l} \left({\tau }_{i}^{l}\ge 0\right)$ , integers ${c}_{i}$ and state gains ${K}_{i}^{1}$ such that (7a) and the following conditions are satisfied:

For $l\in {I}_{i0}$;For $l\in {I}_{i1}$; where

$$\left\{ \begin{gathered} - Q_{i,cont}^{lk} = - Q_{i}^{lk} + \Delta_{0} \left( {4,1} \right)^{T} \left( {Diag_{0} \left( \cdot \right)} \right)^{ - 1} \Delta_{0} \left( {4,1} \right) + c_{i} r_{i} \left( {C_{i}^{l} - E_{i}^{l} K_{i}^{k} } \right)^{T} \left( {C_{i}^{l} - E_{i}^{l} K_{i}^{k} } \right) ; for l \in I_{i0} \hfill \\ - Q_{i,cont}^{lk} = - Q_{i}^{lk} + \Delta_{1} \left( {5,1} \right)^{T} \left( {Diag_{1}^{1} \left( \cdot \right)} \right)^{ - 1} \Delta_{1} \left( {5,1} \right) + \gamma^{ - 2} P_{i} D_{i}^{l} D_{i}^{lT} P_{i} + c_{i} r_{i} \left( {C_{i}^{l} - E_{i}^{l} K_{i}^{k} } \right)^{T} \left( {C_{i}^{l} - E_{i}^{l} K_{i}^{k} } \right) - \tau_{i}^{l - 1} P_{i} ;for l \in I_{i1} \hfill \\ \end{gathered} \right.$$

and ${\Delta }_{0}\left(\mathrm{4,2}\right),{\Delta }_{1}\left(\mathrm{5,3}\right)$ are matrices that are defined as follows:

$$\left\{ \begin{gathered} \Delta_{0} \;is\;a\;4 \times 2\;block\;matrix\;where\;the\;first\;column\;is\;\left[ {H_{{a_{i} }}^{lT} P_{i} ;H_{{b_{i} }}^{lT} P_{i} ; \in_{{a_{i} }}^{l} L_{{a_{i} }}^{l} ; \in_{{b_{i} }}^{l} L_{{b_{i} }}^{l} K_{i}^{k} } \right]and\;the\;other\;is\;zero \hfill \\ \Delta_{1} \;is\;a\;5 \times 3\;block\;matrix\;where\;the\;first\;column\;is\left[ {H_{{\alpha_{i} }}^{lT} P_{i} ;H_{{a_{i} }}^{lT} P_{i} ;H_{{b_{i} }}^{lT} P_{i} ; \in_{{a_{i} }}^{l} L_{{a_{i} }}^{l} ; \in_{{b_{i} }}^{l} L_{{b_{i} }}^{l} K_{i}^{k} } \right]and\;the\;others\;are\;zero \hfill \\ \nabla \;is\;a\;4 \times 1\;block\;matrix\;where\;the\;first\;column\;is\left[ {\tau_{i}^{l} \beta_{i} D_{i}^{l} ;\alpha_{i}^{l} ;\rho_{i}^{l} \overline{x}_{i}^{lT} \Theta_{i}^{l} P_{i}^{ - 1} ; \in_{{\alpha_{i} }}^{l} L_{\alpha i}^{l} } \right] \hfill \\ \end{gathered} \right.$$

$Diag_{1}^{1} \left( \cdot \right),Diag_{1}^{2} \left( \cdot \right)$ and $Diag_{0} \left( \cdot \right)$ are diagonal matrices that are defined as

$$\left\{ \begin{gathered} Diag_{1}^{1} \left( \cdot \right) = diag\left( { \in_{{\alpha_{i} }}^{l} R_{{\alpha_{i} }}^{l - 1} , \in_{{a_{i} }}^{l} R_{{b_{i} }}^{l - 1} , \in_{{b_{i} }}^{l} R_{{b_{i} }}^{l - 1} , \in_{{a_{i} }}^{l} I_{i} , \in_{{b_{i} }}^{l} I_{i} } \right) \hfill \\ Diag_{1}^{2} \left( \cdot \right) = diag\left( {\tau_{i}^{l} P_{i}^{ - 1} ,P_{i}^{ - 1} ,P_{i}^{ - 1} , \in_{{\alpha_{i} }}^{l} I_{i} } \right) \hfill \\ Diag_{0} \left( \cdot \right) = diag\left( { \in_{{a_{i} }}^{l} R_{{a_{i} }}^{{l - 1}{}} , \in_{{b_{i} }}^{l} R_{{b_{i} }}^{l - 1} , \in_{{a_{i} }}^{l} I_{i} , \in_{{b_{i} }}^{l} I_{i} } \right) \hfill \\ \end{gathered} \right.$$

and $diag\left({M}_{1},\cdots ,{M}_{n}\right)$ is a diagonal matrix such that its $\left(i,i\right)$ th entry is ${M}_{i}\left(i=\mathrm{1,2},\cdots ,n\right)$ . Also, semicolons $\left(;\right)$ are used to separate the rows of a matrix. All notations are similar to Theorem 1.

Proof:

See Appendix.

Remark 2:

Equations (14b) and (14c) represent bilinear matrix inequalities (BMIs). For simplicity analogous to Remark 1 and Corollary 1, we can rewrite (14b) and (14c) in terms of LMIs with pre-defined scalar variables. We further remark that, $\mathrm{for} l\in {I}_{i1}$, because $\left(-{Q}_{i}^{lk}-{{\tau }_{i}^{l}}^{-1}{P}_{i}\right)$ is independent of ${\tau }_{i}^{l}, {Q}_{i,cont}^{lk}$ is also independent of ${\tau }_{i}^{l}$. Thus, for (14d), we can set ${\tau }_{i}^{l}=0$ and delete the column and row that includes ${\tau }_{i}^{l},$ resulting in a less restrictive condition.

Remark 3:

For $l\in {I}_{i1}$, if ${D}_{i}^{l}{d}_{i}\left(t\right)\ne 0$ and ${d}_{i}\left(0\right)=0$, then $-{Q}_{i,cont}^{lk}=-{Q}_{i}^{lk}+{{\Delta }_{0}\left(\mathrm{4,1}\right)}^{T}{\left({Diag}_{0}\left(\bullet \right)\right)}^{-1}{\Delta }_{0}\left(\mathrm{4,1}\right)+{\gamma }^{-2}{P}_{i}{D}_{i}^{l}{{D}_{i}^{l}}^{T}{P}_{i}+{c}_{i}{r}_{i}{\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right)}^{T}\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right)$, and (14b) can be rewritten as the following inequality.

If $\left(14a\right)-\left(14d\right)$ hold for $\gamma$, then the latter inequality holds is feasible for all attenuation levels $\widehat{\gamma }>\gamma$. The following theorem denotes the suboptimal solution for the ${H}_{\infty }$ optimal control problem.

Theorem 3

The suboptimal solution for the ${H}_{\infty }$ optimal control problem can be obtained by solving the following minimization problem.

$$\left\{ \begin{gathered} minimize\gamma \hfill \\ subject\,\, to\mathop \smallint \limits_{0}^{\infty } \left| {{\varvec{y}}\left( t \right)} \right|^{2} dt \le \mathop \smallint \limits_{0}^{\infty } \gamma^{2} \left| {{\varvec{d}}\left( t \right)} \right|^{2} dt \hfill \\ \end{gathered} \right.$$

(15)

which can also be stated as follows

$$\left\{ \begin{gathered} minimize\gamma \hfill \\ subject \,\,to\left( {14a} \right), \left( {14b} \right), \left( {14c} \right), and \left( {14d} \right). \hfill \\ \end{gathered} \right.$$

(16)

Remark 4: For comparison, in [35], stability analysis and ${H}_{\infty }$ controller design of continuous-time non-affine fuzzy large-scale systems by using piecewise Lyapunov functions is considered. Extending the piecewise Lyapunov function approach to the fuzzy large-scale system is the main advantage of this paper. Reference [25] which was one of the pioneer works in this field, has considered a particular class of interactions and feedback gains, as the main contribution of the manuscript and also state feedback controller has been used instead of PDC, in this paper. In another work, stability, and stabilization of standard fuzzy large-scale systems, as the main contribution, based on an existing method (PDC), has been the main motivation for considering that article to be published [24]. Stability analysis and ${H}_{\infty }$ controller design of discrete-time standard fuzzy large-scale systems, based on a commonly used method, namely piecewise Lyapunov functions, has been the reason for the publication of [36]. Even, a new stabilization criterion for large-scale T–S fuzzy systems, based on a commonly used method (PDC), as its main contribution, has received attention in [37]. In [37], extending some widely used methods to uncertain fuzzy large-scale systems have been considered as the main contribution of the manuscript. In [33], by using some changes in Lyapunov–Krasovskii functional method, stability conditions, which are less conservative and more applicable than the existing results, have been derived in terms of linear matrix inequalities (LMIs). In the mentioned papers, affine systems have not been considered in fuzzy large-scale systems. Recently, some works have been considered in the field of AFLSS but robust stability, but ${H}_{\infty }$ controller design, nonlinear controller with more flexibility and low computation as will explain in the continuation, have not been considered.

In summary, we observe the following:

• (i). The conditions of Theorems 1, 2 and 3 and Corollary 1 are satisfied only for ${Q}_{i,cont}^{l1}$ and ${K}_{i}^{1}$, and there is no need for ${Q}_{i,cont}^{lk}\left(2\le k\le {c}_{i}\right)$ to be positive. Therefore, the ${K}_{i}^{k}$’s are optional $\left(\mathrm{for }k\ne 1\right)$ and do not affect stability. As a result, the number of state feedback gains is greatly decreased. We remark that ${K}_{i}^{k}(k\ne 1)$ modify the type of response, i.e., the amount of oscillation, damping, settling time, etc. Consequently, there is greater flexibility in the control design. So, giving a new controller with more optional gains, relaxed conditions are one of the majority of the merits of the paper. In the previous papers, the ${H}_{\infty }$ performance for AFLSS, all gains for subsystems must be computed exactly according to all states of the system. But here it is not required to have all gains and some of them can be selected optionally.

• (ii). The theorems presented in this paper, and the proposed method is applicable with much less computation. This method does not include restrictive conditions such as bounded norm. In addition, the proposed method is not a predesigned scheme. That is, it is not necessary to check the stability of the predesigned system by trial and error.

• (iii). In contrast to the PDC method presented [24] in which the control law is based on Lyapunov stability for which ensuring $\dot{V}\left(x,t\right)<0$, is difficult, the approach presented in this paper is simpler.

• (iv). The number of controllers (${c}_{i}$) is also optional for Theorem 1 and Corollary 1. However, for Theorems and 3, it is obtained via matrix inequalities. By choosing a proper ${c}_{i}$, the amount of computation including the number of inequalities and the number of controller gains which have to be designed is reduced.

• (v). Considering (7a), we can use show matrix $M$ as follows:

  $$M = \underbrace {{\left( {\begin{array}{*{20}c} {m_{1}^{1} } & 0 & \cdots & 0 \\ 0 & {m_{2}^{1} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {m_{J}^{1} } \\ \end{array} } \right)}}_{Controler parameters}\underbrace {{\left( {\begin{array}{*{20}c} {\eta_{1} } & { - r_{1} \lambda_{\max } \left( {P_{1} } \right)\delta_{12} } & \cdots & { - r_{1} \lambda_{\max } \left( {P_{1} } \right)\delta_{1J} } \\ { - r_{2} \lambda_{\max } \left( {P_{2} } \right)\delta_{21} } & {\eta_{2} } & \cdots & { - r_{2} \lambda_{\max } \left( {P_{2} } \right)\delta_{2J} } \\ \vdots & \vdots & \ddots & \vdots \\ { - r_{J} \lambda_{\max } \left( {P_{J} } \right)\delta_{J1} } & { - r_{J} \lambda_{\max } \left( {P_{J} } \right)\delta_{J2} } & \cdots & {\eta_{J} } \\ \end{array} } \right)}}_{Interconnection effect matrix}$$

By using Sylvester’s criterion to check for positive definite matrices [21], It is easy to show that these conditions are independent of ${m}_{i}^{1}(i=\mathrm{1,2},\cdots ,J)$, and we can obtain ${\eta }_{i} (i=\mathrm{1,2},\cdots ,J)$. All leading minors have to be positive to guarantee positive-ness of $M$. For $kth$ leading minor $\left({M}_{k}\right)$, we have

$$\left| {M_{k} } \right| = \left| {\begin{array}{*{20}c} {m_{1}^{1} } & 0 & \cdots & 0 \\ 0 & {m_{2}^{1} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {m_{k}^{1} } \\ \end{array} } \right|\left| {\begin{array}{*{20}c} {\eta_{1} } & { - r_{1} \lambda_{max} \left( {P_{1} } \right)\delta_{12} } & \cdots & { - r_{1} \lambda_{max} \left( {P_{1} } \right)\delta_{1k} } \\ { - r_{2} \lambda_{max} \left( {P_{2} } \right)\delta_{21} } & {\eta_{2} } & \cdots & { - r_{2} \lambda_{max} \left( {P_{2} } \right)\delta_{2k} } \\ \vdots & \vdots & \ddots & \vdots \\ { - r_{k} \lambda_{max} \left( {P_{k} } \right)\delta_{k1} } & { - r_{k} \lambda_{max} \left( {P_{k} } \right)\delta_{k2} } & \cdots & {\eta_{k} } \\ \end{array} } \right|$$

$$= m_{1}^{1} m_{2}^{1} \cdots m_{k}^{1} \times \left| {\begin{array}{*{20}c} {\eta_{1} } & { - r_{1} \lambda_{max} \left( {P_{1} } \right)\delta_{12} } & \cdots & { - r_{1} \lambda_{max} \left( {P_{1} } \right)\delta_{1k} } \\ { - r_{2} \lambda_{max} \left( {P_{2} } \right)\delta_{21} } & {\eta_{2} } & \cdots & { - r_{2} \lambda_{max} \left( {P_{2} } \right)\delta_{2k} } \\ \vdots & \vdots & \ddots & \vdots \\ { - r_{k} \lambda_{max} \left( {P_{k} } \right)\delta_{k1} } & { - r_{k} \lambda_{max} \left( {P_{k} } \right)\delta_{k2} } & \cdots & {\eta_{k} } \\ \end{array} } \right|$$

since ${m}_{1}^{1}{m}_{2}^{1}\cdots {m}_{k}^{1}\ge 0$, the only thins has to be checked is

$$\left| {\begin{array}{*{20}c} {\eta_{1} } & { - r_{1} \lambda_{max} \left( {P_{1} } \right)\delta_{12} } & \cdots & { - r_{1} \lambda_{max} \left( {P_{1} } \right)\delta_{1k} } \\ { - r_{2} \lambda_{max} \left( {P_{2} } \right)\delta_{21} } & {\eta_{2} } & \cdots & { - r_{2} \lambda_{max} \left( {P_{2} } \right)\delta_{2k} } \\ \vdots & \vdots & \ddots & \vdots \\ { - r_{k} \lambda_{max} \left( {P_{k} } \right)\delta_{k1} } & { - r_{k} \lambda_{max} \left( {P_{k} } \right)\delta_{k2} } & \cdots & {\eta_{k} } \\ \end{array} } \right| > 0 \forall k = 1,2,3, \cdots ,J$$

• (vi). In the above method, the hyper-ellipsoid technique has been extended to overcome the complexity of AFLSS for designing a new nonlinear controller to guarantee the robust stability and ${H}_{\infty }$ performance of the AFLSS.

• (vii). ${Q}_{i,cont}^{lk}$ is a key parameter in controller design and also in the stability analysis. But according to the controller structure and also the firing regions of rules, they are different for the main system with and without uncertainties. Consider the (A.6) and (A.7),we have to consider ${Q}_{i,cont}^{lk}={Q}_{i}^{lk}$ and when the systems has uncertainties, we have to consider the uncertainties term in ${Q}_{i,cont}^{lk}$, to a reach negative amount for the derivative of the Lyapunov function as follows:

  $$\left\{ \begin{gathered} - Q_{i,cont}^{lk} = - Q_{i}^{lk} + \Delta_{0} \left( {4,1} \right)^{T} \left( {Diag_{0} \left( \cdot \right)} \right)^{ - 1} \Delta_{0} \left( {4,1} \right) + c_{i} r_{i} \left( {C_{i}^{l} - E_{i}^{l} K_{i}^{k} } \right)^{T} \left( {C_{i}^{l} - E_{i}^{l} K_{i}^{k} } \right) ; for l \in I_{i0} \hfill \\ - Q_{i,cont}^{lk} = - Q_{i}^{lk} + \Delta_{1} \left( {5,1} \right)^{T} \left( {Diag_{1}^{1} \left( \cdot \right)} \right)^{ - 1} \Delta_{1} \left( {5,1} \right) + \gamma^{ - 2} P_{i} D_{i}^{l} D_{i}^{lT} P_{i} + c_{i} r_{i} \left( {C_{i}^{l} - E_{i}^{l} K_{i}^{k} } \right)^{T} \left( {C_{i}^{l} - E_{i}^{l} K_{i}^{k} } \right) - \tau_{i}^{l - 1} P_{i} ;for l \in I_{i1} \hfill \\ \end{gathered} \right.$$

Remark 5: To comparison with some works, by referring to some previous studies like [24, 36], and [38] in fuzzy large-scale systems, we will reach some strong points in this paper. In [24], a Decentralized PDC controller is designed for a T-S fuzzy large-scale system. It is evident that some essential assumptions are not considered in this paper. Disturbances are not applied and evaluated for these systems. It is obvious disturbance rejection is one of the most critical part of designing as an effective controller. Besides, the computational burden of the paper is not suitable for today’s approaches. By noticing [36], we can see that disturbances and uncertainties are not considered again in this paper. On the other hand, the computed gains for stabilizing are so big and it will be a negative point causes more costs. In [38], the author designed an output-feedback control problem for a class of switched Takagi–Sugeno. Not only did the author not consider disturbances and uncertainties for the system, but also the proposed algorithm is just applicable for switched systems. It is not possible to apply this method to affine systems. Here, we proposed a nonlinear Pseudo state-feedback controller for affine fuzzy large-scale systems with ${H}_{\infty }$ performance. Using Lyapunov stability, sufficient conditions with low computational effort and free gains are derived in terms of matrix inequalities are a strength part of this work. As it is mentioned, a prominent part of this paper is that the algorithm does not need to compute gains for each subsystem, and due to the proposed example, by computing three gains for six subsystems, the overall system will be stabilized.

Remark 6: To compare with state feedback method, in this paper a nonlinear pseudo state-feedback controller for affine fuzzy large-scale systems is studied, in which, by this algorithm the computational burden is declined dramatically. Besides, in state feedback controller, to stabilize outputs of the system, the exact states and parameters of the system must be existed, but in this paper, it is not required to compute all gains in each subsystem and we can avoid some of them so that they are considered optional. It is one of the main novelties of the proposed method that by having just some of gains the overall system will be stabilized according to the example. In addition, By considering ${u}_{i}\left(t\right)=-\sum_{k=1}^{{c}_{i}}{m}_{i}^{k}\left(t\right){K}_{i}^{k}{x}_{i}\left(t\right)$ in the proposed method, we are using a nonlinear averaging method by computing ${m}_{i}^{k}\left(t\right)$ at instant and we do averaging among some state feedback controllers. So ${m}_{i}^{k}\left(t\right)$ can be considered as varying average coefficients according to the conditions of all subsystems.

Due to Theorem 3, the control synthesis procedure can be summarized as the following algorithm.

4 Numerical Example

In this section, an example is presented to demonstrate the results of the proposed stabilization procedure for affine fuzzy large-scale systems. Consider the following AFLSS, composed of three subsystems described as.

• Subsystem ${S}_{1}:$

  Rule1: ${\mathbf{IF}}\,x_{{11}} \,{\mathbf{is}}\,M_{1}^{1} \,{\mathbf{and}}\,x_{{12}} \,{\mathbf{is}}\,M_{1}^{3} \,{\mathbf{THEN}}\left\{ \begin{gathered} \dot{x}_{1} = \hat{A}_{1}^{1} x_{1} + B_{1}^{1} u_{1} + D_{1}^{1} d_{1} \left( t \right) + \alpha _{1}^{1} + \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne 1} \\ \end{array} }}^{3} C_{{1j}}^{1} x_{j} \hfill \\ y_{1} = C_{1}^{1} x_{1} + E_{1}^{1} u_{1} \hfill \\ \end{gathered} \right.$

  Rule2:${\mathbf{IF}}\,\, x_{11}\, {\mathbf{is}}\,\, M_{1}^{2}\,\, {\mathbf{and}}\,\, x_{12} \,{\mathbf{is}}\,\, M_{1}^{2} \,\,{ }{\mathbf{THEN}}\left\{ \begin{gathered} \dot{x}_{1} = \hat{A}_{1}^{2} x_{1} + B_{1}^{2} u_{1} + D_{1}^{2} d_{1} \left( t \right) + \alpha_{1}^{2} + \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne 1} \\ \end{array} }}^{3} C_{1j}^{2} x_{j} \hfill \\ y_{1} = C_{1}^{2} x_{1} + E_{1}^{2} u_{1} \hfill \\ \end{gathered} \right.$

  Rule3:${\mathbf{IF}}\,\, x_{11}\,\, {\mathbf{is}}\,\, M_{1}^{3}\,\, {\mathbf{and}}\,\, x_{12} \,\,{\mathbf{is}} \,\,M_{1}^{1} \,\,{ }{\mathbf{THEN}}\left\{ \begin{gathered} \dot{x}_{1} = \hat{A}_{1}^{3} x_{1} + B_{1}^{3} u_{1} + D_{1}^{3} d_{1} \left( t \right) + \alpha_{1}^{3} + \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne 1} \\ \end{array} }}^{3} C_{1j}^{3} x_{j} \hfill \\ y_{1} = C_{1}^{3} x_{1} + E_{1}^{3} u_{1} \hfill \\ \end{gathered} \right.$ where

  $$\begin{gathered} \hat{A}_{1}^{1} = \left[ {\begin{array}{*{20}c} {\delta_{1} } & {\delta_{1} } \\ { - \delta_{2} } & { - 4} \\ \end{array} } \right], \hat{A}_{1}^{2} = \left[ {\begin{array}{*{20}c} {\delta_{3} } & {\delta_{2} } \\ 0 & 2 \\ \end{array} } \right] ,\hat{A}_{1}^{3} = \left[ {\begin{array}{*{20}c} {\delta_{1} } & 3 \\ { - 1} & {\delta_{3} } \\ \end{array} } \right], \hfill \\ B_{1}^{1} = \left[ {\begin{array}{*{20}c} {0.5} \\ 0 \\ \end{array} } \right], B_{1}^{2} = \left[ {\begin{array}{*{20}c} {0.5} \\ {0.5} \\ \end{array} } \right], B_{1}^{3} = \left[ {\begin{array}{*{20}c} 0 \\ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} \\ \end{array} } \right],D_{1}^{1} = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right],D_{1}^{2} = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right] \hfill \\ \end{gathered}$$
  $$D_{1}^{3} = \left[ {\begin{array}{*{20}c} 1 \\ 1 \\ \end{array} } \right], \alpha_{1}^{1} = \left[ {\begin{array}{*{20}c} 0 \\ { - 1} \\ \end{array} } \right], \alpha_{1}^{2} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right], \alpha_{1}^{3} = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right], C_{12}^{1} = \left[ {\begin{array}{*{20}c} 1 & { - 1} \\ 0 & 0 \\ \end{array} } \right], C_{13}^{1} = \left[ {\begin{array}{*{20}c} 0 & { - 1} \\ 2 & 0 \\ \end{array} } \right], C_{12}^{2} = \left[ {\begin{array}{*{20}c} 2 & 0 \\ 0 & { - 1} \\ \end{array} } \right], C_{13}^{2} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - 1} & 0 \\ \end{array} } \right]$$
  $$C_{12}^{3} = \left[ {\begin{array}{*{20}c} 2 & 1 \\ 0 & 0 \\ \end{array} } \right], C_{13}^{3} = \left[ {\begin{array}{*{20}c} { - 1} & 0 \\ 0 & { - 2} \\ \end{array} } \right],C_{1}^{1} = \left[ {\begin{array}{*{20}c} 1 \\ 1 \\ \end{array} } \right]^{T} , C_{1}^{2} = \left[ {\begin{array}{*{20}c} { - 1} \\ 1 \\ \end{array} } \right]^{T} , C_{1}^{3} = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right]^{T} , E_{1}^{1} = E_{1}^{2} = E_{1}^{3} = 1$$

  The normalized membership functions of subsystem 1 are shown in Fig. 3.

• Subsystem ${S}_{2}:$

Fig. 3

Membership functions of subsystem ${{\varvec{S}}}_{1}$

Rule1: $\mathbf{I}\mathbf{F} \,\,{x}_{21}\,\, \mathbf{i}\mathbf{s}\,\, {M}_{2}^{1}\,\, \mathbf{a}\mathbf{n}\mathbf{d} \,\,{x}_{22}\,\, \mathbf{i}\mathbf{s}\,\, {M}_{2}^{2}\,\, \mathbf{T}\mathbf{H}\mathbf{E}\mathbf{N}\left\{\begin{array}{c}{\dot{x}}_{2}={\widehat{A}}_{2}^{1}{x}_{1}+{B}_{2}^{1}{u}_{2}+{D}_{2}^{1}{d}_{2}\left(t\right)+{\alpha }_{2}^{1}+\sum_{\begin{array}{c}j=1\\ j\ne 2\end{array}}^{3}{C}_{2j}^{1}{x}_{j}\\ {y}_{2}={C}_{2}^{1}{x}_{2}+{E}_{2}^{1}{u}_{2}\end{array}\right.$

Rule2: $\mathbf{I}\mathbf{F}\,\, {x}_{21}\,\, \mathbf{i}\mathbf{s} \,\,{M}_{2}^{2} \,\,\mathbf{a}\mathbf{n}\mathbf{d}\,\, {x}_{22}\,\, \mathbf{i}\mathbf{s} \,\,{M}_{2}^{1} \,\,\mathbf{T}\mathbf{H}\mathbf{E}\mathbf{N}\left\{\begin{array}{c}{\dot{x}}_{2}={\widehat{A}}_{2}^{2}{x}_{2}+{B}_{2}^{2}{u}_{2}+{D}_{2}^{2}{d}_{2}\left(t\right)+{\alpha }_{2}^{2}+\sum_{\begin{array}{c}j=1\\ j\ne 2\end{array}}^{3}{C}_{2j}^{2}{x}_{j}\\ {y}_{2}={C}_{2}^{2}{x}_{2}+{E}_{2}^{2}{u}_{2}\end{array}\right.$ where.

$\hat{A}_{2}^{1} = \left[ {\begin{array}{*{20}c} {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} & { - \delta _{4} } \\ 2 & {\delta _{1} } \\ \end{array} } \right],\hat{A}_{2}^{2} = \left[ {\begin{array}{*{20}c} { - 4} & {\delta _{4} } \\ {\delta _{5} } & 1 \\ \end{array} } \right]$, $B_{2}^{1} = \left[ {\begin{array}{*{20}c} {0.5} \\ 0 \\ \end{array} } \right],B_{2}^{2} = \left[ {\begin{array}{*{20}c} 0 \\ { - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} \\ \end{array} } \right]$, $D_{2}^{1} = \left[ {\begin{array}{*{20}c} 1 \\ {0.5} \\ \end{array} } \right],D_{2}^{2} = \left[ {\begin{array}{*{20}c} { - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} \\ 0 \\ \end{array} } \right],\alpha _{2}^{1} = \alpha _{2}^{2} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right]$

$$E_{2}^{1} = - 1,E_{2}^{2} = 1.5,C_{{21}}^{1} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ \end{array} } \right],C_{{23}}^{1} = \left[ {\begin{array}{*{20}c} 5 & 0 \\ 0 & 5 \\ \end{array} } \right],C_{{21}}^{2} = \left[ {\begin{array}{*{20}c} { - 1} & 1 \\ 0 & 0 \\ \end{array} } \right],C_{{23}}^{2} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & { - 2} \\ \end{array} } \right],C_{2}^{1} = \left[ {\begin{array}{*{20}c} {0.5} \\ {{\text{ }}{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} \\ \end{array} } \right]^{T} ,C_{2}^{2} = \left[ {\begin{array}{*{20}c} 1 \\ { - 1} \\ \end{array} } \right]^{T} .$$

Subsystem ${S}_{3}:$

Rule1: $\mathbf{I}\mathbf{F}\,\, {x}_{31}\,\, \mathbf{i}\mathbf{s} \,\,{M}_{3}^{1}\,\, \mathbf{a}\mathbf{n}\mathbf{d} \,\,{x}_{32}\,\, \mathbf{i}\mathbf{s}\,\, {M}_{3}^{2} \,\,\mathbf{T}\mathbf{H}\mathbf{E}\mathbf{N}\left\{\begin{array}{c}{\dot{x}}_{3}={\widehat{A}}_{3}^{1}{x}_{3}+{B}_{3}^{1}{u}_{3}+{D}_{3}^{1}{d}_{3}\left(t\right)+{\alpha }_{3}^{1}+\sum_{\begin{array}{c}j=1\\ j\ne 3\end{array}}^{3}{C}_{3j}^{1}{x}_{j}\\ {y}_{3}={C}_{3}^{1}{x}_{3}+{E}_{3}^{1}{u}_{3}\end{array}\right.$

where

$${\widehat{A}}_{3}^{1}=\left[\begin{array}{cc}0& -1\\ 1& {\delta }_{2}\end{array}\right], {B}_{3}^{1}=\left[\begin{array}{c}1.5\\ -0.25\end{array}\right], {D}_{3}^{1}=\left[\begin{array}{c}0\\ 1\end{array}\right], {\alpha }_{3}^{1}=\left[\begin{array}{c}0\\ 0\end{array}\right],{C}_{31}^{1}=\left[\begin{array}{cc}-1& 0\\ 1& 0\end{array}\right], {C}_{32}^{1}=\left[\begin{array}{cc}0& -1\\ 4& 0\end{array}\right], {C}_{3}^{1}={\left[\begin{array}{c}1\\ 0\end{array}\right]}^{T}, {E}_{3}^{1}=2.$$

The normalized membership functions of subsystems 2 and 3 are as follows:

${M}_{2}^{1}\left(x\right)={M}_{3}^{1}\left(x\right)=\frac{1}{7}\left(-x+4\right), {M}_{2}^{2}\left(x\right)={M}_{3}^{2}\left(x\right)=\frac{1}{7}\left(x+3\right)$.

Here we considered ${d}_{1}=0.5, {d}_{2}=0.4, {d}_{3}=0.3$

The uncertainties are considered as follows. It is also assumed that ${\widehat{A}}_{i}^{l}={A}_{i}^{l}+{H}_{ai}^{l}{F}_{ai}^{l}{L}_{ai}^{l}$, where

$$\delta _{1} = \left[ {\left( {1 - 0.25\% } \right)\left( {1 + 0.25\% } \right)} \right]\delta _{2} = \left[ {\left( {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}} - 10\% } \right)\left( {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}} - 10\% } \right)} \right]\delta _{3} = \left[ {\left( {0 - 0.5\% } \right)\left( {0 + 0.5\% } \right)} \right]$$

$${\delta }_{4}=\left[\left(2-40\%\right)\left(2+40\%\right)\right] {\delta }_{5}=\left[\left(-1-15\%\right)\left(-1+15\%\right)\right]$$

and

$$A_{1}^{1} = \left[ {\begin{array}{*{20}c} 1 & {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} \\ { - 1} & { - 4} \\ \end{array} } \right],A_{1}^{2} = \left[ {\begin{array}{*{20}c} 2 & {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} \\ 0 & 2 \\ \end{array} } \right],A_{1}^{3} = \left[ {\begin{array}{*{20}c} 1 & 3 \\ { - 1} & 2 \\ \end{array} } \right],A_{2}^{1} = \left[ {\begin{array}{*{20}c} {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} & 1 \\ 2 & 1 \\ \end{array} } \right],A_{2}^{2} = \left[ {\begin{array}{*{20}c} { - 4} & { - 1} \\ 0 & 1 \\ \end{array} } \right],A_{3}^{1} = \left[ {\begin{array}{*{20}c} 0 & { - 1} \\ 1 & {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} \\ \end{array} } \right]$$

$${F}_{a1}^{1}=diag\left({\xi }_{1},{\xi }_{2}\right) , {F}_{a1}^{2}=\left[\begin{array}{cc}0& {\xi }_{1}\\ {\xi }_{2}& 0\end{array}\right],{F}_{a1}^{3}=diag\left({\xi }_{1},{\xi }_{3}\right),{F}_{a2}^{1}=\left[\begin{array}{cc}0& {\xi }_{4}\\ 0& {\xi }_{1}\end{array}\right],{F}_{a2}^{2}=\left[\begin{array}{cc}0& {\xi }_{4}\\ {\xi }_{5}& 0\end{array}\right], {F}_{a3}^{1}=\left[\begin{array}{cc}0& 0\\ 0& {\xi }_{2}\end{array}\right]$$

$${H}_{a1}^{1}=\left[\begin{array}{cc}0.25& 0\\ 0& 0.1\end{array}\right] , {H}_{a1}^{2}=\left[\begin{array}{cc}0.1& 0.4\\ 0& 0\end{array}\right],{H}_{a1}^{3}=\left[\begin{array}{cc}0.25& 0\\ 0& 0.4\end{array}\right],{H}_{a2}^{1}=\left[\begin{array}{cc}-0.15& 0\\ 0& 0.25\end{array}\right]$$

$${H}_{a2}^{2}=\left[\begin{array}{cc}0.15& 0\\ 0& 0.5\end{array}\right], {H}_{a3}^{1}=\left[\begin{array}{cc}0& 0\\ 0& 0.1\end{array}\right], {L}_{a1}^{1}=\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right], {L}_{a1}^{2}={L}_{a1}^{3}={L}_{a2}^{1}={L}_{a2}^{2}={L}_{a3}^{1}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$$

where ${\xi }_{i}, i=1,\cdots ,5$ are random numbers on interval $[-1, 1]$. Now, by using the MATLAB LMI Toolbox, Theorem 3, and assuming $\gamma =2.432$, the following solution is obtained.

$${\delta }_{12}=2, {\delta }_{21}=1, {\delta }_{31}=2,{\delta }_{13}=2, {\delta }_{23}=2, {\delta }_{32}=4, {c}_{1}={c}_{2}={c}_{3}=2, {K}_{1}^{1}=\left[\begin{array}{cc}68.4747& 36.2931\end{array}\right]$$

$${K}_{1}^{2}=\left[\begin{array}{cc}1.0061 0.5009\end{array}\right] {K}_{2}^{1}=\left[\begin{array}{cc}27.6127 -6.8022\end{array}\right], {K}_{3}^{1}=\left[\begin{array}{cc}69.5951 -44.8869\end{array}\right], {\epsilon }_{a1}^{1}=0.60$$

$${\epsilon }_{a1}^{2}=0.40,{\epsilon }_{a1}^{3}=0.80,{\epsilon }_{a2}^{1}=1.0,{\epsilon }_{a2}^{2}=0.90,{\epsilon }_{a3}^{1}=1.2, {\eta }_{1}^{1}={\eta }_{1}^{2}={\eta }_{1}^{3}=118.0179$$

${\eta }_{2}^{1}={\eta }_{2}^{2}=139.4786, {\eta }_{3}^{1}=188.2272, {\rho }_{1}^{1}=128.9055, {\rho }_{1}^{3}=141.5489, {P}_{1}=\left[\begin{array}{cc}5.5420 & 0.3937\\ 0.3937& 2.8138\end{array}\right], {P}_{2}=\left[\begin{array}{cc}16.626& 1.1811\\ 1.1811& 8.4414\end{array}\right], {P}_{3}=\left[\begin{array}{cc}16.626& 1.1811\\ 1.1811& 8.4414\end{array}\right]$.

Remark 7

According to Algorithms A and B and also as stated in Page 9 (part iv), for the system without uncertainties, ${c}_{i}$ is optional for controller design and ${K}_{i}^{1}$ are extracted from Theorem 1 although the other ${K}_{i}^{k}$ are optional. It is one of the most important merits of this paper. When we consider uncertainties, ${c}_{i}$ is extracted from Theorems 2 and 3. In here, it is not optional and in the best case, the minimization problem (16) can be solved with a predefined ${c}_{i}$.

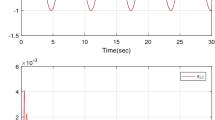
Remark 8: By proposing this example, it has been shown that the algorithm is entirely practical. Here in this example, as is evident in Fig. 4, Fig. 5, and Fig. 6, the trajectories of the three subsystems are leading to zero and they are fixed during the time horizon. So, this means that the overall closed-loop system is stable during the time. And the proposed method is applicable.

Fig. 4

Trajectories of subsystem 1

Fig. 5

Trajectories of subsystem 1

Fig. 6

Trajectories of subsystem 1

Remark 9: In this paper, we remark that the other feedback gains ${K}_{2}^{2}$ and ${K}_{3}^{2}$ are optional and this means by having three gains out of six gains this algorithm is able to stabilize the system. By referring to the cost side of the engineering it means decreasing in costs. This shows the effectiveness of the proposed approach.

5 Conclusion

This paper was dealt with asymptotic stability, robust stabilization, and ${H}_{\infty }$ control of AFLSS, where each subsystem includes offset terms, disturbances and uncertainties. First, a set of asymptotic stability conditions was derived for an AFLSS. It was shown that stabilization can be determined by solving a set of matrix inequalities. Second, this approach was used to stabilize an AFLSS in the presence of parametric uncertainties. For this purpose, a set of stabilization conditions and ${H}_{\infty }$ controllers were presented. Through these conditions, it was shown that there is no need to determine controller gains by solving matrix inequalities. It was also shown that these conditions could be considered as an alternative to BMI or LMI (by predefining decision variables). An example was illustrated by the proposed control method.

Appendix (Proof of Theorems 1 and 2)

Proof of Theorem 1

Consider the function $V\left(x,t\right)$, for an AFLSS in (6), expressed as $V\left(x,t\right)=\sum_{i=1}^{J}{V}_{i}\left({x}_{i},t\right)=\sum_{i=1}^{J}{x}_{i}^{T}{P}_{i}{x}_{i}$, where ${\dot{V}}_{i}\left({x}_{i},t\right)={\dot{x}}_{i}^{T}{P}_{i}{x}_{i}+{x}_{i}^{T}{P}_{i}{\dot{x}}_{i}$. For $l\in {I}_{i1}$, it can be shown that the derivative of ${V}_{i}\left({x}_{i},t\right)$ along the trajectory of $(6)$ can be written as.

$$\begin{gathered} \dot{V}_{i} \left( {x_{i} \left( t \right),t} \right) = \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{J} \mathop \sum \limits_{{l \in I_{i1} }}^{{r_{i} }} \mathop \sum \limits_{k = 1}^{{c_{i} }} \mu_{i}^{l} m_{i}^{k} \left( {\frac{1}{J - 1}\left( {x_{i}^{T} Y_{i}^{lkT} P_{i} x_{i} + D_{i}^{lT} d_{i} \left( t \right)P_{i} x_{i} + \alpha_{i}^{lT} P_{i} x_{i} } \right) + x_{j}^{T} C_{ij}^{lT} P_{i} x_{i} } \right) \hfill \\ + \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{J} \mathop \sum \limits_{{l \in I_{i1} }}^{{r_{i} }} \mathop \sum \limits_{k = 1}^{{c_{i} }} \mu_{i}^{l} m_{i}^{k} \left( {\frac{1}{J - 1}\left( {x_{i}^{T} P_{i} Y_{i}^{lk} x_{i} + x_{i}^{T} P_{i} d_{i} \left( t \right)D_{i}^{l} + x_{i}^{T} P_{i} \alpha_{i}^{l} } \right) + x_{i}^{T} P_{i} C_{ij}^{l} x_{j} } \right){ } \hfill \\ \end{gathered}$$

(A.1)

Note that here $J>1$. By using the following inequality for two vectors $x$ and $y$, $2{x}^{T}y\le \epsilon {x}^{T}{P}^{-1}x+{\epsilon }^{-1}{y}^{T}Py$ in which $P>0$ is a real matrix, we obtain ${{D}_{i}^{l}}^{T}{d}_{i}\left(t\right){P}_{i}{x}_{i}+{x}_{i}^{T}{P}_{i}{d}_{i}\left(t\right){D}_{i}^{l}\le {{\tau }_{i}^{l}}^{-1}{{x}_{i}}^{T}{P}_{i}{x}_{i}+{\tau }_{i}^{l}{{\beta }_{i}}^{2}{{D}_{i}^{l}}^{T}{P}_{i}{D}_{i}^{l}$, Then, it follows that

$$\dot{V}_{i} \left( {x_{i} ,t} \right) \le \sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{j} {\sum\limits_{{l \in I_{i1} }}^{{r_{i} }} {\sum\limits_{k = 1}^{{c_{i} }} {\mu_{i}^{l} m_{i}^{k} } } } \left( {\frac{1}{J - 1}\left( {x_{i}^{T} \left( {Y_{i}^{lkT} P_{i} + P_{i} Y_{i}^{lk} + \tau_{i}^{l - 1} P_{i} } \right)x_{i} + \alpha_{i}^{lT} P_{i} x_{i} + x_{i}^{T} P_{i} \alpha_{i}^{l} + \tau_{i}^{l} \beta_{i}^{2} D_{i}^{lT} P_{i} D_{i}^{l} } \right) + x_{j}^{T} C_{ij}^{lT} P_{i} x_{i} + x_{i}^{T} P_{i} C_{ij}^{l} x_{j} } \right)$$

(A.2)

Because ${\tau }_{i}^{l}{{\beta }_{i}}^{2}{{D}_{i}^{l}}^{T}{P}_{i}{D}_{i}^{l}\ge 0$ and equation (A.2) should be given in terms of matrix inequalities, the following positive scalars are added to (A.2). This implies that each rule of ${I}_{i1}$ is encircled by a hyper-ellipsoid. $\sum_{l\in {I}_{i1}}{\mu }_{i}^{l}\frac{{\rho }_{i}^{l}}{J-1}\left(1-{x}_{i}^{T}{\Theta }_{i}^{l}{x}_{i}+{x}_{i}^{T}{\Theta }_{i}^{l}{\overline{x}}_{i}^{l}+{{\overline{x}}_{i}^{l}}^{T}{\Theta }_{i}^{l}{x}_{i}-{{\overline{x}}_{i}^{l}}^{T}{\Theta }_{i}^{l}{\overline{x}}_{i}^{l}\right)$ where ${\rho }_{i}^{l}$ is a positive scalar and $\left(1-{x}_{i}^{T}{\Theta }_{i}^{l}{x}_{i}+{x}_{i}^{T}{\Theta }_{i}^{l}{\overline{x}}_{i}^{l}+{{\overline{x}}_{i}^{l}}^{T}{\Theta }_{i}^{l}{x}_{i}-{{\overline{x}}_{i}^{l}}^{T}{\Theta }_{i}^{l}{\overline{x}}_{i}^{l}\right)$ is the definition for a hyper-ellipsoid that includes the $l$ th rule ($l\in {I}_{i1}$) of the $i$ th subsystem. Therefore, we obtain

$${\dot{V}}_{i}\left({x}_{i},t\right)\le \sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}\sum_{l\in {I}_{i1}}^{{r}_{i}}\sum_{k=1}^{{c}_{i}}{\mu }_{i}^{l}{m}_{i}^{k}\left(\frac{1}{J-1}\left({x}_{i}^{T}\left({{Y}_{i}^{lk}}^{T}{P}_{i}+{P}_{i}{Y}_{i}^{lk}+{{\tau }_{i}^{l}}^{-1}{P}_{i}\right){x}_{i}+{{\alpha }_{i}^{l}}^{T}{P}_{i}{x}_{i}+{x}_{i}^{T}{P}_{i}{\alpha }_{i}^{l}+{\tau }_{i}^{l}{{\beta }_{i}}^{2}{{D}_{i}^{l}}^{T}{P}_{i}{D}_{i}^{l}\right)+{x}_{j}^{T}{{C}_{ij}^{l}}^{T}{P}_{i}{x}_{i}+{x}_{i}^{T}{P}_{i}{C}_{ij}^{l}{x}_{j}+\frac{{\rho }_{i}^{l}}{J-1}\left({\rm O}_{i}^{l}-{x}_{i}^{T}{\Theta }_{i}^{l}{x}_{i}+{x}_{i}^{T}{\Theta }_{i}^{l}{\overline{x}}_{i}^{l}+{{\overline{x}}_{i}^{l}}^{T}{\Theta }_{i}^{l}{\overline{x}}_{i}^{l}\right)\right)$$

(A.3)

$$=\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}\sum_{l\in {I}_{i1}}^{{r}_{i}}\sum_{k=1}^{{c}_{i}}{\mu }_{i}^{l}{m}_{i}^{k}\left(\frac{-{x}_{i}^{T}{Q}_{i}^{lk}{x}_{i}}{J-1}+{F}_{ij}^{l}\right)+\sum_{l=1}^{{r}_{i}}\sum_{k=1}^{{c}_{i}}{\mu }_{i}^{l}{m}_{i}^{k}\left(-{x}_{i}^{T}{P}_{i}{x}_{i}+\left({{\alpha }_{i}^{l}}^{T}{P}_{i}+{\rho }_{i}^{l}{{\overline{x}}_{i}^{l}}^{T}{\Theta }_{i}^{l}\right){x}_{i}+{x}_{i}^{T}\left({P}_{i}{\alpha }_{i}^{l}+{\rho }_{i}^{l}{\Theta }_{i}^{l}{\overline{x}}_{i}^{l}\right)+{\tau }_{i}^{l}{{\beta }_{i}}^{2}{{D}_{i}^{l}}^{T}{P}_{i}{D}_{i}^{l}+{\rho }_{i}^{l}{\rm O}_{i}^{l}\right)$$

$$=\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}\sum_{l\in {I}_{i1}}^{{r}_{i}}\sum_{k=1}^{{c}_{i}}{\mu }_{i}^{l}{m}_{i}^{k}\left(\frac{-{x}_{i}^{T}{Q}_{i}^{lk}{x}_{i}}{J-1}+{F}_{ij}^{l}\right)+\sum_{l\in {I}_{i1}}^{{r}_{i}}\sum_{k=1}^{{c}_{i}}{\mu }_{i}^{l}{m}_{i}^{k}{\left(\begin{array}{cc}{x}_{i}^{T}& 1\end{array}\right)}^{T}\left[\begin{array}{cc}-{P}_{i}& *\\ {{\alpha }_{i}^{l}}^{T}{P}_{i}+{\rho }_{i}^{l}{{\overline{x}}_{i}^{l}}^{T}{\Theta }_{i}^{l}& {\tau }_{i}^{l}{{\beta }_{i}}^{2}{{D}_{i}^{l}}^{T}{P}_{i}{D}_{i}^{l}+{\rho }_{i}^{l}{\rm O}_{i}^{l}\end{array}\right]\left(\begin{array}{c}{x}_{i}\\ 1\end{array}\right)$$

(A.4)

Here ${F}_{ij}^{l}={x}_{j}^{T}{{C}_{ij}^{l}}^{T}{P}_{i}{x}_{i}+{x}_{i}^{T}{P}_{i}{C}_{ij}^{l}{x}_{j}$ and ${Q}_{i}^{lk}$ are as defined in Theorem 1. Now, let $\left[\begin{array}{cc}-{P}_{i}& *\\ {{\alpha }_{i}^{l}}^{T}{P}_{i}+{\rho }_{i}^{l}{{\overline{x}}_{i}^{l}}^{T}{\Theta }_{i}^{l}& {\tau }_{i}^{l}{{\beta }_{i}}^{2}{{D}_{i}^{l}}^{T}{P}_{i}{D}_{i}^{l}+{\rho }_{i}^{l}{\rm O}_{i}^{l}\end{array}\right]\le 0$ which gives ${\dot{V}}_{i}\left({x}_{i},t\right)\le \sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}\sum_{l=1}^{{r}_{i}}\sum_{k=1}^{{c}_{i}}{\mu }_{i}^{l}{m}_{i}^{k}\left(-\frac{1}{J-1}{x}_{i}^{T}{Q}_{i}^{lk}{x}_{i}+{F}_{ij}^{l}\right)$. Then, we conclude that (7c) implies (A.4). We remark that since ${D}_{i}^{l}{d}_{i}\left(t\right)=0,{\alpha }_{i}^{l}=0$ for $l\in {I}_{i0}$, there is no need to check (A.4) for $l\in {I}_{i0}$. Thereby, for both $l\in {I}_{i0}$ and $l\in {I}_{i1},$ we have

$${\dot{V}}_{i}\left({x}_{i},t\right)\le -\sum_{l=1}^{{r}_{i}}\sum_{k=1}^{{c}_{i}}\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}{\mu }_{i}^{l}{m}_{i}^{k}\left(\frac{1}{J-1}{{x}_{i}}^{T}{Q}_{i}^{lk}{x}_{i}-{F}_{ij}^{l}\right)=-\sum_{k=1}^{{c}_{i}}{m}_{i}^{k}\left(\sum_{l=1}^{{r}_{i}}\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}{\mu }_{i}^{l}\left(\frac{1}{J-1}{{x}_{i}}^{T}{Q}_{i}^{lk}{x}_{i}-{F}_{ij}^{l}\right)\right)$$

$$=-{m}_{i}^{1}\sum_{l=1}^{{r}_{i}}\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}{\mu }_{i}^{l}\left(\frac{1}{J-1}{{x}_{i}}^{T}{Q}_{i}^{l1}{x}_{i}-{F}_{ij}^{l}\right)-\sum_{k=2}^{{c}_{i}}{m}_{i}^{k}\left(\sum_{l=1}^{{r}_{i}}\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}{\mu }_{i}^{l}\left(\frac{1}{J-1}{{x}_{i}}^{T}{Q}_{i}^{lk}{x}_{i}-{F}_{ij}^{l}\right)\right)$$

(A.5)

Because ${\rm H}_{ij}^{lh}=\frac{1}{J-1}{{x}_{i}}^{T}{Q}_{i,cont}^{lh}{x}_{i}-{F}_{ij}^{l}$, (A.5) can be rewritten as

$${\dot{V}}_{i}\left({x}_{i},t\right)\le -{m}_{i}^{1}\sum_{l=1}^{{r}_{i}}\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}{\mu }_{i}^{l}\left({\rm H}_{ij}^{l1}\right)-\sum_{k=2}^{{c}_{i}}\left(\frac{{\left({\sum }_{l=1}^{{r}_{i}}\sum_{\begin{array}{c}j=1\\ i\ne j\end{array}}^{J}{\mu }_{i}^{l}{\rm H}_{ij}^{lk}\right)}^{2}}{\sum_{h=1}^{{c}_{i}}\sum_{l=1}^{{r}_{i}}\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}\left|\left.{\mu }_{i}^{l}{\rm H}_{ij}^{lh}\right|\right.}\right)$$

(A.6)

Therefore, we obtain ${\dot{V}}_{i}\left({x}_{i},t\right)\le -{m}_{i}^{1}\sum_{l=1}^{{r}_{i}}\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}{\mu }_{i}^{l}{\rm H}_{ij}^{l1}$ and as a result

$$\dot{V}\left(x,t\right)=\sum_{i=1}^{J}{V}_{i}\left({x}_{i},t\right)\le -\sum_{i=1}^{J}\sum_{l=1}^{{r}_{i}}\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}{m}_{i}^{1}{\mu }_{i}^{l}{\rm H}_{ij}^{l1}=-\sum_{i=1}^{J}{m}_{i}^{1}\left(\sum_{l=1}^{{r}_{i}}{\mu }_{i}^{l}{{x}_{i}}^{T}{Q}_{i}^{l1}{x}_{i}-\sum_{l=1}^{{r}_{i}}\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}{\mu }_{i}^{l}{F}_{ij}^{l}\right).$$

(A.7)

Using (7b), we obtain ${-{\mu }_{i}^{l}{{x}_{i}}^{T}Q}_{i}^{l1}{x}_{i}\le -{\mu }_{i}^{l}{\eta }_{i}{I}_{i}{\Vert {x}_{i}\Vert }^{2}$. Because $\sum_{l=1}^{{r}_{i}}{\mu }_{i}^{l}=1$ and ${\eta }_{i}=\underset{l}{\mathit{min}}\left({\eta }_{i}^{l}\right)$, we conclude that $-\sum_{l=1}^{{r}_{i}}{\mu }_{i}^{l}{{x}_{i}}^{T}{Q}_{i}^{l1}{x}_{i}\le -{\eta }_{i}{\Vert {x}_{i}\Vert }^{2}\sum_{l=1}^{{r}_{i}}{\mu }_{i}^{l}=-{\eta }_{i}{\Vert {x}_{i}\Vert }^{2}$. Also

$$\sum_{l=1}^{{r}_{i}}{\mu }_{i}^{l}{F}_{ij}^{l}=\sum_{l=1}^{{r}_{i}}{\mu }_{i}^{l}\left({x}_{j}^{T}{{C}_{ij}^{l}}^{T}{P}_{i}{x}_{i}+{{x}_{i}}^{T}{P}_{i}{C}_{ij}^{l}{x}_{j}\right)\le {r}_{i}\Vert {P}_{i}{x}_{i}\Vert \Vert {C}_{ij}^{l}{x}_{j}\Vert \left({n}_{i}+{n}_{j}\right)$$

$$\le {r}_{i}\sqrt{{\left({C}_{ij}^{l}{x}_{j}\right)}^{T}{C}_{ij}^{l}{x}_{j}}\sqrt{{\lambda }_{max}\left({{P}_{i}}^{T}{P}_{i}\right)}\Vert {x}_{i}\Vert \Vert {x}_{j}\Vert \left({n}_{i}+{n}_{j}\right)\le {r}_{i}\Vert {x}_{i}\Vert \Vert {x}_{j}\Vert {\Vert {P}_{i}\Vert }_{2}\underset{l}{\mathit{max}}\left(\Vert {C}_{ij}^{l}\Vert \right)\left({n}_{i}+{n}_{j}\right)$$

(A.8)

where ${n}_{i}$ and ${n}_{j}$ are the number of states in the $i$ th and $j$ th subsystems, respectively. Now, based on (A.7) and the above inequalities, it is clear that $\dot{V}\left(x,t\right)\le \sum_{i=1}^{J}{m}_{i}^{1}\left(-{\eta }_{i}{\Vert {x}_{i}\Vert }^{2}+\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}{r}_{i}\Vert {x}_{i}\Vert \Vert {x}_{j}\Vert {\Vert {P}_{i}\Vert }_{2}{\delta }_{ij}\right)$ where${\delta }_{ij}=\underset{l}{\mathit{max}}\left(\Vert {C}_{ij}^{l}\Vert \right)\left({n}_{i}+{n}_{j}\right)$,$\left\| {P_{i} } \right\|_{2} = \lambda _{{max}} \left( {P_{i} } \right) = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\lambda _{{min}} \left( {T_{i} } \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\lambda _{{min}} \left( {T_{i} } \right)}$}}$, and${{T}_{i}}^{-1}= {P}_{i}$. Therefore$\dot{V}\left(x,t\right)\le \sum_{i=1}^{J}{m}_{i}^{1}\left(-{\eta }_{i}{\Vert {x}_{i}\Vert }^{2}+\sum_{\begin{array}{c}j=1\end{array}}^{J}{r}_{i}\Vert {x}_{i}\Vert \Vert {x}_{j}\Vert {\lambda }_{max}\left({P}_{i}\right){\delta }_{ij}\right)$. The right-hand side this inequality is quadratic in terms of$\left\{\begin{array}{ccc}\Vert {x}_{1}\Vert & \Vert {x}_{2}\Vert & \begin{array}{cc}\cdots & \Vert {x}_{J}\Vert \end{array}\end{array}\right\}$, and can be rewritten as$-\left[\begin{array}{ccc}\Vert {x}_{1}\Vert & \Vert {x}_{2}\Vert & \begin{array}{cc}\cdots & \Vert {x}_{J}\Vert \end{array}\end{array}\right]\times M\times {\left[\begin{array}{ccc}\Vert {x}_{1}\Vert & \Vert {x}_{2}\Vert & \begin{array}{cc}\cdots & \Vert {x}_{J}\Vert \end{array}\end{array}\right]}^{T}$. Now, if $\left(A.7\right)$ is negative and (7b)-(7c) hold, then we obtain$\dot{V}\left(x,t\right)<0$. This procedure was considered when$\sum_{h=1}^{{c}_{i}}\sum_{l=1}^{{r}_{i}}\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}\left|\left.{\mu }_{i}^{l}{\rm H}_{ij}^{lh}\right|\right.\ne 0$. In the case that $\sum_{h=1}^{{c}_{i}}\sum_{l=1}^{{r}_{i}}\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}\left|\left.\left({\mu }_{i}^{l}{H}_{ij}^{lh}\right)\right|\right.=0$ and ${\sum }_{l=1}^{{r}_{i}}\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}\left({\mu }_{i}^{l}{H}_{ij}^{lk}\right)\ge 0$ in (4), we obtain${m}_{i}^{k}=\frac{1}{{c}_{i}}$,, but since${\mu }_{i}^{l}\left(\frac{1}{J-1}{{x}_{i}}^{T}{Q}_{i}^{lk}{x}_{i}-{F}_{ij}^{l}\right)=0$, the above procedure is much simpler and results in$\dot{V}(x,t)\le 0$. In the case of ${\sum }_{l=1}^{{r}_{i}}\sum_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{J}\left({\mu }_{i}^{l}{H}_{ij}^{lk}\right)<0,$ in (4), the result is easy to obtain, although the derivation is omitted here. By using LaSalle’s principle, since the limit set includes only the trivial trajectory$x\equiv 0$, the origin is asymptotically stable. Thus the proof is complete.

Proof of Theorem 2

Consider the following cost function for AFLSS expressed in (12) and (13).

$${J}_{t}={\int }_{0}^{\infty }\left({\left|{\varvec{y}}\left(t\right)\right|}^{2}-{\gamma }^{2}{\left|{\varvec{d}}\left(t\right)\right|}^{2}\right)dt={\int }_{0}^{\infty }\left({{\varvec{y}}}^{T}\left(t\right){\varvec{y}}\left(t\right)-{\gamma }^{2}{{\varvec{d}}\left(t\right)}^{T}{\varvec{d}}\left(t\right)+\frac{dV\left(x,t\right)}{dt}\right)dt-V\left(x\left(\infty \right),\infty \right)$$

(A.9)

It is clear that

$${J}_{t}\le {\int }_{0}^{\infty }\left({{\varvec{y}}}^{T}\left(t\right){\varvec{y}}\left(t\right)-{\gamma }^{2}{{\varvec{d}}\left(t\right)}^{T}{\varvec{d}}\left(t\right)+\frac{dV\left(x,t\right)}{dt}\right)dt={\int }_{0}^{\infty }\sum_{i=1}^{J}\left({{y}_{i}}^{T}{y}_{i}-{\gamma }^{2}{{d}_{i}\left(t\right)}^{T}{d}_{i}\left(t\right)+\frac{d{V}_{i}\left(x,t\right)}{dt}\right)dt$$

(A.10)

For $l\in {I}_{i1}$, using ${y}_{i}$ expressed in (13), $($ A.10) becomes

$$\begin{gathered} \smallint _{0}^{\infty } \sum\limits_{{i = 1}}^{J} {\left\{ {\left[ {\sum\limits_{{k = 1}}^{{c_{i} }} {\sum\limits_{{l \in I_{{i1}} }}^{{r_{i} }} {\mu _{i}^{l} } } m_{i}^{k} \left( {\left( {C_{i}^{l} - E_{i}^{l} K_{i}^{k} } \right)x_{i} } \right)} \right]^{T} \left[ {\sum\limits_{{k = 1}}^{{c_{i} }} {\sum\limits_{{l \in I_{{i1}} }}^{{r_{i} }} {\mu _{i}^{l} } } m_{i}^{k} \left( {\left( {C_{i}^{l} - E_{i}^{l} K_{i}^{k} } \right)x_{i} } \right)} \right] - \gamma ^{2} d_{i} \left( t \right)^{T} d_{i} \left( t \right)} \right\}} dt \hfill \\ + \smallint _{0}^{\infty } \sum\limits_{{i = 1}}^{J} {\left\{ {\sum _{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{J} \sum\limits_{{l \in I_{{i1}} }}^{{r_{i} }} {\sum\limits_{{k = 1}}^{{c_{i} }} {\mu _{i}^{l} } } m_{i}^{k} \left( {\frac{{x_{i}^{T} \hat{Y}_{i}^{{lkT}} P_{i} x_{i} + D_{i}^{{lT}} d_{i} \left( t \right)P_{i} x_{i} + \hat{\alpha }_{i}^{{lT}} P_{i} x_{i} }}{{J - 1}} + x_{j}^{T} C_{{ij}}^{{lT}} P_{i} x_{i} + \frac{{x_{i}^{T} P_{i} \hat{Y}_{i}^{{lk}} x_{i} + x_{i}^{T} P_{i} d_{i} \left( t \right)D_{i}^{l} + x_{i}^{T} P_{i} \hat{\alpha }_{i}^{l} }}{{J - 1}} + x_{i}^{T} P_{i} C_{{ij}}^{l} x_{j} } \right)} \right\}} dt \hfill \\ \end{gathered}$$

(A.11)

Similar to (A.2), by using the inequality $2{x}^{T}y\le \epsilon {x}^{T}{P}^{-1}x+{\epsilon }^{-1}{y}^{T}Py$, for the two vectors $x$ and $y$, we obtain ${x}_{i}^{T}{P}_{i}{d}_{i}\left(t\right){D}_{i}^{l}+{{D}_{i}^{l}}^{T}{d}_{i}\left(t\right){P}_{i}{x}_{i}\le {\gamma }^{-2}{x}_{i}^{T}{P}_{i}{D}_{i}^{l}{{D}_{i}^{l}}^{T}{P}_{i}{x}_{i}+{\gamma }^{2}{{d}_{i}\left(t\right)}^{T}{d}_{i}\left(t\right)$. Similar to (A.2)-(A.3), we conclude that ${J}_{t}\le {\int }_{0}^{\infty }\sum_{i=1}^{J}\left\{{\mathcal{U}}_{i}+{\mathcal{V}}_{i}+{\mathcal{W}}_{i}\right\}dt$, in which

$${\mathcal{U}}_{i}={\left[\sum_{k=1}^{{c}_{i}}\sum_{l\in {I}_{i1}}^{{r}_{i}}{\mu }_{i}^{l}{m}_{i}^{k}\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right){x}_{i}\right]}^{T}\left[\sum_{k=1}^{{c}_{i}}\sum_{l\in {I}_{i1}}^{{r}_{i}}{\mu }_{i}^{l}{m}_{i}^{k}\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right){x}_{i}\right]$$

$$\nu _{i} = \sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{j} {\sum\limits_{{l \in I_{{il}} }}^{{r_{i} }} {\sum\limits_{{k = 1}}^{{c_{i} }} {\mu _{i}^{l} m_{i}^{k} } } } \left( {\frac{{x_{i}^{T} \left( {\hat{Y}_{i}^{{lkT}} P_{i} + P_{i} \hat{Y}_{i}^{{lk}} + \gamma ^{{ - 2}} P_{i} D_{i}^{l} D_{i}^{{lT}} P_{i} + P_{i} - \rho _{i}^{l} \Theta _{i}^{l} + \in _{{\alpha i}}^{{l - 1}} P_{i} H_{{\alpha _{i} }}^{l} R_{{\alpha _{i} }}^{{lT}} H_{{\alpha _{i} }}^{l} P_{i} } \right)x_{i} }}{{J - 1}} + x_{j}^{T} C_{{ij}}^{{lT}} P_{i} x_{i} + x_{i}^{T} P_{i} C_{{ij}}^{l} x_{j} } \right)$$

$${\mathcal{W}}_{i}=\sum_{l\in {I}_{i1}}^{{r}_{i}}\sum_{k=1}^{{c}_{i}}{\mu }_{i}^{l}{m}_{i}^{k}\left(-{x}_{i}^{T}{P}_{i}{x}_{i}+\left({{\alpha }_{i}^{l}}^{T}{P}_{i}+{\rho }_{i}^{l}{{\overline{x}}_{i}^{l}}^{T}{\Theta }_{i}^{l}\right){x}_{i}+{x}_{i}^{T}\left({P}_{i}{\alpha }_{i}^{l}+{\rho }_{i}^{l}{\Theta }_{i}^{l}{\overline{x}}_{i}^{l}\right)+{\rho }_{i}^{l}{\rm O}_{{c}_{i}}^{l}+{\epsilon }_{{\alpha }_{i}}^{l}{{L}_{{\alpha }_{i}}^{l}}^{T}{L}_{{\alpha }_{i}}^{l}\right)$$

(A.12)

Now, from (A.1)-(A.4), we recall that

$$\dot{V}_{i} \left( {x_{i} ,t} \right) \le \sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{j} {\sum\limits_{{l \in I_{{i1}} }}^{{r_{i} }} {\sum\limits_{{k = 1}}^{{c_{i} }} {\mu _{i}^{l} m_{i}^{k} } } } \left( {\frac{1}{{J - 1}}x_{i}^{T} \left( {\hat{Y}_{i}^{{lkT}} P_{i} + P_{i} \hat{Y}_{i}^{{lk}} + \left( {\tau _{i}^{{l - 1}} + 1} \right)P_{i} - \rho _{i}^{l} \Theta _{i}^{l} } \right)x_{i} + x_{j}^{T} C_{{ij}}^{{lT}} P_{i} x_{i} + x_{i}^{T} P_{i} C_{{ij}}^{l} x_{j} } \right) + \sum\limits_{{l \in I_{{i1}} }}^{{r_{i} }} {\sum\limits_{{k = 1}}^{{c_{i} }} {\mu _{i}^{l} } } m_{i}^{k} \left( { - x_{i}^{T} P_{i} x_{i} + \left( {\hat{\alpha }_{i}^{{lT}} P_{i} + \rho _{i}^{l} \bar{x}_{i}^{{lT}} \Theta _{i}^{l} } \right)x_{i} + x_{i}^{T} \left( {P_{i} \hat{\alpha }_{i}^{l} + \rho _{i}^{l} \Theta _{i}^{l} \bar{x}_{i}^{l} } \right) + \tau _{i}^{l} \beta _{i} ^{2} D_{i}^{{lT}} P_{i} D_{i}^{l} + \rho _{i}^{l} {\text{O}}_{i}^{l} } \right)$$

(A.13)

where ${\widehat{Y}}_{i}^{lk}={\widehat{A}}_{i}^{l}-{\widehat{B}}_{i}^{l}{K}_{i}^{k}$. Therefore ${\dot{V}}_{i}\left({x}_{i},t\right)\le \sum_{l\in {I}_{i1}}^{{r}_{i}}\sum_{k=1}^{{c}_{i}}{\mu }_{i}^{l}{m}_{i}^{k}\left({{\alpha }_{i}^{l}}^{T}{P}_{i}{x}_{i}+{x}_{i}^{T}{P}_{i}{\alpha }_{i}^{l}+{\left({H}_{{\alpha }_{i}}^{l}{F}_{{\alpha }_{i}}^{l}\left(t\right){L}_{{\alpha }_{i}}^{l}\right)}^{T}{P}_{i}{x}_{i}+{x}_{i}^{T}{P}_{i}{H}_{{\alpha }_{i}}^{l}{F}_{{\alpha }_{i}}^{l}\left(t\right){L}_{{\alpha }_{i}}^{l}\right)+{Q}_{i}$ where ${Q}_{i}$ are the remaining terms of (A.13). We know the for the given matrices $Q,H,R,E$ of appropriate dimensions, with $Q={Q}^{T}, R={R}^{T}$ and $R>0,$ then $Q+HFE+{E}^{T}{F}^{T}{H}^{T}<0$ for all $F$ satisfying ${F}^{T}F<R$, if and only if there exists some $\epsilon >0$ such that $Q+\epsilon H{H}^{T}+{\epsilon }^{-1}{E}^{T}RE<0$. It can be concluded that ${\dot{V}}_{i}\left({x}_{i},t\right)<0$ if and only if the following inequality holds:

$$\sum_{l\in {I}_{i1}}^{{r}_{i}}\sum_{k=1}^{{c}_{i}}{\mu }_{i}^{l}{m}_{i}^{k}\left({{\alpha }_{i}^{l}}^{T}{P}_{i}{x}_{i}+{x}_{i}^{T}{P}_{i}{\alpha }_{i}^{l}+{{\epsilon }_{{\alpha }_{i}}^{l}}^{-1}{x}_{i}^{T}{P}_{i}{H}_{{\alpha }_{i}}^{l}{R}_{{\alpha }_{i}}^{l}{{H}_{{\alpha }_{i}}^{l}}^{T}{P}_{i}{x}_{i}+{\epsilon }_{{\alpha }_{i}}^{l}{{L}_{{\alpha }_{i}}^{l}}^{T}{L}_{{\alpha }_{i}}^{l}\right)+{Q}_{i}\le 0$$

(A.14)

that results in

$$\dot{V}_{i} \left( {x_{i} ,t} \right) \le \sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{J} {\sum\limits_{{l \in I_{{i1}} }}^{{r_{i} }} {\sum\limits_{{k = 1}}^{{c_{i} }} {\mu _{i}^{l} } } m_{i}^{k} } \left( {\frac{{x_{i}^{T} \left( {\hat{Y}_{i}^{{lkT}} P_{i} + P_{i} \hat{Y}_{i}^{{lk}} + \left( {\tau _{i}^{{l - 1}} + 1} \right)P_{i} - \rho _{i}^{l} \Theta _{i}^{l} + \in _{{\alpha _{i} }}^{{l - 1}} P_{i} H_{{\alpha _{i} }}^{l} R_{{\alpha _{i} }}^{l} H_{{\alpha _{i} }}^{{lT}} P_{i} } \right)x_{i} }}{{J - 1}} + x_{j}^{T} C_{{ij}}^{{lT}} P_{i} x_{i} + x_{i}^{T} P_{i} C_{{ij}}^{l} x_{j} } \right) + \sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{J} {\sum\limits_{{l \in I_{{i1}} }}^{{r_{i} }} {\sum\limits_{{k = 1}}^{{c_{i} }} {\mu _{i}^{l} } } m_{i}^{k} } \left( { - x_{i}^{T} P_{i} x_{i} + \left( {\alpha _{i}^{{lT}} P_{i} + \rho _{i}^{l} \bar{x}_{i}^{{lT}} \Theta _{i}^{l} } \right)x_{i} + x_{i}^{T} \left( {P_{i} \alpha _{i}^{l} + \rho _{i}^{l} \Theta _{i}^{l} \bar{x}_{i}^{l} } \right) + \tau _{i}^{l} \beta _{i} ^{2} D_{i}^{{lT}} P_{i} D_{i}^{l} + \rho _{i}^{l} {\text{O}}_{i}^{l} + \in _{{\alpha _{i} }}^{l} L_{{\alpha _{i} }}^{{lT}} L_{{\alpha _{i} }}^{l} } \right)$$

(A.15)

The second term of (A.15), can also be written as

$$-{x}_{i}^{T}{P}_{i}{x}_{i}+\left({{\alpha }_{i}^{l}}^{T}{P}_{i}+{\rho }_{i}^{l}{{\overline{x}}_{i}^{l}}^{T}{\Theta }_{i}^{l}\right){x}_{i}+{x}_{i}^{T}\left({P}_{i}{\alpha }_{i}^{l}+{\rho }_{i}^{l}{\Theta }_{i}^{l}{\overline{x}}_{i}^{l}\right)+{\tau }_{i}^{l}{{\beta }_{i}}^{2}{{D}_{i}^{l}}^{T}{P}_{i}{D}_{i}^{l}+{\rho }_{i}^{l}{\rm O}_{i}^{l}+{\epsilon }_{{\alpha }_{i}}^{l}{{L}_{{\alpha }_{i}}^{l}}^{T}{R}_{{\alpha }_{i}}^{l}{L}_{{\alpha }_{i}}^{l}$$

$$={\left(\begin{array}{cc}{x}_{i}^{T}& 1\end{array}\right)}^{T}\left[\begin{array}{cc}-{P}_{i}& *\\ {{\alpha }_{i}^{l}}^{T}{P}_{i}+{\rho }_{i}^{l}{{\overline{x}}_{i}^{l}}^{T}{\Theta }_{i}^{l}& {\tau }_{i}^{l}{{\beta }_{i}}^{2}{{D}_{i}^{l}}^{T}{P}_{i}{D}_{i}^{l}+{\rho }_{i}^{l}{\rm O}_{\mathrm{i}}^{l}+{\epsilon }_{{\alpha }_{i}}^{l}{{L}_{{\alpha }_{i}}^{l}}^{T}{L}_{{\alpha }_{i}}^{l}\end{array}\right]\left(\begin{array}{c}{x}_{i}\\ 1\end{array}\right)$$

(A.16)

Using the Schur complement, if the following inequality holds, then ${\mathcal{W}}_{i}$ becomes negative

$$\left[\begin{array}{cc}-{P}_{i}& *\\ {{\alpha }_{i}^{l}}^{T}{P}_{i}+{\rho }_{i}^{l}{{\overline{x}}_{i}^{l}}^{T}{\Theta }_{i}^{l}& {\rho }_{i}^{l}{\rm O}_{\mathrm{i}}^{l}+{\epsilon }_{{\alpha }_{i}}^{l}{{L}_{{\alpha }_{i}}^{l}}^{T}{L}_{{\alpha }_{i}}^{l}\end{array}\right]\le 0 (\mathrm{A}.17)$$

Now by considering (A.13)-(A.17), we conclude that where ${\Upsilon}_{\mathrm{i}}^{l}={\rho }_{i}^{l}{\rm O}_{i}^{l}+{\rho }_{i}^{l}{{\alpha }_{i}^{l}}^{T}{\Theta }_{i}^{l}{\overline{x}}_{i}^{l}+{\left({\rho }_{i}^{l}{{\alpha }_{i}^{l}}^{T}{\Theta }_{i}^{l}{\overline{x}}_{i}^{l}\right)}^{T}$ implies (A.17). By setting ${\tau }_{i}^{l}=0$ inhere, we can obtain a less restrictive condition. Consequently, if the following inequality holds then we obtain${\mathcal{W}}_{\mathrm{i}}\le 0$.

Now, By defining ${\chi }_{i}^{lk}=\sum_{l\in {I}_{\mathrm{i}1}}^{{r}_{i}}{\mu }_{i}^{l}{m}_{i}^{k}\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right){x}_{i}$, we obtain

$$\sum_{k=1}^{{c}_{i}}\sum_{l\in {I}_{i1}}^{{r}_{i}}{\mu }_{i}^{l}{m}_{i}^{k}\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right){x}_{i}=\sum_{k=1}^{{c}_{i}}{\chi }_{i}^{lk}$$

(A.19)

Chebyshev inequality indicates $\forall {v}_{i}\in {\mathbb{R}}^{n\times n}$ we have ${\left(\sum_{i=1}^{m}{v}_{i}\right)}^{T}\left(\sum_{i=1}^{m}{v}_{i}\right)\le m\sum_{i=1}^{m}{{v}_{i}}^{T}{v}_{i}.$ Using Chebyshev inequality, we have

$${\left(\sum_{k=1}^{{c}_{i}}{\chi }_{i}^{lk}\right)}^{T}\left(\sum_{k=1}^{{c}_{i}}{\chi }_{i}^{lk}\right)\le {c}_{i}\sum_{k=1}^{{c}_{i}}\left({\left[\sum_{l\in {I}_{i1}}^{{r}_{i}}{\mu }_{i}^{l}{m}_{i}^{k}\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right){x}_{i}\right]}^{T}\left[\sum_{l\in {I}_{i1}}^{{r}_{i}}{\mu }_{i}^{l}{m}_{i}^{k}\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right){x}_{i}\right]\right)$$

$$\le {c}_{i}{r}_{i}\sum_{k=1}^{{c}_{i}}\sum_{l\in {I}_{i1}}^{{r}_{i}}{\left({\mu }_{i}^{l}{m}_{i}^{k}\right)}^{2}{{x}_{i}}^{T}{\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right)}^{T}\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right){x}_{i}$$

(A.20)

Because $0\le {\mu }_{i}^{l}\le 1, 0\le {m}_{i}^{k}\le 1$, it is clear that ${J}_{t}\le {\int }_{0}^{\infty }\sum_{i=1}^{J}\left\{{c}_{i}{r}_{i}\sum_{k=1}^{{c}_{i}}\sum_{l\in {I}_{i1}}^{{r}_{i}}{\left({\mu }_{i}^{l}{m}_{i}^{k}\right)}^{2}{{x}_{i}}^{T}{\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right)}^{T}\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right){x}_{i}+{\mathcal{V}}_{i}\right\}dt$. We know that for given matrices $Q,H,R,E$ of appropriate dimensions, with $Q={Q}^{T}, R={R}^{T}$ and $R>0,$ then $Q+HFE+{E}^{T}{F}^{T}{H}^{T}<0$ for all $F$ satisfying ${F}^{T}F<R$, if and only if there exists some $\epsilon >0$ such that $Q+\epsilon H{H}^{T}+{\epsilon }^{-1}{E}^{T}RE<0$. Using this and analogous to (A.5)-(A.8), if the following inequality holds

$${{A}_{i}^{l}}^{T}{P}_{i}+{P}_{i}{A}_{i}^{l}-{{K}_{i}^{k}}^{T}{{B}_{i}^{l}}^{T}{P}_{i}-{P}_{i}{B}_{i}^{l}{K}_{i}^{k}+{P}_{i}-{{\rho }_{i}^{l}\Theta }_{i}^{l}+{{\epsilon }_{{\alpha }_{i}}^{l}}^{-1}{P}_{i}{H}_{{\alpha }_{i}}^{l}{R}_{{\alpha }_{i}}^{l}{{H}_{{\alpha }_{i}}^{l}}^{T}{P}_{i}+{\epsilon }_{{a}_{i}}^{l}{{L}_{{a}_{i}}^{l}}^{T}{L}_{{a}_{i}}^{l}$$

$$+{{\epsilon }_{{a}_{i}}^{l}}^{-1}{P}_{i}{H}_{{a}_{i}}^{l}{R}_{{a}_{i}}^{l}{{H}_{{a}_{i}}^{l}}^{T}{P}_{i}+{\epsilon }_{{b}_{i}}^{l}{{K}_{i}^{k}}^{T}{{L}_{{b}_{i}}^{l}}^{T}{L}_{{b}_{i}}^{l}{K}_{i}^{k}+{{\epsilon }_{{b}_{i}}^{l}}^{-1}{P}_{i}{H}_{{b}_{i}}^{l}{R}_{{b}_{i}}^{l}{{H}_{{b}_{i}}^{l}}^{T}{P}_{i}+{\gamma }^{-2}{P}_{i}{D}_{i}^{l}{{D}_{i}^{l}}^{T}{P}_{i}+{c}_{i}{r}_{i}{\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right)}^{T}\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right)\le -{\eta }_{i}^{l}{I}_{i}$$

(A.21)

we obtain ${\mathcal{U}}_{i}+{\mathcal{V}}_{i}\le 0$. Now considering (A.21) as $-{Q}_{i,cont}^{lk}=-{Q}_{i}^{lk}+{{\Delta }_{1}\left(\mathrm{5,1}\right)}^{T}{\left({Diag}_{1}^{1}\left(\bullet \right)\right)}^{-1}{\Delta }_{1}\left(\mathrm{5,1}\right)+{\gamma }^{-2}{P}_{i}{D}_{i}^{l}{{D}_{i}^{l}}^{T}{P}_{i}+{c}_{i}{r}_{i}{\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right)}^{T}\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right)-{{\tau }_{i}^{l}}^{-1}{P}_{i}\le -{\eta }_{i}^{l}{I}_{i}$, and by continuing the same procedure, and using the following inequality, we obtain ${J}_{t}\le 0$.

For l $\in {I}_{i0}$, the procedure is simpler and similar to (A.19)-(A.22). Consequently, it yields

$${\eta }_{i}^{l}{I}_{i}+{{A}_{i}^{l}}^{T}{P}_{i}+{P}_{i}{A}_{i}^{l}-{{K}_{i}^{k}}^{T}{{B}_{i}^{l}}^{T}{P}_{i}-{P}_{i}{B}_{i}^{l}{K}_{i}^{k}+{\epsilon }_{{a}_{i}}^{l}{{L}_{{a}_{i}}^{l}}^{T}{L}_{{a}_{i}}^{l}+{{\epsilon }_{{a}_{i}}^{l}}^{-1}{P}_{i}{H}_{{a}_{i}}^{l}{R}_{{a}_{i}}^{l}{{H}_{{a}_{i}}^{l}}^{T}{P}_{i}+{\epsilon }_{{b}_{i}}^{l}{{K}_{i}^{k}}^{T}{{L}_{{b}_{i}}^{l}}^{T}{L}_{{b}_{i}}^{l}{K}_{i}^{k}+{{\epsilon }_{{b}_{i}}^{l}}^{-1}{P}_{i}{H}_{{b}_{i}}^{l}{R}_{{b}_{i}}^{l}{{H}_{{b}_{i}}^{l}}^{T}{P}_{i}+{c}_{i}{r}_{i}{\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right)}^{T}\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right)\le 0$$

(C.37)

Let $-{Q}_{i,cont}^{lk}=-{Q}_{i}^{lk}+{{\Delta }_{0}\left(\mathrm{4,1}\right)}^{T}{\left({Diag}_{0}\left(\bullet \right)\right)}^{-1}{\Delta }_{0}\left(\mathrm{4,1}\right)+{c}_{i}{r}_{i}{\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right)}^{T}\left({C}_{i}^{l}-{E}_{i}^{l}{K}_{i}^{k}\right)$. To satisfy this latter inequality, the following matrix inequality should hold.

With regards to remarks of Theorem 2, we obtain ${J}_{t}\le 0,$ and the proof is complete.