1 Introduction

Since the seminal work by Zadeh [1], fuzzy set theory and its applications have been widely extended to provide powerful tools to deal with imprecise information in many decision-making problems. A fuzzy set is a class of objects characterized by a membership function which assigns to each element a degree of membership ranging between zero and one. Fuzzy sets were extended by intuitionistic fuzzy sets proposed by [2, 3] characterized by a membership function but also by a non-membership function. Furthermore, neutrosophic sets proposed by [4] extended intuitionistic fuzzy sets by considering a truth-membership function, an indeterminacy-membership function, and a falsity-membership function. Wang et al. [5] introduced the concept of a single-valued neutrosophic sets (SVNS), a subclass of the neutrosophic sets. A SVNS is an instance of neutrosophic set which can be used in real economics and finance applications. Ye [6] introduced trapezoidal neutrosophic sets and developed score and accuracy functions to deal with multiple criteria decision-making (MCDM) problems.

Several recent works rely on neutrosophic sets to approach different problems in multiple research areas. For example [7] proposes neutrosophic linear programming using the concept of possibilistic mean; [8] develop an application in the hotel location selection problem; [9] proposes an approach to pharmaceutical supply chain management; [10] investigate the pricing problems of satellite image data products; [11] study the temperature variation and climate data; [12] approach the problem of offshore wind farm site selection in USA; [13] measure pollution attributes in mega-cities; [14] describe an application for sustainable supplier selection; [15] deal with the assessment of safety in construction; [16] propose a leanness assessment methodology; and [17] explore the key factors which would prevent expansion of the epidemic in the face of incomplete knowledge.

However, one of the limitations in neutrosophic fuzzy numbers is the assumption of linearity of membership functions. Single valued triangular neutrosophic numbers (SVTNN) can only handle incomplete, indeterminate and inconsistent information expressed by means of linear functions. Mondal et al. [18] defined non-linear interval fuzzy numbers with two membership functions (upper and lower). More recently, [19] discussed different types of linear and non-linear neutrosophic trapezoidal numbers. However, this last work is limited to the proposal of a non-linear expression of membership functions without considering its main properties.

In this paper, we develop the concept of non-linear neutrosophic number (NLNN). By considering the set of parameters that characterizes a NLNN, we analytically and graphically explore the implications of selecting alternative values. We pay special attention to extreme values. We also derive more general definitions for the notion of \((\alpha ,\beta ,\gamma )\)-cuts, possibility mean, variance and skewness of a NLNN. We also propose a new possibility score function of a NLNN based on the possibility mean and standard deviation that can be used to better deal with MCDM problems.

Other recent contributions to decision-making considering multiple criteria within a context of uncertainty include [20,21,22,23,24]. In this paper, we follow the approach of dealing with uncertainty by means of NLNN. Table 1 presents a survey on recent MCDM works under uncertainty and shows the research gap covered by this paper. More precisely we propose the use of NLNN to deal with uncertainty to evaluate a set of alternatives in the context of supply chain management. Similarly to the use of the Minkowski distance in several MCDM applications [25, 26], we argue that a NLNN allows practitioners to express fuzziness in both a wider and more specific way. To illustrate our proposal, we describe how can a hybrid model combining Neutrosophic Analytic Hierarchy Process (N-AHP) and Neutrosophic Technique for Order of Preference by Similarity to Ideal Solution (N-TOPSIS) recently proposed by [27] can be generalized by using NLNN.

Table 1 Survey on recent works about MCDM under uncertainty
Full size table

Summarizing, the main contributions of this paper are:

  1. 1.

    An alternative definition for NLNN.

  2. 2.

    A new set of definitions derived from the concept of NLNN.

  3. 3.

    A new score function useful for decision-making applications.

In what follows, Sect. 2 provides some basic definitions about neutrosophic sets. Section 3 develops the concept of NLNN by exploring its properties. Section 4 focuses on the concept of possibility mean, variance and standard deviation of NLNN. Section 5 proposes a new score function. Section 6 illustrates our porposal by means of a real case study. Section 7 provides managerial insights and practical implications and Sect. 8 concludes.

2 Background on Neutrosophic Sets

Since the proposal by Zadeh [1], fuzzy set theory has been broadly used in several research fields. In the same way, Smarandache [4] introduced the concept of neutrosophic set (NS).

Definition 1

[5] Let X be a space of points, with a generic element in X denoted by x. A neutrosophic set A in X is characterized by a truth-membership function \(T_A\), an indeterminacy-membership function \(I_A\) and a falsity-membership function \(F_A\).

\(T_A(x)\), \(I_A(x)\) and \(F_A(x)\) are standard or non-standard subsets of \(\left] {{0}^{-}}{{,1}^{+}} \right[\):

$$\begin{gathered} T_{A} :X \to \left] {0^{ - } ,1^{ + } } \right[ \hfill \\ I_{A} :X \to \left] {0^{ - } ,1^{ + } } \right[ \hfill \\ F_{A} :X \to \left] {0^{ - } ,1^{ + } } \right[ \hfill \\ \end{gathered}$$
(1)

The membership functions must satisfy the condition:

$${{0}^{-}}\le {{T}_{A}}(x)+{{I}_{A}}(x)+{{F}_{A}}\le {{3}^{+}}$$
(2)

A single valued neutrosophic set is a specific type of NS with membership value functions in the interval \(\left[ 0, 1\right]\).

Definition 2

[5] Let X be a space of points, with a generic element in X, denoted by x. A single valued neutrosophic set (SVNS) A in X is characterized by a truth-membership function \(T_A\), an indeterminacy-membership function \(I_A\) and a falsity-membership function \(F_A\). For each point x in X, \(T_A(x)\), \(I_A(x)\), \(F_A(x) \in \left[ 0, 1\right]\).

The sum of \(T_A(x)\), \(I_A(x)\), \(F_A(x)\) must satisfy the condition:

$$0\le {{T}_{A}}(x)+{{I}_{A}}(x)+{{F}_{A}}(x) \le 3$$
(3)

Given a SVNS A in X, \(x=({{T}_{x}},{{I}_{x}},{{F}_{x}})\) is called a single valued neutrosophic number (SVNN) as an element in A.

Definition 3

[28] Let \(x=({{T}_{x}},{{I}_{x}},{{F}_{x}})\) and \(y=({{T}_{y}},{{I}_{y}},{{F}_{y}})\) be two SVNNs. The operations for SVNNs can be defined as follows:

  1. 1.

    \(x\oplus y=({{T}_{x}}+{{T}_{y}}-{{T}_{x}}\times {{T}_{y}},{{I}_{x}}\times {{I}_{y}},{{F}_{x}}\times {{F}_{y}})\)

  2. 2.

    \(x\otimes y=({{T}_{x}}\times {{T}_{y}},{{I}_{x}}+{{I}_{y}}-{{I}_{x}}\times {{I}_{y}},{{F}_{x}}+{{F}_{y}}-{{F}_{x}}\times {{F}_{y}})\)

  3. 3.

    \(\lambda x=(1-{{(1-{{T}_{x}})}^{\lambda }},{{({{I}_{x}})}^{\lambda }},{{({{F}_{x}})}^{\lambda }}),\text { where }\lambda >0\)

Definition 4

[7] An SVNN \({\tilde{A}}=({\underline{a}},a,{\overline{a}});{{w}_{\tilde{A}}},{{y}_{\tilde{A}}},{{u}_{\tilde{A}}})\) is called SVTNN when its truth-membership function \({{T}_{\tilde{A}}}(x)\), indeterminacy-membership function \({{I}_{\tilde{A}}}(x)\) and falsity-membership \({{F}_{\tilde{A}}}(x)\) function are linear and given as follows:

$${{T}_{\tilde{A}}} (x) = \left\{ {\begin{array}{*{20}c} {\frac{{x - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}{{a - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}w_{\tilde{A}} } & {{\text{if}}\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} \le x < a,\,} \\ {w_{\tilde{A}} } & {{\text{if}}\,x = a,} \\ {\frac{{\bar{a} - x}}{{\bar{a} - a}}w_{\tilde{A}} } & {{\text{if}}\,a < x \le \bar{a},} \\ 0 & {{\text{otherwise}}.} \\ \end{array} } \right.$$
(4)
$$I_{\tilde{A}}(x) = \left\{ \begin{array}{llll} \frac{a- x +(x-{\underline{a}}) y_{\tilde{A}}}{a-{\underline{a}}} & {\text{ if }} & {\underline{a}} \le x< a, \\ y_{\tilde{A}} & {\text{ if }} & x = a, \\ \frac{x-a+({\overline{a}}-x)y_{\tilde{A}}}{{\overline{a}}-a} &{\text{if }} & a < x \le {\overline{a}}, \\ 1 & & {\text {otherwise}}. \end{array}\right.$$
(5)
$$F_{\tilde{A}}(x) = \left\{ \begin{array}{lll} \frac{a- x +(x-{\underline{a}}) u_{\tilde{A}} }{a-{\underline{a}}} &{\text{ if }} & {\underline{a}} \le x< a, \\ u_{\tilde{A}} &{\text{ if }} & x = a, \\ \frac{x-a+({\overline{a}}-x)u_{\tilde{A}}}{{\overline{a}}-a} &{\text{ if }} & a < x \le {\overline{a}}, \\ 1 & & \text {otherwise}. \end{array}\right.$$
(6)

In Fig. 1, we show an example of a SVTNN.

Fig. 1
figure 1

A single valued triangular neutrosophic number

Full size image

The notion of \((\alpha ,\beta ,\gamma )\)-cut is also important to solve different problems when using neutrosophic numbers such as optimization.

Definition 5

[7] For a SVTNN \({\tilde{A}}=(({\underline{a}},a,{\overline{a}});w_{\tilde{A}},y_{\tilde{A}},u_{\tilde{A}})\), the \((\alpha ,\beta ,\gamma )\)-cut set is defined as:

$${\tilde{A}}_{(\alpha ,\beta ,\gamma )}=\left\{ \left\langle x,T_{\tilde{A}}(x)\ge \alpha ,I_{\tilde{A}}(x)\le \beta ,F_{\tilde{A}}(x) \le \gamma \right\rangle : x\in X \right\}$$
(7)

which satisfies the following conditions:

$$0\le \alpha \le w_{\tilde{A}}; y_{\tilde{A}}\le \beta \le 1; u_{\tilde{A}}\le \gamma \le 1$$
(8)

and

$$\alpha +\beta +\gamma \le 3.$$
(9)

Thus, the \((\alpha ,\beta ,\gamma )\)-cut set of SVTNN \({\tilde{A}}\), symbolized by \({{\tilde{A}}_{(\alpha ,\beta ,\gamma )}}\), is a crisp subset of set X:

$${{\tilde{A}}_{(\alpha ,\beta ,\gamma )}}=\left\langle {\tilde{A}_{(\alpha )}};{\tilde{A}_{(\beta )}};{\tilde{A}_{(\gamma )}} \right\rangle .$$
(10)

The \((\alpha )\)-cut set of SVTNN \({\tilde{A}}\), symbolized by \({{\tilde{A}}_{(\alpha )}}\) is a closed interval, denoted by:

$${{\tilde{A}}_{(\alpha )}}=\left[ T_{\tilde{A}}^{L}(\alpha ),T_{\tilde{A}}^{U}(\alpha ) \right]$$
(11)

where

$${T_{\tilde{A}}^{L}}(\alpha ) = {\underline{a}}_{\tilde{A}}+{\frac{\alpha }{{w}_{\tilde{A}}}({{a}_{\tilde{A}}}-{\underline{a}}_{\tilde{A}}})$$
(12)
$$T_{\tilde{A}}^{U} (\alpha ) = {\overline{a}}_{\tilde{A}} - \frac{\alpha }{{w_{\tilde{A}} }}({\overline{a}}_{\tilde{A}} - a_{\tilde{A}} ).$$
(13)

The \((\beta )\)-cut set of SVTNN \({\tilde{A}}\), symbolized by \({{\tilde{A}}_{(\beta)}}\) is a closed interval, denoted by:

$${{\tilde{A}}_{(\beta)}}=\left[ I_{\tilde{A}}^{L}(\beta ),I_{\tilde{A}}^{U}(\beta ) \right]$$
(14)

where

$${I_{\tilde{A}}^{L}}(\beta ) = \frac{{a}_{\tilde{A}}-{{y}_{\tilde{A}}{\underline{a}}_{\tilde{A}}-{\beta ({{a}_{\tilde{A}}-{\underline{a}}_{\tilde{A}}})}}}{1-{{y}_{\tilde{A}}}}$$
(15)
$${I_{\tilde{A}}^{U}}(\beta ) = \frac{{a}_{\tilde{A}}-{{y}_{\tilde{A}}{\overline{a}}_{\tilde{A}}+{\beta ({\overline{a}}_{\tilde{A}}-{{a}_{\tilde{A}}}}})}{1-{{y}_{\tilde{A}}}}.$$
(16)

The \((\gamma )\)-cut set of SVTNN number \({\tilde{A}}\), symbolized by \({{\tilde{A}}_{(\gamma)}}\) is a closed interval, denoted by:

$${{\tilde{A}}_{(\gamma)}} = \left[ {F_{\tilde{A}}^{L} (\gamma ),F_{\tilde{A}}^{U} (\gamma )} \right]$$
(17)

where

$${F_{\tilde{A}}^{L}}(\gamma ) = \frac{{a}_{\tilde{A}}-{{u}_{\tilde{A}}{\underline{a}}_{\tilde{A}}-{\gamma ({a}_{\tilde{A}}-{\underline{a}}_{\tilde{A}}}})}{1-{{u}_{\tilde{A}}}}$$
(18)
$${F_{\tilde{A}}^{U}}(\gamma ) = \frac{{a}_{\tilde{A}}-{{u}_{\tilde{A}}{\overline{a}}_{\tilde{A}}+{\gamma ({\overline{a}}_{\tilde{A}}-{{a}_{\tilde{A}}}}})}{1-{{u}_{\tilde{A}}}}.$$
(19)

An important limitation of SVTNN is the assumption of linear functions in its definition. To overcome this drawback, [18] introduced the concept of non-linear interval-valued fuzzy number and [19] presented a single-valued non-linear trapezoidal neutrosophic number with 21 components:

Definition 6

[19] A single-valued non-linear trapezoidal neutrosophic number:

$${\tilde{A}}=(a_1,a_2,a_3,a_4;b_1,b_2,b_3,b_4;c_1,c_2,c_3,c_4; p_1,p_2; q_1, q_2; r_1,r_2, \omega , \rho , \lambda )$$

is a SVNN whose truth membership function \(T_{\tilde{A}}(x)\), indeterminacy membership function \(I_{\tilde{A}}(x)\) and falsity membership function \(F_{\tilde{A}}(x)\) are given, respecting the original notation, as followsFootnote 1:

$$T_{\tilde{A}}(x) = \left\{ \begin{array}{lll} \omega \left( \frac{x-a_1}{a_2-a_1}\right) ^{p_1} &{\text{ if }} & a_1 \le x< a_2, \\ \omega &{\text{ if }} & a_2< x \le a_3, \\ \omega \left( \frac{a_4-x}{a_4-a_3}\right) ^{p_2} &{\text{ if }} & a_3 < x \le a_4, \\ 0 & & {\text {otherwise}} \end{array}\right.$$
(20)
$$I_{\tilde{A}}(x) = \left\{ \begin{array}{lll} \rho \left( \frac{b_2-x}{b_2-b_1}\right) ^{q_1} &{\text{ if }} & b_1 \le x< b_2, \\ 0 &{\text{ if }} & b_2< x \le b_3, \\ \rho \left( \frac{x-b_3}{b_4-b_3}\right) ^{q_2} &{\text{ if }} & b_3 < x \le b_4, \\ \rho & & {\text {otherwise}} \end{array}\right.$$
(21)
$$F_{\tilde{A}}(x) = \left\{ \begin{array}{lll} \lambda \left( \frac{c_2-x}{c_2-c_1}\right) ^{r_1} &{\text{ if }} & c_1 \le x< c_2, \\ 0 &{\text{ if }} & c_2< x \le c_3, \\ \lambda \left( \frac{x-c_3}{c_4-c_3}\right) ^{r_2} &{\text{ if }} & c_3 < x \le c_4, \\ \lambda & & {\text {otherwise}} \end{array}\right.$$
(22)

where \(0 \le T_{\tilde{A}}(x)+I_{\tilde{A}}(x)+F_{\tilde{A}}(x) \le 3\) and where exponents \(p_1, p_2, q_1, q_2, r_1, r_2 \ne 1\) define different kinds of non-linearity.

Finally, the concept of possibilistic mean and variance of fuzzy numbers were introduced by [29]. Later on, [30] proposed definitions for the possibilistic mean \(M({\tilde{A}})\) and standard deviation \(\sigma ({\tilde{A}})\) of triangular intuitionistic fuzzy numbers (TIFN).

Definition 7

[30] The possibilistic mean of a TIFN denoted by \({\tilde{A}}= (({\underline{a}},a, {\overline{a}}), w_{\tilde{A}}, u_{\tilde{A}} )\) is given by:

$$M({\tilde{A}}) = \frac{M_{\mu }({\tilde{A}})+M_{v}({\tilde{A}})}{2}$$
(23)

where \(M_{\mu }({\tilde{A}})\) is the possibilistic mean of the membership function and \(M_{v}({\tilde{A}})\) is the possibilistic mean of the non-membership function computed as follows:

$$M_{\mu }({\tilde{A}}) = \frac{1}{6}({\underline{a}}+4a+{\overline{a}}) w_{\tilde{A}}$$
(24)
$$M_{v}({\tilde{A}}) = \frac{1}{6}({\underline{a}}+4a+{\overline{a}}) (1-u_{\tilde{A}}).$$
(25)

Definition 8

[30] Given a TIFN \({\tilde{A}}=( ({\underline{a}},a, {\overline{a}}), w_{\tilde{A}}, u_{\tilde{A}})\), the possibilistic standard deviation of \({\tilde{A}}\) is given by:

$$\sigma ({\tilde{A}}) = \frac{\sigma _{\mu }({\tilde{A}})+\sigma _{v}({\tilde{A}})}{2}$$
(26)

where \(\sigma _{\mu }({\tilde{A}})\) is the possibilistic standard deviation of the membership function and \(\sigma _{v}({\tilde{A}})\) is the possibilistic standard deviation of the non-membership function computed as follows:

$$\sigma _{\mu }({\tilde{A}}) = \frac{1}{\sqrt{24}}({\underline{a}}-{\overline{a}}) \sqrt{w_{\tilde{A}}}$$
(27)
$$\sigma _{v}({\tilde{A}}) = \frac{1}{\sqrt{24}}({\underline{a}}-{\overline{a}}) \sqrt{(1-u_{\tilde{A}})}.$$
(28)

3 An Alternative Definition of Non-linear Neutrosophic Numbers and Their Main Properties

As mentioned in Sect. 2, an important limitation of SVTNN is the assumption of linear functions in the definition of their membership functions. Even though Definition 6 by [19] can be easily transformed in a non-linear triangular neutrosophic number, it fails to represent non-linear neutrosophic numbers (NLNN) with sufficient precision. More precisely, \(I_{\tilde{A}}(x)\) and \(F_{\tilde{A}}(x)\) do not map parameters \(\rho\) and \(\lambda\) with the minimum values of the functions but with their maximum values. We argue that this feature is a limitation to express the degree of indeterminacy and falsity in a decision-making context. To better characterize these functions, we propose a novel definition of a NLNN by considering sets of parameters \(m=(m_T, m_I, m_F)\) and \(n=(n_T, n_I, n_F)\), with all elements in the range \(\left[ 1,\infty \right]\):

Definition 9

\({\tilde{A}}_{(m,n)}=(({\underline{a}},a,{\overline{a}});w_{\tilde{A}},y_{\tilde{A}},u_{\tilde{A}})\) is a SVNN whose truth-member–ship function \(T_{\tilde{A}}(x)\), indeterminacy-membership function \(I_{\tilde{A}}(x)\) and falsity-membership function \(F_{\tilde{A}}(x)\) are given as follows:

$$T_{{\tilde{A}}} (x) = \left\{ {\begin{array}{*{20}c} {\left[ {1 - \left( {\frac{{a - x}}{{a - {\underline{a}} }}} \right)^{{m_{T} }} } \right]w_{{\tilde{A}}} } & {{\text{if}}\,{\underline{a}} \le x < a,} \\ {w_{{\tilde{A}}} } & {{\text{if}}\,x = a,} \\ {\left[ {1 - \left( {\frac{{a - x}}{{a - \bar{a}}}} \right)^{{n_{T} }} } \right]w_{{\tilde{A}}} } & {{\text{if}}\,a < x \le \bar{a},} \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right.$$
(29)
$$I_{{\tilde{A}}} (x) = \left\{ {\begin{array}{*{20}c} {\left[ {y_{{\tilde{A}}} + (1 - y_{{\tilde{A}}} )\left( {\frac{{a - x}}{{\underline{a}}}} \right)^{{m_{I} }} } \right]} & {{\text{if}}\, {\underline{a}} \le x < a,} \\ {y_{{\tilde{A}}} } & {{\text{if}}\,x = a,} \\ {\left[ {y_{{\tilde{A}}} + (1 - y_{{\tilde{A}}} )\left( {\frac{{a - x}}{{a - \bar{a}}}} \right)^{{n_{I} }} } \right]} & {{\text{if}}\,a < x \le \bar{a},} \\ 1 & {{\text{otherwise}}} \\ \end{array} } \right.$$
(30)
$$F_{{\tilde{A}}} (x) = \left\{ {\begin{array}{*{20}c} {\left[ {u_{{\tilde{A}}} + (1 - u_{{\tilde{A}}} )\left( {\frac{{a - x}}{{\underline{a}}}} \right)^{{m_{I} }} } \right]} & {{\text{if}}\, {\underline{a}} \le x < a,} \\ {u_{{\tilde{A}}} } & {{\text{if}}\,x = a,} \\ {\left[ {u_{{\tilde{A}}} + (1 - u_{{\tilde{A}}} )\left( {\frac{{a - x}}{{a - \bar{a}}}} \right)^{{n_{I} }} } \right]} & {{\text{if}}\,a < x \le \bar{a},} \\ 1 & {{\text{otherwise}}} \\ \end{array} } \right.$$
(31)

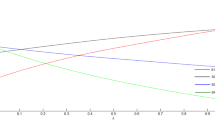
Without loss of generality, Definition 9 also implies that functions \(T_{\tilde{A}}(x)\), \(I_{\tilde{A}}(x)\) and \(F_{\tilde{A}}(x)\) are centered on parameter a. This situation seems reasonable in a context in which uncertainty is expressed around a given reference point. Furthermore, this definition can be easily extended to consider non-linear trapezoidal, pentagonal, hexagonal and higher-order neutrosophic numbers. A visual representation of a NLNN for \(m=(2,2,2)\) and \(n=(2,2,2)\) is shown in Fig. 2. Note that when \(m=(1,1,1)\) and \(n=(1,1,1)\) a NLNN becomes a triangular neutrosophic number as in Definition 4.

Fig. 2
figure 2

Non-linear neutrosophic number with \(m=(2,2,2)\) and \(n=(2,2,2)\)

Full size image

3.1 \((\alpha ,\beta ,\gamma )\)-Cuts of a NLNN

Along the lines of Definition 5, we develop a more general definition for the notions of \((\alpha ,\beta ,\gamma )\)-cuts of a NLNN.

Definition 10

For a NLNN \({\tilde{A}}_{(m,n)}=(({\underline{a}},a,{\overline{a}});w_{\tilde{A}},y_{\tilde{A}},u_{\tilde{A}})\), the \((\alpha ,\beta ,\gamma )\)-cut set is defined as:

$${\tilde{A}}_{(\alpha ,\beta ,\gamma )}=\left\{ \left\langle x,T_{\tilde{A}}(x)\ge \alpha ,I_{\tilde{A}}(x)\le \beta ,F_{\tilde{A}}(x) \le \gamma \right\rangle : x\in X \right\}$$
(32)

which satisfies the following conditions:

$$0\le \alpha \le w_{\tilde{A}}; y_{\tilde{A}}\le \beta \le 1; u_{\tilde{A}}\le \gamma \le 1$$
(33)

and

$$\alpha +\beta +\gamma \le 3.$$
(34)

Thus, the \((\alpha ,\beta ,\gamma )\)-cut set of NLNN \({\tilde{A}}_{(m,n)}\), denoted by \({{\tilde{A}}_{(m,n;\alpha ,\beta ,\gamma )}}\) is a crisp subset of set X:

$${{\tilde{A}}_{(m,n;\alpha ,\beta ,\gamma )}}=\left\langle {{\tilde{A}}_{({{m}_{T}},{{n}_{T}};\alpha )}};{{\tilde{A}}_{({{m}_{I}},{{n}_{I}};\beta )}};{{\tilde{A}}_{({{m}_{F}},{{n}_{F}};\gamma )}} \right\rangle$$
(35)

The \(\alpha\)-cut set of NLNN \({{\tilde{A}}_{(m,n;\alpha ,\beta ,\gamma )}}\), denoted by \({{\tilde{A}}_{({{m}_{T}},{{n}_{T}};\alpha )}}\) is a closed interval, denoted by:

$${{\tilde{A}}_{({{m}_{T}},{{n}_{T}};\alpha )}}=\left[ T_{\tilde{A}}^{L}(\alpha , m_T ),T_{\tilde{A}}^{U}(\alpha , n_T ) \right]$$
(36)

where

$$T_{\tilde{A}}^{L} (\alpha ,m_{T} ) = a_{\tilde{A}} - \left( {1 - \frac{\alpha }{{w_{\tilde{A}} }}} \right)^{{1/m_{T} }} (a_{\tilde{A}} - {\underline{a}} _{\tilde{A}})$$
(37)
$$T_{\tilde{A}}^{U} (\alpha ,n_{T} ) = a_{\tilde{A}} - \left( {1 - \frac{\alpha }{{w_{\tilde{A}} }}} \right)^{{1/n_{T} }} (a_{\tilde{A}} - {\underline{a}} _{\tilde{A}})$$
(38)

The \(\beta\)-cut set of NLNN \({{\tilde{A}}_{(m,n;\alpha ,\beta ,\gamma )}}\), denoted by \({{\tilde{A}}_{({{m}_{I}},{{n}_{I}};\beta )}}\) is a closed interval, denoted by:

$${{\tilde{A}}_{({{m}_{I}},{{n}_{I}};\beta )}}=\left[ I_{\tilde{A}}^{L}(\beta ),I_{\tilde{A}}^{U}(\beta ) \right]$$
(39)

where

$$I_{\tilde{A}}^{L} (\beta ,m_{I} ) = a_{\tilde{A}} - \left( {\frac{{\beta - y_{\tilde{A}} }}{{1 - y_{\tilde{A}} }}} \right)^{{1/m_{I} }} (a_{\tilde{A}} - {\underline{a}} _{\tilde{A}} )$$
(40)
$$I_{\tilde{A}}^{U} (\beta ,n_{I} ) = a_{\tilde{A}} - \left( {\frac{{\beta - y_{\tilde{A}} }}{{1 - y_{\tilde{A}} }}} \right)^{{1/n_{I} }} (a_{\tilde{A}} - {\overline{a}} _{\tilde{A}} ).$$
(41)

The \(\gamma\)-cut set of NLNN \({{\tilde{A}}_{(m,n;\alpha ,\beta ,\gamma )}}\), denoted by \({{\tilde{A}}_{({{m}_{F}},{{n}_{F}};\gamma )}}\) is a closed interval expressed by:

$${{\tilde{A}}_{({{m}_{F}},{{n}_{F}};\gamma )}}=\left[ F_{\tilde{A}}^{L}(\gamma ), F_{\tilde{A}}^{U}(\gamma ) \right]$$
(42)

where

$$F_{\tilde{A}}^{L} (\gamma ,m_{F} ) = a_{\tilde{A}} - \left( {\frac{{\gamma - u_{\tilde{A}} }}{{1 - u_{\tilde{A}} }}} \right)^{{1/m_{F} }} (a_{\tilde{A}} - {\underline{a}} _{\tilde{A}} )$$
(43)
$$F_{\tilde{A}}^{U} (\gamma ,n_{F} ) = a_{\tilde{A}} - \left( {\frac{{\gamma - u_{\tilde{A}} }}{{1 - u_{\tilde{A}} }}} \right)^{{1/n_{F} }} (a_{\tilde{A}} - {\overline{a}} _{\tilde{A}} ).$$
(44)

3.2 Interpretation of Alternative Degrees of Non-linearity

Parameters \(m=(m_T, m_I, m_F)\) and \(n=(n_T, n_I, n_F)\) control the degree of non-linearity of a NLNN and, ultimately, the degree of uncertainty of any membership function because it covers a wider range of possible values of x. This feature is formally expressed by the following remark.

Proposition 1

Given two NLNN \({\tilde{A}}_{(m_1,n_1)}=(({\underline{a}},a,{\overline{a}});w_{\tilde{A}},y_{\tilde{A}},u_{\tilde{A}})\) with \(m_1=(m_{T_1}, m_{I_1}, m_{F_1})\) and \(n_1=(n_{T_1}, n_{I_1}, n_{F_1})\) and \({{\tilde{B}}_{(m_2,n_2)}}=(({\underline{a}},a,{\overline{a}});w_{\tilde{A}},y_{\tilde{A}},u_{\tilde{A}})\) with \(m_2=(m_{T_2}, m_{I_2}, m_{F_2})\) and \(n_2=(n_{T_2}, n_{I_2}, n_{F_2})\), if \(m_1>m_2\) and \(n_1>n_2\), then \({\tilde{A}}_{(m_1,n_1;\alpha ,\beta ,\gamma )}>{\tilde{B}}_{(m_2,n_2;\alpha ,\beta ,\gamma )}\).

Proof

If \(m_1>m_2\) and \(n_1>n_2\), element by element, then \({\tilde{A}}_{(m_1,n_1;\alpha ,\beta ,\gamma )}>{\tilde{B}}_{(m_2,n_2;\alpha ,\beta ,\gamma )}\) because the following set of inequalities holds:

$$T_{\tilde{A}}^{L}(\alpha , m_{T_1})<T_{{\tilde{B}}}^{L}(\alpha , m_{T_2})$$
(45)
$$T_{\tilde{A}}^{L}(\alpha , n_{T_1})>T_{{\tilde{B}}}^{L}(\alpha , n_{T_2})$$
(46)
$$I_{\tilde{A}}^{L}(\beta , m_{I_1})<I_{{\tilde{B}}}^{L}(\beta , m_{I_2})$$
(47)
$$I_{\tilde{A}}^{L}(\beta , n_{I_1})>I_{{\tilde{B}}}^{L}(\beta , n_{I_2})$$
(48)
$$F_{\tilde{A}}^{L}(\gamma , m_{F_1})<F_{{\tilde{B}}}^{L}(\gamma , m_{F_2})$$
(49)
$$F_{\tilde{A}}^{L}(\gamma , n_{F_1})>F_{{\tilde{B}}}^{L}(\gamma , n_{F_2}).$$
(50)

\(\square\)

As a result the degree of non-linearity of a NLNN is a measure of the degree of uncertainty expressed in terms of its \((\alpha ,\beta ,\gamma )\)-cut. Extreme values for elements in m and n would lead to special types of NLNN. If we simultaneously increase the elements of vectors m and n, the area under the curve of \(T_{\tilde{A}}(x)\) and the area above the curve of both \(I_{\tilde{A}}(x)\) and \(F_{\tilde{A}}(x)\) increases. In the limit, a NLNN \(m=(\infty , \infty , \infty )\) and \(n=(\infty , \infty , \infty )\) is an interval crisp set. For instance, a visual representation of a NLNN for \(m=(100,100,100)\) and \(n=(100,100,100)\) is shown in Fig. 3. This kind of NLNN is an expression of a high degree of vagueness or uncertainty around a given number that abruptly disappears when reaching the extremes of the interval.

Fig. 3
figure 3

Non-linear neutrosophic number with \(m=(100,100,100)\) and \(n=(100,100,100)\)

Full size image

On the contrary, values below one in the elements of vectors m and n lead to a reduced degree of uncertainty around a given number. For instance, Fig. 4 is a representation of a NLNN for \(m=(0.5,0.5,0.5)\) and \(n=(0.5,0.5,0.5)\). The truth-membership function of this kind of NLNN is an expression of a reduced degree of vagueness or uncertainty around a given number that decreases more vertically than increases horizontally.

Fig. 4
figure 4

Non-linear neutrosophic number with \(m=(0.5,0.5,0.5)\) and \(n=(0.5,0.5,0.5)\)

Full size image

3.3 Symmetry and Skewness

Definition 9 implies the possibility of symmetry and asymmetry of a NLNN. The notion of symmetry of NLNN is related to the measurement of skewness of a fuzzy variable:

Definition 11

[31] Let \({\tilde{A}}\) be a fuzzy variable with finite expected value \({\mathbb {E}}\big [{\tilde{A}}\big ]\). The skewness (G) of \({\tilde{A}}\) is defined as:

$$G({\tilde{A}})={\mathbb {E}}\left[ ({\tilde{A}}-{\mathbb {E}}\big [{\tilde{A}}\big ])^3\right]$$
(51)

Remark 1

[31] If fuzzy variable \({\tilde{A}}\) has a symmetric membership function, then \(G({\tilde{A}})=0\).

Within the context of NLNN, symmetry is given by the elements of \(m=(m_T, m_I, m_F)\) and \(n=(n_T, n_I, n_F)\) that control for the form of membership functions \(T_{\tilde{A}}(x)\), \(I_{\tilde{A}}(x)\) and \(F_{\tilde{A}}(x)\). As a visual example, Fig. 5 shows an asymmetric NLNN with with \(m=(2,2,2)\) and \(n=(1,1,1)\).

Fig. 5
figure 5

Non-linear neutrosophic number with \(m=(2,2,2)\) and \(n=(1,1,1)\)

Full size image

Following the approach by [30] in the context of intuitionistic fuzzy numbers, we can reasonably assume that the combined skewness of a NLNN is the average of the skewness of its three membership functions.

Definition 12

The skewness \(G({\tilde{A}}_{(m,n)})\) of a NLNN is given by:

$$G({\tilde{A}}_{(m,n)})=\frac{G_T+G_I+G_F}{3}.$$
(52)

Remark 2

If a NLNN \({\tilde{A}}_{(m,n)}\) is characterized by \(m=(m_T, m_I, m_F)\) with \(n=(n_T, n_I, n_F)\) and \(m_T = n_T\), \(m_I=n_I\) and \(m_F=n_F\), then \(T_{\tilde{A}}(x)\), \(I_{\tilde{A}}(x)\) and \(F_{\tilde{A}}(x)\) are symmetric and \(G({\tilde{A}}_{(m,n)})=0\).

Note also that the skweness can be negative and the positive skewness of a membership function can offset the negative skewness of another membership function . Then, we say that a NLNN \({\tilde{A}}_{(m,n)}\), is perfectly symmetric when \(m_T = n_T\), \(m_I=n_I\) and \(m_F=n_F\). We say that a NLNN \({\tilde{A}}_{(m,n)}\), is partially symmetric when at least one of the following identities hold: \(m_T = n_T\), \(m_I=n_I\), \(m_F=n_F\), disregarding its combined skewness. Otherwise, we say that a NLNN is asymmetric.

4 Possibility Mean, Variance and Standard Deviation of a NLNN

Along the lines of the definitions of possibility mean, variance and standard deviation of fuzzy numbers by [29, 30] and [32], we next define the concepts of possibilistic mean, variance and standard deviation of a NLNN.

4.1 Possibility Mean of a NLNN

Definition 13

Given NLNN \({\tilde{A}}_{(m,n)}=({\underline{a}},a,{\overline{a}});w_{\tilde{A}},y_{\tilde{A}},u_{\tilde{A}})\) and its \(\alpha\)-cut set \({{\tilde{A}}_{({{m}_{T}},{{n}_{T}};\alpha )}}=\left[ {\text {T}}_{\tilde{A}}^{L}(\alpha ),{\text {T}}_{\tilde{A}}^{U}(\alpha ) \right]\), the f-weighted lower and upper possibility means of truth-membership function for NLNN \({{\tilde{A}}_{(m,n)}}\) are defined as follows:

$$\overline{M}_{T} (\tilde{A}_{{(m,n)}} ) = \int_{0}^{{w_{{\tilde{A}}} }} {f({\text{Pos}}[\tilde{A}_{{(m,n)}} \le {\text{T}}_{{\tilde{A}}}^{L} ]){\text{T}}_{{\tilde{A}}}^{L} {\text{d}}\alpha = \int_{0}^{{w_{{\tilde{A}}} }} {f(\alpha ){\text{T}}_{{\tilde{A}}}^{L} {\text{d}}\alpha } }$$
(53)
$${\underline{M}}_{T} ({{\tilde{A}}_{(m,n)}} ) = \int_{0}^{{w_{\tilde{A}} }} {f({\text{Pos}}[{{\tilde{A}}_{(m,n)}} \ge {\text{T}}_{\tilde{A}}^{U} ]){\text{T}}_{\tilde{A}}^{U} {\text{d}}\alpha = \int_{0}^{{w_{\tilde{A}} }} {f(\alpha ){\text{T}}_{\tilde{A}}^{U} {\text{d}}\alpha } }$$
(54)

where

$$\text {Pos}[{\tilde{A}}_{(m,n)}\le {{\text {T}}}_{\tilde{A}}^{L}] = \underset{x \le {{\text {T}}}_{\tilde{A}}^{L}}{\text {sup}}\{{{\text {T}}}_{\tilde{A}}^{L}(x)\}=\alpha$$
(55)
$$\text {Pos}[{\tilde{A}}_{(m,n)}\ge {{\text {T}}}_{\tilde{A}}^{U}] = \underset{x \ge {{\text {T}}}_{\tilde{A}}^{U}}{\text {sup}}\{{\text {T}}_{\tilde{A}}^{L}(x)\}=\alpha$$
(56)

and \(f:\left[ 0,w_{\tilde{A}}\right] \rightarrow {\mathbb {R}}\) is a non-negative and monotonic increasing weighting function that satisfies conditions \(\int_{{0}}^{w_{\tilde{A}}} f(\alpha ) = w_{\tilde{A}} \) and \(f(0)=0\).

From Eqs. (36), (53) and (54) if \(f(\alpha )=2\alpha /w_{\tilde{A}}\), \(\alpha \in \left[ 0,w_{\tilde{A}}\right]\), as suggested by [30] as an example, then:

$${\underline{M}}_{T}({{\tilde{A}}_{(m,n)}})={{w}_{\tilde{A}}}\left( \frac{2m_{T}^{2}{{\underline{a}}_{\tilde{A}}}+3{{m}_{T}}{{a}_{\tilde{A}}}+{{a}_{\tilde{A}}}}{(1+2{{m}_{T}})(1+{{m}_{T}})} \right)$$
(57)
$${\overline{M}}_{T}({{\tilde{A}}_{(m,n)}})={{w}_{\tilde{A}}}\left( \frac{2n_{T}^{2}{{\overline{a}}_{\tilde{A}}}+3{{n}_{T}}{{a}_{\tilde{A}}}+{{a}_{\tilde{A}}}}{(1+2{{n}_{T}})(1+{{n}_{T}})} \right).$$
(58)

Then, the f-weighted possibility mean of a truth-membership function is defined as follows:

$${{M}_{T}}({{\tilde{A}}_{(m,n)}})=\frac{{{\underline{M}}_{T}}({{\tilde{A}}_{(m,n)}})+{{\overline{M}}_{T}}({{\tilde{A}}_{(m,n)}})}{2}$$
(59)

Introducing Eqs. (57) and (58) in equation (59), then:

$$M_{T} ({{\tilde{A}}_{(m,n)}} ) = \frac{{w_{\tilde{A}} }}{2}\left( {\frac{{2m_{T}^{2} {\underline{a}} _{\tilde{A}} + 3m_{T} a_{\tilde{A}} + a_{\tilde{A}} }}{{(1 + 2m_{T} )(1 + m_{T} )}} + \frac{{2n_{T}^{2} {\overline{a}}_{\tilde{A}} + 3n_{T} a_{\tilde{A}} + a_{\tilde{A}} }}{{(1 + 2n_{T} )(1 + n_{T} )}}} \right).$$
(60)

The \(\beta\)-cut set of a NLNN is \({{\tilde{A}}_{({{m}_{I}},{{n}_{I}};\beta )}}=\left[ I_{\tilde{A}}^{L}(\beta ),I_{\tilde{A}}^{U}(\beta ) \right]\). Then the g-weighted lower and upper possibility means of the indeterminacy membership function for the NLNN number \({{\tilde{A}}_{(m,n)}}\) are, respectively, defined as follows:

$${\underline{M}} _{I} ({{\tilde{A}}_{(m,n)}} ) = \int_{{y_{\tilde{A}} }}^{1} {g({\text{Pos}}[{{\tilde{A}}_{(m,n)}} \le I_{\tilde{A}}^{L} ])I_{\tilde{A}}^{L} {\text{d}}\beta = \int_{{y_{\tilde{A}} }}^{1} {g(\beta )I_{\tilde{A}}^{L} {\text{d}}\beta } }$$
(61)
$${\overline{M}} _{I} ({{\tilde{A}}_{(m,n)}} ) = \int_{{y_{\tilde{A}} }}^{1} {g({\text{Pos}}[{{\tilde{A}}_{(m,n)}} \le I_{\tilde{A}}^{U} ])I_{\tilde{A}}^{U} {\text{d}}\beta = \int_{{y_{\tilde{A}} }}^{1} {g(\beta )I_{\tilde{A}}^{U} {\text{d}}\beta } }$$
(62)

where

$${\text{Pos}}[{{\tilde{A}}_{(m,n)}} \le {\text{I}}_{\tilde{A}}^{L} ] = \mathop {{\text{sup}}}\limits_{{x \le {\text{I}}_{\tilde{A}}^{L} }} \{ {\text{I}}_{\tilde{A}}^{L} (x)\} = \beta$$
(63)
$${\text{Pos}}[{{\tilde{A}}_{(m,n)}} \le {\text{I}}_{\tilde{A}}^{U} ] = \mathop {{\text{sup}}}\limits_{{x \le {\text{I}}_{\tilde{A}}^{U} }} \{ {\text{I}}_{\tilde{A}}^{U} (x)\} = \beta$$
(64)

and \(g:\left[{y}_{\tilde{A}},1 \right] \rightarrow {\mathbb {R}}\) is a non-negative and monotonic decreasing weighting function that satisfies conditions \(\int_{{y_{{\tilde{A}}} }}^{1} {f(\beta ) = 1 - y_{{\tilde{A}}} } \) and \(g(1)=1\).

From Eqs. (14), (61) and (62) for \(g(\beta ) = \frac{{2(1 - \beta )}}{{(1 - y_{{\tilde{A}}} )}},\beta \in [y_{{\tilde{A}}} ,1]\), as suggested by [30] as an example, then:

$${\underline{M} _{I}} ({{\tilde{A}}_{(m,n)}} ) = (1 - y_{\tilde{A}} )\left( {\frac{{2m_{I}^{2} {\underline{a}} _{\tilde{A}} + 3m_{I} a_{\tilde{A}} + a_{\tilde{A}} }}{{(1 + 2m_{I} )(1 + m_{I} )}}} \right)$$
(65)
$${\overline{M} _{I}} ({{\tilde{A}}_{(m,n)}} ) = (1 - y_{\tilde{A}} )\left( {\frac{{2n_{I}^{2} {\overline{a}} _{\tilde{A}} + 3n_{I} a_{\tilde{A}} + a_{\tilde{A}} }}{{(1 + 2n_{I} )(1 + n_{I} )}}} \right).$$
(66)

The g-weighted possibility mean of indeterminacy membership function defined as follows:

$${{M}_{I}}({\tilde{A}}_{(m,n)})=\frac{{{\underline{M}}_{I}}({{\tilde{A}}_{(m,n)}}+{{\overline{M}}_{I}}({{\tilde{A}}_{(m,n)}})}{2}$$
(67)

Introducing Eqs. (65) y (66) in equation (67), then

$$M_{I} ({{\tilde{A}}_{(m,n)}}) = \frac{{(1 - y_{\tilde{A}} )}}{2}\left( {\frac{{2m_{I}^{2} {\underline{a}} _{\tilde{A}} + 3m_{I} a_{\tilde{A}} + a_{\tilde{A}} }}{{(1 + 2m_{I} )(1 + m_{I} )}} + \frac{{2n_{I}^{2} {\overline{a}}_{\tilde{A}} + 3n_{I} a_{\tilde{A}} + a_{\tilde{A}} }}{{(1 + 2n_{I} )(1 + n_{I} )}}} \right)$$
(68)

The \(\gamma\)-cut set of a NLNN is \({{\tilde{A}}_{({{m}_{F}},{{n}_{F}};\gamma )}}=\left[ F_{\tilde{A}}^{L}(\gamma ),F_{\tilde{A}}^{U}(\gamma ) \right]\). Then, the h-weighted lower and upper possibility means of indeterminacy membership function for the NLNN number \({{\tilde{A}}_{(m,n)}}\) are, respectively, defined as follows:

$${\underline{M}}_{F} ({{\tilde{A}}_{(m,n)}} ) = \int_{{y_{\tilde{A}} }}^{1} {h({\text{Pos}}[{{\tilde{A}}_{(m,n)}} \le F_{\tilde{A}}^{L} ])F_{\tilde{A}}^{L} {\text{d}}\gamma = \int_{{y_{\tilde{A}} }}^{1} {h(\gamma )F_{\tilde{A}}^{L} {\text{d}}\gamma } }$$
(69)
$${\underline{M}}_{F} ({{\tilde{A}}_{(m,n)}} ) = \int_{{y_{\tilde{A}} }}^{1} {h({\text{Pos}}[{{\tilde{A}}_{(m,n)}} \le F_{\tilde{A}}^{U} ])F_{\tilde{A}}^{U} {\text{d}}\gamma = \int_{{y_{\tilde{A}} }}^{1} {h(\gamma )F_{\tilde{A}}^{U} {\text{d}}\gamma } }$$
(70)

where

$${\text {Pos}}[{\tilde{A}}_{(m,n)}\le {\text {F}}_{\tilde{A}}^{L}] = \underset{x \le {\text {F}}_{\tilde{A}}^{L}}{\text {sup}}\{{\text {F}}_{\tilde{A}}^{L}(x)\}=\gamma$$
(71)
$${\text {Pos}}[{\tilde{A}}_{(m,n)}\ge {\text {F}}_{\tilde{A}}^{U}] = \underset{x \ge {\text {F}}_{\tilde{A}}^{U}}{\text {sup}}\{{\text {F}}_{\tilde{A}}^{L}(x)\}=\gamma$$
(72)

and \(h:\left[ {u}_{\tilde{A}},1 \right] \rightarrow {\mathbb {R}}\) is a non-negative and monotonic decreasing weighting function that satisfies conditions \(\int_{{y_{{\tilde{A}}} }}^{1} {f(\gamma ) = 1 - u_{{\tilde{A}}} }\) and \(g(1)=1\).

From Eqs. (17), (69) and (70) for \(h(\gamma )=\frac{2(1-\gamma )}{(1-{u}_{\tilde{A}})}, \gamma \in [{u}_{\tilde{A}},1]\), then:

$${\underline{M}} _{F} ({{\tilde{A}}_{(m,n)}} ) = (1 - u_{\tilde{A}} )\left( {\frac{{2m_{F}^{2} {\underline{a}} _{\tilde{A}} + 3m_{F} a_{\tilde{A}} + a_{\tilde{A}} }}{{(1 + 2m_{F} )(1 + m_{F} )}}} \right)$$
(73)
$${\overline{M}} _{F} ({{\tilde{A}}_{(m,n)}} ) = (1 - u_{\tilde{A}} )\left( {\frac{{2n_{F}^{2} {\overline{a}} _{\tilde{A}} + 3n_{F} a_{\tilde{A}} + a_{\tilde{A}} }}{{(1 + 2n_{F} )(1 + n_{F} )}}} \right).$$
(74)

The h-weighted possibility mean of an indeterminacy membership function defined as follow:

$${{M}_{F}}({{\tilde{A}}_{(m,n)}})=\frac{{\underline{M}_{F}}({{\tilde{A}}_{(m,n)}}+{{\overline{M}}_{F}}({{\tilde{A}}_{(m,n)}})}{2}$$
(75)

Introducing Eqs. (73) y (74) in Eq. (75), then

$$M_{F} ({{\tilde{A}}_{(m,n)}} ) = \frac{{(1 - u_{\tilde{A}} )}}{2}\left( {\frac{{2m_{F}^{2} {\underline{a}} _{\tilde{A}} + 3m_{F} a_{\tilde{A}} + a_{\tilde{A}} }}{{(1 + 2m_{F} )(1 + m_{F} )}} + \frac{{2n_{F}^{2} {\overline{a}}_{\tilde{A}} + 3n_{F} a_{\tilde{A}} + a_{\tilde{A}} }}{{(1 + 2n_{F} )(1 + n_{F} )}}} \right)$$
(76)

Remark 3

If \({{m}_{T}}={{m}_{I}}={{m}_{F}}={{n}_{T}}={{n}_{I}}={{n}_{F}}=1\), then NLNN \({\tilde{A}}_{(m,n)}\) degenerates to a SVTNN and the possibility mean reduces to:

$${{M}_{T}}({\tilde{A}})=\frac{({\underline{a}}+4a+{\overline{a}}){w}_{\tilde{A}}}{6}$$
(77)
$${{M}_{I}} ({\tilde{A}}) = \frac{({\underline{a}}+4a+{\overline{a}})(1 - y_{\tilde{A}} )}{6}$$
(78)
$$M_{F} ({\tilde{A}}) = \frac{{({\underline{a}} + 4a + {\overline{a}})(1 - u_{\tilde{A}} )}}{6}.$$
(79)

Remark 4

If \({{m}_{T}}={{m}_{I}}={{m}_{F}}={{n}_{T}}={{n}_{I}}={{n}_{F}}=1\), with \(0\le {w}_{\tilde{A}}+{u}_{\tilde{A}}\le 1\) and \({y}_{\tilde{A}}=0\), then NLNN \({\tilde{A}}_{(m,n)}\) degenerates to a triangular intuitionistic fuzzy number and the possibility mean reduces to:

$$M_{{w_{\tilde{A}} }} ({\tilde{A}}) = \frac{{({\underline{a}} + 4a + {\overline{a}})w_{\tilde{A}} }}{6}$$
(80)
$$M_{{u_{{\tilde{A}}} }} (\tilde{A}) = \frac{{({\underline{a}} + 4a + \bar{a})(1 - u_{{\tilde{A}}} )}}{6}.$$
(81)

Remark 5

If \({{m}_{T}}={{m}_{I}}={{m}_{F}}={{n}_{T}}={{n}_{I}}={{n}_{F}}=1\), \({{w}_{\tilde{A}}}=1\) and \({{y}_{\tilde{A}}}={{u}_{\tilde{A}}}=0\), then NLNN \({{\tilde{A}}_{(m,n)}}\) degenerates to triangular fuzzy number \({\tilde{A}}=({\underline{a}},a,{\overline{a}})\) and the possibility mean of triangular fuzzy number \({\tilde{A}}=({\underline{a}},a,{\overline{a}})\) reduces to:

$$M({\tilde{A}})=\frac{({\underline{a}}+4a+{\overline{a}})}{6}.$$
(82)

4.2 Possibility Variance of a NLNN

Along the lines of the definitions by [30] in an intuitionistic fuzzy numbers context, we next define the possibility variance of a NLNN:

Definition 14

Given NLNN \({{\tilde{A}}_{(m,n)}}=(({\underline{a}},a,{\overline{a}});~{w}_{\tilde{A}},{y}_{\tilde{A}},~{u}_{\tilde{A}})\) with its \(\alpha\)-cut set \({\tilde{A}}_{({{m}_{T}},{{n}_{T}};\alpha )}=\left[ {\text {T}}_{\tilde{A}}^{L}(\alpha ),{\text {T}}_{\tilde{A}}^{U}(\alpha ) \right]\), the possibility variance of its truth-membership function is defined as follows:

$$V_{T} (\tilde{A}_{{(m,n)}} ) = \int_{0}^{{w_{{\tilde{A}}} }} {f(\alpha )\left( {\frac{{{\text{T}}_{{\tilde{A}}}^{U} - {\text{T}}_{{\tilde{A}}}^{L} }}{2}} \right)^{2} d\alpha }$$
(83)

From Eqs. (37), (38) and (83), and for \(f(\alpha)={\frac{2\alpha}{w_{\tilde{A}}}, \alpha \in [0,w_{\tilde{A}}]}\), we obtain the following expression:

$$V_{T} ({{\tilde{A}}_{(m,n)}} ) = w_{\tilde{A}} \left[ {\frac{{m_{T}^{2} (a_{\tilde{A}}^{2} - {\underline{a}} _{\tilde{A}}^{2} )}}{{4(1 + m_{T} )(2 + m_{T} )}} + \frac{{n_{T}^{2} ({\overline{a}}_{\tilde{A}}^{2} - a_{\tilde{A}}^{2} )}}{{4(1 + n_{T} )(2 + n_{T} )}} - \frac{{n_{T}^{2} m_{T}^{2} (a_{\tilde{A}}^{2} - {\underline{a}} _{\tilde{A}} a_{\tilde{A}} - a_{\tilde{A}} {\overline{a}}_{\tilde{A}} + {\underline{a}}_{\tilde{A}} {\overline{a}}_{\tilde{A}} )}}{{(m_{T} + n_{T} + 2n_{T} m_{T} )(m_{T} + n_{T} + n_{T} m_{T} )}}} \right]$$
(84)

The \(\beta\)-cut set of NLNN is \(\tilde{A}_{{(m_{I} ,n_{I} ;\beta )}} = \left[ {I_{{\tilde{A}}}^{L} (\beta ),I_{{\tilde{A}}}^{U} (\beta )} \right]\). Then, the possibility variance of indeterminacy membership function is defined as follows:

$$V_{I} (\tilde{A}_{{(m,n)}} ) = \int_{{y_{{\tilde{A}}} }}^{1} {g(\beta )\left( {\frac{{I_{{\tilde{A}}}^{U} - I_{{\tilde{A}}}^{L} }}{2}} \right)^{2} {\text{d}}\beta }$$
(85)

From Eqs. (40), (41) and (85), for \(g(\beta ) = \frac{{2(1 - \beta )}}{{(1 - y_{{\tilde{A}}} )}},\beta \in [y_{{\tilde{A}}} ,1]\), we obtain the following expression:

$$V_{I} ({{\tilde{A}}_{(m,n)}} ) = (1 - y_{\tilde{A}} )\left[ {\frac{{m_{T}^{2} (a_{\tilde{A}}^{2} - {\underline{a}} _{\tilde{A}^{2}} )}}{{4(1 + m_{T} )(2 + m_{T} )}} + \frac{{n_{T}^{2} ({\overline{a}}_{\tilde{A}}^{2} - a_{\tilde{A}}^{2} )}}{{4(1 + n_{T} )(2 + n_{T} )}} - \frac{{n_{T}^{2} m_{T}^{2} (a_{\tilde{A}}^{2} - {\underline{a}} _{\tilde{A}} a_{\tilde{A}} - a_{\tilde{A}} {\overline{a}}_{\tilde{A}} +{\underline{a}}_{\tilde{A}} {\overline{a}}_{\tilde{A}} )}}{{(m_{T} + n_{T} + 2n_{T} m_{T} )(m_{T} + n_{T} + n_{T} m_{T} )}}} \right]$$
(86)

The \(\gamma\)-cut set of NLNN is \({\tilde{A}}_{({{m}_{F}},{{n}_{F}};\gamma )}=\left[ F_{\tilde{A}}^{L}(\gamma ),F_{\tilde{A}}^{U}(\gamma ) \right]\). Then, the possibility variance of a falsity membership function is defined as follows:

$$V_{F} (\tilde{A}_{{(m,n)}} ) = \int_{{u_{{\tilde{A}}} }}^{1} {h(\gamma )\left( {\frac{{F_{{\tilde{A}}}^{U} - F_{{\tilde{A}}}^{L} }}{2}} \right)^{2} {\text{d}}\gamma }$$
(87)

From Eqs. (43), (44) and (87), for \(h(\gamma )=\frac{2(1-\gamma )}{(1-{{u}_{\tilde{A}}})}, \gamma \in [{{u}_{\tilde{A}}},1]\), we obtain the following expression:

$$V_{F} ({{\tilde{A}}_{(m,n)}} ) = (1 - u_{\tilde{A}} )\left[ {\frac{{m_{T}^{2} (a_{\tilde{A}}^{2} - {\underline{a}} _{\tilde{A}}^{2} )}}{{4(1 + m_{T} )(2 + m_{T} )}} + \frac{{n_{T}^{2} ({\overline{a}}_{\tilde{A}}^{2} - a_{\tilde{A}}^{2} )}}{{4(1 + n_{T} )(2 + n_{T} )}} - \frac{{n_{T}^{2} m_{T}^{2} (a_{\tilde{A}}^{2} - {\underline{a}}_{\tilde{A}} a_{\tilde{A}} - a_{\tilde{A}} {\overline{a}}_{\tilde{A}} + {\underline{a}}_{\tilde{A}} {\overline{a}}_{\tilde{A}} )}}{{(m_{T} + n_{T} + 2n_{T} m_{T} )(m_{T} + n_{T} + n_{T} m_{T} )}}} \right].$$
(88)

4.3 Possibility Standard Deviation of a NLNN

Definition 15

Given NLNN \({{\tilde{A}}_{(m,n)}}=(({\underline{a}},a,{\overline{a}});~{w}_{\tilde{A}},{y}_{\tilde{A}},~{u}_{\tilde{A}})\) with its \(\alpha\)-cut \({\tilde{A}}_{({{m}_{T}},{{n}_{T}};\alpha )}=\left[ {\text {T}}_{\tilde{A}}^{L}(\alpha),{\text {T}}_{\tilde{A}}^{U}(\alpha ) \right]\), the possibility standard deviation of its truth-membership function is defined as follows:

$$D_T({{\tilde{A}}_{(m,n)}})=\sqrt{{{V}_{T}}({{\tilde{A}}_{(m,n)}})}.$$
(89)

Introducing (84) in Eq. (89):

$$D_{T} ({{\tilde{A}}_{(m,n)}} ) = \left[ {({w_{\tilde{A}}} )\left[ {\frac{{m_{T}^{2} (a_{\tilde{A}}^{2} - {\underline{a}} _{\tilde{A}}^{2} )}}{{4(1 + m_{T} )(2 + m_{T} )}} + \frac{{n_{T}^{2} ({\overline{a}}_{\tilde{A}}^{2} - a_{\tilde{A}}^{2} )}}{{4(1 + n_{T} )(2 + n_{T} )}} - \frac{{n_{T}^{2} m_{T}^{2} (a_{\tilde{A}}^{2} - {\underline{a}} _{\tilde{A}} a_{\tilde{A}} - a_{\tilde{A}} {\overline{a}}_{\tilde{A}} + {\underline{a}} _{\tilde{A}} {\overline{a}}_{\tilde{A}} )}}{{(m_{T} + n_{T} + 2n_{T} m_{T} )(m_{T} + n_{T} + n_{T} m_{T} )}}} \right]} \right]^{{1/2}}$$
(90)

The \(\beta\)-cut set of NLNN is \({{\tilde{A}}_{({{m}_{I}},{{n}_{I}};\beta )}}=\left[ I_{\tilde{A}}^{L}(\beta ),I_{\tilde{A}}^{U}(\beta ) \right]\). Then, the possibility standard deviation of indeterminacy membership function is defined as follows:

$${{D}_{I}}({{\tilde{A}}_{(m,n)}})=\sqrt{{{V}_{I}}({{\tilde{A}}_{(m,n)}})}$$
(91)

Introducing (85) in Eq. (91):

$$D_{I} ({{\tilde{A}}_{(m,n)}} ) = \left[ { (1 - y_{\tilde{A}} )\left[ {\frac{{m_{T}^{2} (a_{\tilde{A}}^{2} - {\underline{a}} _{\tilde{A}}^{2} )}}{{4(1 + m_{T} )(2 + m_{T} )}} + \frac{{n_{T}^{2} ({\overline{a}}_{\tilde{A}}^{2} - a_{\tilde{A}}^{2} )}}{{4(1 + n_{T} )(2 + n_{T} )}} - \frac{{n_{T}^{2} m_{T}^{2} (a_{\tilde{A}}^{2} - {\underline{a}} _{\tilde{A}} a_{\tilde{A}} - a_{\tilde{A}} {\overline{a}}_{\tilde{A}} + {\underline{a}} _{\tilde{A}} {\overline{a}}_{\tilde{A}} )}}{{(m_{T} + n_{T} + 2n_{T} m_{T} )(m_{T} + n_{T} + n_{T} m_{T} )}}} \right]} \right]^{{1/2}}$$
(92)

The \(\gamma\)-cut set of a NLNN is \({{\tilde{A}}_{({{m}_{F}},{{n}_{F}};\gamma )}}=\left[ F_{\tilde{A}}^{L}(\gamma ),F_{\tilde{A}}^{U}(\gamma ) \right]\). Then, the possibility standard deviation of falsity membership function is defined as follows:

$$D_{F} (\tilde{A}_{{(m,n)}} ) = \sqrt {V_{F} (\tilde{A}_{{(m,n)}} )}$$
(93)

Introducing (87) in Eq. (93):

$$D_{F} ({{\tilde{A}}_{(m,n)}} ) = \left[ {(1 - u_{\tilde{A}} )\left[ {\frac{{m_{T}^{2} (a_{\tilde{A}}^{2} - {\underline{a}} _{\tilde{A}}^{2} )}}{{4(1 + m_{T} )(2 + m_{T} )}} + \frac{{n_{T}^{2} ({\overline{a}}_{\tilde{A}}^{2} - a_{\tilde{A}}^{2} )}}{{4(1 + n_{T} )(2 + n_{T} )}} - \frac{{n_{T}^{2} m_{T}^{2} (a_{\tilde{A}}^{2} - {\underline{a}} _{\tilde{A}} a_{\tilde{A}} - a_{\tilde{A}} {\overline{a}}_{\tilde{A}} + {\underline{a}} _{\tilde{A}} {\overline{a}}_{\tilde{A}} )}}{{(m_{T} + n_{T} + 2n_{T} m_{T} )(m_{T} + n_{T} + n_{T} m_{T} )}}} \right]} \right]^{{1/2}}.$$
(94)

Remark 6

If \({{m}_{T}}={{m}_{I}}={{m}_{F}}={{n}_{T}}={{n}_{I}}={{n}_{F}}=1\), then NLNN \({{\tilde{A}}_{(m,n)}}\) degenerates to a SVTNN and the possibility standard deviation reduces to:

$${{D}_{T}}({\tilde{A}})=\frac{({\overline{a}}-{\underline{a}})}{\sqrt{24}}\sqrt{{{w}_{\tilde{A}}}}$$
(95)
$${{D}_{I}}({\tilde{A}})=\frac{({\overline{a}}-{\underline{a}})}{\sqrt{24}}\sqrt{(1-{{y}_{\tilde{A}}})}$$
(96)
$${{D}_{F}}({\tilde{A}})=\frac{({\overline{a}}-{\underline{a}})}{\sqrt{24}}\sqrt{(1-{{u}_{\tilde{A}}})}.$$
(97)

Remark 7

If \({{m}_{T}}={{m}_{I}}={{m}_{F}}={{n}_{T}}={{n}_{I}}={{n}_{F}}=1\), \(0\le {w}_{\tilde{A}}+{u}_{\tilde{A}}\le 1\) and \({y}_{\tilde{A}}=0\), then NLNN \({\tilde{A}}_{(m,n)}\) degenerates to a triangular intuitionistic fuzzy number and its possibility standard deviation reduces to:

$${{D}_{{w}_{\tilde{A}}}}({\tilde{A}})=\frac{({\overline{a}}-{\underline{a}})}{\sqrt{24}}\sqrt{{{w}_{\tilde{A}}}}$$
(98)
$${{D}_{{u}_{\tilde{A}}}}({\tilde{A}})=\frac{({\overline{a}}-{\underline{a}})}{\sqrt{24}}\sqrt{(1-{{u}_{\tilde{A}}})}.$$
(99)

Remark 8

If \({{m}_{T}}={{m}_{I}}={{m}_{F}}={{n}_{T}}={{n}_{I}}={{n}_{F}}=1\), \({w}_{\tilde{A}}=1\) and \({y}_{\tilde{A}}={u}_{\tilde{A}}=0\), then NLNN \({{\tilde{A}}_{(m,n)}}\) degenerates to triangular fuzzy number \({\tilde{A}}=({\underline{a}},a,{\overline{a}})\) and its possibility standard deviation reduces to:

$$D({\tilde{A}})=\frac{({\overline{a}}-{\underline{a}})}{\sqrt{24}}.$$
(100)

5 A New Possibility Score Function for NLNN

Score functions for fuzzy numbers are very important for comparative and ranking purposes in many different applications (see e.g., [32]). In this section, we introduce a new possibility score function for NLNN based on the concepts of possibilistic mean and standard deviation that will be later used in a case study (Sect. 6).

Definition 16

Let \({{\tilde{A}}_{(m,n)}}=(({\underline{a}},a,{\overline{a}});~{w}_{\tilde{A}},{y}_{\tilde{A}},~{u}_{\tilde{A}})\) be a NLNN with truth-membership \({T}_{\tilde{A}}\left( x \right)\), indeterminacy-membership \({I}_{\tilde{A}}\left( x \right)\) and falsity-membership \({F}_{\tilde{A}}\left( x \right)\) of NLNN \({{\tilde{A}}_{(m,n)}}\). Then, a possibility score function \(PS({{\tilde{A}}_{(m,n)}})\) is given as follows:

$$PS({{\tilde{A}}_{(m,n)}})=\frac{P{{S}_{T}}({{\tilde{A}}_{(m,n)}})+P{{S}_{I}}({{\tilde{A}}_{(m,n)}})+P{{S}_{F}}({{\tilde{A}}_{(m,n)}})}{3}$$
(101)

where possibility score functions \(P{{S}_{T}}({{\tilde{A}}_{(m,n)}})\), \(P{{S}_{I}}({{\tilde{A}}_{(m,n)}})\) and \(P{{S}_{F}}({{\tilde{A}}_{(m,n)}})\) related, respectively, to truth-membership \({T}_{\tilde{A}}(x)\), indeterminacy-membership \({I}_{\tilde{A}}(x)\), and falsity-membership \({F}_{\tilde{A}}(x)\), are defined as follows:

$$P{{S}_{T}}({{\tilde{A}}_{(m,n)}})={{M}_{T}}({{\tilde{A}}_{(m,n)}})+{{D}_{T}}({{\tilde{A}}_{(m,n)}})$$
(102)
$$P{{S}_{I}}({{\tilde{A}}_{(m,n)}})={{M}_{I}}({{\tilde{A}}_{(m,n)}})+{{D}_{I}}({{\tilde{A}}_{(m,n)}})$$
(103)
$$P{{S}_{F}}({{\tilde{A}}_{(m,n)}})={{M}_{F}}({{\tilde{A}}_{(m,n)}})+{{D}_{F}}({{\tilde{A}}_{(m,n)}}).$$
(104)

Given \({\tilde{A}}_{(m,n)}=(({\underline{a}},a,{\overline{a}});~{w}_{\tilde{A}},{y}_{\tilde{A}},~{u}_{\tilde{A}})\) and \({{{\tilde{B}}}_{(m,n)}}=(({\underline{b}},b,{\overline{b}});~{{w}_{{{\tilde{B}}}}},{{y}_{{{\tilde{B}}}}},~{{u}_{{{\tilde{B}}}}})\), we have that:

  • If \(P{{S}_{T}}({{\tilde{A}}_{(m,n)}})>P{{S}_{T}}({{\tilde{B}}_{(m,n)}})\Rightarrow {{T}_{\tilde{A}}(x)>{{T}_{\tilde{B}}}}(x)\)

  • If \(P{{S}_{I}}({{\tilde{A}}_{(m,n)}})>P{{S}_{I}}({{\tilde{B}}_{(m,n)}})\Rightarrow {I}_{\tilde{A}}(x)>{{I}_{\tilde{B}}}(x)\)

  • If \(P{{S}_{F}}({{\tilde{A}}_{(m,n)}})>P{{S}_{F}}({{\tilde{B}}_{(m,n)}})\Rightarrow {{F}_{\tilde{A}}(x)>{{F}_{\tilde{B}}}}(x)\).

6 Case Study

In this section, we illustrate how our NLNN are used in practice. More precisely, we build a hybrid model combining Neutrosophic Analytic Hierarchy Process (N-AHP) and Neutrosophic Technique for Order of Preference by Similarity to Ideal Solution (N-TOPSIS). [27] propose a ranking of supply chain risks in the motor industry of Pakistan using N-AHP to obtain weights and N-TOPSIS to compute a score and the final ranking.

6.1 N-AHP

To solve the problem, we propose the following steps. Steps 1, 2, 3 and 4 correspond to N-AHP and steps 5, 6 and 7 to N-TOPSIS.

  1. Step 1

    Hierarchical structure of the problem. [27] establish that the main goal is managing risks in the supply chain. Then, they consider three different criteria: supply chain resilience (C1), supply chain agility (C2) and supply chain robustness (C3). Finally, seventeen supply chain risks are assessed.

  2. Step 2

    Neutrosophic pairwise comparison of criteria. From the aggregation of the expert opinions expressed by a SVTNN with the help of a neutrosophic linguistic scale, a neutrosophic pairwise comparison of criteria is built as shown in Table 2

    Table 2 Neutrosophic pair-wise comparison matrix
    Full size table
  3. Step 3

    Structure the crisp comparison matrix of the criteria. In this step, we transform the neutrosophic pairwise comparison matrix in a deterministic pairwise comparison matrix. To this end, we use different score functions for comparison purposes. [33] propose the following score function under the assumption of linearity of functions:

    $${{S}_{1}}({\tilde{A}})=\frac{{\underline{a}}+a+{\overline{a}}}{8}\times ~(2+{w}_{\tilde{A}}-{y}_{\tilde{A}}-~{u}_{\tilde{A}})$$
    (105)

    Similarly, [27] propose the following score function:

    $${{S}_{2}}({\tilde{A}})=\frac{{\underline{a}}+a+{\overline{a}}}{3}+~{w}_{\tilde{A}}-{y}_{\tilde{A}}-~{u}_{\tilde{A}}$$
    (106)

    In addition to these score functions, we here propose a new possibilistic score function based on Eq. (101) from Definition 16. This score function allows practitioners to use both linear (\(m_1=(1,1,1)\) and \(n_1=(1,1,1)\)) and non-linear functions (\(m_{25}=(25,25,25)\) and \(n_{25}=(25,25,25)\)). As an illustrative example, we use a value of 25 to express a significant degree of non-linearity, although any other value above or below one could have been chosen for this purpose. Tables 3 and 4 contain the deterministic pairwise comparison matrices when using this new score functions.

    Table 3 Deterministic pair-wise comparison matrix for \(m_1\) and \(n_1\)
    Full size table
    Table 4 Deterministic pair-wise comparison matrix for \(m_{25}\) and \(n_{25}\)
    Full size table
  4. Step 4

    Weights for criteria and consistency evaluation. Once the neutrosophic matrix is transformed in a deterministic matrix by means of a score function, weights are computed and consistency is evaluated as recommended by [34]. Table 5 gathers the weights obtained using different score functions.

    Table 5 Weights for criteria
    Full size table

6.2 N-TOPSIS

  1. Step 5

    Neutrosophic decision matrix for each alternative risk and criteria. Table 6 summarizes the opinion of experts revealed by a single value triangular number according to a neutrosophic linguistic scale.

    Table 6 Neutrosophic decision matrix
    Full size table
  2. Step 6

    Deterministic decision matrix for each alternative risk and criteria by means of different score functions similarly to Step 3.

  3. Step 7

    TOPSIS methodology. From the deterministic decision matrix, we implement TOPSIS methodology [35] to establish a ranking of the most vulnerable risks in the supply chain. Table 6 shows the obtained ranking for different score functions.

    Table 7 Supply Chain risk ranking
    Full size table

From the analysis of Table 7, we find two main results.

  • Firstly, in case of assuming that expert opinions are expressed by SVTNN with linear truth-membership (\({T}_{\tilde{A}}\left( x \right)\)), indeterminacy-membership (\({I}_{\tilde{A}}\left( x \right)\)) and a falsity-membership (\({F}_{\tilde{A}}\left( x \right)\)) functions, the rankings obtained by using score function \(PS({{\tilde{A}}_{(m_1,n_1)}})\) are the same than those obtained by using score function \({{S}_{1}}({\tilde{A}})\) proposed by [33]. However, the results are sensibly different to those obtained by using score function \({{S}_{2}}({\tilde{A}})\) proposed by [27].

  • Secondly, assuming linearity of truth-membership (\({T}_{\tilde{A}}\left( x \right)\)), indeterminacy-membership (\({I}_{\tilde{A}}\left( x \right)\)) and falsity-membership (\({F}_{\tilde{A}}\left( x \right)\)) functions as proposed by [33] and [27] may lead to possible errors. From the results of the case study, we obtain different rankings when the expert opinions are expressed with NLNN and \(PS({{\tilde{A}}_{(m_{25},n_{25})}})\) with respect to linearity with \(PS({{\tilde{A}}_{(m_1,n_1)}})\), \({{S}_{1}}({\tilde{A}})\) and \({{S}_{2}}({\tilde{A}})\).

7 Managerial Insights and Practical Implications

Linearity in the assessment of uncertainty imposes some degree of rigidity in exchange for simplicity. The main motivation to introduce non-linearity in the expression of a neutrosophic number is its flexibility. By using NLNN, practitioners are allowed to: (i) control the degree of uncertainty of any membership function by varying the order of non-linearity as shown in Sect. 3.2; and (ii) control the degree of symmetry and skewness of any membership function as mentioned in Sect. 3.3. As a result, we argue that NLNN lead to more realistic decision-making models.

In other works, the order of non-linearity is used either as an expression of ethical principles [36, 37], or as indicative of the balance of solutions [38, 39]. We here follow the approach of using the order of non-linearity as an expression of the uncertainty, hence providing more flexibility to decision-makers. Furthermore, the rest of useful tools such as the possibilistic mean, variance and score functions can be similarly computed. As a result, we achieve a higher degree of generality.

However, NLNN also introduce a higher degree of complexity when compared with their linear counterpart. As summarized in Table 8, NLNN require a larger number of parameters, a more complex informational structure and may involve more computational load. In order to avoid decision fatigue in decision makers, the use of graphical tools such as Figs. 2, 3, 4 and 5 may help understanding the implications of the selection of parameters. In addition to visualization, NLNN parameters can be determined by means of the common interactive process in multiple criteria decision making in which parameters selection and optimization stages are repeated until a satisfactory solution is obtained with the help of an analyst.

Table 8 Pros and cons of linear and non-linear neutrosophic numbers
Full size table

The necessity of adopting NLNN in a MCDM problem will be determined by the degree of flexibility and generality that the decision-maker wants to achieve. When linear functions are not enough to express the opinion of decision-makers, a more general set of functions such as NLNN is required. For instance, let us assume that a decision-maker wants to express a lower degree of uncertainty around parameter a as in Fig. 2 with respect to the triangular neutrosophic number in Fig. 1. NLNN not only allows to a more flexible expression of uncertainty but also allows to control the degree of uncertainty by means of a parameter.

Finally, computational complexity may give rise to some limitations when using NLNN in the context of large optimization problems when solving algorithms are required to obtain solutions. However, this limitation will mainly depend on the particular application, the available computational power and the ability of the state-of-the-art algorithms. In this sense, we would like to recall that in ranking applications such as the one described in Sect. 6, the impact of computational complexity is null.

8 Concluding Remarks

In this paper, we present an alternative definition for NLNN that overcome some of the limitations identified in existing literature. We also develop the main properties of NLNN including the concepts of \((\alpha ,\beta ,\gamma )\)-cuts, possibilistic mean, possibilistic variance and possibilistic standard-deviation. After this new set of definitions, we show how these expressions reduce to the well-known counterpart expressions for intuitionistic, and triangular fuzzy numbers.

Non-linearity allows practitioners to increase the degree of flexibility in the expression of truth, indeterminacy and falsity-membership functions in the context of neutrosophic fuzzy logic. By varying the order of non-linearity, we analyze the implications of selecting alternative values paying special attention to extreme values. More precisely, we find that the \((\alpha ,\beta ,\gamma )\)-cuts are an increasing function of the order of non-linearity (Proposition 1). In addition, we define global skewness as the average of the skewness of the truth, indeterminacy and falsity-membership functions.

A NLNN allows practitioners to express fuzziness in both a wider and more specific way. However, in many decision-making contexts, we need score functions for comparative and ranking purposes in many different applications. A further contribution of this paper is new possibility score function for NLNN based on the concepts of possibilistic mean and standard deviation. We illustrate the use of NLNN by means of a hybrid model in a multiple criteria decision-making context. Summarizing, the main results of this paper are:

  • An alternative definition for NLNN.

  • A new set of definitions derived from the concept of NLNN.

  • A new score function useful for decision-making applications.

We argue that the main advantage of a NLNN is its ability to handle indeterminate and inconsistent information in much wider way than triangular fuzzy numbers. An interesting future line of work is the extension of the analysis to non-linear trapezoidal, pentagonal, hexagonal and higher-order neutrosophic numbers.