Tax evasion and competition in a differentiated duopoly

Abstract

This paper investigates the relation between market competition and firms’ tax evasion in a duopoly with differentiated products under both Bertrand and Cournot conjectures. The previous literature has shown that competition can lead to higher or lower tax evasion. Our paper can help to conciliate these different results by showing that a negative or a positive relation depends on what causes competitive pressure (i.e. an increase of the marginal cost, a higher product substitutability or a change of the mode of competition) and the pre-existing level of competition.

1 Introduction

The level of indirect tax evasion by firms is a relevant concern in many countries. For instance, “the Member States in Europe are collecting around one half of the VAT revenue available to them” (European Commission 2013, p.8).¹ On the other hand, despite its relevance for policy-makers, the literature dealing with the issue of firms compliance is rather scanty in contrast to that studying personal tax compliance: in the recent words of Bayer and Cowell (2009, p. 1131) “the behaviour of firms is sometimes glossed over in the economic analysis of tax policy. In the analysis of tax compliance it is often omitted altogether.”

The knowledge of the relationship between the firms’ market environment and their compliance behaviours represents a key question to enable policy-makers to evaluate qualitatively as well quantitatively the firms’ tax evasion, and to develop properly an effective tax-design. Few papers have investigated this subject, assuming prevalently a perfect competition environment (e.g. Virmani 1989; Cremer and Gahvari 1992, 1993, 1999; Panteghini 2000; and Hashimzade et al. 2010); however, Marrelli and Martina (1988), Goerke and Runkel (2006, 2011), Bayer and Cowell (2009) and Besfamille et al. (2009a, b) have studied imperfect competition. More specifically, few scholars have investigated the relation between the degree of market competitive pressure and firms’ tax evasion, despite intensifying competition and effort against evasion are high on the agenda of policy-makers.

This paper considers the effects of greater competitive pressure on (absolute and relative²) tax evasion in a duopoly market. First, we consider a general functional form for demand under Cournot competition with homogeneous products to provide a better intuition what is generally going on in the model with regard to the effects of marginal costs’ changes on tax evasion. It is shown that decreasing marginal costs reduce the competition level under a sufficiently low slope elasticity. In such a case, more competition may imply either more or less tax evasion, depending on whether the demand is elastic or inelastic, respectively.

Second, while the previous literature focuses on firms acting in a homogenous goods industry, we consider the most used framework with product differentiation (i.e. Dixit 1979; Singh and Vives 1984) in which firms face constant marginal costs and linear demand functions. In particular, the degree of product substitutability and marginal production costs are considered as the competition parameters, and we analyse the effects of a change in these two parameters on absolute and relative evasion.

Third, the cases in which the two firms compete on prices and on quantity are considered, checking whether and how the competition mode affects the results.

To the best of our knowledge, this paper fills a gap in the literature because tax evasion in a differentiated product duopoly has not been so far explored. The main findings are as follows: (1) under Bertrand competition, the effect of increasing competition on tax evasion depends on what triggers more competition (either a higher degree of product substitutability—denoted as “product market competition”—or a lower marginal production cost—denoted as “cost competition”). In particular, (1.1) the degree of differentiation may show an inverted U-shaped relationship with tax evasion, depending on the marginal cost (i.e. a higher degree of product substitutability is more likely to decrease (resp. to increase) tax evasion the higher (resp. the lower) both the marginal production cost and the pre-existing competitive pressure); and (1.2) a higher marginal production cost is more likely to decrease tax evasion the lower the initial level of the marginal cost and the higher the degree of product substitutability; (2) comparing the cases of output and price competition, it is shown that the absolute tax evasion and the relationship between relative evasion and marginal costs are (quantitatively and qualitatively, respectively) the same in both cases. By contrast, an increase in the degree of product substitutability has an univocal effect in the Cournot case (i.e. the higher the degree of product substitutability, the higher the relative evasion); (3) comparing relative evasion in the two competition modes, it is shown that relative tax evasion is larger under Bertrand (resp. Cournot) if the degree of product substitutability is sufficiently high (resp. low) and the marginal production cost is sufficiently low (resp. high). This implies that tax evasion may be higher when the competitive pressure is stronger.

Public policy may affect – directly or, more often, indirectly—competition focusing on the production costs as well as on the competition mode (as widely recognized, price competition is fiercer than output competition) and the degree of product differentiation. As to the latter, the concerns for a public regulation of product differentiation have been noted since Chamberlin (1950) (e.g. Dixit and Stiglitz 1977; Salop, 1979). As regards the former, policy can affect competition through changes in production costs, for instance, “by liberalizing input markets, slashing the bureaucratic burden imposed on firms or by simplifying international trade in inputs” (Goerke and Runkel, 2011, p. 723). The scant literature on this theme has initially pointed out that the economics of tax compliance has “no a priori argument for holding that a more collusive market (as opposed to a more competitive one) should lead to a higher tax declaration, or vice versa.” (Marrelli and Martina 1988, p. 56).

The papers dealing with the theme of the tax evasion/competitive pressure relationship—and thus closest to the present one—are those of Marrelli and Martina (1988) and Goerke and Runkel (2011). Both papers assume a homogeneous product and quantity competition. Noteworthy, those papers show opposite results as regards the sign of the link between competition and tax evasion. In fact, Marrelli and Martina (1988) find that the more competitive the market is, the lower is the tax evaded; moreover, this result holds not only for a symmetric duopoly but also for an asymmetric duopoly with (not too great) differences in production costs.³ Goerke and Runkel (2011) find ambiguous effects of market competition on tax evasion. The relationship is positive (negative) if demand is inelastic (elastic): in fact, a higher degree of competition always raises tax evasion if the demand is linear or concave. Thus, Goerke and Runkel (2011) have the result of Marrelli and Martina (1988) as a special case.

According to Goerke and Runkel (2011, p. 714), two main reasons can explain the appearance in some cases of a sharp difference between their findings and those of Marrelli and Martina (1988): “First, Marrelli and Martina (1988) focus on a conjectural variation parameter to model a change in competition, whereas we look at the impact of deep competition parameters. Second, Marrelli and Martina (1988) assume decreasing absolute risk aversion. The less collusive the market, the smaller are the profits and the higher the risk aversion. This provides firms with the incentive to evade less when competition becomes more intensive. To rule out such risk-driven tax evasion, we suppose firms to be risk neutral.” Another difference between the two papers is that Marrelli and Martina (1988) assume that firms decide the evasion in terms of unpaid taxes and will incur a fine (including the tax) represented by the evaded tax multiplied for a penalty rate larger than one, while Goerke and Runkel (2011) assume that firms decide the evasion in terms of undeclared sales and the penalty is a function increasing and convex in evaded revenues. However, none of these authors considers such assumptions crucial for the results achieved and, thus, their diversity cannot be ascribed to the difference in the definitions of the evasion⁴ and of the penalty. Finally, Marrelli and Martina (1988) (resp. Goerke and Runkel 2011) derive their results under the assumption of linear demand and zero costs (resp. weakly concave—e.g. linear—and iso-elastic demand and constant marginal costs).

Unfortunately for the policy-makers, the policy implications of the two above mentioned papers are in sharp contrast: while Marrelli and Martina (1988) suggest that governments should encourage competition, and a larger competition (either induced by the government itself or by external factors like globalization) allows reducing the effort in the fight against evasion, Goerke and Runkel (2011) argue that policy-makers should be careful in encouraging competition, unless a stronger fight to reduce evasion accompanies it.

Thus, the sharp contrast between the signs of the relationship between competition and evasion emerged in the preceding literature (due to an analysis conducted with homogeneous goods) is a stimulus to reassess the issue, developing a framework with differentiated products (with the degree of product differentiation as a “deep” competition parameter), and firms competing either in prices or output. The aim of the paper is thus to shed further light on the nexus between competitive pressure and tax evasion, a requisite for a fruitful tax policy analysis of the corporate sector.

Moreover, Goerke and Runkel (2011) have already analyzed marginal costs as deep competition parameter. In their model, however, the scale of the marginal costs exerts either a positive or negative effect on tax evasion, but never an U-shaped effect as we detect. On the other hand, those authors treat the number of firms as endogenous, so focusing on the entry effects of tax evasion, while the present paper considers a fixed number of firms. Therefore, the novelty of this paper is to consider the competitive role of products differentiation and, thus, whether and how the competition on the product variety affects tax evasion outcomes and modifies the established results.

Developing a duopoly model with differentiated product under price as well as output competition,⁵ this paper proposes a twofold contribution. On the one hand, it obtains that, in essence, the first (second) suggestion above mentioned about the relation between tax evasion and competitive pressure holds true when the existing level of competition is relatively low (high). On the other hand, it argues that the expected effect of competition changes on firms’ tax evasion depends on its source (i.e. changes in the degree of product differentiation, in production costs, in the competition modes, i.e. on quantities or prices). In fact, the firms’ main strategies to cope with the competitive pressure are cost-reducing interventions or changing the characteristics of their products to reduce their substitutability (e.g. Scherer and Ross 1990). The present paper shows that the choice of which strategy matters for the relationship between competition and tax evasion.

Our results can be also read in the light of Schleifer (2004, p. 414), who recently shows “how competitive pressures lead to the spread of the censured behaviour”, and he investigates five examples of such behaviours: employment of children, corruption, excessive executive pay, corporate earnings manipulation, and involvement of universities in commercial activities. However, he abstracts from the firms’ tax compliance which would be an adequate case of censured activity and a further good candidate for testing his findings. In this respect, the paper’s suggestion as regards the possibility that competition favours unethical behaviours is mixed: for instance such a finding holds true only if the pre-existing competitive pressure is relatively high.

The paper is organised as follows. Section 2 presents the model first under a general demand form with homogenous goods and quantity competition, investigating the effects of marginal costs as a measure of competitive pressure on tax evasion; then, the market equilibrium under price and quantity competition with differentiated products is characterized, showing the link between various competition changes and tax evasion and discussing policy implications. Section 3 summarizes the findings.

2 The model

Preliminary, to understand the basic mechanism behind the relationship between competitive pressure and tax evasion we propose a general functional demand form. For simplicity, we assume homogeneous goods and we focus on the relationship between relative tax evasion and marginal cost in the Cournot case. Here, we assume a constant marginal cost (rather than a general cost function form) as well as Cournot competition to follow Marrelli and Martina (1988) and Goerke and Runkel (2011). Moreover, as regards firms’ risk-neutrality, the evasion variable and the type of penalty function, this paper follows the assumptions of Goerke and Runkel (2011). Because Marrelli and Martina (1988) measure the degree of competition through the conjectural variation parameter and Goerke and Runkel (2011) through the Lerner index (in particular the level of marginal costs), then we also consider both those aspects by analyzing the two polar cases of price and quantity competition with differentiated products as well as the role that marginal costs play.

2.1 Cournot competition with homogenous product and a general form for demand

We assume a general (inverse) demand function $P(Q)$ with standard properties: (i) $P\,^{\prime}( \cdot ) < 0$ and (ii) $P\,^{\prime}( \cdot ) + q_{i} P^{\prime\prime}< 0$, where $Q = (q_{i} + q_{j} )$ with $q_{i}$ and $q_{j}$ denoting firm i and j’s outputs ($i,j = 1,2\;,\;i \ne j$), respectively, and the apex denoting the order of the partial derivative with respect to quantity. Property (ii) implies that the market game is played in strategic substitutes (e.g. Bulow et al. 1985).

Firms have to pay an ad valorem sales tax⁶; however, they may evade part of this tax.

The tax rate of the sales tax is denoted by $t \in (0,1)$. The true tax base of firm i reads $P\,q_{i}$. Firms may understate their sales volume to evade taxes: firm i declares $a_{i} \in [0,P\,q_{i} ]$ as its tax base to the tax authority. Thus firm i’s unreported revenues are given by $P\,q_{i} - a_{i}$. The firm i’s tax bill amounts to $t\,a_{i}$. With a given probability $y \in (0,1)$, tax evasion is detected. If detected, firm i has to pay taxes on full sales revenues, $P\,q_{i}$, and, in addition, a penalty function $T(P\,q_{i} - a_{i} )$ which depends on evaded turnover. Alternatively, the penalty may be assumed to be a function of taxes evaded instead of undeclared revenues, but the equilibrium results, since the level of the tax rate is assumed constant, are qualitatively the same.

The expected penalty is $yT( \cdot )$ and can represent a measure of the expected cost of tax evasion. In the following, we suppose that the detection probability, $y$, is a constant parameter while the penalty function, T, is strictly increasing and convex in evaded revenues. Then, given a convex T and a constant $y$, the expected penalty (or the cost of tax evasion), $yT$, increases and is convex in evaded sales.

Broadly, there are four forms of penalty: automatic financial, automatic nonfinancial, criminal financial, and criminal nonfinancial (Tait 1988). Goerke and Runkel (2011, p. 716) justify the form of the penalty function T (F in their terminology) as follows: “The penalties generally increase with the severity and extent of insufficient tax payments, supporting our assumption that F is increasing in evaded revenues. Moreover, many penalty schemes involve prison sentences for severe tax evasion activities. If F reflects not only monetary but also non-monetary penalties, such prison sentences suggest that F will be convex.” Indeed, in several countries, the properties of the penalty function here proposed are empirically in line with actual penalties. Moreover, countries such as Denmark and Spain (and Ireland with regard to interests to be paid for late tax payments) have the financial penalty increasing in the amount of the tax evaded (see OECD 2009, 2011, 2013).⁷

The cost function of firm i is given by $c_{i} q_{i}$ where $c_{i}$ is the constant marginal cost, assumed to be uniform across firms (i.e. $c_{i} = c_{j} = c$). Firm $i$’s expected net profit is

$$\pi _{i} = y\left\{ {(1 - t)P(q_{i} + q_{j} )q_{i} - cq_{i} - T\left[ {P(q_{i} + q_{j} )q_{i} - a_{i} } \right]} \right\} + (1 - y)\left[ {P(q_{i} + q_{j} )q_{i} - cq_{i} - ta_{i} } \right]$$

(1)

The simultaneous maximisation of (1) with respect to q and a leads to the following couple of first-order conditions (FOCs):

$$U_{i} : = \frac{{\partial \pi _{i} }}{{\partial a_{i} }} = yT\,'( \cdot ) - (1 - y)t = 0$$

(2)

$$V_{i} : = \frac{{\partial \pi _{i} }}{{\partial q_{i} }} = \left[ {P( \cdot ) + q_{i} P'( \cdot )} \right]\left[ {1 - y(t + T'( \cdot ))} \right] - c = 0.$$

(3)

After algebraic passages (see the Appendix), one obtains the following expressions:

• (i)
  $$(3P\,^{\prime} + 2qP\,^{\prime\prime}) = P\,^{\prime}\Big(3 + \frac{2qP\,^{\prime\prime}}{{P\,^{\prime}}}\Big) = P\,^{\prime}(3 + \varepsilon ) < 0 \Leftrightarrow \varepsilon > - 3$$

  (4)

where the elasticity of the slope of inverse demand (or the slope elasticity for short) $\varepsilon = \frac{2qP\,^{\prime\prime}}{{P\,^{\prime}}}$ may be negative or positive depending on whether the demand function is convex or concave.⁸ Moreover, note that the case in which the industry marginal revenue is declining occurs when $\varepsilon > - 2$ (e.g. Dixit 1986, p. 114) which is also the condition for output competition in strategic substitutes.⁹ Furthermore, since it is standard in oligopoly models to assume stability, we recall that the most general stability condition in duopoly requires $3 + \varepsilon > 0$ (Seade 1980a, b),¹⁰ while a stronger stability condition is that each firm’s perceived marginal revenue should be decreasing in the other firms’ total output, that is $2 + \varepsilon > 0$ (Hahn 1962). Finally, we note that when the stability condition holds also the second-order condition—which requires $4 + \varepsilon > 0$—also automatically holds. Therefore, the stability of the Nash equilibrium in the product market and the second-order condition require that the inequality (4) must be satisfied.

• (ii)
  $$(P + 2qP\,^{\prime}) = P(1 + \eta ),$$

where $\eta = \frac{2qP\,^{\prime}}{P}$ is the industry (inverse) price elasticity.¹¹ We assume that the inequality (4) holds. It follows that

• 1
  $$\Delta > 0;$$

  (5)

• 2.
  $$\frac{\partial a}{{\partial c}} = \frac{P(1 + \eta )}{{(1 - t)P\,^{\prime}(3 + \varepsilon )}}\frac{ > }{ < }0 \Leftrightarrow \eta \frac{ < }{ > } - 1$$

  (6)

• 3.
  $$\frac{\partial q}{{\partial c}} = \frac{1}{(1 - t)P\,^{\prime}(3 + \varepsilon )} < 0)$$

  (7)

Once we have the effects of c on declared revenue and output (a and q), we can easily calculate those on price and firm’s revenue ($P$ and $Pq$), as follows:

• 4.
  $$\frac{{\partial P}}{{\partial c}} = 2P'(2q)\frac{{\partial q}}{{\partial c}} > 0$$

  (8)

• 5.
  $$\frac{{\partial (Pq)}}{{\partial c}} = \frac{{\partial P}}{{\partial c}}q + P\frac{{\partial q}}{{\partial c}} = \frac{{\partial q}}{{\partial c}}(2P'q + P) = \frac{{\partial q}}{{\partial c}}P(1 + \eta )\frac{ > }{ < }0 \Leftrightarrow \eta \frac{ < }{ > } - 1$$

  (9)

From (6)–(9) the following remark follows.

Remark 1

The higher the marginal costs are, the lower the output is, and the higher the price is, while firm’s revenue and declared revenue are larger (resp. smaller) depending on whether the demand is elastic (resp. inelastic).

As known, the degree of competition is inversely related to the firms’ market power which, in turn, can be measured by the Lerner index, that is, the difference between the (after-tax) output price and marginal production costs, relative to the (after-tax) output price (e.g. Martin 2001).

The Lerner index¹² is given by $L = \frac{{\left[ {(1 - t)P - c} \right]}}{(1 - t)P}$. Now, we demonstrate the conditions under which an increase in marginal production costs reduces the Lerner index.

Lemma 1

A sufficient condition in order that a higher c implies a higher level of competition is that $\varepsilon > - 1$.

Proof

See the Appendix.

It follows that with a linear demand (where $\varepsilon = 0$) the Lerner index is always increasing with decreasing marginal costs (as will be also shown later in the case of Bertrand competition and differentiated product by Lemma 2).

The effect of an increase of marginal cost c on the Lerner index is twofold: on the one hand a direct negative effect, on the other hand an indirect positive effect through an increase of prices. Whether the second effect may be prevalent depends crucially on the curvature of the demand function: the negative effect always prevails if the demand is concave or not too convex. Therefore, although the effect of c on competition is ambiguous for a convex demand function, Lemma 1 provides a sufficient condition for a clear-cut effect in terms of the curvature of the convex demand function.¹³

Now, let us define the indicators of tax evasion. Following the established literature—e.g. Marrelli and Martina (1988), Virmani (1989), Cremer and Gahvari (1992, 1993, 1999), Goerke and Runkel (2011)—the indicators of tax evasion considered are:

• (i) the absolute tax evasion (i.e., the absolute amount of tax evaded) per firm (E):

  $$E = (1 - y)t(Pq - a)$$

  (10)

• (ii) the relative aggregate tax evasion, e, which represents the fraction of aggregate tax revenues evaded successfully. This is given by the ratio between the total evasion in the entire market, $2E$, and the hypothetical tax revenues ($h$), i.e. the amount of tax revenues that would arise without evasion (i.e. $h = 2tPq$):

  $$e = (1 - y)\left( {1 - \frac{a}{Pq}} \right)$$

  (11)

Now, it is possible to evaluate the effects of c on relative and absolute evasion¹⁴:

$$\begin{aligned} \frac{{\partial e}}{{\partial c}} & = \left\{ { - (1 - y)\frac{{\frac{{\partial a}}{{\partial c}}Pq - a(P\frac{{\partial q}}{{\partial c}} + q\frac{{\partial P}}{{\partial 2q}}\frac{{2\partial q}}{{\partial c}})}}{{\left( {Pq} \right)^{2} }} = - (1 - y)\frac{{\frac{{\partial a}}{{\partial c}}Pq - a\left[ {\frac{{\partial q}}{{\partial c}}(P + 2qP\,')} \right]}}{{\left( {Pq} \right)^{2} }}} \right\}\frac{ > }{ < }0 \\ & \quad \quad \Leftrightarrow - \frac{{P(1 - \left| \eta \right|)(Pq - a)}}{{(1 - t)P\,'(3 - \left| \varepsilon \right|)}}\frac{ > }{ < }0 \Leftrightarrow \eta \frac{ > }{ < } - 1 \\ \end{aligned}$$

(12)

$$\frac{\partial E}{{\partial c}} = \left\{ \begin{gathered} (1 - y)t\left[ {\left( {P\frac{\partial q}{{\partial c}} + q\frac{\partial P}{{\partial 2q}}\frac{2\partial q}{{\partial c}}} \right) - \frac{\partial a}{{\partial c}}} \right] = (1 - y)t\left[ {\left( {\frac{\partial q}{{\partial c}}} \right)(P + 2qP\,^{\prime}) - \frac{\partial a}{{\partial c}}} \right] = \hfill \\ = (1 - y)t\frac{P(1 - \left| \eta \right|) - P(1 - \left| \eta \right|)}{{(1 - t)P\,^{\prime}(3 - \left| \varepsilon \right|)}} \hfill \\ \end{gathered} \right\} = 0$$

(13)

Therefore, the following Result holds.

Result 1: (i) a higher level of competition (i.e. a higher c) may increase (resp. decrease) the relative tax evasion depending on whether demand is inelastic (resp. elastic); (ii) the absolute tax evasion is independent of marginal cost’s changes.

Proof

See the Appendix.

Result 1 (part (i)) provides a general result about the possibility of an inverted U-shaped relation between the degree of competition and tax evasion when demand passes from being inelastic to be elastic.¹⁵ Result 1 is also in line with Goerke and Runkel’s (2011, p. 727) Proposition 3 with regard to the relative tax evasion.¹⁶ However, while those authors obtain this result assuming a specific iso-elastic demand function, we note that its validity holds irrespective of the demand’s convexity or concavity, given a sufficiently low slope elasticity.

Therefore, we may draw a rather general observation: the competitive pressure raises tax evasion when price elasticity tends to be sufficiently high, irrespective of the functional form of demand. This result offers another example of the Schleifer’s findings: a fiercer competition may favour censured behaviours, extending the list of the latter with the activity of tax compliance by firms.

Moreover, Result 1 also offers a policy implication: if to reduce the relative tax evasion is a policy objective, then policy-makers should be cautious to implement pro-competitive policies favouring a reduction in marginal costs,¹⁷ because they risk, for instance in the case of a low slope elasticity $\varepsilon$ and inelastic demand, to raise firms’ market power together with an increase in relative tax evasion.

However, the relationship between competitive pressure and firms’ tax compliance may be better investigated by considering two important aspects: (1) the competition mode—i.e. Cournot and Bertrand, where the latter is notoriously more competitive than the former one (e.g. Singh and Vives, 1984); (2) the degree of product differentiation when products are heterogeneous. To investigate these issues, in the next sections we resort to the most used framework of differentiated oligopoly proposed by Dixit (1979) and Singh and Vives (1984).

2.2 Price competition

To begin with, we consider a standard Bertrand duopoly product game in which firms have to pay an ad valorem sales tax. Preferences of the representative consumer are:

$$U(q_{i} , q_{j} ) \, = z(q_{i} + q_{j} ) - \frac{{ (q_{i}^{2} + 2\gamma q_{i} q_{j} + q_{j}^{2} )}}{2}$$

(14)

where $q_{i}$ and $q_{j}$ denote outputs by firm i and j (i, j = 1, 2, i ≠ j), respectively, $z > 0$, and $\gamma \in (0,1)$ denotes the extent of product differentiation, with goods assumed to be imperfect substitutes. In particular, notice that if $\gamma = 1$, the products of the two firms would be undifferentiated, hence firms compete in the same market. At the other extreme, if $\gamma = 0$, each firm becomes a monopolist in its market. Hence, the higher γ, the higher the degree of product market competition. The derived linear inverse market demand for firm i is (e.g. Singh and Vives 1984):

$$p_{i} (q_{i} , q_{j} ) = z - \gamma q_{j} - q_{i}$$

(15)

From (15) and its counterpart for firm j, we can write product demand for the firm i as:

$$q_{i} (p_{i} ,p_{j} ) = \frac{{z(1 - \gamma ) - p_{i} + \gamma p_{j} }}{{(1 - \gamma^{2} )}}$$

(16)

With differentiated products the true tax base of firm i reads $p_{i} q_{i}$, the firm i’s unreported sales revenues are given by $p_{i} q_{i} - a_{i}$, and $a_{i} \in [0,p_{i} q_{i} ]$.

In particular, strictly following Goerke and Runkel (2011, p. 732), to ensure analytical tractability we assume a quadratic penalty function:

$$T_{i} (.) = \frac{{(p_{i} q_{i} - a_{i} )^{2} }}{2}$$

(17)

Firm i’s expected net profit is given by

$$\pi_{i} = y\left\{ {(1 - t)p_{i} q_{i} - cq_{i} - \frac{{\left( {p_{i} q_{i} - a_{i} } \right)^{2} }}{2}} \right\} + (1 - y)\left\{ {p_{i} q_{i} - cq_{i} - ta_{i} } \right\}$$

(18)

where the first bracketed term in (18) represents firm i’s profit in the case that tax evasion is detected, while the second term represents profit if such an evasion remains undetected. Inserting (16) in (18), one gets from firm i’s FOCS (see Appendix), simultaneously¹⁸ choosing price $p_{i}$ and declared revenues $a_{i}$, the following equilibrium values

$$p_{i} = p_{j} = p = \frac{z(1 - t)(1 - \gamma ) + c}{{(2 - \gamma )(1 - t)}}$$

(19)

$$a_{i} = a_{j} = a = - \frac{{y\left[ {z^{2} (1 - t)^{2} (\gamma - 1) - c\gamma z(1 - t) + c^{2} - t(1 - t)^{2} (1 + \gamma )(2 - \gamma )^{2} } \right] + t(2 - \gamma )^{2} (1 - t)^{2} (1 + \gamma )}}{{y(2 - \gamma )^{2} (1 - t)^{2} (1 + \gamma )}}$$

(20)

Then output at equilibrium is

$$q_{i} = q_{j} = q = \frac{z(1 - t) - c}{{(1 + \gamma )(2 - \gamma )(1 - t)}}$$

(21)

The condition ensuring a positive output is the standard one, that is

$$z > \frac{c}{(1 - t)}$$

(22)

The conditions ensuring that at equilibrium an interior solution¹⁹ for $a$ (that is, $a \in (0,pq)$ do exist and are

$$a > 0\; \Leftrightarrow y > y^\circ = \frac{{t(4 + \gamma^{3} - 3\gamma^{2} )(1 - t)^{2} }}{{z^{2} (1 - t)^{2} (1 - \gamma ) + c\gamma z(1 - t) - c^{2} - t(1 - t)^{2} (4 + \gamma^{3} - 3\gamma^{2} )}}$$

(23)

and

$$a < pq\; \Leftrightarrow \frac{t(1 - y)}{y} > 0$$

(24)

Note that, while (24) is always satisfied by definition, both (22) and (23) are always satisfied when z is sufficiently high, that is when the market “size” is sufficiently large (as usual in the oligopoly literature with linear demand).

It follows that the equilibrium profit (i.e. $\pi_{i} = \pi_{j} = \pi$) is:

$$\pi = \frac{{\left\{ \begin{gathered} (ty)^{2} (2 - \gamma )^{2} (1 - t)(1 + \gamma ) \hfill \\ + 2y\left[ {z^{2} (1 - t)^{2} (1 - \gamma ) - 2cz(1 - t)(1 - \gamma ) + c^{2} (1 - \gamma ) - t^{2} (1 - t)(1 + \gamma )(2 - \gamma )^{2} } \right] + \hfill \\ + t^{2} (2 - \gamma )^{2} (1 - t)(1 + \gamma ) \hfill \\ \end{gathered} \right\}}}{{2y(2 - \gamma )^{2} (1 - t)(1 + \gamma )}}$$

(25)

In this frame, the Lerner index is

$$L = \frac{{(1 - \gamma )\left[ {z(1 - t) - c} \right]}}{z(1 - t)(1 - \gamma ) + c}$$

(26)

Then the following Lemma holds:

Lemma 2

The higher γ, t and c and the lower z, the higher is the degree of competition.

Proof

See the Appendix.

The economic intuition behind Lemma 2 is simple. For instance, focusing only on the parameter c, we can see from (38) that the total effect of marginal cost changes on the Lerner index can be decomposed in a twofold effect: on the one hand, an increase in the marginal cost, c, reduces output and raises the equilibrium price, p (see (33) and (31), respectively); on the other hand, an increase in c has a direct negative effect on the Lerner index, L. For a linear demand, the direct negative effect is stronger than the fall in the market price, p, so that an increase in c unambiguously reduces L.²⁰

In the following, we particularly focus on the relationship between e²¹ and the competition parameters (i.e. c, γ). As regards the absolute tax evasion per firm it is easy to see that it depends only on tax policy parameters:

$$E = \frac{{t^{2} (1 - y)^{2} }}{y}$$

(27)

As expected, an increasing tax rate (detection probability) increases (decreases) the absolute tax evasion per firm:

$$\frac{\partial E}{{\partial t}} = \frac{{2t(1 - y)^{2} }}{y} > 0 ,\frac{\partial E}{{\partial y}} < 0 .$$

(28)

By contrast the relative tax evasion depends also on the competition parameters $(c,\gamma )$:

$$e(c,\gamma ) = \frac{{t(2 - \gamma )^{2} (1 - t)^{2} (1 + \gamma )(1 - y)^{2} }}{{y\left[ {z(1 - t)(1 - \gamma ) + c} \right]\left[ {z(1 - t) - c} \right]}}$$

(29)

Then, the following Propositions hold:

Proposition 1

The relationship between relative tax evasion and marginal cost is U-shaped. Moreover, the lower (higher) the marginal cost (degree of product differentiation), the more likely evasion will be reduced by an increase of marginal cost.

Proof

See the Appendix.

Recalling (12), from Proposition 1 the next Corollary holds.

Corollary 1

Also in the case of Bertrand competition with product differentiation and linear demand Result 1, part (i), holds because Proposition 1 implies that a higher competition stimulates tax evasion only if demand is elastic (and vice versa). ²²

Proposition 2

The relationship between relative tax evasion and degree of product differentiation is inverted U-shaped. Moreover, the higher both the marginal cost and the degree of product differentiation, the more likely evasion will be reduced by an increase in product substitutability.

Proof:

See the Appendix.

The next Corollary focuses on the role played by the product differentiation: more “product” market competition increases tax evasion until a sufficiently high level of such a competition is reached; however, beyond this threshold, the relationship between “product” market competition and tax evasion becomes negative.

Corollary 2

The relationship between relative tax evasion and degree of product differentiation is increasing (resp. decreasing) when.

$$\gamma \frac{ < }{ > }\gamma^\circ = \frac{{2z(1 - t) + 3c - \sqrt { - 12tz(c + tz) + 24tz^{2} + 9c + 12cz - 12z^{2} } }}{z(1 - t)}$$

The content of Propositions 1 and 2 and Corollary 2 can be illustrated through numerical examples. Only for illustrative purposes we fix the following parametric set: $z = 5,\;t = 0.3,\;y = 0.4$, for which in the range of marginal cost values $c \in (0,3.5)$, conditions (22) and (23) hold. Figure 1 shows that evasion is strongly decreasing with the marginal cost when product substitutability is very high and marginal cost is adequately low, while it becomes increasing with the marginal cost when either the product substitutability is sufficiently low or the marginal cost is appropriately high. Figure 2 shows that evasion decreases with the degree of product substitutability when both the latter and the marginal cost are sufficiently high; conversely, if the marginal cost is sufficiently low then it increases with the product substitutability.

Fig. 1

Relative tax evasion (e) as function of the marginal cost (c ∈ (0, 3.5)), for different degrees of product substitutability: with γ = 0.99 (blue solid line), with γ = 0.80 (black dotted line), and with γ = 0.20 (red dashed line). (Note that for all the figures shown in the paper, declared sales and output are always positive and thus not displayed for economy of space.) (color figure online)

Fig. 2

Relative tax evasion (e) as function of the degree of product substitutability (γ ∈ (0, 1)), for different marginal cost values: with c = 3 (red solid line), with c = 2.5 (black dotted line), and with c = 0.50 (blue dashed line) (color figure online)

Now, given Lemma 2, we can state the following Remarks about the relationship between tax evasion and competition. First, we distinguish between the changes in the competitive pressure due to changes in the different competition parameters: a larger competition induced by higher marginal costs (namely, defined as “cost” market competition) and a larger competition induced by less product differentiation (namely, defined as “product” market competition). Second, we consider the pre-existing level of the relative tax evasion for different levels and changes of the competition parameters.

Remark 2

If the market competition in terms of the product substitutability is high, while in terms of the marginal cost is low, increasing competition due to higher marginal costs reduces tax evasion; if the pre-existing market competition is rather high in terms of both “cost” and “product” market competition (i.e. both γ and c sufficiently high) increasing competition through a further rise in the degree of product substitutability reduces tax evasion.

Therefore, a rather high degree of product substitutability (i.e. a sufficiently high “product “ market competition) is always associated with a possible reduction of tax evasion (or, conversely, if the competition is low because of very differentiated products, increasing competition through either a larger product substitutability or larger marginal costs always tends to raise tax evasion).

Remark 3

Although it has been established above that higher marginal costs always increase tax evasion when the product substitutability is high, it is possible that the level of relative tax evasion is higher, for a given sufficiently high level of product substitutability, when the marginal cost is lower. In Fig. 2, for example, it is shown that, for γ > 0.85 tax evasion is larger when c = 0.5 than when c = 2.5. Alternatively, it is possible that the level of relative tax evasion is higher, for a given sufficiently high marginal cost, when the product is more differentiated: for instance, Fig. 1 shows that, for given values of c > 2.5, the level of relative tax evasion is higher when γ = 0.80 than when γ = 0.99.

2.3 Discussion of the main findings

The intuition behind the key results (i.e. Propositions 1 and 2) is based on the following points: (1) sales revenue may be a non-linear function of the two competition parameters, in particular a humped function of the marginal cost and a U-shaped function of the degree of product differentiation; (2) the difference between sales and declared sales (i.e. the undeclared absolute tax base) remains constant for varying competition parameters.

As regards point 1), by observing the numerator of the equilibrium sales revenue

$$pq = \frac{{z^{2} (1 - t)^{2} (1 - \gamma ) + c\gamma z(1 - t) - c^{2} }}{{(2 - \gamma )^{2} (1 - t)^{2} (1 + \gamma )}}$$

(30)

it can be easily seen that for sufficiently low (high) values of c sales are increasing (decreasing) with increasing c (and the higher γ, the more increasing or the less decreasing sales are).²³

As regards point (2), it can be easily seen that the difference between sales and declared sales, $\left( {pq - a} \right)$, does not depend on such competition parameters (see (39)): thus, the relative evasion—given by (11) and rewritten as $(1 - y)\frac{pq - a}{{pq}}$—evidently decreases (increases) with increasing c for existing low (high) values of c (as stated in Proposition 1). Moreover, as regards the role of γ, from the next derivative

$$\frac{\partial (pq)}{{\partial \gamma }} = \frac{{2z^{2} (1 - t)^{2} ( - \gamma^{2} - 1 + \gamma ) + cz(1 - t)(2\gamma^{2} + 2 + \gamma ) - 3c^{2} \gamma }}{{(2 - \gamma )^{3} (1 - t)^{2} (1 + \gamma )^{2} }}$$

(31)

we can see that if c tends to be small, sales revenue is always decreasing in γ, while if both c and γ tend to be large, sales revenue may be increasing in γ. Therefore, in the latter case, the relationship between sales revenue and γ becomes U-shaped and, thus, the relative tax evasion may be an inverted U-shaped function of γ (as stated in Proposition 2).

2.4 Output competition

Under Cournot competition, firm i maximizes $\pi_{i}$ —given by (18) after substitution of (15)—simultaneously choosing output, q_i, and declared revenues, $a_{i}$, taking the rival firm’s output as given. From the FOCs (see the Appendix), we get, respectively, the next equilibrium output and declared sales revenue (the apex C denotes Cournot)

$$q^{C} = \frac{z(1 - t) - c}{{(2 + \gamma )(1 - t)}}$$

(32)

$$a^{C} = \frac{{y\left[ {z^{2} (1 - t)^{2} + c\gamma z(1 - t) + t(1 - t)^{2} (\gamma^{2} + 4\gamma + 4) - c^{2} (1 + \gamma )} \right] - t(1 - t)^{2} (2 + \gamma )^{2} }}{{y(1 - t)^{2} (2 + \gamma )^{2} }}$$

(33)

Also under Cournot Lemma 2 holds true: the higher γ, t and c and the lower z are, the higher is the degree of competition.

The absolute and the relative tax evasion per firm are respectively.

$$E^{C} = \frac{{t^{2} (1 - y)^{2} }}{y}$$

(34)

$$e^{C} (c,\gamma ) = \frac{{t(2 + \gamma )^{2} (1 - t)^{2} (1 - y)^{2} }}{{y\left[ {z(1 - t) + c(1 + \gamma )} \right]^{2} \left[ {z(1 - t) - c} \right]^{2} }}$$

(35)

Thus, the next Proposition holds.

Proposition 3

(1) The absolute tax evasion is identical under Cournot and Bertrand competition; (2) the relationship between relative tax evasion and marginal cost is qualitatively the same of Bertrand (i.e. Prop. 1 also holds true under Cournot); (3) differently from the Bertrand case (i.e. Prop. 2), the relationship between relative tax evasion and product differentiation is unambiguous: the higher the product market competition is, the higher the relative tax evasion is.

Proof

See the Appendix.

After the concise derivation of the results in the Cournot case,²⁴ we are in a position to compare, in next sub-section, the two competition modes with respect to the main aim of the paper, i.e. the nexus between competition changes and tax evasion.

2.5 Modes of competition and tax evasion

As known, competition is fiercer under Bertrand than under Cournot. Then, it is worth to study under which competition mode the unethical evasion behaviour is larger. The relative tax evasion differential is:

$$D: = e^{C} - e = \frac{{\gamma^{2} t(1 - t)^{2} (1 - y)^{2} \left[ {2\gamma z(1 - t) - c(4 - \gamma^{2} + 2\gamma )} \right]}}{{y\left[ {z(1 - t)(1 - \gamma ) + c} \right]\left[ {z(1 - t) - c} \right]\left[ { - z(1 - t) - c(1 + \gamma )} \right]}} > 0$$

(36)

Although (36) looks cumbersome, one can exhaustively depict the effects of the competition parameters via numerical simulations, as Figs. 3 and 4 (based on the same parametric set in Sect. 2.2) display. These figures seem to reveal that the relative tax evasion is larger under Bertrand (Cournot) if the product substitutability (“product” market competition) is sufficiently high (low) and the marginal cost (“cost” market competition) is sufficiently low (high). In detail, the relative tax evasion is larger under Cournot than under Bertrand if there is a high “cost” market competition while a lower (higher) product differentiation essentially plays the role of enlarging (reducing) the differential, as expected by the fact that the higher the degree of differentiation is, the more similar the two competition modes are. A similar logic applies to the converse case of low “cost” market competition. Finally, in the case of relatively intermediate levels of “cost” market competition – as the behaviour of the solid curve in Fig. 4 shows—a reducing product differentiation (a higher “product market” competition) leads to a larger tax evasion under Bertrand.

Fig. 3

Relative tax evasion differential (D) as function of the marginal cost (c ∈ (0, 3)), for different degrees of product substitutability: D with γ = 0.80 (blue dotted line), D with γ = 0.50 (black solid line), and D with γ = 0.20 (red dashed line).Other parameters as in Figs. 1 and 2 (color figure online)

Fig. 4

Relative tax evasion differential (D) as function of the degree of product substitutability ($\gamma \in (0,1)$), for different marginal cost values: D with c = 0.3 (red dotted line), D with c = 1 (black solid line), and D with c = 2 (blue dashed line). Other parameters as in Figs. 1 and 2 (color figure online)

When the competitive pressure is relatively low (i.e. a low c), evasion may be higher under Bertrand (Cournot) depending on whether products are less (more) differentiated. Since Bertrand competition is fiercer than the Cournot one for any degree of product differentiation, then (provided that goods are sufficiently substitutes) tax evasion may be higher in the competition mode with stronger competitive pressure: that is, higher competition may be associated with larger evasion, in line with the Schleifer’s finding.

By contrast, when the competitive pressure is relatively high (i.e. a high c), evasion is always larger under Cournot: this means that the situation with larger firms’ market power is associated with larger evasion, in contrast to the Schleifer’s finding.

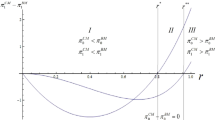
Therefore, by comparing the two standard competition modes with the firms’ tax compliance behaviour, we conclude that the link between competitive pressure and unethical behaviour may be true only when such a pressure is low and products are sufficiently substitutes, while it does not hold true when such a pressure is high, irrespective of the degree of products substitutability. Figure 5 graphically depicts the above reasoning, showing that if $c < 1.4$ then tax evasion may be higher under Bertrand (resp. Cournot) depending on whether products are less (resp. more) differentiated, while if $c > 1.4$ then tax evasion is always larger under Cournot.

Fig. 5

Plot of the zero relative tax evasion differential (D = 0) in the parametric plane (c,γ)

To sum up, also in the case of the comparison between the two competition modes our findings are mixed; therefore, to evaluate the different merits in terms of tax compliance of quantity versus price setting behaviours by firms, policy-makers should take into account the different competitive pressure as measured by the marginal cost and the product differentiation.

3 Conclusions

In this paper we have examined the relationship between tax evasion and competition in a duopoly context. We have preliminarily analysed the Cournot case with homogeneous product under a general form of demand, showing that an adequately low slope elasticity is a sufficient condition for considering a marginal costs’ increase as a fiercer competition and, in such a case, a fiercer competition may imply either more (less) tax evasion depending on whether the demand is elastic (inelastic). As known, firms may tackle with fiercer market competition through either cost-reducing or product differentiation choices, and policies may also encourage (or discourage) indirectly such choices. Thus, we have investigated the above mentioned relationship under Bertrand and Cournot competition modes with differentiated products in the standard Dixit (1979) and Singh and Vives (1984) framework.

The essential message of the paper is the following: increasing competition may imply either more or less evasion depending on whether (i) the existing competitive pressure is more or less fierce, (ii) the competition mode is on price or on quantity, and (iii) the larger competition fierceness is caused by either a rise of the production costs or a higher products substitutability. This message is sufficiently robust because it qualitatively holds under both Bertrand and Cournot modes of competition.²⁵

The policy implication²⁶ is that both tax and antitrust authorities should consider the different effects—as regards tax evasion—of both different sources of possible pro-competitive interventions and different pre-existing competitive pressures.²⁷ As regards the nexus between competition mode and tax compliance behaviour, the finding is that firms evade more (less) when they compete on quantities than when they compete on prices if the “cost” market competition is relatively high (low).

Finally, we have noted that Schleifer (2004) has recently argued that a keener competition, a part from efficiency reasons, may be associated with an increase of socially censored behaviours. Then, the firms’ behaviour in terms of tax evasion could be thought as an unethical behaviour to be studied in relation to the degree of market competition. In this respect, still in contrast to the preceding results by Goerke and Runkel (2011) (resp. by Martina and Marrelli 1988) which would be in line with (resp. in sharp contrast to) the Schleifer’s finding, we find mixed results: higher competition may favour or reduce the firms’ tax evasion depending on the reasons (i.e. different economic parameters) bringing upon such an increase of the competitive pressure and its pre-existing level.

Appendix

1.1 Comparative statics with homogeneous goods under Cournot, general demand

Substituting $U_{i}$ in $V_{i}$, yields:

$$V_{i} : = \left[ {P( \cdot ) + q_{i} P^{\prime}( \cdot )} \right](1 - t) - c = 0$$

To develop comparative statics for duopoly, we base on the symmetric implicit solutions ($a_{i} = a_{j} = a,\;q_{i} = q_{j} = q$) to the system representing the FOCs of each firm’s expected profit maximisation problem. This means that the FOCs may be rewritten as:

$$U: = yT\,^{\prime}\left[ {P(2q)q - a} \right] - (1 - y)t = 0$$

$$V: = \left[ {P(2q) + q_{i} P^{\prime}(2q)} \right](1 - t) - c = 0$$

Let $\theta = i$, where $i = c,y,t$ be a parameter in the expressions ($U$) and ($V$) (that is for firms’ marginal profits). Totally differentiating the expressions ($U$) and ($V$), we have

$$\left[ {\begin{array}{*{20}c} {U_{a}^{^{\prime}} } & {U_{q}^{^{\prime}} } \\ {V_{a}^{^{\prime}} } & {V_{q}^{^{\prime}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{\partial a}{{\partial \theta_{i} }}} \\ {\frac{\partial q}{{\partial \theta_{i} }}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{\partial U}{{\partial \theta_{i} }}} \\ { - \frac{\partial V}{{\partial \theta_{i} }}} \\ \end{array} } \right]$$

where $U_{a}^{{\prime}} : = - yT\,^{\prime\prime}$;$U_{q}^{{\prime}} : = yT\,^{\prime\prime}(P + 2qP\,^{\prime})$; $V_{a}^{{\prime}} : = 0$; $V_{q}^{{\prime}} : = (1 - t)(3P\,^{\prime} + 2qP\,^{\prime\prime})$.

By applying Cramer’s rule, the solution to the above system is

$$\frac{\partial a}{{\partial \theta_{i} }} = \frac{{\left[ {\begin{array}{*{20}c} { - \frac{\partial U}{{\partial \theta_{i} }}} & {U_{q}^{^{\prime}} } \\ { - \frac{\partial V}{{\partial \theta_{i} }}} & {V_{q}^{^{\prime}} } \\ \end{array} } \right]}}{\Delta },\;\frac{\partial q}{{\partial \theta_{i} }} = \frac{{\left[ {\begin{array}{*{20}c} {U_{a}^{^{\prime}} } & { - \frac{\partial U}{{\partial \theta_{i} }}} \\ {V_{a}^{^{\prime}} } & { - \frac{\partial V}{{\partial \theta_{i} }}} \\ \end{array} } \right]}}{\Delta },\;{\text{where}}\;\Delta : = \det \left[ {\begin{array}{*{20}c} {U_{a}^{^{\prime}} } & {U_{q}^{^{\prime}} } \\ {V_{a}^{^{\prime}} } & {V_{q}^{^{\prime}} } \\ \end{array} } \right]$$

Simple calculations yields:

$$\Delta : = - T\,^{\prime\prime}y(1 - t)(3P\,^{\prime} + 2qP\,^{\prime\prime}),$$

$$\frac{\partial a}{{\partial c}} = \frac{P + 2qP\,^{\prime}}{{(1 - t)(3P\,^{\prime} + 2qP\,^{\prime\prime})}},$$

$$\frac{\partial q}{{\partial c}} = \frac{1}{(1 - t)(3P\,^{\prime} + 2qP\,^{\prime\prime})}.$$

1.2 Proof of Lemma 1

(i) Preliminary, we show that

$$\begin{gathered} \frac{{\partial L}}{{\partial c}} = \frac{{(1 - t)^{2} \left( {2P\,'\frac{{\partial q}}{{\partial c}}} \right)P - (1 - t)P - (1 - t)^{2} \left( {2P\,'\frac{{\partial q}}{{\partial c}}} \right)P + c(1 - t)\left( {2P\,'\frac{{\partial q}}{{\partial c}}} \right)}}{{\left( {(1 - t)P} \right)^{2} }}, \hfill \\ \frac{{\partial L}}{{\partial c}}\frac{ < }{ > }0 \Leftrightarrow P\frac{ > }{ < }\frac{c}{{(1 - t)}}\frac{2}{{(3 + \varepsilon )}} \hfill \\ \end{gathered}$$

(A.1)

(ii) Since $P > \frac{c}{(1 - t)}$ is the necessary condition for positive profits, then $\varepsilon > - 1$ suffices in order that the Lerner index increases with decreasing marginal costs. $\hfill\square$

1.3 Proof of Result 1

(i) provided the negativity of (A.1), the proof straightforwardly follows from (21) in the main text;

(ii) the proof straightforwardly follows from (22) in the main text.

1.4 Firm’s FOCs under price competition

Firm i’s expected net profit is given by

$$\pi_{i} = y\left\{ {\left[ {(1 - t)p_{i} - c} \right]\frac{{z(1 - \gamma ) - p_{i} + \gamma p_{j} }}{{(1 - \gamma^{2} )}} - \frac{{\left( {p_{i} \frac{{z(1 - \gamma ) - p_{i} + \gamma p_{j} }}{{(1 - \gamma^{2} )}} - a_{i} } \right)^{2} }}{2}} \right\} + (1 - y)\left\{ {(p_{i} - c)\frac{{z(1 - \gamma ) - p_{i} + \gamma p_{j} }}{{(1 - \gamma^{2} )}} - ta_{i} } \right\}$$

(A.2)

Firm i maximizes $\pi_{i}$, taking as given the rival firm’s price. The FOCs for an interior solution are, with regard to declared revenues

$$\frac{{\partial \pi_{i} }}{{\partial a_{i} }} = 0\; \Leftrightarrow a_{i} = \frac{{y[p_{i} z(1 - \gamma ) + \gamma p_{i} p_{j} - p_{i}^{2} + (1 - \gamma^{2} )t)] - t(1 - \gamma^{2} )}}{{y(1 - \gamma^{2} )}}$$

(A.3)

and, exploiting (A.3), as regards price

$$\frac{{\partial \pi_{i} }}{{\partial p_{i} }} = 0\; \Leftrightarrow p_{i} (p_{j} ) = \frac{{\gamma (p_{j} - z)(1 - t) + z(1 - t) + c}}{2(1 - t)}$$

(A.4)

From (A.4), by substituting for the counterpart for firm j, we get the equilibrium values reported in the main text.

1.5 Proof of Lemma 2

Lemma straightforwardly derives from the following:

$$\begin{gathered} \frac{\partial L}{{\partial c}} = \; - \frac{z(1 - t)(2 - \gamma )(1 - \gamma )}{{\left[ {z(1 - t)(1 - \gamma ) + c} \right]^{2} }} < 0;\quad \frac{\partial L}{{\partial t}} = \; - \frac{cz(2 - \gamma )(1 - \gamma )}{{\left[ {z(1 - t)(1 - \gamma ) + c} \right]^{2} }} < 0; \hfill \\ \frac{\partial L}{{\partial z}} = \;\frac{c(1 - t)(2 - \gamma )(1 - \gamma )}{{\left[ {z(1 - t)(1 - \gamma ) + c} \right]^{2} }} > 0;\quad \frac{\partial L}{{\partial \gamma }} = \; - \frac{{c\left[ {z(1 - t) - c} \right]}}{{\left[ {z(1 - t)(1 - \gamma ) + c} \right]^{2} }} < 0 \hfill \\ \end{gathered}$$

1.6 Proof of Proposition 1

The proof derives from.

$$\frac{\partial e(c,\gamma )}{{\partial c}} = \frac{{t(2 - \gamma )^{2} (1 - t)^{2} (1 + \gamma )(1 - y)^{2} \left[ {2c - \gamma z(1 - t)} \right]}}{{y\left[ {z(1 - t)(1 - \gamma ) + c} \right]^{2} \left[ {z(1 - t) - c} \right]^{2} }}\frac{ > }{ < }0\; \Leftrightarrow \;c\frac{ > }{ < }c^\circ = \frac{z\gamma (1 - t)}{2},$$

(A.5)

Hence, there are always values of c which are below c° and always some values of c which are above c°. Hence, relative tax evasion is always U-shaped in c.

1.7 Proof of Proposition 2

The proof derives from

$$\frac{\partial e(c,\gamma )}{{\partial \gamma }} = \frac{{t(\gamma - 2)(1 - t)^{2} (1 - y)^{2} \left[ {2z(1 - t)(\gamma - \gamma^{2} - 1) + 3c\gamma } \right]}}{{y\left[ {z(1 - t)(1 - \gamma ) + c} \right]^{2} \left[ {z(1 - t) - c} \right]}}\frac{ > }{ < }0\; \Leftrightarrow \;c\frac{ < }{ > }c^\circ = \frac{{2z(1 + \gamma^{2} - \gamma )(1 - t)}}{3\gamma }$$

and, in the spirit of the proof of Proposition 1, there are always values of c which are below c°° and always some values of c which is above c°°. Hence, relative tax evasion is always inverted U-shaped in c.

1.8 Firm’s FOCs under output competition

The first-order conditions for an interior solution are, as regards declared revenues

$$\frac{{\partial \pi_{i} }}{{\partial a_{i} }} = 0\; \Leftrightarrow a_{i} = \frac{{y[q_{i} z - (\gamma q_{i} q_{j} + q_{i}^{2} - t)] - t}}{y}$$

(A.6)

and, exploiting the direct demand function, as regards output

$$\frac{{\partial \pi_{i} }}{{\partial q_{i} }} = 0\; \Leftrightarrow q_{i} = \frac{{z(1 - t) - c - \gamma q_{j} (1 - t)}}{2(1 - t)}$$

(A.7)

From (A.6) and (A.7), by substituting for the counterpart for firm j, we get the equilibrium values reported in the main text.

1.9 Proof of Proposition 3

Part 1): This straightforwardly derives from the fact that $E^{C} = E$

Part 2): Given that²⁸

$$\frac{{\partial e^{C} (c,\gamma )}}{\partial c} = \frac{{t(2 + \gamma )^{2} (1 - t)^{2} \left[ {\gamma z(t - 1) + 2c(1 + \gamma )} \right](1 - y)^{2} }}{{y\left[ {z(1 - t)(1 + \gamma ) - c} \right]^{2} \left[ {z(1 - t) - c} \right]^{2} }}\frac{ > }{ < }0\; \Leftrightarrow \;z\frac{ < }{ > }\frac{2c(1 + \gamma )}{{\gamma (1 - t)}}$$

(A.8)

the proof follows from the simple comparison of (A.5) with (A.8);

Part 3): This straightforwardly follows from

$$\frac{{\partial e^{C} (c,\gamma )}}{\partial \gamma } = \frac{{t(2 + \gamma )(1 - t)^{2} \left[ {2z(1 - t) + c\gamma } \right](1 - y)^{2} }}{{y\left[ {z(1 - t) + c(1 + \gamma )} \right]^{2} \left[ {z(1 - t) - c} \right]}}$$