Modeling on naturalization of inflow and outflow nutrients sources of Blue Nile River at the Lake Tana in Basaltic Plateau of Ethiopia

Abstract

Lake Tana is the largest natural reservoir in Ethiopia and the head water of Abbay basin. However, after building of an irrigation weir and further lying Tunnel to Tana Belles, Lake Tana maximum amplitude of water level canges from 2.18 to 3.56 m that differ substantially in 1.38 m from amplitude of natural water level fluctuation. Understanding the natural characteristics of the Lake is important to know its water balance and for sustainable development. But it is difficult to study the natural characteristics of the Lake and its water balance using the regulated water level and outflow data sets. Thus it is evident that the regulated water level and outflow data sets have to be first naturalized before they are used for any analysis and modeling. Lake level and outflow data that have been collected since 1976 were considered to assess the regulation effect and then for naturalization. Inflows to the Lake from the main tributaries have also been collected to find if there are any correlations with either the Lake Level and/or the outflow. Regression analyses were used to develop the naturalization models. The regression analyses of flows from Gilgel Abay and Gummar with Lake Level shows that there is a very good correlation between them in different seasons. Besides, same has also been observed between Lake Level and out flow. These relationships can be used to naturalize the regulated outflow and water level.

Introduction

Lakes are one of humanity’s most important resources; often viewed as highly productive biological systems (Sewunet 2011).

Anybody who has lived near a Lake can observe the phenomenon of Lake level fluctuation which is characterized by higher water Level during the spring and the last summer season and lower water levels during the autumn season. Such fluctuations are the results of several natural factors but also human activities. The primary the natural factors affecting Lake Levels are amounts of water inflow by rainfall, river inflow, ground water discharge to Lake, the surface and sub-surface runoff, etc., and outflow by evaporation, river outflow. Major influential human factors which affects the Lake level are diversion of water into and out of the basin for the irrigation and other purposes, regulation of outflow and dredging of outlet Tunnels for generation of hydropower. For this purpose the commencement of a seven-gate Chara Chara weir has the capacity to regulate lake stages up to 3 m retaining 2.4 times the annual outflow, the excessively dry period of 2000 and 2001 seems to have resulted in conflict of interest to keep the lake stage against the power house demands (Chebud and Melesse 2009). This weir regulates water storage in Lake Tana over a 3 m range of water levels from 1784 masl2 to 1787 masl (Mccartney et al. 2010). The active storage of the lake between these levels is 9100 Mm3, which represents approximately 2.4 times the average annual outflow. In 2010 Tana Belles Hydropower plant was constructed to receives water from western side of the Lake Tana to Belles River via 12km long, 7.1m diameter tunnel (Salini 2006). The intention is to divert approximately 2985 Mm³ through the tunnel (rather than via the Chara Chara Weir) each year to generate 2310 GWh of electricity (SMEC 2008). But it is difficult to study natural characteristics of the Lake. The adjustment of Lake Level and outflow fluctuation difference can be studied in this research.

The Lake Tana water Level fluctuation is characterized by higher water level during September and lower water level during June. The basic problem resulting from regulation of outflows of the Lake is the construction of a Chara Chara weir and lying of Tunnel to Tana belles typically leads to water level fluctuation that differs substantially from natural water level fluctuation.

The major aim of this research is to developing a naturalization model that used to naturalize regulated Lake Level and Lake Outflow.

Materials and methods

Study area description

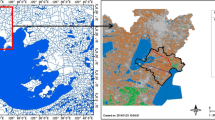
The Lake Tana watershed is one of the sub basins of the Blue Nile River basins (Fig. 1). It is located in Ethiopia’s North-West high lands (12^°00 latitude, 37^°15′ longitude) and has a drainage area of 15092 km². The Tana Lake is a natural lake which covers around 3033 km² areas with a maximum depth of 14 m. It is approximately 84 km long, 66 km wide. Gilgel Abay, Ribbe, Gummera and Megech are the main rivers feeding the lake, contributing more than 93% of the inflow (Kebede et al. 2006). Lake Tana is the main source of the Blue Nile River that is the only natural surface outflow for the Lake. The lake catchment has minimum elevation of approximately 1784 m amsl at east, north and west-south side of the lake on the flood Ribbe, Megech and Gilgel Abay respectively and a maximum elevation of 4107 m amsl at east side of the lake at the boundary of Ribbe catchment (Wale 2008). Lake Tana water surface has its natural mean sea level of 1786 (Daniel 2006).

Fig. 1

Location of the study area

Methodology

Data quality test methods and its applications

The basic statistical analysis of hydrologic time series, the applications of time series analysis in hydrological sciences include development of mathematical models to generate synthetic hydrologic data, to forecast hydrologic events, to identify trends and shifts in hydrologic data, to fill in missing observations, and to extend short hydrologic records (Machiwal and Jha 2012). A set of quantitative observations such as stream flow measured in discrete time interval and arranged in chronological order is an ideal example of time series. The time series to be analyzed may then be thought of as a particular realization, produced by the underlying probability mechanism. The outflow series recorded from Lake Tana out let and the inflow series of Lake Tana are single realizations among other perhaps many different possible realizations in their respective stochastic processes (Azeze 2013).

There are four major steps involved in a time series analysis (McCuen 2003): (i) detection, (ii) analysis, (iii) synthesis and (iv) verification. In the detection step, systematic components of the time series such as trends or periodicity are identified. In the analysis step, the systematic components are analyzed to identify their characteristics including magnitudes, form and their duration over which the effects exist. In the synthesis step, information from the analysis step is accumulated to develop a time series model and to evaluate goodness-of-fit of the developed model. Finally, in the verification step, the developed time series model is evaluated using independent sets of data. In case of this research only the first two steps such as detection and analysis steps were applicable.

The time intervals for most hydrologic time series are hour, day, week, month, season or year. The time series data of inflow to the Lake Tana, outflow from Lake Tana and Lake Tana water level are recorded at daily time interval. But for this research analysis monthly time interval was applicable.

The ability to demonstrate whether a change or trend is present in the climatological data series and to quantify this trend, if it is present in case of this research absence of trend test analysis was applicable to evaluate a change due to regulation of Lake out flow or quantify significant changes on natural Lake Level and outflow.

Regression analysis and its application

Regression analysis is a conceptually simple method for investigating functional relationships among variables. The relationship is expressed in the form of an equation or a model connecting the response or dependent variable and one or more explanatory or predictor variables (John Wiley 2006). The distinction between simple and multiple regressions is determined by the number of predictor variables (simple means one predictor variable and multiple means two or more predictor variables), whereas the distinction between univariate and multivariate regressions is determined by the number of response variables (univariate means one response variable and multivariate means two or more response variables (John Wiley 2006). In Lake Tana the natural Lake level data taken as a response variable and the precipitation, gauged and un gauged stream flows to the Lake, surface and sub-surface runoff to the Lake and ground water discharge to the Lake are taken as a predicator and then this relationship becomes multiple regression equation. In case of this research analysis only the inflows taken as a predictor variable, the Lake level taken as a response variable and the relationship becomes simple regression equation. The Lake level for the Lake outflow becomes a predictor variable and the Lake outflow for the Lake level becomes a response variable and the relationship of this variable becomes simple regression equation.

The values of R² can be used as the good fit relationship of Lake with inflows and Lake Outflow with Lake Level. In case of this study selection of good-fit linear relationship was performed from different techniques such as regression of all-time series data of natural Lake Level with G/Abay and Gummera flow individually and in combined, time series data of seasonal natural Lake Level with seasonal G/Abay flow and Gummera flow individually and in combined.

Generally as shown in Fig. 2 the simplified flow chart of this research methodology can be arranged in work sequence order.

Fig. 2

Methodology flow chart that used in this study

Results and discussion

Missed data infilling

Lake Tana water Level has three recorded station such as Bahirdar, Gorgora and Konzila Lake level recorded station. There is relatively sufficient length of Lake level records since 1959 at Bahirdar Lake level station, and also Konzila and Gorgora Lake level station started to record 1980 and 1990 respectively.

Accourding to historical recorded Lake level data reports, Konzila and Gorgora Lake level recorder station have more missed values and short length of historical time than Bahirdar Lake level recorder station. Therefore, according to data quality principle, only Bahirdar Lake level station recorded data was applicable for analysis of this research.

There is almost full Lake Outflow data From Abay near Bahirdar station from the year 1972. The missed data in the selected records of the Lake Outflow, inflow data and Lake Level have been filled by arithmetic average methods. This method is fast and simple and yields good estimates for single station of data recorders (Ragunath 2006).

Data quality test analysis of natural and regulated lake level and outflow

A time series is said to have trends, if there is a significant correlation (positive or negative) between the observed values and time. Trends and shifts in a hydrologic time series are usually introduced due to gradual natural or human-induced changes in the hydrologic environment producing the time series (Salas 1993). A ‘trend’ is defined as “a unidirectional and gradual change (falling or rising) in the mean value of a variable” (Shahin et al. 1993).

The man-made changes such as the closure of a new dam, the beginning or termination of groundwater pumping, or other such developmental activities may also cause jumps in some hydrologic time series (Haan 1977). The variables that appear to have a trend may actually just represent a change in climatological or hydrological conditions near the monitoring site. Under such conditions, the affected climatological data should be modified so that the values are better representative of the study area as a whole (Hameed et al. 1997).

Natural time series, including hydrologic, climatic and environmental time series, which satisfy the assumptions of homogeneity, randomness, no periodic, non-persistence and stationarity, seem to be the exception rather than the rule. In fact, for all water resources studies involving the use of hydrologic time series data, preliminary statistical analyses must always be carried out to confirm whether the hydrologic time series possess all the required assumptions/characteristics (Adeloye and Montaseri 2002).

Homogeneity test

The term ‘homogeneity’ implies that the data in the series belong to one population, and therefore have a time invariant mean. Non-homogeneity arises due to changes in the method of data collection and/or the environment in which it is done (Fernando and Jayawardena 1994).

Homogeneity test analysis result of Lake level data which recorded before 1996 and after 1996 |u) = 1.65 and 0.08 respectively is less than the critical value u_0.025 = 1.96 at 5% significance level (Table 1). But Test analysis result of all Lake level data |u| = 3.74 greater than the critical value u_0.025 = 1.96. This result shows that the lake level data which recorded before 1996 are heterogeneous with the Lake level data which recorded since 1996. In other words the Lake level data which recorded before 1996 are homogeneous by

itself and the lake level data which recorded since 1996 are homogeneous but the combination of natural regulated Lake level data set are not homogenous and stationary.

Table 1 Homogeneous analysis results of Time series data

Homogeneity test analysis result of natural Lake outflow data set |u) _test = 2.09 less than the critical value u_0.01 = 2.326 at 99% confidence interval. But Test analysis result of combination of natural and regulated Lake outflow data set,and regulated Lake outflow data set |u|_test = 5.62 and 5.91 respectively greater than the critical value u_0.01 = 2.326. This result shows that natural characteristics of Lake outflow and Lake level data which recorded since 1996 were changed their homogeneity due to Lake Outflow regulation.

Homogeneity test analysis result of G/Abay flow and Gummera flow data shows that all-time series data of G/Abay and Gummera flows data set are homogeneous and stationarity with each other at 5% significant level (Table 1).

Absence of trend test analysis

Absence of trend test analysis result of Lake level data which recorded before 1996 and after 1996; t_s = 1.63 and − 0.63 respectively bounded between the critical region t_{(478, 2.5%}) = − 1.966 and t_{(478, 97.5%)} = 1.966 at 5% significance level, but Absence of Trend Test analysis result of all Lake level data t_s = 3.23 not bounded within the critical region. This result shows that characteristics of the lake level data which recorded before 1996 were changes due to Lake Outflow regulation. (Table 2)

Table 2 Absence of Trend test analysis results of time series data sets

Absence of trend test analysis result of Lake outflow data which recorded before 1996 t_s = 2.09 is bounded between the critical region t_(190,1%) = − 2.348 and t_{(190, 99%)} = 2.348, and also t_s = 0.98 is bounded between the critical region t_(152,1%) = − 2.351 and t_(152,99%) = 2.351, but absence of trend test analysis result of Lake outflow data which recorded from 1980 to 2008 t_s = 6.6 not bounded between the critical region at 1% significant level. This result shows that the lake outflow data which recorded before and after 1996 have a different hydrological characteristic (Table 2).

Absence of trend test analysis results of G/Abay and Gummera flow shows that, all-time series data sets are hove no trend, Megech and Ribbe time series data have a trend between them.

This Absence of trend test analysis are takes placed not only using all sequence of time series data sets, but also carried out in individual monthly data set orders in case of maximum, minimum and average monthly data sets.The absence of trend test analysis results of combined Lake level data set shows that except March, April, May, June, July and August all months of data sets have a trend in all three cases such as Maximum, minimum and average data sets at 95% confidence interval, but Absence of trend test analysis results of natural and regulated Lake level data set individually shows that all months of data sets have not trend in all three cases such as Maximum, minimum and average data set at 95% confidence interval. This result indicates that combined some monthly Lake level data sets are changes their natural characteristics due to Lake Outflow regulation.

The absence of trend test analysis results of combined Lake outflow data set shows that except September, November and December all monthly data sets have trend in all three cases such as Maximum, minimum and average data sets at 95% confidence interval, but absence of trend test analysis results of natural Lake outflow data set shows that all months of data sets have no a trend in all three cases such as Maximum, minimum and average data sets at 95% confidence interval and also regulated Lake outflow data set shows that almost all months of data sets are free from a trend in three cases such as Maximum, minimum and average data sets at 95% confidence interval. This result indicates that combined monthly Lake Outflow data sets are changed its natural characteristics by due to Lake Outflow regulation.

Assessing lake level and inflows to the lake relationship

Around 93% Lake Tana’s flow system is governed by four main components: the inflow from surrounding river catchments into the lake such as G/Abay, Gummera, and Megech and Ribbe rivers (Kebede et al. 2006). The remaining 7% supplied of water to the Lake Tana was produced from precipitation fall on the Lake, un gauged runoff to the Lake and ground water discharge to the Lake (Kebbede et al. 2006). So most increasing or decreasing of Lake Level was depends on decreasing and increasing of flow discharge of four major rivers, especially G/Abay and Gummera rivers covers more quantity of water which supplied to the Lake Tana.

As shown in Fig. 3a, b maximum mean monthly historical data of flow for all major rivers were recorded in August while maximum mean monthly historical data of Lake Level and outflow were recorded in September, And also minimum mean monthly historical data of flow for all major rivers were recorded in April and minimum mean monthly historical data of Lake Level and outflow were recorded in June.

Fig. 3

Hydrograph mean monthly data sets

Natural Lake Level and inflows have similar positive gradients during infilling period (June to August) and also have similar negative gradients during decline period (December to February). But for the two remaining seasons have not similar infilling or declined characteristics between them because during autumn season (March to May) inflow hydrographs have decline period (negative gradients) during March & April and have infilling period (positives gradient) during May. But Lake Level hydrographs have decline period (negative gradients during this season (March to May). In addition during spring season from September to November inflow hydrographs have decline period (negative gradients) during September, but Lake Level hydrographs have infilling period (positive gradient) during September. This seasonal relationship of Lake Level and inflows were widely discussed in their linear relationship between them using R² values to determined good-fit relationship.

There is similar seasonal relationship between Lake Level and outflow during infilling and decline period (See Fig. 3b).

• (a) Hydrograph of mean monthly stream flow data sets

• (b) Hydrograph of mean monthly Lake level and outflow data set

Developing naturalization model of lake level and outflow

Making assumptions and restrictions on the natural characteristics and fluctuation of the range of reservoir deemed to be important to reverse the observation into the natural condition (Azeze 2013). The assumption here is that the rising and go down of natural lake level can be depending on gauged and un gauged stream flows to the Lake, precipitation fall on the Lake, surface and sub-surface runoff to the Lake, ground water discharge to the Lake and evapotranspiration from the Lake. This assumption indicates that natural characteristics of the Lake level can be related to natural characteristics of Lake Water components during the unregulated period. Such characteristics well simplify the naturalization process of Lake Level. From these Lake water components, runoff and precipitation does not ongoing throw out the year, so difficult to related with time series data of Lake Level in case of this research. According to previous study ground water discharge and un gauged stream flow to the Lake have a small quantity which compared to the other Lake water components. Then gauged stream flow and evapotranspiration are the basic components to determine the natural characteristics such as rising and go down Lake Level. But to know evapotranspiration from the Lake further detail investigation can be needed and the Lake not response to evapotranspiration. In other words the Lake level not depends on evapotranspiration rather the evapotranspiration depends on Lake Water. Therefore, gauged stream flows are selected for naturalization process of Lake Level.

The Time series data quality test analysis result of stream flow shows that the historical data of Megech and Ribbe stream flow were not homogeneous and safe according to their data quality standards. So for naturalization process of regulated Lake Level only G/Abay and Gummera flows were applicable.

The Linear relationship of natural Lake Level with G/Abay and Gummera stream flows were carried out using linear regression analysis.

This regression analysis was carried out in two ways. This was by using all-time series data of both response and predictor variables and by using seasonal time series data of both response and predictor variables. These two regression analysis have one response variable (natural Lake Level) and two predictor variable (G/Abay and Gummera flow). The relationship of response variable and predictor variable was carried out in four ways such as Lake Level versus G/Abay flow, Lake Level versus Gummera flow, Lake Level versus the sum of G/Abay and Gummera flow and Lake Level versus G/Abay and Gummera flow as separate dependent variable. This analysis used to select the best fit linear relationship of Lake Level versus inflow using R² values.

Linear regression analysis results of all-time series data set of response variable with all-time series data set of predictor variable have very small R² value in those different ways (Table 3). This result indicates that there is seasonal variation between their time series data set.

Table 3 Summary in linear regression analysis of Lake level versus inflow in different ways

According to Linear regression analysis results of summer and winter season the values of R² is more than the other R² values of remaining seasons. From linear relationship of natural Lake Level versus inflow in summer season the R² values of natural Lake versus Gummera flow is 0.85, which is more than the remaining linear relationships. And the linear relationship of natural Lake Level versus inflow in winter season the R² values of natural Lake Level versus sum of G/Abay and Gummera flow is 0.76, which is more than the remaining linear relationships.

This Linear regression analysis result concluded that good-fit relationship of Lake Level and inflows are depending on their seasonality throughout the year. The value of R² = 0.85 in Fig. 5a and the values of R² = 0.76 in Fig. 4b indicates that nearly 76% for December to February and 85% for June to August of the total variability in the Lake Level is accounted by the sum of G/Abay and Gummera flows and Gummera flows, respectively.

Fig. 4

Linear relationship of Lake Level versus inflows in different ways

• (a) Linear relationship of LL versus Gummera in summer

• (b) linear relationship of LL versus sum of inflows in winter.

The seasonal Lake Level is then regressed with the seasonal inflow and a new rating curve that relates the inflow with the corresponding Lake Level has been developed for season of summer and winter. This rating curve equation used to convert summer and winter season of regulated Lake Level to summer and winter natural Lake Level. The reaming season of regulated Lake Level can be naturalized using the concepts of increasing and decreasing time of the natural Lake Level.

This developing Linear rating curve has an empirical equation of the form:

$$ {\text{LL}}_{{{\text{win}}\left( {\text{t}} \right)}} = 0.0 4 {\text{Q}}_{{{ \inf }({\text{t}})}} \, + \, 1 7 8 6 $$

(1)

for winter season

$$ {{\rm LL}}_{{{{\rm sum}}({{\rm t}})}} \, = \,0.00 7 3 {{\rm Q}}_{{{{\rm Gf}}({{\rm t}})}} \, + \, 1 7 8 5. 5 $$

(2)

for summer season

where Q_{inf (t)} is the sum of G/Abay and Gummera flow in m³/s at time t, Q_Gf(t) is Gummera flow in m³/s at time t, and LL_{win (t)} and LL_{sum (t)} is the naturalized Lake Level at time t in m.a.s.l for winter and summer season respectively.

The most reasonable and practical strategy to naturalize the outflow is to find a functional relationship between the outflow and Lake level observed during the unregulated natural conditions. This is due to the fact that increasing and decreasing of the outflow quantity only depends on Lake Level and evapotranspiration from the surface areas of the outflow channel. But the amount of evapotranspiration which evaporated from outflow channel is very small due to short span length from Lake Water to Abay River Gauge.

• (a) Linear relationship of LL and outflow in winter

• (b) Linear relationship of LL and outflow in spring

• (c) Linear relationship of LL and outflow in Summer

• (d) Linear relationship of LL and outflow in Autumn

Lake Level and outflow versus month shows there is seasonality between them throughout the year (Fig. 3b). So to naturalize regulated Lake Outflow first a simple model from seasonal functional relationship of Lake Level and outflow was developed (see Fig. 5). The seasonal outflow is then regressed with the seasonal Lake Level and a new rating curve that relates the Lake level with the corresponding outflow has been developed for all types of seasons of the year.

Fig. 5

Linear relationship of Lake Outflow versus Lake Level

These rating curves have an empirical equation of the form:

$$ {\text{Q}}_{{{\text{oufw}}({\text{t}})}} \, = \, 1 1 4.0 9 {\text{LL}}_{{{\text{win}}\left( {\text{t}} \right)\,}} \, - 20 3 7 3 5 $$

(3)

for winter season

$$ {\text{Q}}_{{{\text{oufsu}}({\text{t}})}} \, = \, 9 9. 10 5 {\text{LL}}_{{{\text{sum}}\left( {\text{t}} \right)\,}} - \, 1 7 6 9 4 7 $$

(4)

for summer season

$$ {\text{Q}}_{{{\text{oufsp}}({\text{t}})}} \, = \, 4 2. 2 8 9 {\text{LL}}_{{{\text{spr}}\left( {\text{t}} \right)\,}} - \, 7 5 4 9 7 $$

(5)

for Spring season

$$ {\text{Q}}_{{{\text{oufa}}({\text{t}})}} \, = \, 4 7 5. 1 6 {\text{LL}}_{{{\text{aut}}\left( {\text{t}} \right)\,}} - \, 8 4 8 7 8 3 $$

(6)

for Autumn season

where Q_{oufw (t)}, Q_{oufsu (t)}, Q_{oufsp (t)} and Q_{oufa (t)} is the outflow in m³/s at time t, and LL_win(t), LL_sum(t), LL_spr(t) and LL_aut(t) is the naturalized Lake Level in m. a.s.l at time t for season of winter,summer, spring and Autumn respectively. Then these developed empirical equations are used to convert the regulated Lake outflow to naturalized Lake Outflow using their corresponding naturalized Lake Level data.

Naturalization of regulated lake level and lake outflow data set

Regulated Lake Level and Lake Outflow must be naturalized before used for different hydrological analysis of Lake Level and outflow. The regulated lake level for winter and summer season can be converted simply using Eqs. 1, 2 by taking the G/Abay inflow data and Gummera flow data which recorded since 1996 as independent variable. Then the remaining seasonal regulated Lake Level can be converted to naturalize Lake Level using backward and forward extrapolation of these two season naturalized Lake Level by developing a simple equation for each year. The hydrograph of natural average Lake Level shows that the infilling period starts from June and continues to September. During this period the hydrograph of natural Lake has a positive slope (See Fig. 6). Then the regulated Lake level of September can be converted to natural Lake Level by using Extrapolation equation of June to August rising hydrograph lines. This equation is developed from June to August naturalized Lake Level versus time index for each year.

Fig. 6

Seasonal variation of natural monthly average Lake Level

The hydrograph of natural average Lake Level shows that decline period was starting from October and continues to May. During this period the hydrograph of natural Lake has a negative slope (See Fig. 6). Then the regulated Lake level of October to November and March to May can be converted to natural Lake Level by using backward and forward extrapolation equation of December to February decline hydrograph lines for each year. This equation is developed from December to February naturalized Lake Level versus time index for each year. The regulated September Lake Level can also naturalized by backward extrapolation of December to February decline hydrograph lines, because of September natural lake level is the peak point of hydrograph of Lake level.

In other words natural characteristics of Lake Level show that decreasing line (recession limb) of Lake Level from September to May almost has similar negative slopes. And also the recession limb of autumn season and spring season underlined with recession limb of winter season. Then using this contextual principle the regulated Lake level of autumn season and spring season can be naturalize by extrapolation of naturalized winter season Lake level by developing simple linear equation from naturalized Lake Level (Fig. 7).

Fig. 7

Naturalized Average Lake Level for winter season versus time index

Then regulated Lake Level which recorded in Autumn season (September to November) and Spring season (March to May) can be naturalized by backward and forward Extrapolation of naturalized winter season (December to February) respectively using developed simple equation for each year.

Generally the result of Naturalization process of Lake Level is plotted as (Fig. 8):

Fig. 8

Time series plot of Lake Level and outflow after naturalization

The historical daily recorded data of natural maximum and minimum Lake Level are 1787.49 m.a.s.l and 1785.31 m.a.s.l respectively and their difference becomes 2.18 m. But the historical daily recorded data of regulated maximum and minimum Lake Level are 1788.02 m.a.s.l and 1784.46 m.a.s.l respectively and their difference becomes 3.56 m. This result indicates that water level fluctuation of regulated Lake level increases 1.63 times natural water Level fluctuation,but after naturalization of the regulated Lake Level maximum and minimum naturalized Lake Level are 1787.45 m.a.s.l and 1785.39 m.a.s.l respectively and their difference becomes 2.06 m. The ratio of naturalized Lake Level to natural Lake Level becomes 0.94. Therefor this developed naturalization model can be decreased the fluctuation factor of regulated Lake Level to natural Lake Level from 1.63 to 0.94.

The regulated Lake outflow for each season can be converted to natural Lake Outflow simply using Eqs. 3 to 6 by taking the corresponding seasonal naturalized Lake Level data as independent variable.

Conclusion

The historical daily recorded data of natural maximum and minimum Lake Level are 1787.49 m.a.s.l and 1785.31 m.a.s.l respectively and their difference becomes 2.18 m. The natural maximum and minimum outflow are 658.13 m³/s and 2.130 m³/sec respectively. But the historical daily recorded data of regulated maximum and minimum Lake Level and outflow are 1788.02 m.a.s.l and 1784.46 m.a.s.l respectively for and their difference becomes 3.56 m for Lake level and 704.96 m³/s and 0.14 m³/s respectively and their difference becomes 704.82 m3/s for Lake outflow. This result indicates that water level fluctuation of regulated Lake Level and outflow increases 1.63 and 1.07 times natural water Level fluctuation of Lake Level and outflow respectively.

Homogeneity test and absence of Trend test analysis of both time series data and similar monthly data set result shows that the Lake Level and outflow data set which recorded before 1996 and after 1996 data sets individually are homogenous and have no trend. But their combination data set are heterogeneous and have a trend. This result indicate that hydrological characteristics of natural Lake Level and outflow are not similar to corresponding regulated Lake Level and outflow .

Water Level fluctuation difference of natural and regulated Lake Level was adjusted by converting regulated Lake Level to natural Lake Level. This was by using seasonal linear regression empirical equation of natural Lake Level versus the sum of G/Abay and Gummera flow for winter season (Dec to Feb) with performance R² value of 0.76 and natural Lake Level versus Gummera flow for summer season (June to August) with performance R² value of 0.85. The remaining season such as September to November and March to May regulated Lake Level was naturalized by backward and forward extrapolation of winter season naturalized Lake Level data set respectively. After naturalization of regulated Lake Level amplitude of water level fluctuation was decreasing from 3.56 to 2.06 m that differ substantially in 0.12 m from amplitude of natural water level fluctuation.

Water Level fluctuation difference of natural and regulated Lake outflow was adjusted by converting regulated Lake outflow to natural Lake outflow using seasonal linear regression empirical equation of natural Lake outflow versus natural Lake Level for each corresponding season such as December to February, March to May, June to August and September to November and their performance R² value are 0.80, 0.85, 0.91, 0.80 respectively.