Abstract
For non-directional drilling cores, selection of samples and the test methods for in situ stress measurements to evaluate the Kaiser effect (KE) were proposed, and the magnitude and direction of the principal stresses were derived from first principles. Based on this approach, the KE for 423 samples in the Burtai and Baode coal mines in the northern Ordos Basin (NOB), China, have been investigated. The results show that the maximum horizontal principal stress (σH), the minimum horizontal principal stress (σh) and the vertical stress (σv) varied with depth and location, and the values increase with increasing depth. Generally, the horizontal stresses play a leading role. For the main stress regimes in the NOB, σH > σh > σv (Burtai Mine, < 172 m; Baode Mine, < 170 m) and σH > σv > σh (Burtai Mine, 170–800 m; Baode Mine, 170–400 m), and the σv > σH > σh stress regimes are mainly distributed in moderately deep to deep coal mines. For rock masses with a depth of 350 m, k ((σH + σh)/2σv) tends to 1, indicating that a deep critical state will gradually emerge. The test results are compared with those for the overcoring (OC) method, the anelastic strain recovery (ASR) method and micro-hydraulic fracturing (HF). The relative errors for σH, σh and σv were 14.90%, 19.67%, 15.47% (Burtai Mine) and 10.74%, 22.76%, 19.97% (Baode Mine), respectively, and the errors are all within an acceptable range, thus verifying the reliability of the KE method. The dominant orientation for the σH (Burtai mine, NE-NNE; Baode Mine, NEE) is obtained via paleomagnetic technology, and the data are consistent with those (NE-NEE) of the earthquake focal mechanism solutions for the area. Based on the Byerlee–Anderson theory, a discussion is given on the levels of stress accumulation in the rock mass of the mines. For dry rocks or hydrostatic pressure rocks, the friction coefficients of the faults are low for both locations, and the values are less than the lower limit (0.6) of the strike-slip faults slip, indicating that the stress fractures at a low level around the study areas are lower than the friction limit stress. The stress accumulation levels in the Baode Mine are slightly larger than those in the Burtai Mine.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
During geological evolution, the crustal rock mass is continuously adjusting and evolving due to the effects of groundwater and precipitation on rock corrosion, pressure dissolution, high-temperature thermal stress, and long-term creep. Consequently, the combined effects result in an in situ stress distribution which is both variable and complex in time and space. Water is not the only key factor which determines the stability of the regional structure, it can also affect the stability of engineered structures such as mines and roadways (Yuan 2017; Qian 2012). With increasing demand for energy and mineral resources and against a background of increased mining activity, deep mining activity is assuming more importance. Engineering problems such as the "three highs and one disturbance" of high in situ stress, high in situ temperature, high water pressure and strong mining disturbance, have become issues in deep mining rock mechanics and engineering (Xie et al. 2015; Bi 2019). Obtaining an accurate measure of the distribution and accumulation level of in situ stress in deep mining scenarios is key to solving some of the above problems.
The studies of Lieurace (1933) on the measurement of surface stress relief paved the way to understanding stress in the surrounding rock mass of a spillway tunnel at the bottom of the Hoover Dam. Since then, in situ stress testing has developed rapidly, and has been widely used in many fields, such as energy utilization, and in diverse sectors including oil, gas, water, geothermal, resource development of coal mines, metal mines, earthquake prediction, nuclear waste disposal, and so on (Su 2002; Wu 2019; Zhang 2020; Cheng 2019). To date, numerous in situ stress testing methods have been reported, but no unified classification standard has been agreed. The test methods may be classified according to data sources and can be roughly divided into five categories: core-based methods, borehole-based methods, geological methods, underground space-based methods and geophysical methods (seismological methods) (Zang and Stephansson 2013; Wang 2014; Stephansson and Brown 2015). However, different test methods reveal different scales of stress information, and the scope of application may also be different. Therefore, several methods need to be used in tandem, preferably methods which are complementary to each other in order to determine the stress state of the rock mass, and to reduce the errors introduced by using different scales of stress information.
The development of the acoustic emission (AE) monitoring system has created conditions for the accurate identification of the Kaiser effect (KE) and its applications. Since Kaiser discovered the phenomenon in 1957 (Michihiro et al. 1985), the KE of sandstone and crystalline rock was confirmed by Goodman (1963) and Kurita and Fujii (1979). Most materials (e.g., marble, gneiss, granite, gabbro, greenstone, porphyry, chalcopyrite; Kiruna magnetite excepted) exhibit a KE (Holcomb 1983; Li and Nordlund 1993). Kanagawa et al. (1976) first attempted to apply the KE in an in situ stress test. To obtain the exact KE point, the uniaxial double cyclic loading mode was proposed by Yoshikawa and Mogi (1989), where the cyclic peak load (σP) must be higher than the estimated previous maximum stress (σHmax), and σP is 30%–80% of the uniaxial compressive strength (σc). At the same time, the deformation rate analysis (DRA) method for in situ stress testing was proposed (Kanagawa et al. 1976). The combined AE-DRA method has since been developed, whereby the vertical stress of siliceous slate in metals mines (Xie et al. 2010) and gypsum rock (Ge et al. 2015) was studied. Although the precise mechanism for the KE has not been completely resolved, the approach has been shown to meet many engineering needs as evidenced by the comparative data for the KE method and field measurements (Qin et al. 1993). At present, most research on the KE is focused on hard magmatic rock, metamorphic rock, and sedimentary rock, while systematic studies on coal measures in sedimentary rock are relatively scarce.
When the main stress state is such that the maximum horizontal principal stress (σH) > minimum horizontal principal stress (σh) > vertical stress (σv), σH > σv > σh and σv > σH > σh, this situation is conducive to reverse fault, strike-slip fault and normal fault activities (Anderson 1942; Byerlee 1978). The changes of the in situ stress values around the fault are complex. The micro hydraulic fracturing (HF) test results for nearly 1000 fault block oil wells around normal and inverse fault areas show that σh is parallel to the fault trajectory (Sun and Zhang 2004). According to the Mohr–Coulomb criterion (Hoek and Brown 2019), when τ ≥ μσn (σn refers to the mormal stress, μ refers to the internal friction coefficient), sliding instability occurs along the fault plane. After analysis of a large set of test data on rock friction and sliding, it was concluded that when the normal stress (σn) is less than 100 MPa, the internal friction coefficient (μ) values for most crustal rocks are between 0.6 and 1.0 (Byerlee 1978). The results of drilling on the continental crust in the German deep hole drilling site (KTB) show that Byerlee's law applies from the surface to a depth of 9.1 km, and the permeable fracture rocks in the range of 3–7 km are very close to the Coulomb fracture line when μ is approximately 0.6. A large number of rock friction mechanical tests in the Three Gorges Dam area are consistent with the latter data (Lavrov 2003), and, moreover, Byerlee’s law is also applicable to granite, limestone, sandstone, and other rocks in the dam area. The rock friction strength was between τ = 1.10 σn and τ = 0.65 σn with an average value of τ = 0.85 σn. According to Byerlee's law, the angle between the maximum principal stress of Anderson fault and the fault plane was 23°–30°, where, according to the Byerlee–Anderson theory, μ can reflect quantitatively the friction strength around a fault. When μ > 0.6, the mechanical strength around the fault is high; when 0.6 > μ > 0.3, it is at medium level; when μ < 0.3, the mechanical strength is weak. Also, the direction of σH and σh can be inferred roughly according to the rock vein, and presence of anticline and syncline etc.
The Shendong mining area is located in the north Ordos Basin. It is the largest coal mining area in China. With increase of mining depth, nonlinear dynamic phenomena occur successively, such as floor heave, spalling, large area roof weighting, gaseous emissions, and so on, all factors which are closely related to in situ stress. In this study, the KE for in situ stress testing was examined based on analysis of drilling cores. Specifically, the distribution law for in situ stress is analyzed, and the stress accumulation level is evaluated. From a theoretical standpoint, this research has practical significance and engineering value when applied to coal mining in the Burtai and Baode mines.
2 Geological setting of the study area
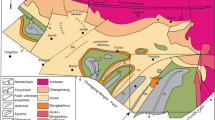
The Burtai mine is located in the south of Dongsheng County, Ordos City. Its geotectonic division belongs to the mid-eastern section of the Yimeng uplift and the northeast section of the Yishan slope in the Ordos syncline of the North China platform. From the regional structure outline map (Zhang et al. 2009; Zhao et al. 2019, 2018; Ye et al. 2006; He 2013), it can be seen that the Burtai mine is located in the northeast of the Wuhai-Ejin Horo banner-Jungar banner deep crust fracture (F11) and has a length of 450 km in an EW–NEE direction. The fractures around it are relatively well developed, such as the Ordos-Dongsheng crust fracture (F10) with a length of 200 km in a NEE direction, and the East Dongsheng basement fracture (F20) with length of 50 km in a NW direction. The complex, broken, uneven and intersecting basement faults lead to a prism and lattice pattern-type structure, which controls the development of fault structures in the upper overburden (Fig. 1b), and constitutes a migration channel for a rise in reducing fluid at depth. This structure has an important influence on the oil, gas, water, and sandstone type uranium deposits in a deep basin. In coal mining, the fracture structure is closely related to mine design, production management, disaster prevention and control, and mine damage.
Regional tectonic outline of the Burtai Mine and the Baode Mine. Notes: F1, Ural Mountains; F2, Hetao Basin; F3, Daqing Mountains; F4, Northern margin of Ordos Basin; F5, Horinger; F6, Hanggin banner-Ejin Horo banner; F7, Wuhai North; F8, Dalad banner; F9, Hanggin banner-Togtoh; F10, Ordos-Dongsheng; F11, Wuhai-Ejin Horo banner-Jungar banner; F12, Uxin banner-Shenmu-Fugu; F13, Linfen-Lishi-Pianguan; F14, Leap Hetao Basin; F15, Leap Ural Mountains; F16, Leap Ural Mountains and Daqing Mountain; F17, Leap Daqing Mountain; F18, South Linhe; F19, Boundary between northern margin of Ordos Basin fault and Lingle fault; F20, East Dongsheng; F21, Leap near NE fault
The structural form of the Burtai mine is a complex syncline, consisting of a series of asymmetric secondary gentle open short-axis folds with a dip of 42°–70° in an NNW direction. Within the envelope, the Yan'an formation strikes N10°W–N50°W. The well field structure is generally a nearly horizontal monoclinic structure (Fig. 1), with a stratum strike of N20°W, a trend of S70°W, a dip of less than 5° and inclined to the SW. During field exploration, no large fault, collapsed column structure or magmatic rock intrusion was found. Except for a reverse fault with a drop of 0.54 m, the remaining faults were normal, medium sized and small faults with a drop of less than 12 m, and the strike was NW.
In the process of coal mining, it was found that small and medium-sized folds and faults were widely developed, and these have a great impact on coal mining. It is considered that the coal-bearing strata of the Yan'an Formation are in unconformity with the lower Yanchang Formation, the upper Zhiluo Formation or the Yijinhuoluo Formation (Jia 2008; Qing 2011). In the late Middle Jurassic, under the N24°–45°E-direction compression, the Yimeng uplift took place, and shallow structural level longitudinal bending fold deformation took place in the Jurassic, which resulted in the formation of the capping-sliding type compound syncline structural style. Conjugate shear joints having a NNE direction developed on the outer side of the secondary fold envelope. In the Cretaceous, under the action of a N46°–65°E nearly horizontal extension, the shear and fault rise and fall led to the occurrence of extensional detachment deformation over a large range, thus forming the widespread development of strata slip faults in the Yan'an formation, which was accompanied by a large number of high angle normal faults and traction folds. Clearly, folds and faults directly affect the distribution of the local stress field.
Baode Mine is located in Baode County, Shanxi Province. Its geotectonic division belongs to the northeast in the Ordos coal accumulating basin, the north section of the West Shanxi fold belt, the west of the Shanxi Fault uplift, the west of the Lvliang structure, and the east of the Yellow River graben. The fractures around it are relatively well developed, such as the Linfen–Lishi–Pianguan crust fracture (F13) in the NS, the Uxin banner-Shenmu-Fugu crust fracture in the NE (F12), and F21 in the NW. The strike of faults in the region is dominated by the near NS, followed by the near WE. The regional tectonic stress field is affected mainly by the Yanshan and Himalayan movement (Yang et al. 2014). In the Yanshan period, the compressional stress was dominant, the extensional stress being secondary, and the NW–SE compressive stress and the NEE–SWW tensile stress were developed. In the Himalayan period, the compressional stress changed to NE–SW; the azimuth of σ1 is N150°E, the dip is 3°, the azimuth of σ3 is N31°E, and the dip is close to 0°, which leads to a large number of tension joints and weakened compression joints. In the Yanshan period, the axial fold of nearly EW deflected to the axial fold of NW. The superposition of two-periods of tectonic movement caused the direction of σ1 to change from NW–SE to NE–SE.
Baode Mine field is dominated by slightly inclined monoclinic strata. The coal seam is trending in a near NS direction and is inclined to the west, with a dip of 3°–10°. The fold and fault are relatively weak, but joints are very developed. The overall axial direction of the fold is nearly EW. Normal faults account for the majority of faults, and their strike is NE, NW and nearly NS. The joints are significantly affected by the lithology, those of Ordovician limestone are relatively well developed, and that of the coal seam is quite different. The shear joints account for the majority, and the X and goose-type shear joints are developed, which are filled by veins of calcite. The landform of the Baode mine is characterized by distinct undulating hills. Subject to long-term water erosion, the thickly covered surface loess features thousands of gullies. The special topography will affect the stress distribution in the mine field.
3 In situ stress testing based on evaluation of KE in borehole cores
3.1 Sample preparation and test methods
For the directional rock block with an undisturbed and shallow bedrock surface or chamber, typically, six or nine small samples (Qin et al. 1993) on the parent rock block are drilled in different directions; the samples are cylindrical or square, with a width to height ratio of 1:2. However, the core of ground drilling is different from that of the shallow layer; that is, most of the drilling holes are straight holes, and it is difficult to achieve orientation of the core. The diameter of the parent rock core is approximately 75 mm, so it is impossible to drill as required, thus it is necessary to reduce the number of small samples being drilled. It is assumed that in evaluating the KE for in situ stress testing based on the non-directional core, the vertical stress is one of the principal stresses and the other two are horizontal stresses. Therefore, it is necessary to process four small cylindrical samples, one along the core axis, and three in a direction perpendicular to the core axis with drillings at 0°, 45° and 90° or 0°, 60° and 120° anticlockwise. The diameter and height of the drilled holes are 25 mm and 50 mm, respectively which conforms to the rock mechanics testing standard. The on-site coring location and sample processing process are depicted in Fig. 2. A total of six drill holes (Burtai, five; Baode, one) were selected for acoustic emission (AE) measurement. In general, the influence of damage from core sampling on the KE can be ignored (Lavrov 2003).
Before the test, two to four sensors were used to collect data for small samples, the sensors were placed in the middle of the sample side, as far as possible away from the upper and lower end faces. To ensure the coupling effect between the sensor and the end face, Vaseline or butter was used as the coupling agent, and the sensors were fixed with adhesive tape or plasticine. In accord with previous work (Qin et al. 1993), the AE monitoring system was configured with a preamplifier gain of 40 dB, a valve value of 45 dB and a sampling rate of 1 MHz.
In uniaxial loading, when the load rate is 0.05–0.25 kN/s or the displacement rate is 0.05–0.60 mm/min, the AE effect is enhanced. An increase in the sample moisture content will lead to a decrease in the AE count and energy, so a natural or dried sample should be used (Yang et al. 2018). When the triaxial loading test is adopted, the stratum stress, where the sample is located, can be estimated in advance to set the confining pressure and load the axial load at a constant rate. When the rock is buried to a shallow depth and the confining pressure is low, the KE can be used for in situ stress testing directly by uniaxial loading.
For identification of the KE inflexion points, most researchers select an AE count or the cumulative counts as the measurement parameters. In our case, the comprehensive identification method, which is mainly the AE count or the cumulative counts, supplemented by the AE energy rate or the count rate increment (RI) is preferred, given that it is easier to determine the KE point. To avoid the interference on the AE by friction at the initial loading stage, the KE points are usually identified using uniaxial double-cycle loading. In general, given that more AE is produced by crack closure at the beginning of loading, the surge point of the first AE cycle should not be selected, and that of the second loading cycle AE should be used as a means to determine the KE point (Fig. 3). Moreover, the first cyclic peak load σP is less than σHmax, σP being approximately 30% of σc.
The specific identification method used in this study is as follows: first, based on the AE count or cumulative counts versus time, the counting group is located, then the inflexion (or surge) point is identified according to the AE energy rate or the IR versus time; then with mutual checking and verification, the KE point is determined. If there are multiple KE points under cyclic loading or if they are not sufficiently clear, the AE-DRA method may be tried. The loading mode is multiple cyclic loading controlled by the load and the displacement. The first cycle σP is less than σHmax, and the next cycle σP is greater than σHmax and less than σe. It is suggested that a reasonable σP in the first cycle is less than 27% of σc for siltstone, fine sandstone, and coarse sandstone, 40% of σc for sandy mudstone, 17% of σc for medium sandstone, 13% of σc for mudstone and limestone, and it does not exceed 63%–70% for σc in the nest cycles (Yang et al. 2018). If further KE point recognition is still not ideal, the method of calculating the fractal dimension using the G-P algorithm can be attempted. In this study, all three methods were used.
3.2 Processing of test data
There are different opinions on how to determine the principal stress direction of non-directional drilling cores (Li and Dong 2009; Fa et al. 2017). This section seeks to clarify the magnitude and direction of the principal stress and establish the necessary equations for calculation. For the plane stress state, the stress components σx, σy and τxy, τxy = − τyx, on the element body are known, and the normal stress (σα) and the shear stress (τα) on any inclined section (α slope) can be obtained by:
If the corresponding Mohr stress circle is established, then σα and τα on slope α can also be obtained. Then, the two principal stress values can be determined as follows:
If the angle between the x-axis and the direction of σH on the rock unit is β, and the clockwise direction is negative, then:
To determine the angle between two principal stresses and the x-axis, first, calculate β and β ± 90° from Eq. (3), and then compare the magnitudes of σx and σy. If σx > σy, the angle between the maximum principal stress (σ1) and the x-axis is β; if σx < σy, the angle between σ1 and the x-axis is β ± 90°; if σx = σy, then β = − 45°. That is to say, σ1 is always inclined to the larger of σx and σy, while σ2 is inclined to the smaller of the two values. At the same time, it is known that the angle between the x-axis and the direction of σH is within ± 90. Thus, β calculated from Eq. (3) is the angle between the x-axis and the direction of σH (Li and Dong 2009; Fa et al. 2017); in fact, there will always be a certain deviation.
From Eqs. (1) to (3), the magnitude and relative directions of the two horizontal principal stresses can be calculated using the least-squares method. If it is not possible to obtain the stress of the axial sample at the KE point along the core, σv can be calculated by the logging density using the following equation:
With increase of depth, the mechanical properties of the rock differ from those nearer to the surface, and the stress is more affected by the pore fluid, which can be characterized in terms of the pore pressure. The KE can only measure the relative constant deformation stress of the rock memory, that is, the effective stress. The real in situ stress value should be the effective stress plus the pore pressure, so the expressions for σH, σh and σv considering the pore pressure are as follows:
3.3 Core orientation using paleomagnetic technology
For non-directional core drilling, the angle between σH and the 0°-mark line can be obtained from the above, while the azimuth of σH relative to the geographic north requires paleomagnetic orientation technology. The sample is processed into a cylinder with a diameter and height of 25 mm and 20 mm, respectively, along the core axis, each testing point process requiring more than five to seven samples. A straight line is drawn along the side which is parallel to the generatrix (0°-mark line of KE sample) with the top of the core facing upwards, and the relative coordinate system is established by rotation around the central axis of the sample. That is, a right-hand coordinate system (Fig. 4) is established, where the X-axis is the extension direction of the sample cross-section dot O toward the 0°-mark line; the Y-axis is a 90° clockwise rotation of the X-axis; the Z-axis is the vertical downward direction of the sample axis; OH is the direction of magnetic north, and the angle between it and the X-axis is the magnetic declination (D), which determines the azimuth of the geographic north; D is positive in a clockwise direction and negative counterclockwise; I between the OJ vector direction and the horizontal plane is the magnetic dip, and I is positive in the northern hemisphere and negative in the southern hemisphere.
In the paleomagnetic test, a 2G superconducting magnetometer (USA) and a MMDT80 thermal demagnetization meter (UK) are used in the thermal demagnetization method. First, the natural remanence (NRM) of the samples are measured, and then the samples are demagnetized and cleaned every 50 °C. The magnetic declination Da, the magnetic inclination Ia and the magnetization of the viscous remanence (VRM) of the samples are measured. Then, D and I for the VRM in the relative coordinate system are obtained by using the principal vector analysis method. Second, the average Da and the average Ia of the VRM at each testing point are counted, and the magnetic declination (D0) of the sampling location relative to the geographic north are noted (Burtai Mine, − 4.65°; Baode Mine, − 4.18°), thus, the azimuth of the sample marker line relative to the geographical north is given by D0—Da. Finally, according to the angle β (β0 or β0 + 90°) between the 0°-mark line and the σH, the azimuth (αN) of σH relative to the geographic north is calculated as:
4 Measurement and analysis of in situ stress
4.1 Distribution characteristics of in situ stress for the Burtai Mine
Five boreholes at the Burtai Mine were selected for in situ stress testing, that is, BK212, BK209, BK213, BK207 and BK220. The depths ranged from 490 to 610 m, the average depth being 546 m. A group of cores were collected at intervals of approximately 100 m from each borehole, and the samples were screened and processed as outlined in Sect. 3.1 before KE testing was performed. A total of 343 cores were processed and 338 KE stress values were obtained. It was noted that 263 cores exhibited a clear KE, accounting for 77.8% of the total, 60 cores were less clear, accounting for 17.8% of the total, and 15 were insignificant, representing 4.4% of the total. Overall, a total of 89 groups of in situ stress data were obtained for the five boreholes, among which for 35 groups it was not possible to obtain a small core along the core axis, thus σv could not be tested. Therefore, linear fitting was carried out based on the measured σv values for 54 groups and then σv at the depths for the various measuring points were calculated by the fitting equation.
4.1.1 Variation of in situ stress with depth for the Burtai mine
The distributions of σH, σh, σv, k, and the azimuth of σH at the measuring points are presented in Fig. 5a–f. The characteristics of the present stress fields for five boreholes and nearby areas in the Burtai mine are as follows:
-
(1)
In the depth region of 610 m, σH is 1.52–21.04 MPa, σh is 1.07–15.76 MPa, and σv is 2.01–20.55 MPa, and, which, for comparison purposes, corresponds to the general stress levels for in situ stress testing for mainland China (Kang et al. 2010). The three principal stress values exhibit specific values which increase with depth (Fig. 5a–f). The fitting equations are as follows:
$$\left. \begin{aligned} &\sigma_{{\text{H}}} = 2.0386 + 0.0241 H \hfill \\ &\sigma_{{\text{h}}} = 1.2091 + 0.0172 H \hfill \\ &\sigma_{{\text{v}}} = - 0.5257 + {0}{{.0273}} H \hfill \\ \end{aligned} \right\}$$(7)Among them, the data of BK209 is too erratic, the fitting coefficient is low, and the values for the other boreholes are greater than 0.7. The large variability of data is caused mainly by the heterogeneity of the rocks as a result of the different lithologies, structure, bedding, and so on. It can be seen from Eq. (7) that σv increases most rapidly with increase of depth. In shallow mines, the horizontal stress is large. In deep mines, σv tends to be close to σH.
-
(2)
Based on past experience and judgment (Wang 2014), there are 39 cores with σh < 10 MPa, accounting for 44% of the total; 42 cores with σh < 18 MPa, accounting for 47% of the total; and 8 cores with σH > 18 MPa, accounting for 9% (Table 1). Among them, there are 34 groups above 350 m, 29 groups with σh < 10 MPa, accounting for 85% of the total; 55 groups below 350 m, 11 groups with σh < 10 MPa, accounting for 20% of the total, and 66% with 10 < σh < 18 MPa. Therefore, the in situ stress field in the Burtai mine is low at depths above 350 m and at a medium level below 350 m.
-
(3)
The main stress regimes are as follows: σH > σh > σv (< 172 m, I) and σH > σv > σh (170–800 m, II). There are 15 cores in category I, accounting for 17% of the total; 46 cores in category II, accounting for 52% of the total. The former reflect a reverse fault stress mechanism, and the latter reflect a strike-slip fault stress mechanism. The σv > σH > σh stress regime is distributed mainly below 800 m, according to Eq. (7), and it is deeper than that (600 m) of the same stress regime in underground coal mines in China (Kang et al. 2010); these results are consistent with the southern Qinshui Basin (825 m) and western Guizhou province (750 m) (Chen et al. 2017). The stress state is in good agreement with a large number of extensional structures such as slip faults which have developed in the Yan'an formation in the Burtai mine field.
-
(4)
The ratio of σH to σv is 0.19–2.33, with an average value of 1.20 and a mean square deviation of 0.37; the ratio of σh to σv is 0.14–1.97 with an average value of 0.83 and a mean square deviation of 0.31; k is 0.16–2.06 with an average value of 1.02 and a mean square deviation of 0.32. Among 89 groups of principal stress data, there are 61 with σH > σv, accounting for 68.5% of the total. Generally, horizontal stress plays a leading role. The results are in accord with the transverse isotropic crustal stress model, which can be expressed as follows:
$$\sigma_{{\text{H}}} = \frac{1 - \nu }{{\nu_{{{XZ}}} }} \times \sigma_{{\text{v}}}$$(8)This model can better reflect the in situ stress characteristics of sedimentary rock strata, and when v = 0.25, vXZ = 0.5 and σH = 1.5 σv, the smaller vXZ is, the larger k is.
-
(5)
The variation of k with depth is shown in Eq. (9). Compared with the k envelope (Eq. (10)), obtained by Brown and Hoek for the world (Jia 2008), in general, the progressive values are different, but they are basically the same for the progressive values of the inner envelope. It can be seen from Fig. 6a that there are 41 data with k > 1, accounting for 46.1% of the total. Above 350 m, the range for k is wider. With increase of depth, the range of k becomes narrower. At 350 m, k = 0.98, a value that is close to 1. The rock mass is in a deep critical state.
$$\left. \begin{aligned} &k = \frac{126}{H} + 0.625 \hfill \\ &\frac{35}{H} + 0.285 < k < \frac{350}{H} + 0.6 \hfill \\ \end{aligned} \right\}$$(9)$$\left. \begin{aligned} &k = \frac{800}{H} + 0.4 \hfill \\ &\frac{100}{H} + 0.3 < k < \frac{1500}{H} + 0.5 \hfill \\ \end{aligned} \right\}$$(10) -
(6)
The ratio of σH to σh is 1.07–2.96 with an average value of 1.53 and a mean square deviation of 0.44. The difference between σH and σh is generally large. Meanwhile, the maximum shear stress ((σ1 − σ3) / 2) is 0.31–6.89 MPa with an average value of 2.05 MPa and a mean square deviation of 1.18 MPa. This leads to a mixed extension of rock-shear type, which provides conditions for the development of joints and faults, and this is also one of the reasons for the development of small and medium-sized faults in the Yan'an Formation. According to statistical data of Jia (2008), the Yan'an formation in the Burtai mine developed small and medium-sized high angle normal faults, which consist of small graben, horst, and stepped faults. These faults provide direct evidence for large shear stress in the rock mass.
-
(7)
The in situ stresses at the same depth are different for different lithologies; for example, the sand mudstone σH of groups 11–13 in BK209 is 2.18 times that of the medium sandstone groups 21 and 22 in BK212; the sand mudstone σH of groups 61–63 in BK209 is 1.42 times that of siltstone groups 41–43 in BK209; the sand mudstone σH of groups 51–53 in BK220 is 1.36 times that of fine sandstone groups 41–43 in BK207, and so on. The most important reason for these observations is that the σc of sandy mudstone is generally high, 30–60 MPa, however, some of the stress values are over 80 MPa, and the bearing stress is large; in contrast, the σc of sandstone is typically low, mostly being less than 30 MPa, with high porosity and weak cementation, so the bearing stress is small.
4.1.2 Direction of in situ stress in the Burtai mine
Sixteen parent rock cores of depth 100–603 m in the Burtai mine were selected for paleomagnetic orientation. The strata were, respectively, the Yijinhuoluo formation, the Zhiluo formation and the Yan'an formation. The lithology is mainly siltstone, fine sandstone, medium sandstone, coarse sandstone, and so on. At one of the measuring points, we failed to obtain the principal stress direction based on the KE, so it was not possible to determine the azimuth relative to the North coordinate for that location. The stereoscopic projections and the orthogonal projections of the magnetization directions for some samples are presented in Fig. 7. The test results for the samples are given in Table 2, and Fig. 8a shows the σH azimuth half-rose for the samples.
A change of the remanent magnetization direction after demagnetization, and the intensity of magnetization and the direction of samples can be seen from inspection of. The trend of the change in the magnetization vector for the same group of samples is basically the same, and the differences between different lithologic samples are large. In the case of D131 and D132 in BK207, which consist of coarse sandstones, the thermal demagnetization ranges from 50° to 500°. After each step, the magnetic declination and dip of the VRM are both relatively stable. However, the magnetization vectors for D511 and D512 of medium sandstone turn, and the intensity is weakened after demagnetization at 500°, so this location should be rejected. The principles to be followed in the selection of the thermal demagnetization points include the following: α95 confidence ErAng ± error < 16; more than three selected points; and temperatures above 100°–200°.
Among the 63 measuring points indicated in Fig. 8a, there is 22 σH orientations between N30°E and N75°E, accounting for 34.92% of the total, and 14 between N30°E and N75°E, accounting for 22.22% of the total. Therefore, the dominant orientation of σH in the Burtai mine is NE-NNE, followed by NW.
Studies based on a focal mechanism solution, HF and hole wall collapse in the Ordos area show that the orientation of σH is NE-NEE. The orientation obtained by the paleomagnetic method combined with KE is consistent with the above results, although some measuring points are quite different. This is mainly related to the local geological structure, the rock mass structure and error in the testing process. Based on a large number of observations on the geological structure of the mines and geological surveys of the surface (Jia 2008), it is believed that the fault strike of the mine field is mainly NNE, followed by NW, and the basic pattern of the extensional structure is the capping-sliding type. Thus, the orientation of σH is parallel to the fault trend. When the angle between the orientation of σH and the axial direction of the roadway is 0°–30°, this is conducive to mine stability.
4.2 Distribution characteristics of in situ stress tests for the Baode mine
A borehole beside the Baode power plant was selected for the in situ stress tests. The depth of the borehole was 416 m. A group of cores were collected every 50 m; 85 cores were processed and 85 KE stress values were obtained. There were 44 cores with a clear KE stress point, accounting for 51.8% of the total, there were 19 cores with less clear points, accounting for 22.4% of the total, and there were 22 cores with insignificant KE points, reflecting 25.8% of the total. Overall, a total of 24 groups of in situ stress data were obtained, including 13 groups with measured σv and 11 groups with σv calculated by the fitting equation.
4.2.1 Variation of in situ stress with depth the Baode mine
The distributions of σH, σh, σv, k, and the azimuth of σH at the measuring points are illustrated in Fig. 5. The characteristics of the present stress field due to the power plant and nearby areas in the Baode mine are as follows:
-
(1)
In the range up to a depth of 420 m, σH is 3.99–15.15 MPa, σh is 0.71–9.63 MPa, and σv is 1.26–10.01 MPa. The three main stress values are all erratic but increase with depth (Fig. 5g). The fitting equations are as follows:
$$\left. \begin{aligned} &\sigma_{{\text{H}}} = {3}{{.5656 + 0}}{.0161} H \hfill \\ &\sigma_{{\text{h}}} = {0}{{.7081 + 0}}{.0189} H \hfill \\ &\sigma_{{\text{v}}} ={-0}{{.5935 + 0}}{.0267} H \hfill \\ \end{aligned} \right\}$$(11) -
(2)
There are 23 cores with σh < 10 MPa, accounting for 96% of the total, and only one with 10 < σh < 18 MPa (Table 1). Therefore, it can be inferred that the in situ stress in the Baode mine is in the low in situ stress field category.
-
(3)
The main stress regimes are as follows: σH > σh > σv (< 170 m, I) and σH > σv > σh (170–400 m, II). There are 10 stress regimes belonging to either categories I or II, and which account for 42% of the total, respectively. The σv > σH > σh stress regime is distributed mainly at a depth below 400 m, according to Eq. (11), and it is shallower than that (600–750 m) of the same stress regime in underground coal mines in China (Kang et al. 2010; Chen et al. 2017).
-
(4)
The ratio of σH to σv is 0.72–3.61 with an average value of 1.76 and a mean square deviation of 0.81; the ratio of σh to σv is 0.31–1.68 with an average value of 0.96 and a mean square deviation of 0.34; k is 0.66–2.44 with an average value of 1.36 and a mean square deviation of 0.50. Among the 24 groups of the principal stress data, there are 20 groups in the category σH > σv, accounting for 83.3% of the total.
-
(5)
The variation of k with depth is presented in Eq. (12). The variation is similar to the envelope line of k obtained by Brown and Hoek (world basis); however, there are some differences in the progressive value, which is close to those of 0.3 and 0.5 for the inner and outer envelope lines, respectively. With reference to Fig. 6b, there are 18 data with k > 1, accounting for 75% of the total. Above 350 m, the range for k is wider. With increase in depth, the range for k becomes narrower. At 350 m, k = 1.02, which is close to 1. Much like the Burtai mine, the rock mass is in a deep critical state.
$$\left. \begin{aligned} &k = \frac{72}{H} + 0.817 \hfill \\ &\frac{70}{H} + 0.32 < k < \frac{210}{H} + 0.46 \hfill \\ \end{aligned} \right\}$$(12) -
(6)
The ratio of σH to σh is 1.07–7.38 with an average value of 2.04 and a mean square deviation of 1.42. The difference between σH and σh is generally large. Meanwhile, (σ1-σ3) / 2 is 0.24–4.44 MPa with an average value of 1.46 MPa and a mean square deviation of 0.86 MPa, which leads to large shear stress in the rock mass, providing favorable conditions for the development of joints and faults in the mine.
4.2.2 Direction of in situ stress for the Baode mine
Eight parent rock cores from 99.1 to 340.6 m at the Baode power plant were selected for paleomagnetic orientation. The relevant strata are the Shangshihezi formation, the Shanxi formation, the Taiyuan formation and the Fengfeng formation. The lithology is mainly fine sandstone, medium sandstone, sandy mudstone, mudstone, and limestone. The test results for the samples are presented in Table 3 and the σH azimuth half-rose of the samples is given in Fig. 8b.
Among the 19 measuring points in Fig. 8b, there are 14 σH orientations between NS and N45°E, accounting for 73.7% of the total. Therefore, the dominant orientation of σH in the Baode mine is NEE, which is generally consistent with the NNE-NE direction obtained from solution of the regional focal mechanism.
5 Discussion
5.1 Comparison of results for in situ stress testing
5.1.1 Comparison of results for in situ stress testing in the Burtai Mine
In situ stress testing of three boreholes (Fig. 2, light green) by OC in the first and second panels of the Burtai Mine was performed by staff of Anhui University of Science and Technology. The depth for testing was 348 m. The KE stresses for three measuring points close to this depth were selected for analysis, and although the locations were different, the terrain was flat at these locations.
According to the data of Table 3, the stress values for KE for 7 measuring points in the Burtai Mine are greater than those for OC representing 77.8% of the total. The relative errors for σH were 6.44%–25.37%, those for σh were 10.94%–34.49%, those for σv were 12.66%–19.35%, and those for the three principal stresses were 14.90%, 19.67% and 15.47%, respectively. Therefore, the errors for the test results between KE and OC were small. Considering the different test locations, the errors were considered to be within an acceptable range for field measurements, and which clearly can satisfy the requirements for engineering stability and geological evaluation, hence verifying the reliability of the KE for in situ stress assessment.
In situ stress testing by HF in the Yitai mining area and the Hongqinghe area of the Dongsheng coal field was performed (Liu 2011), and KE stresses for ten measuring points close to this depth were selected. Stress levels at three measuring points were calculated by Eq. (7), and the results are shown in Table 3. The eighteen stress levels for KE are greater than those for HF, and account for 54.5% of the total. The relative errors for σH were 9.81%–45.24%, those for σh were 0%–51.73%, those for σv were 0.65%–81.80%, and those for the three principal stresses were 21.40%, 17.64% and 23.79%, respectively. Due to the influence of depth and the geological structure, the relative errors were relatively high above 100 m, and the test result was also erratic. However, considering the change of location of the measuring points and the occurrence of the coal seam, the errors of the test results were considered to be within an acceptable range. Therefore, the test results for the two independent methods are judged to be reasonably consistent.
Three major tectonic movements, that is, Indochina, Yanshan and Xishan occurred in the Mesozoic and Cenozoic strata in the Ordos Basin. At the end of the Jurassic, the basin was subject to horizontal tectonic compression in an NWW-SEE direction and a second tectonic thermal event. These events resulted in the formation of σH in an NWW-SEE and EW and NW–SE and conjugate shear fractures in the Jurassic Yan'an Formation (Gao et al. 2020; Ju et al. 2019). From the late Cretaceous to Paleogene, the basin was subjected to NNE-SSW horizontal tectonic compression and a third tectonic thermal event occurred, resulting in a strata denudation thickness of 600–3200 m (Ma et al. 2020; Meng 2016; Ng et al. 2017). Under tectonic compression and uplift denudation, σH in NNE-SSW and NS and NE-SW conjugate shear fractures were formed in the Late Jurassic, the Cretaceous and the Neogene. Under the thrust or nappe action of peripheral faults into the basin, the basin was uplifted as a whole, and low angle or interlayer sliding occurred, forming a slip thrust fault, which released the energy accumulated by orogeny movements around the basin, and the strata were clearly not deformed (Li et al. 2014; Wu et al. 2017; Xiao et al. 2020). However, most of the basement faults have been activated, and the deep fractures have obvious control on the shallow ones.
During field exploration, 11 large and medium-sized faults have developed in the northern Shenmu mine area of the Shenfu coalfield, all of which are tensional high angle normal faults with a NW strike and a dip of 55°–80°. The drop is 10–80 m, and the extension is less than 16 km. It can be inferred that the σ1 direction is roughly N40°E–N80°E (Ju et al. 2015, 2020; Li et al. 2019). Based on the results for the focal mechanism solution, HF, borehole collapse, OC, fault sliding vector and earthquake surface rupture (Ju et al. 2017; Wang et al. 2018; Deng and Sheng 2015; Sheng et al. 2015), it is considered that the present σ1 direction in the north Ordos area is NE-NEE. In the Yitai mining area, there are six points of ten measuring points σ1 in a N28.3°E–N54.1°E direction, and four in a N18.9°W–N63.6°W direction, most of which are NE; the orientations of the three fracture surfaces of the hydraulic fracture holes are N65.0°E, N61.0°E, and N54.0°E in the Hongqinghe mining area, and generally being in a NE-NEE direction.
In situ stress testing of 42 coal seams in the Burtai mine was performed by staff at Taiyuan University of Technology. σ1 is approximately N30°E, which is vertical to the roadway axis of the 42103-working face, and there is large tectonic stress. The results for this study show that the dominant orientation of σH in the Burtai mine is NE-NNE, followed by NW, and that of σH in the Baode mine is NEE (Sect. 5.1.2). These orientations are related to the Triassic and Jurassic tectonic movements in the Ordos Basin. σH in an NWW-SEE direction is formed by the Yanshan movement, and σH in an NNE-SSW direction is the product of Himalayan movement. The two periods of tectonic movement since the Mesozoic have resulted in a deflection of the σH orientation in the Shendong mining area. At the same time, the dominant orientation of σH in the Burtai mine is also roughly consistent with the main strike fault (near NEE) for the surface Huhewusu ditch in the south. Therefore, the present σH orientation in the Shendong mining area obtained by KE combined with the paleomagnetic orientation data is consistent with the above results; however, some measuring points are quite different, and this is mainly related to the local geological structure, the rock mass structure, the topography and landforms, and the errors in the testing process.
5.1.2 Comparison of the results for in situ stress testing for the Baode mine
In situ stress testing of three boreholes (Fig. 2, light green) by OC in the third panel of the Baode mine was carried out by staff of the Anhui University of Science and Technology. The depth was 485 m. KE stresses for three measuring points close to this depth were selected and Eq. (11) was used to calculate the stresses at the number 2 # and 6 # measuring points. According to Table 4, the seven stress values for KE are greater than those for OC, accounting for 77.8% of the total. The relative errors for σH were 8.46%–12.41%, those for σh were 27.18%–35.65%, those for σv were 34.82%–45.59%, and those for the principal stress were 9.91%, 30.82% and 39.84%, respectively, among which the errors between the fitting equation and OC were the largest.
The stress levels measured by the KE were compared with those by ASR (Xu 2018) with cores at the same depth in the same borehole being selected. The samples for groups 51–53 and 62–64 in Table 4 were selected for KE, and those of BD-2 (275.5 m) and BD-6 (346.0 m) were selected for ASR, among which the average values for σH, σh and σv of groups 51–53 were 8.28, 6.16 and 7.31 MPa, respectively, and those for σH, σh and σv of BD-2 were 6.8, 4.7 and 7.3 MPa, with relative errors of 17.90%, 23.71% and 0.08%; the average values for σH, σh and σv of groups 62–64 were 8.34, 6.91 and 9.41 MPa, respectively, and those for σH, σh and σv of BD-6 were 7.9, 7.3 and 9.4 MPa with relative errors of 5.22%, 5.68% and 0.13%. The average relative errors for the principal stresses were 11.56%, 14.69%, and 0.11%, respectively.
It can be seen that the errors for the test results of the KE method and the ASR method are small, and those for KE and OC are larger. Considering the different test locations, and that the two groups of data were calculated by Eq. (11), if the two groups are removed, the errors are considered to be within an acceptable range, which can meet the requirements for stability analysis and engineering geology evaluation. Thus, the reliability of KE has been verified.
5.2 Analysis of the stress accumulation level in the rock
Based on the Byerlee Anderson theory and in situ stress testing, the stress state for boreholes in the two mines may be represented, as illustrated in Fig. 9. None of the six boreholes has a measurement point with μ > 0.6, and σH is all on the left of the lower limit of the Byerlee range, and μ < 0.3. Below 350 m, a small amount of data in the Burtai mine is between 0.6 > μ > 0.3, which indicates that with an increase of depth, the stress accumulation level is increasing. Therefore, it can be concluded that the friction strength of the faults around the boreholes in the two mines is weak, the stress level is low, and the faults can be considered to be in a relatively calm period. Also, the faults and the surrounding areas are in a relatively stable state.
Sliding failure caused by an increase of shear stress is a common fracture phenomenon in the Earth's crust. The main controlling factors are the maximum shear stress and the normal stress of the vertical shear plane. Therefore, the μmd and μmh calculated based on in situ stress are also indicators which may be used to characterize the regional stress accumulation level (Jamison and Cook 1980). The relationship between μm and μ is as follows:
where the expressions for indexes μmd and μmh are as follows:
and where σ1, σ3 and P0 represent the maximum principal stress, the minimum principal stress, and the pore pressure, respectively. In the shallow low permeability rocks of the crust, P0 is roughly equal to the static pressure of the water column (Townend and Zoback 2000). To some extent, μmd and μmh only represent the stress accumulation level, which is independent of the stress direction. The larger the value, the greater is the shear stress around the fault, and the higher is the stress accumulation level, hence the greater the possibility of fault activity, and vice versa (Jamison and Cook 1980). The shallow μm is mostly approx. 0.7, and the deep μm is approx. 0.5 (Tuncay and Ulusay 2008), thus when μm is 0.5–0.7, the crustal stress accumulation is in its friction limit state; when μm is close to 0.5–0.7, the stress accumulation level is higher; when μm is less than 0.3, then the level is lower.
The distribution of μmd and μmh with depth in the two mines is illustrated in Fig. 10. In dry rock, the μmd for the Burtai mine is 0.04–0.76 with an average value of 0.24 and a mean square deviation of 0.14, among which, μmd > 0.1, accounts for 87.6% of the total; also, there are only two points with μmd > 0.6, and these are 0.76 and 0.75; there are 66 points with μmd < 0.3, accounting for 74.2% of the total and 85 points with μmd < 0.5, accounting for 95.5% of the total. The μmd values for the Baode mine range from 0.03–0.76 with an average value of 0.32 and a mean square deviation of 0.19, among which, μmd > 0.1 accounts for 87.5% of the total, and there are only three points with μmd > 0.6, these being 0.60, 0.76 and 0.61, respectively; there are 13 points with μmd < 0.3, accounting for 54.2% of the total; there are 19 points with μmd < 0.5, which accounts for 79.2% of the total. The average values for μmd are 0.33 (Burtai mine) and 0.42 (Baode mine) above 170 m, and the average values are both 0.23 below 170 m. In hydrostatic pressure rock, after removal of four outliers for the Burtai mine, μmh are 0.05–0.89, with an average value of 0.32 and a mean square deviation of 0.19, among which, μmh > 0.1, which accounts for 91.8% of the total; there are only 8 points with μmh > 0.6; there are 49 points with μmh < 0.3, accounting for 57.6% of the total; there are 71 points with μmh < 0.5, accounting for 83.5% of the total. For the Baode mine, after removal of two outliers, the μmh values range from 0.04 to 0.74 with an average value of 0.31 and a mean square deviation of 0.19, among which, μmh > 0.1, account for 86.4% of the total, and only one with μmh > 0.1, it being 0.74; there are 13 points with μmh < 0.3, accounting for 59.1% of the total; there are 17 points with μmh < 0.5, accounting for 77.3% of the total. The average values for μmh are 0.47 (Burtai mine) and 0.50 (Baode mine) above 170 m, and 0.35 (Burtai mine) and 0.32 (Baode mine) below 170 m.
Whether for dry rocks or hydrostatic pressure rocks, the friction coefficients for faults in the two mines are low, the average values for μmd being 0.23–0.33 and 0.23–0.44, and for μmh being 0.35–0.47 and 0.32–0.50, respectively, values which are less than the lower limit (0.6) of strike-slip fault systems. The data show that the fracture stress state around the study area is lower than the friction limit state, which is at a low level on the whole; moreover, the risk of seismic activity is low. Historically, the number of earthquakes in Ordos City and its vicinity has been low, and of relatively low intensity, however, the regional in-site stress is in the accumulation phase, which, therefore, does not exclude the possibility of micro earthquakes occurring. Based on critical comparison of the mines, the stress accumulation in the Baode mine is greater than that of the Burtai mine.
6 Conclusions
Based on elastic mechanics and paleomagnetic reorientation technology, an in situ stress test method based on the KE of borehole cores is established. The method has been used to test for and analyze the distribution characteristics of present stresses in and around boreholes of the Burtai and Baode mines. The test results have been compared with the results from the OC, ASR and HF methods. Based on the Byerlee-Anderson theory, the stress accumulation level of the rock masses are discussed. The main conclusions are as follows:
-
(1)
For non-directional drilling cores, and based on the elastic mechanics, the magnitude and direction of the principal stress measured by KE have been derived. The angle between the direction of σH and the marker line is β0 or β0+90°. The azimuth of σH relative to the geographic north was calculated as D0-Da-β.
-
(2)
The σH, σh and σv in the two mines increased with increasing depth. The ratios of σH, σh to σv are 1.20, 0.83 (Burtai Mine), and 1.76 and 0.96 (Baode Mine), respectively. The k values are 1.02 (Burtai Mine) and 1.36 (Baode Mine). In general, the horizontal stresses play a leading role. The ratio of σH to σh is 1.53 (Burtai Mine) and 2.04 (Baode Mine), and (σ1- σ3)/2 is 2.05 MPa (Burtai Mine) and 1.46 MPa (Baode Mine). The main stress regimes in the NOB are as follows: σH > σh > σv (Burtai Mine, < 172 m; Baode Mine, < 170 m) and σH > σv > σh (Burtai Mine, 170–800 m; Baode Mine, 170–400 m), and the σv > σH > σh stress regime is distributed mainly in moderately deep to deep coal mines. For rock masses with a depth of 350 m, k ((σH + σh)/2σv) tends to 1, indicating that a deep critical state will gradually emerge.
-
(3)
The test results were compared with the results for the OC, ASR and HF methods. The relative errors for σH, σh and σv were 14.90%, 19.67%, 15.47% (Burtai Mine) and 10.74%, 22.76%, 19.97% (Baode Mine), and the errors were within an acceptable range, which meet the requirements for geological evaluation and stability analysis of the engineering rock mass, thus verifying the reliability of the KE method.
-
(4)
The dominant orientation for σH in the Burtai mine is NE-NNE, followed by NW, and that for σH for the Baode mine is NEE. The orientations are related to the Triassic and Jurassic tectonic movement in the Ordos Basin. σH in NWW-SEE was formed by the Yanshan movement, and σH in NNE-SSW was the product of the Himalayan movement, which is consistent with that (NE-NEE) of earthquake focal mechanisms in this area.
-
(5)
Under the influence of dry rocks or hydrostatic pressure rocks, the friction coefficient of faults were both low, the average values of μmd being 0.23–0.33 (Burtai Mine), 0.23–0.44 (Baode Mine), and μmh being 0.35–0.47 (Burtai Mine) and 0.32–0.50 (Baode Mine), values which are less than the lower limit of strike-slip faults slip, indicating that the fracture stress with a low level around the study area is lower than the friction limit stress. The stress accumulation level for the Baode mine is slightly larger than that in the Burtai mine.
References
Anderson EM (1942) The dynamics of faulting and dyke formation, with applications to Britain. Nature 62(4):651–652. https://doi.org/10.1086/626182
Bi YL, Xiao L, Liu RR (2019) Response of arbuscular mycorrhizal fungi and phosphorus solubilizing bacteria to remediation abandoned solid waste of coal mine. Int J Coal Sci Technol 6(4):603–610
Brown ET, Hoek E (1978) Trends in relationships between measured in-situ stresses and depth. Int J Rock Mech Min Sci Geo 15(4):211–215. https://doi.org/10.1016/0148-9062(78)91227-5
Byerlee JD (1978) Friction of rocks. Pure Appl Geophys 116(4/5):615–626. https://doi.org/10.1007/bf00876528
Chen SD, Tang DZ, Tao S, Xu H, Li S, Zhao JL, Ren PF, Fu HJ (2017) In-situ stress measurements and stress distribution characteristics of coal reservoirs in major coalfields in China: Implication for coalbed methane (CBM) development. Int J Coal Geol 182:66–84. https://doi.org/10.1016/j.coal.2017.09.009
Cheng LL, Sun HY, Zhang Y, Zhen SF (2019) Spatial structure optimization of mountainous abandoned mine land reuse based on system dynamics model and CLUE-S model. Int J Coal Sci Technol 6(1):113–126
Deng SQ, Sheng SZ (2015) The crustal stress field around the Ordos block. North Chin Earthq Sci 33(2):55–62
Fa L, Xie BZ, Xi BJ, Shen N, Zhang SL (2017) A method for predicting principal stresses of underground rock. J Xi’an Univ Posts Telecomm 22(3):87–92. https://doi.org/10.13682/j.issn.2095-6533.2017.03.016
Gao Y, Jiang ZX, James LB, Zhang JG (2020) Soft-sediment deformation structures as indicators of tectono-volcanic activity during evolution of a lacustrine basin: a case study from the Upper Triassic Ordos Basin. China Mar Petrol Geol 115(5):104250. https://doi.org/10.1016/j.marpetgeo.2020.104250
Ge WF, Zhang F, Chen M, Jin Y, Lu YH, Hou B (2015) Research on geostress measurement using DRA-Kaiser method in salt-gypsum formation. Chin J Rock Mech Eng 34(1):3138–3142. https://doi.org/10.13722/j.cnki.jrme.2014.0132
Goodman RE (1963) Subaudible noise during compression of rocks. Geol Soc Am Bull 74(4):487–490. https://doi.org/10.1130/0016-7606(1963)74[487:sndcor]2.0.co;2
He ZJ (2013) The application of gravity and magnetic data processing and interpretation in regional tectonic analysis of Ordos Basin. Chin Univ Geosci (Beijing), Beijing
Hoek E, Brown ET (2019) The Hoek-Brown failure criterion and GSI–2018 edition. J Rock Mech Geotech Eng 11:445–463. https://doi.org/10.1016/j.jrmge.2018.08.001
Holcomb DJ (1983) Using acoustic emissions to deter coal in-situ stress: problems and promises 57:11–21
Jamison DB, Cook NGW (1980) Note on measured values for the state of stress in the Earth’s crust. J Geophys Res Sol Ea 85(B4):1833–1838. https://doi.org/10.1029/JB085iB04p01833
Jia JW (2008) Study on the geometry of extensional structure in the Burtai well field. J Chin Coal Soc 33(11):1253–1256
Ju JF, Xu JL, Zhu WB (2015) Longwall chock sudden closure incident below coal pillar of adjacent upper mined coal seam under shallow cover in the Shendong coalfield. Int J Rock Mech Min 77:192–201. https://doi.org/10.1016/j.ijrmms.2015.04.004
Ju W, Jiang B, Qin Y, Wu CF, Wang G, Qu ZH, Li M (2019) The present-day in-situ stress field within coalbed methane reservoirs, Yuwang Block, Laochang Basin, south China. Mar Petrol Geol 102(5):61–70. https://doi.org/10.1016/j.marpetgeo.2018.12.030
Ju W, Niu XB, Feng SB, You Y, Xu K, Wang G, Xu HR (2020) Present-day in-situ stress field within the Yanchang Formation tight oil reservoir of Ordos Basin, central China. J Petrol Sci Eng 187(4):106809. https://doi.org/10.1016/j.petrol.2019.106809
Ju W, Shen J, Qin Y, Meng SZ, Wu CF, Shen YL, Yang ZB, Li GZ, Li C (2017) In-situ stress state in the Linxing region, eastern Ordos Basin, China: implications for unconventional gas exploration and production. Mar Petrol Geol 86(9):66–78. https://doi.org/10.1016/j.marpetgeo.2017.05.026
Kanagawa T, Hayashi M, Nakasa H (1976) Estimation of spatial geo-stress components in rock samples using the Kaiser effect of acoustic emission. Doboku Gakkai Ronbunshu 258:63–75
Kang HP, Zhang X, Si L, Wu Y, Gao F (2010) In-situ stress measurements and stress distribution characteristics in underground coal mines in China. Eng Geol 116:333–345. https://doi.org/10.1016/j.enggeo.2010.09.015
Kurita K, Fujii N (1979) Stress memory of crystalline rocks in acoustic emission. Geophys Res Lett 6(1):9–12. https://doi.org/10.1029/GL006i001p00009
Lavrov A (2003) The Kaiser effect in rocks: principles and stress estimation techniques. J Rock Mech Min Sci 40(2):151–171. https://doi.org/10.1016/s1365-1609(02)00138-7
Li C, Nordlund E (1993) Experimental verification of the Kaiser effect in rocks. Rock Mech Rock Eng 26(4):333–351. https://doi.org/10.1007/BF01027116
Li GQ, Yan DT, Zhuang XG, Zhang Z, Fu HJ (2019) Implications of the pore pressure and in situ stress for the coalbed methane exploration in the southern Junggar Basin. China Eng Geol 262(11):105305. https://doi.org/10.1016/j.enggeo.2019.105305
Li Y, Tang DZ, Xu H, Yu TX (2014) In-situ stress distribution and its implication on coalbed methane development in Liulin area, eastern Ordos basin. China J Petrol Sci Eng 122(10):488–496. https://doi.org/10.1016/j.petrol.2014.08.010
Li YX, Dong PC (2009) In-situ stress measurement of reservoir using Kaiser effect of rock. Chin J Rock Mech Eng 28(S1):2802–2802. https://doi.org/10.3321/j.issn:1000-6915.2009.z1.033
Lieurance RS (1933) Stresses in foundation at Boulder (Hoover) dam. U.S. Bureau of Reclamation Technical Memorandum, vol 12, p 346
Liu J (2011) In-situ stress measurements and study on distribution characteristics of stress fields in underground coal mines in Yitai mining area. J Chin Coal Soc 36(4):562–566. https://doi.org/10.3724/SP.J.1077.2011.00271
Ma WJ, Hou LH, Luo X, Liu JZ, Tao SZ, Guan P, Cai YW (2020) Generation and expulsion process of the Chang 7 oil shale in the Ordos Basin based on temperature-based semi-open pyrolysis: Implications for in-situ conversion process. J Petrol Sci Eng 190(7):107035. https://doi.org/10.1016/j.petrol.2020.107035
Meng ZP, Shi XC, Li GQ (2016) Deformation, failure and permeability of coal-bearing strata during longwall mining. Eng Geol 208(5):69–80. https://doi.org/10.1016/j.enggeo.2016.04.029
Michihiro K, Fujiwara T, Yoshioka H (1985) Study on estimating geostresses by the Kaiser effect of AE. In: U.S. symposium on rock mechanics. https://doi.org/10.1016/0148-9062(86)90772-2
Ng HM, Ge LL, Du ZY, Wang SR, Ma C (2017) Satellite radar interferometry for monitoring subsidence induced by longwall mining activity using Radarsat-2, Sentinel-1 and ALOS-2 data. Int J Appl Earth Obs 61(9):92–103. https://doi.org/10.1016/j.jag.2017.05.009
Peng SS, Li HM, Zhou Y (2015) Study on strata control in Shendong and Zhungeer mining areas. Science Press, Beijing
Qian QH (2012) Challenges and countermeasures for safety of underground engineering construction. Chin J Rock Mech Eng 31(10):1945–1956
Qin SQ, Li ZD, Zhang XY, Deng RG (1993) Introduction to rock acoustic emission technology. Southwest Jiaotong University Press, Chengdu
Qing LH (2011) Study on mechanism of overburden rock failure during coal mining with shallow depth and thin bedrock. Procedia Eng 26:228–235. https://doi.org/10.1016/j.proeng.2011.11.2162
Sheng SZ, Wan YG, Huang JC, Bu YF, Li X (2015) Present tectonic stress field in the Circum-Ordos region deduced from composite focal mechanism method. Chin J Geophys 58(2):436–452. https://doi.org/10.6038/cjg20150208
Stephansson O, Brown ET (2015) Rock stress and rock stress measurements: a review. Eng Geol 49(1):81–82. https://doi.org/10.1016/S0013-7952(97)85629-3
Su SR (2002) Influence of fault structure on in-situ stress field and its engineering application. Science Press, Beijing
Sun ZQ, Zhang JH (2004) Variation of in-situ stresses before and after occurrence of geologic fault structure. Chin J Rock Mech Eng 23:3964–3969
Townend J, Zoback MD (2000) How faulting keeps the crust strong. Geology 28(5):399–402. https://doi.org/10.1130/0091-7613(2000)28%3c399:hfktcs%3e2.0.co;2
Tuncay E, Ulusay R (2008) Relation between Kaiser effect levels and pre-stresses applied in the laboratory. Int J Rock Mech Min Sci 45(4):524–537. https://doi.org/10.1016/j.ijrmms.2007.07.013
Wang CH (2014) Brief review and outlook of main estimate and measurement methods for in-situ stress in rock mass. Geol Rev 60(5):971–996. https://doi.org/10.3969/j.issn.0371-5736.2014.05.003
Wang LL, Jiang B, Wang JL, Qu ZH (2018) Effects of in-situ stress and joint on permeability of the coal bed in Linfen block, southeastern Ordos Basin, China. Russ Geol Geophys 59(3):299–312. https://doi.org/10.1016/j.rgg.2018.03.008
Wang SM, Zhang YP (1999) Study on the formation, evolution and coal accumulating regularity of the Jurassic Ordos Basin. Earth Sci Front 6(1):147–155. https://doi.org/10.16509/j.georeview.2014.05.005
Wu QH, Li XB, Weng L, Li QF, Zhu YJ, Luo R (2019) Experimental investigation of the dynamic response of prestressed rockbolt by using an SHPB-based rockbolt test system. Tunn Undergr Sp Tech 93:103088. https://doi.org/10.1016/j.tust.2019.103088
Wu S, Tang DZ, Li S, Wu HY, Hu X, Zhu XG (2017) Effects of geological pressure and temperature on permeability behaviors of middle-low volatile bituminous coals in eastern Ordos Basin, China. J Petrol Sci Eng 153(5):372–384. https://doi.org/10.1016/j.petrol.2017.03.034
Xiao W, Lv XJ, Zhao YL, Sun HX, Li JQ (2020) Ecological resilience assessment of an arid coal mining area using index of entropy and linear weighted analysis: a case study of Shendong Coalfield, China. Ecol Indic 109(2):105843. https://doi.org/10.1016/j.ecolind.2019.105843
Xie HP, Gao F, Ju Y (2015) Research and exploration of deep rock mechanics. Chin J Rock Mech Eng 34(11):2161–2178. https://doi.org/10.15961/j.jsuese.201700025
Xie Q, Qiu P, Yu XB, Carlos DG (2010) Initial stress measurements with AE and DRA combined technique. J Chin Coal Soc 35(4):559–564. https://doi.org/10.1016/S1876-3804(11)60004-9
Yang DH, Zhao YX, Zhang C, Teng T, He X, Wang W, Han PH (2018) Experimental study on the influence of cyclic loading on Kaiser effect of sedimentary rocks. Chin J Rock Mech Eng 37(12):2697–2708. https://doi.org/10.13722/j.cnki.jrme.2018.0394
Yang F, Yang XC, Jiang B, Zhou K, Chen CH (2014) Analysis on tectonic characteristics and tectonic stress field in Baode area. Coal Sci Tech 42(7):92–97. https://doi.org/10.13199/j.cnki.cst.2014.07.024
Ye FW, Liu DC, Huang XF, Zhang BJ (2006) Study on fault tectonics in northen Ordos Basin using Post remote sensing application technology. Uran Geol 22(3):182–189. https://doi.org/10.1007/s11769-006-0026-1
Yoshikawa S, Mogi K (1989) Experimental studies on the effect of stress history on acoustic emission activity: a possibility for estimation of rock stress. J A E 8:113–123
Yuan L (2017) Scientific conception of precision coal mining. J Chin Coal Soc 42(1):1–7. https://doi.org/10.13225/j.cnki.jccs.2016.1661
Zang A, Stephansson O (2013) Crustal stress field. Seismological Press, Beijing, pp 90–230
Zhang DS, Ma LQ, Wang XF, Fan GW (2009) Aquifer-protective mining technique and its application in shallowly buried coal seams in Northwest of China. Procedia Earth Planet Sci 1(9):60–67. https://doi.org/10.1016/j.proeps.2009.09.012
Zhang H, Meng ZP, He ZL (2000) Study on tectonic stress field in the Ordos coal basin. J Chin Coal Soc 25(S1):1–5. https://doi.org/10.13225/j.cnki.jccs.2000.s1.002
Zhang K, Li HF, Han JM, Jiang BB, Gao J (2020) Understanding of mineral change mechanisms in coal mine groundwater reservoir and their influences on effluent water quality: a experimental study. Int J Coal Sci Technol. https://doi.org/10.1007/s40789-020-00368-3
Zhang YQ, Shi W, Liao CZ, Hu B (2006) Fault kinematic analysis and change in late mesozoic tectonic stress regimes in the peripheral zones of the Ordos Basin, North China. Acta Geol Sin 80(5):639–647. https://doi.org/10.1016/S1001-8042(06)60011-0
Zhao JL, Tang DZ, Lin WJ, Qin Y, Xu H (2019) In-situ stress distribution and its influence on the coal reservoir permeability in the Hancheng area, eastern margin of the Ordos Basin, China. J Nat Gas Sci Eng 61(1):119–132. https://doi.org/10.1016/j.jngse.2018.09.002
Zhao JL, Tang DZ, Qin Y, Xu H (2018) Experimental study on structural models of coal macrolithotypes and its well logging responses in the Hancheng area, Ordos Basin, China. J Petrol Sci Eng 166(8):658–672. https://doi.org/10.1016/j.petrol.2018.03.073
Zoback MD (2007) Reservoir geomechanics. Cambridge University Press, New York
Acknowledgements
This study was supported by the Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi (2019L0772), the Key Research Development Program of Shanxi Province (201903D121070), the Key Research Development Program of Datong City in Shanxi Province (2019013), Shenhua Shendong Coal Branch Technology Innovation Project (HT2017–4307), and Ph.D. Research Startup of Shanxi Datong University. The authors especially thank Senior engineer Guijun Song, Erlin Wang and Guoqiang Xie of Shendong Coal Branch for their help in the on-site core collection and thank Professor Yixin Zhao for his assistance in drafting the paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yang, D., Ning, Z., Li, Y. et al. In situ stress measurement and analysis of the stress accumulation levels in coal mines in the northern Ordos Basin, China. Int J Coal Sci Technol 8, 1316–1335 (2021). https://doi.org/10.1007/s40789-021-00407-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40789-021-00407-7