1 Introduction

Acoustic emission (AE) or microseismic (MS) technology have become an important mean to study rock failure process and determine stability of rock mass because of its capability in real-time monitoring of signal released by rock in external damage (Liu et al. 2017; Přikryl et al. 2003; Xiao et al. 2016; Wang et al. 2017; Cao et al. 2016; Hall et al. 2006; He et al. 2014; Li and Li 2017). After excavation of underground engineering, the free side of rock mass tends to be under tensile state which adversely affects stability of the underground rock engineering. The mechanical responses of rock material under pressure and tensile state are quite different. Therefore, AE signal characteristics and constitutive model of the rock under the tensile state need to be studied exclusively.

The generation and propagation of cracks inside rock under compressive stress are very complex, which contain shear fracture, tensile fracture and also accompanied by sliding friction between the damage surface and particles. All of the generation of fractures, vibration and friction could produce AE signals, resulting in difficulty in identification and in-depth analysis of AE signal (Katsuyama 1996). Brazil split method is preferentially adopted in rock tensile test (ISRM 1978). The inner stress distribution of cylindrical specimen subjected to radial loading is more complicated, and highly concentrated compressive stress is around the vicinity of the loading point, while tensile stress dominates in the vicinity of specimen center, so it is difficult to distinguish the generation mechanism of AE signals in Brazil split tests. The mechanism of rock fracture under directs tensile is simpler; the internal micro-fracture is caused by tensile stress only. The AE signal also corresponds to tensile fracture. The physical basis is more reasonable to propose tensile constitutive model with AE signals as the damage factor for rock materials.

Stavrogin et al. (1986) carried out direct tensile, splitting and uniaxial compression AE tests on sandstone and limestone specimens. The results showed that AE activities of rock specimens under direct tensile was different from that of splitting and uniaxial compression. There were few AE events in the whole process, which can only be monitored when rock specimen was nearly destructed. Li et al. (2010) carried out uniaxial compression and direct tensile tests on two typical hard rock and soft rock specimens. The relationship between tensile stress, strain and AE count rate was obtained. Their results showed that, under tensile stress, there was basically no AE event during initial loading but sudden increasing of AE occurs before destruction. Nasseri et al. (2011) conducted fracture toughness measurements in granites and AE technique was adopted to monitor real-time crack initiation and propagation under tension, the creation of a significant fracture process zone surrounding the propagating main crack was been confirmed. Chen et al. (2012), Li et al. (2013) studied AE characteristics of Beishan granite under direct tensile, uniaxial compression and triaxial compression, and founded influence of different stress conditions on rock failure and AE characteristics. It is considered that initiation and expansion of fracture under the condition of tensile stress are the main mechanism to control specimen destruction, which leads to later appearance of AE signal. AE signal will accumulate rapidly once it occurs, which means macroscopic damage occurrence of specimen. Tham et al. (2005) analyzed direct tensile mechanical properties and AE activity of 2-D rock specimens and associated acoustic emission, regarding that AE activity associated with micro-fractures.

In the aspect of direct tensile damage model of rock, Jin and Qian (1998) proposed nonlinear elasticity constitutive equation by analyzing increasing law of inelastic deformation under tensile stress. Yu et al. (1998) obtained the relationship between energy consumption in tensile damage and internal damage by direct tensile static, dynamic failure experiments and optical analysis of the failure surface. Based on the micro-cracks propagation criterion and extended rate hypothesis, Jiang et al. (2013) obtained damage change and evolution direction of the rock by using integral principle. The damage constitutive equation of the brittle rock under uniaxial tension was established.

Rock is a natural geological material consisting mineral particles and pore fissures in complex distribution. Due to its strong non-uniform characteristics, it is difficult to determine the variation of micro-damage within the rock. In the above theoretical models, damage variables are mostly guided by single fracture propagation, and then the rock is assumed to agree with statistical distribution law. In fact, generation and propagation of rock damage will release corresponding AE signals. Therefore, there is physical significance in definition of damage factor with AE signals. In addition, the above direct tensile AE test results also show that AE activity under direct tension is significantly different from that under compression. If existence of massive tensile micro-damage can be determined by monitoring AE signals and tensile damage model, it will be of great help to determine stability of rock engineering. In this paper, direct tensile test was conducted on two kinds of marble with monitoring the AE activity, and tensile damage constitutive model was established based on AE parameters to explore failure mechanism of direct tensile status on marble.

2 Experiment method

A pair of spherical hinge pullers was used to eliminate the unevenness on two ends the specimen, so that tensile stress can be axially centered. Two threaded steel caps were used to connect the specimen and the spherical hinge puller. One end of transmission steel cap adopted threaded connection puller, while the other end was processed into a flat surface and stuck with the specimen. Acrylate adhesive was selected, whose tensile strength was up to 24 MPa, which met tensile test requirements of most rock.

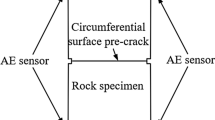
The rock specimens were drilled from two kinds of marble base which were pink coarse-grained marble and white fine-grained marble, and were processed into Ф50 × 100 mm cylindrical specimens according to rock mechanics test standard (Bieniawski and Bernede 1979). Four axial strain gauges and two transverse strain gauges with size of 2 × 10 mm were arranged symmetrically on the surface of middle area of the specimen, which would measure the axial strain and transverse strain, respectively. Strain datum was recorded in real time using XL2101C programmable static resistance strain monitor. SANS servo testing machine was used to conduct loading, which has the maximum loading capacity as 200 kN. Displacement control loading model was adopted, and the loading and unloading rate was 0.05 mm/min. Cyclic loading test also conducted on the two kinds of marble, in first loading cycle, the loading level was set to 1 MPa, when loading value reached 1 MPa then unloading the specimen; in second loading cycle, the loading level was 2 MPa, and in third cycle the level was 3 MPa, etc. The loading cycles are added continuously till the specimen is fractured in the test. There were eight specimens had been prepared for each kind of marble, and named to A1–A8 and B1–B8, respectively. A1–A5 and B1–B5 were tested in direct tensile loading, and A6–A8 and B6–B8 were tested in cyclic tensile loading. AE signals were collected by DS5.0 AE monitor with a sampling frequency of 3 mHz. PAC’s Nano-30 AE sensors were adopted, whose best response frequency range was 125–750 kHz. The preamplifier gain was 40 dB and threshold was set to 10 mV. Both ends of the specimen were evenly arranged with three AE sensors which were homologous in upper and lower position with 120° included angle in the center, as shown in Fig. 1. For reason that the power system of SANS machine is in its lower part, the signals of channel 3 which connect to a sensor on the upper end of specimens was chosen to analyzed in the article.

Fig. 1
figure 1

The sketch and photo of set-up for direct tensile AE test on rock specimens. a Schematic diagram of test device, b photo of the mounted specimen

Full size image

3 Experiment results

3.1 Mechanical parameter of the specimens

The main mechanical parameters of the two kinds of rocks (pink coarse-grained marble and white fine-grained marble) were obtained via uniaxial tensile and compressive test. For specimens in the compressive test, take the average value of test results of each group, as shown in Table 1. The uniaxial tensile stress–strain curves of two kinds of specimens are shown in Fig. 2.

Table 1 Mechanical parameters of the two kinds of marble specimens
Full size table
Fig. 2
figure 2

Tensile stress–strain curves of marble specimens in the two groups. a Group A, b Group B

Full size image

The two kinds of marble are middle hard rock. For pink marble in group A, the average compressive strength is 92.7 MPa, average tensile strength is 3.5 MPa and compressive strength and tensile strength ratio(C–T ratio) is 26.5; for white marble in group B, the average compressive strength is 86.4 MPa, tensile strength is 6.5 MPa and C–T ratio is 13.3. Although marble is relatively homogeneous rock, the uniaxial tensile strengths of these specimens are with big discreteness. The standard deviation of group A is 0.63 MPa, its ratio to average value is 0.18; standard deviation of group B is 1.12 MPa, its ratio to average value is 0.17. For specimens of both groups, compressive strength is not proportional to tensile strength. From fracture surface of specimens (Fig. 3), specimen in group A is coarse-grained marble comprising coarse particles with size around 1 mm and sticking substance. The strength of sticking substance between particles under tensile state is obviously smaller than that of the particles, so tensile fracture mainly occurs in the sticking substance. Specimens in group B are dense fine-grained marble with well homogeneity, so the elastic modulus and tensile strength are higher. In the compressed state, the micro weak parts between particles of group A has little effect on macro shear and friction damage, as well as coarse particles have higher shear strength, so the compressive strength of group A marble is higher than that of group B. It also shows that mechanical response of rock material is related to stress state in addition to its own mineral composition and structure. The mechanical constitutive and strength criterion of rock under direct tensile state should be discussed specially.

Fig. 3
figure 3

Photographs of fracture surface for two marble specimens. a Specimen A2, b specimen B3

Full size image

The tensile stress–strain curves in Fig. 2 show that the whole tensile process of specimens in group A are almost nonlinear. The tensile tangent modulus decreases monotonically with increasing of stress level, indicating that tensile strength between inner particles of the specimens are strong unevenness. The tensile stress–strain curves of specimens in group B were basically linearly increased in whole loading process, especial for specimen B1, B2 and B3, indicating that tensile strengths of internal crystal of specimens in group B are relatively uniform. In addition, tensile modulus of specimens in group B is also significantly higher and more uniform than that in group A. As shown in Fig. 2b, linear parts of tensile curves of B1–B4 are almost completely coincided.

3.2 AE activity for specimens under direct tensile process

Figures 4 and 5 shows AE activity of the two kinds of marble specimens during direct tensile test, where σv and εv is the vertical stress and strain in tensile test, respectively. The relationship between stress, AE energy rate and axial strain are given. Compared to the numbers of AE events occur in compressive tests (Hou 2017), there are obviously less in direct tensile test and almost no AE events were detected at the initial loading stage. The energy of most AE events is less than 300 mV except few AE events occurring at macroscopic fractured moment. In comparison of the two groups’ marble, AE events for group A occurred earlier and with more quantity during the whole loading process than group B. Obvious AE activity occurs after loading level exceeding 80% of damage strength for the specimen B2. The first half loading stage of specimen B5 is almost linear, and almost no AE occurs. While, when loading level exceeds 50% of B5’s tensile strength, AE events begins to occur in large quantity, and the loading process becomes to non-linear.

Fig. 4
figure 4

AE activities during the whole directly tensile process for specimens in A group. a Specimen A1, b specimen A2

Full size image
Fig. 5
figure 5

AE activities during the whole directly tensile process for specimens in B group. a Specimen B2, b specimen B5

Full size image

3.3 AE activity in tensile cyclic loading test

Figure 6 shows the stress–strain curves for two groups of marble under directly tensile cyclic loading. It can be seen that cyclic loading has no significant effect on tensile strength and failure process of the specimens. Similar to axial compression cyclic loading, tensile loading and unloading process cannot be repeated yet, and the next loading cycle is linear when loading stress level is less than that in the previous loading cycle, and becomes to non-linear when it exceeds the previous loading level.

Fig. 6
figure 6

Stress-strain curves in cycle tensile loading for the two groups of specimens. a A6 specimen, b B6 specimen

Full size image

The internal microcracks of the specimen increases with increasing of tensile loading, the portions of inner particles that can bear tensile stress decreases, and the decreasing of tangent modulus is the apparent behavior. During unloading cycle, the unspoiled particles recover its deformation, but the failure particles such as the generation and propagation of microcracks cannot be recovered. Portion of loading energy is consumed with the increasing of microcracks. In reloading cycles, the portions that can bear tensile loading in specimen is reduced compared with the previous loading, resulting in the reducing of its tensile modulus which shown in weakened linear characteristic. This is opposite to reloading linear characteristic that reinforcement in compression cyclic loading for rock specimens (You 2007). Figure 7 shows the variation of tensile modulus of the two kinds of marble under different loading cycles. It can be seen that specimens in group B with more uniform and compact particles has less reduction in elastic modulus in the cyclic loading. While specimens in group A with stronger non-uniformity has larger reduction in elastic modulus in the cyclic loading and each cyclic tensile process produces more micro damage in it.

Fig. 7
figure 7

Variation of elastic modulus in different tensile loading cycle

Full size image

Figure 8 shows the relationship of loading level and AE cumulative energy during the tensile cyclic loading process. The KE Points refers to Kaiser Effect point that occurs when AE activity recovers during repeated loading. There is also significant Kaiser Effect during tensile cyclic loading on rock specimens. AE signal reappears when loading stress level is beyond maximum stress level in previous loading. There is no AE signal occurrence during the unloading process. The Kaiser Effect in tensile loading also proves the phenomenon of damage accumulation in rock material under tensile state.

Fig. 8
figure 8

Variation of stress and AE energy in the tensile cyclic loading, a A6 specimen, b B6 specimen

Full size image

4 Tensile constitutive equation based on AE energy

AE event is an accompaniment signal of generation of micro-crack within the rock. Its quantity and magnitude reflect density and size of micro-cracks, especially for the rock specimens in direct tensile state. Because there is almost no noise signal caused by loading contact and sliding friction of particles, AE signals and tensile micro-damage have a better correspondence.

4.1 Tensile damage factor

The basic principle of damage mechanics is that the main mechanism of material deterioration is decreasing of effective bearing area caused by micro-defect. Hence, concept of damage factor is introduced (Rabotnov 1969):

$$D = \frac{{A_{\text{d}} }}{A}$$
(1)

where D is damage factor, D = 0 for completely non-damaged state of material, D = 1 for completely loss of bearing loading capacity. A is the area with damage, that is, apparent area of the specimen; Ad is the total area of micro-defect of specimen, (A − Ad) is effective bearing area. For non-uniform rock materials, area of micro-defects is difficult to measure, especially in the process of loading, as micro-fracture area will change with the load increasing.

Assuming that the marble specimen is intact material before tensile loading, the occurrence of AE events indicates that generation of damage in the specimens. With cumulative value of AE energy to indicate the magnitude of internal damage, the damage factor can be defined by AE energy parameter:

$$D_{e} = \left( {\frac{{\sum\nolimits_{i = 1}^{n} {e_{i} } }}{{E_{n} }}} \right)$$
(2)

where De is damage factor based on AE energy parameter; i is count of AE event when load is at a certain level; ei is the energy of that AE event; En is the total accumulative energy of AEs when the specimen is completely failure, its value can be obtained through AE experiments. Since ei and En are respectively energy of single AE event and cumulative energy with the same unit, De is dimensionless quantity.

4.2 Damage constitutive model in tensile state for rock material

According to the aforementioned test results, the essence of tensile stress–strain relationship is the process of generation and propagation of micro-cracks in the rock. The damaged portion of specimens have lost the ability to bear tensile stress, but stress–strain relationship of the rest portion which bear the tensile loading still conforms to Hooke’s law for elastic material.

$$\tilde{\sigma }_{t} = \frac{{F_{t} }}{{A - A_{d} }} = E\varepsilon$$
(3)

where \(\tilde{\sigma }_{t}\) is effective stress; Ft is applied tensile loading; E is elastic modulus of the loaded material; ε is strain. Substitute Eq. (1) in, then Eq. (3) can be expressed with damage factor:

$$\sigma_{t} = E\varepsilon (1 - D)$$
(4)

Substitute the damage factor De which defined by AE energy into Eq. (4), then:

$$\sigma_{t} = E\varepsilon (1 - D_{e} ) = E\varepsilon \left[ {1 - \left( {\frac{{\sum\nolimits_{i = 1}^{n} {e_{i} } }}{{E_{n} }}} \right)} \right]$$
(5)

Figure 9 shows the comparison of theoretical and experimental results of stress–strain relationship for the two kinds of marble, and the variation of damage factor with strain increasing. It can be seen that the theoretical simulation curve based on AE energy parameters can well represent directly tensile stress–strain relationship for the two kinds marble.

Fig. 9
figure 9

Comparison of the theoretical simulated results based on AE energy factor and the test results. a Specimen A1, b specimen A2, c specimen B2, d specimen B5

Full size image

The constitutive equation in formula (5) contains only two constants, i.e., initial elastic modulus and cumulative AE energy of the rock, which represent material characteristics and accumulative amount of internal micro-defects respectively, indicating that quasi-static tensile failure process of rock is determined by the two constants. Compared with other tensile damage equations (Qin et al. 2003; Zhou and Xu 2009), the constants of initial damage factor is taken out and the initial value of specimen’s damage factor De is 0 for all rock material. Although ideal rock material without any defects is not reality, it is hard to quantize the initial damage level in practical application. In addition, the initial elastic modulus which can be easily gotten from test has contained the initial damage factor implicitly. If initial damage value is added to the equation, then the initial damage factor would be considered repeatedly. The damage parameter De which initial level is 0 in Eq. (5) accumulatively increases in the loading process and mutates to the level De= 1 when the maximum tensile strain is reached, which indicates the transition of gradual micro-damage accumulation to sudden macroscopic fracture in rock specimens.

The two material constants in this tensile constitutive equation can be tested by AE system and servo test machine. Due to the directly tensile state, AE signal is less disturbed by loading noise, and the threshold value collected by AE equipment can be set on a lower level, so that more AE signals, especially low energy signals, can be collected. Meanwhile, AE signals should be collected via multiple channels, and the average value of cumulative AE energy from all acquisition channels could be taken to reduce error that collected by only single channel.

5 Conclusions

The directly tensile tests on two kinds of marble specimens were conducted and the AE signal were acquired and analyzed. The mechanical response and characteristic of AE activity under directly tensile process were obtained. The tensile constitutive equation based on AE energy parameters was proposed and cumulative damage character for marble specimens was analyzed. Following conclusions can be drawn:

  1. (1)

    Tensile strength of marble has a strong discreteness, which is more sensitive to micro-defects and particle composition within the rock. The tensile stress–strain curve is obviously nonlinear, with tensile tangent modulus decreasing with the load increase. In the cyclic loading, elastic modulus of the specimen decreases compared with that in the previous loading, and showed that its linearity decreases due to increasing of internal micro-defect in it.

  2. (2)

    Compared with AE signal in compressive test, it has less quantity and smaller energy in the directly tensile tests. AE activity is well corresponding to nonlinear deformation of specimens under tensile loading process. At the initial stage of elastic deformation, almost no AE event occurs, but at nonlinear deformation stage, AE occurs in large volumes, and its quantity and energy relate to the variation of tensile tangent modulus. AE Kaiser Effect can be clearly observed during tensile cyclic loading.

  3. (3)

    Based on the theory of damage mechanics, the damage factor of rock material were proposed by AE energy, and tensile damage constitutive equation needing two material constants was established, which was proved to be in good agreement with the experimental result.