Introduction

In an experiment, missing observations are often arisen, particularly when the experimental units are breeding or biological varieties. Consider, for instance, a long-term experiment in which different safflower genotypes were planted in a blocking design to determine their yields. During the experiment, it is very likely that one or more plants of a variety in a block be missed due to a limited experimental unit or being withered; this will result in the problem of missing an observation completely at random. The missing values could cause a major problem in the statistical analysis of an experiment and might adversely affect the results, causing bias in treatment effect estimation and the upward sum of squares, increasing the estimate variability, or may diminish the power of testing treatment effects. Therefore, the missing problem should be carefully treated. The attempts to resolve such a problem go back many years ago when it was suggested that the vacant cell be filled by the estimation of the lost observation [1, 2]. Later, the missing problem has been studied for different designs; Cornish [3] discussed how to estimate missing values in incomplete block designs (IBD). Baird and Kramer [4] considered the Balanced IBD with several missing values. Apart from the pre-mentioned estimating method of missing observations, an exact method to deal with the missing values has been considered by some researchers, which is the so-called “general regression significance test” [5]. This method has been mostly studied for the analysis of covariance [6,7,8]. Recently, the exact scheme is highlighted by Sirikasemsuk, et al. [9] where the adjusted regression sum of squares of the randomized complete block design (RCBD) with a missing observation was calculated mathematically.

The problem of missing values is less discussed in ARCBD. ARCBD is an unbalanced design that is obtained from an RCBD, including the control treatments, by distributing a numerous number of added new genotypes randomly to blocks with the aim of studying them. ARCBD has been introduced by Federer [10] to deal with the screening stage of the breeding program, where the experimenters face a large number of new treatments (genotypes) (see also [11] for more details). Consider a randomized complete block design where genotypes are augmented randomly in all of the blocks by proliferating the number of experimental units within blocks. Therefore, each block includes only once each of the c control treatments, so-called checks. Therefore, the blocks and treatment effects are orthogonal. The genotypes run without replication in the experiment; that is, each appears only in one of the blocks. Several classes of Augmented block designs have been developed. Federer and Crossa [11] give a review of augmented designs. [12,13,14] developed SAS code for analyzing the data that come from augmented designs.

As mentioned above, a common approach is to estimate the missing value and used it for analyzing the data. This is a method so-called approximate [5]; however, the estimated value intrinsically differs from the original value and hence may cause a bias in results. There are two issues with this approach. First is the uncertainty about the estimated missing value especially, if there are some ambiguities and indeterminacies in the data itself and the second is the potential for the inefficiency of the approximate approach. Neither the classic analysis is able to provide information regarding the measure of indeterminacy to analyze the genotypes precisely nor the approximate method is enough reliable to make inferences, unbiasedly.

In classic statistics, all classes of augmented designs have been considered and analyzed, yet to the best of our knowledge, there is still a vacancy for these designs in the uncertain environment. Accordingly, several researchers have employed fuzzy sets and intuitionistic fuzzy sets in their investigations to effectively tackle the presence of uncertainty and ambiguity within the data. In this context, Kumar [15] highlighted a new method for addressing the type-2 intuitionistic fuzzy transportation problem. Naveed et al. [16] have focused on the analysis of interval-valued fuzzy soft sets and the application of IVFSS algorithm in the risk assessment of prostate cancer. Kumar [17] provided an innovative approach to address the challenges posed by intuitionistic fuzzy solid transportation problems. Kumar [18] furnished a facile approach toward resolving type-2 and type-4 fuzzy transportation predicaments. Kumar [19] introduced a novel technique for resolving transportation problems that fall under the type-1 and type-3 fuzzy categories. A novel category of orthopair fuzzy sets called “ (2, 1) -fuzzy sets” was proposed by Al-shami [20]. These sets employ a pair of values within the unit interval to indicate the degrees of membership and non-membership. A comparison with other fuzzy set types was made, and essential operations and properties were suggested alongside their potential applications in multi-criteria decision-making techniques. Al-shami and Mhemdi [21] presented a generalized frame for orthopair fuzzy sets known as (m, n) -fuzzy sets, along with their practical applications in methods for making decisions involving multiple criteria. Al-shami et al. [22] introduced a novel extension of fuzzy soft sets known as (a, b) -fuzzy soft sets.

Although fuzzy sets and intuitionistic fuzzy sets can be viewed as a broader space of classical set theory, neutrosophic sets surpass fuzzy sets by introducing a third parameter called indeterminacy. Indeterminacy assesses the degree of uncertainty or incompleteness in a statement, improving the representation of uncertainty by incorporating not only the degree of membership and non-membership but also the degree of indeterminacy. Besides, computations with neutrosophic sets are less complex, leading to more efficient use of time and resources. Thus, neutrosophic sets are more effective than intuitionistic fuzzy sets in clustering complex datasets with overlapping information and can manage multiple degrees of overlap and contradictions that intuitionistic fuzzy sets struggle with. There are more discussions in the literature about the differences between neutrosophic statistics (NS) and other types of statistics. Smarandache [23] demonstrated that NS are more general than interval statistics in many cases and gave examples of how neutrosophic algebra can provide greater accuracy. For instance, NS deals with all types of indeterminacy, whereas interval statistics only deals with indeterminacy represented by intervals. Accordingly, neutrosophy has led to the development of new mathematical theories, such as neutrosophic set theory, probability, statistics, and logic. These theories generalize classical and fuzzy counterparts and have practical applications in various fields.

We have considered the missing value in ARCBD and raised some ambiguities in data, such as the indeterminacy, the pre-unknown number of new treatments in ARCBD, erroneous estimating of the missing value, and imprecise F test. The probable inadequacy of the classic and fuzzy methods to deal with such complexity motivated us to utilize NS. In this paper, the indeterminacies are tackled by examining the analysis of missing values in NS framework, which provides additional information about the level of uncertainty. Moreover, an exact method for dealing with a missing value was suggested through the NS to came up with a more precise analysis in ARCBD. This is for the first time that the augmented block design is discussed in neutrosophic environment, while also focusing on the issue of missing value.

The concept of NS has been introduced by Smarandache [24]. Aslam [25] explained the differences between fuzzy statistics, NS, and classic statistics. As Smarandache [23] explained, NS is much broader than interval statistics because it deals with all types of indeterminacy including non-well-known sample size, neutrosophic random variable, and neutrosophic probability distributions. Aslam [26] has discussed the neutrosophic ANOVA method. AlAita and Aslam [27] highlighted the application of neutrosophic analysis of covariance to neutrosophic completely random designs, neutrosophic randomized complete block designs, and neutrosophic split-plot designs. The utilization of neutrosophic statistical analysis for split-plot designs was discussed by AlAita et al. [28]. [29] suggested post hoc multiple comparison tests under NS. Neutrosophic correlation and simple linear regression have been discussed by Salama et al. [30]. Analysis of neutrosophic multiple regression has been suggested by Nagarajan, et al. [31]. Jafar et al. [32] proposed a novel approach for site selection in solid waste management systems through the development of distance and similarity measures using max–min operators of neutrosophic hypersoft sets. Jafar et al. [33] have constructed trigonometric similarity metrics for neutrosophic hypersoft sets and employed them to select renewable energy sources. Jafar et al. [34] proposed utilizing similarity measures such as tangent, cotangent, and cosine within a neutrosophic environment for the purpose of selecting academic programs. The matrix theory for neutrosophic hypersoft set and its application in multiattributive multicriteria decision-making problems were analyzed by Jafar and Saeed [35]. In the very most recent years, numerous neutrosophic statistical studies have been discussed [36,37,38,39,40,41,42,43,44].

Neutrosophic normality

The following offers some basic concepts regarding the neutrosophic random variables that will be advantageous in the subsequent sections.

The \(X_N{\in }\left[ X_L{,\ }X_U\right] \) is a neutrosophic random variable with indeterminacy interval, \(I_N,\) and is written as \(X_N{=\ }X_L{+\ }X_UI_N\), where \(X_L\) is determinate part and \(X_UI_N\) is indeterminate part, where \(I_N{\in }{[}I_L,I_U{]}\) is measure of uncertainty. Clearly, \(X_N\) is reduced to the classical random variable at \(I_L=0.\)

Definition 1

[28] Suppose that \(X_N\) is a neutrosophic random variable with neutrosophic normal distribution with population mean and variance \({\mu }_N\) and \({\sigma }^{{2}}_N,\) respectively if the neutrosophic mean and variance can be found as

$$\begin{aligned}{} & {} \!\!\!{\mu }_N{\in }\left[ \frac{\sum ^N_{i{=1}}{X_{Li}}}{N},\frac{\sum ^N_{i{=1}}{X_{Ui}}}{N}\right] ;\quad {\ }{\mu }_N{\in }\left[ {\mu }_L{,\ }{\mu }_U{\ }\right] \,\, \textrm{and}\\{} & {} \!\!\!{\sigma }^{{2}}_N{\in }\left[ \frac{\sum ^N_{i{=1}}{{\left( X_{Li}-{\mu }_L\right) }^{{2}}}}{N},\frac{\sum ^N_{i{=1}}{{\left( X_{Ui}{-}{\mu }_U\right) }^{{2}}}}{N}\right] ; \quad {\sigma }^{{2}}_N{\in }{[}{\sigma }^{{2}}_L,{\sigma }^{{2}}_U{]}. \end{aligned}$$

Definition 2

[28] Suppose a random sample of size n, selected from a population of size N, contains indeterminate observations. The estimated neutrosophic sample mean \({{\overline{x}}}_N\) and the variance \(s^{{2}}_N\), are expressed by;

$$\begin{aligned}{} & {} {{\overline{x}}}_N{\in }\left[ \frac{\sum ^n_{i{=1}}{x_{Li}}}{n},\frac{\sum ^n_{i{=1}}{x_{Ui}}}{n}\right] {;} {{\overline{x}}}_N{\in }\left[ {{\overline{x}}}_L{,\ }{{\overline{x}}}_U \right] \,\, \textrm{and} \\{} & {} s^{{2}}_N{\in }\left[ \frac{\sum ^n_{i{1}}{{\left( x_{Li}{-}{{\overline{x}}}_L\right) }^{{2}}}}{n{-1}},\frac{\sum ^n_{i{=1}}{{\left( x_{Ui}-{{\overline{x}}}_U\right) }^{{2}}}}{n{-1}}\right] ; s^{{2}}_N{\in }{[}s^{{2}}_L,s^{{2}}_U{]}. \end{aligned}$$

Neutrosophic model of augmented randomized complete and incomplete block designs

The neutrosophic statistical model for a NARCBD with a blocks, c checks and v new treatments can be formulated as follows:

$$\begin{aligned} y_{Nhijg}= & {} {\mu }_N+{\alpha }_{Ni}+{\tau }_{Nqj}+{\tau }_{Nlig} +{\varepsilon }_{Nhijg},\nonumber \\ i= & {} 1,2,\ldots ,b,\ \ j=1,2,\ldots ,c,\ \ g=1,2,\ldots ,n_{(li)}\nonumber \\ \end{aligned}$$
(1)

The neutrosophic form of \(y_{Nhijg}\) can be expressed as

$$\begin{aligned} y_{Nhijg}=y_{Lhijg}+y_{Uhijg}I_N;\ I_N\in \left[ I_L,\ I_U\right] , \end{aligned}$$

where \(h=l\ or\ q\) stands for the neutrosophic effects associated with new treatments or checks, respectively, \({\mu }_N\) is a neutrosophic overall mean, \({\alpha }_{Ni}\) is the neutrosophic effect of the ith block, \({\tau }_{Nqj}\) is the neutrosophic effect of the jth check, \({\tau }_{Nlig}\) is the neutrosophic effect of the g th new treatment in the ith block, and \({\varepsilon }_{Nhijg}\) is the random error with neutrosophic zero mean and variance \({\sigma }^2_N\). It is assumed that the errors are independent and neutrosophic normally distributed. Let \({v}=\sum ^b_{i=1}{n_{(li)}}\) refer to the number of new treatments, c for the number of check treatments, and b for the number of blocks; therefore,\(e={v}+c\) is the total number of new and check treatments and the total number of all plots in the blocks is n; i.e., \(n={v}+bc\). Formula (1) is also the model for neutrosophic augmented incomplete block design (NAIBD) in which one or more c checks do not appear in some blocks; therefore, \(n<{v}+bc.\) Throughout the paper in the context of neutrosophic ANOVA, the \({SS}_{NT},\ {SS}_{NTr},\ {SS}_{NB}\) and \({SS}_{NE}\), \({SS}_{N.}{\in }\left[ {SS}_{L.},\ {SS}_{U.}\right] ,\) stand for the neutrosophic sum of squares (\( SS_N \)) total, treatment, block, and error, respectively, and the subscript N denotes the neutrosophic context.

Estimation of neutrosophic parameters

Neutrosophic approximate analysis (NAA)

The neutrosophic analysis for an ARCBD is studied by AlAita and Talebi [45]. Now, consider the problem of losing a check in a block completely at random; for example, rth check in block m. In the classic statistics, the missing observation is estimated by minimizing the sum of squares errors and assumed as the true value to analyze the data by lessening one degrees of freedom of the error. Such an approach can be extended to NS by estimating the neutrosophic missing observation by \(y^*_{Nqmr}=\frac{{{by}_{Nqm.}+cy}_{Nq.r}-y_{Nq..}}{\left( c-1\right) \left( b-1\right) }=[y^*_{Lqmr},\ y^*_{Uqmr}]\), where throughout the paper the notion (.) means the sum over the related indices. However, a poor estimate of missing observation may lead to inefficient inference about treatments. A simulation study will be subsequently conducted for a more detailed analysis of this issue.

Neutrosophic exact analysis (NEA)

For a more precise analysis of data that includes missing values in the NARCBD, an exact analytical approach is proposed to address neutrosophic missing values in the NARCBD. By missing a check in NARCBD, one face with an incomplete block hence the design is a NAIBD in terms of control treatments, regardless of the new treatments. The design that involves a missing check treatment within a block is regarded as an NAIBD and will be analyzed, accordingly. Note that the unbalanced blocks deface the orthogonality between blocks and checks due to not having all checks in each block. Consequently, this contravenes control and new treatments estimation and gives invalid sums of squares which are not sum to a right total. To response to the need of the required adjustment, the exact approach is accomplished based on the complete case analysis of the observations for the NAIBD. It should be noted that the results in NAIBD is a generalization of NIBD where the new treatments will be ignored.

To estimate the model parameters of a NAIBD where it is assumed an observation is missing completely at random, e.g., the rth check treatment in the mth block for any r and m, the least squares normal equations (NEs) are

$$\begin{aligned}{} & {} {\mu }_N:{(v+}bc{-1)}{{\hat{\mu }}}_N{+(}b{-1)}\sum ^c_{j=1{,}j{\ne }r}{{{\hat{\tau }}}_{Nqj}}{+(}b{-2)}{{\hat{\tau }}}_{Nqr}\nonumber \\{} & {} \quad +\sum ^b_{i{=1}}{n_{li}}{{\hat{\alpha }}}_{Ni}-{{\hat{\alpha }}}_{Nm}=y_{N...}, \end{aligned}$$
(2)
$$\begin{aligned}{} & {} {\alpha }_{Nm}:{(}c+n_{lm}{-1)(}{{\hat{\mu }}}_N+{{\hat{\alpha }}}_{Nm})\nonumber \\{} & {} \quad +\sum ^c_{j=1{, }j{\ne }r}{{{\hat{\tau }}}_{Nqj}}+\sum ^{n_{lm}}_{g{=1}}{{{\hat{\tau }}}_{Nlmg}=y_{N..m}}, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} {\tau }_{Nqr}:{(}b{-1)(}{{\hat{\mu }}}_N+{{\hat{\tau }}}_{Nqr}{)-}{{\hat{\alpha }}}_{Nm}=y_{Nqr.}, \end{aligned}$$
(4)
$$\begin{aligned}{} & {} {\tau }_{Nlmg}:{{\hat{\mu }}}_N+{{\hat{\tau }}}_{Nlmg}+{{\hat{\alpha }}}_{Nm}=y_{Nlmg}. \end{aligned}$$
(5)

By solving NEs (2–5) under the constraints \(\sum ^b_{i{=1}}{{{\hat{\alpha }}}_{Ni}{=0}}\), \(\sum ^c_{j{=1}}{{{\hat{\tau }}}_{Nqj}}+\sum ^b_{i{=1}}{\sum ^{n_{li}}_{g{=1}}{{{\hat{\tau }}}_{Nlig}{=0}}}\), the neutrosophic estimates of the parameters in (1) are

$$\begin{aligned}{} & {} \!\!\!{{\hat{\mu }}}_N{=}\frac{{1}}{(v{+}c)}\left( y_{N...}{-}\frac{(b{-}1)}{b}\sum ^c_{j=1,j{\ne }r}{y_{Nq.j}{-}(b{-}2){{\hat{y}}}_{Nq.r}}\right. \\{} & {} \qquad \quad \left. -\sum ^b_{i=1, i\ne m}{n_{li}{{\hat{\alpha }}}_{Ni}} +\frac{\left( {1-(b-1)}n_{lm}\right) }{b{-1}}{\hat{\alpha }}_{Nm}\right) , \\{} & {} \!\!\!{{\hat{\alpha }}}_{Nm}=\frac{{1}}{b{(}c{-1)}} \left( by_{Nqm.}-\sum ^c_{j=1{, }j{\ne }r}{y_{Nq.j}}\right) ,\\{} & {} \!\!\!{{\hat{\tau }}}_{Nqr}={{\hat{y}}}_{Nq.r}+\frac{{{\hat{\alpha }}}_{Nm}}{b-1}-{{\hat{\mu }}}_N, \\{} & {} \!\!\!{{\hat{\tau }}}_{Nlmg}=y_{Nlmg}-{{\hat{\alpha }}}_{Nm}-{{\hat{\mu }}}_N,~{{\hat{\alpha }}}_{Ni}=\frac{y_{qi.}}{c}-{{\hat{\mu }}}_{Nq},\\{} & {} \!\!\!{{\hat{\tau }}}_{Nqj}=\frac{y_{Nq.j}}{b}-{{\hat{\mu }}}_N={{\hat{y}}}_{Nq.j}-{{\hat{\mu }}}_N, \textrm{and} \\{} & {} \!\!\!{{\hat{\tau }}}_{Nlig}=y_{Nlig}-{{\hat{\alpha }}}_{Ni}-{{\hat{\mu }}}_N{,} \quad g=1,2,\ldots , n_{li}{,}\\{} & {} \!\!\! i=1,2,\ldots ,b,\quad i{\ne }m,\quad j=1,2,\ldots ,c,\quad j{\ne }r \end{aligned}$$

where \({{\hat{\mu }}}_{Nq}=\frac{{(}bc{-}b{-}c{)}y_{Nq..}+by_{Nqm.}+cy_{Nq.r}}{bc{(}b{-}{1)(}c{-1)}}.\)

In the same manner, as above, the neutrosophic estimates of the parameters of the reduced treatment- and block-models, obtained by deleting the block and treatment effects from (1), can be calculated, respectively.

Neutrosophic testing of effects

To test the neutrosophic parameters in NARCBD, a need is to calculate the \({SS}_{NT}\) and neutrosophic adjusted(adj) and unadjusted(unadj) sums of squares for the blocks, treatments (new and check) and the NSS for error in the NARCBD.

$$\begin{aligned}{} & {} \!\!\!{SS}_{NT}=\sum ^b_{i=1}{\sum ^c_{j=1}{y^2_{Nqij}+}}\sum ^b_{i=1}{\sum ^{n_{(li)}}_{g=1}{y^2_{Nlig}}}\\{} & {} \qquad \quad \qquad -\frac{y^2_{N\dots }}{n};~{SS}_{NT}\in \left[ {SS}_{LT},\ {SS}_{UT}\right] , \\{} & {} \!\!\!{SS}_{NB(\textrm{unadj})}=\sum ^b_{i=1,\ i\ne m}{\frac{y^2_{N.i.}}{c+n_{(li)}}+\frac{y^2_{N.m.}}{c-1+n_{(lm)}}-\frac{y^2_{N\dots }}{n}};\\{} & {} \!\!\!{SS}_{NB{(\textrm{unadj})}}\in \left[ {SS}_{LB{(\textrm{unadj})}},\ {SS}_{UB{(}{\textrm{unadj})}}\right] , \\{} & {} \!\!\!{SS}_{NTr{(\textrm{unadj})}}=\frac{1}{b}\sum ^c_{j=1,{}j\ne r}{y^2_{Nq.j}+\frac{1}{b-1}y^2_{Nq.r}}\\{} & {} \qquad \qquad \quad \qquad \qquad +\sum ^b_{i=1}{\sum ^{n_{(li)}}_{g=1}{y^2_{Nlig}}-\frac{y^2_{N\dots }}{n}};\\{} & {} \!\!\!{SS}_{NTr{(\textrm{unadj})}}\in \left[ {SS}_{LTr{(\textrm{unadj})}},\ {SS}_{UTr{(\textrm{unadj})}}\right] , \\{} & {} \!\!\!SS_{NB{(}{\textrm{adj}}{)}}=P_N=\frac{{1}}{c}\sum ^b_{i=1,\ i\ne m}{y^{{2}}_{Nqi.}}\\{} & {} \qquad \quad \quad \quad \quad +\frac{\left( by_{Nqm.}-\sum ^c_{j=1,{}j\ne r}{y_{Nq.j}}\right) \left( y_{Nqm.}+\frac{y_{Nq.r}}{b{-1}}\right) }{b{(}c{-1)}}\\{} & {} \qquad \qquad \qquad -{{\hat{\mu }}}_{Nq}\sum ^b_{i=1,\ i\ne m}{y_{Nqi.}};~SS_{NB{(}{\textrm{adj}}{)}}\\{} & {} \qquad \qquad \qquad \in \left[ SS_{LB{(}{\textrm{adj}}{)}},\ SS_{UB{(}{\textrm{adj}}{)}}\right] , \\{} & {} \!\!\!{SS}_{NTr{(}\textrm{adj}{)}}={SS}_{NTr{(un}\textrm{adj}{)}}-{SS}_{NB{(un}\textrm{adj}{)}}\\{} & {} \qquad \quad \qquad \quad \quad +P_N;~ {SS}_{NTr{(}\textrm{adj}{)}}\\{} & {} \qquad \quad \qquad \quad \quad \in \left[ {SS}_{LTr{(}\textrm{adj}{)}},\ {SS}_{UTr{(}\textrm{adj}{)}}\right] , \end{aligned}$$
$$\begin{aligned}{} & {} \!\!\!SS_{NE}=\sum ^b_{i{=1}}{\sum ^c_{j{=1}}{y^{{2}}_{Nqij}-}}\frac{\sum ^c_{j{=1,}j{\ne }r}{y^{{2}}_{Nq.j}}}{b}\\{} & {} \qquad \quad \quad -\frac{y^{{2}}_{Nq.r}}{b{-1}}{-}P_N;~SS_{NE}\in \left[ SS_{LE},\ SS_{UE}\right] , \\{} & {} \!\!\!{SS}_{N\textrm{Check}{(\textrm{unadj})}}=\frac{1}{b}\sum ^c_{j=1,{}j\ne r}{y^2_{Nq.j}}\\{} & {} \qquad \qquad \qquad \qquad +\frac{1}{b-1}y^2_{Nq.r}-\frac{y^2_{Nq..}}{bc};\\{} & {} \!\!\!{SS}_{N\textrm{Check}{(\textrm{unadj})}}\in \left[ {SS}_{L\textrm{Check}{(\textrm{unadj})}}, {SS}_{U\textrm{Check}{(\textrm{unadj})}}\right] , \\{} & {} \!\!\!{SS}_{N\textrm{Check}{(\textrm{adj})}}=\frac{\sum ^c_{j=1}{y^2_{Nq.j}}}{b}-\frac{y^2_{Nqm.}}{c(c-1)}\\{} & {} \qquad \qquad \qquad \qquad +\frac{(by_{Nqm.}+cy_{Nq.r}-y_{Nq..})}{bc(b-1)(c-1)}-\frac{y^2_{Nq..}}{bc};\\{} & {} \!\!\!{SS}_{N\textrm{Check}{(\textrm{adj})}}\in \left[ {SS}_{L\textrm{Check}{(\textrm{adj})}},\ {SS}_{U\textrm{Check}{(\textrm{adj})}}\right] , \\{} & {} \!\!\!{SS}_{N\textrm{new}}=\sum ^b_{i=1}{\sum ^{n_{(li)}}_{g=1}{y^2_{Nlig}}-\frac{y^2_{Nl..}}{{v}}};\\{} & {} \!\!\!{SS}_{N\textrm{new}}\in \left[ {SS}_{Lnew},\ {SS}_{Unew}\right] , \\{} & {} \!\!\!{SS}_{N{\textrm{new}\ and\ \textrm{new}\ \times \ ch}}={SS}_{NTr{(\textrm{adj})}}-{SS}_{N\textrm{Check}{(\textrm{adj})}};\\{} & {} \!\!\!{SS}_{N{\textrm{new}\ and\ \textrm{new}\ {\times } \ ch}}\in \left[ {SS}_{L{\textrm{new}\ and\ \textrm{new}\ {\times } \ ch}},\right. \\{} & {} \qquad \qquad \qquad \left. {SS}_{U{\textrm{new}\ and\ \textrm{new}\ {\times } \ ch}}\right] , \\{} & {} \!\!\!{SS}_{N{new\ \times \ \textrm{check}}}={SS}_{NTr{(\textrm{unadj})}}{-}{SS}_{N\textrm{Check}{(\textrm{unadj})}}{-}{SS}_{N\textrm{new}};\\{} & {} \!\!\!{SS}_{N{new\ \times \ \textrm{check}}}\in \left[ {SS}_{L{\textrm{new}\ \times \ \textrm{check}}},\ {SS}_{U{\textrm{new}\ \times \ \textrm{check}}}\right] , \textrm{and} \end{aligned}$$

neutrosophic mean squares and neutrosophic test statistics \(F_N\) are obtained as in the NANOVA Tables 1 and 2. The \(F_N\in [F_L,F_U]\), and the neutrosophic form of \(F_N\) is \(F_N=F_L+F_UI_{F_N};\ I_{F_N}\in [I_{F_L},I_{F_U}]\), where \(F_L\) and \(F_UI_{F_N}\) are determinate and indeterminate parts of each proposed test (see Aslam [46]). This test reduces to a test under classic statistic if \(I_{F_N}\) = 0 and \(I_{F_N}\)can be calculated by \({\left( F_U-F_L\right) }/{F_U.}\) Accordingly, the neutrosophic p value is \(p_N\in \left[ p_L,p_U\right] ,\) where \(p_L\) and \(p_U\) correspond to \(F_L\) and \(F_U\), respectively.

Neutrosophic hypotheses and decision rules

To test the blocks, checks and new treatments the null and alternative hypotheses are:

\( H_{N0}:{\alpha }_{Ni}=0\ \ {v}s\ \ H_{N1}:\mathrm{at\ least\ one\ \alpha }_{Ni}\ne 0,~i=1,\ 2,\ldots ,\ b, \)

\( H_{N0}:{\tau }_{Nqj}=0\ \ {v}s\ \ H_{N1}:\mathrm{at\ least\ one\ \tau }_{Nqj}\ne 0,~j=1,\ 2,\ldots ,\ c, \)

\( H_{N0}:{\tau }_{Nlig}=0\ \ {v}s\ \ H_{N1}:\mathrm{at\ least\ one\ \tau }_{Nlig}\ne 0,~g=1,\ 2,\ldots ,\ n_{(li)}. \)

The null hypothesis is not rejected if \(\textrm{min}\{p_\mathrm{N-value}\}\ge \alpha \), where \(\alpha \) is a level of significance. Conversely, the null hypothesis is rejected if \(\textrm{max}\left\{ p_\mathrm{N-value}\right\} <\alpha \). Under the neutrosophic normality assumption and if \(H_{N0}\) is correct, the \(p_N\)-value is obtained from F-distribution with the related degrees of freedom as given in the ANOVA Tables. Following [10], we present two ANOVA tables for unadjusted (A) and adjusted blocks (B), respectively. Two ANOVA tables are provided, one for unadjusted blocks (A) and the other for adjusted blocks (B). In the NANOVA Tables 1 and 2, the calculation formulas for testing the formulated neutrosophic hypotheses have been summarized for a NIBD as a NARCBD with a missing control treatment. In Table 2, the New by check interaction effect with one degree of freedom is separated which allows for testing the new genotypes. We provide a code in R for computing these NANOVA Tables. A code in R is made available for the computation of these NANOVA Tables.

Table 1 NANOVA Table (A) for NARCBD with a missing check
Full size table
Table 2 NANOVA Table (B) for NARCBD with a missing check
Full size table

Numerical example and simulation

In this section, the proposed NS for dealing with a missing value in an ARCBD is numerically assessed. For this purpose, a set of real neutrosophic data with uncertain observations from NARCBD with a missing check will be analyzed. A simulation study will also be contrived for evaluation. To assess the efficiency of the neutrosophic exact method for missing value analysis, the \(F_N{\in }[F_L,F_U]\) tests for the treatment effects are calculated and compared with the existing tests under classic statistics in terms of uncertainty.

Real data example

An experiment was run in three parts of a farm at the Isfahan University of Technology to study the safflower plant breeding program. In this experiment, 99 cultivars of safflower (an oil and medicinal plant) genotypes were planted using an NARCBD with three blocks. Each block contains 8 control (check) treatments and 25 genotypes (new treatments). The oil seed functions of the plants were measured and recorded in Table 8 (see the Appendix). To assess the exact analysis approach in this study, a check treatment is deleted (for instance, G35 being eliminated from the third block). The NANOVA Tables for this set of data including sums of squares (\({SS}_N\)) and the observed F-test statistics (\(F_N\)) with corresponding p values (\(p_N\)) are calculated based on the neutrosophic approximate and the proposed exact methods of dealing with a missing value in NARCBD. The results for the approximate method are summarized in Table 3 based on the neutrosophic estimate of missing observation \(y^{{*}}_{Nqmr}=\frac{{{by}_{Nqm.}+cy}_{Nq.r}{-}y_{Nq..}}{\left( c{-1}\right) \left( b{-1}\right) }=\left[ {600.6071,}\ {602.9157}\right] .\) Neutrosophic ANOVA Tables 4 and 5 present the results of the exact method for dealing with the same missing observation.

Simulation study

Now, by the following simulation study, the efficiency of the exact approach will be compared to the approximate method, as well as classic and neutrosophic statistics in analyzing data that contains missing values in NARCBD. For this purpose, the empirical neutrosophic type I error and the power of the test for neutrosophic treatment effects at a given nominal significant level were calculated. The simulation was carried out for the given number of treatments and blocks which are already presented in various existing examples (e.g., [10]). The data are first generated from the corresponding neutrosophic normal distribution. Then, by assuming nominal significant levels at 0.05 and 0.01, the MC method was employed to compute both the empirical neutrosophic type I error and the power of the test for neutrosophic treatment effects. The simulation was replicated 10,000 times for both methods.

Table 3 NANOVA for the NARCBD safflower experiment with a missing check (approximate approach)
Full size table
Table 4 NANOVA Table (A) for the NARCBD safflower experiment with a missing check (exact approach)
Full size table
Table 5 NANOVA Table (B) for the NARCBD safflower experiment with a missing check (exact approach)
Full size table

To calculate the neutrosophic empirical Type I error rate and the test power for an MC experiment, the following steps need to be completed (Figs. 1, 2):

MC simulation to compute \({{\alpha }}_{{\textrm{Empirical}}}\)

Step 1: The random sample \(x^{(i)}_{N1},x^{(i)}_{N2},\ldots ,\ x^{(i)}_{Nn}\) is generated from the neutrosophic normal standard distribution under \(H_{N0}\), \(i=1,2,\ldots ,10{,}000\).

Step 2: The \(F_{Ni}\)-test is computed under \(H_{N0}\).

Step 3: The results are recorded by assigning a value of \(I_{Ni}=1\) when the \(H_{N0}\) is rejected, and \(I_{Ni}=0\) otherwise.

Step 4: The ratio \(\frac{1}{10,000}\sum ^{10,000}_{i=1}{I_{Ni}}\) is computed and take it as \({\alpha }_{\textrm{Empirical}}\).

Step 5: The neutrosophic coefficient factor \(NCF=\frac{\alpha }{{\alpha }_{\textrm{Empirical}}}\) is computed.

MC simulation to compute \({\textrm{Power}}_{\textrm{Empirical}}\)

Step 1: The random sample \(x^{(i)}_{N1},~x^{(i)}_{N2},\dots ,\ x^{(i)}_{Nn}\) is generated from the neutrosophic normal standard distribution under \(H_{N1}\), \(i=1,2,\dots ,10{,}000\). For instance, \(({\mu }_{N1},{\mu }_{N2},{\mu }_{N3},{\mu }_{N4})=(0,1,2,4)\).

Step 2: The \(F_{Ni}\)-test is computed under \(H_{N1}\).

Step 3: The results are recorded by assigning a value of \(I_{Ni}=1\) when the \(H_{N1}\) is rejected, and \(I_{Ni}=0\) otherwise.

Step 4: The ratio \(\frac{1}{10,000}\sum ^{10,000}_{i=1}{I_{Ni}}\) is computed and take it as \(\textrm{Power}_\textrm{Empirical}\).

Step 5: The \(\textrm{Power}_\mathrm{Empirical({adj})}=NCF\times \textrm{Power}_\textrm{Empirical}\) is computed.

Fig. 1
figure 1

MC simulation for calculating \( \alpha _\textrm{Empirical} \) and NCF

Full size image
Fig. 2
figure 2

MC simulation for calculating Power\(_\mathrm{Empirical (adj)} \)

Full size image
Table 6 Empirical type I error rate for NARCBD with a missing check \( \left( b,\ c,{\ v},\ n\right) \) \(={(3,\ 4,\ 8,\ 20)} \)
Full size table
Fig. 3
figure 3

Empirical \({\alpha }\) of classic approximate and exact approaches for ARCBD \( (b=3,~c= 4, ~{v}=8,~n=20)\) with a missing check

Full size image
Fig. 4
figure 4

Empirical \({\alpha }_N\) of NAA and NEA for NARCBD \( (b=3,~c= 4, ~{v}=8,~n=20) \) with a missing check

Full size image

In this section, the calculations were completed using the R software. To achieve this, a code was created within the R program. The R program is a popular option for carrying out data analysis due to its strong statistical features and visualization capabilities. As an open-source programming language, users can access and customize the source code according to their specific requirements. Additionally, R offers a cost-effective solution for data analysis since it can be downloaded and used free of charge. R is frequently employed by data analysts and scientists, and many possess familiarity with its functions. The use of R can make the data science process unique and exciting because of its ability to perform various advanced and complex statistical computations. Moreover, R can present interpreted data graphically, making scientific reports easier to comprehend. The program’s capacity to compute enormous amounts of data quickly is also noteworthy [47,48,49,50]. Specifically, an R code was developed for this simulation study, taking advantage of the software’s exceptional ability to calculate and provide the necessary simulation materials.

The simulated neutrosophic type I error for exact and approximate methods were calculated and summarized in Table 6. The performance of the exact scheme is reliable due to having a close empirical type one error with the nominal \(\alpha \), but the approximate method exposes an inflated empirical type I error which means the null hypothesis is overly rejected. That is, the treatments may erroneously be considered significant. Meanwhile, the neutrosophic empirical type one error for both approximate and exact methods is better than the classic statistics. The superiority of exact over approximate method as well as neutrosophic over classic is evidently figured in Figs. 3 and 4. Figures 3 and 4 display classic empirical type I error, \({\alpha }_L\), and neutrosophic, \({\alpha }_N\), respectively, obtained for 200 times repetitions of the simulation. The empirical \({\alpha }_N\) for the exact method disperses around the nominal \(\alpha \)- level.

To measure the deviation proportion of empirical type I error from nominal more precisely, the neutrosophic coefficient factor (NCF) was defined as NCF = nominal \(\alpha {-}\textrm{level}/\textrm{Empirical}\) type I error = [ LCF, UCF] and calculated in the last columns of Table 6 for both approximate and exact methods. The closer NCF is to 1 prefigures the more precision of a method.

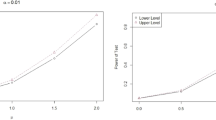
Table 7 Simulation results for NARCBD with a missing check \((b=3,~c=4,~{v}=8,~n=20)\) for Check treatment means \(\delta =\left( {\mu }_{N1},~{\mu }_{N2},~{\mu }_{N3},~{\mu }_{N4}\right) \) and different values of new treatments \(\left( {\mu }_{Ni}=0,~{\mu }_{Nj}=1\right) \),  \(i=1,\ldots ,4,~j=5, \ldots , 8\)
Full size table

For more investigation, the power of testing the neutrosophic treatment effects using NANOVA was also calculated for both methods. The results are recorded in Table 7 for NARCBD with \(\left( b{,\ }c{,\ v,\ }n\right) =\left( {3,\ 4,\ 8,\ 20}\right) \) and different sets of check means, \(\left( {\mu }_{N1},~{\mu }_{N2},~{\mu }_{N3},~{\mu }_{N4}\right) \) and new treatments given in the Tables for 0.05 and 0.01 significant levels. For more understanding, the results in Table 7 are graphically displayed in Figures 5 and 6; without loss of generality, the powers were plotted in ascending order. Figure 5 demonstrates the power of the treatment test for the classic exact (upper bound) and approximate (lower bound) methods, revealing the superiority of the exact proposed method. Figure 6 is the neutrosophic version of Fig. 5 with the same conclusion for the superiority of the exact method. Moreover, the neutrosophic color spectrum above the classic lower bound indicates the superiority of the neutrosophic model.

Discussion

This study was administrated with the aim of improving the analysis of uncertain and indeterminate data in the framework of NS for an augmented block design with a missing value. In classic statistics, the unrecorded observation is estimated and is used as the true value to analyze the data; however, the estimated value is intrinsically neutrosophic due to not matching the original value, exactly. Therefore, it is logical to use NS to deal with the estimated missing data.

Fig. 5
figure 5

Power curves of classic approximate and exact approaches for ARCBD \( (b=3,~c= 4, ~{v}=8,~n=20) \) with a missing check

Full size image
Fig. 6
figure 6

Power curves of NAA and NEA for NARCBD \( (b=3,~c= 4, ~{v}=8,~n=20) \) with a missing check

Full size image

In this study, the basic analytical needs were formulated for ANOVA of an ARCBD in the neutrosophic context in the presence of a missing value, though it is also useable for classic statistics; then, the proposed method was assessed by a set of real safflower plant data, numerically. A simulation study was also performed to see how precise are the neutrosophic approximate and exact methods. To assess the performances of these methods the empirical type I error and the power of the test for treatment effects have been used. The neutrosophic results disclosed a better performance than the classic; moreover, the proposed exact method performance was more efficient than the approximate method. For more illustration, the results showed that the empirical \( \alpha \) is a little inflated than that of nominal level in the approximate method, while, it was compatible with the nominal \( \alpha \) for the exact method. Interestingly, the exact method, either classic or neutrosophic, indicated a higher power of test than the neutrosophic approximate method. The results in Tables 6 and 7 and Figs. 3, 4, 5, 6 reveal the superiority of the proposed approach in this study. More advantages of the proposed neutrosophic model are tabulated below. Some disadvantages are also listed.

The code written in the R program for NACRBD with missing values, given online in the supplemental material, provides the NANOVA in which the adjusted unbiased \( SS_N \) of neutrosophic treatment effect is directly calculated. Moreover, the neutrosophic treatment effect is decomposed to check and new treatments. This eventuated to having the \( F_N \)-test statistics and \( p_N \)-values for each effect, separately. Furthermore, the \( F_N \)-tests in NANOVA offer greater flexibility, applicability, and information when compared with the existing F-tests for classic ARCBD in uncertain environments. Moreover, the post hoc test for each of the neutrosophic treatments as well as the new by check interaction is presented in this program which is crucial for determining the significant new genotypes. This code fills the calculation gap and the mistaken analysis of the data in classic ACRBD with a missing value.

Advantages

Disadvantages

The neutrosophic exact proposes approach in this study is more efficient than that of existing approximate method for dealing with missing value

Neutrosophic statistical models is more complex than traditional statistical models due to the incorporation of neutrosophic set theory

Neutrosophic logic furnishes a mathematical structure for depicting levels of indeterminacy which can aid researchers in addressing the intricacies that arise from real-world data

The results obtained from neutrosophic statistical models may be difficult to be interpreted due to the inherent uncertainty in the data and model assumptions

The neutrosophic model is more flexible and versatile that allows for the handling of uncertainty and indeterminacy in data and analysis in diverse contexts

Understanding of the indeterminacy in a system is both in a subjective and an objective sense such as uncertainty or vagueness that sometimes, it is hard to be redefined from a formal point of view

Using a neutrosophic model enables one to collect novel information from linguistic sources not present in a classic model

 

Using NARCBD decline the limitation on the number of new treatments that can be included in the experiment

 

The neutrosophic approach reduces the computational complexity and time, though having more complex mathematical formula

 

Neutrosophic model leads to a more powerful test than that of classic one

 

Utilizing the neutrosophic models leads to more comprehensive, precise, dependable, and enlightening outcomes

 

Limitations and future research directions

This paper deals with the issue of one missing values; however, this can be extended to more than a missing value which make the problem become more complicated. For instance, in the case of two missing values, one encounter with three distinct scenarios in terms of missing cells. In the future study, the aim could be of delving this issue and extend the results to the problem of numerous missing values. Upon detecting a biased problem resulting from missing values, there are various methods to address the resolving the biasedness. Selecting a method that effectively minimizes bias is of utmost importance. The exact method proposed in this study has been limited to the ARCBD. However, in the future studies, the problem of missing values can be studied in any augmented design including augmented Latin square design, row-column design, split-plot design, etc. Finally, this study is limited to neutrosophic normality; however, in the real life, there are messy data which may not be normal. For example, data with heavy- or skewed-tail distributions are very often appeared which should be considered in the future studies.

Conclusions

The indeterminacies in data oblige ones to employ the neutrosophic type of data analysis; yet, due to the existing error and vagueness in the environment in the usual situations, applying the neutrosophic model could evermore lead to an improvement of the results. However, it must be noted that this is always an advance in methodology, making the improvement significant. Here, in this study, the proposed exact approach made the difference. Nevertheless, the progress in the computational aspect and developing a new code in the R software program should not be disregarded. This was the first attempt to consider the missing values as uncertainty matter and propose the neutrosophic model to deal with it in addition to considering the intrinsic indeterminacies in data. Moreover, all are applied for a design that is not simple, though it is very useable. Although it is conceivable that missing neutrosophic analysis using a detailed approach leads to a more efficient result, the lack of an analytical base for such an approach has prevented us from enjoying such an advantage. This study has provided a suitable environment for data analysis in such conditions. The proposed neutrosophic exact approach and obtained NANOVA, including the \( F_N \)-tests, offer greater accuracy, flexibility, applicability, and information when compared with the existing F-tests in uncertain environments.

Table 8 Data for safflower genotypes (observation values in blocks)
Full size table

Supplemental material

The code in R for computational materials in this manuscript can be accessed through the following link. https://github.com/AbdAita/augmented_designs.