Introduction

With the rapid proliferation of artificial intelligence technology, multi-agent systems (MASs) are widely utilized in complex tasks due to their autonomous, distributed and coordinated characteristics [1]. With the maturity of target recognition and localization technologies, multi-agents are expected to supersede humans for efficient patrol and rescue tasks in dangerous environments. Multi-agent search strategies have been widely studied, and search tasks are completed according to the cooperative strategies between the control system and agents [2,3,4].

For multi-agent multi-target (MAMT) search strategies, traditional algorithms usually employ random search methods [5, 6] and grid search methods [7]. However, random search methods require accurate knowledge of the environment in advance, which is a tough task in practical applications. Since the search trajectory is fixed, the search efficiency of the grid search will be affected by the target location. Therefore, traditional algorithms [5,6,7] are not suitable in complex environments where targets are not fixed.

The emergence of deep reinforcement learning (DRL) is beneficial to solve the problem that the agents can perform information interaction and decision-making in unknown environments. For MAMT search strategies, traditional reinforcement learning (RL) algorithms such as Q-Learning [8] and Policy Gradient [9] algorithms are not suitable for multi-agent dynamic environments. This is because that during the training of agents, the policy adjustment of each agent will make the environment to become extremely unstable, which leads to difficulty in the convergence of the system. To solve this problem, many algorithms based on multi-agent training have been proposed, e.g., Deep Q-Learning Networks (DQN) [10] and deep deterministic policy gradient (DDPG) algorithms [11]. Although the above algorithms [10, 11] solve the problem of unstable environment to a certain extent, DRL is prone to cause the strategies to fall into local optima, which leads to the low robustness of the MAS. In addition, the sparse rewards in DRL will cause the algorithm to iterate slowly and even difficult to converge.

To address the above concerns, we design a MiniMax Multi-agent Deep Deterministic Policy Gradient based on Parallel Hindsight Experience Replay (PHER-M3DDPG) algorithm. The main contributions of this paper are summarized as follows:

  • As to existing multi-agent reinforcement learning methods, the policy of each agent can be very sensitive and fragile to the policies of the agents other than itself. Therefore, to enhance the system robustness, we leverage the minimax strategy to define the objective function, which takes the external disturbance received by the agents as part of the cumulative reward. By doing so, the reward space of the agents can be expanded to enhance the exploration ability of agents.

  • To address the problem of sparse rewards, we employ a hindsight experience replay mechanism to improve the sampling strategy of experience replay and promote the utilization efficiency of the sampled data. Different from the existing methods of avoiding repeated sampling in the same batch of data, we divide the experience data into multiple batches and put them into multiple threads for processing. By doing this, data diversity and the utilization of experience data can be improved.

  • We verify the effectiveness of the proposed algorithm in the MAMT search scenario. Evaluation results show that the PHER-M3DDPG algorithm can adaptively adjust the strategies of agents and outperform the existing algorithms in terms of convergence speed and task completion time.

Related work

This section will review the related work from the following three aspects: (1) traditional algorithms for multi-target search; (2) RL algorithms for multi-target search; (3) solutions for sparse rewards.

Traditional algorithms for multi-target search

For studies in known environments, Luo et al. [12] adopted genetic algorithm to obtain the shortest path and conducted target search in a two-dimensional stationary environment. Li et al. [13] adopted a Grover quantum search algorithm based on weighted target superposition, and the target search task is accomplished by approximating the probability of each target as the corresponding weight coefficient. Sisso et al. [14] proposed a robust satisfaction algorithm based on the information gap theory, which allows the agents search for stationary targets on a given map. Baum et al. [15] proposed a search- theoretic algorithm based on the rate of return maps and formulated a collaborative unmanned aerial vehicles (UAVs) search plan to complete the search for stationary targets. Garcia et al. [16] proposed a new scheme for multi-agent coordinated search to find multiple targets in a search area. In unknown environments, based on the Nash equilibrium in game theory, Sujit et al. [17] designed a strategies theory for uncertainty reduction in a search space to make the agents search for targets. Leahy et al. [18] adopted multiple noisy binary sensors to track the movement of objects in a Markov chain with symmetrical false-alarm and missed-detection probabilities in a discrete environment. Chen et al. [19] proposed a meta-heuristic algorithm to solve the pickup and delivery problem of multi-robots where each robot can carry multiple packages. However, due to the randomness of the targets in the unknown environment, the traditional algorithms [12,13,14,15,16,17,18,19] drastically degrade the search efficiency and are not suitable for the dynamic and complex environment.

RL algorithms for multi-target search

To improve the searching efficiency of the agents, DRL [20] is utilized to train the strategies of multi-agent to implement the information interaction. Cao et al. [21] utilized the Asynchronous Advantage Actor-Critic (A3C) network structure to generate search strategies for various unknown environments to complete the multi-target search. Wang et al. [22] adopted the target localization algorithm of DQN and multi-task learning to design a new reward function to reduce the number of search steps of the agents in each localization. Sun et al. [23] proposed a robust UAV autonomous aerial refueling detection and tracking strategy, which includes a deep learning-based detector and an RL-based tracker to achieve rapid acquisition of target positions during the tracking phase. In the generative adversarial architecture algorithm for neural architecture search, Shi et al. [24] took the generator as the search target and adopted a distributed search algorithm based on RL to update the controller parameters to improve the efficiency of architecture search. Chen et al. [25] utilized an enhanced multi-agent RL to coordinate multiple UAVs for real-time target tracking. In RL, the reward function plays an important role, and the agents optimize the policies based on the reward. In the multi-target search scenario, due to the complex reward mechanism, the reward is sparse or even no reward is given to agents, which hinders the effective learning of the agents.

Solutions for sparse rewards

To address these concerns, it is necessary to construct dense rewards to improve the efficiency of system exploration [26]. At present, the solutions to the problem of sparse rewards mainly consist of the following three categories: multi-target learning [27, 28], reward design and learning [29, 30], and experience replay mechanism [31, 32]. Wang et al. [27] proposed a DRL algorithm based on non-professional assistance, which explores the state space by reshaping the environmental interaction behavior policy to help the agent achieve the goal. Vecchietti et al. [28] utilized unsuccessful experiences and took them as successful experiences achieving different goals to improve the training performance on the task. To improve the efficiency of the robot trajectory planning algorithms in unstructured working environments with obstacles, Xie et al. [29] proposed an orientation reward function by modeling position and orientation constraints to reduce the blindness of exploration. For the target recognition problem, Zeng et al. [30] adopted inverse RL to design a reward function, so that the target can be more accurately identified. Kang et al. [31] proposed a DDPG algorithm based on the double network priority experience replay mechanism, which divides the importance of samples in the experience replay mechanism to improve the convergence speed of the algorithm. Na et al. [32] proposed a bio-inspired collision avoidance strategy by utilizing virtual pheromones, which combined highlight experience replay with a deep deterministic policy gradient algorithm to increase the sampling rate. However, in the complex and dynamic multi-target search environment, the above algorithms [27,28,29,30,31,32] will consume more computational resources in the selection of targets in the complex dynamic multi-target search environment and cannot be extended to on-policy learning algorithms.

Therefore, in the complex environment of MAMT search, to solve the problem of sparse rewards while improving the system efficiency, robustness and transferability, we designed the PHER-M3DDPG algorithm. The agents make real-time decisions through a centralized training and decentralized execution architecture in a continuous and complex environment.

Background and preliminary

Markov decision process

Markov decision process (MDP) is a stochastic dynamic optima decision process based on Markov process theory, i.e., the next state of the system is only related to the current state. In MDP, actions are considered, and the next state of the system is related not only to the current state, but also to the current action taken. A Markov process can be represented by a quintuple \(M = (s,a,p,R,\gamma )\), where s is the state set of the system; \(a = ({a_1},{a_2},...,{a_N})\) is the set of actions in the state s; p is the state transition probability; R is the reward function related to state and action. \(\gamma \ (0 \le \gamma \le 1)\) is the discount factor for calculating the cumulative income of the whole process. The total return of the system at time t is \({G^t} = {R^{t + 1}} + \gamma {R^{t + 2}} + \cdots + {\gamma ^n}{R^{t + N}}\), which means that the farther away from the current state s, the smaller the impact is.

Deterministic policy gradient algorithm

The deterministic policy gradient (DPG) algorithm introduces the deterministic idea into the policy gradient algorithm and employs a deterministic function \(a = {\mu _\theta }(s)\) to represent the policy. In the current state, the action chosen by the DPG algorithm is a determinate value rather than a probability distribution. The gradient of the objective function \(J(\theta ) = {E_{s \sim {\rho ^\mu }}}[R(s,a)]\) is given by

$$\begin{aligned} J(\theta ) = {E_{s \sim \mathrm{{\mathcal{D}}}}}[{\nabla _\theta }{\mu _\theta }(s){\nabla _a}{Q^\mu }(s,a){\vert _{a = {\mu _\theta }(s)}}], \end{aligned}$$
(1)

where \(\mathrm{{\mathcal{D}}}\) is the experience replay buffer, and \({Q^\mu }(s,a)\) is the value Q of the evaluation action generated when the action is selected according to the strategy \(\mu \) in the state s. Since the action space a is continuous, the strategy \(\mu \) is also continuous.

Fig. 1
figure 1

The architecture of the PHER-M3DDPG algorithm

Full size image

PHER-M3DDPG algorithm

As shown in Fig. 1, the PHER-M3DDPG algorithm is mainly based on MDP and the Multi-Agent Deep Deterministic Policy Gradient (MADDPG) algorithm and employs the minimax objective optimization strategy to improve the cumulative reward of the agents. To solve the problem of sparse rewards generated during the exploration process, the PHER-M3DDPG algorithm adopts a parallel hindsight mechanism. The exploration space is increased by involving virtual targets, and the collected data is batched and put into multiple threads for processing to improve the utilization efficiency of the sampled data.

Architecture design of the PHER-M3DDPG algorithm

A. Reward value design

In the multi-target search environment, both the number of the agents and the targets are N. The aims of agents are to reach the corresponding target points in the shortest time. In the process of task execution, it is necessary to execution collision avoidance among agents as well as between the agents and the obstacles. The reward of the agents depends on the distance to the target points and whether a collision occurs. The reward value of agent i (denoted as \({r_i}\)) is formulated as

$$\begin{aligned} {r_i} = - \min \left\{ {D({a_i},t{g_i})\vert \forall i \in \{ 1,2,...,N\} } \right\} + C, \end{aligned}$$
(2)

where \({a_i}\) denotes agent i, \(t{g_i}\) denotes the target point of agent i, and \(D({a_i},t{g_i})\) denotes the distance between agent i and target i and is calculated by

$$\begin{aligned} D({a_i},t{g_i}) = \sqrt{{{({x_i} - {x_i}')}^2} + {{({y_i} - {y_i}')}^2}}, \end{aligned}$$
(3)

where \(({x_i},{y_i})\) and \(({x_i}',{y_i}')\) are the coordinates of \({a_i}\) and \(t{g_i}\), respectively. C is the indicator of collision among agents and is given as

$$\begin{aligned} C = \left\{ \begin{array}{l} \ -1,\mathrm{{ \quad if\ collision\ occurs\ among\ agents;}}\\ \quad 0,\mathrm{{ \quad otherwise}}\mathrm{{.}} \end{array} \right. \end{aligned}$$
(4)
Fig. 2
figure 2

Scene settings. a Without interference. b With interference

Full size image

B. Optimization objective formulation

The PHER-M3DDPG algorithm is a multi-agent RL algorithm based on the Actor-Critic network architecture [33]. The PHER-M3DDPG algorithm takes fixed discrete time as the step and interacts with the environment in real time to generate data. The optimal joint strategy \(\pi (a\vert s)\) learned from the previous experience is calculated as

$$\begin{aligned} \pi (a\vert s) = \prod \limits _{i \in N} {{\pi _i}({a_i}\vert s)}, \end{aligned}$$
(5)

where \({\pi _i}\) is the strategy of agent i. The multi-agent RL algorithm is an objective optimization problem in multi-agent non-stationary environment. The objective function is denoted as \({\pi ^*}\) and is calculated by

$$\begin{aligned} {\pi ^*} = \arg \mathrm{{ }}\max {E_\pi }\bigg (\sum \limits _{i = 1}^N {R_i^t} \bigg ), \end{aligned}$$
(6)

where \(R_i^t\) denotes the cumulative reward of agent i at time t.

C. Search strategy formulation

Different from the random strategy search algorithm [34], the PHER-M3DDPG algorithm adopts a heterogeneous search strategy, i.e., the Actor network adopts a random strategy update to ensure sufficient exploration, and the Critic network adopts a deterministic search strategy to reduce the size of sampled data. The random gradient descent method is given as \({\nabla _{{\theta _i}}}J({\theta _i})\) and is formulated as

$$\begin{aligned} {\nabla _{{\theta _i}}}J({\theta _i})= & {} {E_{\textrm{x},a \sim \mathrm{{\mathcal{D}}}}}[{\nabla _{{\theta _i}}}{\mu _i}({o_i})\nonumber \\{} & {} \times {\nabla _{{a_i}}}Q_i^{\vec {\mu } }(\textrm{x},{a_1},{a_2},...,{a_N}){\vert _{{a_i} = {\mu _i}({o_i})}}], \end{aligned}$$
(7)

where \({o_i}\) and \({a_i}\) denote the observation value and action value of agent i, respectively. \(\textrm{x} = ({o_1},{o_2},...,{o_N})\) denotes the observation space, \(\vec {\mu } = ({\mu _1},{\mu _2},...,{\mu _N})\) denotes the set of strategies \(\mu \), \(Q_i^{\vec {\mu } }\) denotes a centralized action value function learned by agent i, and \({\nabla _{{\theta _i}}}{\mu _i}({o_i}){\vert _{{a_i} = {\mu _i}({o_i})}}\) denotes the action \({a_i}\) that selects agent i according to the policy \(\mu \). The Critic network for each agent is iteratively updated by minimizing the loss function \(\mathrm{{\mathcal{L}}}({\theta _i})\) and is calculated by

$$\begin{aligned} \mathrm{{\mathcal{L}}}({\theta _i}) = {E_{\textrm{x},a,r,\textrm{x}'}}[{(Q_i^\mu (\textrm{x},{a_1},{a_2},...,{a_N}) - y)^2}], \end{aligned}$$
(8)

where y is the temporal difference (TD) target value and is formulated as

$$\begin{aligned} y = {r_i} + \gamma Q_i^{\mu '}(\textrm{x}',a{'_1},a{'_2},...,a{'_N}){\vert _{a{'_j} = \mu {'_j}({o_j})}}, \end{aligned}$$
(9)

where \(\mu '\) is the target policy for delaying soft update parameters. We maximize the Q value of the action-value function by minimizing the loss function to find the appropriate action.

Minimax optimization

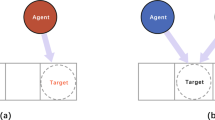
In the process of multi-target search, the strategy of an agent is not optimized in terms of acquiring information, which may result in unfair behavior. In addition, as the strategies of other agents change, the learning strategy of the agent we are training cannot be updated in time, resulting in the system falling into the local optimum [35]. As shown in Fig. 2, to solve this problem, we introduce a minimax objective optimization and update the strategy to enhance the robustness of the agent by considering the worst case for the agent itself.

To improve the robustness of the system, we add interference to the MAS for analysis. Figure 2a is the search scene in the normal state without interference from competing agents. Figure 2b shows that the interfering agents will compete with the agent to find the targets, which will lead to a change in the strategy learned by the agent being trained. Therefore, the purpose of adopting the minimax strategy is to optimize the objective function of the multi-agent system during training and enhance the robustness of each agent. Compared with Eq. (1), the minimax objective function is defined as \({\max _{{\theta _i}}}{J_M}({\theta _i})\), where the \({J_M}({\theta _i})\) is given by

$$\begin{aligned} {J_M}({\theta _i})&= {E_{s \sim {\rho ^\mu }}}[R_i^t]\nonumber \\&= \mathop {\min }\limits _{a_{j \ne i}^t} {E_{s \sim {\rho ^\mu }}}\bigg [\sum \limits _{t = 0}^T {{\gamma ^t}{r_i}({s^t},a_1^t,a_2^t,...,a_N^t)\left| {_{a_i^t = \mu (o_i^t)}\bigg ]} \right. }, \end{aligned}$$
(10)
$$\begin{aligned}&= {E_{{s^0} \sim \rho }}\bigg [\mathop {\min }\limits _{a_{j \ne i}^0} Q_{M,i}^\mu ({s^0},a_1^0,a_2^0,...,a_N^0){\vert _{a_i^0 = \mu (o_i^0)}}\bigg ], \end{aligned}$$
(11)

where \({a^0} = (a_1^0,a_2^0,...,a_N^0)\) is the set of agent actions at time \(t=0\). In Eq. (10), the state \({s^{t + 1}}\) of the agent at time \(t+1\) depends not only on the state probability distribution \({\rho ^\mu }\), but also on the action strategy \({\mu _i}(o_i^t)\). In Eq. (11), \(\mathop {\min }\nolimits _{a_{j \ne i}^0} Q_{M,i}^\mu \) denotes the robustness of minimizing the action value function \(Q_{M,i}^\mu \) of other agents to select the worst action to train agent i.

According to Eqs. (10) and (11), we know that the objective function is optimized by maximizing the minimum action value function of other agents. Therefore, after involving the minimum value to Eq. (7), the policy gradient descent method is updated as

$$\begin{aligned}{} & {} {\nabla _{{\theta _i}}}{J_M}({\theta _i}) \nonumber \\{} & {} \quad = {E_{\textrm{x} \sim \mathcal{D}}}{\left[ \begin{array}{l} {\nabla _{{\theta _i}}}{\mu _{{\theta _i}}}({o_i}){\nabla _{{a_i}}}Q_{M,i}^{\vec {\mu } }(\textrm{x},a_1^ \star ,...,{a_i},...,a_N^ \star )\vert \\ \mathrm{{ }}{a_i} = {\mu _i}({o_i})\\ \mathrm{{ }}a_{j \ne i}^ \star = \arg {\min _{{a_{j \ne i}}}}Q_{M,i}^{\vec {\mu } }(\textrm{x},{a_1},{a_2},...,{a_N}) \end{array} \right] _.} \nonumber \\ \end{aligned}$$
(12)

When calculating the target Q value, we involve the minimum value and update the loss function as follows

$$\begin{aligned} \mathrm{{\mathcal{L}}}({\theta _i}) = {E_{\textrm{x},a,r,\textrm{x}'\sim \mathcal{D}}}\left[ {{{(Q_{M,i}^\mu (\textrm{x},{a_1},{a_2},...,{a_N}) - y)}^2}} \right] , \nonumber \\ \end{aligned}$$
(13)

where y is the TD target value and is calculated as

$$\begin{aligned}{} & {} y = {r_i} + \gamma Q_{M,i}^{\mu '}(\textrm{x}',a'^ \star _1,...,a{'_i},...\nonumber \\{} & {} \quad ,a'^ \star _N ){\vert _{a{'_j} = \mu {'_i}({o_i}),a'^ \star _{j \ne i} = \arg \mathop {\min }\limits _{a{'_{j \ne i}}} Q_{M,i}^{\mu '}(\textrm{x}',a{'_1},a{'_2},...,a{'_N}),}} \end{aligned}$$
(14)

where \(\mu {'_i}\) denotes the target policy of agent i with delay parameter \(\theta {'_i}\).

Parallel hindsight experience replay

In the MAMT search process, there is a sparse binary reward, i.e., the agents will receive a reward only when the task is completed. In this environment, the MAS is difficult to converge. To solve this problem, the Hindsight Experience Replay (HER) mechanism is introduced.

The data in traditional experience replay is represented as \(({s^t},{a^t},{r^t},{s^{t + 1}})\), while the HER mechanism involves an extra parameter: target G, i.e., \(({s^t},{a^t},{r^t},{s^{t + 1}},g),g \in G\). G is divided into the desired goal and the completion goal. The desired goal is the final goal of the task, and the completion goal is the goal that has been completed at the current time step, which is also expressed as a virtual goal. In tasks with sparse rewards, the agents will only obtain a positive reward after completing the desired goal. However, there are not many cases of reaching the desired goal, which also causes the agents to fail to learn a better policy [31]. The HER mechanism makes the reward “intensive” by replacing the currently completed goal with the desired goal with a certain probability, thereby reducing the difficulty of obtaining the reward for the task. In the MAMT search process, the experience replay data method in the HER mechanism is formulated as \(({s^t},{a^t},{r^t},{s^{t + 1}},e{g^t},a{g^t},a{g^{t + 1}})\), where \({s^t}\) denotes the state of the agent at time t, \({a^t}\) denotes the action of the agent at time t, and \({r^t}\) denotes the reward obtained by the agent at time t, \(e{g^t}\) denotes the desired goal of the agent at time t, \(a{g^t}\) denotes the goal that the agent has completed at time t, and \(a{g^{t + 1}}\) denotes the goal that the agent has completed at time t+1.

It can be seen from Eq. (12) that the gradient update method \({\nabla _{{\theta _i}}}{J_M}({\theta _i})\) of the objective function is related to the sampling of the experience replay pool. The K pieces of experience data are randomly obtained from the sampling pool. The data is divided into multiple batches, and the amount of data in each batch is k. Both K and k are integers. Assume that the time required for sampling k pieces of data from the experience replay pool is T. There is a certain mapping relationship between T and \({\nabla _{{\theta _i}}}{J_M}({\theta _i})\), i.e., \(f:T \rightarrow {\nabla _{{\theta _i}}}{J_M}({\theta _i})\). Then, if K/k threads are executed parallel, the time for each thread to take k pieces of data from the experience replay pool is still T, i.e.,

$$\begin{aligned} T = f(\nabla _{{\theta _i}}^1{J_M}({\theta _i})) = \cdots = f(\nabla _{{\theta _i}}^{K/k}{J_M}({\theta _i})). \end{aligned}$$
(15)

Since \(\nabla _{{\theta _i}}^1{J_M}({\theta _i}),...,\nabla _{{\theta _i}}^{K/k}{J_M}({\theta _i})\) are all sampled from the experience replay pool \(\mathcal{D}\), it can be seen from Eq. (15) that parallel processing in the same time expands the throughput of experience data by K/k times, which increases the diversity of data and improves the sampling efficiency.

The details of the PHER-M3DDPG algorithm are summarized in the Algorithm 1.

figure a
  1. (1)

    Initialization (Lines 1–3): The PHER-M3DDPG algorithm adopts the framework of centralized training and decentralized execution. The parameters of the Actor network and Critic network are initialized and updated during training according to learning steps, and the Maximum step length is \({E_{\max }}\). In addition, the sampled data size K and the batch of data size k are initialized.

  2. (2)

    Experience storage (Lines 5–7): During the training process, the action \(a =({a_1},{a_2},...,{a_N})\), reward and new state \(x'\) generated by the agents are stored in the experience replay pool \(\mathrm{{\mathcal{D}}}\) as a quadruple \((x,a,r,x')\).

  3. (3)

    Parallel data processing (Lines 8–13): During the entire training episodes, K/k threads are started when each time K steps are executed. Thread i initializes worker i, i = 1,2,..., K/k. Thread i samples k pieces of experience data from the experience replay pool. The policy loss for k pieces of experience data is calculated by TD bias \(\delta \). The deviation \(\delta \) is calculated by

    $$\begin{aligned} \delta = {(y - {Q^\pi }(s,{a_1},{a_2},...,{a_N}))^2}. \end{aligned}$$
    (16)
  4. (4)

    Parameter update (Lines 14–17): During the training process, the observation value \(\textrm{x} = ({o_1},{o_2},...,{o_N})\) of the agents is utilized as the input of the Actor network to generate the policy \({\mu _\theta }(s)\). The parameters of the Actor network for each agent are updated by the policy gradient, which is formulated as

    $$\begin{aligned}{} & {} {\nabla _{{\theta _i}}}J \approx \frac{1}{S}\sum \limits _j {{\nabla _{{\theta _i}}}{\mu _i}(o_i^j)} {\nabla _{{a_i}}}Q_{M,i}^\mu ({x^j},a_1^j,a_2^j,...,\nonumber \\{} & {} \qquad \qquad a_N^j){\vert _{{a_i} = {\mu _i}(o_i^j)}}. \end{aligned}$$
    (17)

In addition, we update the Critic network in the main network learner according to the sub-thread worker i with the largest loss function value, which is calculated by

$$\begin{aligned} \mathrm{{\mathcal{L}}}({\theta _i}) = \frac{1}{S}{\sum \nolimits _j {\left( {({y^j} - Q_i^\mu ({x^j},a_1^j,a_2^j,...,a_N^j)} \right) } ^2}, \end{aligned}$$
(18)

where \(Q_i^\mu \) is the Q value generated when agent i selects an action according to strategy \(\mu \). The loss of the system is minimized by the update of Critic network, i.e., maximize the Q value. In addition, the choice of action is related to the Q value.

Complexity analysis

The PHER-M3DDPG algorithm is endowed with an experience replay buffer and 2(K/k +1) Actor-Critic neural networks. During the off-line training and online execution phases, the nonlinear mapping of states to actions is achieved by deep neural networks. Suppose that the Actor-network contains J fully connected layers, and the Critic network contains L fully connected layers, the time complexity of the PHER-M3DDPG algorithm (denoted as \({T_\mathrm{{PHER - M3DDPG}}}\)) is given by

$$\begin{aligned}{} & {} {T_\mathrm{{PHER - M3DDPG}}} \nonumber \\{} & {} \quad = 2(K/k + 1) \times \sum \limits _{j = 0}^{J -1} {{u_{\mathrm{{actor}},j}}{u_{\mathrm{{actor}},j + 1}}\,}\nonumber \\{} & {} \qquad { + \,2(K/k + 1)} \sum \limits _{l = 0}^{L - 1} {{u_{\mathrm{{critic}},l}}{u_{\mathrm{{critic}},l +1}}} \nonumber \\{} & {} \quad = {O\bigg (\sum \limits _{j = 0}^{J - 1}{{u_{\mathrm{{actor}},j}}{u_{\mathrm{{actor}},j + 1}}} \, + \,\sum \limits _{l = 0}^{L - 1} {{u_{\mathrm{{critic}},l}}{u_{\mathrm{{critic}},l + 1}}}} \bigg ), \nonumber \\ \end{aligned}$$
(19)

where \({u_{\mathrm{{actor}},j}}\) denotes the number of neurons in the layer j of the Actor network, and \({u_{\mathrm{{critic}},l}}\) denotes the number of neurons in the layer l of the Critic network.

The fully connected neural network consists of a matrix of \(P \times Q\) and a bias of Q. Therefore, the number of storage unit required by a fully connected neural network is \((P + 1) \times Q\), and thus the space complexity is O(f). In addition, it is also necessary to allocate storage space to the experience replay pool B to store information in the process of training, and the space complexity is O(B). Therefore, the space complexity of the PHER-M3DDPG algorithm (denoted as \({S_\mathrm{{PHER - M3DDPG}}}\)) is given by

$$\begin{aligned}{} & {} {S_\mathrm{{PHER - M3DDPG}}}\nonumber \\{} & {} \quad = (K/k + 1) \times \sum \limits _{j = 0}^{J - 1} {({u_{\mathrm{{actor}},j}}\, + \,1){u_{\mathrm{{actor}},j + 1}}} \,\nonumber \\{} & {} \qquad + \,\,(K/k + 1) \times \sum \limits _{l = 0}^{L - 1} {({u_{\mathrm{{critic}},l}}\, + \,1){u_{\mathrm{{critic}},l + 1}}} \, + \,B \nonumber \\{} & {} \quad = \,\underbrace{{O\bigg (\sum \limits _{j = 0}^{J - 1} {{u_{\mathrm{{actor}},j}}{u_{\mathrm{{actor}},j + 1}}} \, + \,\,\sum \limits _{l = 0}^{L - 1} {{u_{\mathrm{{critic}},l}}{u_{\mathrm{{critic}},l + 1}}}} \bigg )}_{O(f)}\nonumber \\{} & {} \qquad + {O(B)}. \end{aligned}$$
(20)

In the distributed execution stage, only the trained actor network is needed. Therefore, the space complexity of the execution phase is formulated as

$$\begin{aligned} {O\bigg (\sum \limits _{j = 0}^{J - 1} {{u_{\mathrm{{actor}},j}}{u_{\mathrm{{actor}},j + 1}}}}\bigg ) + O(B), \end{aligned}$$
(21)

and the time complexity is formulated as

$$\begin{aligned} {O\bigg (\sum \limits _{j = 0}^{J - 1} {{u_{\mathrm{{actor}},j}}{u_{\mathrm{{actor}},j + 1}}}}\bigg ). \end{aligned}$$
(22)

Performance evaluation

Simulation settings

We verify the performance of the PHER-M3DDPG algorithm through numerical simulation experiments. Experimental platform is built based on Intel(R) Core (TM) i5-8500 and Tensorflow 1.14. As shown in Fig. 3, we employ OpenAI Gym [36] to build the simulation environment of the MAMT search and train the agents based on the “simple_spread” environment in Gym. The experimental parameters are shown in Table 1.

Fig. 3
figure 3

The simulation environment in Gym

Full size image
Table 1 Simulation parameters
Full size table

Results analysis

In this section, to prove the scalability of the algorithm, we first analyze the convergence of the average reward value with a different number of agents. Secondly, we demonstrate the performance change of the PHER-M3DDPG algorithm with different number of CPUs and k. Finally, in terms of task completion time and convergence, we compare the PHER-M3DDPG algorithm with four related algorithms.

A. Extensibility analysis

To prove the scalability of our proposed model, we set both the number of the agents and the targets as N, and the number of obstacles as J. As shown in Fig. 4, we perform experiments with the agents of 3, 4, 5, and 6, respectively. From the figure, we can see that regardless of the number of agents, the average reward curve of the system can reach a state of convergence. Without loss of generality, we select the number of agents as 3 as a reference.

Fig. 4
figure 4

Analysis of mean episode reward convergence with different number of the agents

Full size image
Fig. 5
figure 5

The time of task completion with different number of CPUs. a The number of CPUs is 2. b The number of CPUs is 4. c The number of CPUs is 6

Full size image

B. Four related comparison algorithms

MADDPG: The MADDPG [37] algorithm adopts the framework of centralized training and decentralized execution, so that the agent can search for targets in a continuous action space.

HER-MADDPG: Based on the MADDPG algorithm, an HER mechanism is added to optimize the objective function to solve the problem of sparse rewards.

HER-M3DDPG: The HER-M3DDPG algorithm adopts minimax strategy and the HER mechanism, and mainly solves the problems of poor robustness in MASs [38, 39].

PER-MATD3: The PER-MATD3 algorithm is improved based on the double-delay deep deterministic policy gradient algorithm [40], which is mainly utilized to solve the problems of Q overestimation and poor sampling efficiency of the system in MADDPG.

C. Performance comparisons

(1) Performance analysis with different number of CPUs

As shown in Fig. 5, We train in three systems with 2, 4, and 6 CPUs, respectively, and analyze the time required for the agents to complete the task.

  • As the number of CPUs increases, the agents take less time to complete the task, and the shortest time can reach 45 s.

  • The time required for agents to complete the task is not only related to the number of CPUs, but also the choice of k. We comprehensively consider the selection of k with different number of CPUs and found that the optimal batch of data is k = 128.

According to the above figures, we can see that the more number of CPUs, the less time the system needs to process tasks. The choice of k directly affects our training speed. Therefore, to more intuitively see the optimal k with different number of CPUs, we compare the task completion time at 40,000 episodes of agents. From Fig. 6, we know that when the number of CPUs is 2 or 4, the time taken by the agent to complete the task changes greatly. Therefore, the number of k greatly affects the training of agents. It can be seen from the figure that the time required for agents to complete the task is closest to the average level when k = 128, i.e., the optimal batch of data is k = 128.

Fig. 6
figure 6

The task completion time of the agent with 40,000 episodes

Full size image

((2) Collision rate and stability analysis with different values of k

As shown in Fig. 7a, we train the agents with different numbers of k. The training results show that the PHER-M3DDPG algorithm tends to converge around 2000 episodes, and the collision rate approaches 0 around 6000 episodes.

As shown in Fig. 7b, to see the fluctuation of the curve more intuitively, we utilize boxplots for comparative analysis in the three cases of \(k =32\), 64, and 128. From the simulation results, as the value of k increases, the fluctuation of the curve gradually becomes smaller. When k = 128, the curve is the most stable one, and the effect of system training is better.

Fig. 7
figure 7

Collision rate and stability analysis. a Collision rate between agents. b Stability of collision rates across batches

Full size image

(3) Performance comparisons with four related schemes

As shown in Fig. 8, to verify the performance of the PHER-M3DDPG algorithm, we analyze it from three aspects: algorithm convergence, rate of winning and completion time of task.

Fig. 8
figure 8

Performance comparison. a Convergence analysis. b Winning rate comparison. c The task completion time comparison

Full size image

  • From Fig. 8a, we know that the PHER-M3DDPG algorithm reaches the convergence state in about 5000 episodes. It is proved that the parallel hindsight experience replay mechanism can effectively improve the data utilization rate and accelerate the convergence speed of the system.

  • As shown in Fig. 8b, to demonstrate the superiority of the PHER-M3DDPG algorithm in the environment of the MAMT search, we compare the reward values of different algorithms within 5000 episodes. The comparison results show that within 5000 episodes, the winning rate of the PHER-MADDPG algorithm is obviously superior to other algorithms. Due to solving the sparse rewards problem, the PHER-MADDPG algorithm can better train agents and improve the search efficiency of multi-agent cooperation.

  • Due to the original environment, the agents have the problem of sparse rewards in the process of searching for the target. Therefore, the HER mechanism is adopted to set dense rewards during the task to motivate agents to find the targets faster. As shown in Fig. 8c, due to the large float of the curve fluctuations in M3DDPG training, to better compare the task completion time, we compared the PHER-M3DDPG algorithm with three different algorithms with 40,000 episodes. Through comparative experiments, we know that the PHER-M3DDPG algorithm reaches a convergence state in about 1000 episodes. Compared with the other four algorithms, the task completion time of agents with the PHER-M3DDPG algorithm is about 42 s. From the figure, we know that the curve of the PHER-M3DDPG algorithm is more stable, which shows that the minimax strategy can better enhance the robustness of the system.

Discussion

In this section, we focus on the limitations of the model used in this paper and the superiority of our algorithm over other ideas. The main limitation of this paper is that we set the searched target to a static state, which greatly reduces the complexity of the environment and allows the agents to learn the optimal strategy faster. However, the positions of the targets and the agents in each episode are randomly initialized so that the agents can adapt their strategy to different environments. To highlight the superiority of the PHER-M3DDPG algorithm, we have analyzed three aspects: theory, model, and simulation. Experiments show that compared with other multi-agent reinforcement learning algorithms, our algorithm can achieve convergence faster in a multi-target search environment and can complete the required tasks in a shorter time.

Conclusion

In this paper, we have studied a strategy of the MAMT search based on DRL. First, to enhance the robustness of the system, we have designed a learning structure based on minimax strategy, which adaptively adjusts the learning strategy of the agent by optimizing the cumulative reward of the agent. Then, we have designed a parallel hindsight experience replay mechanism to process the experience data in batches, which improves data diversity and solves the problem of sparse rewards in the MAMT search environment. Finally, we have shown that the PHER-M3DDPG algorithm yields better performance in terms of convergence efficiency and task completion time. At present, multi-agent target tracking has received widespread academic attention, and applying deep reinforcement learning to dynamic targets is a good choice to improve the flexibility of multi-agent systems. In the future, we will expand this paper to address the problem of dynamic target tracking.