Introduction

Simulation-based optimization has gradually been widely used in complex engineering systems due to advances in high-fidelity simulation technology [1,2,3]. Numerous types of expensive simulations such as the finite element method (FEM) or computational fluid dynamics (CFD) are applied in various practical engineering problems. However, the high-precision simulation is generally accompanied by a huge time consumption. In addition, practical engineering problems are frequently limited by various constraints, which makes the global optimization more complicated compared to unconstrained problems. Therefore, this paper focuses on the common expensive inequality-constrained optimization problem in practice, which can be expressed in the following form:

$$ \begin{gathered} \min f(x)\quad \quad \quad \quad x \in [lb,ub] \hfill \\ s.t. \, C_{i} (x) \le 0,\quad \quad i = 1, \cdot \cdot \cdot ,m, \hfill \\ \end{gathered} $$
(1)

where \(f(x)\) denotes the objective function to be optimized, \([lb,ub]\) refers to the upper and lower limits of the design space, \(C_{i} (x)\) and m represents the \(i{\text{th}}\) inequality constraint and the total number of constraints, respectively. In this study, \(f(x)\) and \(C_{i} (x)\) are presupposed to be time-consuming black-box functions and are assumed to be available simultaneously through a single function evaluation. Gradient-based optimization strategies are powerless for simulation-based optimization problems since computer simulation input and output have no analytical relationship [4]. Evolutionary algorithms (EAs), including but not limited to naturally inspired or swarm intelligence algorithms, have excellent optimization ability and do not need to rely on gradient information. Well-known algorithms belonging to EAs such as Genetic Algorithm (GA) [5], Particle Swarm Optimization (PSO) [6], Differential Evolution (DE) [7], and Evolutionary Programming (EP) [8] are frequently employed in different sorts of optimization problems. Since most EAs are developed for unconstrained optimization problems, they are combined with constrained handling techniques to extend their ability to handle constrained ones. Wang et al. [9] introduced an algorithm termed as C2oDE by making use of the idea of CoDE [10]. C2oDE trades off constraints and objectives by extending CoDE with two generations considering the degree of constraint violation and the optimal value of the objective function, respectively. On this basis, offspring are selected by combining feasibility rule and ε constraint method. Wang et al. [11] proposed CORCO to balance constraints and objective functions by exploiting the correlation between them. A two-stage mechanism is adopted, with one stage mining the correlation between the two, and the other stage updating and replacing to make use of the correlation.

Most existing EAs, as we all know, take tens of thousands of function evaluations to provide potentially optimal solution. However, a single time-consuming simulation in practical engineering usually takes tens of minutes or even hours. This time-consuming, also called computationally expensive, property makes EAs unsuitable for direct application to such optimization problems. Therefore, data-driven optimization [12, 13] is proposed to solve this kind of optimization problem by properly utilizing the data obtained in the historical function evaluation. Unlike conventional EAs, data-driven optimization employs surrogate model to partially replace the time-consuming function evaluation, and it combines the appropriate model management procedures to organize the surrogate model and guide the optimization direction. Data-driven optimization can be divided into two categories: online and offline optimization, depending on whether the optimization is supplemented with new data [12], and the online category is also known as surrogate-assisted evolutionary optimization. Surrogate models [14], also known as meta-models, are mathematical models that approximate the response of complex time-consuming simulations using data with a limited sample size. The surrogate model is significantly less time-consuming to construct and predict than the simulation.

Various surrogate models have been successively proposed by scholars, such as Kriging, Radial Basis Function (RBF) [15], Polynomial Response Surface (PRS) [16], Artificial Neural Network (ANN) [17], and have been utilized to solve practical engineering problems effectively. Jones et al. [18] introduced the efficient global optimization (EGO) algorithm by designing expected improvement (EI) criterion to screen promising candidate points. The EI criterion leverages the prediction and uncertainty of the Kriging model to enable EGO to reach a reasonable balance between global and local search [19]. Dong et al. [20] developed a multi surrogate-assisted optimization algorithm that simultaneously utilizes the prediction information provided by Kriging, RBF and PRS, and evaluates the merit of candidate sample points based on a scoring mechanism. Pan et al. [21] presented surrogate-assisted hybrid optimization algorithm (SAHO) that combines teaching–learning-based optimization (TLBO) [22] and DE [7]. These two algorithms run alternately, taking advantage of their advantages in global exploration and local exploitation ability, respectively. In addition, SAHO employed an RBF-based pre-screening strategy to select promising individuals. The above algorithm is designed for unconstrained optimization problems and cannot handle problems with constraints. Regis [23] proposed the algorithm called ConstrLMSRBF to screen feasible and low constraint violation solutions using the predictive value of RBF and distance metrics. Although the ConstrLMSRBF is capable of handling constrained optimization problems, the algorithm must rely on at least one feasible solution to start. However, this is quite challenging to obtain feasible solutions in the initial stage of optimization for real engineering problems with small feasible domains. Dong et al. [24] proposed a Kriging-based optimization algorithm called SCGOSR, which uses a multi-start strategy to mine information of the Kriging models. However, SCGOSR performed poorly on some cases due to the limitation of Kriging model accuracy.

From the above introduction, it is clear that DE and PSO are the two most popular frameworks for constructing data-driven optimization methods. Considering that Harris Hawks Optimization (HHO) algorithm performs better than DE and PSO in mechanical design, motor design and other problems, this study proposes the Data-Driven Harris Hawks Constrained Optimization (DHHCO) to solve such optimization problems by exploiting the superior search performance of HHO and the powerful nonlinear prediction capability of Kriging. DHHCO proposes a data-driven optimization framework covering the data generation, data screening, and data utilization phases that can effectively balance exploration and exploitation. Improve the original HHO algorithm and combine it with EOBL-based diversity strategy to achieve high quality and diverse candidate data generation. Kriging-based data-driven strategy is proposed to leverage the existing expensive sample data and the predictive power of the Kriging model for data screening and utilization. DHHCO's data-driven holistic framework efficiently guides the direction of optimization, enabling it to effectively handle costly constrained optimization problems. The main contributions of this study are summarized as follows: 1. a novel data-driven optimization framework is proposed, combining HHO’s meta-heuristic exploration and Kriging model prediction mechanisms; 2. an improved HHO is presented to generate candidate individuals that balance the local search and global exploration; 3. the Kriging-based data-driven strategy leverages existing data to exploits potential optimal while reducing computational consumption. 4. The presented DHHCO has superior performance on various benchmark cases and has been successfully applied to practical structural optimization problems. The remainder of this paper is organized as follows. "Preliminaries" gives some preliminaries to establish the basis for the subsequent proposed algorithm. The proposed algorithm is described in detail in "Data-driven Harris Hawks constrained optimization". "Experimental design and results" reports and discussed the experimental results with the benchmark functions and a practical engineering case. "Conclusion" gives the conclusions of this study.

Preliminaries

Kriging model

Kriging model is a statistical interpolation model originated in geology and extended to simulate computer experiments by Sacks et al. [25]. Subsequently, the Kriging model has been extensively studied and implemented in a variety of engineering field. Kriging realizes the estimation by interpolating the spatial correlation between the known samples and the unknown points to be predicted. The estimate value of Kriging is composed of a trend function and a random term, and can be expressed as follows.

$$ \widehat{y}\left( {\mathbf{x}} \right) = \beta_{0} + z\left( {\mathbf{x}} \right), $$
(2)

where \(\beta_{0}\) and \(z\left( {\mathbf{x}} \right)\) are constant and random terms, respectively.

The random term \(z\left( {\mathbf{x}} \right)\) obeys a Gaussian process with zero mean, and the covariance of \(z\left( {\mathbf{x}} \right)\) at two arbitrary points is formulated as

$$ {\text{Cov}}\left[ {z\left( {{\mathbf{x}}^{\left( i \right)} } \right),z\left( {{\mathbf{x}}^{\left( j \right)} } \right)} \right] = \sigma^{2} R\left( {{\mathbf{x}}^{\left( i \right)} ,{\mathbf{x}}^{\left( j \right)} } \right), $$
(3)

where \(R\left( {{\mathbf{x}}^{\left( i \right)} ,{\mathbf{x}}^{\left( j \right)} } \right)\) and \(\sigma^{{2}}\) represent the spatial correlation function and the variance of \(z\left( {\mathbf{x}} \right)\), respectively. The Gaussian correlation exponential functions used in this study can be represented as

$$ R\left( {{\mathbf{x}}^{\left( i \right)} ,{\mathbf{x}}^{\left( j \right)} } \right) = \exp \left( { - \sum\limits_{k = 1}^{d} {\theta_{k} \left| {x_{k}^{\left( i \right)} - x_{k}^{\left( j \right)} } \right|^{2} } } \right),\forall \theta_{k} \in {\mathbb{R}}^{ + } , $$
(4)

where \(d\) is the number of design variable and \(\theta\) is a parameter vector with \(d\) elements.

Under the assumption of zero mean square error at existing sample points, the predicted value and predicted mean square error of the unknown point can be expressed as

$$ \hat{y}\left( {\mathbf{x}} \right) = \beta^{*} + {\mathbf{r}}\left( {\mathbf{x}} \right)^{T} {\mathbf{R}}^{ - 1} \left( {{\mathbf{y}} - {\mathbf{1}}\beta^{*} } \right) $$
(5)
$$ s^{2} \left( {\mathbf{x}} \right) = \hat{\sigma }^{2} \left( {1 - {\text{r}}\left( {\mathbf{x}} \right)^{T} {\mathbf{R}}^{ - 1} {\text{r}}\left( {\mathbf{x}} \right)} \right) + \hat{\sigma }^{2} \frac{{\left( {1 - {\text{r}}\left( {\mathbf{x}} \right)^{T} {\mathbf{R}}^{ - 1} {\text{r}}\left( {\mathbf{x}} \right)} \right)^{{2}} }}{{{\mathbf{1}}^{T} {\mathbf{R}}^{ - 1} {\mathbf{1}}}}, $$
(6)

where \(\beta^{*}\) is the estimated hyper-parameter vector, \({\mathbf{R}}\) is the correlation matrix composed of known samples, \({\mathbf{r}}\left( {\mathbf{x}} \right)\) is the correlation vector representing the correlation between the point to be predicted and known points. \({\mathbf{R}}\) and \({\mathbf{r}}\left( {\mathbf{x}} \right)\) can be formulated as

$$ {\mathbf{R}}{ = }\left[ {\begin{array}{*{20}c} {R\left( {{\mathbf{x}}^{\left( 1 \right)} ,{\mathbf{x}}^{\left( 1 \right)} } \right)} & {R\left( {{\mathbf{x}}^{\left( 1 \right)} ,{\mathbf{x}}^{\left( 2 \right)} } \right)} & \cdots & {R\left( {{\mathbf{x}}^{\left( 1 \right)} ,{\mathbf{x}}^{\left( m \right)} } \right)} \\ {R\left( {{\mathbf{x}}^{\left( 2 \right)} ,{\mathbf{x}}^{\left( 1 \right)} } \right)} & {R\left( {{\mathbf{x}}^{\left( 2 \right)} ,{\mathbf{x}}^{\left( 2 \right)} } \right)} & \cdots & {R\left( {{\mathbf{x}}^{\left( 2 \right)} ,{\mathbf{x}}^{\left( m \right)} } \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {R\left( {{\mathbf{x}}^{\left( m \right)} ,{\mathbf{x}}^{\left( 1 \right)} } \right)} & {R\left( {{\mathbf{x}}^{\left( m \right)} ,{\mathbf{x}}^{\left( 2 \right)} } \right)} & \cdots & {R\left( {{\mathbf{x}}^{\left( m \right)} ,{\mathbf{x}}^{\left( m \right)} } \right)} \\ \end{array} } \right] \in {\mathbb{R}}^{m \times m} ,{\mathbf{r}}\left( {\mathbf{x}} \right){ = }\left[ {\begin{array}{*{20}c} {R\left( {{\mathbf{x}}^{\left( 1 \right)} ,{\mathbf{x}}} \right)} \\ {R\left( {{\mathbf{x}}^{\left( 2 \right)} ,{\mathbf{x}}} \right)} \\ \vdots \\ {R\left( {{\mathbf{x}}^{\left( m \right)} ,{\mathbf{x}}} \right)} \\ \end{array} } \right] \in {\mathbb{R}}^{m} . $$
(7)

\(\beta^{*}\) and \(\hat{\sigma }^{{2}}\) in Eqs. (5–6) can be obtained by maximizing the logarithm likelihood function.

$$ \beta^{*} = \left( {{\mathbf{1}}^{T} {\mathbf{R}}^{ - 1} {\mathbf{1}}} \right)^{ - 1} {\mathbf{1}}^{T} {\mathbf{R}}^{ - 1} {\mathbf{y}} $$
(8)
$$ \hat{\sigma }^{{2}} { = }\frac{{1}}{m}\left( {{\mathbf{y}} - {\mathbf{1}}\beta^{*} } \right)^{T} {\mathbf{R}}^{{ - 1}} \left( {{\mathbf{y}} - {\mathbf{1}}\beta^{*} } \right). $$
(9)

Harris Hawks optimization

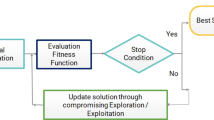
HHO algorithm, proposed by Heidari et al. [26], is a biologically inspired swarm intelligence algorithm inspired by behaviors such as cooperation and chasing during predation process of Harris Hawks. HHO mimics the behavior of Harris Hawks in predation, where a flock of Harris Hawks cooperate and use strategies to capture their prey. Specifically, HHO formulates several intelligent tactics in the predation process, such as soft siege, hard siege, and progressive rapid dives, and adopts corresponding tactics according to the different states of the prey, effectively imitating the hunting process of the Harris Hawks. HHO is divided into two phases of exploration and exploitation, according to the escaping energy of the prey. Dynamically adopt different predation styles in different phases according to different states of the prey. The overall flow of the HHO algorithm is illustrated in Fig. 1. The HHO algorithm, like most heuristics, consists of two phases: exploration and exploitation.

Fig. 1
figure 1

Flowchart of the HHO algorithm

Full size image

Exploration phase

In exploration phase, the Harris Hawk relies on keen vision to scout and track its prey. In this phase, HHO implements two strategies to simulate the search behavior of Harris Hawk. One strategy is based on the location of other individuals and prey in the population, and the other is a random tree detect strategy. Two strategies are selected and executed by random parameter q. The update of the corresponding individual position can be formulated as Eq. (10)

$$ {\varvec{x}}_{i,new}^{d} = \left\{ \begin{gathered} x_{rand}^{d} - r_{1} \left| {x_{rand}^{d} - 2r_{2} {\varvec{x}}_{i,old}^{d} } \right|\quad \quad \quad \quad \quad \qquad \qquad \qquad q \ge 0.5 \hfill \\ ({\varvec{x}}_{rabbit,t}^{d} - x_{m}^{d} ) - r_{3} (LB^{d} + r_{4} (UB^{d} - LB^{d} ))\quad \quad \, q < 0.5 \hfill \\ \end{gathered} \right. $$
(10)

where \(x_{rabbit}\), \(x_{t}\) and \(x_{t + 1}\) represent the position of the prey, the current position of the Hawks and the updated position of the Hawks, respectively. \(x_{m}\) is the mean of the Hawks population position vector. \(r_{1} \sim r_{4}\) and q are random numbers between 0 and 1. \(UB\) and \(LB\) denote the upper and lower boundaries of the design space, respectively. \(x_{m}\) can be calculated by Eq. (11)

$$ x_{m} = \frac{1}{N}\sum\limits_{i = 1}^{N} {x_{i} } , $$
(11)

where \(x_{i}\) represents the position of each hawk, and there are a total of \(N\) Hawks in the current population.

Transition phase

The HHO algorithm transitions from the exploration to the exploitation phase, as the optimization process proceeds. Shifting between the two phases is governed by the escape energy of the prey. And when entering the exploitation phase, the algorithm will take different predation strategies and actions according to the energy value. The escape energy of the prey can be formulated as

$$ E = 2E_{0} \left(1 - \frac{t}{T}\right), $$
(12)

where \(E\) and \(T\) denote the escape energy of the prey and the maximum number of iterations of the algorithm, respectively. \(E_{{0}}\) is the initial escape energy of the prey, which is a random number between − 1 and 1 updated in each iteration, and t denotes the number of current iterations. When \(E_{{0}}\) is less than 0, the closer to − 1 indicates that the prey is almost exhausted. On the contrary, when \(E_{{0}}\) is greater than 0, it means that the prey is full of energy. \(E\) is stochastic and dynamically changing and tends to get smaller gradually, as the algorithm iterates. When the value of \(\left| E \right|\) is greater than 1, the exploration phase is implemented, and vice versa, the algorithm performs the exploitation phase.

Exploitation phase

At the exploitation phase, the HHO algorithm conducts a surprise attack strategy on the identified prey. Hawks adopt corresponding hunting strategies according to the different escape behaviors of prey, because the escape form of prey is very complicated. HHO uses a random number r between 0 and 1 to indicate whether the prey can successfully escape or not. When the value of r is less than 0.5, it indicates that the prey successfully escaped, and on the contrary, the escape failed. There are four different strategies in the exploitation phase, \(E\) and \(r\) jointly determine which of the four strategies is used. When \(\left| E \right|\) is greater than 0.5, the HHO performs a soft besiege, and when \(\left| E \right|\) is less than 0.5, a hard besiege is implemented.

(1) Soft besiege.

For the case of \(r \ge 0.5\) and \(\left| E \right| \ge 0.5\), the prey has relatively high physical strength. Therefore, the Hawks adopt a soft encirclement strategy and then make a surprise attack. This soft besiege can be formulated as follows:

$$ x_{i,new} = (x_{rabbit} - x_{i} ) - E\left| {J_{i} x_{rabbit} - x_{i} } \right| $$
(13)
$$ J_{i} = 2(1 - r_{5} ), $$
(14)

where \(J\) is a random number representing jump strength and \(r_{5}\) is a random number between 0 and 1.

(2) Hard besiege.

For the case of \(r \ge 0.5\) and \(\left| E \right| < 0.5\), the prey's physical strength is not sufficient to support escape. The Hawks implement a hard besiege strategy to encircle violently. The hard besiege process can be expressed as follows:

$$ x_{i,new} = x_{rabbit} - E\left| {x_{rabbit} - x_{i} } \right|. $$
(15)

(3) Soft besiege with progressive rapid dives.

For the case of \(r < 0.5\) and \(\left| E \right| \ge 0.5\), the prey has plenty of energy and a chance to make a successful escape, so the Hawks adopt a more intelligent strategy on the basis of soft besiege. HHO uses levy flight (LF) to simulate the escape route of prey. It consists of two ways of updating individuals, and if the position movement of the first is not improved, the second is implemented. Specific strategies can be described as follows:

$$ Y_{i} = x_{rabbit} - E\left| {J_{i} x_{rabbit} - x_{i} } \right| $$
(16)
$$ Z_{i} = Y_{i} + L_{i} \cdot LF(D) $$
(17)
$$ x = \left\{ \begin{gathered} Y{\text{ if }}F(Y) < F(x(t)) \hfill \\ Z{\text{ if }}F(Z) < F(x(t)) \hfill \\ \end{gathered} \right., $$
(18)

where D represents the number of design variables, F stands for fitness value, LF is the levy flight function, which can be formulated as:

$$ LF(x) = 0.01 \times \frac{\mu \times \sigma }{{\left| \upsilon \right|^{{\frac{1}{\beta }}} }}, \, \sigma = \left( {\frac{{\Gamma (1 + \beta ) \times \sin \left( {\frac{\pi \beta }{2}} \right)}}{{\Gamma \left( {\frac{1 + \beta }{2}} \right) \times \beta \times 2^{{\left( {\frac{\beta - 1}{2}} \right)}} }}} \right)^{{\frac{1}{\beta }}} , $$
(19)

where \(\mu\) and \(\upsilon\) are both random numbers between 0 and 1, \(\beta\) is a constant with a value of 1.5.

(4) Hard besiege with progressive rapid dives.

For the case of \(r < 0.5\) and \(\left| E \right| < 0.5\), the prey can escape successfully, although the physical strength of the prey is not very sufficient. Hawks implement hard besiege to reduce the distance between their entire flock and their prey. The position update of Hawks can be formulated as:

$$ Y^{\prime} = x_{rabbit} - E\left| {J_{i} x_{rabbit} - x_{m} } \right| $$
(20)
$$ Z^{\prime} = Y^{\prime} + S \cdot LF(D) $$
(21)
$$ x = \left\{ \begin{gathered} Y{\text{ if }}F(Y) < F(x(t)) \hfill \\ Z{\text{ if }}F(Z) < F(x(t)) \hfill \\ \end{gathered} \right., $$
(22)

where \(x_{m}\) is the average position of individuals in the current population.

Data-driven Harris Hawks constrained optimization

The general framework of DHHCO

The overall framework of DHHCO is shown in Fig. 2. DHHCO's data-driven optimization process consists of four parts: the initialization phase, the data generation phase, the data screening phase, and the data utilization phase. The joint action of the four phases achieves an efficient balance between global exploration and local exploitation. The pseudocode of DHHCO is given in detail in Algorithm 2. In the initial phase, Optimized Latin Hypercube Sampling (OLHS) is employed to generate initial sample points and evaluate these points with the true function to obtain the initial data set. In the data generation phase, the improved HHO and EOBL-based diversity strategy work together to generate diverse and high-quality candidate data. Three improvements were made to the original HHO, each of which is described in "Improved HHO". EOBL-based diversity strategy is explained in "EOBL-based diversity strategy". Subsequently, Kriging-based data-driven strategy is proposed to leverage the existing expensive sample data and the predictive power of the Kriging model for data screening and utilization. In the data screening phase, the individual selection strategy is presented to screen promising individuals in the candidate data for subsequent true function evaluation, which is explained in detail in "Individual selection strategy". In the data utilization phase, the surrogate model constructed with the acquired expensive data is used to search for the predicted optimal solution, and in addition, a data-driven dynamic population construction is proposed. The corresponding details are described in "Management of Kriging model" and "Data-driven population construction", respectively. The Kriging-based data-driven strategy manages the Kriging models and screens promising samples for real function evaluation, and updates the dataset and Kriging models with supplementary expensive sample data. DHHCO continues to iterate until the stopping criteria are met.

Fig. 2
figure 2

Overall optimization flow of DHHCO

Full size image
figure a

Improved HHO

The HHO is responsible for the update of individuals in the population in each iteration and has a critical impact on the quality of candidate data generation. Three strategies are used to modify the original HHO in DHHCO to improve the HHO to generate high-quality candidate data.

Logarithmic spiral exploration strategy

At the beginning of the HHO algorithm, the entire design space and relatively sparsely sampled regions are extensively explored to initially determine several promising optimal regions. Logarithmic Spiral (LS) is a common geometric model in nature, similar to many biological movement paths, and is widely used in many heuristic algorithms such as Whale Optimization Algorithm (WOA) [27] and Moth Flame Optimization (MFO) [28]. Such logarithmic trajectory improves the distribution of the individuals generated by the algorithm in the design space compared with the linear trajectory. The individual update of the LS-based exploration strategy can be described as follows

$$ \left| {{\varvec{x}}_{rabbit,t}^{d} - {\varvec{x}}_{i,t}^{d} } \right| \times e^{bl} \times \cos \left( {2\pi l} \right) + {\varvec{x}}_{rabbit,t}^{d} \quad \quad R < 0.5 $$
(23)

where l is a random number between − 1 and 1, b is the control parameter for the shape of the logarithmic, \(R\) is a random number between 0 and 1.

The size of \(l\) determines how close the position is to the prey. A schematic diagram of the exploration of LES is shown in Fig. 3. Obviously, as \(l\) decreases from 1 to − 1, the distance between the eagle and the prey gradually gets closer. The ability to explore the design space will be enhanced with the help of the unconventional spiral random position of LS.

Fig. 3
figure 3figure 3figure 3

Iterative results of DHHCO on the 13 cases

Full size image

Quadratic interpolation exploitation strategy

The quadratic interpolation exploitation strategy is introduced in the original HHO algorithm to improve the ability of the individuals generated by the algorithm to jump out of local optima. Quadratic interpolation (QI) utilizes the properties of a parabola to fit the objective function using three known points. Using the extremum points provided by quadratic interpolation for local search is an effective method. QI has also been shown to be effective in combination with various algorithms [29,30,31].

In this paper, the QI technique is performed on the population in each iteration. More specifically, three individuals in the population are taken as a group, N (population size) groups of unique combinations are randomly generated to obtain the corresponding QI solutions. Then, the QI solutions corresponding to each group of three individuals are obtained and formulated as follows:

$$ x_{QI}^{d} = \frac{1}{2}\frac{{[(x_{3}^{d} )^{2} - (x_{2}^{d} )^{2} ]F(x_{1} ) + [(x_{1}^{d} )^{2} - (x_{3}^{d} )]F(x_{2} ) + [(x_{2}^{d} )^{2} - (x_{1}^{d} )^{2} ]F(x_{3} )}}{{(x_{3}^{d} - x_{2}^{d} )F(x_{2} ) + (x_{1}^{d} - x_{3}^{d} )F(x_{2} ) + (x_{2}^{d} - x_{1}^{d} )F(x_{2} )}}, $$
(24)

where \(x_{i}\) represents three individuals in any group, and \(F\left( {x_{i} } \right)\) denotes their corresponding objective function value.

The QI solutions generated by the constantly updated population can effectively improve the exploiting performance and improve the convergence speed of the algorithm.

Nonlinear transition strategy

To achieve a more reasonable balance between exploration and exploitation, the parameter E in the original HHO is modified. The parameter E in the original HHO decreases linearly with the increase of the number of iterations. In the second half of the algorithm, \(\left| E \right|\) is always less than 1, which causes the algorithm to only perform exploitation. This can get stuck in a local optimum for the case where the algorithm fails to locate the global optimum region at the end of the exploration phase. Therefore, a nonlinear dynamically updated E is proposed to overcome the disadvantage of premature convergence that may result from the original linear decreasing trend. The designed parameter \(E\) is formulated as follows:

$$ E = 2 \cdot \left| {y^{t} } \right| - 2 \cdot \tan \left(0.6 \cdot \frac{t}{T}\right) $$
(25)
$$ y^{t} = 1 - 2 \cdot (y^{t - 1} )^{2} , $$
(26)

where \(y^{t}\) is the chaotic sequence in the range − 1 to 1.

It is obvious that the introduced nonlinear parameter \(E\) effectively overcomes the limitation of only performing exploitation in the second half of the algorithm, and enhances the global search ability of the algorithm.

EOBL-based diversity strategy

To improve the global search performance of DHHCO, the EOBL strategy is embedded in it. Opposition-based learning (OBL) was proposed by Tozhoosh [32] and was subsequently widely used in the field of computational intelligence. The basic idea of OBL is to evaluate the current solution and its opposition solution at the same time to enhance the diversity of candidate solutions of the algorithm, and then select the better one to participate in the subsequent evolution. Zhong et al. [33] theoretically demonstrate that the use of OBL can improve the probability of finding a global optimal solution. OBL is also widely incorporated into optimization algorithms to improve performance. Zhou and Wang [34] developed EOBL on the basis of OBL, with the help of elite individuals to generate more promising opposite solutions. It is reported in [34] that the opposite solutions of elite individuals are more likely to fall in the global optimal region. Moreover, EOBL technology has also been successfully applied to various algorithms to improve their performance [35,36,37]. Adopting EOBL strategy to enhance population diversity during random search of Hawks in DHHCO. The implementation steps of EOBL in DHHCO are as follows:

Step 1: Select the individual with the best fitness of the population in the current iteration as the elite individual.

Step 2: Determine dynamic boundaries based on the current population.

Step 3: Use the EOBL strategy to obtain the opposite solution for each individual in the population.

Step 4 Determine whether the generated opposite solution exceeds the range of design space.

Step 5: Merge the original population and its corresponding opposite solution and perform function evaluation using the surrogate model constructed in "Kriging-based data-driven strategy".

To save computational cost, the objective and constraint values corresponding to the current solution and the opposite solution are preliminarily evaluated by the surrogate model constructed in "Kriging-based data-driven strategy". The reason for using a surrogate model for prediction in step 5 here is to save computation.

Kriging-based data-driven strategy

Management of Kriging model

To improve the efficiency of DHHCO in dealing with computationally expensive problems, the Kriging model is used to organize and manage the existing expensive data and utilize them to guide the direction of the search for optimization.

Step 1: The expensive samples evaluated by the precious simulation are archived into the dataset, and the sample data and their corresponding objective and constraint data are stored in dataset.

Step 2: Construct or update Kriging models for the objective function and each constraint function based on the expensive sample dataset.

Step 3: Implement the improved HHO algorithm to find the optimal on the Kriging models to obtain the predicted global optimal solution.

Step 4: Select candidate sample data generated by multiple strategies combined with pre-screening strategies.

Step 5: Evaluate the predicted global optimal solution and several other promising individuals obtained by other strategies with the true function, and supplement the obtained expensive data into the dataset.

Step 6: Repeat Steps 2 to 5 until the DHHCO meets the stopping condition.

Individual selection strategy

In each iteration of HHO, a large number of candidate samples are generated based on the improved HHO and the EOBL-based strategy. In order to reduce the number of calls of expensive real function evaluation and improve the optimization efficiency of the algorithm, an individual selection strategy based on Kriging model is used to screen candidate samples. Specifically, for each individual in the population in the DHHCO process, according to the escape energy, the strategy corresponding to the exploration or exploitation phase will be adopted to generate M (M > 1) individuals, and then the EOBL strategy will be used to generate the opposite solutions of these solutions. In order to reduce the influence of constraints of different magnitudes on individual pre-screening, inspired by [38], an individual selection strategy is designed based on the idea of ranking. For these generated several candidate sample data, the following screening criterion are used to select the best individual for true function evaluation.

(1) If all the individuals in the set of individuals to be compared are infeasible solutions of the Kriging prediction.

$$ F(x_{i} ,{\varvec{Y}},{\varvec{C}}) = R_{Nv} (c_{i} (x_{i} )) + \sum\nolimits_{i = 1}^{m} {R_{\phi }^{i} } {\text{(c}}_{i} (x_{i} ){) } $$
(27)

(2) If the individuals in the set of individuals to be compared have both feasible and infeasible solutions predicted by Kriging.

$$ F(x_{i} ,{\varvec{Y}},{\varvec{C}}) = R_{f} (Y_{i} ) + R_{Nv} (c_{i} (x_{i} )) + \sum\nolimits_{i = 1}^{m} {R_{\phi }^{i} (c_{i} (x_{i} ))} , $$
(28)

where \(R_{f}\), \(R_{\phi }\) and \(R_{Nv}\) indicate the ascending ranking of the individual's objective and constraints violation size, and number of violations, respectively.

Obviously, for a set of candidate samples that are all infeasible solutions, the above comparison criterion is more concerned with the degree of violation of the constraints of the infeasible solutions than the objective value, which facilitates the DHHCO to search for feasible solutions. For a set that contains both feasible and infeasible solutions, the objective and constraints of candidate sample data are balanced. Individuals that violate the constraints slightly are also likely to have good fitness values. It is worth noting that the ranking indicators based on constraints can effectively reduce the impact of different magnitudes of constraint values.

Data-driven population construction

IN DHHCO, data-driven population construction strategy is designed to make full use of the acquired expensive sample data. In each iteration of DHHCO, the individuals in the current population are reconstructed, and different reconstruction strategies are adopted according to the escape energy. For the case where \(\left| E \right|\) is greater than 1, the sample with best \(F\) value in the dataset is selected, and then the remaining \(p - 1\) samples are randomly selected from the sample set, where \(p\) is the population size. This construction mode enhances the diversity and dispersion of individuals in the population and promotes extensive exploration of the design space in the early stage of the algorithm. For another case where \(\left| E \right|\) is less than 1, the data in the dataset is sorted according to the fitness value, and the top \(p\) samples are regarded as the individuals of the current population. Compared to the previous construction mode, this one focuses on the best samples in the sample set to enhance the DHHCO's exploiting around these potential optimal areas. During the DHHCO cycle, two data-driven population construction modes switch adaptively according to the parameter \(E\).

Experimental design and results

Experimental settings

To investigate the effectiveness of DHHCO, it is compared with six well-known and recently published algorithms including SCGOSR [24], CEI [39], ConstrLMSRBF [23], HHO [26], C2oDE [9], CORCO [11]. Specifically, the first three algorithms are counted as surrogate-assisted optimization algorithms, while the last three are considered as heuristic algorithms. The above comparison algorithms have been shown to be effective in handling expensive constrained optimization problems and outperform many other algorithms such as EGO, MSSR [40], KCGO [41], CoDE, COMDE and FROFI. The inequality constraint cases of CEC2006 [42] are adopted to verify the effect of DHHCO and the characteristics of these cases are listed in Table 1. Two groups of experiments are set up with different maximum number of function evaluations (maxNFE) for fair comparison, because the surrogate-assisted algorithms consume less function evaluation times than the heuristic.

Table 1 Characteristics of numerical benchmark cases
Full size table

Ablation experiment

This section performs an ablation experiment on DHHCO. Based on previous theoretical explanations, the main components of DHHCO include the improved HHO, EOBL-based diversity strategy, individual selection strategy and data-driven population construction part. To evaluate the effectiveness of each component, an experimental comparison was performed on the proposed original algorithm with its four variants including DHHCO-w/o-IHHO, DHHCO-w/o-EOBL, DHHCO-w/o-PS and DHHCO-w/o-PC. DHHCO-w/o-IHHO discards the improvement strategy for HHO (IHHO) and uses the original HHO algorithm. DHHCO-w/o-EOBL discards the EOBL-based diversity strategy (EOBL) and produces offspring individuals only by improved HHO. DHHCO-w/o-PS discards individual selection strategy (PS) uses the penalty function approach to screen the offspring individuals. DHHCO-w/o-PC discards data-driven population construction (PC) and selects the top N solutions in the current database to form the population in each iteration.

The ablation experiment adopts the CEC2006 as the benchmark problems. The equality constraint problems are not considered in this work, and 13 of these arithmetic cases are selected as test problems. Each algorithm was run 20 times independently to weaken the effect of randomness. The mean values of the optimal values from 20 independent experiments are listed in Table 2. The best results among the five algorithms are highlighted in bold.

Table 2 Comparison results between DHHCO and its variants on CEC2006 cases
Full size table

From Table 2, we observe that DHHCO outperforms DHHCO-w/o-IHHO in 11 out of 13 cases, for the other three variants are 12, 8, and 11 times, respectively. According to the average ranking, DHHCO has the best performance among the five algorithms. DHHCO-w/o-PS has the best results among the four variants, ranking second only to DHHCO. DHHCO-w/o-PS lacks the individual selection strategy compared to DHHCO, and the penalty function approach that prefers feasible solutions may ignore the useful information contained in infeasible solutions. The other three variants weakened the diversity of DHHCO producing offspring to varying degrees, causing them to rank further down the list. Among them, EOBL-based diversity strategy has the greatest impact on the optimization results. The potential reason for this is the ability of EOBL to produce candidates that differ more from the current offspring individuals. Similarly, DHHCO-w/o-PC selects only the portion of the current optimum as the population, which compromises population diversity, and DHCO-w/o-IHHO lacks the improvement of the original HHO exploration and mining strategy, which deteriorates the global search performance. It is worth noting that except for the cases where the DHHCO-w/o-PC and DHHCO-w/o-IHHO fail to find feasible solutions on g10 and g16 in some experiments, all five algorithms find feasible solutions stably on the remaining cases. This precisely verifies that the improved HHO and population construction strategies, which are exactly the missing strategies in both DHHCO-w/o-IHHO and DHHCO-w/o-PC algorithms, can improve the global search ability of the corresponding algorithms. Therefore, it can be concluded that the combination of IHHO, EOBL, PS and PC strategies in DHHCO can effectively improve the global optimization capability.

Comparison with surrogate-based optimization algorithms

IN this section, DHHCO is compared with surrogate-assisted optimization algorithms, including SCGOSR, CEI and ConstrLMSRBF, and the maxNFE is set to 200. For these three comparison algorithms, the default parameter values from their original papers [23, 24, 39]. For DHHCO, the population size and number of candidate individuals are set to 3 and 10, respectively. The initial number of sampling points is \(2d + 1\), and \(d\) is the problem dimension. The statistical results are summarized in Table 3 and all algorithms are run for 20 independent repetitions to eliminate randomness. ConstrLMSRBF is abbreviated as CLMSRBF in Table 3 for brevity and SR denotes the successful ratio of finding feasible solutions in total runs. A run is regarded as successful if at least one feasible solution is found within MaxNFE.

Table 3 Comparisons of statistical results on CEC2006 cases (MaxNFE = 200)
Full size table
Table 4 Comparisons of statistical results on CEC2006 cases (MaxNFE = 500)
Full size table

It is clearly seen that DHHCO is able to find feasible solutions on all cases. The SCGOSR algorithm has challenges in solving g10 and g18, with only a one-quarter success rate of finding a feasible solution. CEI is not always stable on g16 and g18 and may fail to find a feasible solution. ConstrLMSRBF performed poorly on g04, g06, g10 and g16, for which none of them could find a feasible solution. In general, DHHCO is more stable and robust than the other three algorithms. As seen in Table 3, DHHCO finds known optimal vicinity on most of the cases and outperforms the other three algorithms on g01, g09, g12 and g19. For the other cases except g06 and g07, DHHCO and SCGOSR performed comparably, but DHHCO was more stable and finds the approximate optimal solution in all repeated tries. SCGOSR outperforms DHHCO on g06 and g07, but their results are very close. CEI has the opportunity to find the global optimum on half of the cases. However, its convergence performance is worse compared to DHHCO and SCGOSR, and the best and average values are not as good as these two algorithms such as on g02, g06, g07, g09, g18 and g19. The ConstrLMSRBF algorithm encountered difficulties with these cases, and it had difficulty converging or even finding a feasible solution in some cases. It is worth noting that ConstrLMSRBF performs the best among the four algorithms for the g02 case, which is attributed to the modeling advantage of the RBF model for high-dimensional problems. In conclusion, DHHCO outperforms the other three algorithms in terms of stability and robustness for 13 CEC2006 cases.

Figure 3 illustrates the iterative results of DHHCO, which shows the historical data generated by DHHCO throughout the search process and a clearer supplemental graph near the best points is plotted. Intuitively, most of the iterative graphs exhibit a similar situation, where the samples generated by initial DoE are mostly infeasible solutions with widely varying objective function values, while the points generated during the iterative process are mainly feasible solutions or globally optimal regions. This is due to the fact that the initial DOE samples extensively in the design space and gradually samples in the feasible region and the promising global optimum region as the iteration of DHHCO proceeds. This phenomenon is particularly evident on the g07, g08 and g10, where there are no feasible ones in the initial sampling points, and more and more feasible solutions are found as the iteration continues. It is also verified that DHHCO can still guide the correct search direction even when the initial all infeasible points. It is worth noting that due to the role of the global exploration mechanism of DHHCO, although the optimal area has been found, it will still explore in the area far from the current optimal area. This avoids DHHCO getting stuck in local optima to find the global optima.

Comparison with meta-heuristic algorithms

Since DHHCO integrates a meta-heuristic search mechanism, it is compared with three meta-heuristic algorithms including HHO itself. The maxNFE of the four algorithms is 500, and the other parameters of DHHCO are consistent with "Experimental settings". For HHO, C2oDE, CORCO, the population size is defined as 10, and all the other parameters remain at their default values [9, 11, 26]. Table 4 lists the comparison results of the four algorithms. There is no doubt that DHHCO can achieve better results than those in Table 4 after 500 FEs. For many cases (e.g., g01, g06, g07), DHHCO can roughly obtain the true global optimal. On the contrary, these three algorithms may always fail on some cases. For instances, HHO can hardly deal with g10 and g16, while C2oDE and CORCO cannot solve g10 and g18. Moreover, C2oDE and CORCO achieve lower SR on g01 and g09, respectively. Relatively, the three compare algorithms achieve better performance on g02, g04, g08, g09, g12 and g24, since these cases have larger feasible space. Among the rest three comparison algorithms, C2oDE and CORCO outperform the HHO in terms of robustness, since they are more likely to identify the feasible solutions. It is obvious that more function calls are required for C2oDE and CORCO to identify the feasible area. DHHCO achieves robust global optimization by combining HHO heuristic search mechanism and Kriging prediction capability. From the above results, it can be observed that the proposed DHHCO is highly competitive compared with not only SBO but also meta-heuristic algorithms.

Engineering applications

Blended-Wing-Body underwater gliders (BWBUGs) [43] play an important role in scientific and commercial fields due to their advantages of low cost and capability for long gliding range and have got considerable amount of attention in recent years. Inside the glider, there are several pressure-resistant cabins to guarantee that the pricey instruments and equipment installed operate properly in the deep-sea environment. These cabins are connected and fixed to the wing frame by the fixing frame of the cabin. The cabin fixing frame is such a critical structure that it fixes the position of the cabin relative to the shape and is the main load-bearing structure when it is lifted. In this work, we seek to increase the lightweight effect on the premise of reducing the design cost, while also satisfying the constraints of stress and deformation. The geometric description is shown in Fig. 4, which defines seven design variables including thickness parameters (T1, H1, H2 and D) and size parameters (DR, L and T2).

Fig. 4
figure 4

Illustration of BWBUG’s cabin fixing frame

Full size image

The objective for this BWBUG engineering case is to minimize the weight of cabin fixing frame. The cabin fixing frame is mainly affected by two loading: the weight of three pressure cabins in the fuselage, and the gravity of the wing structure and skin. The von Mises stress and maximum deformation of the fixing frame are employed to measure the strength of the fixing frame. To ensure the performance of the fixing frame, two constraints are imposed in this optimization: the maximum of von Mises stress of fixing frame should be less than allowable stress and the maximum total deformation should be less than allowable deformation. In addition to the above constraints, the design variables are restricted by lower and upper bounds given in Eq. (29). The specific mathematical formula of BWBUG fixing frame optimization problem is expressed as,

$$ \begin{gathered} {\text{min }}m(D,DR,L,H1,H2,T1,T2) \hfill \\ s.t.\quad \sigma_{\max } (D,DR,L,H1,H2,T1,T2) \le \gamma \sigma_{s} \hfill \\ \quad \quad \mu_{\max } (D,DR,L,H1,H2,T1,T2) \le \left[ \mu \right] \hfill \\ {\text{where}}\quad {20} \le D \le 40;{ 285} \le DR \le 315;{ 30} \le L \le 40 \hfill \\ \quad \quad \quad {15} \le H1 \le 25;{ 15} \le H2 \le 25 \hfill \\ \quad \quad \quad {8} \le T1 \le 15;{ 55} \le T2 \le 70 \hfill \\ \end{gathered} $$
(29)

where m denotes the weight of the cabin fixing frame, \(\sigma_{s}\) is the yield strength, \(\gamma\) is a safety factor, and \(\left[ \mu \right]\) is allowable deformation. In this engineering case, aluminum alloy is applied for the fixing frame, \(\sigma_{s}\), \(\gamma\) and \(\left[ \mu \right]\) are set to 280Mpa, 1.3 and 12 mm, respectively.

From the comparative analysis results in "Comparison with surrogate-based optimization algorithms", DHHCO and SCGOSR have the best performance, and these two algorithms are employed to implement the optimization for comparison. Fifteen sample points are generated by OLHS as the initial DoE samples, and 200 simulations are set as the computational budget in total. For fair comparison, DHHCO and SCGOSR adopt the same DoE samples in the initial stage.

DHHCO discovered a better solution than SCGOSR after performing 200 simulations. The historical iteration curves of the two algorithms are drawn in Figs. 5 and 6. Intuitively, DHHCO spends about 60 simulations to find the vicinity of the optimal solution, and then according to its exploration mechanism, it explores other unknown areas to search for the global optimal solution, and finally converges to the optimal solution. However, SCGOSR may get stuck in a local optimum area after 100 simulation calls. Table 5 lists comparable results for two algorithms. DHHCO obtains the best feasible solution with the minimum weight m = 2.13 kg. Compared with the best DoE sample, DHHCO achieves about 18.7% weight reduction, while SCGOSR only achieves an 15.8% improvement. Besides, Figs. 7, 8 and 9 illustrate the optimal simulation results of DoE, DHHCO and SCGOSR. The comparison results demonstrate the efficiency of DHHCO in optimizing this engineering case. In conclusion, DHHCO can deal with both benchmark cases and simulation-based engineering example.

Fig. 5
figure 5

Objective value iterative curve of DHHCO

Full size image
Fig. 6
figure 6

Objective value iterative curves of SCGOSR

Full size image
Fig. 7
figure 7

Equivalent stress and total deformation results of DoE’s best sample

Full size image
Fig. 8
figure 8

Equivalent stress and total deformation results of DHHCO’s best solution

Full size image
Fig. 9
figure 9

Equivalent stress and total deformation results of SCGOSR’s best solution

Full size image
Table 5 Optimization results under a total of 200 simulations budget
Full size table

Conclusion

In this work, a data-driven Harris Hawks constrained optimization noted as DHHCO is proposed to solve the black-box optimization problems with computationally expensive objective and constraints. In the proposed DHHCO, the improved HHO framework combined with EOBL-based diversity strategy to efficiently explore the design space and generate promising individuals. Kriging-based data-driven strategy utilizes existing expensive data to guide optimization directions and screen candidate individuals to save computational effort. To demonstrate the performance of DHHCO, it is tested on 13 benchmark cases via comparing with 3 surrogate-based algorithms and 3 heuristic algorithms and DHHCO performs more efficiently and stably. Moreover, DHHCO is successfully used to the lightweight design of the cabin fixing frame of a BWBUG, realizing lightest fixing frame structure and guarantee the constraints. The test results demonstrate the effectiveness and practicability of the proposed DHHCO for solving both numerical benchmarks and real-world engineering optimization problems.