Introduction

Two-person non-cooperative competitions exist universally in real-world practices. The selection of the optimal competitive strategy is vital for players to survive from current intensified competitive circumstances. Nevertheless, on account of the large number of optional strategies, competitive strategy group decision making (CSGDM) has become an extremely challenging issue facing decision makers. Hence, CSGDM problems in two-person non-cooperation competitions have captured increasing attention from specialists and practitioners [1, 2].

Matrix game theory is an effective tool for portraying two-person non-cooperation competitions and has been applied to some fields such as advertising, biology, emergency and military issues [3,4,5]. Matrix game theory considers the characteristics of players’ non-cooperative behaviors and aims to solve the conflict of interests between players. The players in a matrix game aim at maximizing their own benefits, which highly abstracts from CSGDM problems. CSGDM via solving a matrix game can not only obtain the optimal strategy in the form of probabilities but also get the value of the game, which is hard to achieve with most other methods. In addition, results obtained by matrix game are able to reflect the divergence degree between any two alternatives, while most other methods, for instance, multi-attribute decision-making (MADM) methods [6,7,8], usually order the strategies based on simple sorting results.

The general model of matrix game utilizes crisp values [9]; however, the complexity of real world determines that players cannot estimate exactly payoff outcome. Under this circumstance, fuzzy matrix game methods in uncertain environments can be viewed as an interesting topic for CSGDM problems. To describe the complicated uncertain scenarios, Zadeh [10] introduced the definition of fuzzy sets, assigning a grade of membership to each object belongs to the fuzzy sets. After that, fuzzy sets have been applied into many competitive strategy decision-making problems in uncertain situations widely because they can character the complex world more accurately [11, 12]. Atanassov [13] modified the version of fuzzy sets and first proposed the concepts of intuitionistic fuzzy sets (IFSs) which are nonstandard fuzzy subsets. The users can evaluate the support for and against membership of each object in the IFSs synchronously. A distinguishing feature of the IFSs is that the summation of the support for membership degree \(u\) and the support against membership degree \(v\) satisfies the condition that \(u + v \le 1\). Nevertheless, IFSs cannot express some particular attributes if \(u + v > 1\). Although Yager [14] developed the Pythagorean fuzzy sets (PFSs) in which \(u^{2} + v^{2} \le 1\) to depict decision-making systems with intricate fuzzy messages, PFSs are also restricted by real world. To solve this plight thoroughly, Yager [15] explored q-rung orthopair fuzzy sets (q-ROFSs) by means of broadening the scopes of IFSs and PFSs. The q-ROFSs, satisfying \(u^{q} + v^{q} \le 1\), are generalizations of IFSs and PFSs because q-ROFSs can be transformed into different forms by choosing different values of parameter \(q\). Obviously, q-ROFSs are more general and can expand the range of users’ application. Due to the high efficiency of q-ROFSs, many scholars have made some contributions under the q-ROF circumstances currently. For example, Yang et al. [16] initiated q-rung orthopair fuzzy interaction weighted Heronian mean operators by considering the interactive characteristics of decision matrix. Liu and Wang [17] established q-rung orthopair fuzzy generalized Maclaurin symmetric mean operators to tackle MADM problems. Zeng et al. [18] proposed a novel induced weighted logarithmic distance measure for handling MADM problems within q-ROF environment. Riaz et al. [19] introduced two q-ROF hybrid aggregation operators and applied q-ROF TOPSIS method to cope with a transport policy problem. Garg et al. [20] and Liu et al. [21] improved q-ROFSs and developed complex q-rung orthopair fuzzy set (Cq-ROFS) for dealing with awkward and complicated information. Thereafter, Garg et al. [22] presented generalized dice similarity measures for Cq-ROFSs. Mahmood and Ali [23] investigated a novel TOPSIS MADM method based on a complex q-rung orthopair fuzzy correlation coefficient measure. Riaz et al. [24] combined the idea of q-ROFS and m-polar fuzzy set to propose q-rung orthopair m-polar fuzzy sets which are generalizations of Pythagorean m-polar fuzzy sets [25]. Although there are some researches, regarding matrix game methods by utilizing IFSs and PFSs, can be found in the existing literatures, they will lose efficacy in complicated CSGDM problems where \(u^{2} + v^{2} > 1\). Therefore, it is vacant but crucial to explore fuzzy matrix game methods for CSGDM problems in q-rung orthopair fuzzy contexts.

The determination of experts’ weights is a momentous link belongs to the process of CSGDM, which has direct impacts on the final results. The more accurate the experts’ weights are, the more valid the decision result is. Most of the existing literatures have taken a constant experts’ weight assumption in the study process [26,27,28]. However, due to the fact that experts are discrepant concerning knowledge backgrounds, experiences, psychological behaviors or some aspects, the importance degrees of experts are often dissimilar and tend to be changed. Thus, it is reasonable to assign each expert a weight dynamically according to the individual experts’ basic information and evaluation results. Even if several scholars have attempted to eliminate the irrationality caused by constant decision makers’ weights in decision process via variable weights theory [29, 30], the experts’ individual evaluation abilities are neglected in most decision-making processes. To remedy this gap, this paper established a hybrid dynamic expert weight determining method integrating the credibility degree of experts and discrepancy degree of subjective evaluation information provided by experts. Inspired by Zhang [31], an expert credibility analysis scale consists of experts’ individual information is designed to reflect the experts’ assessment abilities and credibility degree. In addition, considering that distance is an efficient mathematical implement for measuring the discrepancy degree between two objects [32,33,34], a q-rung orthopair fuzzy Hausdorff distance measure, generalizations of Hamming distance and Euclidean distance, is defined for calculating the discrepancy degree of subjective evaluation information.

On account of the foregoing analyses, this paper aims at proposing a novel two-person fuzzy matrix game method for tackling CSGDM problems accurately and efficiently. In brief, the contributions of this manuscript mainly consist of three aspects:

  1. (i)

    q-ROFSs, generations of IFSs and PFSs, are employed to express the uncertainty and vague of competitive strategy group decision-making environment, which can extend the application range of the proposed approach.

  2. (ii)

    With the help of a credibility analysis scale and q-ROF Hausdorff distance, a novel expert weight calculation method, combining both objective individual and subjective evaluation information, is developed to determine the variable experts’ weights legitimately and comprehensively.

  3. (iii)

    A fuzzy two-person matrix game within the q-ROF environment is formulated to select the optimal mixed strategies in the form of probabilities, which can portray the behavior characteristics of participants in competitive strategy group decision-making problems.

  4. (iv)

    An illustrative example, regarding the selection of the most desirable market share competitive strategy, is conducted. Several comparative analyses and sensitive analyses are performed to verify the availability of the proposed approach. The experimental results show that the proposed game method can directly obtain the priorities of the competitive strategies with high efficiency, little calculation burden and low calculation complexity.

The remaining structure of this paper is as follows: the basic concepts, including q-rung orthopair fuzzy sets, Hausdorff distance as well as two-person matrix game, are briefly reviewed in the next section. The third section proposes a two-person matrix game on the strength of the variable weights’ theory and q-ROFS. In the fourth section, an illustrate example, several comparative analyses and sensitivity analyses are presented to verify the availability of the proposed approach, and then the advantages with limitations of the proposed approach are stated. Finally, the last section discusses the conclusion of this paper.

Preliminaries

q-rung orthopair fuzzy set

The q-rung orthopair fuzzy set (q-ROFS) [15] was explored to remedy the shortages of IFSs and PFSs. The general definitions and operational laws of q-ROFSs are as shown follows.

Definition 1 [15]

Suppose \(X\) be a space of points. A q-ROFS \(A\) on \(X\) can be characterized as

$$ A{ = }\left\{ {\left. {\left\langle {x,u_{A} (x),v_{A} (x)} \right\rangle } \right|x \in X} \right\}, $$
(1)

where for all \(x \in X\), \(u_{A} :X \to \left[ {0,1} \right]\) indicates membership grade and \(v_{A} :X \to \left[ {0,1} \right]\) indicates non-membership grade of \(x\), severally, with \(0 \le (u_{A} (x)^{q} + v_{A} (x)^{q} ) \le 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} (q \ge 1)\). The uncertainty degree is described as \(\pi_{A} (x) = (u_{A} (x)^{q} + v_{A} (x)^{q} - u_{A} (x)^{q} v_{A} (x)^{q} )^{1/q}\). For convenience’s sake, \(\left\langle {u_{A} (x),v_{A} (x)} \right\rangle\) is named as a q-ROFN, symbolized by \(A = \left\langle {u_{A} ,v_{A} } \right\rangle\).

Definition 2 [35]

The score value \(S(A)\) and accuracy value H(A) of a q-ROFN \(A\) can be given by

$$ S(A) = u_{A}^{q} - v_{A}^{q} , \, H(A) = u_{A}^{q} + v_{A}^{q} {\text{ for }}q \in \left[ {1, + \infty } \right). $$
(2)

Obviously, \(S(A) \in \left[ { - 1,1} \right]\) and \(H(A) \in \left[ {0,1} \right]\). The larger the score \(S(A)\) and the accuracy degree \(H(A)\) are, the greater \(A\) is.

On this basis, a comparative approach of q-ROFNs is presented as follows.

Definition 3 [35]

Suppose \(a = \left\langle {u_{a} ,v_{a} } \right\rangle\) and \(b = \left\langle {u_{b} ,v_{b} } \right\rangle\) are two q-ROFNs. Then, they obey the following comparative rules:

  1. (i)

    If \(S(a) > S(b)\), then \(a > b\);

  2. (ii)

    If \(S(a) = S(b)\), then

If \(H(a) > H(b)\), then \(a > b\);

If \(H(a) = H(b)\), then \(a = b\).

Let \(\alpha = \left\langle {u,v} \right\rangle\), \(\alpha_{1} = \left\langle {u_{1} ,v_{1} } \right\rangle\), and \(\alpha_{2} = \left\langle {u_{2} ,v_{2} } \right\rangle\) be any three q-ROFNs. Then, the fundamental algorithms can be represented as follows:

  1. (1)

    \(\alpha^{c} = \left\langle {v,u} \right\rangle\);

  2. (2)

    \(\alpha_{1} \oplus \alpha_{2} = \left\langle {(u_{1}^{q} + u_{2}^{q} - u_{1}^{q} u_{2}^{q} )^{1/q} ,v_{1} v_{2} } \right\rangle\);

  3. (3)

    \(\lambda \alpha_{1} = \left\langle {(1 - (1 - u_{1}^{q} )^{\lambda } )^{1/q} ,v_{1}^{\lambda } } \right\rangle\), for any \(\lambda > 0\);

  4. (4)

    \(Max\left\langle {\alpha_{1} ,\alpha_{2} } \right\rangle = \left\langle {\max \left\{ {u_{1} ,u_{2} } \right\},\min \left\{ {v_{1} ,v_{2} } \right\}} \right\rangle\);

  5. (5)

    \(Min\left\langle {\alpha_{1} ,\alpha_{2} } \right\rangle = \left\langle {\min \left\{ {u_{1} ,u_{2} } \right\},\max \left\{ {v_{1} ,v_{2} } \right\}} \right\rangle\).

Based on the aforementioned algorithms of q-ROFNs, Liu and Wang [35] introduced and analyzed the q-ROFWA operator.

Definition 4 [35]

Let \(\tilde{a}_{k} = \left\langle {u_{k} ,v_{k} } \right\rangle (k = 1,2,...,n)\) be a collection of q-ROFNs with weight vector \(w = (w_{1} ,w_{2} ,...,w_{n} )^{T}\) such that \(0 \le w_{k} \le 1\) and \(\sum\nolimits_{k = 1}^{n} {w_{k} = 1}\), then, the q-rung orthopair fuzzy weight averaging (q-ROFWA) operator is

$$ q - ROFWA(\tilde{a}_{1} ,\tilde{a}_{2} ,...,\tilde{a}_{n} ) = w_{1} \tilde{a}_{1} \oplus w_{2} \tilde{a}_{2} \oplus ... \oplus w_{n} \tilde{a}_{n} = \left\langle {(1 - \mathop \prod \limits_{k = 1}^{n} (1 - u_{k}^{q} )^{{w_{k} }} )^{1/q} ,\mathop \prod \limits_{k = 1}^{n} v_{k}^{{w_{k} }} } \right\rangle . $$
(3)

Hausdorff distance

The Hausdorff distance measures how far two non-empty compact subsets \(A\) and \(B\) resemble mutually with their positions in a Banach space \(S\), which is initially put forward by Nadler [36]. Let \(d(a,b)\) be a metric for \(S\). \(d(z,A) = \min \left\{ {d(z,a)\left| {a \in A} \right.} \right\}\). The Hausdorff measure \(H^{*} (A,B) = \mathop {\max }\limits_{a \in A} d(a,B)\) is one-way. \(H(A,B)\) is defined by \(H(A,B) = \max \left\{ {H^{*} (A,B),H^{*} (B,A)} \right\}\). If \(S = \Re\), for any two intervals \(A = \left[ {a_{1} ,a_{2} } \right]\) and \(B = \left[ {b_{1} ,b_{2} } \right]\), the Hausdorff distance \(H(A,B)\) is given by \(H(A,B) = \max \left\{ {\left| {a_{1} - b_{1} } \right|,\left| {a_{2} - b_{2} } \right|} \right\}\).

Two-person matrix game

A review of the classical two-person matrix game [37] is presented in this subsection. \(S^{m} = \left\{ {x \in R_{ + }^{m} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} e^{T} x = 1} \right\}\) and \(S^{n} = \left\{ {y \in R_{ + }^{n} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} e^{T} y = 1} \right\}\), in which \(e^{T} = (1,1,...,1)\) is a vector of “ones”, are the pure strategies space of player I and II, severally. \(x_{i} (i = 1,2,...,n)\) is the probability that player I chooses pure strategy \(s_{i} \in S^{m}\) which belongs to the mixed strategy \(x = (x_{1} ,x_{2} ,...,x_{n} )^{T}\) of player I. Similarly, \(y_{j} (j = 1,2,...,m)\) is the probability in which player II chooses pure strategy \(s_{j} \in S^{n}\) which pertains to the mixed strategy \(y = (y_{1} ,y_{2} ,...,y_{m} )^{T}\) of player II. Let \(X\) and \(Y\) consist of all mixed strategies of player I and II, respectively. \(A = (a_{ij} )_{m \times n}\) is the payoff matrix of player I when player I chooses pure strategy \(s_{i}\) and player II chooses pure strategy \(s_{j}\) simultaneously.

Suppose player I and II play a two-person matrix game \(G\). Player I’s expected payoff is the scalar \(x^{T} Ay = \sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {x_{i} a_{ij} y_{j} } }\) if player I and II choose mixed strategies \(x \in X\) and \(y \in Y\) concurrently. Player I’s expected gain-floor can be acquired via the formula \(v_{G} (x) = \min \left\{ {\left. {x^{T} Ay} \right|y \in Y} \right\}\). The convention is to assume that player I pursues the maximizing yield; on the contrary, player II aims at the minimizing yield. Therefore, the minimum is attained in virtue of pure strategy \(y_{j} \in S^{n}\) as follows:

$$ v_{G} (x) = \min \left\{ {\left. {x^{T} A_{j} } \right|j = 1,2,...,n} \right\} = \min \left\{ {\left. {\sum\nolimits_{i = 1}^{m} {x_{i} a_{ij} } } \right|j = 1,2,...,n} \right\}, $$
(4)

where \(A_{j} = (a_{1j} ,a_{2j} ,...,a_{mj} )^{T}\) is the jth column of the payoff matrix \(A\). Thus, to maximize \(v_{G} (x)\), a mixed strategy \(x^{*} \in X\) should be chosen by player I to obtain

$$ v_{G} (x^{*} ) = \max \left\{ {\left. {v_{G} (x)} \right|x \in X} \right\}. $$
(5)

Such \(v_{G} (x^{*} )\) is termed as player I’s gain-floor, expressed as \(v_{G} = v_{G} (x^{*} )\), and \(x^{*} \in X\) is the optimal mixed strategy for player I in the two-person matrix game \(G\).

Similarly, the player II’s expected loss-ceiling of choosing mixed strategy \(y\) is

$$ \omega {}_{G}(y) = \max \left\{ {\left. {A_{i} y} \right|i = 1,2,...,m} \right\} = \max \left\{ {\left. {\sum\nolimits_{j = 1}^{n} {a_{ij} y_{j} } } \right|i = 1,2,...,m} \right\}, $$
(6)

where \(A_{i} = \left\{ {a_{i1} ,a_{i2} ,...,a_{in} } \right\}\) is the ith row of the payoff matrix \(G\). Thus, to obtain

$$ \omega {}_{G}(y^{*} ) = \min \left\{ {\left. {\omega {}_{G}(y)} \right|y \in Y} \right\}, $$
(7)

a mixed strategy \(y^{*} \in Y\) should be chosen by player II.

Such \(\omega {}_{G}(y^{*} )\) is named as player II’s loss-ceiling, expressed as \(\rho_{G} = \omega {}_{G}(y^{*} )\), and \(y^{*} \in Y\) is the optimal mixed strategy for player II in the matrix game \(G\).

Apparently, Eqs. (6) and (8) are original dual linear programming problems for player I and II. Therefore, \(\max \left\{ {v_{G} } \right\}\) is equivalent to \(\min \left\{ {\rho_{G} } \right\}\). Their equal value is termed as the game \(G^{\prime}s\) value, indicated as \(V_{G} = v_{G} = \rho_{G}\).

The proposed two-person non-cooperative matrix game group decision-making approach

In this section, a two-person non-cooperative fuzzy matrix game based on the variable weight theory and q-ROFSs is proposed to deal with competitive strategy group decision-making problems.

Description of competitive strategy group decision-making problems

Suppose a two-person non-cooperative matrix game be constituted by player I and II. Let finite sets \(\delta = \left\{ {\delta_{1} ,\delta_{2} ,...,\delta_{m} } \right\}\) and \(\beta = \left\{ {\beta_{1} ,\beta_{2} ,...,\beta_{n} } \right\}\) be the finite strategy sets of player I and II, severally. The optimal solution of the two-person non-cooperative matrix game can be obtained by the following three stages: (1) preparatory stage. Considering the costs and benefits of strategies, a group of \(t\) experts evaluates the respective advantages of player I’s and II’s competitive strategies using q-ROFNs and derive payoff matrices. Let

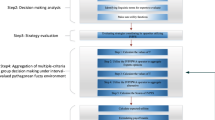
$$ A^{k} = (a_{ij}^{k} )_{m \times n} = \left[ {\begin{array}{*{20}c} {(u_{11}^{k} ,v_{11}^{k} )} & {(u_{12}^{k} ,v_{12}^{k} )} & {...} & {(u_{1n}^{k} ,v_{1n}^{k} )} \\ {(u_{21}^{k} ,v_{21}^{k} )} & {(u_{22}^{k} ,v_{22}^{k} )} & {...} & {(u_{2n}^{k} ,v_{2n}^{k} )} \\ {...} & {...} & {...} & {...} \\ {(u_{m1}^{k} ,v_{m1}^{k} )} & {(u_{m2}^{k} ,v_{m2}^{k} )} & {...} & {(u_{mn}^{k} ,v_{mn}^{k} )} \\ \end{array} } \right] $$

be the kth expert’s judgment matrix. (2) Computation stage: in this stage, an extended variable weighting approach is designed to aggregate the weighted payoff matrix on the basis of q-ROFWA operator. \(w_{k} (k = 1,2,...,t)\) is the initial kth expert’ weight satisfying \(w_{k} \in \left[ {0,1} \right]\) and \(\sum\limits_{k = 1}^{t} {w_{t} = 1}\), which is calculated based on the self-evaluation value of kth expert \(G_{k} (k = 1,2,...,t)\). On the basis of this, a novel Hausdorff distance measure for q-ROFNs is introduced to construct the variable expert weight \(\tilde{w}_{k} (k = 1,2,...,t)\). Utilizing the q-ROFWA operator, a comprehensive payoff matrix can be got. (3) Decision stage: the optimal strategies are chosen with a two-person matrix game via linear programming (LP). The game results are in the form of probability which have higher credibility. To present the main procedures of the proposed approach explicitly, a flowchart is plotted as displayed in Fig. 1.

Fig. 1
figure 1

The conceptual structure of the proposed method

Full size image

The group decision-making approach

Step 1: Calculate the experts weights via variable weight assignment method

Step 1.1 Determine the initial experts’ weights using credibility analysis scale

The experts’ credibility indexes are shown in Table 1. The initial experts’ weights can be calculated utilizing the following two formulas:

$$ G_{k} = E_{1}^{k} + E_{2}^{k} + ... + E_{6}^{k} $$
(8)
$$ w_{k} = \frac{{G_{k} }}{{\sum\nolimits_{k = 1}^{t} {G_{k} } }}. $$
(9)
Table 1 Expert credibility analysis scale
Full size table
Step 1.2 Compute the variable experts’ weights based on Hausdorff distance for q-ROFNs

Distance for the evaluation matrix can be used to measure the difference degree among experts [38,39,40,41]. Meanwhile, according to Hastie and Kameda [42], majority rules perform quite well in group decisions, at levels comparable to rules that require more resources for instance the average rule of individual judgment. Hence, based on the majority rules, the greater the sum of the differences between an expert and other experts is, the less reliable expert’s evaluation. Inspired by this inference, the variable experts’ weights can be obtained on the basis of a Hausdorff distance for q-ROFNs.

Let \(\tilde{A}\) and \(\tilde{B}\) be two q-ROFNs in a finite set \(X = \left\{ {x_{1} ,x_{2} ,...,x_{n} } \right\}\). \(I_{{\tilde{A}}} (x_{i} )\) and \(I_{{\tilde{B}}} (x_{i} )\) are two subintervals in \(\left[ {0,1} \right]\) with \(I_{{\tilde{A}}} (x_{i} ) = \left[ {u_{{\tilde{A}}}^{q} (x_{i} ),1 - v_{{\tilde{A}}}^{q} (x_{i} )} \right]\) and \(I_{{\tilde{B}}} (x_{i} ) = \left[ {u_{{\tilde{B}}}^{q} (x_{i} ),1 - v_{{\tilde{B}}}^{q} (x_{i} )} \right]\), \(i = 1,2,...,n\). \(H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} ))\) is defined as the Hausdorff distance between \(I_{{\tilde{A}}} (x_{i} )\) and \(I_{{\tilde{B}}} (x_{i} )\). The Hausdorff distance between \(\tilde{A}\) and \(\tilde{B}\) is

$$ \begin{gathered} d_{H} (\tilde{A},\tilde{B}) = H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} )) = \max \left\{ {\left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{B}}}^{q} (x_{i} )} \right|,\left| {1 - v_{{\tilde{A}}}^{q} (x_{i} ) - (1 - v_{{\tilde{B}}}^{q} (x_{i} ))} \right|} \right\} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} {\kern 1pt} \max \left\{ {\left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{B}}}^{q} (x_{i} )} \right|,\left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{B}}}^{q} (x_{i} )} \right|} \right\}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ \end{gathered} $$

The normalized Hausdorff distance \(d_{NH} (\tilde{A},\tilde{B})\) from \(\tilde{A}\) to \(\tilde{B}\) is as the following formula:

$$ d_{NH} (\tilde{A},\tilde{B}) = \frac{1}{n}\sum\limits_{i = 1}^{n} {H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} )) = } \frac{1}{n}\sum\limits_{i = 1}^{n} {\max \left\{ {\left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{B}}}^{q} (x_{i} )} \right|,\left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{B}}}^{q} (x_{i} )} \right|} \right\}} . $$
(10)

Example 1

Assume two q-ROFSs \(A = \left( {0.5,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0.6,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0.39} \right)\) and \(B = \left( {0.4,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0.7,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0.35} \right)\), then the following results can be obtained by applying Eq. (10):

\(d_{NH} (A,B) = \frac{1}{1}\max \left\{ {\left| {0.25 - 0.16} \right|,\left| {0.36 - 0.49} \right|} \right\} = 0.13\).

The following proposition is given to guarantee the reasonability of Eq. (10).

Proposition 1

Let \(X = \left\{ {x_{1} ,x_{2} ,...,x_{n} } \right\}\) be a fixed set. The defined normalized distance \(d_{NH} (\tilde{A},\tilde{B})\) between q-ROFNs \(\tilde{A}\) and \(\tilde{B}\) has the following properties (\(P_{1}\))–(\(P_{4}\)):

(\(P_{1}\)) \(0 \le d_{NH} (\tilde{A},\tilde{B}) \le 1\);

(\(P_{2}\)) \(d_{NH} (\tilde{A},\tilde{B}) = 0\) if and only if \(\tilde{A} = \tilde{B}\);

(\(P_{3}\)) \(d_{NH} (\tilde{A},\tilde{B}) = d_{NH} (\tilde{B},\tilde{A})\);

(\(P_{4}\)) If \(\tilde{A} \subseteq \tilde{B} \subseteq \tilde{R}\), then \(d_{NH} (\tilde{A},\tilde{B}) \le d_{NH} (\tilde{A},\tilde{R})\) and \(d_{NH} (\tilde{B},\tilde{R}) \le d_{NH} (\tilde{A},\tilde{R})\).

Proof

Obviously, \(d_{NH} (\tilde{A},\tilde{B})\) confirms to the properties \(P_{1} - P_{3}\).

(\(P_{4}\)) Due to \(\tilde{A} \subseteq \tilde{B} \subseteq \tilde{C}\), thus \(u_{{\tilde{A}}}^{q} (x_{i} ) \le u_{{\tilde{B}}}^{q} (x_{i} ) \le u_{{\tilde{C}}}^{q} (x_{i} )\), \(v_{{\tilde{A}}}^{q} (x_{i} ) \ge v_{{\tilde{B}}}^{q} (x_{i} ) \ge v_{{\tilde{C}}}^{q} (x_{i} )\), \(\forall x_{i} \in X\).

\(H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} )) = \max \left\{ {\left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{B}}}^{q} (x_{i} )} \right|,\left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{B}}}^{q} (x_{i} )} \right|} \right\}\),

\(H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{C}}} (x_{i} )) = \max \left\{ {\left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{C}}}^{q} (x_{i} )} \right|,\left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{C}}}^{q} (x_{i} )} \right|} \right\}\),

\(H(I_{{\tilde{B}}} (x_{i} ),I_{{\tilde{C}}} (x_{i} )) = \max \left\{ {\left| {u_{{\tilde{B}}}^{q} (x_{i} ) - u_{{\tilde{C}}}^{q} (x_{i} )} \right|,\left| {v_{{\tilde{B}}}^{q} (x_{i} ) - v_{{\tilde{C}}}^{q} (x_{i} )} \right|} \right\}\).

Case 1. If \(\left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{C}}}^{q} (x_{i} )} \right| \ge \left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{C}}}^{q} (x_{i} )} \right|\), \(H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{C}}} (x_{i} )) = \left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{C}}}^{q} (x_{i} )} \right|\). However, \(\left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{B}}}^{q} (x_{i} )} \right| \le \left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{C}}}^{q} (x_{i} )} \right| \le \left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{C}}}^{q} (x_{i} )} \right|\) and \(\left| {v_{{\tilde{B}}}^{q} (x_{i} ) - v_{{\tilde{C}}}^{q} (x_{i} )} \right| \le \left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{C}}}^{q} (x_{i} )} \right| \le \left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{C}}}^{q} (x_{i} )} \right|\). Based on the inequalities above, \(H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} )) \le H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{C}}} (x_{i} ))\) and \(H(I_{{\tilde{B}}} (x_{i} ),I_{{\tilde{C}}} (x_{i} )) \le H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{C}}} (x_{i} ))\) can be obtained without a hitch. Hence, \(d_{NH} (\tilde{A},\tilde{B}) \le d_{NH} (\tilde{A},\tilde{C})\) and \(d_{NH} (\tilde{B},\tilde{C}) \le d_{NH} (\tilde{A},\tilde{C})\).

Case 2. If \(\left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{C}}}^{q} (x_{i} )} \right| \le \left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{C}}}^{q} (x_{i} )} \right|\), \(H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{C}}} (x_{i} )) = \left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{C}}}^{q} (x_{i} )} \right|\). However, \(\left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{B}}}^{q} (x_{i} )} \right| \le \left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{C}}}^{q} (x_{i} )} \right| \le \left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{C}}}^{q} (x_{i} )} \right|\) and \(\left| {u_{{\tilde{B}}}^{q} (x_{i} ) - u_{{\tilde{C}}}^{q} (x_{i} )} \right| \le \left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{C}}}^{q} (x_{i} )} \right| \le \left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{C}}}^{q} (x_{i} )} \right|\). On the contrary, \(\left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{B}}}^{q} (x_{i} )} \right| \le \left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{C}}}^{q} (x_{i} )} \right|\) and \(\left| {u_{{\tilde{B}}}^{q} (x_{i} ) - u_{{\tilde{C}}}^{q} (x_{i} )} \right| \le \left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{C}}}^{q} (x_{i} )} \right|\). Based on the inequalities above, \(H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} )) \le H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{C}}} (x_{i} ))\) and \(H(I_{{\tilde{B}}} (x_{i} ),I_{{\tilde{C}}} (x_{i} )) \le H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{C}}} (x_{i} ))\). Hence, \(d_{NH} (\tilde{A},\tilde{B}) \le d_{NH} (\tilde{A},\tilde{C})\) and \(d_{NH} (\tilde{B},\tilde{C}) \le d_{NH} (\tilde{A},\tilde{C})\). Thus, the containment property (\(P_{4}\)) is proved.

Proposition 2

The proposed normalized Hausdorff distance \(d_{NH} (\tilde{A},\tilde{B})\) between q-ROFNs \(\tilde{A}\) and \(\tilde{B}\) increases as the \(q\) increases.

Proof

  1. (i)

    If \(\left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{B}}}^{q} (x_{i} )} \right| \ge \left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{B}}}^{q} (x_{i} )} \right|\) and \(u_{{\tilde{A}}}^{q} (x_{i} ) \ge u_{{\tilde{B}}}^{q} (x_{i} )\), \(H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} )) = u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{B}}}^{q} (x_{i} )\). Then, \(\frac{{\partial H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} ))}}{\partial q} = q(u_{{\tilde{A}}}^{q - 1} (x_{i} ) - u_{{\tilde{B}}}^{q - 1} (x_{i} )) \ge 0\) which proves that with the increase of \(q\), the Hausdorff distance \(H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} ))\) increases. Therefore, the proposed normalized Hausdorff distance \(d_{NH} (\tilde{A},\tilde{B})\) between q-ROFNs \(\tilde{A}\) and \(\tilde{B}\) increases with the increasing value of \(q\).

  2. (ii)

    If \(\left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{B}}}^{q} (x_{i} )} \right| \ge \left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{B}}}^{q} (x_{i} )} \right|\) and \(u_{{\tilde{A}}}^{q} (x_{i} ) \le u_{{\tilde{B}}}^{q} (x_{i} )\), \(H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} )) = u_{{\tilde{B}}}^{q} (x_{i} ) - u_{{\tilde{A}}}^{q} (x_{i} )\). Then, \(\frac{{\partial H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} ))}}{\partial q} = q(u_{{\tilde{B}}}^{q - 1} (x_{i} ) - u_{{\tilde{A}}}^{q - 1} (x_{i} )) \ge 0\) which proves that with the increase of \(q\), the Hausdorff distance \(H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} ))\) increases. Therefore, the proposed normalized Hausdorff distance \(d_{NH} (\tilde{A},\tilde{B})\) between q-ROFNs \(\tilde{A}\) and \(\tilde{B}\) increases with the increasing value of \(q\).

  3. (iii)

    If \(\left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{B}}}^{q} (x_{i} )} \right| \le \left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{B}}}^{q} (x_{i} )} \right|\) and \(v_{{\tilde{A}}}^{q} (x_{i} ) \ge v_{{\tilde{B}}}^{q} (x_{i} )\), \(H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} )) = v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{B}}}^{q} (x_{i} )\). Then, \(\frac{{\partial H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} ))}}{\partial q} = q(v_{{\tilde{A}}}^{q - 1} (x_{i} ) - v_{{\tilde{B}}}^{q - 1} (x_{i} )) \ge 0\) which proves that with the increase of \(q\), the Hausdorff distance \(H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} ))\) increases. Therefore, the proposed normalized Hausdorff distance \(d_{NH} (\tilde{A},\tilde{B})\) between q-ROFNs \(\tilde{A}\) and \(\tilde{B}\) increases with the increasing value of \(q\).

  4. (iv)

    If \(\left| {u_{{\tilde{A}}}^{q} (x_{i} ) - u_{{\tilde{B}}}^{q} (x_{i} )} \right| \le \left| {v_{{\tilde{A}}}^{q} (x_{i} ) - v_{{\tilde{B}}}^{q} (x_{i} )} \right|\) and \(v_{{\tilde{B}}}^{q} (x_{i} ) \ge v_{{\tilde{A}}}^{q} (x_{i} )\), \(H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} )) = v_{{\tilde{B}}}^{q} (x_{i} ) - v_{{\tilde{A}}}^{q} (x_{i} )\). Then, \(\frac{{\partial H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} ))}}{\partial q} = q(v_{{\tilde{B}}}^{q - 1} (x_{i} ) - v_{{\tilde{A}}}^{q - 1} (x_{i} )) \ge 0\) which proves that with the increase of \(q\), the Hausdorff distance \(H(I_{{\tilde{A}}} (x_{i} ),I_{{\tilde{B}}} (x_{i} ))\) increases. Therefore, the proposed normalized Hausdorff distance \(d_{NH} (\tilde{A},\tilde{B})\) between q-ROFNs \(\tilde{A}\) and \(\tilde{B}\) increases with the increasing value of \(q\).

Proposition 2 means that for the same evaluation information, the increasing parameter value of \(q\) can cause miscalculation of Hausdorff distance between q-ROFNs \(\tilde{A}\) and \(\tilde{B}\). In other words, it is not a sensible choice giving the experts more freedom sometimes.

The variable expert weight \(\tilde{w}_{k} (k = 1,2,...,t)\) can be calculated as

$$ \tilde{w}_{k} = \frac{{w_{k} \sum\nolimits_{l = 1}^{t} {(1 - d_{NH} (A^{k} ,A^{l} ))} }}{{\sum\nolimits_{k = 1}^{t} {w_{k} } \sum\nolimits_{l = 1}^{t} {(1 - d_{NH} (A^{k} ,A^{l} ))} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (k = 1,2,...,t;l = 1,2,...,t;l \ne k). $$
(11)

As can be observed from Eq. (11), the initial expert weight \(w_{k}\), obtained on the basis of experts’ individual information, plays an important role in the calculation process of \(\tilde{w}_{k}\). On the other hand, it can be easily seen that the variable expert weight \(\tilde{w}_{k}\) changes with \(d_{NH} (A^{k} ,A^{l} )\), and the variation of subjective information evaluated by experts can result in the change of \(d_{NH} (A^{k} ,A^{l} )\). Thus, the proposed expert weight dynamic determination model is capable of taking into account the objective individual information of experts and varying with changeable subjective evaluation information to make the decision results more reliable in a real scenario.

Step 2. Obtain the overall payoff matrix by the q-ROFWA operator

Player I’s comprehensive payoff matrix \(\overline{A} = (\overline{u}_{ij} ,\overline{v}_{ij} )\) can be constructed by aggregating all payoff values \(a_{ij}^{k} (i = 1,2,..,m;j = 1,2,...,n)\) to the overall preference value \(\overline{a}_{ij} (i = 1,2,..,m;j = 1,2,...,n)\) utilizing the \(q - ROFWA\) operator:

$$ \overline{a}_{ij} = \left( {\overline{u}_{ij} ,\overline{v}_{ij} } \right) = q - ROFWA(a_{ij}^{1} ,a_{ij}^{2} ,...,a_{ij}^{t} ) = \left\langle {(1 - \mathop \prod \limits_{k = 1}^{t} (1 - (u_{ij}^{k} )^{q} )^{{\tilde{w}_{k} }} )^{1/q} ,\mathop \prod \limits_{k = 1}^{t} (v_{ij} )^{{\tilde{w}_{k} }} } \right\rangle . $$
(12)

Step 3. Select the optimal strategies via two-person non-cooperative matrix game theory

Step 3.1 Construct expected payoffs of player I and II

The expected payoff of player I can be computed by the following formula:

$$ \tilde{E} = x^{T} Ry = \left( {(1 - \prod\limits_{j = 1}^{m} {\prod\limits_{i = 1}^{n} {(1 - \overline{u}_{ij}^{q} )^{{x_{i} y_{j} }} )^{1/q} ,\prod\limits_{j = 1}^{m} {\prod\limits_{i = 1}^{n} {\overline{v}_{ij}^{{x_{i} y_{j} }} } } } } } \right), $$
(13)

which is a q-ROFN. Stated as earlier, the expected payoff of player II can be obtained via the equation

$$ - \tilde{E} = x^{T} ( - R)y = \left( {(1 - \prod\limits_{i = 1}^{n} {\prod\limits_{j = 1}^{m} {(1 - \overline{v}_{ij}^{q} )^{{x_{i} y_{j} }} )^{1/q} ,\prod\limits_{i = 1}^{n} {\prod\limits_{j = 1}^{m} {\overline{u}_{ij}^{{x_{i} y_{j} }} } } } } } \right){\kern 1pt} , $$
(14)

which is still a q-ROFN. Denote the maximum payoff of player I and the minimum payoff of player II as \(v_{G}\) and \(\rho_{G}\), respectively, which can be calculated using the following two expressions:

\(v_{G} = \left( {\tilde{u},\tilde{v}} \right) = (\mathop {\min }\limits_{y \in Y} (1 - \prod\limits_{j = 1}^{n} {\prod\limits_{i = 1}^{m} {(1 - \overline{u}_{ij}^{q} )^{{x_{i} y_{j} }} )^{1/q} ,\mathop {\max }\limits_{y \in Y} (\prod\limits_{j = 1}^{n} {\prod\limits_{i = 1}^{m} {\overline{v}_{ij}^{{x_{i} y_{j} }} ))} } } }\),

\(\rho_{G} = \left( {\tilde{\mu },\tilde{\gamma }} \right) = (\mathop {\max }\limits_{x \in X} (1 - \prod\limits_{i = 1}^{m} {\prod\limits_{j = 1}^{n} {(1 - \overline{v}_{ij}^{q} )^{{x_{i} y_{j} }} )^{1/q} } } ,\mathop {\min }\limits_{x \in X} (\prod\limits_{i = 1}^{m} {\prod\limits_{j = 1}^{n} {\overline{u}_{ij}^{{x_{i} y_{j} }} } } ))\).

The two-person matrix game \(G\) gains a fuzzy value \(V_{G}\) if \(V_{G} = v_{G} = \rho_{G}\).

Step 3.2 Determine the optimal competitive strategies of player I and II

According to Eq. (6), solving the following non-linear multi-objective programming model can generate the gain-floor of player I and a maximum strategy \(x^{*}\):

$$ \max \left\{ {v_{G} } \right\} = \left\{ {\max (\tilde{u}),\min (\tilde{v})} \right\} $$
(M-1)
$$ s.t. \, \left( {1 - \prod\limits_{i = 1}^{m} {\prod\limits_{j = 1}^{n} {(1 - \overline{u}_{ij}^{q} )^{{x_{i} y_{j} }} } } } \right)^{1/q} \ge \tilde{u}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (j = 1,2,...,n) $$
$$ \prod\limits_{i = 1}^{m} {\prod\limits_{j = 1}^{n} {\overline{v}_{ij}^{{x_{i} y_{j} }} } } \le \tilde{v}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j = 1,2,...,n $$
$$ e^{T} x = 1 $$

\(\tilde{u} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde{v} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_{i} \ge 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 1,2,...,m)\).

Obviously, the existing methods cannot directly solve the above non-linear programming (NLP) model. Thus, inspired by Li [37], a novel approach based on the weighted average theory is proposed to transform model (M-1) into the standard LP model.

For \(0 \le \tilde{u} \le 1\), \(\max \left\{ {\tilde{u}} \right\}\) is equivalent to \(\min \left\{ {1 - \tilde{u}} \right\}\) which is equivalent to \(\min \left\{ {\ln (1 - \tilde{u})} \right\}\). \(\min \left\{ {\ln (1 - \tilde{u})} \right\}\) is equivalent to \(\min \left\{ {\ln (1 - \tilde{u}^{q} )} \right\}\). Hence, \(\max \left\{ {\tilde{u}} \right\}\) is equivalent to \(\min \left\{ {\ln (1 - \tilde{u}^{q} )} \right\}\) for \(0 \le \tilde{u} \le 1\). Similarly, \(\min \left\{ {\tilde{v}} \right\}\) is equivalent to \(\min \left\{ {\ln (\tilde{v})} \right\}\). Thus, model (M-1) can be transformed into

$$ \min \left\{ {\lambda \ln (1 - \tilde{u}^{q} ) + (1 - \lambda )\ln (\tilde{v})} \right\} $$
(M-2)
$$ s.t. \, \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {x_{i} y_{j} (\lambda \ln (} } 1 - \overline{u}_{ij}^{q} ) + (1 - \lambda )\ln \overline{v}_{ij} ) \le \lambda \ln (1 - \tilde{u}^{q} ){\kern 1pt} {\kern 1pt} + {\kern 1pt} {\kern 1pt} (1 - \lambda )\ln \tilde{v}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (j = 1,2,...,n) $$
$$ e^{T} x = 1 $$
$$ \tilde{u} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde{v} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_{i} \ge 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 1,2,...,m), $$

except for \(\overline{u}_{ij} = 1\), \(\tilde{u} = 1\), \(\overline{v}_{ij} = 0\), \(\tilde{v} = 0\). \(\lambda\) is the weight determined by players, which measures the objectives’ priorities.

In light of that the set \(Y\) is compact and finite, it is reasonable to transform model (M-2) into the linear model (M-3) as follows:

$$ \min \left\{ {\lambda \ln (1 - \tilde{u}^{q} ) + (1 - \lambda )\ln (\tilde{v})} \right\} $$
$$ s.t. \, \sum\limits_{i = 1}^{m} {x_{i} (\lambda \ln (1 - \overline{u}_{ij}^{q} ) + (1 - \lambda )\ln \overline{v}_{ij} ) \le \lambda \ln (1 - \tilde{u}^{q} ) + {\kern 1pt} {\kern 1pt} (1 - \lambda )\ln \tilde{v}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (j = 1,2,...,n)} $$
$$ e^{T} x = 1 $$
$$ \tilde{u} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde{v} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_{i} \ge 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 1,2,...,m){.} $$

In a same analysis, according to Eq. (7), solving the following non-linear multi-objective programming model can generate the loss-ceiling of player II and a minimum strategy \(y^{*}\):

$$ \min \left\{ {\rho_{G} } \right\} = \left\{ {\min (\tilde{\mu }),\max (\tilde{\gamma })} \right\} $$
(M-4)
$$ s.t. \, \left( {1 - \prod\limits_{i = 1}^{m} {\prod\limits_{j = 1}^{n} {(1 - \overline{v}_{ij}^{q} )^{{x_{i} y_{j} }} } } } \right)^{1/q} \le \tilde{\mu }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 1,2,...,m) $$
$$ \prod\limits_{i = 1}^{m} {\prod\limits_{j = 1}^{n} {\overline{u}_{ij}^{{x_{i} y_{j} }} } } \ge \tilde{\gamma }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2,...,m $$
$$ e^{T} y = 1 $$
$$ \tilde{\mu } \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde{\gamma } \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y_{j} \ge 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (j = 1,2,...,m){.} $$

Obviously, for \(\tilde{\mu } \in \left[ {0,1} \right]\), \(\min \left\{ {\tilde{\mu }} \right\}\) is equivalent to \(\max \left\{ {1 - \tilde{\mu }} \right\}\). \(\max \left\{ {1 - \tilde{\mu }} \right\}\) is equivalent to \(\max \left\{ {\ln (1 - \tilde{\mu })} \right\}\) for \(\tilde{\mu } \in \left[ {0,1} \right)\). Hence,

$$ \max \left\{ {\lambda \ln (1 - \tilde{\mu }^{q} ) + (1 - \lambda )\ln (\tilde{\gamma })} \right\} $$
(M-5)
$$ s.t. \, \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {x_{i} y_{j} (\lambda \ln (} } 1 - \overline{u}_{ij}^{q} ) + (1 - \lambda )\ln \overline{v}_{ij} ) \ge \lambda \ln (1 - \tilde{\mu }^{q} ){\kern 1pt} {\kern 1pt} + {\kern 1pt} {\kern 1pt} (1 - \lambda )\ln \tilde{\gamma }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({\kern 1pt} i = 1,2,...,m) $$
$$ e^{T} y = 1 $$
$$ \tilde{\mu } \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde{\gamma } \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y_{j} \ge 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (j = 1,2,...,n){.} $$

except for \(\overline{u}_{ij} = 1\), \(\tilde{\mu } = 1\), \(\overline{v}_{ij} = 0\), \(\tilde{\gamma } = 0\). \(\lambda\) is the weight determined by players, which measures the objectives’ priorities.

In light of that the set \(X\) is compact and finite, it is reasonable to transform model (M-5) into the linear model (M-6) as follows:

$$ \max \left\{ {\lambda \ln (1 - \tilde{\mu }^{q} ) + (1 - \lambda )\ln (\tilde{\gamma })} \right\} $$
(M-6)
$$ s.t. \, \sum\limits_{j = 1}^{n} {y_{j} (\lambda \ln (1 - \overline{u}_{ij}^{q} ) + (1 - \lambda )\ln \overline{v}_{ij} ) \ge \lambda \ln (1 - \tilde{\mu }^{q} ) + {\kern 1pt} {\kern 1pt} (1 - \lambda )\ln \tilde{\gamma }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 1,2,...,m)} $$
$$ e^{T} y = 1 $$
$$ \tilde{\mu } \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde{\gamma } \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y_{j} \ge 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (j = 1,2,...,n){.} $$

However, \(\ln (1 - \overline{u}_{ij}^{q} ) \to - \infty\), and/or \(\ln (\overline{v}_{ij} ) \to - \infty\) if \(\overline{u}_{ij}^{q} = 1\), and/or \(\overline{v}_{ij} = 0\). Under these circumstances, model (M-3) and (M-6) are meaningless. To expand the application of the proposed method, the following NLP models should be formulated:

$$ \min \left\{ {(1 - \tilde{u}^{q} )^{\lambda } (\tilde{v})^{1 - \lambda } } \right\} $$
(M-7)
$$ s.t. \, \mathop \prod \limits_{i = 1}^{m} \left[ {(1 - \overline{u}_{ij}^{q} )^{\lambda } (\overline{v}_{ij} )^{1 - \lambda } } \right]^{{x_{i} }} \le (1 - \tilde{u}^{q} )^{\lambda } (\tilde{v})^{1 - \lambda } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (j = 1,2,...,n) $$
$$ e^{T} x = 1 $$
$$ \tilde{u} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde{v} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_{i} \ge 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 1,2,...,m) $$

and

$$ \max \left\{ {(1 - \tilde{\mu }^{q} )^{\lambda } (\tilde{\gamma })^{1 - \lambda } } \right\} $$
(M-8)
$$ s.t. \, \mathop \prod \limits_{j = 1}^{n} \left[ {(1 - \overline{u}_{ij}^{q} )^{\lambda } (\overline{v}_{ij} )^{1 - \lambda } } \right]^{{y_{j} }} \le (1 - \tilde{\mu }^{q} )^{\lambda } (\tilde{\gamma })^{1 - \lambda } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 1,2,...,m) $$
$$ e^{T} y = 1 $$
$$ \tilde{\mu } \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde{\gamma } \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y_{j} \ge 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (j = 1,2,...,n){.} $$

Let \(L = (1 - \tilde{u}^{q} )^{\lambda } (\tilde{v})^{1 - \lambda }\) and \(T = (1 - \tilde{\mu }^{q} )^{\lambda } (\tilde{\gamma })^{1 - \lambda }\). Then, \(0 \le L \le 1\) since \(\lambda \in \left[ {0,1} \right]\), \(0 \le 1 - \tilde{u}^{q} \le 1\) and \(0 \le \tilde{v} \le 1\). Similarly, \(0 \le T \le 1\). Thus, (M-7) and (M-8) can be overtyped into the NLP models as follows:

$$ \min \left\{ L \right\} $$
(M-9)
$$ s.t. \, \mathop \prod \limits_{i = 1}^{m} \left[ {(1 - \overline{u}_{ij}^{q} )^{\lambda } (\overline{v}_{ij} )^{1 - \lambda } } \right]^{{x_{i} }} \le L{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (j = 1,2,...,n) $$
$$ e^{T} x = 1 $$
$$ \tilde{u} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde{v} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_{i} \ge 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 1,2,...,m) $$

and

$$ \max \left\{ T \right\} $$
(M-10)
$$ s.t. \, \mathop \prod \limits_{j = 1}^{n} \left[ {(1 - \overline{u}_{ij}^{q} )^{\lambda } (\overline{v}_{ij} )^{1 - \lambda } } \right]^{{y_{j} }} \le T{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 1,2,...,m) $$
$$ e^{T} y = 1 $$
$$ \tilde{\mu } \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde{\gamma } \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y_{j} \ge 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (j = 1,2,...,n){.} $$

Evidently, models (M-9) and (M-10) are original dual linear programming problems for player I and II. According to the duality theorem, \(\max \left\{ T \right\}\) is equivalent to \(\min \left\{ L \right\}\). The optimal strategies of players can be obtained by solving models (M-9) and (M-10) via simplex methods.

Illustrative example

In this section, to demonstrate the availability of the proposed group decision-making method, a market share competition between two new energy electric vehicles sharing companies is exemplified.

Case description

Due to the advantages of energy conservation and pollution reduction, new energy electric vehicles become more and more popular in Shanghai, China. Two new energy electric vehicles sharing companies \(A\) and \(B\) compete for market share in Shanghai market. The company \(A\) was formed by the cooperation of two big companies, which has more than 3673 branches. The company \(B\) is a local brand in Shanghai and owns over 226 branches. The company \(A\) has advantages in company size, branch quantity, usability. For the company \(B\), it has the techniques of backstage big data processing provided by a national renowned college’s smart grid center located in Shanghai and uses only pure electric cars, which can improve the satisfaction of green consumers. Although the unit price are different with the vehicle type, there is no big difference in unit price between the two companies. Since an increase in one company’s market share means a decrease in another company’s market share, the competition game between \(A\) and \(B\) belongs to a two-person matrix game. The company \(A\) and \(B\) consider the following three strategies to maximum market share: \(\eta_{1}\)(improving the quality subscribers), \(\eta_{2}\)(advertising investment) and \(\eta_{3}\)(technology improvement). Five experts \(e_{1} - e_{5}\) comprehensively evaluate the relative competitive advantages between the companies \(A\) and \(B\) considering the factors including capital demand, labor cost, time cost, execution difficulty coefficient and sustainability, and give the payoff matrices of the companies \(A\) and \(B\). Table 2 shows the payoff matrices of the company \(A\) evaluated by the five experts. Due to \(\max \left\{ {(u_{ij}^{k} )^{1} + (v_{ij}^{k} )^{1} } \right\} = (0.6)^{1} + (0.8)^{1} = 1.4 \ge 1\) and \(\max \left\{ {(u_{ij}^{k} )^{2} + (v_{ij}^{k} )^{2} } \right\} = (0.6)^{2} + (0.8)^{2} = 1 \ge 1\), IFSs and PFSs cannot describe this market share competition. Note that \(\max \left\{ {(u_{ij}^{k} )^{3} + (v_{ij}^{k} )^{3} } \right\} = (0.6)^{3} + (0.8)^{3} = 0.728 < 1\). Hence, to conquer the shortcomings of IFSs and PFSs in depicting this illustrative example, q-ROFS is utilized as the evaluation language by assigning the parameter value of \(q\) to 3.

Table 2 The payoff matrices of the company \(A\)
Full size table

Illustration of the proposed method

Step 1: Calculate the experts’ weights via variable weight assignment method

Step 1.1 Determine the initial experts’ weights using credibility analysis scale

Based on the objective credibility information provided by the five experts, the initial experts weights can be obtained using the Eqs. (8) and (9) as \(w_{k} = (0.2177,0.2177,0.2016,0.1774,0.1855)\). From Table 3 which presents the main results of Step 1.1, the ordering of experts’ total credibility index is \(G_{1} = G_{2} > G_{3} > G_{5} > G_{4}\) in accordance with the ranking of experts’ evaluation credibility. This confirms the accuracy of the initial experts’ weights obtained by this step.

Table 3 The initial experts’ weights based on credibility information
Full size table

Step 1.2 Compute the variable experts’ weights based on Hausdorff distance for q-ROFNs

First, the Hausdorff distances between the experts are calculated by Eq. (10). After that, the variable experts’ weights are computed via Eq. (11) as \(\tilde{w}_{k} = (0.1778,0.2363,0.1935,0.2022,0.1902)\). The above results are shown in Table 4. Compared to the initial weights in Table 3, the experts’ weights vary with respect to the difference degree of experts. First, the big difference between Expert 1 and other experts signifies that the payoff matrix evaluated by Expert 1 may exist biased errors resulted from some key evaluation factors such as knowledge deficits. Thus, the ordering weight of Expert 1 falls from first to fifth. Second, the Expert 2’s and 4’s ordering weights move up because of relatively small differences with others. Next, the ordering weight of Expert 3 and 5 are constant. The final ranking result of experts weights, \({\text{w}}_{5} > w_{1} > w_{3} > w_{2} > w_{4}\), reveals that the dynamic experts weight, derived by the hybrid weight determination model, can not only combine objective individual information but also make efficient adjustments according to changes in subjective evaluation information.

Table 4 The variable experts’ weights calculated via Hausdorff distance
Full size table

Step 2. Obtain the overall payoff matrix by the q-ROFWA operator

On the basis of the subjective payoff information of the company \(A\) and the variable experts’ weights, the company \(A^{\prime}s\) overall payoff matrix can be aggregated by Eq. (12) as shown in Table 5.

Table 5 The overall payoff matrix of the company \(A\)
Full size table

Step 3. Select the optimal strategies by a two-person non-cooperative matrix game theory

According to the company \(A^{\prime}s\) overall payoff matrix calculated in the previous step, the optimal strategies of \(A\) and \(B\) are obtained via model (M-9) and (M-10), respectively. Table 6 presents the results. It is easily to see that the optimal strategies of \(A\) and \(B\) are constant regardless of the changes in the weight \(\lambda\). The optimal strategy of the company \(A\) and \(B\) are \((0,1,0)\) and \((0,0,1)\), respectively. The company \(A^{\prime}s\) expected payoff is equal to the expected payoff of \(B\) as \(E(x^{*} ,y^{*} ) = (0.6315,0.4445)\). The above results show that the company \(A\) only considers the strategy \(\eta_{2}\) to compete with \(B\) when the company \(B\) takes the competitive strategy \(\eta_{3}\).

Table 6 The optimal strategies of the company \(A\) and \(B\)
Full size table

Sensitivity analysis

It can be observed that the parameter \(q\) plays a crucial part in the proposed two-person non-cooperative matrix game group decision-making approach. To study the sensitivity of the parameter \(q\), let the value of \(q\) increase one unit at a time until 10 in the above example.

Figure 2 displays how the variation of \(q\) impacts the total Hausdorff distance between each expert and the other experts. Obviously, the increasing of \(q\) decreases the Hausdorff distance between each experts simultaneously even though the payoff matrices provided by the experts are unaltered. It means that as the parameter \(q\) increases, the difference degree between any two experts is preposterously reduced. Hence, the greater value of \(q\) is not better because it will generate the incorrect experts’ difference degrees.

Fig. 2
figure 2

The experts’ total Hausdorff distance with different \(q\)

Full size image

Figure 3 illustrates the dynamic expert weights’ ordering changes. Specifically, only the Expert 2’s weight ordering is constant, however, the rest of the experts’ weight orderings have changed in varying degrees. Expert 1’s weight remains unchanged at the last place when \(q\) changes from 3 to 5, but when \(q\) is greater than 5, it rises to the fourth place. For Expert 3 and 5, their weights order fluctuate depending on the value of the parameter \(q\). Besides, as the value of \(q\) increases, the order of Expert 5 is more and more backward until it becomes the last one. Based on the foregoing analyses, it is necessary for experts to choose the appropriate parameter \(q\) prudently because the expert weights ordering results are allergic to the variation of \(q\).

Fig. 3
figure 3

The changes in the experts’ weights ranking ordering with different \(q\)

Full size image

Table 7 shows the impacts of the different \(q\) on the market share matrix game solution. Note that Table 7 only displays the summary results because the game results are same regardless of the weight \(\lambda ^{\prime}s\) variation. Firstly, the optimal strategy and strategies ranking of \(B\) are unchanged. Next, the optimal strategy of \(A\) has changed from \((0,1,0)\) to \((0,0,1)\) when the value of \(q\) changes from 3 to 10, which means that the company \(A\) will takes strategy \(\eta_{3}\) to compete with \(B\) in these cases. In addition, the expected payoff \(E(x^{*} ,y^{*} )\) changes with the different \(q\). Concretely, the winning gains of \(A\) and \(B\) increase in the value of \(q\). Inversely, the increasing of \(q\) makes the losses of failure decrease. Seemingly, the larger the parameter value of \(q\), the better the decision result. However, this verdict is unauthentic because improper parameter values of \(q\) lead to significant biases in the expert weights and the total Hausdorff distance between each expert and the other experts. These biases distort the final decision-making results.

Table 7 The two-person matrix game results via the different \(q\)
Full size table

From the above analyses, it is easily to find that the value of \(q\) has vital adverse influence on the proposed method. In other word, although the greater the \(q\), the more freedom the experts have, the proposed method will be impacted by the increasing value of \(q\) negatively. On the one hand, the increasing value of \(q\) will bridge the gap on Hausdorff distance between the experts, which may impact the correct calculation of the variable experts weights. On the other hand, the winning probabilities increase with \(q\) and the aggregated payoff matrix has changes, which causes the computing deviations of matrix game optimal solutions. Hence, the minimal value of \(q\) should be chosen meeting the condition that \(0 \le (u_{A} (x)^{q} + v_{A} (x)^{q} ) \le 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} (q \ge 1)\) where for all \(x \in X\), \(u_{A} :X \to \left[ {0,1} \right]\) indicates membership grade and \(v_{A} :X \to \left[ {0,1} \right]\) indicates non-membership grade of \(x\), respectively.

Comparative analysis

In this subsection, the stability and superiorities of the proposed approach are demonstrated and highlighted through comparative analyses.

Comparison with other fuzzy evaluation languages

There have been several fuzzy languages improved to describe complex decision-making problems since FSs was proposed. To examine the effectiveness of q-ROFS, it is compared with some classic and novel fuzzy languages including FS [10], IFS [13], PFS [14], spherical fuzzy set [43], bipolar soft set [44] and bipolar picture fuzzy set [45]. The corresponding results are concluded as follows:

  • FS is characterized by a single membership function and ignores the non-membership degree of an object. Hence, this fuzzy set cannot describe fuzzy decision-making problems as q-ROFS can.

  • As special cases of q-ROFSs, IFS and PFS are unable to depict situations where \(u + v > 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} u^{2} + v^{2} > 1\).

  • Spherical fuzzy set and bipolar soft set, generalizations of IFS, are also invalid when \(u + v > 1\).

  • Bipolar picture fuzzy set, a reformative extension of PFS, loses its efficacies if \(u^{2} + v^{2} > 1\).

On the basis of the above comparisons, it can be easily observed that q-ROFS has dominant advantages of portraying complexity systems because it can be transformed into different forms by choosing different values of parameter \(q\).

Comparison with other expert weight calculation methods

Over the past few years, several expert weight assignment methods have been put forward. The devised hybrid dynamic expert weight determination model is compared with three representative categories of weight assignment methods to emphasize its advantages. Table 8 displays the main characteristics of different expert weight calculation methods. The comparative results show that the proposed model is a powerful tool to assign reasonable weight to experts, which can portray experts’ objective individual information and vary with subjective evaluation information.

Table 8 Characteristics of different expert weight calculation methods
Full size table

Comparison with other fuzzy matrix game solution methods

In addition to the weighted average method integrated into the proposed approach, ideal point method and sequential optimization method, widely applied in market share competition strategy selection problems, are also classical methods to solve fuzzy matrix models. Hence, the validity of the proposed method is demonstrated in comparisons with ideal point method [52] and sequential optimization method [53] based on the aforementioned illustrative example. The comparative results are shown in Table 9.

Table 9 The results of two comparative analyses
Full size table

Table 9 shows that there is no significant difference in optimal strategies obtained by the three methods, which verifies the accuracy of the proposed approach. However, compared to the proposed approach, the ideal point method and sequential optimization method have the following two shortcomings: (1) Heavy calculation burden cannot be avoided. Both the ideal point method and the sequential optimization method require two steps to solve four linear programming models, while the proposed approach only needs to solve two linear programming models at once. (2) Intermediate variables are needed. To measure differences between the ideal point and alternatives, distance variables are inevitably introduced into the ideal point method. Similarly, in the calculation process of the fuzzy sequential optimization method, intermediate variables are designed to define comparative laws of fuzzy numbers. The presence of intermediate variables increases computation complexities of the above two method.

According to the above three comparative analyses, the superiorities of the proposed approach in solving competitive strategy decision-making problems are highlighted. Regardless of the number of alternative strategies, the proposed approach can obtain the correct optimal strategies in the form of probability with high efficiency, little calculation burden and low calculation complexity.

Advantages with limitations of the proposed approach

In light of the above comparative analyses, the proposed approach for addressing intricate competitive strategy group decision-making problems has the following advantages:

  1. (i)

    The fuzzy evaluation language utilized by this paper, q-ROFS, is capable of conveying more complex information than part of existing sets such as FS, IFS, PFS, spherical fuzzy set, bipolar soft set and bipolar picture fuzzy set. It can adapt to changes in the language environment.

  2. (ii)

    The devised expert weight determination model integrates the objective individual information and subjective evaluation information, which is more reasonable and close to the actual expert weights.

  3. (iii)

    The proposed two-person non-cooperative fuzzy matrix game decision-making method is less affected by the number of competitive strategies, and can present the specific difference degree of each strategy rather than simple ranking results.

On the other hand, the proposed approach has some limitations:

  1. (1)

    This approach cannot be applied under some particular fuzzy circumstances where various membership functions are independently.

  2. (2)

    Competitive strategy group decision-making problems in non-linear nature are powerless to be handled via the proposed approach which uses linear membership and non-membership function.

Conclusion

A two-person non-cooperative fuzzy matrix game method integrating the superiorities of variable experts’ weights and q-ROFSs is devised to handle competitive strategy group decision-making problems in this paper. First, q-ROFS is utilized to present the payoff matrices provided by experts, which renders experts more freedom of evaluation and describes the uncertainties of CSGDM problems more flexibly because the parameter value of q can be chosen according to the information expression range. Next, a new mechanism to calculate the variable experts’ weights is formulated, taking the objective and subjective weights of experts into consideration simultaneously, based on the q-ROF Hausdorff distances among the experts and the initial weights calculated with experts’ individual information. Then, the q-ROFWA operator is implemented to compute the comprehensive payoff matrices of the players. After that, a q-ROF two-person matrix game is formulated to select the optimal mixed strategy which can present the priorities of the competitive strategies explicitly and concretely. In addition, an illustrative example, several comparative analyses and sensitivity analyses are performed to highlight the superiorities of the proposed approach, the insights show that the optimal strategies in the form of probabilities are close to competitive strategy selection practice, and the proposed approach as a CSGDM method with high efficiency, low computation complexity and little calculation burden. Besides, although the increasing parameter value of q gives the experts more freedom, it would cause decision-making biases. Hence, the minimum value of q that satisfies the language constraints should be chosen with the same evaluation information.

In the future, the following two research directions can be pursued. As a starter, the proposed method can be extended resort to utilizing other forms of fuzzy language such as neutrosophic sets [54, 55] and linear Diophantine fuzzy sets [56,57,58]. Moreover, the proposed fuzzy matrix game is between two persons, and future researches can focus on fuzzy multi-player game method for competitive strategy group decision-making problems.