Approaches for multicriteria decision-making based on the hesitant fuzzy best–worst method

Abstract

Hesitant fuzzy preference relations (HFPRs) have been widely applied in multicriteria decision-making (MCDM) for their ability to efficiently express hesitant information. To address the situation where HFPRs are necessary, this paper develops several decision-making models integrating HFPRs with the best worst method (BWM). First, consistency measures from the perspectives of additive/multiplicative consistent hesitant fuzzy best worst preference relations (HFBWPRs) are introduced. Second, several decision-making models are developed in view of the proposed additive/multiplicatively consistent HFBWPRs. The main characteristic of the constructed models is that they consider all the values included in the HFBWPRs and consider the same and different compromise limit constraints. Third, an absolute programming model is developed to obtain the decision-makers’ objective weights utilizing the information of optimal priority weight vectors and provides the calculation of decision-makers’ comprehensive weights. Finally, a framework of the MCDM procedure based on hesitant fuzzy BWM is introduced, and an illustrative example in conjunction with comparative analysis is provided to demonstrate the feasibility and efficiency of the proposed models.

Introduction

In multicriteria decision-making (MCDM) problems, we need to choose the best alternative/alternatives according to several determined criteria from a set of alternatives [1,2,3]. Different approaches have been developed from different perspectives, where preference relations (PRs) are one of the commonly used technologies. Their principle is to rank alternatives in view of the priority weight vector obtained from pairwise comparisons of the alternatives [4]. According to the evaluation scale of the pairwise comparisons, PRs can be divided into fuzzy PRs (FPRs) and multiplicative PRs (MPRs). The former uses the [0, 1] scale, and the latter expresses the comparison with [1/9, 9]. In the process of developing PRs, consistency analysis is necessary to avoid contradictory ranking. Tanino [5] developed two consistency concepts for FPRs, namely, additive consistent FPRs and multiplicative consistent FPRs. The former indicates additive transitivity, and the latter shows multiplicative transitivity. For MPRs, Saaty [6] defined the concept of multiplicatively consistent MPRs, which indicates the multiplicative transitivity among three related comparisons. Since then, MCDM approaches based on two types of PRs have been proposed [7,8,9,10,11,12].

Noticeably, FPRs and MPRs only employ an exact numeric value to denote the membership degree of pairwise comparisons, which limits the applications because hesitant information exists extensively in MCDM problems. To address this issue, Torra and Narukawa [13] employed several values in [0, 1] to denote the pairwise comparisons and developed the concept of hesitant fuzzy set (HFS). The primary advantage of HFS is that several values can be used to represent decision makers’ hesitant information; it can also overcome the shortcoming of fuzzy sets, which use only one value. Since the concept of HFS has been proposed, a large number of studies focusing on HFS have been developed [14,15,16]. Later, Xia and Xu [17] introduced the concept of hesitant fuzzy preference relations (HFPRs). Following the original work of Xia and Xu [17], many MCDM approaches based on HFPRs have been developed. For example, MCDM approaches are based on additive consistent HFPRs [18,19,20], MCDM approaches are based on multiplicatively consistent HFPRs [21,22,23], and MCDM approaches are based on multiplicatively consistent hesitant MPRs (HMPRs) [24, 25]. According to the principle of using the number of elements, including hesitant fuzzy elements (HFEs), these approaches can be classified into four categories [21]. A concise literature review of these approaches is presented as follows and summarized in Table 1.

Table 1 A summary of different consistent HFPRs

(1) Consider only one FPR derived from HFPRs [26, 27]. This method is also named optimistic consistency; that is, a reduced FPR with the highest consistency degree is derived from HFPRs. The optimistic consistency method can reflect the highest consistency degree of HFPRs, but it cannot reflect the hesitancy of decision-makers. It leads to substantial information loss. (2) Based on ordered FPRs derived from normalized HFPRs [28, 29]. This method also named normalized consistency. The normalized consistency requires that any two HFEs have an equal number of elements; if two HFEs have an unequal number of elements, a normalized process is needed. In the review of the previous work [30], the shorter HFE needs to add some values until two HFEs have the same number of elements in the normalized process. Therefore, the normalized consistency method may distort the original information provided by decision-makers. (3) Based on all possible FPRs, including HFPRs [18, 31]. This method defines the concept of consistent HFPRs as too restricted. It is difficult for decision-makers to provide such pairwise comparisons in the actual decision-making process. (4) Based on the derived FPRs for each value in HFEs [32, 33]. The main feature of this method is that it considers all the evaluation information and neither adds values to HFEs nor removes values from HFEs. Compared with (3), this method only used some possible FPRs, including HFPRs.

Rezaei [34] developed a novel MCDM method named the best–worst method (BWM), which can be taken as an enhancement of the traditional analytic hierarchy process (AHP). With the BWM, it can remedy the drawbacks of AHP in terms of numerous comparisons and low consistency [35]; thus, it is much easier to use. At the same time, the weights derived from the BWM are more reliable than the AHP, as it only needs to provide the best and worst vectors [36, 37]. Due to these advantages, the BWM has attracted wide attention from scholars [38,39,40,41,42,43]. For example, Ming et al. [44] managed patient satisfaction in a blood-collection room integrated with BWM and probabilistic linguistic gained and lost dominance score method. Karimi et al. [45] introduced a fully fuzzy BWM with a triangular fuzzy number. Chen and Ming [46] developed a smart product service module integrated with a BWM and data envelopment analysis. Liang et al. [47] established the thresholds for the consistency ratios. Mohammadi and Rezaei [48] introduced the Bayesian BWM for group decision-making problems. In addition, an overview of the BWM can be found in [49].

The concept of HFPRs has been introduced, and several scholars have studied some MCDM methods based on BWM. However, there are still some important issues that need to be further studied. (1) The concept of additive/multiplicatively consistent HFPRs. As HFPRs, additive/multiplicatively consistent HFPRs develop in considering one FPR derived from HFPRs, which may lead to information loss [50]; develops in considering ordered FPRs derived from normalized HFPRs may distort the preference information [50, 51]; and develops in considering all possible FPRs in HFPRs seems too restrictive [31]. (2) The different expertise levels of decision-makers and the complexity of MCDM problems lead to the appearance of uncertainty in decision-making processes. In these cases, uncertain techniques, such as fuzzy numbers, interval numbers and triangular fuzzy numbers, were integrated with the BWM. Unfortunately, few scholars have studied integrating BWM with HFEs. (3) In the review of the previous work related to BWM, the scholars study the maximum absolute differences are minimized problem are transferred to two list of same compromise limit constraints. Considering that decision-makers with different constraints may have different compromise limits, it is necessary to study the maximum absolute differences when the minimized problem is transferred to two lists of different compromise limit constraints.

To eliminate the abovementioned defects, consider the advantage of HFS in showing the evaluation information and the advantage of BWM in solving MCDM problems. It is necessary to propose a new hesitant fuzzy BWM for MCDM. In this study, consistency measures from the perspectives of additive/multiplicative consistent hesitant fuzzy best worst preference relations (HFBWPRs) are defined. Several decision-making models are developed in view of the proposed additive consistency and multiplicative consistency measures. The primary contributions of this study are summarized as follows:

• 1. Consistency measures from the perspectives of additive/multiplicatively consistent HFBWPRs are introduced, which integrate the advantages of HFPRs and BWM.

• 2. Several decision-making models are developed in view of the proposed additive/multiplicatively consistent HFBWPRs. The main characteristic of the constructed models is that they consider all the values included in the HFBWPRs and consider the same and different compromise limit constraints.

• 3. An absolute programming model is developed to obtain the decision-makers’ objective weights utilizing the optimal priority weight vector information, and the calculation of decision-makers’ comprehensive weights is provided.

The remainder of the paper is organized as follows. In "Preliminaries", some basic knowledge of FPRs, HFS, HFPRs and the BWM is introduced. In "Hesitant fuzzy BWM", the concepts of additive/multiplicatively consistent HFBWPRs are presented, and several decision-making models are developed in view of the proposed additive consistency and multiplicative consistency measures. In "A framework of MCDM procedure based on hesitant fuzzy BWM", an absolute programming model is developed to obtain the decision-makers’ objective weights, and a procedure for MCDM problems with hesitant fuzzy BWM is given. In "Illustrative example", the proposed methods are illustrated by an example, and a comparative analysis is provided. Finally, conclusions are presented in "Conclusion".

Preliminaries

In this section, some basic knowledge of FPRs, HFS, HFPRs and the BWM is introduced.

FPRs

Let $X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$ denote a finite set of alternatives, where $x_{i}$ represents the ith alternate. Orlovsky [52] developed the concept of FPRs.

Definition 1

[52]. An FPR on a set of alternatives X is represented by a matrix $H = \left( {r_{ij} } \right)_{n \times n} \subset X \times X$, where $r_{ij}$ is interpreted as the degree to which alternative $x_{i}$ is preferred to $x_{j}$. Furthermore, $r_{ij}$ should satisfy the following conditions: $r_{ij} + r_{ji} = 1$, $r_{ii} = 0.5$ for all $i,j \in N$.

To measure the rationality of FPRs provided by decision-makers, the concepts of additive consistent and multiplicative consistent FPRs were introduced.

Definition 2

[5]. Let $H = \left( {r_{ij} } \right)_{n \times n}$ be an FPR, and $W = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)$ be the priority weight vector derived from R, where $w_{i} \in \left[ {0,1} \right]$ and $\sum\nolimits_{i = 1}^{n} {w_{i} } = 1$. For all $i,j \in N$, the FPR is additive consistency if $r_{ij} = \frac{1}{2}\left( {w_{i} - w_{j} } \right) + 0.5$ and FPR is multiplicative consistency if $r_{ij} = \frac{{w_{i} }}{{w_{i} + w_{j} }}$.

HFS and HFPRs

To express the hesitant information, Torra and Narukawa [13] introduced an effective tool which named HFS.

Definition 3

[13]. Let X be a fixed set. Accordingly, a HFS E on X is defined in terms of a function $h_{E} \left( x \right)$ that when applied to X returns a finite subset of [0, 1].

To be easily understood, Xia and Xu [53] utilized the following mathematical symbol to express the HFS:$E = \left\{ { < x,h_{E} \left( x \right) > \left| {x \in X} \right.} \right\}$. Where $h_{E} \left( x \right)$ is a set of values in [0, 1] representing the possible membership degrees of the element x in X to E, and $h_{E} \left( x \right)$ is named HFE and denoted as $h{ = }\left\{ {\gamma^{s} \left| {s = 1,2, \ldots ,\# h} \right.} \right\}$, $\# h$ is the number of elements including in h.

With the effective of HFE, Xia and Xu [17] proposed the concept of HFPRs. However, the need for sequence relationships of the elements including in HFPRs, this leads to some complexity in actual application. To address this issue, Xu et al. [54] developed a new definition of HFPRs that does not need to arrange the elements in descending or ascending sequence.

Definition 4

[54]. Let $X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$ be a fixed set, HFPRs on X is represented by a matrix $R = \left( {h_{ij} } \right)_{n \times n} \subset X \times X$, where $h_{ij} { = }\left\{ {\gamma_{ij}^{s} \left| {s = 1,2, \ldots ,\# h_{ij} } \right.} \right\}$ is a HFE indicating the possible preference degrees of alternative $x_{i}$ is preferred to alternative $x_{j}$. For all $i,j \in N$, $h_{ij}$ should satisfy: $\gamma_{ij}^{s} + \gamma_{ji}^{{\# h_{ij} - s + 1}} = 1$, $\gamma_{ii}^{{}} = 0.5$, $\# h_{ij} = \# h_{ji}$, where $\gamma_{ij}^{s}$ refers to the sth element in $h_{ij}$.

Integrating into Tanino [5]’s additive consistency and the concept of HFPRs, Xu et al. [55] developed the concept of additive consistent HFPRs.

Definition 5

[55]. Let R be the same as those given in Definition 4. If R satisfies the following condition: $\frac{1}{2}\left( {w_{i} - w_{j} } \right) + 0.5 = \gamma_{ij}^{1} \;or\;\gamma_{ij}^{2} \;{\text{or}}\; \ldots \;{\text{or}}\;\gamma_{ij}^{{\# h_{ij} }} \,$. Then R is called additive consistent HFPR, where $W = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)$ is the priority weight vector derived from R.

Similarly, integrating into Tanino [5]’s multiplicative consistency and the concept of HFPRs, Zhu and Xu [56] developed the concept of multiplicative consistent HFPRs.

Definition 6

[56]. Let R be the same as those given in Definition 4. If R satisfies the following condition: $\frac{{w_{i} }}{{w_{i} + w_{j} }} = \gamma_{ij}^{1} \;or\;\gamma_{ij}^{2} \;or\; \cdots \;or\;\gamma_{ij}^{{\# h_{ij} }} \,$, then R is called multiplicative consistent HFPR.

BWM

BWM is a frequently used MCDM technique since it was developed by Rezaei [34]. Later, Li et al. [10] extended this method to the evaluation scale as a number from 0.1 to 1 to address FPRs. It mainly includes the following steps:

Step 1: Define the decision criteria.

The decision criteria are defined on the basis of alternatives’ characteristics and denoted as $\left\{ {c_{1} ,c_{2} , \ldots ,c_{n} } \right\}$.

Step 2: Identify the best and worst criteria.

How to identify the best and worst criteria is puzzled by decision-makers when using the BWM. Some scholars developed it with the out-degree and in-degree of the node [57] and belief degree [58], while more scholars suggested that with respect to decision-makers’ professional judgment [59].

Step 3: Determine the priority of the best criterion over each of the other criteria.

When the best criteria are identified, the decision-makers determine the priority of the best criterion over each of the other criteria as a number from 0.1 to 1 and denote it as $A_{Bj} = \left( {a_{B1} ,a_{B2} , \cdots ,a_{Bn} } \right)$. The value $a_{Bj}$ is the priority of the best criterion over the jth criterion and $a_{BB} = {0}{\text{.5}}$, where the evaluation result is an FPR.

Step 4: Determine the priority of each criterion over the worst criteria.

Similarly, when the worst criteria are identified, the decision-makers determine the priority of each criterion over the worst criteria as a number from 0.1 to 1 and denote it as $A_{jW} = \left( {a_{1W} ,a_{2W} , \ldots ,a_{nW} } \right)$. The value $a_{jW}$ is the priority of the jth criterion over the worst criteria and $a_{WW} = {0}{\text{.5}}$, where the evaluation result is an FPR.

Step 5: Calculate the optimal weights of the criteria.

To obtain the optimal weight of each criterion, there are two cases, including Case 1: suppose the FPRs have additive consistency. We form the pairs $\frac{1}{2}\left( {w_{B} - w_{j} } \right) + 0.5 - a_{Bj}$ and $\frac{1}{2}\left( {w_{j} - w_{W} } \right) + 0.5 - a_{jW}$ and then try to minimize the maximum of $\left| {\frac{1}{2}\left( {w_{B} - w_{j} } \right) + 0.5 - a_{Bj} } \right|$ and $\left| {\frac{1}{2}\left( {w_{j} - w_{W} } \right) + 0.5 - a_{jW} } \right|$ for each j. Based on the theory of maximum–minimum, the optimal weight model is constructed as follows:

$$ \begin{aligned} & \min \;z = \varsigma \\ & {\text{s}}.{\text{t}}.\;\;\left\{ {\begin{array}{*{20}l} {\left| {\frac{1}{2}\left( {w_{B} - w_{j} } \right) + 0.5 - a_{Bj} } \right| \le \varsigma ,} \hfill & {\quad \forall \,j} \hfill \\ {\left| {\frac{1}{2}\left( {w_{j} - w_{W} } \right) + 0.5 - a_{jW} } \right| \le \varsigma ,} \hfill & {\quad \forall \,j} \hfill \\ {\sum\nolimits_{j = 1}^{n} {w_{j} = 1} } \hfill & {} \hfill \\ {w_{j} \ge 0} \hfill & {} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

(1)

Case 2: Suppose the FPRs have multiplicative consistency. We form the pairs $\frac{{w_{B} }}{{w_{B} + w_{j} }} - a_{Bj}$ and $\frac{{w_{j} }}{{w_{j} + w_{W} }} - a_{jW}$ and then try to minimize the maximum of $\left| {\frac{{w_{B} }}{{w_{B} + w_{j} }} - a_{Bj} } \right|$ and $\left| {\frac{{w_{j} }}{{w_{j} + w_{W} }} - a_{jW} } \right|$ for each j. Similarly, to Eq. (1), the optimal weight model is constructed as follows:

$$ \begin{aligned} & \min \;z = \varsigma \\ & {\text{s}}.{\text{t}}.\;\;\left\{ {\begin{array}{*{20}l} {\left| {\frac{{w_{B} }}{{w_{B} + w_{j} }} - a_{Bj} } \right| \le \varsigma ,} \hfill & {\quad \forall \,j} \hfill \\ {\left| {\frac{{w_{j} }}{{w_{j} + w_{W} }} - a_{jW} } \right| \le \varsigma ,} \hfill & {\quad \forall \,j} \hfill \\ {\sum\nolimits_{j = 1}^{n} {w_{j} = 1} } \hfill & {} \hfill \\ {w_{j} \ge 0} \hfill & {} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

(2)

Step 6: Calculate the consistency ratio of FPRs.

Since the optimal weights of each criterion are derived from different models, there are also two cases to calculate the consistency ratio.

Case 1: We derive the optimal solution $\varsigma_{A}$ by solving model (1), and combining the consistency index $\delta_{A}$ presented in Table 2, the consistency ratio of FPRs is calculated as follows: ${\text{CR}}_{A} = \frac{{\varsigma_{A} }}{{\delta_{A} }}$.

Table 2 Consistency index for BWM with additive consistent FPRs

Case 2: Similarly, we derive the optimal solution $\varsigma_{M}$ by solving model (2), and combining the consistency index $\delta_{M}$ presented in Table 3, the consistency ratio of FPRs is calculated as follows: ${\text{CR}}_{M} = \frac{{\varsigma_{M} }}{{\delta_{M} }}$.

Table 3 Consistency index for BWM with multiplicatively consistent FPRs

Step 7: Improve the consistency of FPRs.

When a desired consistency level is not achieved, the consistency of FPRs can be improved by modifying some values, including in the FPRs. Two issues need to be considered in this process: the first issue is how to determine the threshold of consistency, and the second issue is how to modify the values to improve the consistency. For the first one, some scholars developed it with the Monte Carlo simulation method [60], while more scholars suggested that decision-makers determine it with respect to the background of practical decision problems [10]. For the last one, several scholars designed different algorithms based on different decision environments, such as intuitionistic fuzziness [57], hesitant fuzzy linguistics [61], and probabilistic hesitant fuzziness [10].

Remark 1

The consistency index for the fuzzy BWM presented in Tables 2 and 3 includes only the numbers ranging from 0.1 to 1, and other numbers, including those in [0,1], can be determined according to Eq. (13) if BWM with additive consistent FPR or Eq. (21) if the BWM has a multiplicatively consistent FPR, which is developed in [10].

Hesitant fuzzy BWM

In this section, we first introduce the concepts of additive/multiplicatively consistent HFBWPRs and then develop several programming models for deriving priority weight vectors from the proposed HFBWPRs, which include two cases. That is, programming models consider the same and different compromise limit constraints.

Additive and multiplicative consistent HFBWPRs

To further consider Definitions 5 and 6, the concepts of additive and multiplicatively consistent HFPRs are defined on the basis of relationships between the formula consisting of priority weights and the values included in HFEs. However, the relationships present in Definitions 5 and 6 only consider the relationships between one priority weight formula and all the values included in HFPRs but cannot reflect the hesitancy of decision-makers. It is reasonable that every value included in HFPRs has a relationship to one priority weight formula. That is, the additive and multiplicatively consistent HFPRs are in accordance with the derived FPRs with respect to each fixed value. Integrating HFPRs into the idea of BWM, new concepts for additive and multiplicatively consistent HFBWPRs are developed as follows.

Definition 7

Let R be the same as those given in Definition 4. Then, R is called additive consistent HFBWPRs if the elements of best and worst including in R satisfy the following conditions:

$$ \left\{ {\begin{array}{*{20}l} {\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5 = \sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} ,} } \hfill & {\quad k = 1,2, \ldots ,\prod\nolimits_{j = 1}^{n} {\# h_{Bj} } } \hfill \\ {\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5 = \sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} ,} } \hfill & {\quad k = 1,2, \ldots ,\prod\nolimits_{j = 1}^{n} {\# h_{jW} ,} } \hfill \\ \end{array} } \right. $$

(3)

for all $j = 1,2, \ldots ,n$, where $w_{j}^{k}$ are the priority weights such that $w_{j}^{k} \ge 0$,$j = 1,2, \ldots ,n$,$\sum\nolimits_{\begin{subarray}{l} j = 1 \\ j \ne B \end{subarray} }^{n} {w_{j}^{k} } + w_{B}^{k} = 1$, for all $k = 1,2, \ldots ,\prod\nolimits_{j = 1}^{n} {\# h_{Bj} }$ or $\sum\nolimits_{\begin{subarray}{l} j = 1 \\ j \ne W \end{subarray} }^{n} {w_{j}^{k} } + w_{W}^{k} = 1$, for all $k = 1,2, \ldots ,\prod\nolimits_{j = 1}^{n} {\# h_{jW} }$, the above two equations hold at least one of them. In addition, $\alpha_{Bj}^{s}$, $s = 1,2, \ldots ,\# h_{Bj}$ and $\beta_{jW}^{s}$, $s = 1,2, \ldots ,\# h_{jW}$ are two lists of 0–1 indicator variables that satisfy $\sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} } = 1$ and $\sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} } = 1$.

In a similar way, the concept of multiplicatively consistent HFBWPRs is developed as follows.

Definition 8

Let R be the same as those given in Definition 4. Then, R is called multiplicatively consistent HFBWPRs if the elements of best and worst, including in R, satisfy the following conditions:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{w_{B}^{k} }}{{w_{B}^{k} + w_{j}^{k} }} = \prod\nolimits_{s = 1}^{{\# h_{Bj} }} {\left( {\gamma_{Bj}^{s} \,} \right)}^{{\alpha_{Bj}^{s} }} ,} \hfill & {\quad k = 1,2, \ldots ,\prod\nolimits_{j = 1}^{n} {\# h_{Bj} } } \hfill \\ {\frac{{w_{j}^{k} }}{{w_{j}^{k} + w_{W}^{k} }} = \prod\nolimits_{s = 1}^{{\# h_{jW} }} {\left( {\gamma_{jW}^{s} \,} \right)}^{{\beta_{jW}^{s} }} ,} \hfill & {\quad k = 1,2, \ldots ,\prod\nolimits_{j = 1}^{n} {\# h_{jW} ,} } \hfill \\ \end{array} } \right. $$

(4)

for all $j = 1,2, \ldots ,n$. The meanings of symbols $w_{j}^{k}$, $\alpha_{Bj}^{s}$ and $\beta_{jW}^{s}$ are the same as those given in Eq. (3).

Remark 2

It can be easily found that the additive and multiplicatively consistent HFBWPRs present in Definitions 7 and 8 only consider the elements of best and worst; that is, the elements including in the Bth row and Wth column are considered. Other elements, including in R, do not require satisfying Eq. (3) or Eq. (4).

Example 1

Let R be an HFPR obtained from pairwise comparisons of four criteria, namely, $x_{1}$, $x_{2}$, $x_{3}$ and $x_{4}$, where $R = \left[ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ {0.{3}} \right\}} & {\left\{ {0.5,0.6,0.7} \right\}} & {\left\{ {0.{5}} \right\}} \\ {\left\{ {0.{7}} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.{7}} \right\}} & {\left\{ {0.{6},0.{7}} \right\}} \\ {\left\{ {0.3,0.4,0.5} \right\}} & {\left\{ {0.{3}} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.{8}} \right\}} \\ {\left\{ {0.{5}} \right\}} & {\left\{ {0.{3},0.{4}} \right\}} & {\left\{ {0.{2}} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right]$. Suppose $x_{3}$ is the best criterion and $x_{4}$ is the worst criterion. According to Definition 7, if $\left\{ \begin{gathered} \frac{1}{2}\left( {w_{3}^{1} - w_{1}^{1} } \right) + 0.5 = 0.3\alpha_{31}^{1} + 0.4\alpha_{31}^{2} + 0.5\alpha_{31}^{3} ;\quad \frac{1}{2}\left( {w_{3}^{2} - w_{1}^{2} } \right) + 0.5 = 0.3\alpha_{31}^{1} + 0.4\alpha_{31}^{2} + 0.5\alpha_{31}^{3} \hfill \\ \frac{1}{2}\left( {w_{3}^{3} - w_{1}^{3} } \right) + 0.5 = 0.3\alpha_{31}^{1} + 0.4\alpha_{31}^{2} + 0.5\alpha_{31}^{3} ;\quad \frac{1}{2}\left( {w_{3}^{1} - w_{2}^{1} } \right) + 0.5 = 0.3;\quad \frac{1}{2}\left( {w_{3}^{1} - w_{4}^{1} } \right) + 0.5 = 0.8 \hfill \\ \frac{1}{2}\left( {w_{1}^{1} - w_{4}^{1} } \right) + 0.5 = 0.5;\quad \frac{1}{2}\left( {w_{2}^{1} - w_{4}^{1} } \right) + 0.5 = 0.6\beta_{24}^{1} + 0.7\beta_{24}^{2} ;\quad \alpha_{31}^{1} + \alpha_{31}^{2} + \alpha_{31}^{3} = 1;\quad \beta_{24}^{1} + \beta_{24}^{2} = 1 \hfill \\ \end{gathered} \right.$ holds, then R is called additive consistent HFBWPRs.

Deriving priority weight vectors from HFBWPRs with the same compromise limit constraint

Consistency of PRs is related to rationality. By comparison, inconsistent PRs often lead to misleading solutions. Therefore, developing approaches to obtain the expected consistency level is necessary. However, only a few scholars have focused on optimization-based methods to obtain the expected consistent HFBWPRs at present. Therefore, in this section, several mathematical programming models are proposed to obtain acceptable consistent HFBWPRs that consider the minimized deviation from the target of the goal. There are two cases, namely, deriving priority weight vectors from HFBWPRs based on additive consistency and multiplicative consistency.

Case 1; Deriving priority weight vectors from additive consistent HFBWPRs

According to the definition of additive consistent HFBWPRs, we obtain $\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5 = \sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} }$ and $\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5 = \sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} }$. The priority weights of complete additive consistent HFBWPRs can be derived by solving a list of equations $\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5 = \sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} }$, $j = 1,2, \ldots ,n$, $k = 1,2, \ldots ,\prod\nolimits_{j = 1}^{n} {\# h_{Bj} }$ and $\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5 = \sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} }$, $j = 1,2, \cdots ,n$, $k = 1,2, \ldots ,\prod\nolimits_{j = 1}^{n} {\# h_{jW} }$. However, the abovementioned equations do not constantly hold in general given a deviation between $\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5$ and $\sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} }$ for each pair of possible value $\left( {B,j_{0} } \right)$ with $j_{0} = 1,2, \ldots ,n$ for each $s = 1,2, \ldots ,\# h_{Bj}$. Similarly, there is also a deviation between $\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5$ and $\sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} }$ for each pair of possible value $\left( {j_{0} ,W} \right)$ with $j_{0} = 1,2, \ldots ,n$ for each $s = 1,2, \ldots ,\# h_{jW}$. Moreover, the more $\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} }$ and $\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} }$ approaches to 0, the more valid and reasonable the priority weights are.

In this regard, motivated by the idea developed in Rezaei [34], the priority weight vectors are obtained by minimizing the maximum absolute differences $\left| {\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} } } \right|$ and $\left| {\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} } } \right|$. Thus, the following programming models can be constructed:

$$ \begin{aligned} & \min \quad z^{k} = \varsigma \\ & {\text{s}}.{\text{t}}.\;\;\left\{ {\begin{array}{*{20}l} {\left| {\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} } } \right| \le \varsigma } \hfill & {} \hfill \\ {\left| {\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} } } \right| \le \varsigma } \hfill & {} \hfill \\ {\alpha_{{Bj_{0} }}^{s} \left( {\sum\nolimits_{\begin{subarray}{l} j = 1 \\ j \ne B \end{subarray} }^{n} {w_{j}^{k} } + w_{B}^{k} - 1} \right) = 0,} \hfill & {\quad \forall \;k = 1,2, \ldots ,\prod\nolimits_{j = 1}^{n} {\# h_{Bj} } } \hfill \\ {\beta_{{j_{0} W}}^{s} \left( {\sum\nolimits_{\begin{subarray}{l} j = 1 \\ j \ne W \end{subarray} }^{n} {w_{j}^{k} } + w_{W}^{k} - 1} \right) = 0,} \hfill & {\quad \forall \;k = 1,2, \ldots ,\prod\nolimits_{j = 1}^{n} {\# h_{jW} } } \hfill \\ {\left( {\alpha_{{Bj_{0} }}^{s} = 1} \right) \vee \left( {\beta_{{j_{0} W}}^{s} = 1} \right),} \hfill & {\quad j_{0} = 1,2, \ldots ,n} \hfill \\ {\sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} } = 1,\quad \sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} } = 1} \hfill & {} \hfill \\ {\alpha_{Bj}^{s} = 0 \vee 1,} \hfill & {\quad s = 1,2, \ldots ,\# h_{Bj} } \hfill \\ {\beta_{jW}^{s} = 0 \vee 1,} \hfill & {\quad s = 1,2, \ldots ,\# h_{jW} } \hfill \\ {w_{j}^{k} \ge 0,} \hfill & {\quad \varsigma \ge 0} \hfill \\ {j = 1,2, \ldots ,n} \hfill & {} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

(5)

In Eq. (5), the first and second constraints are derived from the theory of maximum–minimum; the third constraint is hold when $\alpha_{{Bj_{0} }}^{s} = 1$, which ensure that all the values including in the HFBWPRs are considered. Similarly, when $\alpha_{{j_{0} W}}^{s} = 1$, the fourth constraint is hold. The fifth constraint ensures that at least one of the third and fourth constraints holds. In addition, the sixth to eighth constraints indicates that $\alpha_{Bj}^{s}$ and $\beta_{jW}^{s}$ are two lists of 0–1 indicator variables. Solving Eq. (5), a list of priority weight vectors $w_{{}}^{k}$, $k = 1,2, \ldots ,t$, where $t = \prod\nolimits_{j = 1}^{n} {\# h_{Bj} } + \prod\nolimits_{j = 1}^{n} {\# h_{jW} }$ can be derived. Since $w_{{}}^{k}$ can be viewed as the possible priority weight vector of R.

Remark 3

Solving Eq. (5), a list of priority weight vectors $w_{{}}^{k}$, $k = 1,2, \ldots ,t$, are derived. However, in most cases, we will obtain more than two identical priority weight vectors.

Based on the ideas of Zhang et al. [31] and Wu et al. [62]. The distance between $w_{{}}^{k}$ and R is developed to select the best priority weight vector of R.

Definition 9

Let $R = \left( {h_{ij} } \right)_{n \times n} \subset X \times X$ be an HFBWPR, and $w_{{}}^{k} { = }\left( {w_{1}^{k} ,w_{2}^{k} , \cdots ,w_{n}^{k} } \right)$, $k = 1,2, \cdots ,t$ be a list of priority weight vectors derived from Eq. (5). Then, the distance between $w_{{}}^{k}$ and $R$ is developed as follows:

$$ d_{1} \left( {w^{k} ,R} \right) = \frac{1}{{2\left( {n - 1} \right)}}\left( {\sum\limits_{j = 1}^{n} {\left| {\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5 - \sum\limits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} } } \right|} + \sum\limits_{j = 1}^{n} {\left| {\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5 - \sum\limits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} } } \right|} } \right). $$

(6)

It can be easily found that the distance $d_{1} \left( {w^{k} ,R} \right)$ reflects the sum of the average of the absolute deviation between $\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5$ and $\sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} }$ for the elements including in the $B$ th row and the absolute deviation between $\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5$ and $\sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} }$ for the elements including in the Wth column. The number of above absolute deviations is $2\left( {n - 1} \right)$, and the coefficient presented in Eq. (6) ensures the value range in interval [0, 1]. It is natural that the optimal priority weight vector minimizes the deviation $d_{1} \left( {w^{k} ,R} \right)$. As a consequence, the priority weight vector of $R$ is developed as follows.

Definition 10

Let $R$ and $w_{{}}^{k}$ be the same as those given in Definition 9. Then, the priority weight vector of $R$ is developed as follows:

$$ w^{k * } = \left( {w_{1}^{k * } ,w_{2}^{k * } , \ldots w_{n}^{k * } } \right) = \arg \,\min_{{w^{k} }} d_{1} \left( {w^{k} ,R} \right), $$

(7)

where the symbol arg represents the correspondence of the priority weight vector $w_{{}}^{k}$ in the minimum distance $d_{1} \left( {w^{k} ,R} \right)$, which is obtained from Eq. (6).

Remark 4

There may be more than one priority weight vector, including in $\min_{{w^{k} }} d_{1} \left( {w^{k} ,R} \right)$; that is, sometimes the solution of Eq. (7) is not unique. In this case, the priority weight vector R is developed as:

$$ w^{k*} = \left( {w_{1}^{k*} ,w_{2}^{k*} , \ldots ,w_{n}^{k*} } \right) = \left( {\frac{1}{{l_{0} }}\sum\limits_{k = 1}^{{l_{0} }} {w_{1}^{k} } ,\frac{1}{{l_{0} }}\sum\limits_{k = 1}^{{l_{0} }} {w_{2}^{k} } , \ldots ,\frac{1}{{l_{0} }}\sum\limits_{k = 1}^{{l_{0} }} {w_{n}^{k} } } \right), $$

(8)

where $w_{i}^{k}$, $i = 1,2, \cdots ,n$, and it indicates that the number of priority weight vectors included in $\min_{{w^{k} }} d_{1} \left( {w^{k} ,R} \right)$ is $l_{0}$. It can be easily found that the priority weight vectors are derived from the average value of $w_{i}^{k}$, $k = 1,2, \cdots ,l_{0}$.

Case 2. Deriving priority weight vectors from multiplicatively consistent HFBWPRs

Similar to the idea of additive consistent HFBWPRs presented in case 1, the following programming models can be constructed when we consider multiplicatively consistent HFBWPRs.

$$ \begin{aligned} & \min \quad z^{k} = \varsigma \\ & {\text{s}}.{\text{t}}.\;\;\left\{ {\begin{array}{*{20}l} {\left| {\frac{{w_{B}^{k} }}{{w_{B}^{k} + w_{j}^{k} }} - \prod\limits_{s = 1}^{{\# h_{Bj} }} {\left( {\gamma_{Bj}^{s} {\mkern 1mu} } \right)^{{\alpha_{Bj}^{s} }} } } \right| \le \varsigma } \hfill & {} \hfill \\ {\left| {\frac{{w_{j}^{k} }}{{w_{j}^{k} + w_{W}^{k} }} - \prod\limits_{s = 1}^{{\# h_{jW} }} {\left( {\gamma_{jW}^{s} {\mkern 1mu} } \right)^{{\beta_{jW}^{s} }} } } \right| \le \varsigma } \hfill & {} \hfill \\ {\alpha_{{Bj_{0} }}^{s} \left( {\sum\limits_{{\mathop {j = 1}\limits_{j \ne B} }}^{n} {w_{j}^{k} + w_{B}^{k} - 1} } \right) = 0,} \hfill & {\quad \forall \;k = 1,2, \ldots ,\prod\limits_{j = 1}^{n} {\# h_{Bj} } } \hfill \\ {\beta_{{j_{0} W}}^{s} \left( {\sum\limits_{{\mathop {j = 1}\limits_{j \ne W} }}^{n} {w_{j}^{k} + w_{W}^{k} - 1} } \right) = 0,} \hfill & {\quad \forall \;k = 1,2, \ldots ,\prod\limits_{j = 1}^{n} {\# h_{jW} } } \hfill \\ {\left( {\alpha_{{Bj_{0} }}^{s} = 1} \right) \vee \left( {\beta_{{j_{0} W}}^{s} = 1} \right),} \hfill & {\quad j_{0} = 1,2, \ldots ,n} \hfill \\ {\sum\limits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} } = 1,\quad \sum\limits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} } = 1} \hfill & {} \hfill \\ {\alpha_{Bj}^{s} = 0 \vee 1,} \hfill & {\quad s = 1,2, \ldots ,\# h_{Bj} } \hfill \\ {\beta_{jW}^{s} = 0 \vee 1,} \hfill & {\quad s = 1,2, \ldots ,\# h_{jW} } \hfill \\ {w_{j}^{k} \ge 0,} \hfill & {\quad \varsigma \ge 0} \hfill \\ {j = 1,2, \ldots ,n} \hfill & {} \hfill \\ \end{array} } \right.. \\ \end{aligned} $$

(9)

The difference between Eqs. (5) and (9) is that we use multiplicatively consistent HFBWPRs in the first and second constraints of Eq. (9) to replace additive consistent HFBWPRs in the first and second constraints of Eq. (5), the rest of the constraints are exactly the same. The meaning of symbols presents in Eq. (9) is the same as those given in Eq. (5). Similar to additive consistent HFBWPRs, the distance between $w_{{}}^{k}$ and R is developed to select the best priority weight vector R.

Definition 11

Let $R = \left( {h_{ij} } \right)_{n \times n} \subset X \times X$ be an HFBWPR, and let $w_{{}}^{k} { = }\left( {w_{1}^{k} ,w_{2}^{k} , \cdots ,w_{n}^{k} } \right)$, $k = 1,2, \cdots ,t$ be a list of priority weight vectors derived from Eq. (9). Then, the distance between $w_{{}}^{k}$ and R is developed as follows.

$$\begin{aligned} d_{2} \left( {w^{k} ,R} \right) &= \frac{1}{{2\left( {n - 1} \right)}}\left( {\sum\limits_{j = 1}^{n} {\left| {\frac{{w_{B}^{k} }}{{w_{B}^{k} + w_{j}^{k} }} - \prod\limits_{s = 1}^{{\# h_{Bj} }} {\left( {\gamma_{Bj}^{s} {\mkern 1mu} } \right)^{{\alpha_{Bj}^{s} }} } } \right|}} \right. \\ &\quad\left. {+ \sum\limits_{j = 1}^{n} {\left| {\frac{{w_{j}^{k} }}{{w_{j}^{k} + w_{W}^{k} }} - \prod\limits_{s = 1}^{{\# h_{jW} }} {\left( {\gamma_{jW}^{s} {\mkern 1mu} } \right)^{{\beta_{jW}^{s} }} } } \right|} } \right). \end{aligned}$$

(10)

The difference between Eqs. (6) and (10) is that we use multiplicatively consistent HFBWPRs in the first and second sections of Eq. (10) to replace additively consistent HFBWPRs in the first and second sections of Eq. (6). The meaning of symbols presents in Eq. (10) is the same as those given in Eq. (6). Similar to additive consistent HFBWPRs, the priority weight vector of R is developed as follows.

Definition 12

Let $R$ and $w_{{}}^{k}$ be the same as those given in Definition 11. Then, the priority weight vector of R is developed as follows:

$$ w^{k * } = \left( {w_{1}^{k * } ,w_{2}^{k * } , \ldots ,w_{n}^{k * } } \right) = \arg \,\min_{{w^{k} }} d_{2} \left( {w^{k} ,R} \right). $$

(11)

Remark 5

There may be more than one priority weight vector, including in $\min_{{w^{k} }} d_{2} \left( {w^{k} ,R} \right)$. In this case, the priority weight vector $R$ is developed according to Eq. (8).

Deriving priority weight vectors from HFBWPRs with different compromise limit constraints

In the above programming models, the constraints $\left| {\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} } } \right| \le \varsigma$ and $\left| {\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} } } \right| \le \varsigma$ present in Eq. (5) or $\left| {\frac{{w_{B}^{k} }}{{w_{B}^{k} + w_{j}^{k} }} - \prod\nolimits_{s = 1}^{{\# h_{Bj} }} {\left( {\gamma_{Bj}^{s} \,} \right)}^{{\alpha_{Bj}^{s} }} } \right| \le \varsigma$ and $\left| {\frac{{w_{j}^{k} }}{{w_{j}^{k} + w_{W}^{k} }} - \prod\nolimits_{s = 1}^{{\# h_{jW} }} {\left( {\gamma_{jW}^{s} \,} \right)}^{{\beta_{jW}^{s} }} } \right| \le \varsigma$ present in Eq. (9) with the same compromise limit $\varsigma$ for all j, $j = 1,2, \ldots ,n$. This is unreasonable in some circumstances because different HFEs, including HFBWPRs, have different numbers of elements; in other words, different numbers of elements may express different hesitant degrees of HFEs. It is more reasonable that for different HFEs corresponding to different compromise limits $\varsigma_{j}$ for different $j$, $j = 1,2, \cdots ,n$. There are also two cases, that is, deriving priority weight vectors from HFBWPRs based on additive consistency and multiplicative consistency.

Case 1: Deriving priority weight vectors from additive consistent HFBWPRs

In view of the above analysis, the maximum absolute differences are minimized, and the problem $\min \;\max \;\left\{ {\left| {\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} } } \right|,\;\left| {\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} } } \right|} \right\}$ can be transferred to two lists of different compromise limit constraints; that is, $\left| {\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} } } \right| \le \varsigma_{j}$ and $\left| {\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} } } \right| \le \varsigma_{j}$ for different j and $j = 1,2, \ldots ,n$. Thus, the following programming models are constructed:

$$ \begin{aligned} & \min \quad z^{k} = \sum\limits_{j = 1}^{n} {\varsigma_{j} } \\ & {\text{s}}.{\text{t}}.\;\;\left\{ {\begin{array}{*{20}l} {\left| {\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5 - \sum\limits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} } } \right| \le \varsigma_{j} } \hfill & {} \hfill \\ {\left| {\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5 - \sum\limits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} } } \right| \le \varsigma_{j} } \hfill & {} \hfill \\ {\alpha_{{Bj_{0} }}^{s} \left( {\sum\limits_{{\mathop {j = 1}\limits_{j \ne B} }}^{n} {w_{j}^{k} + w_{B}^{k} - 1} } \right) = 0,} \hfill & {\quad \forall \;k = 1,2, \ldots ,\prod\limits_{j = 1}^{n} {\# h_{Bj} } } \hfill \\ {\beta_{{j_{0} W}}^{s} \left( {\sum\limits_{{\mathop {j = 1}\limits_{j \ne W} }}^{n} {w_{j}^{k} + w_{W}^{k} - 1} } \right) = 0,} \hfill & {\quad \forall \;k = 1,2, \ldots ,\prod\limits_{j = 1}^{n} {\# h_{jW} } } \hfill \\ {\left( {\alpha_{{Bj_{0} }}^{s} = 1} \right) \vee \left( {\beta_{{j_{0} W}}^{s} = 1} \right),} \hfill & {\quad j_{0} = 1,2, \ldots ,n} \hfill \\ {\sum\limits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} } = 1,} \hfill & {\quad \sum\limits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} } = 1} \hfill \\ {\alpha_{Bj}^{s} = 0 \vee 1,} \hfill & {\quad s = 1,2, \ldots ,\# h_{Bj} } \hfill \\ {\beta_{jW}^{s} = 0 \vee 1,} \hfill & {\quad s = 1,2, \ldots ,\# h_{jW} } \hfill \\ {w_{j}^{k} \ge 0,} \hfill & {\quad \varsigma \ge 0} \hfill \\ {j = 1,2, \ldots ,n} \hfill & {} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

(12)

The difference between Eqs. (5) and (12) is that we use $\varsigma_{j}$ in the first and second constraints of Eq. (12) to replace $\varsigma$ in the first and second constraints of Eq. (5), and use $\sum\nolimits_{j = 1}^{n} {\varsigma_{j} }$ in the objective function of Eq. (12) to replace $\varsigma$ in the objective function of Eq. (5), the rest of the constraints are exactly the same. The meaning of symbols presents in Eq. (12) is the same as those given in Eq. (5).

Case 2. Deriving priority weight vectors from multiplicatively consistent HFBWPRs

Similar to the idea of additive consistent HFBWPRs presented in case 1, the following programming models can be constructed when we consider multiplicatively consistent HFBWPRs.

$$ \begin{aligned} & \min \quad z^{k} = \sum\limits_{j = 1}^{n} {\varsigma_{j} } \\ & {\text{s}}.{\text{t}}.\;\;\left\{ {\begin{array}{*{20}l} {\left| {\frac{{w_{B}^{k} }}{{w_{B}^{k} + w_{j}^{k} }} - \prod\limits_{s = 1}^{{\# h_{Bj} }} {\left( {\gamma_{Bj}^{s} {\mkern 1mu} } \right)}^{{\alpha_{Bj}^{s} }} } \right| \le \varsigma_{j} } \hfill & {} \hfill \\ {\left| {\frac{{w_{j}^{k} }}{{w_{j}^{k} + w_{W}^{k} }} - \prod\limits_{s = 1}^{{\# h_{jW} }} {\left( {\gamma_{jW}^{s} {\mkern 1mu} } \right)}^{{\beta_{jW}^{s} }} } \right| \le \varsigma_{j} } \hfill & {} \hfill \\ {\alpha_{{Bj_{0} }}^{s} \left( {\sum\limits_{{\mathop {j = 1}\limits_{j \ne B} }}^{n} {w_{j}^{k} + w_{B}^{k} - 1} } \right) = 0,} \hfill & {\quad \forall \;k = 1,2, \ldots ,\prod\limits_{j = 1}^{n} {\# h_{Bj} } } \hfill \\ {\beta_{{j_{0} W}}^{s} \left( {\sum\limits_{{\mathop {j = 1}\limits_{j \ne W} }}^{n} {w_{j}^{k} + w_{W}^{k} - 1} } \right) = 0,} \hfill & {\quad \forall \;k = 1,2, \ldots ,\prod\limits_{j = 1}^{n} {\# h_{jW} } } \hfill \\ {\left( {\alpha_{{Bj_{0} }}^{s} = 1} \right) \vee \left( {\beta_{{j_{0} W}}^{s} = 1} \right),} \hfill & {\quad j_{0} = 1,2, \ldots ,n} \hfill \\ {\sum\limits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} } = 1,} \hfill & {\quad \sum\limits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} } = 1} \hfill \\ {\alpha_{Bj}^{s} = 0 \vee 1,} \hfill & {\quad s = 1,2, \ldots ,\# h_{Bj} } \hfill \\ {\beta_{jW}^{s} = 0 \vee 1,} \hfill & {\quad s = 1,2, \ldots ,\# h_{jW} } \hfill \\ {w_{j}^{k} \ge 0,} \hfill & {\quad \varsigma \ge 0} \hfill \\ {j = 1,2, \ldots ,n} \hfill & {} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

(13)

The difference between Eqs. (9) and (13) is that we use $\varsigma_{j}$ in the first and second constraints of Eq. (13) to replace $\varsigma$ in the first and second constraints of Eq. (9), and use $\sum\nolimits_{j = 1}^{n} {\varsigma_j}$ in the objective function of Eq. (13) to replace $\varsigma$ in the objective function of Eq. (9), the rest of the constraints are exactly the same. The meaning of symbols presents in Eq. (13) is the same as those given in Eq. (9).

Remark 6

When solving Eqs. (12) and (13), a list of compromise limit constraint values $\varsigma_{j}$ and $j = 1,2, \ldots ,n$ are derived. In these cases, we use the value $\max \left\{ {\left. {\varsigma_{j} } \right|j = 1,2, \ldots ,n} \right\}$ to replace the value $\varsigma_{A}$ and $\varsigma_{M}$ present in step 6 of Sect. 2.3 when calculating the consistency ratio of FPRs.

A framework of MCDM procedure based on hesitant fuzzy BWM

In this section, including three subsections, the first subsection introduces hesitant fuzzy MCDM problems, the second subsection develops a method to derive the weights of decision-makers, and the last subsection introduces a framework of the MCDM procedure based on hesitant fuzzy BWM.

Hesitant fuzzy MCDM problems

Hesitant fuzzy MCDM problems involve m alternatives denoted as $A = \left\{ {a_{1} ,a_{2} , \ldots ,a_{m} } \right\}$. Each alternative is assessed based on several feature criteria $C = \left\{ {c_{1} ,c_{2} , \ldots ,c_{n} } \right\}$. Let $E = \left\{ {e_{1} ,e_{2} , \ldots ,e_{z} } \right\}$ be a set of decision-makers and $\tau = \left( {\tau_{1} ,\tau_{2} , \ldots ,\tau_{z} } \right)$ be the decision-makers’ weight vector. The evaluation of the alternative $a_{i}$, $i = 1,2, \ldots ,m$ with respect to the feature criterion is provided by the moderator, which is an HFE and denotes as $h{ = }\left\{ {\gamma^{s} \left| {s = 1,2, \ldots ,\# h} \right.} \right\}$. We assume that the weights of criteria and decision-makers are completely unknown. Decision-makers are invited to determine the weights of the criteria. The evaluation of the criteria $c_{j}$, $j = 1,2, \ldots ,n$ with pairwise comparisons is provided by decision-maker $e_{k}$, $k = 1,2, \ldots ,z$, which are the HFPRs and denoted as $h_{k} = \left\{ {\gamma_{k}^{s} \left| {s = 1,2, \ldots ,\# h} \right.} \right\}$.

Derive the weights of the decision-makers

In this subsection, an optimization model is constructed to derive the objective weights of decision-makers with complete unknown information. Considering that decision-makers in the MCDM process typically construct from different knowledge backgrounds and have varied expertise in the domain area, each decision-maker has different judgment values, which influences the solution differently. Therefore, each decision-maker has a different importance weight when collecting the priority weights of the criteria. Given that the decision-maker whose judgment values are far away from the collect judgment values indicates that the judgment values he/she provides are the least reliable, the decision-maker should endow a smaller weight value. By comparison, the decision-maker whose judgment values are close to the collect judgment values indicates that the judgment values he/she provides are the most reliable, and the decision-maker should endow a larger weight value. On this basis, the optimization model is constructed as follows:

$$ \begin{aligned} & \min \quad z = \sum\limits_{k = 1}^{z} {\sum\limits_{i = 1}^{n} {\left| {w_{i}^{k * } - \sum\limits_{k = 1}^{z} {\tau_{k}^{o} w_{i}^{k*} } } \right|} } \\ & {\text{s}}.{\text{t}}.\;\;\left\{ {\begin{array}{*{20}l} {\sum\limits_{k = 1}^{z} {\tau_{k}^{o} = 1} } \hfill \\ {0 \le \tau_{k}^{o} \le 1} \hfill \\ {k = 1,2, \ldots ,z.} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

(14)

In Eq. (14), $w_{i}^{k * }$, and $i = 1,2, \ldots ,n$ are the priority weight vectors of the criteria provided by decision-maker $e_{k}$. If we consider the maximum absolute differences to be a minimized problem with the same compromise limit constraints, then $w_{i}^{k * }$ is obtained from Eqs. (5), (6) and (7) suppose HFBWPRs with additive consistency or obtained from Eqs. (9), (10) and (11) suppose HFBWPRs with multiplicative consistency. Moreover, if we consider that the maximum absolute differences are minimized problems with different compromise limit constraints, then $w_{i}^{k*}$ is obtained from Eqs. (6), (7) and (12) suppose HFBWPRs with additive consistency or obtained from Eqs. (10), (11) and (13) suppose HFBWPRs with multiplicative consistency.

According to the knowledge of decision-makers, the subjective weights of decision-makers are given in advance as $\tau_{k}^{s}$ with $\tau_{k}^{s} \ge 0$ and $\sum\nolimits_{k = 1}^{z} {\tau_{k}^{s} = 1}$. Therefore, the comprehensive weight $\tau_{k}^{{}}$ of the $k$ th decision-maker is calculated as follows:

$$ \tau_{k}^{{}} = \theta \tau_{k}^{o} + \left( {1 - \theta } \right)\tau_{k}^{s} , $$

(15)

where $k = 1,2, \ldots ,z$ and the parameter $\theta$ $\left( {0 \le \theta \le 1} \right)$ tradeoffs the subjective weights and objective weights of decision-makers. In general, we set $\theta = 0.5$.

A framework of MCDM procedure based on hesitant fuzzy BWM

The proposed decision-making procedure is summarized in the following steps.

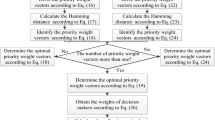
Step 1: Define the decision criteria and provide the evaluation values.

The decision criteria are defined on the basis of alternatives’ characteristics, which are determined by the moderator, and the evaluation of the alternatives with respect to the decision criteria is also provided by the moderator, which is denoted as $R = \left( {h_{ij} } \right)_{m \times n}$. $h_{ij}$ is an HFE indicating the evaluation value of alternative $a_{i}$ under the criteria $c_{j}$.

Step 2: Identify the best and worst criteria.

According to the determination criteria, the decision-makers provide their pairwise comparison judgment matrices and denote them as $R_{k} = \left( {h_{ij,k} } \right)_{n \times n} \subset X \times X$, $k = 1,2, \ldots ,z$. $h_{ij,k} = \left\{ {\gamma_{ij,k}^{s} \left| {\quad s = 1,2, \ldots ,\# h_{ij} } \right.} \right\}$ is an HFPR indicating that the possible preference degrees of criteria $c_{i}$ are preferred to criteria $c_{j}$. Then, the score function of criteria $c_{i}$ is calculated as follows [53]:

$$ s\left( {h_{i,k} } \right) = \frac{1}{{\# h_{ij} }}\sum\limits_{j = 1}^{n} {\sum\limits_{s = 1}^{{\# h_{ij} }} {\gamma_{ij,k}^{s} } } ,\quad i = 1,2, \ldots ,n. $$

(16)

For decision-maker $e_{k}$, the best and worst criteria can be determined based on the score function; that is, the maximal value of $s\left( {h_{i,k} } \right)$ is the best criterion, and the minimum value is the worst criterion.

Step 3: Calculate the optimal weights of the criteria.

To obtain the optimal weight of each criterion, there are two cases, including.

Case 1: Suppose HFPRs with additive consistent HFBWPRs. If we consider the maximum absolute differences to be a minimized problem with the same compromise limit constraints, then the priority weight vectors of the criteria are obtained from Eqs. (5), (6) and (7); otherwise, if we consider the maximum absolute differences to be a minimized problem with different compromise limit constraints, the priority weight vectors of the criteria are obtained from Eqs. (6), (7) and (12).

Case 2: Suppose HFPRs with multiplicatively consistent HFBWPRs. If we consider the maximum absolute differences to be a minimized problem with the same compromise limit constraints, then the priority weight vectors of the criteria are obtained from Eqs. (9), (10) and (11); otherwise, if we consider the maximum absolute differences to be a minimized problem with different compromise limit constraints, the priority weight vectors of the criteria are obtained from Eqs. (10), (11) and (13).

Step 4: Calculate the consistency ratio.

Since the optimal weight of each criterion is derived from different models, there are also two cases to calculate the consistency ratio.

Case 1: Solving models (5) or (12), we derive the optimal solution $\varsigma_{A}$ and use the consistency index $\delta_{A}$ presented in Table 2. The consistency ratio is calculated according to ${\text{CR}}_{A} = \frac{{\varsigma_{A} }}{{\delta_{A} }}$.

Case 2: Solving models (9) or (13), we derive the optimal solution $\varsigma_{M}$ and use the consistency index $\delta_{M}$ presented in Table 3. The consistency ratio is calculated according to ${\text{CR}}_{M} = \frac{{\varsigma_{M} }}{{\delta_{M} }}$.

Step 5: Improve the consistency of FPRs.

Suppose the threshold of consistency is determined by the moderator. If a desired consistency level is not achieved, the consistency of FPRs can be improved by modifying some values, including in the FPRs. To save space, we only present the case in which the HFBWPRs with additive consistency and the maximum absolute differences are minimized problems with the same compromise limit constraint; other cases can be developed in a similar way.

In the improving process, the identification rule and direction rule are sequentially considered. First, identify the position that needs to be adjusted. In the first phase, we determine the maximum difference between $\left| {\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} } } \right|$ and $\varsigma$, and $\left| {\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} } } \right|$ and $\varsigma$. The maximum difference corresponds to the value $\gamma_{Bj}$ or $\gamma_{jW}$ that needs to be adjusted. In the second phase, determine the range that can be adjusted. If $\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} } + \varsigma = 0$ or $\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} } + \varsigma = 0$, the adjustment range is determined as $\gamma_{Bj} \; \in \left\{ {\left[ {0,1} \right] \wedge \left[ {\gamma_{Bj} ,\gamma_{Bj} + \varsigma } \right]} \right\}$ or $\gamma_{jW} \; \in \left\{ {\left[ {0,1} \right] \wedge \left[ {\gamma_{jW} ,\gamma_{jW} + \varsigma } \right]} \right\}$. If $\frac{1}{2}\left( {w_{B}^{k} - w_{j}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{Bj} }} {\alpha_{Bj}^{s} \gamma_{Bj}^{s} } - \varsigma = 0$ or $\frac{1}{2}\left( {w_{j}^{k} - w_{W}^{k} } \right) + 0.5 - \sum\nolimits_{s = 1}^{{\# h_{jW} }} {\beta_{jW}^{s} \gamma_{jW}^{s} } - \varsigma = 0$, the adjustment range is determined as $\gamma_{Bj} \; \in \left\{ {\left[ {0,1} \right] \wedge \left[ {\gamma_{Bj} - \varsigma ,\gamma_{Bj} } \right]} \right\}$ or $\gamma_{jW} \; \in \left\{ {\left[ {0,1} \right] \wedge \left[ {\gamma_{jW} - \varsigma ,\gamma_{jW} } \right]} \right\}$. For a better understanding, algorithm 1 for improving the consistency of FPRs is depicted in Fig. 1.

Fig. 1

The algorithm of improving the consistency of FPR

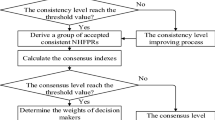
Step 6: Determine the weights of decision-makers.

First, the objective weights of the decision-makers are derived with respect to Eq. (14), and then the comprehensive weights of decision-makers are determined according to Eq. (15).

Step 7: Compute the collective optimal priority weights of the criteria.

The collective optimal priority weights of the criteria are determined by the following formula:

$$ \lambda_{i} = \sum\limits_{k = 1}^{z} {\tau_{k} } w_{i}^{k*} ,\quad i = 1,2, \ldots ,n, $$

(17)

where $\tau_{k}$ is the weight of decision-maker $e_{k}$, and $w_{i}^{k * }$ is the optimal priority weight vector determined from Step 3.

Step 8: Calculate the collective evaluation values.

The collective evaluation values are calculated by the hesitant fuzzy weighted averaging (HFWA) operator [53]:

$$ {\text{HFWA}}\left( {a_{i} } \right) = \cup_{{\gamma_{ij} \in h_{ij} }} \left\{ {1 - \prod\limits_{j = 1}^{n} {\left( {1 - \gamma_{ij} } \right)^{{\lambda_{j} }} } } \right\},\quad i = 1,2, \ldots ,n, $$

(18)

where $\lambda_{j}$ is the collective optimal priority weight vector determined from Eq. (17).

Step 9: Rank the alternatives.

The ranking order of all alternatives is obtained by the scores of collective evaluation values ${\text{HFWA}}\left( {a_{i} } \right)$, $i = 1,2, \ldots ,n$. The maximal scores of ${\text{HFWA}}\left( {a_{i} } \right)$ are the best alternative.

The proposed decision-making procedure is depicted in Fig. 2.

Fig. 2

The framework of the decision-making process based on hesitant fuzzy BWM

Remark 7

In Step 2, more than two identical scores may be derived from different criteria. In this case, the best and worst criteria can be determined with respect to the deviation function that is developed in Xia and Xu [53].

Remark 8

In Step 4, since there may be more than one priority weight vector, including Eq. (7) or Eq. (11). In this case, the consistency ratio of the optimal weights can be determined according to the following formula:

$$ {\text{CR}}_{A}^{^\circ } = \min \left\{ {\left. {\frac{{\varsigma_{A}^{k} }}{{\delta_{A}^{k} }}} \right|k = 1,2, \ldots ,l_{ \circ } } \right\}, $$

(19)

where $\varsigma_{A}^{k}$, $k = 1,2, \ldots ,l_{ \circ }$ is the optimal solution of model (5) or model (9) and indicates that the number of priority weight vectors included in Eq. (7) or Eq. (11) is $l_{0}$.

Remark 9

The algorithm for improving the consistency of FPRs developed in Step 5 is motivated by the idea presented in Mou et al. [57]. The proof of the algorithm’s convergence is developed in a similar way.

Illustrative example

There are three subsections. The first subsection introduces the selection of the most important project problems, the second subsection illustrates the use of the proposed methods, and the comparative analysis and discussion is conducted in the last subsection.

Case description

With the development of the rural economy in China, there are an increasing number of opportunities for enterprises to develop in the countryside. Currently, a series of preferential policies have been adopted in the rural areas of China, and many large domestic companies have taken part in the investment of rural infrastructure, making rural areas that had no prospects for development previously more attractive. Currently, many enterprises in our country choose to develop in rural areas. People in every industry in China are optimistic about the development of rural areas, and everyone believes that they will earn a large profit if invested in rural industries.

The enterprise’s board of director has to plan the development of strategy initiatives for the following several years. Suppose that there are five possible projects, denoted as (1) $a_{1}$ agricultural processing plant industry; (2) $a_{2}$ rural express industry; (3) $a_{3}$ rural logistics industry; (4) $a_{4}$ rural e-commerce industry; and (5) $a_{5}$ early childhood education in rural areas, to be evaluated. It is necessary to compare these projects to select which is the most important from the point view of their importance, taking into account four criteria suggested by the enterprise’s board of director from the perspectives of (1) $c_{1}$ the future development; (2) $c_{2}$ the risk of the investment; (3) $c_{3}$ the size of revenue; and (4) $c_{4}$ impact on the environment.

The evaluation of the alternative $a_{i}$, $i = 1,2, \ldots ,5$ with respect to four feature criteria is provided by the enterprise’s board of director, which is an HFE and demonstrated in Table 4. The weights of the criteria in this decision problem are completely unknown. To derive the weights of criteria, three decision-makers from related fields are invited to take part in the decision process. First, three decision-makers are asked to provide their opinion relative to each criterion. Because of the uncertainty of the criteria, it is difficult for decision-makers to use just one value to provide their pairwise evaluation values. To facilitate the elicitation of their evaluation values, HFE is just an effective tool to address such situations. Three decision-makers provide their evaluation with HFPRs, as demonstrated in matrices 1–3.

$$ \begin{aligned} R_{1} & = \left[ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ {0.{2}} \right\}} & {\left\{ {0.5,0.6,0.7} \right\}} & {\left\{ {0.{5}} \right\}} \\ {\left\{ {0.{8}} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.{7}} \right\}} & {\left\{ {0.{8},0.{9}} \right\}} \\ {\left\{ {0.3,0.4,0.5} \right\}} & {\left\{ {0.{3}} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.{6}} \right\}} \\ {\left\{ {0.{5}} \right\}} & {\left\{ {0.{1},0.{2}} \right\}} & {\left\{ {0.{4}} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right] \\ R_{2} & = \left[ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ {0.{8},0.{9}} \right\}} & {\left\{ {0.8} \right\}} & {\left\{ {0.{7},0.{8}} \right\}} \\ {\left\{ {0.{1},0.{2}} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.7} \right\}} \\ {\left\{ {0.2} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.{4}} \right\}} \\ {\left\{ {0.{2},0.{3}} \right\}} & {\left\{ {0.{3}} \right\}} & {\left\{ {0.{6}} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right]\quad {\text{and}} \\ R_{3} & = \left[ {\begin{array}{*{20}c} {\left\{ {0.5} \right\}} & {\left\{ {0.{6}} \right\}} & {\left\{ {0.{5},0.6,0.7} \right\}} & {\left\{ {0.{7}} \right\}} \\ {\left\{ {0.{4}} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.{6}} \right\}} & {\left\{ {0.{6}} \right\}} \\ {\left\{ {0.3,0.4,0.5} \right\}} & {\left\{ {0.{4}} \right\}} & {\left\{ {0.5} \right\}} & {\left\{ {0.{6}} \right\}} \\ {\left\{ {0.{3}} \right\}} & {\left\{ {0.{4}} \right\}} & {\left\{ {0.4} \right\}} & {\left\{ {0.5} \right\}} \\ \end{array} } \right]. \\ \end{aligned} $$

Table 4 Evaluation of the alternatives with respect to four feature criteria

Illustration of the proposed methods

In this subsection, we only present the case in which HFPRs are provided by three decision-makers with additively consistent HFBWPRs, and a similar method can be developed when HFPRs have multiplicatively consistent HFBWPRs. The procedures for determining the most important project using the proposed methods are discussed below, and there are two cases.

Case 1: The maximum absolute differences are minimized problems with the same compromise limit constraint.

Step 1: Define the decision criteria and provide the evaluation values.

The decision criteria have been defined, and three decision-makers’ evaluation values have been provided, as demonstrated in matrices 1–3.

Step 2: Identify the best and worst criteria.

According to Eq. (16), for decision-maker $e_{1}$, we have:

$s\left( {c_{1} } \right) = 1.{8}$; $s\left( {c_{2} } \right) = 2.{8}5$; $s\left( {c_{3} } \right) = {1}{\text{.8}}$ and $s\left( {c_{4} } \right) = 1.{3}5$. Since $s\left( {c_{2} } \right) > s\left( {c_{3} } \right){ = }s\left( {c_{1} } \right) > s\left( {c_{4} } \right)$, we have the best criterion $c_{2}$ and the worst criterion $c_{4}$.

For decision-maker $e_{2}$, we have:

$s\left( {c_{1} } \right) = 2.9$; $s\left( {c_{2} } \right) = 1.85$; $s\left( {c_{3} } \right) = 1.6$ and $s\left( {c_{4} } \right) = 1.65$. Since $s\left( {c_{1} } \right) > s\left( {c_{2} } \right) > s\left( {c_{4} } \right) > s\left( {c_{3} } \right)$, we have the best criterion $c_{1}$ and the worst criterion $c_{3}$.

For decision-maker $e_{3}$, we have:

$s\left( {c_{1} } \right) = 2.{4}$; $s\left( {c_{2} } \right) = {2}{\text{.1}}$; $s\left( {c_{3} } \right) = {1}{\text{.9}}$ and $s\left( {c_{4} } \right) = {1}{\text{.6}}$. Since $s\left( {c_{1} } \right) > s\left( {c_{{2}} } \right) > s\left( {c_{{3}} } \right) > s\left( {c_{{4}} } \right)$, we have the best criterion $c_{1}$ and the worst criterion $c_{{4}}$.

Step 3: Calculate the optimal weights of the criteria.

First, calculate the weights of the criteria, according to Eq. (5), for decision-maker $e_{1}$, we have:

$$ \begin{aligned} & \min \quad z^{k} = \varsigma \\ & {\text{s}}.{\text{t}}.\;\;\left\{ {\begin{array}{*{20}l} {\left| {\frac{1}{2}\left( {w_{2}^{k} - w_{1}^{k} } \right) + 0.5 - 0.{8}} \right| \le \varsigma } \hfill & {} \hfill \\ {\left| {\frac{1}{2}\left( {w_{2}^{k} - w_{3}^{k} } \right) + 0.5 - 0.{7}} \right| \le \varsigma } \hfill & {} \hfill \\ {\left| {\frac{1}{2}\left( {w_{2}^{k} - w_{4}^{k} } \right) + 0.5 - \left( {0.{8}\alpha_{24}^{1} + 0.{9}\alpha_{24}^{2} } \right)} \right| \le \varsigma } \hfill & {} \hfill \\ {\left| {\frac{1}{2}\left( {w_{1}^{k} - w_{4}^{k} } \right) + 0.5 - 0.{5}} \right| \le \varsigma } \hfill & {} \hfill \\ {\left| {\frac{1}{2}\left( {w_{3}^{k} - w_{4}^{k} } \right) + 0.5 - 0.{6}} \right| \le \varsigma } \hfill & {} \hfill \\ {\alpha_{24}^{s} \left( {w_{1}^{k} + w_{2}^{k} + w_{3}^{k} + w_{4}^{k} - 1} \right) = 0} \hfill & {} \hfill \\ {\alpha_{24}^{1} + \alpha_{24}^{2} = 1} \hfill & {} \hfill \\ {\alpha_{24}^{s} = 0 \vee 1,} \hfill & {\quad s = 1,2} \hfill \\ {\alpha_{24}^{s} = 1,} \hfill & {\quad s = 1,2} \hfill \\ {w_{j}^{k} \ge 0} \hfill & {} \hfill \\ {\varsigma \ge 0} \hfill & {} \hfill \\ {k = 1,2} \hfill & {} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

By solving this optimization model, when $\alpha_{{{24}}}^{{1}}$ and $\alpha_{{{24}}}^{2}$, respectively, set 1, we obtain:

$$ \begin{aligned} & z^{{1}} { = 0}{\text{.0;}}\;w_{{1}}^{{1}} { = 0}{\text{.05}},\;w_{{2}}^{{1}} { = 0}{\text{.65}},\;w_{{3}}^{{1}} { = 0}{\text{.25}}\;{\text{and}}\;w_{4}^{{1}} { = 0}{\text{.05}}. \\ & z^{2} { = 0}{\text{.04;}}\;w_{{1}}^{2} { = 0}{\text{.04}},\;w_{{2}}^{2} { = 0}{\text{.72}},\;w_{{3}}^{2} { = 0}{\text{.24}}\;{\text{and}}\;w_{4}^{2} { = 0}{\text{.0}}. \\ \end{aligned} $$

Similarly, for decision-maker $e_{{2}}$, when $\alpha_{12}^{{1}}$, $\alpha_{12}^{2}$, $\alpha_{14}^{{1}}$ and $\alpha_{14}^{2}$ are set to 1, we can obtain,

$$ \begin{aligned} z^{{1}} & { = 0}{\text{.0;}}\;w_{{1}}^{{1}} { = 0}{\text{.65,}}\;w_{{2}}^{{1}} { = 0}{\text{.05,}}\;w_{{3}}^{{1}} { = 0}{\text{.05}}\;{\text{and}}\;w_{4}^{{1}} { = 0}{\text{.25}}. \\ z^{2} & { = 0}{\text{.03}};\;w_{{1}}^{2} { = 0}{\text{.73,}}\;w_{{2}}^{2} { = 0}{\text{.0,}}\;w_{{3}}^{2} { = 0}{\text{.07}}\;{\text{and}}\;w_{4}^{2} { = 0}{\text{.2}}. \\ z^{3} & { = 0}{\text{.0}};\;w_{{1}}^{3} { = 0}{\text{.65}};\;w_{{2}}^{3} { = 0}{\text{.05}};\;w_{{3}}^{3} { = 0}{\text{.05}}\;{\text{and}}\;w_{4}^{3} { = 0}{\text{.25}}. \\ z^{4} & { = 0}{\text{.03}};\;w_{{1}}^{4} { = 0}{\text{.73}};\;w_{{2}}^{4} { = 0}{\text{.0}};\;w_{{3}}^{4} { = 0}{\text{.07}}\;{\text{and}}\;w_{4}^{4} { = 0}{\text{.2}}. \\ \end{aligned} $$

Moreover, for decision-maker $e_{{3}}$, when $\alpha_{13}^{{1}}$, $\alpha_{13}^{2}$ and $\alpha_{13}^{3}$, respectively, set 1, we can obtain,

$$ \begin{aligned} z^{{1}} & { = 0}{\text{.03;}}\;w_{{1}}^{{1}} { = 0}{\text{.38}},\;w_{{2}}^{{1}} { = 0}{\text{.25}},\;w_{{3}}^{{1}} { = 0}{\text{.32}}\;{\text{and}}\;w_{4}^{{1}} { = 0}{\text{.05}}. \\ z^{2} & { = 0}{\text{.0}};\;w_{{1}}^{2} { = 0}{\text{.45,}}\;w_{{2}}^{2} { = 0}{\text{.25}},\;w_{{3}}^{2} { = 0}{\text{.25}}\;{\text{and}}\;w_{4}^{2} { = 0}{\text{.05}}. \\ z^{3} & { = 0}{\text{.03}};\;w_{{1}}^{3} { = 0}{\text{.52}},\;w_{{2}}^{3} { = 0}{\text{.25}},\;w_{{3}}^{3} { = 0}{\text{.18}}\;{\text{and}}\;w_{4}^{3} { = 0}{\text{.05}}. \\ \end{aligned} $$

Second, derive the optimal priority weight vector.

First, utilize Eq. (6) to obtain the distance between $w_{{}}^{k}$ and $R_{k}$, for decision-maker $e_{1}$, we have:$d_{1} \left( {w^{{1}} ,R_{{1}} } \right) = 0.{07}$ and $d_{1} \left( {w^{2} ,R_{{1}} } \right) = 0.{09}$. Since there is only one priority weight vector included in Eq. (7), then the optimal priority weight vector can be determined as follows: $w^{1 * } = \left( {0.05,0.{6}5,0.{2}5,0.{0}5} \right).$

Similarly, for decision-maker $e_{{2}}$, we can obtain.

$d_{1} \left( {w^{1} ,R_{2} } \right) = d_{1} \left( {w^{3} ,R_{2} } \right) = 0$ and $d_{1} \left( {w^{2} ,R_{2} } \right) = d_{1} \left( {w^{{4}} ,R_{2} } \right) = {0}{\text{.03}}$. Since there is only one priority weight vector included in Eq. (7), then the optimal priority weight vector can be determined as follows: $w^{2 * } = \left( {0.{6}5,0.{0}5,0.{0}5,0.{2}5} \right)$.

Moreover, for decision-maker $e_{{3}}$, we can obtain.

$d_{1} \left( {w^{{1}} ,R_{3} } \right) = d_{1} \left( {w^{3} ,R_{3} } \right) = 0.028$ and $d_{1} \left( {w^{2} ,R_{3} } \right) = 0$. Since there is only one priority weight vector included in Eq. (7), then the optimal priority weight vector can be determined as follows: $w^{3 * } = \left( {0.45,0.25,0.25,0.05} \right)$.

Step 4: Calculate the consistency ratio.

According to ${\text{CR}}_{A} = \frac{{\varsigma_{A} }}{{\delta_{A} }}$, for decision-maker $e_{1}$, we have ${\text{CR}}_{1} = \frac{0.0}{{0.{1}}} = {0}$; for decision-maker $e_{2}$, we have ${\text{CR}}_{2} = 0$; and for decision-maker $e_{3}$, we have ${\text{CR}}_{3} = 0$.

Step 5: Improve the consistency of FPRs.

Since the consistency ratio values ${\text{CR}}_{1}$, ${\text{CR}}_{2}$ and ${\text{CR}}_{3}$ are equal to 0, we have that $R_{1}$, $R_{2}$ and $R_{3}$ are completely consistent, and their consistency does not need to be further improved.

Step 6: Determine the weights of decision-makers.

According to Eq. (14), the objective weights of decision-makers $e_{1}$, $e_{{2}}$ and $e_{{3}}$ are determined as follows:$\tau_{1}^{o} = 0$, $\tau_{2}^{o} = 0$ and $\tau_{3}^{o} = 1$. Suppose the subjective weights of decision-makers are provided by the enterprise’s board of director, which are equal values $\tau_{1}^{s} = \tau_{2}^{s} = \tau_{3}^{s} = \frac{1}{3}$; then, according to Eq. (15), the comprehensive weights of decision-makers $e_{1}$, $e_{{2}}$ and $e_{{3}}$ are calculated as follows: $\tau_{1}^{{}} = \tau_{2}^{{}} = \frac{1}{3}$ and $\tau_{3}^{{}} = \frac{2}{3}$.

Step 7: Compute the collective optimal priority weights of the criteria.

With respect to Eq. (17), the collective optimal priority weights of the criteria are calculated as follows:$\lambda_{1} = 0.4167$, $\lambda_{2} = 0.2833$, $\lambda_{3} = 0.2167$ and $\lambda_{4} = 0.0833$.

Step 8: Calculate the collective evaluation values.

According to Eq. (18), the collective evaluation values are calculated by the HFWA operator as follows:

$$ \begin{aligned} {\text{HFWA}}\left( {a_{1} } \right) & = \left\{ {0.5757,0.9557,0.9506,0.9609,0.9637,0.9604,0.9670,0.9632,0.9708} \right\}, \\ {\text{HFWA}}\left( {a_{2} } \right) & = \left\{ {0.9350,0.9455,0.9597,0.9683,0.9731} \right\},\;\;{\text{HFWA}}\left( {a_{3} } \right) = \left\{ {0.8516,0.8833,0.9414,0.9449,0.95} \right\} \\ {\text{HFWA}}\left( {a_{4} } \right) & = \left\{ {0.8912,0.9079,0.9586,0.9452,0.9538,0.9750,0.9735} \right\}\;\;{\text{and,}} \\ {\text{HFWA}}\left( {a_{5} } \right) & = \left\{ {0.8736,0.9073,0.9113,0.9389,0.9475,0.9519,0.9595} \right\}. \\ \end{aligned} $$

Step 9: Rank the alternatives.

According to Eq. (16), the score values of collective evaluation values are derived as follows: $s\left( {{\text{HFWA}}\left( {a_{1} } \right)} \right) = 0.7686$, $s\left( {{\text{HFWA}}\left( {a_{2} } \right)} \right) = 0.7970$, $s\left( {{\text{HFWA}}\left( {a_{3} } \right)} \right) = 0.7619$, $s\left( {{\text{HFWA}}\left( {a_{4} } \right)} \right) = 0.8257$ and $s\left( {{\text{HFWA}}\left( {a_{5} } \right)} \right) = 0.8112$. Since $s\left( {{\text{HFWA}}\left( {a_{4} } \right)} \right) > s\left( {{\text{HFWA}}\left( {a_{5} } \right)} \right) > s\left( {{\text{HFWA}}\left( {a_{2} } \right)} \right) > s\left( {{\text{HFWA}}\left( {a_{1} } \right)} \right) > s\left( {{\text{HFWA}}\left( {a_{3} } \right)} \right)$, the ranking order of all alternatives is obtained as $a_{4} \succ a_{5} \succ a_{2} \succ a_{1} \succ a_{3}$. Thus, the rural e-commerce industry is the most important project to invest.

Case 2: The maximum absolute differences are minimized problems with different compromise limit constraints.

Step $1^{\prime }$ and Step $2^{\prime }$ are the same as those given in Step 1 and Step 2.

Step $3^{\prime }$: Calculate the optimal weights of the criteria.

First, calculate the weights of the criteria, according to Eq. (12), for decision-maker $e_{1}$, we have:

$$ \begin{aligned} & \min \quad z^{k} = \sum\limits_{i = 1}^{5} {\varsigma_{i} } \\ & {\text{s}}.{\text{t}}.\left\{ {\begin{array}{*{20}l} {\left| {\frac{1}{2}\left( {w_{2}^{k} - w_{1}^{k} } \right) + 0.5 - 0.{8}} \right| \le \varsigma_{1} } \hfill & {} \hfill \\ {\left| {\frac{1}{2}\left( {w_{2}^{k} - w_{3}^{k} } \right) + 0.5 - 0.{7}} \right| \le \varsigma_{2} } \hfill & {} \hfill \\ {\left| {\frac{1}{2}\left( {w_{2}^{k} - w_{4}^{k} } \right) + 0.5 - \left( {0.{8}\alpha_{24}^{1} + 0.{9}\alpha_{24}^{2} } \right)} \right| \le \varsigma_{3} } \hfill & {} \hfill \\ {\left| {\frac{1}{2}\left( {w_{1}^{k} - w_{4}^{k} } \right) + 0.5 - 0.{5}} \right| \le \varsigma_{4} } \hfill & {} \hfill \\ {\left| {\frac{1}{2}\left( {w_{3}^{k} - w_{4}^{k} } \right) + 0.5 - 0.{6}} \right| \le \varsigma_{5} } \hfill & {} \hfill \\ {\alpha_{24}^{s} \left( {w_{1}^{k} + w_{2}^{k} + w_{3}^{k} + w_{4}^{k} - 1} \right) = 0} \hfill & {} \hfill \\ {\alpha_{24}^{1} + \alpha_{24}^{2} = 1} \hfill & {} \hfill \\ {\alpha_{24}^{s} = 0 \vee 1,} \hfill & {\quad s = 1,2} \hfill \\ {\alpha_{24}^{s} = 1,} \hfill & {\quad s = 1,2} \hfill \\ {w_{j}^{k} \ge 0} \hfill & {} \hfill \\ {\varsigma_{j} \ge 0,} \hfill & {\quad j = 1,2, \ldots ,5\quad } \hfill \\ {k = 1,2} \hfill & {} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

By solving this optimization model, when $\alpha_{{{24}}}^{{1}}$ and $\alpha_{{{24}}}^{2}$ respectively set 1, we obtain:

$$ \begin{aligned} z^{{1}} & { = 0}{\text{.0;}}\;\varsigma_{1} = \varsigma_{2} = \varsigma_{3} = \varsigma_{4} = \varsigma_{5} = 0.0,\;w_{{1}}^{{1}} { = 0}{\text{.05,}}\;w_{{2}}^{{1}} { = 0}{\text{.65,}}\;w_{{3}}^{{1}} { = 0}{\text{.25}}\;{\text{and}}\;w_{4}^{{1}} { = 0}{\text{.05}}. \\ z^{2} & { = 0}{\text{.1}};\;\varsigma_{1} = \varsigma_{2} = \varsigma_{4} = \varsigma_{5} = 0.0,\;\varsigma_{3} = 0.1,\;w_{{1}}^{{1}} { = 0}{\text{.05}},\;w_{{2}}^{{1}} { = 0}{\text{.65}},\;w_{{3}}^{{1}} { = 0}{\text{.25}}\;{\text{and}}\;w_{4}^{{1}} { = 0}{\text{.05}}. \\ \end{aligned} $$

Similarly, for decision-maker $e_{{2}}$, when $\alpha_{12}^{{1}}$, $\alpha_{12}^{2}$, $\alpha_{14}^{{1}}$ and $\alpha_{14}^{2}$ are set to 1, we can obtain.

$$ \begin{aligned} z^{{1}} & = {0}{\text{.0;}}\;\varsigma_{1} = \varsigma_{2} = \varsigma_{3} = \varsigma_{4} = \varsigma_{5} = 0.0,\;w_{{1}}^{{1}} { = 0}{\text{.65}},\;w_{{2}}^{{1}} { = 0}{\text{.05}},\;w_{{3}}^{{1}} { = 0}{\text{.05}}\;{\text{and}}\;w_{4}^{{1}} { = 0}{\text{.25}}. \\ z^{2} & = {0}{\text{.1;}}\;\varsigma_{2} = \varsigma_{3} = \varsigma_{5} = 0.0,\;\varsigma_{1} = 0.07,\;\varsigma_{4} = 0.03,\;w_{{1}}^{2} { = 0}{\text{.67}},\;w_{{2}}^{2} { = 0}{\text{.0}},\;w_{{3}}^{2} { = 0}{\text{.07}}\;{\text{and}}\;w_{4}^{2} { = 0}{\text{.27}}. \\ z^{3} & = {0}{\text{.0}};\;\varsigma_{1} = \varsigma_{2} = \varsigma_{3} = \varsigma_{4} = \varsigma_{5} = 0.0,\;w_{{1}}^{3} { = 0}{\text{.65}},\;w_{{2}}^{3} { = 0}{\text{.05}},\;w_{{3}}^{3} { = 0}{\text{.05}}\;{\text{and}}\;w_{4}^{3} { = 0}{\text{.25}}. \\ z^{4} & = {0}{\text{.1}};\;\varsigma_{1} = \varsigma_{2} = \varsigma_{3} = \varsigma_{4} = 0.0,\;\varsigma_{5} = 0.1\;w_{{1}}^{4} { = 0}{\text{.7}},\;w_{{2}}^{4} { = 0}{\text{.1}},\;w_{{3}}^{4} { = 0}{\text{.1}},\;{\text{and}}\;w_{4}^{4} { = 0}{\text{.1}}{.} \\ \end{aligned} $$

Moreover, for decision-maker $e_{{3}}$, when $\alpha_{13}^{{1}}$, $\alpha_{13}^{2}$ and $\alpha_{13}^{3}$ respectively set 1, we can obtain.

$$ \begin{aligned} z^{{1}} & = {0}{\text{.1,}}\;\varsigma_{1} = \varsigma_{3} = \varsigma_{4} = \varsigma_{5} = 0.0,\;\varsigma_{2} = 0.1,\;w_{{1}}^{{1}} { = 0}{\text{.45}},\;w_{{2}}^{{1}} { = 0}{\text{.25}},\;w_{{3}}^{{1}} { = 0}{\text{.25}}\;{\text{and}}\;w_{4}^{{1}} { = 0}{\text{.05}}. \\ z^{2} & = {0}{\text{.0}},\;\varsigma_{1} = \varsigma_{2} = \varsigma_{3} = \varsigma_{4} = \varsigma_{5} = 0.0,\;w_{{1}}^{2} { = 0}{\text{.45}},\;w_{{2}}^{2} { = 0}{\text{.25}},\;w_{{3}}^{2} { = 0}{\text{.25}}\;{\text{and}}\;w_{4}^{2} { = 0}{\text{.05}}. \\ z^{3} & = {0}{\text{.1}},\;\varsigma_{1} = \varsigma_{3} = \varsigma_{4} = \varsigma_{5} = 0.0,\;\varsigma_{2} = 0.1,\;w_{{1}}^{{1}} { = 0}{\text{.45}},\;w_{{2}}^{{1}} { = 0}{\text{.25}},\;w_{{3}}^{{1}} { = 0}{\text{.25}}\;{\text{and}}\;w_{4}^{{1}} { = 0}{\text{.05}}{.} \\ \end{aligned} $$

Second, derive the optimal priority weight vector.

First, utilize Eq. (6) to obtain the distance between $w_{{}}^{k}$ and $R_{k}$, for decision-maker $e_{1}$, we have:$d_{1} \left( {w^{{1}} ,R_{{1}} } \right) = d_{1} \left( {w^{2} ,R_{{1}} } \right) = 0.{07}$. Since there is only one priority weight vector including in Eq. (7), then the optimal priority weight vector can be determined as follows:

$$ w^{1 * } = \left( {0.05,0.{6}5,0.{2}5,0.{0}5} \right). $$

Similarly, for decision-maker $e_{{2}}$, we can obtain.

$d_{1} \left( {w^{1} ,R_{2} } \right) = d_{1} \left( {w^{3} ,R_{2} } \right) = 0$ and $d_{1} \left( {w^{2} ,R_{2} } \right) = d_{1} \left( {w^{{4}} ,R_{2} } \right) = {0}{\text{.03}}$. Since there is only one priority weight vector including in Eq. (7), then the optimal priority weight vector can be determined as follows:

$$ w^{2 * } = \left( {0.{6}5,0.{0}5,0.{0}5,0.{2}5} \right). $$

Moreover, for decision-maker $e_{{3}}$, we can obtain,

$d_{1} \left( {w^{{1}} ,R_{3} } \right) = d_{1} \left( {w^{3} ,R_{3} } \right) = 0.028$ and $d_{1} \left( {w^{2} ,R_{3} } \right) = 0$. Since there is only one priority weight vector including in Eq. (7), then the optimal priority weight vector can be determined as follows: $w^{3 * } = \left( {0.45,0.25,0.25,0.05} \right)$.

Step $4^{^{\prime}}$: Calculate the consistency ratio.

According to ${\text{CR}}_{A} = \frac{{\varsigma_{A} }}{{\delta_{A} }}$, for decision-maker $e_{1}$, we have: $CR_{1} = \frac{0.0}{{0.{1}}} = {0}$; for decision-maker $e_{2}$, we have: $CR_{2} = 0$; for decision-maker $e_{3}$, we have: $CR_{3} = 0$.

Step $5^{\prime }$: Improve the consistency of FPRs.

Since the consistency ratio values ${\text{CR}}_{1}$, ${\text{CR}}_{2}$ and ${\text{CR}}_{3}$ are equal to 0, we have $R_{1}$, $R_{2}$ and $R_{3}$ are completely consistency, the consistency of them do not need to be further improved.

Since the collective optimal priority weights of the criteria are the same as in case 1, Steps $6^{\prime }$ to $9^{\prime }$ are the same as those given in Steps 6–9, and the best choice is the same as in case 1.

Comparative analysis and discussion

To validate the feasibility of the proposed method, we conducted a comparative study with other methods based on the same illustrative example.

Mi and Liao [35] investigated the BWM with hesitant fuzzy information and then developed three different models to derive the priority weights of criteria with respect to diverse objectives. That is: (1) score-based method. The score values of HFEs are used to denote the most possible values of HFEs; (2) normalization-based method. The HFEs are extended to those with equal lengths according to decision-makers’ attitudes. (3) Regression-based method. Each possible value of pairwise comparisons is traversed without ignoring or adding any information. The shortcomings of the score-based method are that the HFEs are translated into different score values, which may lead to the loss of information. The shortcomings of the normalization-based method are that different values are added into shorter HFEs, which may distort the original information provided by decision-makers. The regression-based method is the most similar to the methods proposed in this study. To save space, only the regression-based method is conducted with a comparative study with the proposed methods. The calculation process is shown as follows.

Step 1: Calculate the individual weights of the criteria.

Suppose the HFPRs are provided by three decision-makers with additive consistency. According to the method presented in [35], for decision-maker $e_{1}$, we have:

$$ \begin{aligned} & \min \quad z = \varsigma \\ & {\text{s}}.{\text{t}}.\;\;\left\{ {\begin{array}{*{20}l} {\left| {\frac{1}{2}\left( {w_{2}^{{}} - w_{1}^{{}} } \right) + 0.5 - 0.{8}} \right| \le \varsigma } \hfill & {} \hfill \\ {\left| {\frac{1}{2}\left( {w_{2}^{{}} - w_{3}^{{}} } \right) + 0.5 - 0.{7}} \right| \le \varsigma } \hfill & {} \hfill \\ {\left| {\frac{1}{2}\left( {w_{2}^{{}} - w_{4}^{{}} } \right) + 0.5 - \left( {0.{8}\alpha_{24}^{1} + 0.{9}\alpha_{24}^{2} } \right)} \right| \le \varsigma } \hfill & {} \hfill \\ {\left| {\frac{1}{2}\left( {w_{1}^{{}} - w_{4}^{{}} } \right) + 0.5 - 0.{5}} \right| \le \varsigma } \hfill & {} \hfill \\ {\left| {\frac{1}{2}\left( {w_{3}^{{}} - w_{4}^{{}} } \right) + 0.5 - 0.{6}} \right| \le \varsigma } \hfill & {} \hfill \\ {w_{1}^{{}} + w_{2}^{{}} + w_{3}^{{}} + w_{4}^{{}} = 1} \hfill & {} \hfill \\ {\alpha_{24}^{1} + \alpha_{24}^{2} = 1} \hfill & {} \hfill \\ {\alpha_{24}^{s} = 0 \vee 1,} \hfill & {\quad s = 1,2} \hfill \\ {w_{j}^{{}} \ge 0} \hfill & {} \hfill \\ {\varsigma \ge 0} \hfill & {} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

By solving this optimization model, we obtain:

$$ z{ = 0}{\text{.0;}}\;w_{{1}}^{{}} { = 0}{\text{.05}},\;w_{{2}}^{{}} { = 0}{\text{.65}},\;w_{{3}}^{{}} { = 0}{\text{.25}}\;{\text{and}}\;w_{4}^{{}} { = 0}{\text{.05}}. $$

Similarly, for decision-maker $e_{{2}}$, we can obtain,

$$ z{ = 0}{\text{.0;}}\;w_{{1}}^{{}} { = 0}{\text{.65}},\;w_{{2}}^{{}} { = 0}{\text{.05}},\;w_{{3}}^{{}} { = 0}{\text{.05}}\;{\text{and}}\;w_{4}^{{}} { = 0}{\text{.25}}. $$

Moreover, for decision-maker $e_{{3}}$, we can obtain,

$$ z{ = 0}{\text{.0;}}\;w_{{1}}^{{}} { = 0}{\text{.45}};\;w_{{2}}^{{}} { = 0}{\text{.25}};\;w_{{3}}^{{}} { = 0}{\text{.25}}\;{\text{and}}\;w_{4}^{{}} { = 0}{\text{.05}}. $$

Step 2: Compute the collective optimal priority weights of the criteria.

Suppose the decision-makers’ weights are the same as those given in Step 6, that is, $\tau_{1}^{{}} = \tau_{2}^{{}} = \frac{1}{3}$ and $\tau_{3}^{{}} = \frac{2}{3}$. With respective to Eq. (17), the collective optimal priority weights of the criteria are calculated as follows: $\lambda_{1} = 0.4167$, $\lambda_{2} = 0.2833$, $\lambda_{3} = 0.2167$ and $\lambda_{4} = 0.0833$.

For a better comparison, the results obtained by Mi and Liao [35]’s method and the proposed methods are summarized in Table 5.

Table 5 The ranking results of the different methods

As shown in Table 5, the ranking values are the same when compared with Mi and Liao [35] method and the proposed methods. This confirms the feasibility of the proposed methods. The possible reasons for the consistency are explained as follows: Mi and Liao [35] method and the proposed methods both integrate the consistent HFPRs and BWM and determine the best priority weight vector. However, in the review of the calculation process, the definitions of the consistent HFPRs are different from Mi and Liao [35] method and the proposed methods, In Mi and Liao [35] method, the consistency definitions based on one FPR derived from HFPRs, that is, optimistic consistency, while the proposed methods the consistency definitions are based on the derived FPRs for each value in HFEs. The ways to determine the best priority weight vector are also different. The best priority weight vector was derived from the mathematical programming model in Mi and Liao [35] method, while the proposed methods were derived from the proposed distance formulas. Moreover, the proposed methods consider the consistency checking and improving process, while Mi and Liao [35] method fails to this.

In addition, although the ranking values are the same when compared with the proposed methods with the same and different compromise limit constraints, in the review of the calculation process, we find that the weights of the criteria are different for some FPRs. This confirms the necessity of considering different compromise limit constraints. For a better comparison, the results obtained by Mi and Liao [35] method and the proposed methods are summarized in Table 6.

Table 6 The weights of criteria derived from different methods

According to the comparison analysis, the method proposed in this study has the following advantages over other existing methods.

• 1. The consistency measures from the perspectives of additive consistent and multiplicatively consistent HFBWPRs are defined based on the relationships between each fixed value and their corresponding priority weight vector. It can then avoid information loss and distortion, and the ranking result obtained from the proposed methods seems more reasonable.

• 2. The ways to determine the best priority weight vector developed in this study consider the case when more than one priority weight vector has the same minimum distance.

• 3. The proposed methods consider the consistency checking and improving process, and the ranking result obtained from the proposed methods seems more convincing.

Conclusion

To address the situation where HFPRs are necessary, this paper develops several decision-making models integrating HFPRs with BWM. First, consistency measures from the perspectives of additive/multiplicatively consistent HFBWPRs are introduced. Second, several decision-making models are developed in view of the proposed additive/multiplicatively consistent HFBWPRs. Third, an absolute programming model is developed to obtain the decision-makers’ objective weights utilizing the optimal priority weight vector information, and the calculation of comprehensive weights of decision-makers is provided. Finally, a framework of the MCDM procedure based on hesitant fuzzy BWM is introduced, and an illustrative example in conjunction with comparative analysis is used to demonstrate that the proposed models are feasible and efficient for practical MCDM problems.

The present study provides several significant contributions to MCDM problems with HFPRs. They are summarized as follows: (1) consistency measures from the perspectives of additive/multiplicatively consistent HFBWPRs are introduced, which integrate the advantages of HFPRs and BWM. The proposed hesitant fuzzy BWM based on HFPRs provides us with a very useful method for MCDM in fuzzy environments. (2) Several decision-making models are developed in view of the proposed additive/multiplicatively consistent HFBWPRs and consider the same and different compromise limit constraints. In view of this, the MCDM methods developed in this study have wide practical applications. (3) An absolute programming model is developed to obtain the decision-makers’ objective weights utilizing the optimal priority weight vector information. It provides us with a new way to derive decision-makers’ weights. In our future research, the proposed methods are extended to hesitant fuzzy linguistic preference relations, and the proposed methods are applied to solve other practical MCDM problems. In addition, since the results given in this study are consistent, inconsistency is not considered. How to solve the weight vector by minimizing the inconsistency of the hesitant fuzzy BWM is also an area of future research.