Introduction

Optimization of the production cost has become an imperative component for every successful and robust manufacturing corporation. To design the mathematical modeling for an optimal production cost affected by making a decision in fuzziness, incomplete information. From the real-world, it is generally problematic to construct crisp models for these types of situations. It is also a predictable state of affairs that we recognize fuzzy optimization as the process by which indecision and inaccuracy in optimization problems are implemented. With the existence of fuzzy linear programming problems, many researchers introduced some methods for solving these problems [1] solved fuzzy linear programming problems through the simplex method. Maleki et al. [2] have implemented linear problem programming with fuzzy variables and expanded the primary simplex approach to solving fuzzy cost coefficients of LPP. In addition, the system for FLP problems by confined decision variables has generalized. With ample literature, we deduce from an unusual perspective, the theory and approach of optimization with the fuzzy-valued objective function [3,4,5,6,7], and their references. The feasible set was described via inequalities functions specified through crisp functions, i.e., the only opportunity to survive fuzziness in the areas is measured [8,9,10], and also studied the data in which the alternatives are not explained. Sometimes it is difficult to construct the models for uncertain information, and authors have tried to hypothesis all possibilities according to available data. Gao et al.[58] conducted a thorough review of the plannings for smart, energy-related manufacturing systems. In this paper, an approach has been carried out to build the triangular and trapezoidal fuzzy numbers for uncertainties. Meanwhile, the fuzzy numbers with a realistic approach have been used in different fields like decision-making, data analysis [11, 12], engineering problems [13, 14], etc. With the help of these fuzzy numbers’ assistance, we can resolve numerous optimization problems. A different process on fuzzy triangular numbers (FTN) improved subtraction and division [15]. Also, many modified operations are used to enhance triangular and trapezoidal fuzzy numbers [16,17,18,19,20,21], which might affect optimizing an FLP.

Aforementioned, many researchers had used applications of these fuzzy numbers to optimize the fuzzy linear programming problems such as an approach of ranking a fuzzy number and fuzzy triangular number [22] to solve linear programming problem. A research paper by Chakraborty et al. [23] FLP suggested that all the coefficients and decision variables would be represented by fuzzy triangular numbers, and all the constraints would be of fuzzy equality or inequality type. An innovative way for solving FLP by applying the Lexicography method has been proposed [24], in which the latest pattern for solving FLP using (L-R) fuzzy numbers and a lexicographical method has been applied in addition to classical linear programming. A novel algorithm is proposed [25] built on an innovative lexicographic ordering on TFN to explain the FFLP by changing it to its corresponding a MOLP. Broumi S et al. [57] proposed to define the shortest neutrosophic path, taking account of valued neutrosophic interval numbers, trapezoidal interval, and triangular value, for the length of the path in a network of neutrosophic numbers. Chandrawat et al. [26] carried out a study on modeling and optimization Production Cost using FLP with symmetric and right-angle triangular fuzzy numbers. In this study, the right angle triangular fuzzy number has been utilized to illustrate the membership grade of the optimized fuzzy LPP. Additionally, various components of triangular fuzzy numbers [27, 28] are used to design the reliability parameters to build industrial systems. Lathamaheswari et al. [59] proposed to the soft-weighted arithmetic operator a three-way type-2 interval with their demanded mathematical characteristics and also applied the proposed methodology in a profit-assessed decision-making problem. The symmetric fuzzy numbers were used in the objective and right-hand side constraints of the fuzzy linear programming problem [29,30,31]. Optimization is a systematic effort, under particular circumstances, to achieve better profit margins and reasonable results. de Andrés-Sánchez [56], the fuzzy version of such a form was being enhanced by proposing and evaluating three triangular approximations when the underlies are fuzzy triangular numbers for asset values, uncertainty, and free interest rates Liu and Rahbar [32] have defined the optimized cost as a genuine and steady decrease in the unit cost of the administration services offered without giving up its rationality for the said use. Rajguru and Mahatme [33] demonstrated various ways and systems for streamlining and controlling activities where numerous development ventures cannot meet their time and cost objectives. Jarkas and Abdulaziz [34] revealed that the performance of work repetition seldom increased and decreased to minimize the project time and cost. Also, the building project was executed without crashing. Al Haj and El-Sayegh [35] utilized What's Best solver to find an appropriate approach to the optimization problem. The findings are important and enable the project managers to participate in new trade-offs among time, cost and flexibility. The idea of learning curves came from experiences that made the execution of repetitive tasks simpler, easier and even quicker. Yang [36] observed that when an operation or task has been carried out without interruption, time and expenses will be minimized which in turn increase the quality and success rate of job. Farghal and Everett [37] have concluded that the learning curve phenomenon had been utilized in most of the construction projects. Kelley [38] and Fulkerson [39] have significantly contributed to formulating the time–cost tradeoff problem as a linear programming model. Moder and Phillips [40] introduced formulations of dual linear programming. Bertsimas et al. [41] suggested a robust integer programming problem, even where cost coefficients and data are subject to uncertainty within the constraints of an integer programming problem. Ahmed et al. [42] build a multistage stochastic integer programming formulation for a multistage capital expansion investment model in an ambiguous environment. Modeling unknown demand and expense parameters and fixed cost functions through a scenario tree approach to production management model economies of scale. Zhao et al. [43] introduced a multiobjective optimization model that capitalizes on a big data analysis. It was applied to the green supply chain, which minimizes the inherent risks of handling hazardous materials, associated carbon emissions, and costs. Huang et al. [44], has established a spatial and transient numerical model for the vital arranging of future bioethanol supply chains. The scheduling objective is to reduce costs over the entire planning horizon for the entire biofuel supply chain, from the biofuel supply chain to end users, while meeting demand, resources and technology requirements. This model has been utilized as a case study in California to assess the financial potential and foundation prerequisites for the creation of bioethanol from eight waste biomass sources. Jafari et al.[54] suggested that a model of fuzzy mathematical programming should optimize the desires of the nurses to work in their desirable shifts and reduce total surplus nurses, to fulfil every day's requirements. Leung et al. [8] proposed a robust model for optimizing production at several sites to solve the uncertainty problem, minimizing overall costs, including production costs, inventory costs, labor costs and its variation, Xiao et al. [45] Implement a joint optimization model that minimizes overall costs, including production costs, preventive maintenance, reduced repair costs for unforeseen failures and waiting costs. In previous approaches, the common goal was to minimize costs and for which precise data values have been assumed. Nevertheless, in real-life issues, the measured data values are often imprecise due to incomplete or impracticable details. In these cases, Fuzzy Linear Programming (FLP) contribute to improved and more appropriate models, by working with inappropriate data and constraints. Several researchers have studied the different characteristics of FLP problems in the last five decades and suggested various models for tackling LP problems through fuzzy numbers.

Tanaka et al. [46] first introduced the fuzzy mathematical programming and Bellman and Zadeh [47], which was based on a fuzzy decision structure to address LP parameter issues imprecision with fuzzy imperatives and objective functions. Zimmerman [48] has implemented an FLP formula in a crisp problem model using an existing algorithm and categorized FLP problems into symmetric and non-symmetric. Amid et al. [49] clarifies that there is no difference in the symmetric issue between the amounts of the objective and the restrictions, whereas the destinations and limitations are not identical in non-symmetric issues have different amounts. Tanaka and Asai [50] proposed a likely formulation of LP with a crisp decision coefficient and fuzzy decision variables. Verdegay [51] proposed and used the idea of a fuzzy objective constructed on the norm of fuzzification to explain FLP problems. Herrera et al. [52] analyzed the mathematical problem as fuzzy numbers and often included fuzzy coefficients as the concept of a feasibly specified set. Ganeshan and Veeramani [30] have suggested an FLP model with symmetrical trapezoidal fuzzy numbers. Wang and Peng J [53], the designs of the optimal r-best solution and r-worst solution of FNLPP were discussed and the proposed linear model for the optimal weight vector of the attributes was amended in [55].They have demonstrated fuzzy analogs for some primary LP axioms without translating them into crisp LP problems. Dong et al. [19] were designed a new fuzzy linear model with trapezoidal fuzzy numbers (TrFNs) being all target coefficients, scientific coefficients, and devices. The order relationship of the TrFNs is initially measured using the estimate of the TrFNs interval. The trapezoidal linear fuzzy system was converted into an objective interval program based on the order relationship of the TrFNs. In this study, newly constructed composite triangular and trapezoidal fuzzy LPP models have been proposed to deal with probabilistic increment \({p}_{j}\) in one direction and probabilistic decrement \({p}_{i}\) in other direction in the basic availability bi of classical optimization and analyzing the result with targeted membership grade.

The rest of the paper is arranged accordingly: “Problem identification” explains the problem identification. “Preliminaries” briefly summarizes the essential preliminaries related to the theory of fuzzy set and fuzzy number in optimization—the mathematical programming model of the problems introduced in “Mathematical modeling”. “Case study and data identification” presents a case study and data identification. To illustrate the idea presented in this paper, a numerical representation of the composite—triangular and trapezoidal FLP is provided in “Numerical result”. “Comparison between all the models with different cases” discusses the comparison of the models. Eventually, “Conclusion” provides some concrete conclusions and recommendations for future research.

Problem identification

Rail Coach Factory, Kapurthala, a premier coach manufacturing unit of Indian Railways, was established in 1986. It is situated in the Kapurthala district of Punjab, India. RCF has moved on to become the largest and most modern coach manufacturing unit of Indian Railways. We visited the site and observed the data that more than 36,000 RCF built coaches are traversing our nation's length and breadth. Every year RCF is adding more than 1600 coaches to this fleet, including AC and Non-AC coaches for Broad Gauge. These coaches have higher speed potential (up to 180 kmph), higher carrying capacity, aesthetically pleasing looks, and above all, superior safety features built into its design.

Though with selective indigenization, these coaches' costs have been brought down to one-third of their original cost, still these are 50–80% costlier than the conventional coaches. These coaches were hitherto confined to only premium trains like Rajdhani and Shatabdi Express due to higher costs. So till 2009, RCF was manufacturing around 100 such coaches every year. Derive the benefits of this superior technology on a broader scale; a decision was taken in 2009–2010 to switch over to stainless steel coach manufacturing completely. Hence the data [60] of the production costs of different coaches for the year 2010–2011 were considered input, and the total cost has been targeted as a prime objective see Table 2. It was observed that owing to certain procedural changes, maybe technical shifting, the actual production cost was fluctuating or uncertain, and the uncertainty is classified by Tables 3, 4, 5. Hence it is challenging to optimize the production cost in this inflexibility of creation expenses for various mentors. Therefore, the present study has been carried out by proposing newly constructed composite triangular and trapezoidal fuzzy LPP models to deal with it.

Preliminaries

In this section, some of the definitions, principles, and contexts of fuzzy logic have been discussed.

Fuzzy set and its components

The system of the fuzzy set was presented by Zadeh [41], and it was further improved by Zadeh [42]. It is an impressive technique for signifying instinctive or inaccurate evidence in different situations. A fuzzy set is defined as the universal space of real number with the membership function which assumes values in the range 0–1, in diverge to a classical set, where the transformation for a component in the universe among membership and non-membership in the specified set is unexpected and well defined. So, a fuzzy set is a set that consists of elements changing the degree of membership in the set, i.e., a fuzzy set is a more general concept of the classical set. It is written as a set of pairs {x, \({\upmu }_{{\rm A}}\)(X), where \({\upmu }_{{\rm A}}\)(X) is the membership grade, and X is the universal set}. The α-cut of the fuzzy set, denoted by \({{ \alpha }}_{{\upmu }_{{\rm A}}}\left(x\right),\) is a set consisting of those elements of a universal set whose membership function is either greater than or equal to the value of α. But if the membership function is greater than the value of α, it is called a strong α-cut of a fuzzy set. The mathematical notation of these are expressed as:

$${{ \alpha }}_{{\upmu }_{{\rm A}}}\left(x\right)=\{x|{\upmu }_{{\rm A}}({\rm X})\ge { \alpha }\}$$
(1)
$${{{ \alpha }}^{+}}_{{\upmu }_{{\rm A}}}\left(x\right)=\{x|{\upmu }_{{\rm A}}({\rm X})>{ \alpha }\}$$
(2)

where \({{ \alpha }}_{{\upmu }_{{\rm A}}}\left(x\right) \,\, {{{{\rm and} \,\, \alpha }}^{+}}_{{\upmu }_{{\rm A}}}\left(x\right)\) stands for the membership functions of fuzzy set A and \({\upmu }_{{\rm A}}\)(X) represents the α-cut of a fuzzy set A at the level. Moreover, in Eq. (2), the value of α is equal to zero, then it is termed as the support of the fuzzy set; the mathematical representation is given in Eq. 3.

$${\rm supp}(A)=\{x|{\upmu }_{{\rm A}}({\rm X})> 0\}$$
(3)

The height of a fuzzy set denoted by h(A) is defined as the largest of membership values of the elements contained in that set. For a normal fuzzy set, \(h(A)\) = 1. A fuzzy set is convex, if \({\upmu }_{{\rm A}}\){ λ \({x}_{1}\)+(1- λ)\({x}_{2}\)} ≥ \({\rm min}\{{\upmu }_{{\rm A}}\)(\({x}_{1}), {\upmu }_{{\rm A}}\)(\({x}_{2})\} ,\) Where 0 ≤ λ ≤ 1.

Fuzzy number

Fuzzy numbers are a precise form of fuzzy sets, which are signified by the membership functions with the resulting properties given by Kolesárová [21]: (a) Fuzzy set must be a normal fuzzy set, (b) must be bounded supports (c) is convex and (d) \({\rm have}\,\, \,\, {{ \alpha }}_{{\upmu }_{{\rm A}}}\left(x\right)\) that are closed for every α \(\in \left({\rm 0,1}\right].\) Although there exist numerous types of membership functions that fulfill the above necessities for fuzzy numbers, the triangular and trapezoids fuzzy number is the most commonly used fuzzy numbers which were explained by Lorterapong and Moselhi [21], modified by Pedrycz and Gomide [26], which have different applications of the fuzzy numbers.

Fuzzy linear programming

Classical LPPs are the minimum or maximum values under linear inequalities or linear function equations. The standard form of LPP is represented by

$${\rm Max} / {\rm Min }Z = {\sum_{j=1}^{n}}{{{c}_{j}}}{{x}_{j}}$$
$${\rm Subject to }\sum_{j=1}^{n}{{a}}_{ij}{x}_{j} \le {\rm or}\ge {b}_{i}$$
$${{\rm Where}, \quad x}_{j}\ge 0,\quad i, j\in {\mathbb{N}}$$
(4)

The function to be Max \(Z\) or Min \(Z\) is called an objective function. The \({{c}_{j}}\) are called cost coefficients. The A = [\({{a}}_{ij}]\) matrix is called a restriction matrix and the b = \({<{b}_{1}, {b}_{2},\dots , {b}_{m}>}^{T}\) is called a vector on the right side. where x = \({<{x}_{1}, {x}_{2},\dots , {x}_{n}>}^{T}\) is the vector of variables.

The standard form of fuzzy linear programming is represented by

$${\rm Max }Z=\sum_{j=1}^{n}{{c}_{j}}{x}_{j}$$
$${\rm Subject to }\sum_{j=1}^{n}{{a}}_{ij}{x}_{j }\le {\bar{b}_{i}}$$
$${{\rm Where}, \quad x}_{j}\ge 0,\quad i, j\in {\mathbb{N}}$$
(5)

where \(\tilde{b}_{i}\) is the right triangular fuzzy number represented in Fig. 1. Concerning the increase in the availability of restrictions, the fuzzy number can be presented in the above Eq. (5). The membership function would be described as follows.

$$ \tilde{b}_{i} = \left\{ {\begin{array}{ll} 1 & {{\text{when}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x \le b} \\ {\frac{{b_{i} + p_{i} - x}}{p}} & {{\text{when}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} b_{i} \le x \le b_{i} + p_{i} } \\ 0 & {{\text{when}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x \ge b_{i} + p} \\ \end{array} } \right.{\mkern 1mu} {\mkern 1mu} $$
(6)
Fig. 1
figure 1

Representation of the membership function for \(\tilde{b}_{i}\)

Full size image

The coefficient on the right is the membership function, i.e., the availability of restrictions. Optimize such a problem, the optimum values' lower and upper boundaries need to be estimated. The lower bound (Zl) value is

$${\rm Max }{ {\varvec{Z}}}_{{\varvec{l}}}=\sum_{j=1}^{n}{{c}_{j}}{x}_{j}$$
$${\rm Subject to}\sum_{j=1}^{n}{{a}}_{ij}{x}_{j}\le {b}_{i}$$
$${\rm Where}, {x}_{j}\ge 0, i,j\in {\mathbb{N}},{\rm x} \epsilon {\rm R}.$$
(7)

The optimal values upper bound (\({{\varvec{Z}}}_{{\varvec{u}}})\) is as follows

$${{\rm Max }{\varvec{Z}}}_{{\varvec{u}}}=\sum_{j=1}^{n}{{c}_{j}}{x}_{j}$$
$${\rm Subject to }\sum_{j=1}^{n}{{a}}_{ij}{x}_{j}\le {b}_{i}{ p}_{i}+$$
$${{\rm Where},\quad x}_{j}\ge 0, \quad i,j\in {\mathbb{N}},{\rm x} \epsilon {\rm R}$$
(8)

where, \({p}_{i}\) is an increase in the probabilistic availability of restrictions. In this case, the total probabilistic increase of access to restrictions is determined by the right coefficient.

The Simplex method can now be used to find a solution for the lower and upper bounds of the LPPs. Using these lower and upper bounds, the optimized fuzzy LPP is obtained as follows.

$$ {\text{Max Z}} = \lambda $$
$${{\rm Subject to }\lambda (Z}_{u}-{Z}_{l})- \sum_{j=1}^{n}{{c}_{j}}{x}_{j}\le -{Z}_{l}$$
$$\uplambda ({p}_{i)}+\sum_{j=1}^{n}{{a}}_{ij}{x}_{j \le {b}_{i}}+{p}_{i}$$
(9)

where, \({x}_{j}\ge 0, i,j\in {\mathbb{N}}\) and λ \(\in \left({\rm 0,1}\right)\) is membership grade.

Mathematical modeling

The standard form of FLP in Eq. (5) is considered to be the composite fuzzy triangular number \({\bar{b}_{i}}\) = (\({b}_{i}-{p}_{i }\sim {b}_{i}\sim {b}_{i}+{p}_{i })\) as a consequence of increased and decreased availability of restrictions. Thus the membership function for \({\bar{b}_{i}}\) is defined as follows:

$${{\bar{b}}}_{i} =\left\{\begin{array}{ll} 1 & when \quad x =\\ \frac{x-}{}& when\le x\le \\ \frac{{b}_{i}+{p}_{k}-x}{{p}_{k}}& when\le x\le {b}_{i}+{p}_{k}\\ 0 &otherwise\end{array}\right. $$
(10)

The coefficient on the right side is the membership function, i.e., the availability of restrictions, where x \(\epsilon \) R.

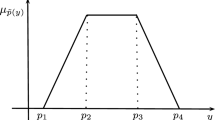
The values of \({{\bar{b}}}_{i}\) according to their membership function are graphically represented in Fig. 2:

Fig. 2
figure 2

Membership grade of total availability in the triangular fuzzy LPP

Full size image

Similarly, in certain situations, the total availability of any constrain can be inflexible from the one requirement to the other, and again it can be intensified and declined by any probabilistic increment and decrement. Such type of problems \({\bar{b}_{i}}\) (\({b}_{i}-{p}_{i }\sim {b}_{i}{\cong {b}_{i}^{*}\sim b}_{i}+{p}_{i })\) can be represented by the trapezoidal fuzzy number, given in Eq. (5), now presented due to an increase from above and decreases from below of the interval in the availability of constraints. The membership function representation for \({{\bar{b}}}_{i}\) is as follows:

$${{\bar{b}}}_{i} =\left\{\begin{array}{ll}1 & \quad when \le x\le {b}_{i}^{*}\\ \frac{x-}{} & \quad when \le x\le \\ \frac{-x}{} &\quad when\, {b}_{i}^{*}\le x\le \\ 0 & \quad otherwise\end{array}\right.$$
(11)

The coefficient on the right side is the membership function, i.e., the availability of restrictions, where x \(\epsilon \) R.

The values of \({{\bar{b}}}_{i}\) according to their membership function are graphically represented in Fig. 3.

Fig. 3
figure 3

Membership grade of total availability in the trapezoidal fuzzy LPP

Full size image

Solution methodology

According to the composite fuzzy triangular number \({\bar{b}_{i}}\) (\({b}_{i}-{p}_{i }\sim {b}_{i}\sim {b}_{i}+{p}_{i })\) the general structure of the optimal values of the lower, static, and upper bounds are defined below:

The lower bound (\({{\varvec{Z}}}_{{\varvec{l}}}\)) –

$${\rm Max}{ {\varvec{Z}}}_{{\varvec{l}}}=\sum_{j=1}^{n}{{c}_{j}}{x}_{j}$$
$${\rm Subject to }\sum_{j=1}^{n}{{a}}_{ij}{x}_{j}\le {b}_{i}-{p}_{i}$$
$${{\rm Where}, x}_{j}\ge 0, i,j\in {\mathbb{N}}$$
(12)
$$ {\text{The static bound}}({\mathbf{Z}}_{{\mathbf{s}}} ) \,\, {-} $$
$${\rm Max}{ {\varvec{Z}}}_{{\varvec{s}}}=\sum_{j=1}^{n}{{c}_{j}}{x}_{j}$$
$${\rm Subject to }\sum_{j=1}^{n}{{a}}_{ij}{x}_{j}\le {b}_{i}$$
$${{\rm Where}, x}_{j}\ge 0, \quad i,j\in {\mathbb{N}}$$
(13)
$$ {\text{The upper bound}} \,\, ({\mathbf{Z}}_{{\mathbf{u}}} ) \,\, {-} $$
$${\rm Max}, \,\,\, { {\varvec{Z}}}_{{\varvec{u}}}=\sum_{j=1}^{n}{{c}_{j}}{x}_{j}$$

Subject to \(\sum_{j=1}^{n}{{a}}_{ij}{x}_{j}\le {b}_{i}-{p}_{i}\)

$${{\rm Where}, x}_{j}\ge 0,\quad i, j\in {\mathbb{N}}$$
(14)

The solution for lower and upper bounds of LPP’s is obtained by the Simplex method. The two different optimized fuzzy LPP model is obtained by using these lower and upper bounds.

Optimized composite triangular fuzzy LPP model-I

$$ {\rm Max}\;Z\; = \lambda \;\;{\text{Sub}}{\text{. to}} $$
$$ \lambda (Z_{s} - Z_{l} ) - \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \le - Z_{l} $$
$$ \lambda (p_{i} ) + \sum\limits_{j = 1}^{n} {a_{ij} x_{j} \le b_{i},} $$
$$ \lambda (Z_{u} - Z_{s} ) - \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \le - Z_{s} $$
$$\lambda \left({p}_{i}\right)+{\sum }_{j=1}^{n}{a}_{ij}{x}_{j} \le {b}_{i}+{p}_{k}$$
$${x}_{j}\ge 0\quad i,j,k\in {\mathbb{N}}$$
(15)

Optimized composite triangular fuzzy LPP model-II:-

$$ {\rm Max}\;Z = \lambda \;{\text{Subject to}} $$
$$ \lambda (Z_{s} - Z_{l} ) - \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \le - Z_{l} $$
$$ \lambda (p_{i} ) + \sum\limits_{j = 1}^{n} {a_{ij} x_{j} \le b_{i} \,\,} $$
$$ \lambda (Z_{u} - Z_{l} ) - \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \le - Z_{l} $$
$$\lambda \left({p}_{i}+{p}_{k}\right)+{\sum }_{j=1}^{n}{a}_{ij}{x}_{j} \le {b}_{i}+{p}_{k}$$
$${x}_{j}\ge 0\quad i,j,k\in {\mathbb{N}}$$
(16)

The membership grade on behalf of primary LPP is given by Eq. (16) fuzzy optimized LPP. Here λ signifies the membership grade and \({Z}_{u}, {Z}_{s} \,\, and \,\, {Z}_{l}\) are the upper, static, and lower bounds. \(\sum\nolimits_{j = 1}^{n} {c_{j} x_{j} }\) is the objective function of the primary LPP, \({p}_{k} \,\, and \,\, {p}_{i}\) is the probabilistic increment and decrement, respectively, in the availability of the constraints.

Similarly, according to the trapezoidal fuzzy number \({\bar{b}_{i}}\) (\({b}_{i}-{p}_{i }\sim {b}_{i}{\cong {b}_{i}^{*}\sim b}_{i}+{p}_{i })\) the general structure of the least lower, lower, upper bounds and the most upper bound of the optimal values are defined below.

The least lower bound (\({{\varvec{Z}}}_{{\varvec{l}}}^{\boldsymbol{*}}\))

$${{\rm Max }{\varvec{Z}}}_{{\varvec{l}}}^{\boldsymbol{*}}=\sum_{j=1}^{n}{{c}_{j}}{x}_{j}$$
$${\rm Subject to }\sum_{j=1}^{n}{{a}}_{ij}{x}_{j}\le {b}_{i}-{p}_{i}$$
$${{\rm Where}, x}_{j}\ge 0,\quad i,j\in {\mathbb{N}}$$
(17)
$$ {\text{The lower bound}}({\mathbf{Z}}_{{\mathbf{l}}} ) $$
$${{\rm Max }{\varvec{Z}}}_{{\varvec{l}}}=\sum_{j=1}^{n}{{c}_{j}}{x}_{j}$$
$${\rm Subject to }\sum_{j=1}^{n}{{a}}_{ij}{x}_{j} \le {b}_{i}$$
$${{\rm Where},x}_{j}\ge 0, \quad i,j\in {\mathbb{N}}$$
(18)

The upper bound (Zu)

$${{\rm Max }{\varvec{Z}}}_{{\varvec{u}}}=\sum_{j=1}^{n}{{c}_{j}}{x}_{j}$$
$${\rm Subject to }\sum_{j=1}^{n}{{a}}_{ij}{x}_{j} \le {b}_{i}^{*}$$
$${{\rm Where}, x}_{j}\ge 0,\quad i,j\in {\mathbb{N}}$$
(19)

Now the most upper bound (\({{\varvec{Z}}}_{{\varvec{u}}}^{\boldsymbol{*}}\))

$${{\rm Max }{\varvec{Z}}}_{{\varvec{u}}}^{\boldsymbol{*}}=\sum_{j=1}^{n}{{c}_{j}}{x}_{j}$$
$${\rm Subject to }\sum_{j=1}^{n}{{a}}_{ij}{x}_{j} \le {b}_{i}^{*}+{p}_{i}^{*}$$
$${{\rm Where}, x}_{j}\ge 0, \quad i,j\in {\mathbb{N}}$$
(20)

The solution for lower and upper bounds of LPP’s can be obtained by using the Simplex method. Two different optimized fuzzy LPP model is obtained by using these lower and upper bounds.

Optimized trapezoidal fuzzy LPP model-I

$$ {\rm Max}\;Z = \lambda \;{\text{Sub}}{\text{. to}} $$
$$ \lambda (Z_{l} - Z_{l} *) - \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \le - Z_{l} * $$
$$ \lambda (p_{i} ) + \sum\limits_{j = 1}^{n} {a_{ij} x_{j} \le b_{i} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} $$
$$ \lambda (Z_{u} * - Z_{u} ) - \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \le - Z_{u} $$
$$\lambda \left({p}_{i}^{*}\right)+{\sum }_{j=1}^{n}{a}_{ij}{x}_{j} \le {b}_{i}^{*}+{p}_{k}^{*}$$
$${x}_{j}\ge 0\quad i,j,k\in {\mathbb{N}}$$
(21)

Optimized fuzzy LPP model (II)

$$ Max\;Z = \lambda \;{\text{Sub}}{\text{. to}} $$
$$ \lambda (Z_{l} - Z_{l} *) - \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \le - Z_{l} * $$
$$ \lambda (p_{i} ) + \sum\limits_{j = 1}^{n} {a_{ij} x_{j} \le b_{i}, x_{j} > {0},} $$
$$ \lambda (Z_{u} - Z_{l} *) - \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \le - Z_{l} * $$
$$ \lambda (p_{i} + b_{i} * - b_{i} ) + \sum\limits_{j = 1}^{n} {a_{ij} x_{j} \le b_{i} *, x_{j} > {0},\,\,\begin{array}{*{20}c} {} & {} & {} & {\begin{array}{*{20}c} {} & {} & {} \\ \end{array} } \\ \end{array} } $$
$$ \lambda (Z_{u} * - Z_{l} *) - \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \le - Z_{l} * $$
$$\lambda \left({ {b}_{i}^{*}-{b}_{i}+{p}_{i}^{*}+p}_{i}\right)+{\sum }_{j=1}^{n}{a}_{ij}{x}_{j} \le {b}_{i}^{*}+{p}_{k}^{*}$$
$${x}_{j}\ge 0 \quad i,j,k\in {\mathbb{N}}$$
(22)

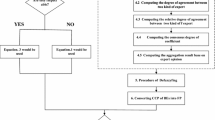
This fuzzy optimized LPP is given the membership grade for our primary LPP. Here λ signifies the membership grade and \({Z}_{l}^{*},\) \({Z}_{l}, {{Z}_{u}and Z}_{u}^{*}\) are the least lower, lower, upper, and most upper bounds, respectively. \(\sum\nolimits_{j = 1}^{n} {c_{j} x_{j} }\) is the objective function of the initial LPP, \({p}_{i}^{*}\) and \({p}_{i}\) is the probabilistic increment and decrement, respectively, in the availability of the constraints.The described methodology can be expressed by the following flow chart (Fig. 4).

Fig. 4
figure 4

Proceedure of the proposed method

Full size image

Illustrative example

In this section, we take an example and find the optimal value of the objective function with the baseline method [48] and the proposed method.

$${\rm Max }Z=5{x}_{1}+3{x}_{2}$$
$${\rm Subject to }3{x}_{1}+{x}_{2}\le {\bar{b}_{1}}$$
$$2{x}_{1}+5{x}_{2}\le {\bar{b}_{2}}$$

where, \({x}_{1}, {x}_{2}\ge 0 ,\) \({\bar{b}_{1}} \,\,{\rm and}\,\,\) \({\bar{b}_{2}}\) are the fuzzy numbers.

And the following Table 1 shows the comparison between the optimum values achieved by the baseline and the proposed method.

Table 1 Comparision of optimum value through the baseline and proposed method
Full size table
Table 2 Coach wise different manufacturing cost for the year 2010–11
Full size table

Case study and data identification

The data specified under is of the Rail Coach Factory (RCF), Kapurthala, Punjab, India of 2010–2011. This data indicates the built-up cost (in ‘lacs’ ‘1,00,000′) of different kinds of constraints of coaches.

Where \({C}_{{\rm Lab}.}\)= Labor cost of different coaches, \({C}_{{\rm Mat}.}\)= Material cost of different coaches, \({C}_{{\rm Aoh}}\)= Administrative overhead charge of different coaches, \({C}_{{\rm foh}}\)= Factory overhead charges of different coaches, \({C}_{{\rm Toh}}\)= Township overhead charges of different coaches, \({C}_{{\rm Soh}}\)= Shop overhead charges of different coaches, \({C}_{{\rm Tot}}\) = Total overhead cost including the petty overhead of different coaches, \({C}_{{\rm Pc}}\)= Performa charges of different coaches, \({C}_{{\rm Tc}}\)= Total cost of different coaches. All costs are in lacs (Indian National Rupees)

According to the complexity of the data, the optimization of targeted constraints might vary. Study of optimization strategies for realistic situations, the skewness and Kurtosis characteristics play a broader role. In the year 2010–2011, different coaches' total production cost is taken as an objective function to be minimized concerning the other constraints. The total availability of constraints \({C}_{Lab.}\), \({C}_{Mat.},\) \({C}_{foh}\), \({C}_{Aoh}\), \({C}_{Toh}\), \({C}_{Soh}\), \({C}_{Tot}\) \(,{C}_{Pc}\) and \({C}_{Tc}\) are 153.2, 2328.22, 256.56, 197.13, 41.23, 18.67, 513.61, 93.83 and 3088.88 lacs, respectively. Each constraint of concerned data has the same nature that is the coefficients of the skewness (\({\gamma }_{1}>0\)) and the coefficients of the Kurtosis (\({\beta }_{1}<0\)), which follows the positive skewness and Platykurtic distribution.

But the total availability of the constraints can be extended with some probabilistic increment, decrement, and reach to \({b}_{i}+{p}_{j},{b}_{i}-{p}_{i}.\) Therefore, a newly constructed composite triangular and trapezoidal fuzzy LPP is suggested to minimize the overall production cost.

Numerical result

To deal with the described situation, the following cases have been identified.

Case I: Unbounded feasibility with zero skewness

The production cost is targeted with at least basic availability for all constraints. It is optimized when basic availability is fluctuating by the increment of average quantity in one direction and a decrement of average quantity in another direction. The fluctuation is shown by Table 3 one direction and intensified by the average in the other direction.

Table 3 Symmetric increment and decrement in the total basic available cost for zero skewness
Full size table

Case II: Bounded feasibility with zero skewness

Case II is similar to case I to justify the feasible bounded region. The Performa charge is included with at least availability, and all other constraints are included with at most availability. Here, the Performa charge is considered at least available because this situation provides the bounded solution and gives the optimal value, which is nearest to the feasible most optimum solution.

Case III: Unbounded feasibility with positive skewness

The production cost is targeted with at least basic availability for all constraints, and it is optimized when the basic availability of all constraints are fluctuating by a decrement of average quantity in one direction and by the increment of maximum quantity in another direction. The fluctuation is shown in Table 4.

Table 4 Non-symmetrical increment and decrement in the total basic available cost for positive skewness
Full size table

Case IV: This case is an extension of the case–II where the membership grade is constant and gives a full degree of satisfaction for a small fluctuation, say minimum quantity in both directions of the basic availability of all constraints. The membership grade is further declined if there are a certain increment and decrement in the inflexible interval of basic availability. For example- (\(b_{i} - p_{i}\sim{{b}}_{i} {\sim{b}}_{i}^* {\sim{b}}_{i}^* - p_{i}^*\)). The minimum production cost is targeted with almost basic availability for all constraints and the least basic Proforma charge availability. The fluctuation is shown in Table 5:

Table 5 The probabilistic increments and decrements in the extension of total basic available cost
Full size table

Case V: This case is an extension of the case–I where the membership grade is constant and give a full degree of satisfaction for a small fluctuation, say minimum quantity in both directions of the basic availability of all constraints. The membership grade is further declined if there are a certain increment and decrement in the inflexible interval of basic availability (\(b_{i} - p_{i}{\sim{b}}_{i}{\sim{b}}_{i}^*{\sim{b}}_{i}^* + p_{i}*\)). The minimum production cost is targeted at the most basic availability for all constraints. The fluctuation is shown in Table 5.

Discussion of numerical results

Using the described methodology, the modeling of production cost is being done, and the Fuzzy numbers for all cost parameters have been derived. The lower bound, static bound, and upper bound are calculated, and the optimized fuzzy linear programming problem (OFLPP) has been constructed using the lower and upper bound, and then the credibility of optimized cost has been illustrated.

Analysis of all proposed cases has been given in the following sections:

Result analysis case-I

The production cost of RCF can be minimized using the cost parameter. The production's total basic cost is rupees 3088.749 (in lacs), and it can be extended and declined until rupees 3243.177, 2934.311(in lacs), respectively. The optimum production cost has been obtained to get the maximum membership grade. It shows that total production cost provides the highest credibility if the optimized cost is considered equal to rupees 3088.749 (in lacs). The credibility of production cost is being decreased if it is tending towards rupees 2934.311 and 3243.177 (in lacs).

Equation 23 and Fig. 5 show the fuzzy number for optimized membership grade:

Fig. 5
figure 5

The relation between membership grade of optimized production cost with \({\lambda }_{1}\) and \({\lambda }_{2}\) of Case-I

Full size image
$${\varvec{\uplambda}}=\left\{\begin{array}{ll}1 & when \,x=3088.7496\\ \frac{x-2934.3116}{154.438}&when\, 2934.3116\le x\le 3088.7496\\ \frac{3243.1771-x}{154.42}& when\, 3088.7496\le x\le 3243.1771\\ 0 &otherwise\end{array}\right.$$
(23)

Using the structure of optimized composite triangle fuzzy LPP, Model-I illustrate the Optimized minimum cost 3088.7273 unit with the membership grade \({\lambda }_{1}=0.00104521,\) and the minimized and greatest minimized costs 2934.466 and 3243.017 units, respectively. Similarly, optimized composite triangle fuzzy LPP, Model-II illustrate the Optimized minimum cost 3027.414 unit with the membership grade \({\lambda }_{2}=0.30143,\) and minimized and the greatest minimized costs 2980.86 and 3196.62 units, respectively.

Result analysis case-II

In this situation, the production cost can be increased and reduced to 3243.1770 and 2934.3110 (in lakes), respectively, and the total cost of production is 3088.7490 (in lakes). The optimal cost of production has been achieved to achieve optimum membership grades. The overall production cost is shown to have an optimum reputation if the optimized costs are substantially equal to 3088,749 (in lakes). However, if the production cost remains at 2934.3110 and 3243.1770 (in lakes), the reputation of production costs is declining.

Equation 24 and Fig. 6 show the fuzzy number for optimized membership grade:

Fig. 6
figure 6

The relation between membership grade of optimized production cost with \({\lambda }_{1}\) and \({\lambda }_{2}\) of Case-II

Full size image
$${\varvec{\uplambda}}=\left\{\begin{array}{ll}1 & when\, x=3098.9125\\ \frac{x-2943.9593}{154.9500}& when\, 2943.9593\le x\le 3098.9125\\ \frac{3253.8350-x}{154.9500} & when\, 3098.9125\le x\le 3253.8350\\ 0& otherwise\end{array}\right.$$
(24)

Model-I then reveals the Optimized Minimum Cost 3098.997 unit for membership grade \({\lambda }_{1}=0.0005434397443\), and the minimized and greatest minimized costs, respectively, 2944.0435 and 3253.7509 units, respectively, and Model-II, emphasizes the optimized minimum cost of 3037.033 points for membership grade \({\lambda }_{2}=0.3003278249\) and the minimized and greatest minimized costs of 2990.4961 and 3207.2998 units, respectively.

Result analysis of case-III

The total basic cost is 3088,749 (in lacs) and can be raised to 2934,3110 (in lacs) and decreased, respectively, to 3409.20 (in lacs). It shows that total production costs should be respected as long as the optimized costs are significantly equal to 3088.7490((in lacs). The reputation of the cost of production is reduced by heading towards 2934.3110 (in lacs) and 3409.2000 (in lacs).

Equation 25 and Fig. 7 show the fuzzy number for optimized membership grade:

Fig. 7
figure 7

The relation between membership grade of optimized production cost with \({\lambda }_{1}\) and \({\lambda }_{2}\) of Case-III

Full size image
$${\varvec{\uplambda}}=\left\{\begin{array}{ll}1& when \,x=3088.7496\\ \frac{x-2934.3116}{154.438} & when \,2934.3116\le x\le 3088.7496\\ \frac{3409.2022-x}{320.4520} & when \,3088.7496\le x\le 3409.2022\\ 0& otherwise\end{array}\right.$$
(25)

Now, Model-I and Model-II measured values are shown in Table 6 using the structure optimized triangle composite fuzzy LPP.

Table 6 Show calculated values of Model I and Model II of FLLP of Case-III
Full size table

Result analysis of case-IV

Under this situation, the total basic production cost would demonstrate full fulfillment from 3026.4 to 3118 rupees (under lakes). It can be increased and decreased to 3225.8 and 2918.6 rupees (in lakes), respectively. Achieve the optimum level of membership grade, and the optimum manufacturing costs have been collected. This indicates that the overall production costs are extremely reliable because the adjusted costs are significantly similar to those specific costs (from 3026.4 to 3118), for which the membership grade is inflexible. The reputation of the cost of production is lowered as it heads towards the higher prices of 2918.6 and 3225.8 (in lakes), respectively.

Equation 26 and Fig. 8 show the fuzzy number for optimized membership grade:

Fig. 8
figure 8

The relation between membership grade of optimized production cost with \({\lambda }_{1}\) and \({\lambda }_{2}\) of Case-IV

Full size image
$${\varvec{\uplambda}}=\left\{\begin{array}{ll}1 & when \,3026.4\le x\le 3118\\ \frac{x-2918.6}{107.8} & when \,2918.6<x<3026.4\\ \frac{3225.8-x}{107.8} & when \,3118<x<3225.8\\ 0& otherwise\end{array}\right.$$
(26)

Similarly, Table 7 displays the calculated values of Model-I and Model-II using the structure optimized Trapezoidal fuzzy LPP.

Table 7 Show calculated values of Model I and Model II of FLLP of Case-IV
Full size table
Table 8 Show calculated values of Model I and Model II of FLLP of Case-V
Full size table

Result analysis of case-V

Similarly, the total production cost would indicate the maximum degree of satisfaction and varies from 3042.7297 to 3134.7889 (in lacs). It can be extended and degraded by 2934.3209 (in lacs) to 3243.1968. It indicates that the actual production cost is more accurate if the adjusted cost is approximately the same as the basic membership (3042.7297 to 3134.7889). The credibility of the production cost is decreased if the expenditure (in lakes) is 2934.3209 and 3243.1968, respectively.

Equation 27 and Fig. 9 show the fuzzy number for optimized membership grade:

Fig. 9
figure 9

The relation between membership grade of optimized production cost with \({\lambda }_{1}\) and \({\lambda }_{2}\) of Case-V

Full size image
$${\varvec{\uplambda}}=\left\{\begin{array}{l}1 when\, 3042.7297\le x\le 3134.7889\\ \frac{x-2934.3209}{108.4088} when\, 2934.3209 <x<3042.7297\\ \frac{3243.196-x}{108.4079} when\, 3134.7889 <x<3243.1968\\ 0 otherwise\end{array}\right.$$
(27)

Likewise, Table 8 displays the measured values of Model I and Model II with the structure of Trapezoidal optimized fuzzy LPP.

Comparison between all the models with different cases

Figure 10, in the form of a bar chart, shows different models' performances to get the optimized. It is observed that the costs obtained by model II are more appropriate as compared to model I of composite triangular LPP and the cost obtained by model I are more appropriate as compared to the model II of trapezoidal LPP. The overall performance of the trapezoidal LPP model—I is better than all other models. Trapezoidal LPP model—I reduced approximately 50% destruction in production cost compared to 26% of trapezoidal LPP model—II, 0.1% of the Composite triangular LPP model—I and 30% of Composite triangular LPP model—II. The overall performance of the trapezoidal LPP model—I is better than all other models. Trapezoidal LPP model—I reduced approximately 62% production cost compared to 32% of trapezoidal LPP model—II, 0.05% of the Composite triangular LPP model—I and 30% of Composite triangular LPP model—II.

Fig. 10
figure 10

The performances of different models for different cases and their extension. Overall, it can be seen from the results that further this approach is extended to solve the other real-life complex problems [61,62,63,64,65,66,67,68,69,70,71,72,73,74]

Full size image

Conclusion

In this paper, the comparative study of modeling and optimizing the production cost of railway coaches of RCF Kapurthala via composite triangular fuzzy and trapezoidal fuzzy linear programming problem (FLPP) is proposed. Due to probabilistic increment and decrement in the availability of different constraints, the real production cost was fluctuating or uncertain. Therefore, the descriptions of five different incertitude situations are formulated, and the realistic models to extenuate the annihilation in the production cost optimization have been given in the article. Here, in the first attempt, the credibility of optimized cost via two different composite triangular FLP models is examined, and the results were compared with its extension, i.e., trapezoidal FLP model. The entire cost has been aimed to optimize regarding the constraints of \( {C}_{Lab.}\), \({C}_{Mat.},\) \({C}_{foh}{C}_{Aoh}\), \({C}_{Toh}\), \({C}_{Soh}\), \({C}_{Tot}\) \(,{C}_{Pc}\) and \({C}_{Tc}\). The lower, least lower, static, upper, and most upper bounds have been calculated for each situation, and then systems of optimized FLP were constructed. The credibility of each model of composite triangular and trapezoidal FLP for all situations has been obtained and using these membership grades the minimum and greatest minimum cost have been exemplified. The performance of each model of composite triangular fuzzy linear programming to all situations was compared with the trapezoidal fuzzy linear programming problem model. In all proposed situations for the greatest lower and least upper cost, it was observed that the composite triangular FLP model II is more appropriate as compared to model I and trapezoidal FLP model I is more appropriate as compared to model II and model I and II of composite triangular FLP. Hence, overall, the trapezoidal fuzzy LPP model I performance is the best among all proposed models. It shows a better degree of conciliation than composite triangular fuzzy LPP models and trapezoidal fuzzy LPP model II.