Introduction

Cryptography is an art of converting the plaintext into ciphertext using a secret key and vice-versa. It aims to secure information from eavesdroppers, interceptors, rivals, intruders, enemies, and assailants Bauer [5]. The prime concentration is on the frameworks for ensuring the confidentiality of information and techniques for the exchange of authentication keys and protocols between communicators Lindell and Katz [29]. The best-known approach is the use of the symmetrical and asymmetrical methods of encryption and decryption.

Modern cryptography uses algebraic number theory Diffie and Hellman [11], Steiner et al. [49], Balasubramaniam and Muthukumar [3], Eftekhari[16] to endorse a variety of cryptography algorithms. In authentication and encryption, the RSA cryptosystem and elliptic curve-based schemes are the best known public-key cryptography Zhou and Tang [56]. The RSA algorithm protection depends, however, on its prime factorization Meneses et al. [32]. If the size of the prime numbers is increased then the security of the encryption algorithm also increased; however, which also increases the calculation complexity and costs.

Diffie and Hellman [11]’s public-key exchange algorithm is a key distribution algorithm. It enables two communicating devices to agree upon a common encryption key through an unstable medium by sharing a key between them. In several fields, this exchange process, and the secret key are used, such as authentication of identity, data encryption, the security of data privacy. This scheme suffers from a MITM attack.

It is, therefore, necessary to search for innovative methods of secured and low costs protocol for the generation/exchange of cryptographic keys. This is a big challenge as attacker E may not be able to deduce the key, although he may partake the ability to follow the algorithm framework. The process of synchronization of the neural network provides an ability to address immense exchange problems Chen et al. [7], Liu et al. [31], Chen et al. [6], Wang et al. [52], Wang et al. [53], Xiao et al. [54], Zhang and Cao [55], Wang et al. [51], Dong et al.[15]. Neural cryptography has recently been recognized as capable of achieving this aim through neural synchronization Rosen-Zvi et al. [40] through in-depth integration and analysis of Artificial Neural Network (ANN) Lakshmanan et al. [28], Ni and Paul [35].

A special Artificial Neural Network (ANN) framework called the Tree Parity Machine (TPM) is used in this proposed technique. On both the sender and the receiver end, two TPM networks with similar configurations are used. These two networks are synchronized by generating random input vector and exchanging the outputs of such networks and preserving the secret of the synaptic weight. Two users A and B can generate a cryptographic key that is difficult for the attacker to infer, even though the attacker is aware of the algorithm structure and communication channel. In this paper, a Generative Adversarial Network (GAN)-based PRNG is proposed for generating the input vector to the neural synchronization process. This research is motivated by the work of Abadi and Andersen [1] in the learning of encoding methods by the neural network, which suggests that even a neural network can represent a good PRNG function. The intention is also derived from security requirements: there are some potentially useful characteristics of a hypothetical neural-network-based PRNG. This requires the ability, through more training, to make ad hoc alterations to the generator, which can constitute the backbone of strategies for dealing with the type of non-statistical threats presented by Kelsey et al. [25].

The rest of this paper is organized accordingly. Section 2 deals with related works. Section 3 deals with the proposed methodology. Sections 4 and 5 deal with security analysis and the results respectively. Conclusions are given in Sect. 6 and references are given at the end.

Related works

Several efforts are being made with neural networks to produce PRNG sequences by Desai et al. [10], Desai et al. [9], Tirdad and Sadeghian [50], Jeong et al. [21]. Tirdad and Sadeghian [50] and Jeong et al. [21], have described the most effective methods. The previous was using Hopfield neural networks to avoid convergence and promote dynamic behavior, whereas the latter used a random data sample-trained LSTM to acquire indices in the pi digits. In statistical randomness tests, these two papers reported a great result. However, no method sought to train a PRNG neural network end-to-end, rather than using the networks as modules of more complicated algorithms. RosenZvi et al. [40] and Kanter et al. [23] successfully created equal states of their internal synaptic weight when two ANNs have been trained using a particular learning rule. Kinzel and Kanter [26] and Ruttor et al. [42] described that a chance of an attack is declining if the network’s weight range get increases and the assailant’s calculation cost increases, as its effort increases exponentially, as users’ effort becomes polynomial. Sarkar and Mandal [44], Sarkar et al. [48], Sarkar et al. [46], Sarkar and Mandal [45], Sarkar et al. [47] proposed schemes which enhanced the security of the protocol by enhancing the synaptic depths of TPM and henceforth counteracting the attacks of the brute power of the attacker. It is found that the amount of security provided by the TPM synchronization also can be improved by introducing a large set of neurons and entries of each neuron in the hidden layers. Allam et al. [2] described an authentication algorithm using previously shared secrets. As a result, the algorithm attains a very high degree of defense without increasing synchronization time. Ruttor [41] described that lower values of the hidden unit have negative safety implications. Klimov et al. [27], compute whether or not two networks synchronize their weights. In connection with performance measurements of TPM network performance measurements, Dolecki and Kozera [12] proposed a frequency analysis technique that permits the assessment before completion of the synchronization rate of two TPM networks with a determined value that is not related to their differences in synaptic weights. Santhanalakshmi et al. [43] and Dolecki and Kozera [13] evaluate the efficiency of coordinated usage of genetic algorithm and the Gaussian distribution respectively. As a result, the random weight’s replacement with optimum weights decreases the time of synchronization. Pu et al. [39] carry out an algorithm, which combines ”true random sequences” with a TPM network that shows more complex dynamic behaviors which enhances encryption efficiency and attack resistance. According to the analysis, a safe, uniform and distribution for the synaptic weight values of the TPM networks are produced. Further, the Poisson’s distribution changes in each simulation run with the results as steps are move ahead towards synchronization. In the light of rules leading to the creation of TPM synchronization, Mu and Liao [33] and Mu et al. [34] describes the heuristic of minimum hamming distances. To test the security level of the final TPM network structure, the proposed heuristic rule was used. Concerning improvements to initial TPM network infrastructure, Gomez et al. [19] observed that the synchronization period is reduced from 1.25 ms to less than 0.7 ms with an initial assignment of the weights between 15 to 20%. The number of steps is also decreased from 220 to less than 100. Niemiec [36] is proposing a new concept for the main quantity reconciliation process using TPM networks. Dong and Huang [14] proposed a complex value-based neural network for neural cryptography. Here all the inputs and the outputs are complex value. But, this technique takes a significant amount of time to complete the synchronization process.

From this survey, it has been observed that all works in progress in neural cryptography are based on the mutual synchronization of two neural networks. To synchronize with n numbers of neural networks needs \(n^{2} \) number of synchronization. Also, it is rare to study the generation of good random input vector through robust pseudo-random number generator in the neural synchronization process. Existing TPM does not perform authentication steps in parallel with synchronization. The proposed technique performs cluster synchronization in logarithmic time instead of generating separate keys for individual communication in quadratic time. By implementing a deep learning technique such as GAN Goodfellow et al. [20] to design a PRNG that produces PRNG sequences explicitly, this paper develops the specific task. This paper, using the NIST Bassham et al. [4] test suite, introduces two simple structures and tests their power as PRNGs. A framework that is simple, conceptually efficient, and reliable is the general result of these modifications. Nearly 95 % of NIST tests can be consistently passed by the trained generator, indicating that the adversarial procedure is extremely effective in training the network to act as a PRNG. Findings are comparable to those of Tirdad and Sadeghian [50], and Jeong et al. [21], outperforming a range of regular PRNGs. This proposed cluster synchronization has several advantages that are as follows:

  1. (1)

    This proposed technology provides GAN-based robust random input vectors for the synchronization process.

  2. (2)

    To enhance the security a complex internal architecture of TPM is used.

  3. (3)

    An increase in the weight range of the neural network increases the complexity of a successful attack exponentially but the effort to build the neural key decreases over the polynomial time.

  4. (4)

    The proposed technique also offers synchronization and authentication steps in parallel.

Different parametric tests are performed to check the robustness and randomness of the GAN generated input vector. Python is used for the implementation of the technique and statistical analysis is done using R.

Proposed methodology

A key aspect of many security algorithms is Pseudo-Random Number Generators (PRNG). One of the focus is to decide how a GAN system can learn how to produce randomized sequences of numbers, and if such a system might be used in a security context as a PRNG. By suggesting the use of GAN to train an ANN to act as a PRNG, this paper presents a new approach to its implementation. Consequently, the generator learns to generate values that cannot be predicted by the attacker.

This paper demonstrates that even a tiny feed-forward completely linked ANN can be efficiently trained by a GAN to generating PRNG sequences with strong statistical characteristics. In this paper, a GAN-based common input vectors generation for neural synchronization is proposed. The proposed technique considers the range of input and output values as a set U. Table 1 lists the variables used in this GAN-based PRNG for neural synchronization.

Table 1 Symbol Description of GAN-based PRNG for Neural Synchronization
Full size table

The members of set U are all unsigned integer of 16 bits. PRNG can be represented as a following Eq. 1.

$$\begin{aligned} \begin{array}{@{}l}\phi (s):U\rightarrow U^{n}\end{array} \end{aligned}$$
(1)

Here, s is the seed value. The seed value is random which helps to generate a complete random common input vector that in turn satisfies the randomness in the purview of the NIST test suite for randomness. Here n can be considered a very large number. The model also can be characterized by individual outputs using Eq. 2.

$$\begin{aligned} \begin{array}{@{}l}\phi ^\nabla (s,\;C_i):T\rightarrow U\end{array} \end{aligned}$$
(2)

Here \(C_i \) is the present internal state, and T represents the all tuples set \((s,\;C_i) \). To approximate, \(\phi (s) \) a function G(s) is used. Consider an input \(O_t \) that leads to the following Eq. 3, which approximates \(\phi ^\nabla (s,\;C_i) \), with the dimension network output.

$$\begin{aligned} \begin{array}{@{}l}G^\nabla (s,\;O_t):U^{t+1}\rightarrow U^{n}\end{array} \end{aligned}$$
(3)

For any fixed s value the model G(s) is presented by concatenating generator’s output sequences \(\forall t\;G^\nabla (s,\;O_t) \).

$$\begin{aligned} \begin{array}{@{}l}\left| G(s)\right| \in \theta (n^{t})\end{array} \end{aligned}$$
(4)

It follows the Eq. 4, for the length of the full sequence G(s) . The model will reduce the adversary’s probability of accurately predicting future outputs from previous outputs. This model can be subdivided into discriminative and predictive model.

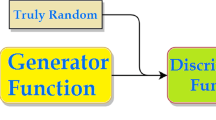
Each n-bit produced by the generator in the predictive approach is divided in such a way so that the \((n-1) \) bits act as an input for the predictor, and the label is designated by the n-th bit. Following Fig. 1 describes the discriminative approach.

Fig. 1
figure 1

Discriminative approach

Full size image

Figure 2 describes the predictive approach.

Fig. 2
figure 2

Predictive approach

Full size image

The generator consists of a fully connected feed-forward neural network, which is shown in the Eq. 5.

$$\begin{aligned} \begin{array}{@{}l}G^\nabla (s,\;O_1):U^{2}\rightarrow U^{8}\end{array} \end{aligned}$$
(5)

The input vector contains a s value and a scalar \(O_1 \). In this model, four hidden layers of thirty units and one output layer of eight units is considered shown in Fig. 3. The Leaky ReLU activation function gets used by the input layer and the hidden layer. Mod activation function is applied to the output layer, mapping values into the desired range while avoiding other pitfalls of sigmoid and \(\tan h \).

Fig. 3
figure 3

Structure of the generator: Fully Connected Layers and ReLU and mod activation function

Full size image

A Convolution Neural Network (CNN) is used as a discriminator using the following Eq. 6.

$$\begin{aligned} \begin{array}{@{}l}D(r):U^{8}\rightarrow [0,1]\end{array} \end{aligned}$$
(6)

where, r is an 8-long vector. The generator generates this r. The discriminator generates a scalar p(true) inside [0, 1], which is likely to belong to either class. The discriminator is made up of 4 stacked CNN layers each having four filters, a kernel size of two, and stride one, followed by a layer of max-pooling and 2 fully connected layers each having four and one respectively. The stack of convolution layers allows the network to identify complex input patterns. The least-squares loss is considered for discriminative purpose. Figure 4 shows the structure of the discriminator.

Fig. 4
figure 4

Structure of discriminator

Full size image

A Convolution Neural Network (CNN) is used as a predictor using the following Eq. 7.

$$\begin{aligned} \begin{array}{@{}l}P(r_{split}):U^{7}\rightarrow U\end{array} \end{aligned}$$
(7)

where \(r_{split} \) is the output vector of the generator with the last variable is discarded. The label is designated by the n-th bit which is served as a predictor’s input. Both the discriminator and predictor have the same design. But their input size and meaning of the result are different from each other. An absolute difference loss is used for the predictive purpose. NIST statistical test for randomness is performed on a variety of output generated for a particular seed for both before and after training. Next, the initialization of the predefined evaluation data set D is performed. It consists of input vector \(I_i\in U^{2} \) in the form \([s,O_{1i}]\), so that the random \(s\in I_i \) is fixed to the same random value \(\forall i~\) and all experiments. For \(I_i \) the offset \(O_{1i} \) starts at zero for \(I_0 \) and increases sequentially for the following vectors. Consider, arbitrarily \(s=20 \) then \(D=\left[ \left[ 20,0\right] ,\;[20,1],\;[20,2],\;...\;\right] \)

A generator is used to produce vectors for all vectors in D before training. Here, the only floating-point output is considered. Floating-point output is rounded down to the nearest integer. When the outputs are distributed uniformly across a range \([a,b]\) where \(a,b\in {\mathbb {R}}^{+} \), then they distributed uniformly across the range \([a,b]\) where \(a,b\in {\mathbb {Z}}^{+} \) .

Generator performance is being assessed after and before training using the NIST test. The procedure is repeated for at least twenty times for discriminative and predictive approaches.

Here, a complete binary tree framework is used to synchronize the cluster of TLTPM. Each TLTPM is considered as a node of a tree framework shown in Fig. 5. In a complete binary tree, a node with no child is called a leaf node. Consider \(j=1 \) at initial round (j is the round number) and \(leaves=8 \). Then the binary tree gets divided into \(\frac{no.\;of\;leaves}{2^{j}} \) subtrees each with \(2^{j} \) leaves i.e. four subtrees with two leaves. Siblings are involved in mutual learning at height four.

Fig. 5
figure 5

Group TLTPM synchronization at Initial State

Full size image

In round 1 siblings become synchronized using the mutual learning step shown in Fig. 6. From each subtree, a node is nominated as a leader among the nodes having the same parents to perform the next round of operation.

Fig. 6
figure 6

Group TLTPM synchronization at first round

Full size image

In round 2 when \(j=2 \) and \(leaves=8 \), the tree gets divided into two subtrees with four leaves at height 3 shown in Fig. 7. In this way next rounds are performed until the root node at height 1 is synchronized.

Fig. 7
figure 7

Group TLTPM synchronization at second round

Full size image

On the completion of the synchronization process, all the nodes in the cluster become synchronized based on a common cluster session key. Table 2 lists the parameters used in this article.

Table 2 Symbol Description of TLTPM
Full size table

This special neural network TLTPM is composed of M no. of input neurons for each H no. of hidden neurons. TLTPM has an only neuron in its output. TLTPM works with binary input, \(\alpha _{u,v}\in \{-1,+1\} \). The mapping between input and output is described by the discrete weight value between \(-\kappa \) and \(+\kappa \), \(\beta _{u,v}\in \{-\kappa ,-\kappa +1,\;\dots ,\;+\kappa \} \).

In TLTPM u-th hidden unit is described by the index \(u\;=\;1,\dots ,H \) and that of \(v\;=\;1,\dots ,M \) denotes input neuron corresponding to the u-th hidden neuron of the TLTPM. Consider there are \(H1,\;H2,\;H3 \) numbers of hidden units in the first, second, and third hidden layers respectively. Each hidden unit of the first layer calculates its output by performing the weighted sum over the present state of inputs on that particular hidden unit. Each hidden unit of the second layer calculates its output by performing the weighted sum over the hidden units of the first layer on that particular hidden unit. Similarly, each hidden unit of the third layer calculates its output by performing the weighted sum over the hidden units of second layer on that particular hidden unit. The calculation for the first hidden layer is given by Eq. 8.

$$\begin{aligned} \begin{array}{@{}l} \begin{array}{l} h_u=\frac{1}{\sqrt{M}}\alpha _u.\beta _u =\frac{1}{\sqrt{M}}\sum \limits _{v=1}^{M}\alpha _{u,v\;}\beta _{u,v\;}\end{array}\end{array} \end{aligned}$$
(8)

\(signum(h_u) \) define the output \(\gamma _u \) of the u-th hidden unit. (in Eq. 9),

$$\begin{aligned} \begin{array}{@{}l}\gamma _u=signum(h_u)\end{array} \end{aligned}$$
(9)

If \(h_u=0 \) then \(\gamma _u\; \)is set to \(-1 \) to make the output in binary form. If \(h_u>0 \) then \(\gamma _u\; \)is mapped to \(+1 \), which represents that the hidden unit is active. If \(\gamma _u\;=-1 \) then it denotes that the hidden unit is inactive (in Eq. 10).

$$\begin{aligned} \begin{array}{@{}l}signum(h_u)=\left\{ \begin{array}{l@{\quad }c}-1&{}if\;h_u\le 0\\ +1&{}if\;h_u>0\end{array}\right. \end{array} \end{aligned}$$
(10)

The product of the hidden neurons of the third layer denotes the ultimate result of TLTPM. This is represented by \(\zeta \) is (in Eq. 11),

$$\begin{aligned} \begin{array}{@{}l}\zeta =\prod \limits _{u=1}^{H3}\gamma _u\end{array} \end{aligned}$$
(11)

The value of \(\zeta \) is mapped in the following way (in Eq. 12),

$$\begin{aligned} \begin{array}{@{}l}\zeta =\left\{ \begin{array}{lc}-1&{}if\;\gamma _u=-1,\;is\;odd\\ +1&{}if\;\gamma _u=-1,\;is\;even\end{array}\right. \end{array} \end{aligned}$$
(12)

\(\zeta =\gamma _1 \), if only one hidden unit (\(H=1 \)) is there. \(\zeta \) value can be the same for\(\;2^{H-1} \) different \((\gamma _1,\;\;\gamma _{2,\;\dots ,\;}\gamma _H) \) representations.

If the output of two parties disagrees, \(\zeta ^{A}\ne \zeta ^{B} \), then no update is allowed on the weights. Otherwise, follow the following rules:

Table 3 Comparison of p_Value between proposed TLTPM and the existing CVTPM
Full size table

s TPM be trained from each other using Hebbian learning rule inzel and Kanter [26] (in Eq. 13).

$$\begin{aligned} \begin{array}{@{}l}\begin{array}{l}\begin{array}{l}\beta _{u,v}^{+}=fn(\beta _{u,v\;}+\alpha _{u,v}\zeta \Theta (\gamma _u\zeta )\;\end{array} \Theta (\zeta ^{A}\zeta ^{B}))\end{array}\end{array} \end{aligned}$$
(13)

In the Anti-Hebbian learning rule, both TPM is learned with the reverse of their output Kinzel and Kanter [26] (in Eq. 14).

$$\begin{aligned} \begin{array}{@{}l}\begin{array}{l}\begin{array}{l}\beta _{u,v}^{+}=fn(\beta _{u,v\;}-\;\alpha _{u,v}\zeta \Theta (\gamma _u\zeta )\;\end{array}\Theta (\zeta ^{A}\zeta ^{B}))\end{array}\end{array} \end{aligned}$$
(14)

If the set value of the output is not imperative for tuning given that it is similar for all participating TPM then random-walk learning rule Kinzel and Kanter [26], is used (in Eq. 15).

$$\begin{aligned} \begin{array}{@{}l}\begin{array}{l}\begin{array}{l}\beta _{u,v}^{+}=fn(\beta _{u,v\;}+\alpha _{u,v}\Theta (\gamma _u\zeta )\;\end{array}\Theta (\zeta ^{A}\zeta ^{B}))\end{array}\end{array} \end{aligned}$$
(15)

If \(X=Y \) then \(\Theta \left( X,Y\right) =1 \) Otherwise, If \(X\ne Y \) then \(\Theta \left( X,Y\right) =0 \). Only weights are updated which are in hidden units with \(\gamma _u=\zeta \). \(fn(\beta ) \) is used for each learning rule (in Eq. 16).

$$\begin{aligned} \begin{array}{@{}l}\begin{array}{l}fn(\beta )=\left\{ \begin{array}{lc}signum(\beta )\kappa &{}for\;\left| \beta \right| >\kappa \\ \beta &{}otherwise\end{array}\right. \end{array}\end{array} \end{aligned}$$
(16)

The likelihood distribution of the weight values in u-th hidden neuron of two TLTPM is represented by \((2\kappa \;+\;1) \) (in Eq. 17).

$$\begin{aligned} \begin{array}{@{}l}pb_{a,b}^{u}=P(\beta _{u,v}^{A}=a\;\wedge \;\beta _{u,v}^{B}=b)\end{array} \end{aligned}$$
(17)

The standard order parameters [18] can be calculated as functions of \(pb_{a,b}^{u} \) shown in Eq. 18, 19, and 20.

$$\begin{aligned} Q_u^{A}= & {} \frac{1}{M}\beta _U^{A}\beta _U^{A}\nonumber \\= & {} \sum \limits _{a=-\kappa }^\kappa \sum \limits _{b=-\kappa }^\kappa a^{2}\;pb_{a,b}^{u} \end{aligned}$$
(18)
$$\begin{aligned} Q_u^{B}= & {} \frac{1}{M}\beta _U^{B}\beta _U^{B}\nonumber \\= & {} \sum \limits _{a=-\kappa }^\kappa \sum \limits _{b=-\kappa }^\kappa b^{2}\;pb_{a,b}^{u} \end{aligned}$$
(19)
$$\begin{aligned} Q_u^{AB}= & {} \frac{1}{M}\beta _U^{A}\beta _U^{B}\nonumber \\= & {} \;\sum \limits _{a=-\kappa }^\kappa \sum \limits _{b=-\kappa }^\kappa ab\;pb_{a,b}^{u} \end{aligned}$$
(20)

Tuning is represented by the normalized overlap [18] given in Eq. 21.

$$\begin{aligned} \rho _u^{AB}=\frac{\beta _u^{A}}{\sqrt{\beta _u^{A}.\beta _u^{A}}} \frac{\beta _u^{B}}{\sqrt{\beta _u^{B}.\beta _u^{B}}}=\frac{R_u^{AB}}{\sqrt{Q_u^{A}.Q_u^{B}}}\times \end{aligned}$$
(21)

Calculate the entropy [8] using Eq. 22.

$$\begin{aligned} \begin{array}{@{}l}\begin{array}{l}S_u^{AB}= -M\;\sum \limits _{a=-\kappa }^\kappa \sum \limits _{b=-\kappa }^\kappa \;pb_{a,b}^{u}\ln \;pb_{a,b}^{u} \end{array} \end{array} \end{aligned}$$
(22)

The weight’s entropy in a single hidden neuron is represented by Eqs. 23 and 24.

$$\begin{aligned}&\begin{array}{@{}l}\begin{array}{l}S_u^{A}= -M\;\sum \nolimits _{a=-\kappa }^\kappa \left( \sum \limits _{b=-\kappa }^\kappa \;pb_{a,b}^{u}\right) \\ ln\left( \sum \limits _{b=-\kappa }^\kappa \;pb_{a,b}^{u}\right) \end{array} \end{array} \end{aligned}$$
(23)
$$\begin{aligned}&\begin{array}{@{}l}\begin{array}{l}S_u^{B}= -M\;\sum \limits _{b=-\kappa }^\kappa \left( \sum \limits _{a=-\kappa }^\kappa \;pb_{a,b}^{u}\right) \\ ln\left( \sum \limits _{a=-\kappa }^\kappa \;pb_{a,b}^{u}\right) \end{array}\end{array} \end{aligned}$$
(24)

Using Eqs. 22, 23, and 24 the common information Cover and Thomas [8] of A’s and B’s represented using Eq. 25.

$$\begin{aligned} \begin{array}{@{}l}\begin{array}{l}In^{AB}=\sum \limits _{u=1}^{H}\left( S_u^{A}+S_u^{B}-S_u^{AB}\right) \end{array}\end{array} \end{aligned}$$
(25)

The likelihood to observe \(\gamma _u\alpha _{u,v}=+1 \) or \(\gamma _u\alpha _{u,v}=-1 \) are not equal, but depend on the related weight \(\beta _{u,v} \) (in Eq. 26).

$$\begin{aligned} \begin{array}{@{}l}\begin{array}{l}P\left( \gamma _u\alpha _{u,v}=1\right) =\frac{1}{2}\left( 1+erf\left( \frac{\beta _{u,v}}{\sqrt{MQ_u-\beta _{u,v}^{2}}}\right) \right) \end{array}\end{array} \end{aligned}$$
(26)

\(\gamma _u\alpha _{u,v}=signum(\beta _{u,v}) \) occurs more frequently than \(\gamma _u\alpha _{u,v}=-\;signum(\beta _{u,v}) \), the stationary likelihood distribution of the weights for \(t\rightarrow \infty \), is computed using Eq. 19 for the transition likelihood Ruttor et al. [42]. This is represented using Eq. 27.

$$\begin{aligned} \begin{array}{@{}l}\begin{array}{l}P\left( \beta _{u,v}=\beta \right) = p_0\prod _{i=1}^{\left| \beta \right| }\frac{1+erf\left( \frac{i-1}{\sqrt{MQ_u-\left( i-1\right) ^{2}}}\right) }{1-erf\left( \frac{i}{\sqrt{MQ_u-i^{2}}}\right) }\end{array}\end{array} \end{aligned}$$
(27)

Here the normalization constant \(p_0 \) is given by Eq. 28.

$$\begin{aligned} \begin{array}{@{}l}\begin{array}{l}p_0=\left( \sum \limits _{\beta =-\kappa }^\kappa \prod \limits _{i=1}^{\left| \beta \right| }\frac{1+erf\left( \frac{i-1}{\sqrt{MQ_u-\left( i-1\right) ^{2}}}\right) }{1-erf\left( \frac{i}{\sqrt{MQ_u-i^{2}}}\right) }\right) ^{-1}\end{array}\end{array} \end{aligned}$$
(28)

For \(M\rightarrow \infty \), the parameter of the error functions will be ruled out, so that the weights stay consistently dispersed shown in Eq. 29.

$$\begin{aligned} \begin{array}{@{}l}\sqrt{Q_u(t=0)}=\sqrt{\frac{\kappa (\kappa +1)}{3}}\end{array} \end{aligned}$$
(29)

Otherwise, if M is finite, the likelihood distribution represented using order parameter \(Q_u \), shown in the following Eq. 30.

$$\begin{aligned} \begin{array}{@{}l}Q_u=\sum \limits _{\beta =-\kappa }^\kappa \beta ^{2}P\left( \beta _{u,v}=\beta \right) \end{array} \end{aligned}$$
(30)

Intensifying it in terms of \(M^{-1/2} \)results Ruttor et al. [42] in Eq. 31.

$$\begin{aligned} Q_u= & {} \frac{\kappa (\kappa +1)}{3}+\frac{8\kappa ^{4}+16\kappa ^{3}-10\kappa ^{2}-18\kappa +9}{15\sqrt{3\pi \kappa (\kappa +1)}}\frac{1}{\sqrt{M}}\nonumber \\&+O\left( \frac{\kappa ^{4}}{M}\right) \end{aligned}$$
(31)

In the case of \(1\ll \kappa \ll \sqrt{M} \), the asymptotic performance of the order parameter is represented using Eq. 32.

$$\begin{aligned} \begin{array}{@{}l}Q_u\sim \frac{\kappa (\kappa +1)}{3}\left( 1+\frac{8}{5\sqrt{3\pi }}\frac{\kappa }{\sqrt{M}}\right) \end{array} \end{aligned}$$
(32)

First-order approximation [42] of \(Q_u \) is given by Eq. 33.

$$\begin{aligned} Q_u= & {} \frac{\kappa (\kappa +1)}{3}-\frac{8\kappa ^{4}+16\kappa ^{3}-10\kappa ^{2}-18\kappa +9}{15\sqrt{3\pi \kappa (\kappa +1)}}\frac{1}{\sqrt{M}}\nonumber \\&+O\left( \frac{\kappa ^{4}}{M}\right) \end{aligned}$$
(33)

This systematically converges to (in Eq. 34).

$$\begin{aligned} \begin{array}{@{}l}Q_u\sim \frac{\kappa (\kappa +1)}{3}\left( 1-\frac{8}{5\sqrt{3\pi }}\frac{\kappa }{\sqrt{M}}\right) \end{array} \end{aligned}$$
(34)

If \(\zeta ^{A}=\zeta ^{B} \), but \(\gamma _u^{A}\ne \gamma _u^{B} \), the weight of one hidden neuron is changed. The weights execute an anisotropic diffusion in case of attractive steps (in Eq. 35).

$$\begin{aligned} \begin{array}{@{}l}pb_{a,b}^{u+}=\frac{1}{2}\left( pb_{a+1,b+1}^{u}+pb_{a-1,b-1}^{u}\right) \end{array} \end{aligned}$$
(35)

Repulsive steps, as an alternative, are equal to normal diffusion steps (in Eq. 36),

$$\begin{aligned} \begin{array}{@{}l}\begin{array}{l}pb_{a,b}^{u+}=\frac{1}{4}\left( pb_{a+1,b}^{u}+pb_{a-1,b}^{u}+pb_{a,b+1}^{u}+pb_{a,b-1}^{u}\right) \end{array}\end{array}\nonumber \\ \end{aligned}$$
(36)

on the same lattice. \(\triangle \rho s_{attr}(\rho ) \) and \(\triangle \rho s_{repu}(\rho ) \) are random variables. \(\triangle \rho s_{attr} \) and \(\triangle \rho s_{repu} \) are the step size for attractive and repulsive respectively shown in Eqs. 37 and 38.

$$\begin{aligned}&\begin{array}{@{}l}\begin{array}{l}\begin{array}{l}\triangle \rho s_{attr}=\frac{3}{\kappa \left( \kappa +1\right) }(1-\sum \limits _{v=-\kappa }^{+\kappa }\left( 2v+2\right) pb_{\kappa ,v}\end{array}+pb_{\kappa ,\kappa })\;\end{array}\end{array} \end{aligned}$$
(37)
$$\begin{aligned}&\begin{array}{@{}l}\begin{array}{l}\triangle \rho s_{repu}=-\frac{3}{\kappa \left( \kappa +1\right) }\left( \sum \limits _{v=-\kappa }^{+\kappa }\frac{v}{2}\;\left( pb_{\kappa ,j}-pb_{-\kappa ,v}\right) \right) \end{array}\end{array} \end{aligned}$$
(38)

At the initial state of the synchronization, it has its highest Klimov et al. [27] effect (in Eq. 39),

$$\begin{aligned} \begin{array}{@{}l}\begin{array}{l}\triangle \rho s_{attr}\left( \rho =0\right) =\frac{12\kappa }{\left( \kappa +1\right) {(2\kappa +1)}^{2}}\sim \frac{3}{\kappa ^{2}}\end{array}\end{array} \end{aligned}$$
(39)

Weights are uncorrelated as shown in Eq. 40.

$$\begin{aligned} \begin{array}{@{}l}pb_{a,b}\left( \rho =0\right) =\frac{1}{{(2\kappa +1)}^{2}}\end{array} \end{aligned}$$
(40)

Highest consequence (in Eq. 41),

$$\begin{aligned} \begin{array}{@{}l}\begin{array}{l}\triangle \rho s_{repu}\left( \rho =1\right) =\\ \frac{3}{\left( \kappa +1\right) \left( 2\kappa +1\right) }\sim -\frac{3}{2\kappa ^{2}}\end{array}\end{array} \end{aligned}$$
(41)

is achieved for complete harmonized weights (in Eq. 42).

$$\begin{aligned} \begin{array}{@{}l}pb_{a,b}(\rho =1)=\left\{ \begin{array}{lc}(2\kappa +1)^{-1}&{}for\;a=b\\ 0&{}for\;a\ne b\end{array}\right. \end{array} \end{aligned}$$
(42)

The weights are updated if \(\zeta ^{A}=\zeta ^{B} \). \(\epsilon _u \) is the generalization error. In common overlap for H hidden neurons,\(\;\epsilon _u=\epsilon \), the likelihood is represented using Eq. 43.

$$\begin{aligned} \begin{array}{@{}l}\begin{array}{l}Pb_{id}=Pb\left( \zeta ^{A}=\zeta ^{B}\right) =\sum \nolimits _{u=0}^{H/2}\left( \frac{H}{2u}\right) \left( 1-\epsilon \right) ^{H-2u}\epsilon ^{2u}\end{array}\end{array}\nonumber \\ \end{aligned}$$
(43)

For synchronization of TLTPM with \(H\;>\;1 \), the likelihood of attractive as well as repulsive are represented using by Eqs. 44 and 45.

$$\begin{aligned}&\begin{array}{@{}l}\begin{array}{l}Pb_{attr}^{B}=\frac{1}{2Pb_{id}}\sum \limits _{u=0}^{\left( \frac{H-1}{2}\right) }\left( \frac{H-1}{2u}\right) \left( 1-\epsilon \right) ^{H-2u}\epsilon ^{2u}\end{array}\end{array} \end{aligned}$$
(44)
$$\begin{aligned}&\begin{array}{@{}l}\begin{array}{l}Pb_{repu}^{B}=\frac{1}{Pb_{id}}\sum \limits _{u=1}^{H/2}\left( \frac{H-1}{2u-1}\right) \left( 1-\epsilon \right) ^{H-2u}\epsilon ^{2u}\end{array}\end{array} \end{aligned}$$
(45)

For \(H\;=\;3 \), this leads to Klimov et al. [27] following Eqs. 46 and 47.

$$\begin{aligned}&\begin{array}{@{}l}Pb_{attr}^{B}=\dfrac{1}{2}\frac{\left( 1-\epsilon \right) ^{3}+(1-\epsilon )\epsilon ^{2}}{\left( 1-\epsilon \right) ^{3}+3(1-\epsilon )\epsilon ^{2}}\end{array} \end{aligned}$$
(46)
$$\begin{aligned}&\begin{array}{@{}l}Pb_{repu}^{B}=\dfrac{2(1-\epsilon )\epsilon ^{2}}{\left( 1-\epsilon \right) ^{3}+3(1-\epsilon )\epsilon ^{2}}\end{array} \end{aligned}$$
(47)

Harmonization time \(Tm_{r,s} \) for the two random walk beginning at position s and distance r. \(Rf_{r,s} \) is the time of the first reflection Ruttor et al. [42]. \(Tm_{r,s} \) is given by Eq. 48.

$$\begin{aligned} \begin{array}{@{}l}Tm_{r,s}=Rf_{r,s}+\sum \nolimits _{v=1}^{r-1}Rf_{v,1}\end{array} \end{aligned}$$
(48)

The Eq. 41 leads to Eq. 49.

$$\begin{aligned} \begin{array}{@{}l}\left\langle Tm_{r,s}\right\rangle =\left\langle m-r+1\right\rangle s-s^{2}+\frac{1}{2}(r-1)(2m-r)\end{array} \end{aligned}$$
(49)

Tuning time Tm for arbitrarily selected beginning positions of the 2 random walkers represented using Eqs. 50 and 51.

$$\begin{aligned}&\begin{array}{@{}l}\left\langle Tm\right\rangle =\frac{2}{m^{2}}\sum \limits _{r=1}^{m-1}\sum \limits _{s=1}^{m-r}\left\langle Tm_{r,s}\right\rangle =\frac{(m-1)^{2}}{3}+\frac{(m-1)}{3m}\end{array} \end{aligned}$$
(50)
$$\begin{aligned}&\begin{array}{@{}l}\begin{array}{l}\left\langle Tm^{2}\right\rangle =\frac{2}{m^{2}}\sum \limits _{r=1}^{m-1}\sum \limits _{s=1}^{m-r}\left\langle T{m^{2}}_{r,s}\right\rangle \\ \qquad \ \,\quad =\frac{(17m^{5}-51m^{4}+65m^{3}-45m^{2}+8m+6)}{90m}\end{array}\end{array} \end{aligned}$$
(51)

The mean attractive steps needed to achieve a harmonized state increases nearly proportional to \(m^{2} \) is given by Eq. 52.

$$\begin{aligned} \begin{array}{@{}l}\left\langle Tm\right\rangle \sim \frac{1}{3m^{2}}\sim \frac{4}{3\kappa ^{2}}\end{array} \end{aligned}$$
(52)

This result is fixed with the scaling performance \(\langle tm_{synch}\rangle \) \(\propto \kappa ^{2} \) found for TPM harmonization Kanter et al. [23].

The standard deviation of Tm is shown in Eq. 53,

$$\begin{aligned} \begin{array}{@{}l}\begin{array}{l}SD_{Tm}=\sqrt{\frac{(7m^{6}-11m^{5}-15m^{4}+55m^{3}-72m^{2}+46m-10)}{90m^{2}}}\end{array}\end{array} \end{aligned}$$
(53)

system size \(m\;=\;2\kappa \;+\;1 \). \(SD_{Tm} \) is proportional asymptotically to \(\left\langle Tm\right\rangle \) shown in Eq. 54.

$$\begin{aligned} \begin{array}{@{}l}SD_{Tm}\sim \sqrt{\frac{7}{10}}\left\langle Tm\right\rangle \end{array} \end{aligned}$$
(54)

Security analysis

Geometric attack

In this proposed technique a geometric attack is considered on TLTPM. The likelihood of \(\gamma _u^{E}\ne \gamma _u^{A} \) is represented using the prediction error Ein-Dor and Kanter [17] using Eq. 55,

$$\begin{aligned} \begin{array}{@{}l}\varepsilon _u^{p}=\frac{1}{2}\left[ 1-erf\left( \frac{\rho _u}{\sqrt{2(1-\rho _u^{2}}}\frac{\left| h_u\right| }{\sqrt{Q_u}}\right) \right] \end{array} \end{aligned}$$
(55)

of the perceptron. When the u-th hidden neuron does not agree and rest of all hidden units has a condition of \(\gamma _v^{E}\ne \gamma _v^{A} \), then the likelihood Ruttor et al. [42] of a modification using the geometric attack is shown using Eq. 56.

$$\begin{aligned} P_k^{+}= & {} \int _0^\infty \left( \frac{2}{\sqrt{2\pi Q}}\right) ^{H} \left( \int _{h_u}^\infty \frac{1-\epsilon ^{P}(h)}{1-\epsilon }e^{-\frac{h^{2}}{2Q\;}}dh\;\right) ^{H-k}\nonumber \\&\times \left( \int _{h_u}^\infty \frac{\epsilon ^{P}(h)}{\epsilon }e^{-\frac{h^{2}}{2Q\;}}dh\;\right) ^{k-1} \frac{\epsilon ^{P}(h_u)}{\epsilon }e^{-\frac{h_u^{2}}{2Q\;}}dh_u \nonumber \\ \end{aligned}$$
(56)

For identical order parameters \(Q=Q_v^{E\;} \)and \(R=R_j^{AE\;} \) and various outputs \(\gamma _v^{A}\ne \gamma _v^{E} \). Then the likelihood for a modification of \(\gamma _u^{E}\ne \gamma _u^{A}\; \)is shown using Eq. 57.

$$\begin{aligned} P_k^{+}= & {} \int _0^\infty \left( \frac{2}{\sqrt{2\pi Q}}\right) ^{H} \left( \int _{h_u}^\infty \frac{1-\epsilon ^{P}(h)}{1-\epsilon }e^{-\frac{h^{2}}{2Q\;}}dh\;\right) ^{H-k}\nonumber \\&\times \left( \int _{h_u}^\infty \frac{\epsilon ^{P}(h)}{\epsilon }e^{-\frac{h^{2}}{2Q\;}}dh\;\right) ^{k-1}\frac{\epsilon ^{P}(h_u)}{\epsilon }e^{-\frac{h^{2}}{2Q\;}}dh_u \end{aligned}$$
(57)

By using the same equation the likelihood for an incorrect modification of \(\gamma _u^{E}=\gamma _u^{A}\; \) is shown with the help of equation 58.

$$\begin{aligned} P_k^{-}&=\int _0^\infty \left( \frac{2}{\sqrt{2\pi Q}}\right) ^{K} \left( \displaystyle \int _{h_i}^\infty \frac{1-\epsilon ^{P}(h)}{1-\epsilon }e^{-\frac{h^{2}}{2Q\;}}dh\;\right) ^{K-k-1`}\nonumber \\&\times \left( \displaystyle \int _{h_i}^\infty \frac{\epsilon ^{P}(h)}{\epsilon }e^{-\frac{h^{2}}{2Q\;}}dh\;\right) ^{k}\frac{1-\epsilon ^{P}(h_u)}{1-\epsilon }e^{-\frac{h_u^{2}}{2Q\;}}dh_u\nonumber \\ \end{aligned}$$
(58)

\(\gamma _u^{E}\ne \gamma _u^{A} \) condition is satisfied and in total there is an even number of hidden units that satisfied this condition then no geometric modification is done. Equation 59 represents this.

$$\begin{aligned} \begin{array}{@{}l}P_{r,1}^{E}=\sum \limits _{u=1}^{H/2}\left( \frac{H-1}{2u-1}\right) \left( 1-\epsilon \right) ^{H-2u}\epsilon ^{2u}\end{array} \end{aligned}$$
(59)

Second part of \(P_r^{E} \) can be represented using Eq. 60.

$$\begin{aligned} \begin{array}{@{}l}P_{r,2}^{E}=\sum \limits _{u=1}^{H/2}\left( \frac{H-1}{2u-1}\right) P_{2u-1}^{-}\left( 1-\epsilon \right) ^{H-2u+1}\epsilon ^{2u-1}\end{array} \end{aligned}$$
(60)

Third part of \(P_r^{E} \) can be represented using Eq. 61.

$$\begin{aligned} P_{r,3}^{E}=\sum \limits _{u=1}^{(H-1)/2}\left( \frac{H-1}{2u}\right) \nonumber \\ \left( 1-P_{2u+1}^{+}\right) \left( 1-\epsilon \right) ^{-2u-1}\epsilon ^{2u+1} \end{aligned}$$
(61)

If \(H\;>\;1 \) then the probability value of attractive steps and repulsive steps in the u-th hidden unit are represented using Eqs. 62 and 63.

$$\begin{aligned} P_a^{E}= & {} \frac{1}{2}\left( 1-\sum \limits _{v=1}^{3}P_{r,v}^{E}\right) \end{aligned}$$
(62)
$$\begin{aligned} P_r^{E}= & {} \sum \limits _{v=1}^{3}P_{r,v}^{E} \end{aligned}$$
(63)

Attractive steps are performed when \(H=\;1 \). If \(H\;=\;3 \) probability value can be calculated using Eq. 56, that forms Eq. 64 and 65.

$$\begin{aligned} P_a^{E}= & {} \frac{1}{2}\left( 1+2P_g\right) \left( 1-\epsilon \right) ^{2}\epsilon +\frac{1}{2}\left( 1-\epsilon \right) ^{3}\nonumber \\&+\frac{1}{2}\left( 1-\epsilon \right) ^{2}+\frac{1}{6}\epsilon ^{3} \end{aligned}$$
(64)
$$\begin{aligned} P_r^{E}= & {} 2\left( 1-P_g\right) \left( 1-\epsilon \right) ^{2}\epsilon +2\left( 1-\epsilon \right) \epsilon ^{2}+\frac{2}{3}\epsilon ^{3} \end{aligned}$$
(65)
Table 4 Comparison of p_Value of NIST Frequency Test
Full size table

Authentication Steps

In TLTPM input of both parties A and B acts as a common secret. The probability of an input vector \(\alpha ^{A/B}(t) \)having a particular parity \(p\in \{0,1\} \) is 0.5. For authentication purpose this parity will at this moment use the output bit \(\zeta ^{A/B} \). At any given time t with common inputs for both parties, the probability of identical output is given in Eq. 66.

$$\begin{aligned} \begin{array}{@{}l}P(\zeta ^{A}(t)=p=\zeta ^{B}(t))=\frac{1}{2}\end{array} \end{aligned}$$
(66)

Given a number \(n\;(1\le n\le \alpha ) \) of pure authentication steps, in which one transmits the parity of the consequent input vector as output \(\zeta ^{A/B} \)directly, the probability that the two parties subsequently produce the same output n times (and thus are likely to have the same n inputs) decreases exponentially with n i.e. \(P(\zeta ^{A}(t)=p=\zeta ^{B}(t))=\frac{1}{2^{n}} \). For statistical security of \(\varepsilon \in [0,1]\) select \(n=\alpha \) authentication steps such that \(1-\frac{1}{2^\alpha }\ge \varepsilon \) which can be computed as \(\alpha =\log _2\left[ \frac{1}{1-\varepsilon }\right] \). With \(\alpha =14 \) the achievable statistical security \(\varepsilon =0.9999 \) i.e. 99.9999%. The synchronization period for this technique therefore increases by \(\alpha \) authentication steps depending on the necessary level of security \(\varepsilon \). Select a certain bit subpattern in the input vector used for authentication only, such that the security threshold will be reached soon enough with a certain probability. Inputs are uniformly distributed so the last m bits is also uniformly distributed. Now select those entries that possess a defined bit sub-pattern (e.g. 0101 for \(m=4 \)). The probability of such a fixed bit sub pattern of m bit to occur is \(\frac{1}{2^{m}} \), because each bit has a fixed value with a probability of 0.5. Thus, for four bits, on average every sixteenth input would be used for authentication. Authentication step is performed when the subpattern arises and then one of the party sends out the parity of the consequent input vector as output \(\zeta ^{A/B} \) . This will only occur at the other party if it has the same inputs. Such an authentication does not manipulate the learning process at all. Because of the truth that the inputs are secret, an attacker cannot know when exactly such an authentication procedure takes place.

Table 5 Results after 500,000 simulations with different values of \(H1-H2-H3-M-\kappa \)
Full size table
Table 6 Results after 1000,000 simulations for the (8-8-8-16-8) and (8-8-8-8-128) combinations
Full size table
Table 7 Comparison of synchronization time for fixed network size and variable learning rules and synaptic depth in proposed TLTPM and existing CVTPM method
Full size table

Secret key space analysis

Consider n number of cascading encryption/decryption techniques is used to encrypt/decrypt the plaintext with the help of a neural synchronized session key. Then a session key of length [(number of cascaded encryption technique in bits) + (three bits combinations of encryption/ decryption technique index) + (length of n number of encryption/decryption keys in bits) + (length of n number of session keys in bits)] i.e. \([\;8+\;\left( 3\times n\right) +\;\left( 128\times n\right) +\left( 128\times n\right) \;]\) bits to \([\;8+\;\left( 3\times n\right) +\;\left( 256\times n\right) +(256\times n)]\) number of bits. So, \(\frac{[\;8+\;\left( 3\times n\right) +\;\left( 128\times n\right) +(128\times n)]}{8}=\left[ 1+\frac{\left( 3\times n\right) }{8}+16n+16n\right] =32n \) to \(\frac{[\;8+\;\left( 3\times n\right) +\;\left( 256\times n\right) +(256\times n)]}{8}=\Big [1+\frac{\left( 3\times n\right) }{8}+32n+32n\Big ]=64n \) numbers of characters.

Therefore, the total number of keys = \({256}^{64n} \). Attacker checks with half of the possible key in an average, the time needed at 1 decryption/ \(\mu s=0.5\times {256}^{64n} \mu s = 0.5\times 2^{8\times 64n} \mu s = 0.5\times 2^{512n} \mu s = 2^{(512n-1)} \mu s\).

Consider any single encryption using the neural key of size 512 bit which is hypothetically approved and needed to be analyzed in the context of the time taken to crack a ciphertext with the help of the fastest supercomputers available at present. In this neural technique to crack a ciphertext, the number of permutation combinations on the neural key is \(2^{512}\;=\;1.340780\;\times \;{10}^{154} \) trials for a size of 512 bits only. IBM Summit at Oak Ridge, U.S. invented the fastest supercomputer in the world with 148.6 PFLOPS i.e. means \(148.6\;\times \;{10}^{15} \) floating-point computing/second. Certainly, it can be considered that each trial may require 1, 000 FLOPS to undergo its operations. Hence, the total test needed per second is\(\;148.6\;\times \;{10}^{12} \). Total no. of sec. a year have = \(365\;\times \;24\;\times \;60\;\times \;60\;=\;31,536,000 \) sec. The total number of years for Brute Force attack: \((1.340780\;\times {10}^{154})/(\;148.6\;\times \;{10}^{12}\times 31,536,000)=2.86109\;\times \;{10}^{132}\) years.

Results and analysis

For result and simulation purpose, an Intel Core i7 10th Generation, 2.6 GHz processor, 16 GB RAM is used. Comprehensive and needful security views have been focused to affect acquaintance security and robustness issues. The precision of \({10}^{-15} \) decimal has been used in arithmetic operations according to the authenticated IEEE Standard 754.

True randomness was ensured in the proposed transmission technique by passing the fifteen tests contained in that suite. These tests are very useful for such a proposed technique with high robustness. A probability value (p-Value) determines the acceptance or rejection of the input vector generated by the GAN. Table 2 contains the results of NIST 15 Statistical tests NIST [37] on the generated random input vector. This table also represents the comparison of p_Value between the proposed TLTPM and the existing CVTPM technique Dong and Huang [14]. Here, p_Value of the proposed TLTPM of the average of 5 and 10 iterations, and p_Value of the existing CVTPM of the average of 10 iterations are represented. From Table 3, it has been seen that in the NIST statistical test p_Value of the proposed TLTPM has outperformed than the CVTPM. This confirms that the GAN-generated input vector has better randomness than the existing CVTPM.

The result of the frequency test indicates a ratio of 0 and 1 in the generated random sequence. Here, the value of the frequency test is 0.696413 which is quite average Kanso and Smaoui [22] and better than the result of frequency test 0.1329 in Karakaya et al. [24], and 0.632558 in Patidar et al. [38] 0.629806 in Liu et al. [30]. Comparison of p_Value of NIST frequency Test is given in Table 4.

The results of simulations for different \(H1-H2-H3-M-\kappa \) are shown in Table 5. The number of minimum and maximum synchronization steps indicates a number of minimum and maximum steps to synchronize the weight of the two networks. The column for the average steps indicates the sum of all simulations conducted. The minimum and maximum synchronization time columns indicate the minimum and maximum time in seconds required to synchronize the weights of the two networks. The successful synchronization of the attacker E column shows successfully how many instances that the attacking network imitated the behaviors of the other two networks for total simulations performed. Finally, the percentage of successful synchronization of the attacker E (%) column shows successfully the percentage of total simulations shown by the earlier column.

As shown in Table 5, the best results for the defense against the attacking network are the combinations (8-8-8-16-8) and (8-8-8-8-128), respectively. E did not mimic the behaves of A and B’s TLTPM in any of the 500,000 simulations. Table 6 shows that the best combination of values for the trio is (8-8-8-16-8).

Table 7 shows the comparison of synchronization time for fixed network size and variable learning rules and synaptic depth in the proposed TLTPM and existing CVTPM method. From the table, it has been seen that a trend towards an increase in the synchronization steps as the range of weight values \(\kappa \) increases in all three learning rules. For small \(\kappa \) values, Hebbian takes fewer synchronization steps than the other two learning rules in the range of 5 to 15, but as the \(\kappa \) value increases the Hebbian rule, more steps are taken to synchronize than the other two learning rules. Here, the Anti-Hebbian rules take less time than the other two learning rules in the 20 to 30 range. Random Walk outperforms 35 and beyond. As a result, an increase in the value of the \(\kappa \) security of the system can be increased.

Conclusion and future scope

In this paper, a GAN-based public-key exchange protocol is proposed. By presenting several alterations to the GAN system, this research makes lots of innovative contributions. This paper presents a rationalization of the GAN framework applicable to this work, in which a reference dataset that the generator should acquire knowledge to mimic is not included in the GAN. Also, instead of a recurrent network, this work design the statefulness of a PRNG that used a feed-forward neural network with additional non-random ”counter” inputs. For generating different key lengths using neural synchronization process various combinations of \(H1-H2-H3-M-\kappa \) with variable network size are considered. The security and synchronization time of GAN-based TLTPM is also being investigated. A geometric attack is also considered and it has been shown that it has a lower success rate. GAN-based TLTPM security is found to be higher than TPM with the same set of TPM network parameters. Finally, a variety of results and analysis are performed to confirm the experimental results. As future work, a more comprehensive analysis of security is planning to carry out. Also, different nature-inspired optimization algorithms will be considered for the optimization of weights value for faster synchronization purposes.