Introduction

Reinforcement learning stems from an experiment on the behaviors of cats in 1898 by Thorndike [20]. With the development of science and application, the concept of deep reinforcement learning (DRL) is proposed. DRL is a interdiscipline of reinforcement learning and deep learning to cope with environments with high dimensions [17]. In DRL field, multi-agent systems raise much attention, since they own the ability to deal with complex tasks by the cooperation of individual agents. Thus, the study among multi-agent systems is important.

Owing to the widespread application in resource allocation [1], machine learning [21], and robot control [25], and so on, distributed optimization problem over multi-agent systems has drawn much attention in recent years. In resolving process, agents can only communicate with their neighbors and the optimal solutions of distributed optimization problems are calculated based on their interaction. In past few decades, many research results have emerged for distributed optimization problems with sorts of constraints (see [3, 14, 18] and references therein). In [18], a topology network is introduced to solve a distributed optimization problem, where time delays are considered in the communication process among agents. By augmented Lagrange multiplier method, a nonsmooth distributed optimization problem with inequality constraints is studied in [29]. Moreover, a penalty method is utilized in [14] for distributed optimization to simplify constraints on an undirected topology graph.

Neurodynamic approach is a powerful tool in distributed optimization problems as well as traditional optimizations. For solving optimizations, Xia et al. [24] proposed a neurodynamic approach with global convergence. In [22], a second-order distribution dynamics is introduced to solve an optimization without constraints. In application of neurodynamic approaches, time delays are often inevitable. To consider the influence of time delays, Zeng et al. presented a continuous-time algorithm with time-varying delays and studied their stabilities in [31, 32]. To be suitable for computers, discrete-time recurrent algorithms are also considered in [30].

In recent years, for the purpose of realizing the goal of reducing the layers of related models, penalty method has attracted great attention among scholars. In [33], a discrete-time algorithm is proposed to solve distributed optimization problem without constraints. Authors in [33] discuss the convergence and error tolerance with the help of estimating a penalty parameter in advance. To solve distributed optimization problems with double local constraints, a neurodynamic approach is proposed in [16] by projection and regularization methods. It is worth noting that the computational burden may increase when applying neural network in [16] to solve distributed optimization problems with complex structures. For the broader application, Jiang et al. [8] proposed a penalty-like continuous-time algorithm for distributed optimization problems with affine equality and convex inequality constraints without considering penalty method.

It can be seen that distributed optimization problems are detailed studied with sorts of constraints and topology graphs according to above research findings. And it is worth noting that the computational complexity varies among different models. To introduce a proper algorithm to simply the calculation and complexity, the penalty method utilized in [14] is also considered here. Besides, we construct a projection-based continuous-time algorithm to solve distributed optimization problems with equality and inequality constraints over multi-agent systems in this paper. The main contributions of this paper are listed as follows:

  1. 1.

    In this paper, a continuous-time algorithm is proposed to resolve distributed optimization problem over multi-agent systems. Since the local cost functions and inequality constraint functions are studied without smoothness assumption, the distributed optimization problem here is more general than the one in [15]. Moreover, algorithm is constructed as a differential inclusion system, which is more flexible than the general gradient systems such as [6, 26].

  2. 2.

    By introducing penalty method, the distributed optimization problem with equality and inequality constraints is transformed into a new one. Thus, the distributed optimization problem can be solved by the algorithm which can be applied into the reformulated problem. Compared with conventional approach for distributed optimization problems in [12], penalty method has the advantage of reducing the dimension of models.

  3. 3.

    From any initial point, the states of the continuous-time algorithm are sure to enter equality constraint in a fixed time. This property guarantees the algorithm to possess the advantage of simplifying the distributed optimization problems by ignoring one of the constraints after a period time. Since fixed entering time is obtained without calculating \((AA^\mathrm {T})^{-1}\), the continuous-time algorithm is easier to be applied than algorithm in [11].

  4. 4.

    Different from conventional approaches which rely on introducing Laplace matrix to guarantee the consensus, the continuous-time algorithm realizes the consensus in the process of dealing with penalty terms. Compared with algorithm in [12], approach herein has fewer state variables, which is more preferable in application fields.

The rest parts are organized as follows. In the section “Preliminaries and problem description”, some necessary preliminaries are first introduced. The targeted distributed optimization problem and the reformulated one are given in the section “Problem reformulation and neurodynamic approach”. In the section “Problem reformulation and neurodynamic approach”, we propose a continuous-time algorithm and discuss the convergence of its states. Double numerical examples are proposed in the section “Simulations” to verify the performance of the presented algorithm. In the section “Conclusions”, the conclusion of this paper and our future works are summarized.

Preliminaries and problem description

This section presents some basic concepts containing graph theory and nonsmooth analysis as well as some necessary lemmas. Then, our studied problem is introduced.

Graph theory and nonsmooth analysis

A graph \({\mathcal {G}}({\mathcal {N}},{\mathcal {E}})\) is utilized in this paper to depict the information sharing among agents, where \({\mathcal {N}}=\{1,2,\ldots ,m\}\) means the set of agents and \({\mathcal {E}}\subset {\mathcal {N}}\times {\mathcal {N}}\) represents an edge set. An edge \(e_{ij}\) exists between a pair of agents (i, j) if they can communicate with each other. Denote that \({\mathcal {N}}_i\) is the neighbor set of agent i, which is \({\mathcal {N}}_i=\{j\in {\mathcal {N}}:e_{ij}\in {\mathcal {E}}\}\). And a graph is called undirected if \((i,j)\in {\mathcal {E}}\) implies \((j,i)\in {\mathcal {E}}\). A path between agents i and j in graph \({\mathcal {G}}\) is a sequence of edges \((i,i_1),(i_1,i_2),\ldots ,(i_k,j)\), where \(i_1,i_2,\ldots ,i_k\in {\mathcal {N}}\). Undirected graph \({\mathcal {G}}\) is said to be connected if there is a path between any pair of agents.

Definition 1

[4] Let \(\varPsi :{\mathbb {R}}^n\rightarrow {\mathbb {R}}\) be Lipschitz continuous near \(u_0\in {\mathbb {R}}^n\). The generalized directional derivative of  \(\varPsi \) at \(u_0\) is defined as:

$$\begin{aligned} \varPsi ^0(u_0;v)=\limsup \limits _{u\rightarrow u_0,s\downarrow 0}\frac{\varPsi (u+sv)-\varPsi (u)}{s}. \end{aligned}$$

Also, if \(\varPsi ^0(u_0;v)=\varPsi '(u_0;v)\), \(\varPsi \) is said to be regular at \(u_0\), where:

$$\begin{aligned} \varPsi '(u_0;v)=\lim \limits _{s\downarrow 0}\frac{\varPsi (u_0+sv)-\varPsi (u_0)}{t}. \end{aligned}$$

Proposition 1

[4] Suppose the function \(\varPsi :{\mathbb {R}}^n\rightarrow {\mathbb {R}}\) is convex. Then, the subdifferential of \( \varPsi \) at \( u_0\in {\mathbb {R}}^n\) is:

$$\begin{aligned}&\partial \varPsi (u_0)=\{\gamma \in {\mathbb {R}}^n :\langle \gamma ,u-u_0\rangle \le \varPsi (u)-\varPsi (u_0),\\&\forall u\in {\mathbb {R}}^n \}. \end{aligned}$$

Proposition 2

[4] If \(\varPsi :{\mathbb {R}}^n\rightarrow {\mathbb {R}}\) is Lipschitz continuous near \(u_0\in {\mathbb {R}}^n\) with Lipschitz constant \(\alpha \), then the following items hold:

(1) \(\partial \varPsi (u_0)\) is upper semicontinuous at \(u_0\);

(2) \(\partial \varPsi (u_0)\) is a nonempty convex compact set;

(3) \(\Vert \xi \Vert \le \alpha \) for any \(\xi \in \partial \varPsi (u_0)\).

Lemma 1

[4] If \(\varPsi :{\mathbb {R}}^n\rightarrow {\mathbb {R}}\) is convex on \(\varOmega \subseteq {\mathbb {R}}^n\), then for any \(u_1,u_2\in \varOmega \), the subdifferential of \(\varPsi \) satisfies:

$$\begin{aligned} \langle u_1-u_2,\xi _1-\xi _2\rangle \ge 0, \end{aligned}$$

for any \(\xi _1\in \partial \varPsi (u_1)\) and \(\xi _2\in \partial \varPsi (u_2)\).

Due to Proposition 2.3.6 in [4], a convex function \(\varPsi :{\mathbb {R}}^n\rightarrow {\mathbb {R}}\) is also regular.

Lemma 2

[4] (Chain rule) Assume that \(x(t):{\mathbb {R}}\rightarrow {\mathbb {R}}^n\) is differentiable and Lipschitz, if function \(V:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\) is regular at x(t), then we have:

$$\begin{aligned} {\dot{V}}(x(t))=\langle \xi ,{\dot{x}}(t)\rangle , \forall \xi \in \partial V(x(t)), \end{aligned}$$

for \({\mathrm {a.e.}}~t\in [0,+\infty ).\)

Several necessary lemmas

Consider a system

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{u}}(t)=-\alpha u(t)^{2-\frac{a}{b}}-\beta u(t)^{\frac{a}{b}}\\&u(0)=u_0, \end{aligned} \right. \end{aligned}$$
(1)

where \(u(t),u_0\in {\mathbb {R}}^n\), \(\alpha ,\beta \) are positive constants and \(a,b>0\) are odd integers satisfying \(a<b\).

Definition 2

For any initial point \(u(0)=u_0\in {\mathbb {R}}^n\), if there exists a \(T>0\), such that:

(1) \(\lim \limits _{t\rightarrow T}\Vert u(t)-u^*\Vert =0\);

(2) \(\Vert u(t)-u^*\Vert =0, t>T\),

where \(u^*\) is an equilibrium point of system (1).  Then,  the equilibrium point of  system (1) is said to be fixed-time stable.

Lemma 3

[34] The original of system (1) is fixed-time stable and upper bound of the time can be calculated as:

$$\begin{aligned} T\le \frac{\pi b}{2\sqrt{\alpha \beta }(b-a)}. \end{aligned}$$

Lemma 4

[4] Suppose that \(\varOmega _1,\varOmega _2\subseteq {\mathbb {R}}^n\) are closed convex sets satisfying \({\mathrm {int }}(\varOmega _1\cap \varOmega _2)\ne \emptyset \), then for \(u_0\in \varOmega _1\cap \varOmega _2\):

$$\begin{aligned} N_{\varOmega _1\cap \varOmega _2}(u_0)=N_{\varOmega _1}(u_0)+N_{\varOmega _2}(u_0), \end{aligned}$$

where \(N_{\varOmega }(u_0)\) is the normal cone to \(\varOmega \subseteq {\mathbb {R}}^n\) at \(u_0\), which is defined as \(N_{\varOmega }(u_0)=\{\xi \in {\mathbb {R}}^n| \langle \xi ,u_0-u\rangle \ge 0,\forall u\in \varOmega \}.\)

Lemma 5

[34] Suppose that \(\varOmega \subseteq {\mathbb {R}}^n\) is a nonempty closed convex set. Then, for any \(u\in {\mathbb {R}}^n\), the projection operator:

$$\begin{aligned} \varPi _{\varOmega }(u)=\arg \min \limits _{v\in \varOmega }\Vert v-u\Vert \end{aligned}$$

has the following propositions:

(1) \(\Vert \varPi _{\varOmega }(u)-u\Vert \) is continuous at u;

(2) \(\nabla (\Vert \varPi _{\varOmega }(u)-u\Vert ^2)=-2(\varPi _{\varOmega }(u)-u)\).

Distributed optimization problem

In this paper, we consider a network consisted of m agents over an undirected graph \({\mathcal {G}}\) to cooperatively solve the distributed optimization problem as follows:

$$\begin{aligned} \begin{aligned} \min ~~~~&\sum _{i=1}^m f_i(x)\\ {\mathrm {s.t.}}~~~~&g_i(x)\le 0,\\&A_i x=b_i,i=1,2,\ldots ,m, \end{aligned} \end{aligned}$$
(2)

where \(x\in {\mathbb {R}}^n\), \(f_i:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\) are local cost functions and \(g_i(x)=(g_{i1}(x), g_{i2}(x),\ldots ,g_{ip_i}(x))^\mathrm {T}:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^{p_i}\) may be nonsmooth, \(A_i\in {\mathbb {R}}^{q\times n}\) are row full rank matrixes and \(b_i\in {\mathbb {R}}^{q}\). For convenience, we denote:

$$\begin{aligned}&S_i=\{x\in {\mathbb {R}}^n| g_i(x)\le 0\}, \\&\varOmega _i=\{x\in {\mathbb {R}}^n| A_ix=b_i\}, \end{aligned}$$

for \(i=1,2,\ldots ,m\). In this paper, we default there exists at least one minimum of distributed optimization problem (2).

For solving distributed optimization problem (2), some useful assumptions are first introduced here.

Assumption 1

The graph \({\mathcal {G}}\) is undirected and connected.

Assumption 2

The Slater condition of distributed optimization problem (2) holds, \({\mathrm {i.e.}}\), there exists a \({\tilde{x}}\in {\mathbb {R}}^n\), such that \(g_i({\tilde{x}})< 0\) as well as \(A_i{\tilde{x}}=b_i\) for \(i=1,2,\ldots ,m\). Besides, the sets \(S_i\) are bounded; that is \(\exists M_i>0,\) such that \(S_i\subseteq B({\tilde{x}},M_i)\) for \(i=1,2,\ldots ,m\).

Assumption 3

The local cost functions \(f_i(x)\) are all convex and Lipschitz on \({\mathbb {R}}^n\) with the Lipschitz constant L.

Remark 1

The Assumptions 1–3 are widely adistributed optimization problems in solving distributed optimization problems, such as [12, 15]. Assumption 1 guarantees agents can communicate with their neighbors. In addition, Assumptions 2-3 imply that distributed optimization problem (2) is solvable.

Problem reformulation and neurodynamic approach

In this section, based on penalty method, the distributed optimization problem (2) is equivalently converted to a new one. Besides, a neurodynamic approach is proposed to solve the obtained distributed optimization problem.

Problem reformulation

Consider the following distributed optimization problem:

$$\begin{aligned} \begin{aligned} \min ~~&\sum _{i=1}^m f_i(x_i)+\sigma \sum _{i=1}^m G_i(x_i)+\lambda \sum _{i=1}^m\sum _{j\in {\mathcal {N}}_i}\Vert x_i-x_j\Vert \\ {\mathrm {s.t.}}~~&x_i\in \varOmega _i,i=1,2,\ldots ,m, \end{aligned} \end{aligned}$$
(3)

where \(f_i\) are from distributed optimization problem (2), \(\varOmega _i=\{x\in {\mathbb {R}}^n| A_i x_i=b_i\}\), the functions \(G_i(x_i)=\sum \limits _{k=1}^{p_i}\max \{g_{ik}(x_i),0\}\), and \(\sigma ,\lambda >0\) are penalty parameters.

Proposition 3

Let Assumption 2 holds, and then, the functions \(G_i(x_i)\) in distributed optimization problem (3) are coercive, that is:

$$\begin{aligned} \lim _{\Vert x_i\Vert \rightarrow +\infty }G_i(x_i)=+\infty , \end{aligned}$$
(4)

for \(i=1,2,\ldots ,m\).

Let \({\tilde{g}}=-\max _{1\le i\le m,1 \le k\le p_i}\{g_{ik}({\tilde{x}})\}\). Then, we have the following conclusion.

Theorem 1

Suppose that Assumptions 1–3 hold. If \(\varOmega _i=\varOmega _j,i,j\in \{1,2,\ldots ,m\}\), then there exist \(\sigma _0=\frac{ML}{m{\tilde{g}}}\) and \(\lambda _0=m(L+\sigma _0)\), such that distributed optimization problem (3) is equivalent to distributed optimization problem (2) with \(\sigma >\sigma _0\) and \(\lambda >\lambda _0\).

Proof

Consider a distributed optimization problem as follows:

$$\begin{aligned} \begin{aligned} \min ~~&\sum _{i=1}^m f_i(x)+\sigma \sum _{i=1}^m G_i(x)\\ {\mathrm {s.t.}}~~&x\in \varOmega _i,i=1,2,\ldots ,m; \end{aligned} \end{aligned}$$
(5)

then, we will first prove distributed optimization problem (2) is equivalent to problem (5).

Suppose that \(x^*\) is an optimal solution to distributed optimization problem (2), which yields:

$$\begin{aligned} 0\in \sum _{i=1}^m \partial f_i(x^*)+N_{S\bigcap \varOmega }(x^*), \end{aligned}$$
(6)

where \(S=\bigcap _{i=1}^m S_i\) and \(\varOmega =\bigcap _{i=1}^m \varOmega _i\). According to Assumption 2 and Lemma 4, \({\mathrm {int }}(S)\cap \varOmega \ne \emptyset \) implies that:

$$\begin{aligned} \begin{aligned} N_{S\bigcap \varOmega }(x^*)&=N_{S}(x^*)+N_{\varOmega }(x^*)\\&=\sum _{i=1}^mN_{S_i}(x^*)+\sum _{i=1}^mN_{\varOmega _i}(x^*). \end{aligned} \end{aligned}$$
(7)

Similar to [28], we have:

$$\begin{aligned} N_{S_i}(x^*)=\bigcup \limits _{\mu \ge 0}\mu \partial G_i(x^*)=\sum _{k\in I_{i0}(x^*)} [0,+\infty )\partial g_{ik}(x^*), \end{aligned}$$
(8)

where \(I_{i0}(x^*)=\{k\in \{1,2,\ldots ,p_i\}:g_{ik}(x^*)=0\}\). Thus, combining (7) with (8), it can be obtained that:

$$\begin{aligned} N_{S\bigcap \varOmega }(x^*)=\sum _{i=1}^m\sum _{k\in I_{i0}(x^*)} [0,+\infty )\partial g_{ik}(x^*)+\sum _{i=1}^mN_{\varOmega _i}(x^*). \end{aligned}$$
(9)

By (6), there exists a \(\xi ^*\in N_{S\bigcap \varOmega }(x^*)\), such that \(-\xi ^*\in \sum _{i=1}^m \partial f_i(x^*)\). Then, it is obvious that \(\Vert \xi ^*\Vert \le L\), where L is the Lipschitz constant of \(f_i(x)\) given in Assumption 3.

Hence, there exist \(\sigma _{ik}\in [0,+\infty )\), \(\varsigma _{ik}^*\in \partial g_{ik}(x^*)\) for \(k\in I_{i0}(x^*)\) as well as \(\tau _{i}^*\in N_{\varOmega _i}(x^*) \), such that:

$$\begin{aligned} \xi ^*=\sum _{i=1}^m\sum _{k\in I_{i0}(x^*)} \sigma _{ik}\varsigma _{ik}^*+\sum _{i=1}^m\tau _{i}^*. \end{aligned}$$
(10)

Then, one has:

$$\begin{aligned} \sigma _{0}\ge \sigma _{ik}, \end{aligned}$$
(11)

for any \(k\in I_{i0}(x^*)\). If (11) does not hold, then there exists \(\sigma _{ik_{0}}>\sigma _{0},k_{0}\in I_{i0}(x^*)\). It follows that:

$$\begin{aligned} \begin{aligned} \langle \xi ^* ,x^*-{\tilde{x}}\rangle&=\sum _{i=1}^m\left\langle \sum _{k\in I_{i0}(x^*)} \sigma _{ik}\varsigma _{ik}^*+\tau _{i}^*,x^*-{\tilde{x}}\right\rangle \\&=\sum _{i=1}^m\sum _{k\in I_{i0}(x^*)}\sigma _{ik} \big \langle \varsigma _{ik}^*, x^*-{\tilde{x}}\big \rangle \\&\quad +\sum _{i=1}^m\big \langle \tau _{i}^*, x^*-{\tilde{x}}\big \rangle , \end{aligned} \end{aligned}$$
(12)

where \({\tilde{x}}\in \varOmega \bigcap {\mathrm {int}}(S)\) is from Assumption 2. Since \(\varsigma _{ik}^*\in \partial g_{ik}(x^*)\), then by Definition 1, one has:

$$\begin{aligned} g_{ik}({\tilde{x}})-g_{ik}(x^*)\ge \langle \varsigma _{ik}^*,{\tilde{x}}-x^*\rangle , \end{aligned}$$
(13)

for any \(k\in I_{i0}(x^*),i\in \{1,2,\ldots ,m\}\). Besides, \(\tau _{i}^*\in N_{\varOmega _i}(x^*) \) and Lemma 4 imply that:

$$\begin{aligned} \langle \tau _{i}^*,{\tilde{x}}-x^*\rangle \le 0. \end{aligned}$$
(14)

for any \(i\in \{1,2,\ldots ,m\}\). Substituting (13) and (14) into (12), it can be immediately obtained that:

$$\begin{aligned} \begin{aligned} \langle \xi ^* ,x^*-{\tilde{x}}\rangle&\ge -\sum _{i=1}^m\sum _{k\in I_{i0}(x^*)}\sigma _{ik} g_{ik}({\tilde{x}})\\&\ge \sum _{i=1}^m\sum _{k\in I_{i0}(x^*)}\sigma _{ik} {\tilde{g}}\ge m\sigma _{ik_0} {\tilde{g}},\\ \end{aligned} \end{aligned}$$
(15)

which together with \(\sigma _{ik_{0}}>\sigma _{0},k_{0}\in I_{i0}(x^*)\) and \(\sigma _0=\frac{ML}{m{\tilde{g}}}\) mean:

$$\begin{aligned} \langle \xi ^* ,x^*-{\tilde{x}}\rangle > M L. \end{aligned}$$

It contradicts with the fact:

$$\begin{aligned} \langle \xi ^* ,x^*-{\tilde{x}}\rangle \le \Vert \xi ^*\Vert \cdot \Vert x^*-{\tilde{x}}\Vert \le ML. \end{aligned}$$

Thus, (11) holds and it delivers:

$$\begin{aligned} \begin{aligned} \xi ^*&=\sum _{i=1}^m\sum _{k\in I_{i0}(x^*)} \sigma _{ik}\varsigma _{ik}^*+\sum _{i=1}^m\tau _{i}^*\\&\in \sum _{i=1}^m\sum _{k\in I_{i0}(x^*)} \sigma _{ik}\partial g_{ik}(x^*)+\sum _{i=1}^mN_{\varOmega _i}(x^*) \\&\subseteq \sigma \sum _{i=1}^m\sum _{k\in I_{i0}(x^*)} [0,1]\partial g_{ik}(x^*)+N_{\varOmega }(x^*)\\&= \sigma \sum _{i=1}^m\partial G_{i}(x^*)+N_{\varOmega }(x^*), \end{aligned} \end{aligned}$$
(16)

for any \(\sigma >\sigma _0\). Moreover, \(-\xi ^*\in \sum _{i=1}^m \partial f_i(x^*)\) and (16) show:

$$\begin{aligned} \begin{aligned} 0\in \sum \limits _{i=1}^m \partial f_i(x^*)+\sigma \sum _{i=1}^m\partial G_{i}(x^*)+N_{\varOmega }(x^*), \end{aligned} \end{aligned}$$

which implies that \(x^*\) is an optimal solution to distributed optimization problem (5). It is not difficult to prove that the minimum of distributed optimization problem (5) is also the optimal solution to problem (2). Hence, the equivalence of distributed optimization problem (2) and (5) has been testified.

On the other hand, by the proof of Theorem 1 in [33], if \(\lambda >\lambda _0=m(L+\sigma _0)\), the optimal solutions of distributed optimization problem (5) also minimize the cost function in (3) and vice versa. Therefore, the distributed optimization problem (2) is equivalent to problem (3) with \(\sigma >\sigma _0\) and \(\lambda >\lambda _0\).\(\square \)

Remark 2

Penalty method is a widely adopted approach in solving optimization problems with sorts of constraints, such as [19, 28] and so on. By introducing penalty parameters, one can reduce the dimension of related algorithms. In this paper, we introduce double penalty parameters to reformulated original distributed optimization problem into a new one. Compared with the conventional continuous-time algorithm in [12], the model herein has the advantages of owning lower state variables.

According to Theorem 1, the equivalence of distributed optimization problem (2) and (3) are based on \(\varOmega _{i}=\varOmega _j,i,j\in \{1,2,\ldots ,m\}\). Let \(\varOmega _{i}=\varOmega \), where:

$$\begin{aligned} \varOmega \triangleq \{x\in {\mathbb {R}}^n| Ax_i=b\}, \end{aligned}$$

and \(A_i=A\in {\mathbb {R}}^{mn}\) and \(b_i=b\in {\mathbb {R}}^{m}\) for \(i=1,2,\ldots ,m\). In the following part of this paper, we will default this condition.

Projection-based continuous-time algorithm

To solve distributed optimization problem (3), a projection-based continuous-time algorithm is proposed as follows:

$$\begin{aligned} \begin{aligned}&{\dot{x}}_i(t)\in |v_i(t)|^{2-\frac{a}{b}}{\mathrm {sign}}(v_i(t))+|v_i(t)|^{\frac{a}{b}}{\mathrm {sign}}(v_i(t))\\&~~~~~~~~~-u_i(t)+|u_i(t)|{\mathrm {sign}}(v_i(t)), \end{aligned} \end{aligned}$$
(17)

where

$$\begin{aligned} \begin{aligned}&u_i(t)=\partial f_{i}(x_i(t))+\sigma \partial G_i(x_i(t)) +2\lambda \sum \limits _{j\in {\mathcal {N}}_i}\partial \Vert x_i(t)-x_j(t)\Vert \\&v_i(t)=\varPi _{\varOmega }(x_i(t))-x_i(t); \end{aligned} \end{aligned}$$

a, b are positive odds and satisfy \(a<b\), \(\partial f_i(\cdot ),\partial G_i(\cdot )\) and \(\partial \Vert \cdot \Vert \) are subdifferentials of corresponding functions, \(\sigma ,\lambda >0\) are penalty parameters, and \(\varPi _{\varOmega }\) represent the projection operator on the sets \(\varOmega =\{x\in {\mathbb {R}}^n| Ax_i=b\}\). It is worth noticing \(|u_i|=\{|\xi _i|:\xi _i\in u_i\}\) for \(i=1,2,\ldots ,m\) in (17).

Remark 3

The continuous-time algorithm (17) is mainly composed of the following two parts:

(1): The terms \(|v_i(t)|^{2-\frac{a}{b}}{\mathrm {sign}}(v_i(t))+|v_i(t)|^{\frac{a}{b}}{\mathrm {sign}}(v_i(t))\) and \(|u_i(t)|{\mathrm {sign}}(v_i(t))\) are utilized to guarantee the states of continuous-time algorithm (17) will enter \(\varOmega ,i=1,2,\ldots ,m\) in fixed time.

(2): The terms \(-\partial f_{i}(x_i(t))-\sigma \partial G_i(x_i(t))-2\lambda \) \(\sum _{j\in {\mathcal {N}}_i}\partial \Vert x_i(t)-x_j(t)\Vert \) are the subdifferentials of objective function in distributed optimization problem (3). They can be regarded as a gradient descent method and ensure the states of continuous-time algorithm (17) converge to an optimal solution of distributed optimization problem (3).

The projection-based continuous-time algorithm (17) can be also expressed by the following form:

$$\begin{aligned} \begin{aligned}&\dot{{\mathbf {x}}}(t)\in |{\mathbf {v}}(t)|^{2-\frac{a}{b}}\mathrm {\mathbf {sign}}({\mathbf {v}}(t))+|{\mathbf {v}}(t)|^{\frac{a}{b}}\mathrm {\mathbf {sign}}({\mathbf {v}}(t))\\&~~~~~~~~~-{\mathbf {u}}(t)+|{\mathbf {u}}(t)|\mathrm {\mathbf {sign}}({\mathbf {v}}(t)), \end{aligned} \end{aligned}$$
(18)

where \({\mathbf {x}}={\mathrm {col}}\{x_1,x_2,\ldots ,x_m\}\), \({\mathbf {v}}={\mathrm {col}}\{v_1,v_2,\ldots ,v_m\}\) and \({\mathbf {u}}={\mathrm {col}}\{u_1,u_2,\ldots ,u_m\}\). The continuous-time algorithm (17) is the distributed form of (18) and it can be seen that algorithm (17) is fully distributed.

Proposition 4

The equilibrium point of continuous-time algorithm (18) is an optimal solution to distributed optimization problem (3) and vice versa.

Convergence analysis

In this part, with the help of Lyapunov method and above preliminaries, we will study the convergence of continuous-time algorithm (17).

Theorem 2

Let Assumptions 1–3 hold. For any initial point \({\mathbf {x}}(0)={\mathbf {x}}^0={\mathrm {col}}\{x_1^{(0)},x_2^{(0)},\ldots ,x_m^{(0)}\}\in {\mathbb {R}}^{mn}\), the state solution \({\mathbf {x}}(t)\) of neural network (18) will converge to \(\varvec{\Omega }=\varOmega _1\times \varOmega _2\times \cdots \times \varOmega _m\) and stays in it in fixed time.

Proof

Suppose that \({\mathbf {x}}(t)={\mathrm {col}}\{x_1(t),x_2(t),\ldots ,x_m(t)\}\) is the solution with initial point \({\mathbf {x}}^{(0)}\in {\mathbb {R}}^n\). By the definition of subdifferential, there exist \(\eta _i(t)\in \partial f_{i}(x_i(t))\), \(\gamma _i (t)\in \partial G_i(x_i(t))\), and \(\theta _i(t)\in \sum _{j\in {\mathcal {N}}_i}\partial \Vert x_i(t)-x_j(t)\Vert \), such that:

$$\begin{aligned} \xi _i(t)=\eta _i(t)+\sigma \gamma _i (t)+ 2\lambda \theta _i(t), \end{aligned}$$
(19)

for \({\mathrm {a.e.}}~t\ge 0,\) where \(\xi _i(t)\in u_i(t)\) is a vector.

Consider the Lyapunov function:

$$\begin{aligned} V_{i}(x_i)=\frac{1}{2}(\varPi _{\varOmega }(x_i)-x_i)^2. \end{aligned}$$

According to Lemma 5 and (19), we can take the derivative of \(V_i(x)\) along \(x_i(t)\) as follows:

$$\begin{aligned} \begin{aligned}&\frac{\mathrm {d}}{\mathrm {d}t}V_{i}(x_i(t))\\&\quad =-\langle \varPi _{\varOmega }(x_i(t))-x_i(t), {\dot{x}}_i(t) \rangle \\&\quad =-\big \langle v_i(t), -\xi _i(t)+|\xi _i(t)|{\mathrm {sign}}(v_i(t))\big \rangle \\&\quad \qquad -|v_i(t)|^{3-\frac{a}{b}}-|v_i(t)|^{1+\frac{a}{b}}, \end{aligned} \end{aligned}$$
(20)

for \({\mathrm {a.e.}}~t\ge 0\).

Since \(\langle v_i(t), \xi _i(t)\rangle -|\xi _i(t)||v_i(t)|\le 0 \), then it follows from (20) that:

$$\begin{aligned} \begin{aligned}&\frac{\mathrm {d}}{\mathrm {d}t}V_{i}(x_i(t))\\&\quad \le -|v_i(t)|^{3-\frac{a}{b}}-|v_i(t)|^{1+\frac{a}{b}}\\&\quad =-(v_i^2(t))^{\frac{3b-a}{2b}}-(v_i^2(t))^{\frac{a+b}{2b}}\\&\quad =-(2V_{i}(x_i(t)))^{\frac{3b-a}{2b}}-(2V_{i}(x_i(t)))^{\frac{a+b}{2b}}. \end{aligned} \end{aligned}$$
(21)

Let \(\rho _i(x_i)=\sqrt{2V_i(x_i)}\), and then, it can be immediately obtained that:

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}\rho _{i}(x_i(t))\le -\big (\rho _{i}(x_i(t))\big )^{2-\frac{a}{b}}-\big (\rho _{i}(x_i(t))\big )^{\frac{a}{b}}. \end{aligned} \end{aligned}$$
(22)

By Lemma 3, we have \(\lim \limits _{t\rightarrow T}\rho _{i}(x_i(t))=0\), which also implies \(\lim _{t\rightarrow T}V_{i}(x_i(t))=0\) for \(i=1,2,..,m\). Thus, we have:

$$\begin{aligned} \varPi _{\varOmega }(x_i^*)=x_i^*, \end{aligned}$$

for \(i=1,2,..,m\), which means for any initial point \({\mathbf {x}}^0={\mathrm {col}}\{x_1^{(0)},x_2^{(0)},\ldots ,x_m^{(0)}\}\in {\mathbb {R}}^{mn}\), \({\mathbf {x}}(t)\) will enter the set in fixed time and T is bounded by:

$$\begin{aligned} T\le \frac{b\pi }{2(b-a)}. \end{aligned}$$

\(\square \)

Remark 4

It is worth noting that the property of entering one of the constraints or feasible region is possessed by many continuous-time algorithms for solving optimization problems, such as [8, 11, 19, 34]. This proposition guarantees the continuous-time algorithm (17) which has the advantages of simplifying the distributed optimization problems by ignoring one of the constraints once the states enter this set. Compared with [11], the continuous-time algorithm (17) in constructed and fixed entering time is obtained without calculating \((AA^\mathrm {T})^{-1}\), which is easier to be applied in engineering fields.

Lemma 6

[2] (Opial) Suppose that \(x:[0,+\infty ) \) is a curve. Then, x(t) will be convergent to a point in \(C\subseteq {\mathbb {R}}^n\) (\(C\ne \emptyset \)) as \(t\rightarrow +\infty \) if and only if the following two tips are satisfied

(1) All accumulation points of \(x(\cdot )\) are in C;

(2) For any \(x^*\in C\), \(\lim _{t\rightarrow +\infty }\Vert x(t)-x^*\Vert \) exists.

Theorem 3

Assume that Assumptions 1–3 hold, then for any initial point \({\mathbf {x}}(0)={\mathbf {x}}^0={\mathrm {col}}\{x_1^{(0)},x_2^{(0)},\ldots ,x_m^{(0)}\}\in {\mathbb {R}}^{mn}\), the state solution \({\mathbf {x}}(t)\) of neural network (17) will converge to its equilibrium point.

Proof

Suppose \({\mathbf {x}}^*={\mathrm {col}}\{x_1^{*},x_2^{*},\ldots ,x_m^{*}\}\) and \(C^*\) are an equilibrium point and equilibrium point set of neural network (18). According to Theorem 2, from initial point \({\mathbf {x}}^0={\mathrm {col}}\{x_1^{(0)},x_2^{(0)},\ldots ,x_m^{(0)}\}\in {\mathbb {R}}^{mn}\), the state solution \({\mathbf {x}}(t)\) of neural network (17) will enter \(\varvec{\Omega }\) in fixed time. And the fixed time \(T\le \frac{b\pi }{2(b-a)}.\) In other words, we can immediately get:

$$\begin{aligned} x_i(t)=\varPi _{\varOmega }(x_i(t)), \end{aligned}$$

for \(t\ge T\). Hence, we have \(v_i(t)= 0, t\ge T\).

Then, the neural network can be simplified as:

$$\begin{aligned} \begin{aligned}&{\dot{x}}_i(t)\in -u_i(t), \end{aligned} \end{aligned}$$
(23)

for \(t\ge T\), where \(u_i(t)\) is from (17). In the following part, we will study the convergence of continuous-time algorithm (23).

Consider the Lyapunov function:

$$\begin{aligned} W(t)=\frac{1}{2}\sum _{i=1}^m\Vert x_i(t)-x_i^*\Vert ^2, \end{aligned}$$
(24)

on \(t\in [T,+\infty )\). Taking the derivative of W(t), there exist \(\eta _i(t)\in \partial f_{i}(x_i(t))\), \(\gamma _i (t)\in \partial G_i(x_i(t))\) and \(\theta _i(t)\in \sum _{j\in {\mathcal {N}}_i}\partial \Vert x_i(t)-x_j(t)\Vert \), such that:

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}W(t)=&\sum _{i=1}^m\langle x_i(t)-x_i^*,{\dot{x}}_i(t)\rangle \\ =&-\sum _{i=1}^m\langle x_i(t)-x_i^*,\eta _i(t)\rangle - \sigma \sum _{i=1}^m\langle x_i(t)\\&-x_i^*,\gamma _i (t)\rangle -2 \lambda \sum _{i=1}^m\sum \limits _{j\in {\mathcal {N}}_i}\langle x_i(t)-x_i^*,\theta _i(t)\rangle \end{aligned} \end{aligned}$$
(25)

for \({\mathrm {a.e.}}~t\ge T\).

Since \({\mathbf {x}}^*\) is an equilibrium point of algorithm (18), it is also an equilibrium point of algorithm (23). Thus, there exist \(\eta _i^*\in \partial f_{i}(x_i^*)\), \(\gamma _i^*\in \partial G_i(x_i^*)\), and \(\theta _i^*\in \sum \limits _{j\in {\mathcal {N}}_i}\partial \Vert x_i^*-x_j^*\Vert \), such that:

$$\begin{aligned} \begin{aligned} 0=\eta _i^*+\sigma \gamma _i^*+2\lambda \theta _i^*, \end{aligned} \end{aligned}$$
(26)

for \(i=1,2,\ldots ,m\), which means that:

$$\begin{aligned} \begin{aligned} 0=\sum _{i=1}^m\langle x_i(t)-x_i^*, \eta _i^*+\sigma \gamma _i^*+2\lambda \theta _i^*\rangle . \end{aligned} \end{aligned}$$
(27)

Combining (25) and (27), we have:

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}W(t)=&-\sum _{i=1}^m\langle x_i(t)-x_i^*,\eta _i(t)-\eta _i^*)\rangle \\&-\sigma \sum _{i=1}^m\langle x_i(t)-x_i^*,\gamma _i (t)-\gamma _i^*\rangle \\&-2 \lambda \sum _{i=1}^m\sum \limits _{j\in {\mathcal {N}}_i}\langle x_i(t)-x_i^*,\theta _i(t)-\theta _i^*\rangle . \end{aligned} \end{aligned}$$
(28)

Due to the fact that \(f_i(x_i)\), \(G_i(x_i)\), and \(\sum _{j\in {\mathcal {N}}_i}\partial \Vert x_i-x_j\Vert \) are convex functions, then by Lemma 1, it follows:

$$\begin{aligned} \begin{aligned}&\langle x_i(t)-x_i^*,\eta _i(t)-\eta _i^*\rangle \ge 0,\\&\langle x_i(t)-x_i^*,\gamma _i (t)-\gamma _i^*\rangle \ge 0,\\&\sum \limits _{j\in {\mathcal {N}}_i}\langle x_i(t)-x_i^*,\theta _i(t)-\theta _i^*\rangle \ge 0, \end{aligned} \end{aligned}$$

for \({\mathrm {a.e. }}~t\ge T\) and \(i=1,2,\ldots ,m\).

Hence, it can be immediately obtained by (28) that:

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}W(t)\le 0, \end{aligned}$$

for \({\mathrm {a.e. }}~t\ge T\). Because of the nonnegativeness of \(\sum _{i=1}^m\Vert x_i(t)-x_i^*\Vert ^2\), we can declare that \(\lim _{t\rightarrow +\infty }W(t)\) exists.

On the other hand, for the convenience of discussion, let:

$$\begin{aligned} \begin{aligned} K({\mathbf {x}})=\sum _{i=1}^m \Big (f_i(x_i)+\sigma G_i(x_i)+\lambda \sum _{j\in {\mathcal {N}}_i}\Vert x_i-x_j\Vert \Big ), \end{aligned} \end{aligned}$$
(29)

where \({\mathbf {x}}={\mathrm {col}}\{x_1,x_2,\ldots ,x_m\}\) and \( \varvec{\Omega }=\varOmega _1\times \varOmega _2\times \cdots \times \varOmega _m\). It is clear that \(\liminf _{t\rightarrow +\infty }K({\mathbf {x}}(t))\ge \min _{{\mathbf {x}}\in \varvec{\Omega }}\{K({\mathbf {x}})\}. \) If \( \liminf _{t\rightarrow +\infty }K({\mathbf {x}}(t))>\min _{{\mathbf {x}}\in \varvec{\Omega }}\{K({\mathbf {x}})\}, \) which means that, for any \(\varepsilon >0\), there exists \({\tilde{T}}>T\), such that:

$$\begin{aligned} K({\mathbf {x}}(t))>\min \limits _{{\mathbf {x}}\in \varvec{\Omega }}\{K({\mathbf {x}})\}+\varepsilon . \end{aligned}$$
(30)
Table 1 Comparison of algorithms for solving distributed optimization problems
Full size table

Since \({\mathbf {x}}^*={\mathrm {col}}\{x_1^{*},x_2^{*},\ldots ,x_m^{*}\}\) is an equilibrium point of continuous-time algorithm (18), by Proposition 4, \({\mathbf {x}}^*\) is also an optimal solution to distributed optimization problem (3). It is obvious that:

$$\begin{aligned} K({\mathbf {x}}^*)=\min \limits _{{\mathbf {x}}\in \varvec{\Omega }}\{K({\mathbf {x}})\}. \end{aligned}$$

For the reason that \(x_i(t)\in \varOmega \) for \(t\ge T\), then \(x(t)\in \varvec{\Omega }\) for \(t\ge {\tilde{T}}>T\). By (25) and (30), we have:

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}W(t)\le \min \limits _{x\in \varvec{\Omega }}\{K({\mathbf {x}})\}-K({\mathbf {x}}(t)) \le -\varepsilon \end{aligned}$$
(31)

for \(t\ge {\tilde{T}}\). The first inequality holds by Definition 1, which is utilized to demonstrate that:

$$\begin{aligned} \begin{aligned}&\langle x_i-x_i^*,\eta _i\rangle \le f_i(x_i^*)-f_i(x_i),\\&\langle x_i-x_i^*,\gamma _i\rangle \le G_i(x_i^*)-G_i(x_i),\\&2\sum \limits _{j\in {\mathcal {N}}_i}\langle x_i-x_i^*,\theta _i\rangle \le \sum \limits _{j\in {\mathcal {N}}_i}\big (\Vert x_i^*-x_j^*\Vert -\Vert x_i-x_j\Vert \big ), \end{aligned} \end{aligned}$$

where \(\eta _i\in \partial f_{i}(x_i)\), \(\gamma _i\in \partial G_i(x_i)\), and \(\theta _i\in \sum _{j\in {\mathcal {N}}_i}\partial \Vert x_i-x_j\Vert \). By calculating integral of (31) from \({\tilde{T}}\) to \(+\infty \), we have:

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty }\left( \sum _{i=1}^m\Vert x_i(t)-x_i^*\Vert ^2\right) =-\infty , \end{aligned}$$
(32)

which leads to a contradiction. Hence, we obtain \(\liminf _{t\rightarrow +\infty }K({\mathbf {x}}(t))=\min _{{\mathbf {x}}\in \varvec{\Omega }}\{K({\mathbf {x}})\}. \)

Thus, there exists a time sequence \(\{t_n\}\), such that:

$$\begin{aligned} \lim \limits _{n\rightarrow +\infty }K({\mathbf {x}}(t_n))=\min \limits _{x\in \varvec{\Omega }}\{K({\mathbf {x}})\}, \end{aligned}$$

which delivers by (31) that \(W(t_n)\rightarrow 0\) as \(n\rightarrow +\infty \). Since \(\lim _{t\rightarrow +\infty }W(t)\) exists, we can get:

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty }W(t)=\lim \limits _{t\rightarrow +\infty }\left( \frac{1}{2}\sum _{i=1}^m\Vert x_i(t)-x_i^*\Vert ^2\right) =0. \end{aligned}$$

Therefore, \({\mathbf {x}}^*\in C^*\) is an accumulation of \({\mathbf {x}}(t)\). By Lemma 6, it can be concluded that \({\mathbf {x}}(t)\) of neural network (18) will converge to its equilibrium point. \(\square \)

According to Proposition 4, the equilibrium point of neural neural network (17) is an optimal solution to distributed optimization problem (2). Then, we have the following conclusion:

Corollary 1

Assume that Assumptions 1–3 hold, then for any initial point \({\mathbf {x}}^0={\mathrm {col}}\{x_1^{(0)},x_2^{(0)},\ldots ,x_m^{(0)}\}\in {\mathbb {R}}^n\) and \(\sigma>\sigma _0,\lambda >\lambda _0\), then the states \({\mathbf {x}}(t)\) of continuous-time algorithm (18) will converge to an optimal solution to distributed optimization problem (2).

Remark 5

In [12], distributed optimization problem (2) has been studied under the similar assumptions in this paper. With the help of Laplacian matrix, authors in [12] proposed a differential inclusion system and proved the consensus and convergence of agents. Different from [12], the continuous-time algorithm (17) achieves convergence by a transformed distributed optimization problem. Compared with algorithm in [12], continuous-time algorithm (17) has fewer state variables, which is more preferable in application fields. Here, we also introduce some algorithms to solve distributed optimization problems in Table 1 to make detailed comparisons.

Simulations

This section presents two numerical examples to show the viability of the conclusion above and the projection-based continuous-time algorithm. Details are given as follows:

Fig. 1
figure 1

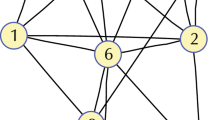
Interaction topology of the three-agent system in Example 1

Full size image
Fig. 2
figure 2

Trajectories \((x_{i,1},x_{i,2},x_{i,3})\) of the states of continuous-time algorithm (17)

Full size image
Fig. 3
figure 3

Transient behaviors of agents’ state solutions of continuous-time algorithm (17) in Example 1

Full size image

Example 1

A three-agent-system communicating over an undirected connected graph is considered in this example and its interaction topology is presented in Fig. 1. The distributed optimization problem is depicted as:

$$\begin{aligned} \begin{aligned} \min ~&\sum _{i=1}^3 f_i(x_i)\\ {\mathrm {s.t.}}~~&x_{i,1}-2x_{i,2}+x_{i,3}=1 \\ ~~~~~~&x_{i,1}^2+x_{i,2}^2+x_{i,3}^2-8\le 0, \end{aligned} \end{aligned}$$
(33)

where \(x_i=(x_{i,1},x_{i,2},x_{i,3})^\mathrm {T}\in {\mathbb {R}}^3\) is the decision variable of agent i. And the local cost function of distributed optimization problem (33) is defined as:

$$\begin{aligned} f_i(x_i)=M^{\mathrm {T}}x_{i}+q,\quad i=1,2,3, \end{aligned}$$
(34)

where \(q=2\) is a constant and \(M=(1,3,4)^{\mathrm {T}}\). The equality constraint set is \(\varOmega =\{x_i\in {\mathbb {R}}^3: x_{i,1}-2x_{i,2}+x_{i,3}=1\}\) to be specific. It is obvious that \(A=(1,-2,3)\) is a full-row-rank matrix and \(b=1\). In addition, the inequality constraint functions \(g_i(x_i)=x_{i,1}^2+x_{i,2}^2+x_{i,3}^2-8,i=1,2,3.\) The sets \(S_i=\{x_i:g_i(x_i)\le 0\}\) are nonempty and satisfy that \({\mathrm {int}}(\varOmega )\bigcap S_i\ne \emptyset \). Also, as the gradient of \(f_i(x_i)\) can be calculated as \(\nabla f_i(x_i)=M=[1,3,4]^{\mathrm {T}},i=1,2,3\), apparently, it is bounded on the equality constraint set. Thus, all assumptions in this paper are satisfied.

Simulation results are presented in Figs. 2 and 3, which shows the trajectories of \((x_{i,1},x_{i,2},x_{i,3})^{\mathrm {T}}\) of states with random initial values \(x_1^{(0)}=(2,1,-1)^{\mathrm {T}}\), \(x_2^{(0)}=(4,-3,2)^{\mathrm {T}}\) and \(x_3^{(0)}=(1,2,-2.4)^{\mathrm {T}}\). The colored area in Fig. 2 is the feasible region of distributed optimization problem (33) and the above-mentioned initial points are marked as black ones. Besides, the star in red means an optimal solution of distributed optimization problem (33). It is easy to find that the state solutions of continuous-time algorithm (17) enter the equality constraint in finite time and stay in it thereafter. After that, the trajectories of all the three agents converge to the equilibrium point \((-0.3,-2.5,-1.233)^{\mathrm {T}}\). The transient behaviors of the three agents’ solutions of continuous-time algorithm (17) are also presented in Fig. 3.

Remark 6

In [9], Jia et al. proposed a generalized neural network for solving distributed optimization problems with inequality constraints only. Thus, the model cannot be immediately applied into distributed optimization problem (33) in Example 1. On the other hand, the continuous-time algorithm (17) is also suitable for distributed optimization problems in [9] under the condition that there is no equality constraint of distributed optimization problem (2) or the equality constraints are satisfied after the fixed time given in Theorem 2. Therefore, compared with neural network in [9], continuous-time algorithm (17) is more flexible when solving different distributed optimization problems.

Fig. 4
figure 4

Interaction topology of the six-agent system in Example 2

Full size image
Fig. 5
figure 5

Transient behaviors of the states of continuous-time algorithm (17) of the six agents in Example 2

Full size image

Example 2

Consider a six-agent network with the communication topology shown in Fig. 4. And the distributed optimization problem is given as follows:

$$\begin{aligned} \begin{aligned} \min ~&\sum _{i=1}^6 f_i(x_i)\\ {\mathrm {s.t.}}~~&x_{i,1}+x_{i,2}-2x_{i,3}=3, \\ ~~~~~~&x_{i,1}^2+x_{i,2}^2+ix_{i,3}^2-5\le 0. \end{aligned} \end{aligned}$$
(35)

The local cost functions of distributed optimization problem (35) are given as:

$$\begin{aligned} f_i(x_i)={\mathcal {M}}_i^{\mathrm {T}}x_i+q,\quad i=1,2,3,4,5,6, \end{aligned}$$
(36)

where \({\mathcal {M}}_i=(1,3,i)^\mathrm {T}\) is relevant to each agent. Calculating the gradient of \(f_i(x_i)\), one derives \(\nabla f_i(x_i)={\mathcal {M}}_i\). Despite the variability of the local cost functions, the boundedness of its gradient over the equality constraint set can still be guaranteed with a limited number of agents. It can be seen that \(A=(1,1,-2)\) is a full-row-rank matrix and:

$$\begin{aligned} g_i(x_i)=x_{i,1}^2+x_{i,2}^2+ix_{i,3}^2-5. \end{aligned}$$

Apparently, distributed optimization problem (35) meets the requirements of the conditions assumed in this paper, for instance, the boundedness of the inequality constraint set and the nonemptiness of the feasible region.

The transient behaviors of the states of continuous-time algorithm (17) are presented in detail in Fig. 5, in which \(x_{i,j}(t)\) represents the trajectories of states. Starting from initial points \(x_1^{(0)}=(1.2,-2,-2.2)^{\mathrm {T}}\), \(x_2^{(0)}=(0.8,-2.5,-2.4)^{\mathrm {T}}\), \(x_3^{(0)}=(0.5,-2.8,-2.6)^{\mathrm {T}}\), \(x_4^{(0)}=(-0.5,-3,-2.8)^{\mathrm {T}}\), \(x_5^{(0)}=(-0.2,-3.3,-3.2)^{\mathrm {T}}\), and \(x_6^{(0)}=(-0.7,-3.5,-3.5)^{\mathrm {T}}\), the states of continuous-time algorithm (17) converge to an optimal solution \({\tilde{x}}=(-1.447,-2.509,-3.478)^{\mathrm {T}}\) of (35). The detailed movements of the three components of the decision variables are also presented in subplots of Fig. 5.

Conclusions

In this paper, a projection-based continuous-time algorithm is proposed to solve distributed optimization problems with equality and inequality constraints over multi-agent systems. By exact penalty method, the distributed optimization problem is reformulated to a new one without inequality constraints and consensus constraints. It is proved that from any initial points, the states of continuous-time algorithm will enter the equality constraint set of the transformed distributed optimization problem in fixed time. And states of continuous-time algorithm are proved to be convergent to an optimal solution of the original distributed optimization problem. Compared with existed models and approaches, the continuous-time algorithm has the advantages of owning fewer state variables. Besides, the states of continuous-time algorithm can find an optimal solution of distributed optimization problem under mild assumptions. Since the penalty method has the weakness of calculating penalty parameters, the application of continuous-time algorithm may be limited in solving more complex distributed optimization problems. In our future work, we will consider to construct a algorithm independent of penalty method.