Knowledge-guided multiobjective particle swarm optimization with fusion learning strategies

Abstract

Multiobjective particle swarm optimization (MOPSO) algorithm faces the difficulty of prematurity and insufficient diversity due to the selection of inappropriate leaders and inefficient evolution strategies. Therefore, to circumvent the rapid loss of population diversity and premature convergence in MOPSO, this paper proposes a knowledge-guided multiobjective particle swarm optimization using fusion learning strategies (KGMOPSO), in which an improved leadership selection strategy based on knowledge utilization is presented to select the appropriate global leader for improving the convergence ability of the algorithm. Furthermore, the similarity between different individuals is dynamically measured to detect the diversity of the current population, and a diversity-enhanced learning strategy is proposed to prevent the rapid loss of population diversity. Additionally, a maximum and minimum crowding distance strategy is employed to obtain excellent nondominated solutions. The proposed KGMOPSO algorithm is evaluated by comparisons with the existing state-of-the-art multiobjective optimization algorithms on the ZDT and DTLZ test instances. Experimental results illustrate that KGMOPSO is superior to other multiobjective algorithms with regard to solution quality and diversity maintenance.

Introduction

Multiobjective optimization problems (MOPs) are complex optimization problems that are widely used but difficult to solve in the real world. They have gradually garnered the attention of researchers due to their challenging nature in that they require the efficient and effective optimization of multiple conflicting objectives simultaneously. Generally, for single-objective optimization problems (SOPs), the goal is to find a global optimal solution. However, there is no absolute optimal solution for MOPs because the optimization of one objective may deteriorate the performance of other objectives. In contrast, The goal of solving MOPs is to obtain a set of equivalent tradeoff solutions, which are also called Pareto optimal solutions. Currently, multiobjective optimization is a hotspot in the field of artificial intelligence and evolutionary computing. To solve MOPs, many multiobjective algorithms are studied by researchers. Some popular and advanced algorithms include NSGA-II [1], PREA [2], MOEA/D [3], SPEA/R [4], NMPSO [5], etc. Recent research on multiobjective algorithms can be found in [6].

In recent years, a well-supported superiority encourages the development of the PSO algorithm. It has been well studied and successfully applied to address SOPs due to its advantages of fast convergence and simple nature. PSO has shown excellent optimization performance and potential in SOPs. Meanwhile, it also shows promising optimization performance in tackling MOPs. In addition, PSO is performed to solve MOPs and it is successfully applied to robot path planning [7], renewable energy systems [8], scientific workflow scheduling [9], image classification [10] and other problems [11, 12]. These theories and applications promote the research of PSO algorithm in the field of MOPs.

Different from the challenges faced when addressing SOPs, two particular issues need to be solved while solving MOPs using the PSO algorithm. The first problem is how to select and update the appropriate individual best position (Pbest) and global best position (Gbest) of the particles. In PSO, Pbest stores the historically best individual experience, and Gbest reflects the cooperation and sharing of information among particles. They jointly guide the evolutionary direction of the whole population and are great influences on the performance of the algorithm. Therefore, it is important to reasonably select the right Pbest and Gbest. The second problem is how to balance the convergence of the algorithm and the diversity of the population. Although PSO exhibits a rapid convergence speed, it easily falls into a local optimal solution due to the rapid loss of population diversity in the later stage of the algorithm. Therefore, the key to improve the performance of PSO is finding a reasonable balance between the convergence of the algorithm and the diversity of the population [13]. In recent years, knowledge-guided learning strategies have become a research hotspot. It is essential to use previous experience or information to guide the learning and evolution of the current population. For the PSO algorithm, it is necessary to carefully consider how to make use of the evolution information of multiple superior particles to promote the coevolution among population to obtain better optimization results.

In recent years, a variety of multiobjective PSO algorithms have been proposed to address the above two problems. Coello et al. first proposed the original multiobjective PSO algorithm [14]. In this algorithm, the Pareto dominance concept is used to determine the proper Gbest and Pbest of the particles, and an external archive is adopted to store the nondominated solutions of the population. The experiments show that this algorithm is effective for solving MOPs, but it experiences difficulties when address MOPs with complex landscapes. The existing multiobjective PSO algorithms can be classified into the following two categories. The first category is based on the Pareto dominance. In this strategy, several different technical schemes are used to randomly select the Gbest to guide the population toward the Pareto-optimal front. Agrawal et al. chose the Gbest from an external archive by using a roulette selection strategy. However, this method is random and inefficient [15]. Sierra et al. developed the OMOPSO algorithm by using the concepts of $\epsilon$-dominance and crowding distance to select the appropriate Gbest [16]. However, this algorithm easily causes the swarm expansion problem. To avoid this problem, Nebro et al. proposed a velocity-constrained multiobjective PSO algorithm called SMPSO. In this algorithm, an effective velocity constraint strategy is proposed to prevent particles from moving out of the search space [17]. Wang et al. proposed a multiobjective PSO algorithm using a parallel cell coordinate system, named pccsAMOPSO. In this algorithm, the feedback information obtained from the evolutionary process are used to dynamically adjust the exploration and development capabilities of the algorithm [18]. Zhang et al. proposed the CMOPSO algorithm in which a competitive mechanism [19], motivated by the competitive swarm optimizer [20], is employed to replace the velocity updating equation of the PSO algorithm. The leader is selected based on pairwise comparison and the random angle selection approach. The results show that CMOPSO is highly competitive with other PSO algorithms. In addition, other technologies have also been proposed and applied to the improvement of multiobjective PSO algorithms, such as the ranking-based strategy [21], the grid-based approach [22] and the reference-point-based domination method [23, 24].

The second category is based on decomposition strategy, which follows the MOEA/D framework. In this strategy, an MOP is decomposed into a set of SOPs. Therefore, the traditional PSO algorithm can be directly applied to address MOPs. Three typical multiobjective PSO algorithms are MOPSO/D [25], SDMOPSO [26], and dMOPSO [27]. Dai et al. proposed a novel decomposition-based multiobjective PSO (MPSO/D) algorithm for solving MOPs [28]. The direction vector is used to divide the target space of the problem into subregions. The crowding distance is used to select the appropriate leader, and the neighbors of a particle are employed to determine the Gbest. Research illustrates that MPSO/D is superior to NSGAII and MOEA/D in terms of convergence and diversity. Liu et al. proposed a dynamic multipopulation particle swarm optimization algorithm based on decomposition and prediction behavior, which is called DP-DMPPSO [29]. In this algorithm, each optimization objective is independently optimized and the optimal information is shared among the entire population. An objective space decomposition-based strategy is proposed to update the external archive. Furthermore, a prediction technique is used to accelerate the convergence speed of the population. Experiments show that this algorithm is highly competitive with other PSO algorithms. In [30], an MP/SO/DD with different ideal points for each reference vector was proposed for MOPs. The ideal point on the reference vector is designed to force the population to converge to the Pareto-optimal front more quickly. However, as reported in [31, 32], the lack of dominance may cause the multiobjective PSO algorithm to not be well and uniformly distributed to the Pareto-optimal front in some MOPs with complex landscape. Therefore, some multiobjective PSOs that combine dominance and decomposition strategies are gradually being studied to balance the global and local search of PSO. Moubayed et al. proposed a D2MOPSO algorithm that incorporates dominance with decomposition strategy. The decomposition strategy is used to transform the MOPs into a set of subproblems, and the dominance plays an essential role of building an external archive to select the right leader. After listening to the advantages of these two strategies, the algorithm shows strong competitiveness and efficiency [33].

As mentioned above, the main concerns of the improved MOPSO algorithm are to tackle the problems of premature convergence and insufficient diversity, and to select promising leaders from the external archive. The diversity of the population plays an essential role in the performance of the algorithm. Higher diversity in the early stage of the algorithm can improve the global search ability of the algorithm, and in the later stage of the algorithm, it is also very indispensable to improve the local search ability of the algorithm. Most of the existing MOPSO algorithms suffer from insufficient population diversity or high computational cost. Therefore, research on to obtain a uniformly distributed Pareto optimal set at a low computational cost is very promising. Motivated by the above analysis, in this paper, a knowledge-guided multiobjective particle swarm optimization using multiple learning strategies is proposed to address MOPs. The main novel aspects of this work are summarized as follows.

• A leader selection strategy based on the angle of the reference point is adopted to select the global leader corresponding to each individual.

• The two-stage evolutionary strategy based on neighborhood knowledge search is incorporated into KGMOPSO. In stage I, the evolutionary information of the promising leader selected from the external archive is used to accelerate the convergence performance of the algorithm. In stage II, the previous best experience of each particle is used to guide the population evolution and balance exploration and development capabilities.

• A dynamic individual similarity detection strategy and a diversity enhancement strategy are incorporated into KGMOPSO to prevent premature convergence of the algorithm and rapid loss of diversity.

• A maximum and minimum crowding distance strategy is developed to enable updating of the external archive to obtain an accurate and uniform Pareto-optimal set.

The remainder of this paper is organized as follows. “Related work” introduces related works, including the basic concepts related to MOPs, Pareto dominance and fundamental PSO algorithm. In “The proposed KGMOPSO”, the detailed explanation of KGMOPSO is given. The experimental results and comparison analysis are described in “Experimental studies”. Finally, the conclusions are provided in “Conclusion”.

Related work

Multiobjective optimization problems

In general, an MOP can be defined as

$$\begin{aligned} \begin{aligned}&\mathrm{{Minimize}} \quad {F(x)}=({f_{1}(x)},{f_{2}(x)}, \ldots ,{f_{M}}(x))^\mathrm{{T}} \\&\mathrm{{Subject}}\;\mathrm{{to}}: \; \begin{array}{l} {g_i}(x) \ge 0,i = 1,2, \ldots ,{N_I}\\ {h_j}(x) = 0,j = 1,2, \ldots ,{N_E} \end{array} \end{aligned} \end{aligned}$$

(1)

where x = ($x_1$, $x_2$, $\ldots$ , $x_D$) $\in$ $\Omega$, $\Omega$ represents the decision space, D is the dimension of decision vector x, M represents the number of optimization objectives, $N_\mathrm{{I}}$ and $N_\mathrm{{E}}$ are the number of inequality constraints and equality constraints, respectively. For MOPs, because there are conflicts among the optimization objectives, the goal is to obtain a set of compromise solutions determined by the Pareto dominance relationship [34].

A solution vector x strictly dominates the solution vector y, expressed as x $\prec$ y , if and only if $\forall$ i $\in$ 1, 2, $\ldots$, M, $f_{i}(x)$ $\le$ $f_{i}(y)$ and at least the following holds: $\exists$ j $\in$ 1, 2, $\ldots$, M, $f_{i}(x)$ < $f_{i}(y)$. If there is no solution x dominated by any other solution y, then this solution x is considered to be the Pareto-optimal solution. The set of Pareto-optimal solution is called Pareto-optimal set (PS), and its value in each objective space is called Pareto-optimal front (PF), which is denoted as:

$$\begin{aligned} \begin{aligned} PF = \{ F(x) = {({f_1}(x),{f_2}(x), \ldots ,{f_M}(x))^\mathrm{{T}}}|x \in PS\} \end{aligned} \end{aligned}$$

(2)

Particle swarm optimization

The PSO algorithm was first proposed by Kennedy and Eberhart in 1995 for solving continuous optimization problems [35, 36]. It originates from the simulation of the foraging behaviors of flocks of birds. In PSO, a feasible solution of the problem is abstractly represented as a particle, and the optimal solution of the problem is found through evolutionary strategies that are different from that of evolutionary algorithms. Without loss of generality, particle i with D problem dimensions consists of three components, including the historically best position found by each particle, named $\mathbf{Pbest} ^{d}_{i}=[pbest^{1}_{i}, pbest^{2}_{i}, \ldots , pbest^{D}_{i}]$, the current velocity $\mathbf{v} ^{d}_{i}=[v^{1}_{i}, v^{2}_{i}, \ldots , v^{D}_{i}]$ and the current position $\mathbf{x} ^{d}_{i}=[x^{1}_{i}, x^{2}_{i}, \ldots , x^{D}_{i}]$. In addition, during the evolutionary process, a global best position $\mathbf{Gbest} =[gbest^{1}, gbest^{2}, \ldots , gbest^{D}]$, found by the entire population, is shared with each particle. The evolutionary strategy of the PSO algorithm is expressed as follows:

$$\begin{aligned} v_i^d(t+1)= & {} w \cdot v_i^d(t) + {c_1} \cdot {r_1} \cdot (Pbest_i^d(t) - x_i^d(t)) \nonumber \\&+\, {c_2} \cdot {r_2} \cdot (Gbes{t^d}(t) - x_i^d(t)) \end{aligned}$$

(3)

$$\begin{aligned} x_i^d(t+1)= & {} x_i^d(t) + v_i^d(t+1) \end{aligned}$$

(4)

where $d=1, 2,\ldots , D$ represents the dth dimension of the optimization problem, $\omega$ is the inertia weight that is used to balance the global and local searches during PSO, $r_{1}$ and $r_{2}$ are two uniformly random numbers in the interval [0, 1], and $c_{1}$ and $c_{2}$ are acceleration factors, representing the extent of influence of one’s own experience and that of the swarm on the evolution of the population, generally, they are set to 2.0 [37].

Main challenges and motivations

When addressing MOPs, the selection of individual and global leaders needs to be carefully considered. This is because there is no unique optimal solution for MOPs. Some common methods include stochastic methods, dynamic neighborhood strategies, niche techniques, and ranking-based methods [38,39,40]. In general, The fewer global leaders choices, the greater the pressure is increased to the population, which results in a fast convergence but a poor diversity [41]. Therefore, the balance between population diversity and convergence speed is also the main factor affecting the algorithm’s performance. Some research shows that the population diversity of MOPSO algorithm is obviously insufficient, which leads to the failure of the MOPSO to obtain a set of outstanding nondominated solutions [42, 43]. Although the MOPSO algorithm has the advantage of fast convergence, it is easy to prematurely perform convergence activities when solving complex and high-dimensional MOPs. Therefore, based on the above analysis, the global leaders of all particles are appropriately selected from the external archive based on neighborhood knowledge in our proposed KGMOPSO algorithm. In addition, the population diversity is dynamically managed, which helps balance the exploration and development capabilities of the algorithm. The details are introduced in the next section.

The proposed KGMOPSO

Two-stage evolutionary strategy based on neighborhood knowledge search

Compared with other evolutionary algorithms, the evolution of the PSO algorithm is performed using the best experience of an individual and the entire population. This ensures that the PSO algorithm achieves a fast convergence speed and more efficient optimization performance [44]. However, it should be noted that when solving MOPs, the goal is to obtain a set of uniformly distributed Pareto-optimal solutions. The PSO algorithm tends to converge prematurely, and it is difficult to converge to the real PF. Therefore, in this paper, an effective knowledge-guided multiobjective particle swarm optimization algorithm is proposed to balance convergence and diversity.

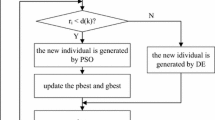
Knowledge-guided search is a promising method for solving complex problems and it has been studied by many scholars in different fields [45, 46]. Zhao et al. proposed an OD-RVEA algorithm where the optimal solution of each subproblem is updated by a direction-guided variation strategy to achieve rapid convergence [47]. Their comparative experiment indicates that OD-RVEA offers preferable performance to those of preceding algorithms. Ghosh et al. proposed an efficient strategy in which the most promising evolutionary information from past generations is retained and used to generate offspring [48]. This strategy is integrated with the winners of the CEC, and the experimental results demonstrate that this leads to a significant improvement in the performance of the algorithm. The best search information is incorporated into the evolutionary process of the population, and the performance of the algorithm is effectively improved. Therefore, in this paper, a two-stage evolutionary strategy based on neighborhood knowledge search is proposed, as shown in Fig. 1. In stage I, two different leaders are selected from the external archive through the leader selection strategy based on the reference point angle, which is explained in detail in the following section. The evolution direction is constructed by the two extreme points that are selected from the external archive to guide the evolutionary process of the whole population. The nondominated solutions obtained by the KGMOPSO algorithm are expected to quickly identify the area where the real PF is located. The role of stage I is to enhance the global exploration capability of the algorithm. In stage II, the population approximates the PF based on the search results in stage I. Therefore, the local search capability of the algorithm needs to be strengthened gradually in order to obtain a set of outstanding nondominated solutions. The individual particle’s best experience is used as a guide particle to the evolution of the population. By using the best experience of each particle to guide the evolution of the population, the convergence ability of the algorithm may be limited to some extent, but the diversity of the population is enhanced gradually. Algorithm 1 gives the pseudocode for this strategy, and the details are shown in the following section.

Fig. 1

Two-stage framework of KGMOPSO

Leader selection based on the reference point angle

The goal of MOPs is to obtain a set of nondominated solutions rather than a single optimal solution. When applying the PSO algorithm to tackle MOPs, an essential problem to be solved is choosing an appropriate leader for each individual. A good leader can guide a population to evolve in a better direction, and a poor leader can cause the algorithm to converge too slowly and fall into a local optimum. Therefore, this paper proposes a leader selection strategy based on the angle of the reference point. Different from randomly selecting two nondominated solutions for comparison to select the appropriate leader, we design the reference point corresponding to each nondominated solution based on the target value of two adjacent individuals in a ring topology. A diagram showing the main frame of the proposed leader selection strategy based on the angle of the reference point is given in Fig. 2. The specific processes are as follows.

First, the sorting is carried out in ascending order according to the objective of each nondominated solution in the external archive. Second, the coordinate of the reference point (rpoint) corresponding to each nondominated solution i in the objective space is obtained by Eq. (5).

$$\begin{aligned} rpoint^m_i = \left\{ \begin{array}{l} \mathrm{{PF}}_{i + 1}^m - |\mathrm{{PF}}_{i + 1}^m - \mathrm{{PF}}_{i - 1}^m|,\;i \ne {{1}} \ne N\\ \mathrm{{PF}}_i^m,\; \mathrm{{Otherwise}} \end{array} \right. \end{aligned}$$

(5)

where $\mathrm{{PF}}_i^m$ is the mth objective value of the ith nondominated solution in PF, N is the number of nondominated solutions obtained by KGMOPSO.

Fig. 2

Leader selection strategy based on reference point angle

The coordinates of the reference point i are equal to the coordinates of the individual $i+1$ minus the distances between the individual $i+1$ and the individual $i-1$ in each objective space. Then, the included angle between the current particle i and each reference point is calculated by Eq. (6).

$$\begin{aligned} \theta _i = \arccos \left( \frac{{rpoint_i \cdot \mathrm{{PF}}_i}}{{\sqrt{|rpoint_i{|^2} + |\mathrm{{PF}}_i{|^2}} }}\right) \end{aligned}$$

(6)

where $|$ $\cdot$ $|$ represents the norm of the vector.

Finally, the nondominated solutions corresponding to the minimum and maximum angles are selected as $Leader_1$ and $Leader_2$, respectively. It is important to note that the reference point of the extreme point in PF is itself. The traditional selection strategy based on the angle between the individual and each nondominated solution mostly uses the information about the particles themselves for comparison, in contrast, the information about the neighborhood of particles is used to generate the corresponding reference points in this paper. The ring topology of the population is adopted, and the appropriate leader is selected through the comparison of the reference points. This strategy can effectively strengthen the diversity of the selected nondominated solutions to some extent, especially in the case of low population diversity. Algorithm 2 gives the pseudocode for the leader selection strategy.

Stage I: approach the real PF

The goal of stage I is to locate the best search space, which is expected to approach the real PF as closely as possible. Each particle learns from a search direction obtained by the leader selection strategy based on the reference point angle introduced in “Leader selection based on the reference point angle”. In stage I, an efficient knowledge-guided evolutionary strategy is designed, which is expressed as follows:

$$\begin{aligned} \begin{aligned} v_i^d(t+1)&= w \cdot v_i^d(t) + {c_1} \cdot {r_1} \cdot (pbest_i^d(t) - x_i^d(t)) \\&\quad + {c_2} \cdot {r_2} \cdot (Leader_1^d(t) - x_i^d(t)) + \phi \\&\quad \cdot (Leader_1^d(t) - Leader_2^d(t)) \end{aligned} \end{aligned}$$

(7)

where $Leader_1$ and $Leader_2$ are the leaders obtained by the leader selection strategy using the reference point angle, and $\phi$ is the influence factor, which indicates the influence of the direction of the leader on the evolutionary process of the individual. It can be calculated by Eq. (8).

$$\begin{aligned} \phi = 0.5 + rs \cdot \left( 1 - \frac{iter}{t\cdot maxIter}\right) \end{aligned}$$

(8)

where iter represents the current number of iterations, maxIter is the maximum number of iterations, t is the two-stage division coefficient, which is set to 0.5 in this paper, and rs is a random number in the range $[-1, 1]$. Equation (7) shows that the evolutionary direction between different leaders is incorporated into the KGMOPSO algorithm. Compared with the traditional MOPSO algorithm, this strategy can improve global search and convergence performance of the algorithm due to the guidance of the leader’s evolution knowledge.

However, it should be noted that not all problems result in accurately searching for the real PF area in stage I, especially problems with complex landscape topologies. If there are enough iterations, KGMOPSO undoubtedly obtains the real PF due to its advantages in the global search described above. However, this usually increases the computational cost of the algorithm. Therefore, in KGMOPSO, stage II is designed to balance the algorithm’s convergence and accuracy.

Stage II: enhanced search

Through the search process of stage I, KGMOPSO is expected to find a promosing search range that is close to the real PF with high probability. Therefore, the goal of stage II is to strengthen the local search and ensure that the KGMOPSO algorithm can obtain an excellent nondominated PS. A simplified velocity updating mechanism is designed, as shown below:

$$\begin{aligned} v_i^d(t+1) = w \cdot v_i^d(t) + \chi \cdot (Pbest_i^d(t) - x_i^d(t)) \end{aligned}$$

(9)

where $\chi$ is the influence factor, which controls the influence level of the historically best individual experience, calculated by Eq. (10).

$$\begin{aligned} \chi = 0.5 + rs \cdot \frac{i}{N} \end{aligned}$$

(10)

where rs has the same meaning as it in Eq. (8), and i=1, 2, $\ldots$, N represents the number of particles. In stage II, due to the lack of a global leader, the convergence speed of the algorithm is relatively slower than that of stage I. Therefore, in stage II, the diversity and enhancement of the local search are the central problems that are considered. From Eq. (9), due to the effect of the influence factor $\chi$, the KGMOPSO algorithm has a certain perturbation ability, which is conducive to the local search and maintain the diversity of the population.

According to the above description, stage I is necessary and important for stage II and the proposed KGMOPSO algorithm to obtain a well-distributed PF. Under the joint action of stage I and stage II, KGMOPSO can overcome the shortcomings of the traditional MOPSO algorithm and achieve a balance between the global and local search.

Similarity detection and diversity enhancement

Although the PSO algorithm achieves a fast convergence rate, it can easily and quickly lose population diversity when solving MOPs, which causes the algorithm to fail to converge to the real PF. Therefore, ensuring that the algorithm possesses sufficient population diversity during runtime is crucial to the optimization performance of the algorithm. An individual similarity detection technology is introduced to measure the diversity of the population for each generation, which is described as:

$$\begin{aligned} \mathrm{{sim}} = \dfrac{{\sum \nolimits _{i = 1}^N {\sum \nolimits _{d = 1}^D {\left| \frac{{x_i^d - m{e^d}}}{{x_{\max }^d - x_{\min }^d}}\right| } } }}{N} \end{aligned}$$

(11)

where $me^d$ is the average value of the population in the dth dimension, and $x^d_\mathrm{{max}}$ and $x^d_\mathrm{{min}}$ represent the maximum and minimum values of individuals in the dth dimension, respectively. By calculating the individual similarity of each generation, the diversity of the population can be dynamically measured. It is favorable to prevent the algorithm from falling into a local optimum.

There is no doubt that maintaining sufficient diversity is essential for promoting the search capabilities of the algorithm. Therefore, this paper proposes a new strategy to enhance population diversity. In this strategy, the Euclidean distance between individuals is calculated. The entire population is divided into two groups, and each group implements different mutation strategies to maintain the diversity of the population. The detailed steps are described below.

Step 1: Calculate the Euclidean distance between individuals in the decision space;

Step 2: Sort all the individuals, and select half of the individuals with the larger distance as one group (named group 1), and the rest as another group (named group 2).

Step 3: For group 1, when a random number is less than 0.5, the negation strategy is executed by Eq. (12); otherwise, a nondominated solution is randomly selected from an external archive for replacement.

$$\begin{aligned} x_i^d = \mathrm{{Upper}}(x_i^d) + \mathrm{{Lower}}(x_i^d) - x_i^d \end{aligned}$$

(12)

where $\mathrm{{Upper}}(x_i^d)$ and $\mathrm{{Lower}}(x_i^d)$ represent the upper and lower limits of the ith particle in the dth dimension, respectively.

For group 2, when a random number is less than 0.5, a Gaussian mutation strategy based on individuals and randomly selected leaders is performed by Eq. (13). On the contrary, the individual does not undergo any changes.

$$\begin{aligned} \begin{aligned} x_i^d = \left\{ \begin{array}{l} N(r\cdot x_i^d + (1 - r)\cdot g^d, |x_i^d - g^d|), \; \mathrm{{if}\; \mathrm{{rand}} < 0}{{.5}}\\ x_i^d,\; {\text {Otherwise}} \end{array} \right. \end{aligned} \end{aligned}$$

(13)

where r is a random number in the interval [0, 1], $g^d$ represents a nondominated solution randomly selected from the external archive, and $N(\cdot )$ is a Gaussian distribution function.

In addition, the computational cost of the algorithm may increase when the diversity operation is excessively performed. An effective method is proposed to solve this problem. When the population similarity is lower than a preset threshold, it indicates that there are too many identical or similar individuals in the population, and the diversity enhancement strategy needs to be implemented. Otherwise, the diversity enhancement strategy is not implemented. To reasonably evaluate the similarity of individuals for each generation, this paper adopts a dynamic method for setting the threshold, as shown in Eq. (14).

$$\begin{aligned} \mathrm{{Threshold}}(iter) = C\cdot \left( 1- {\left( \frac{iter}{{1.25 \cdot maxIter}}\right) ^2}\right) \end{aligned}$$

(14)

where C is a fixed constant, which is set to 0.45 in this paper.

Maximum and minimum crowding distance

In general, to obtain a uniformly distributed PF, the redundant individuals in the external archive should be deleted. In [1], the crowding distance is first used as a method to judge the distance between nondominated solutions. A large crowding distance means that the more dispersed the individuals are, the better the diversity of the population. Inspired by [49], this paper proposes a pair of improved crowding distances, which are called the maximum and minimum crowding distances. Through this strategy, the nondominated solutions with good distributions are retained as much as possible, in contrast, the nondominated solutions with poor distributions are removed. The calculation process of the maximum and minimum crowding distances mainly involves two steps. The first step is to calculate the crowding distances, which are used in [1], of the individual on each objective space, including the maximum distance $\mathrm{{CD}}_\mathrm{{max}}$, minimum distance $\mathrm{{CD}}_\mathrm{{min}}$, and average distance $\mathrm{{CD}}_\mathrm{{average}}$. The second step is to calculate the proposed crowding distance of each individual using the criteria shown in Eq. (15).

$$\begin{aligned} \mathrm{{CD}}_i^m = \left\{ \begin{array}{l} \mathrm{{CD}}_{\max }^m,\;if\;\mathrm{{CD}}_i^m \ge \mathrm{{CD}}_\mathrm{{average}}^m\\ \mathrm{{CD}}_{\min }^m,\;if\;\mathrm{{CD}}_i^m < \mathrm{{CD}}_\mathrm{{average}}^m \end{array} \right. \end{aligned}$$

(15)

where m = 1, 2, $\ldots$, M is the index of the objective function.

To clearly explain the maximum and minimum crowding distance strategies, a simple example is given, as shown in Fig. 3. Assume that there are four nondominated solutions distributed on the PF, in which nondominated solution 1 and nondominated solution 4 are extreme points need to be retained in the PF. The goal is to find a poor solution from nondominated solution 2 and nondominated solution 3. As shown in Fig. 3a, we first calculate the crowding distance of nondominated solution 2 and nondominated solution 3 in each objective space. From Fig. 3a, the crowding distance of nondominated solution 2 is equal to $\mathrm{{CD}}_{21}$ + $\mathrm{{CD}}_{22}$ and $\mathrm{{CD}}_{31}$ + $\mathrm{{CD}}_{32}$ for the nondominated solution 3. Secondly, the $\mathrm{{CD}}_\mathrm{{max}}$, $\mathrm{{CD}}_\mathrm{{min}}$, and $\mathrm{{CD}}_\mathrm{{average}}$ are calculated according to the crowding distance between nondominated solution 2 and nondominated solution 3 in each objective space. Next, Eq. (14) is used to calculate the proposed maximum and minimum crowding distance of each nondominated solution. Finally, they are sorted in ascending order to delete the nondominated solution with the minimum crowding distance, as shown in Fig. 3b. The remaining solution is the nondominated solution that needs to be retained, as shown in Fig. 3c. The good nondominated solutions can be retained by setting the maximum and minimum crowding distances, and they realize the balance of convergence and diversity of the algorithm by incorporating the leader selection strategy.

Fig. 3

Examples of maximum and minimum crowding distances

The overall framework of KGMOPSO

Based on the above description, the KGMOPSO algorithm is composed of a knowledge-guided two-stage evolutionary strategy, an individual similarity measurement and diversity enhancement strategy, and a maximum and minimum crowded distance strategy. Through different evolution strategies, KGMOPSO can balance the global and local search capabilities well. The individual similarity detection technique is adopted to dynamically measure the diversity of the population, and the diversity is enhanced by the proposed diversity enhancement strategy. The improved crowding distance strategy is employed, and the nondominated solutions are screened to obtain the approximate real PF of the problem. In addition, a simulated binary crossover (SBX) and polynomial mutation (PM) are also incorporated into the KGMOPSO algorithm [50, 51]. In KGMOPSO, the update scheme of individual leader is that when the new individual dominates the current individual leader, the new individual is regarded as new individual leader. Half of the probability is used to select one of the individuals as the current individual leader if the two individuals do not dominate each other. Algorithm 3 gives the overall framework of the proposed KGMOPSO algorithm.

Experimental studies

Test problems

In this paper, two popular test instances, including the ZDT [52] and DTLZ test instances [53], are employed to show the high effectiveness of KGMOPSO. These test problems possess different landscape characteristics, such as multimodality, convexity and discontinuity. Therefore, it is very challenging to optimize these problems by using the proposed KGMOPSO and other multiobjective algorithms. The two test instances used in this paper contain a total of twelve MOPs, of which the first five test problems (i.e., ZDT1 to ZDT4 and ZDT6) are biobjective problems from the ZDT test instance. The last seven problems (i.e., DTLZ1 to DTLZ7) are three-objective problems from the DTLZ test instance. The number of decision variables is set as 30 for ZDT1-ZDT3 and 10 for ZDT4 and ZDT6. For the DTLZ1 test problems, M + 4 decision variables are used, DTLZ2-DTLZ6 use M+9 decision variables, and the last problem is set uses M + 19 decision variables, in which M is the number of objective functions. Table 1 gives the main features of these two benchmark instances.

Table 1 The main features of the ZDT and DTLZ test instances

Performance metrics

In our study, to comprehensively analyze KGMOPSO, three quantitative performance metrics are adopted for all the chosen algorithms for performance evaluation, including the inverted generational distance (IGD) [54], the hypervolume (HV) [55] and the distribution indicator of a nondominated solution (spread) [1]. These three performance indicators quantificationally evaluate the multiobjective optimization algorithm in terms of the convergence, diversity and uniformity of the nondominated solutions. A small IGD or spread value and a large HV value obtained by any algorithm indicates that the optimization performance of the algorithm is remarkable and outstanding.

Let S represent a set of nondominated solutions that are uniformly sampled from the real PF and let $S'$ be the set of nondominated solutions achieved by a multiobjective optimization algorithm. Therefore, the IGD metric can be described as:

$$\begin{aligned} {\mathrm{{IGD}}(S,S')} = \frac{\sum \nolimits _{i = 1}^{|S|}{d({S_i},S')}}{|S|} \end{aligned}$$

(16)

where $i=1, 2, \ldots , |S|$, |S| is the number of nondominated solutions in S, and $d(S, S')$ represents the minimum Euclidean distance between the ith member of S and any member of $S'$. If the IGD value is smaller, it indicates that the distribution of the nondominated solution is closer to the real PF.

Table 2 The parameter settings for all the algorithms

Table 3 IGD results of all algorithms on the ZDT test instances

Table 4 HV results of all algorithms on the ZDT test instances

Table 5 Spread results of all algorithms on the ZDT test instances

Fig. 4

Plots of nondominated solutions obtained by KGMOPSO on the ZDT test problems

Fig. 5

The results of nondominated solutions obtained by six comparison algorithms on the ZDT3 problem

The HV metric can be explained as follows:

$$\begin{aligned} \mathrm{{HV}} = \delta \cdot \left( \bigcup \limits _{x \in S'} {[{f_1}(x),c_1^r]} \times \cdots [{f_m}(x),c_m^r]\right) \end{aligned}$$

(17)

where $\delta$ represents the Lebesgue measure and $c_m^r$ is the reference point in the mth objective space. In general, a larger HV value indicates that the quality of the nondominated solution obtained by the algorithm is reliable.

The spread indicator ($\varDelta$) is defined as follows:

$$\begin{aligned} \varDelta = \frac{{{d_f} + {d_l} + \sum \nolimits _{i = 1}^{N - 1} {|{d_i} - \bar{d}|} }}{{{d_f} + {d_l} + (N - 1)\bar{d}}} \end{aligned}$$

(18)

where N is the number of nondominated solutions, $d_i$ represents the Euclidean distance from the ith nondominated solution to its neighboring solution, $\bar{d}$ is the average value of $d_i$, and $d_f$ and $d_l$ are the Euclidean distances between the extreme solution obtained by the algorithm and the boundary solution. If the spread value is smaller, it means that the distribution and quality of the nondominated solution obtained by the algorithm is satisfactory.

Experimental settings

In our experiments, the performance of KGMOPSO is validated through comparisons with two existing state-of-the-art multiobjective evolutionary algorithms and four advanced multi-objective PSO algorithms, including NSGA-II [1], SPEA/R [4], dMOPSO [27], MPSO/D [28], MMOPSO [34] and NMPSO [5].

For a fair comparison, the population size for each algorithm is set to 100. If the algorithm requires an external archive, its size is set to 100. For each ZDT test problem, the maximum number of function evaluations and DTLZ test instances on each test problem for each algorithm is 100,000 and 200,000, respectively. Three performance indicators are calculated by using 500 points uniformly sampled from the true PF for the ZDT test instances and 5000–10,000 points for the DTLZ test instances. To reduce the influence of experimental error, each algorithm runs independently 25 times on each problem. The average value and standard deviation of the experimental results are given to compare the optimization performance of these algorithms. The source codes of all the above algorithms come from the PlatEMO platform [56]. Table 2 summarizes the main parameter settings for all the algorithms.

Experimental results and analysis

Experimental results on the ZDT test problems

In this paper, the ZDT test problems are employed to analyze the capability of the KGMOPSO algorithm to handle problems with two optimization objectives. Tables 3,  4 and  5 give the values of IGD, HV and spread for seven multiobjective optimization algorithms on the ZDT test problems, respectively. The best result on each problem obtained by any algorithm is highlighted.

The experimental results indicate that the proposed KGMOPSO algorithm achieves the best optimization performance on most of ZDT test problems. It obtains the best IGD values on the ZDT1, ZDT2 and ZDT4 problems, as shown in Table 3. Except the NSGA-II algorithm which obtains the best results on the ZDT3 problem and the dMOPSO algorithm which achieves the outstanding performance on the ZDT6 problem, the other algorithms do not obtain the best optimization result on the ZDT test problems in terms of IGD. From Table 4, compared with six multiobjective optimization algorithms, KGMOPSO obtains the best HV results on all ZDT problems, which shows that the KGMOPSO algorithm can obtain the best optimization results when solving optimization problems with two objectives and with discontinuous and convex properties. In addition, as shown in Table 5, the KGMOPSO algorithm obtains the best spread result on the ZDT1$\sim$ZDT4 problems. In the case of ZDT6, the spread value of the KGMOPSO algorithm is relatively worse than those of NSGA-II, dMOPSO and MPSOD but better than those of the SPEA/R, MMOPSO and NMPSO algorithms. The dMOPSO algorithm obtains the best spread value for the ZDT6 problem. The other algorithms fail to obtain the best result on any of the ZDT problems. Figure 4 shows the distribution of the nondominant solutions obtained by the KGMOPSO algorithm when solving the ZDT test problems. We can see that the nondominated solution obtained by KGMOPSO can approximate the true PF. For the sake of comparison, we choose the representative ZDT3 problem, which is disconnected and multimodal. Figure 5 shows the final results obtained by the other six algorithms on this problem. NSGA-II and MMOPSO obtain similar results to that of KGMOPSO. However, other algorithms do not converge well to the real PF, especially the NMPSO algorithm. Therefore, it can be concluded that the KGMOPSO algorithm exhibits a relatively reliable and efficient performance in addressing the ZDT instances.

Table 6 IGD results of seven multiobjective algorithms on the DTLZ test instances

Table 7 HV results of seven multiobjective algorithms on the DTLZ test instances

Table 8 Spread results of seven multiobjective algorithms on the DTLZ test instances

Fig. 6

Distribution of solutions obtained by these algorithms on the DTLZ1 problem

Fig. 7

Distribution of solutions obtained by these algorithms on the DTLZ7problem

Experimental results on the DTLZ test problems

Tables 6,  7 and  8 represent the IGD, HV and spread results obtained by the KGMOPSO algorithm and six multiobjective optimization algorithms on the DTLZ problems with three optimization objectives, respectively. The best results for each problem are highlighted. The results demonstrate that the KGMOPSO algorithm possesses a strong competitive advantage in solving DTLZ test problems with three optimization objectives. It can be seen from Table 6 that KGMOPSO obtains the best IGD result on the DTLZ6 and DTLZ7 functions. The MPSOD algorithm obtains the best value for DTLZ1, DTLZ2 and DTLZ4. NSGA-II and NMPSO obtain the best results on DTLZ3 and DTLZ7, respectively. Other multiobjective algorithms fail to obtain the best IGD values. Although the KGMOPSO algorithm only obtains the best IGD values on DTLZ6 and DTLZ7 functions, for HV, which is shown in Table 7, compared with other multiobjective algorithms, the proposed KGMOPSO algorithm obtains the best results on DTLZ2, DTLZ4 and DTLZ7. Table 8 shows that the KGMOPSO algorithm obtains the best spread value for DTLZ5 and DTLZ6, which indicates that the KGMOPSO algorithm achieves a very good distribution for these two problems. MPSOD does not obtain the best HV result on any of the DTLZ test problems, but it possesses advantages on DTLZ1, DTLZ2 and DTLZ4. NMPSO achieves the best result on DTLZ3, but it achieves a mediocre performance in terms of spread. The NSGA-II, SPEAR, dMOPSO and NMPSO algorithms do not show higher competitive advantages in HV. NSGA-II obtains the best spread value on the DTLZ7 problem, and dMOPSO obtains the best spread value on DTLZ3 problem. Figures 6 and 7 show the distributions of the nondominated solutions obtained by the seven algorithms on the DTLZ1 and DTLZ7 test problems. The results show that the nondominated solutions obtained by the proposed KGMOPSO algorithm exhibit high diversity and are better distributed. Considering the overall performance across the DTLZ test instances and three performance metrics, the proposed KGMOPSO algorithm in this paper possesses highly competitive and can be deemed a promising algorithm when solving MOPs with three optimization objectives.

Discussion and analysis

Based on the above experimental results, the proposed KGMOPSO algorithm is competitive compared to other multiobjective algorithms on most of the test problems, which indicates that KGMOPSO has acceptable optimization performance and can obtain a better approximation along with the real PF. The main reason is that under stage I, the global search capability of the algorithm is improved by the knowledge learning of Pareto-optimal solution in the external archive, and the algorithm has better exploration and development capabilities through effective management of diversity. However, KGMOPSO fails to obtain the best result in some problems, such as DTLZ3, but the differences brought by KGMOPSO are not significant. As shown in Tables 6, 7, and  8, KGMOPSO achieves the best result on almost half of the test problems. Moreover, the results obtained by KGMOPSO are better than NSGA-II, SPEA/R, and MMOPSO and second only to the NMPSO and MPSOD on the whole. According to the distribution of solutions shown in Figs. 4 and  5, KGMOPSO is superior to other comparison algorithms. The work demonstrates that the nondominated solutions obtained by KGMOPSO has good uniformity and distribution, which indicates that KGMOPSO is useful for MOPs. However, as the number of objectives increases, the experimental results show that the KGMOPSO algorithm is generally satisfactory. Figures 6 and 7 show the distribution of the Pareto-optimal solution of the algorithm on DTLZ1 and DTLZ7. We can see that when solving the optimization problem of three objectives, the Pareto-optimal front is not obtained very well by the proposed KGMOPSO, but the overall result is acceptable. Tables 6, 7 and  8 also shows the performance results of the KGMOPSO algorithm on three performance indicators. The overall optimization performance is better than most algorithms, and further improvements will also be developed. In a word, from the existing results, the comprehensive performance of KGMOPSO is acceptable and better than most multiobjective algorithms.

Conclusion

To address the difficulties of MOPSO in managing diversity and selecting favorable leaders, this paper proposes a novel MOPSO algorithm for tackling MOPs. In this algorithm, multiple optimization strategies are incorporated into the proposed KGMOPSO algorithm. A knowledge-guided two-stage evolutionary strategy is designed to improve the algorithm’s global and local search capabilities, and a selection strategy based on the reference point angle is performed to choose the appropriate leaders. Moreover, an individual similarity detection and diversity enhancement strategy is adopted to avoid the problem of insufficient diversity in current population. Finally, an improved crowding distance technology is designed to screen appropriate nondominated solutions. To evaluate the efficiency and advantages of KGMOPSO, KGMOPSO is subjected to twelve test instances. The computational results indicate that KGMOPSO has highly competitive in comparison with other multiobjective algorithms. However, KGMOPSO possesses some disadvantages when addressing problems with complex landscapes, such as DTLZ3; the convergence speed is relatively insufficient, and further improvement is needed.

The KGMOPSO algorithm and its related strategies will be further modified in future research, and it will be considered to address the practical problems.