A novel entropy-based weighted attribute selection in enhanced multicriteria decision-making using fuzzy TOPSIS model for hesitant fuzzy rough environment

Abstract

The existing approaches of multicriteria decision-making (MCDM) process might yield unreliable and questionable results. The notable challenges of MCDM approaches are rank reversal paradox and uncertainty. The prime inspiration for researchers is the MCDM for hesitant fuzzy sets (HFSs). In some scenarios, the decision-makers could not choose one from numerous values while expressing their preferences. HFS which is the extension of fuzzy sets (FS) is found to be helpful in solving such decision-making (DM) problems. The DM process is revolutionized with the commencement of powerful and efficient tools of data representation for expressing vagueness and uncertainty in data sets as FSs (both generalized and hesitant ones). This paper copes with one such novel approach that involves entropy-based attribute weighting, followed by an evaluation of approximate sets in the fuzzy rough framework. Correlation of the input alternatives in respect of evaluation criteria and the output class is evaluated. With the fuzzy technique for ordered preference by similarity to ideal solutions (FTOPSIS), the generated correlation matrix is utilized for calculating the degree of closeness ($\delta$) of the output classes to the input alternatives. This paper made a novel contribution of performance indicator centered on FTOPSIS for the hesitant fuzzy rough domain. The proposed method’s efficiency is established through comprehensive and systematic experimentation on datasets utilized by researchers globally. The proposed algorithms prove its ability to handle datasets that involve human-like hesitant thinking in the MCDM system by contrasting with the existing ones.

Introduction

For decades, MCDM has remained as an inexorable topic of research. Optimum selection of alternatives considerably affects the DM of picking a suitable one from a provided set of conflicting criteria. The uncertainty and vagueness involved with the human DM process could be effectually modeled by FS theory. MCDM embraces attributes, decision methods, selection criteria, and even subjective estimation of experts [1]. Improvisation in classical FSs [2] was done for handling the uncertainties and vagueness. Extended versions of FSs embrace fuzzy rough sets (FRS) [3] which could handle the indiscernible datasets effectually in a fuzzy framework. Researchers made countless attempts for incorporating real-life complex scenarios that involve uncertainty into the datasets and solve it utilizing FTOPSIS [4–7]. It has now been meticulously adopted in several use cases on account of its simplicity, comprehensive mathematical concept along with computational efficiency. The extension of the classical TOPSIS approach in regard of fuzzy logic, namely FTOPSIS, has also been effectively implemented in disparate applications like Networks, Supply Chain Management, Defense Industry, Construction, Healthcare, etc., FTOPSIS was employed in countless practical use cases, starting from choosing a suitable supplier for manufacturing through assessment of service quality and ending at selection and ranking of the renewable energy (RE) sources, confirming that is widely implemented in innumerable practical issues. Additionally, the energy policies’ selection and ranking of the RE sources are the eminent challenges tackled by FTOPSIS. Hence, there TOPSIS studies are becoming popular regarding the problems, which consider sustainable development, environment, and RE sources. Decision-makers present variable opinions for the alternatives, which brings uncertainty. HFS has an imperative role in modeling such uncertainty. This difference in opinions could be due to inadequate information or their different backgrounds. Researchers have widely explored HFSs in respect of the aggregation operators (AOs), various information measures as well as their application on DM [8]. Expert assessment of the attributes is done utilizing probable membership values that the attribute could possibly take. HFSs were proffered by [9] and were intensively utilized by researchers in respect of AOs for DM [10–12]. An outline of trends and tools associated with HFSs was studied by [13]. A fusion of the Rough Sets (RS) model and HFSs was explored by [14] by rendering an axiomatic and constructive mathematical framework. Probabilistic and Pawlak’s models were propounded by [15]. Enhanced concept associated to approximate precision and roughness for hesitant fuzzy compatible rough space was examined by [16]. Dual HFSs and associated AOs were studied by [17]. Attribute reduction was intensively examined by [18]. The utilization of decision-theoretic RSs for the purpose of resolving DM problems in HFSs was carried out by [19]. However, it might be difficult or expensive to develop criteria set, wherein all criteria are independent in certain situations. In some real-life scenarios, on account of the higher uncertainty of the situation and the restricted cognition of human thinking, it is hard for decision-makers to make a choice in selecting merely one alternative as of a candidate alternative set or evaluation arguments set to show their preference. They might highly hesitate amongst several alternatives or evaluation arguments. In these similar scenarios, it is reasonable to formulate a new DM rule or build a tool that permits decision-makers to express their judgments or preferences on several objects with individual degrees of hesitation. Consequently, it is requisite to comprehensively study the HFSs with inter-active criteria and construct an MCDM approach by considering the interaction amongst criteria. This paper has brought about a pioneering work in the FRSs field as it bridges the gap from RSs to HFSs for attribute reduction. It can elevate the DM efficiency and lessen the decision pressure, because, here, the decision-makers are permitted to express their preference in form of entropy centered weighted attribute selection.

The forthcoming section handles preliminaries of hesitant FRSs, as well as RSs, and is followed by methodology and experimentation. A detailed explanation of proposed work and its implementation on two disparate cases of hesitant fuzzy data sets are done in subsequent sections.

Preliminaries

Here, the basic RS and FRS concepts are expounded in detail.

Definition 1

[20] Consider information system ‘I’, universes of discourse ‘X’, non-empty finite set ‘A’, and attribute value ‘$Y_{a}$’ where I = (X, A). ${\text{for}}\;{\text{every}}\;a:X \to Y_{a} \;{\text{for}}\;{\text{every}}\;a \in \, A$. And, ‘A’ that is a decision system could be defined as $A = (C \cup \, D)$, where C and D are a set of conditional and decision attributes, respectively. The core notion in RS theory exists in finding the lower approximations (LA) as well as upper approximations (UA) centered on IND (P)-equivalence relation, where

$$ {\text{IND}}\left( P \right) = \{ \left( {x,y} \right) \in U^{2} |\forall a \in P\;{\text{such}}\;{\text{that}}\;a(x) = a(y)\} . $$

(1)

Definition 2

[20] If $(x,y) \in {\text{IND}}(P)$, then (x, y) is indiscernible by ‘P’ attribute. Consider an equivalence class generated as of IND (P) as $[x]_{P}$. Here, the LA is $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{P} X$ and UA is $\bar{P}X$, and both are evaluated as

$$ \begin{aligned}& \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{P} X = \{ x|[x]_{p} \subseteq X\} \hfill \\& \bar{P}X = \{ x|[x]_{p} \cap X \ne 0\} . \hfill \\ \end{aligned} $$

(2)

The tuples $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{P} X$ and $\bar{P}X$ are termed an RS:

Definition 3

[20, 21] The considered positive region comprises all objects which could be positively classified to the classes of U/Q. The determination of dependence between the attributes is proffered by Eq. (3).

$$ \gamma_{P} (Q) = \frac{{|{\text{POS}}_{P} (Q)|}}{|U|}. $$

(3)

By determining the change in the dependence, while a feature is added or removed, significance of the feature is evaluated by [20, 22].

The issue of crisp LA and UA adversely influences the classification accuracy and is effectually handled by FRS explained in [3, 23, 24].

Definition 4

The definitions of Membership functions for fuzzy LA and fuzzy UA are proffered as Eq. (4)

$$ \begin{aligned} \mu_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{P} X}} (F_{i} ) & = \inf_{x} \hbox{max} \{ 1 - \mu_{{F_{i} }} (x),\mu_{X} (x)\} \hfill \\ \mu_{{\bar{P}X}} (F_{i} ) & = \sup_{x} \hbox{min} \{ \mu_{{F_{i} }} (x),\mu_{X} (x)\} , \hfill \\ \end{aligned} $$

(4)

where $F_{i}$—fuzzy equivalence classes belonging to U/P.

A fuzzy positive area is then evaluated using extension principle as:

$$ \mu_{{{\text{POS}}_{P} (Q)}} (x) = \mathop {\sup }\limits_{X \in U/Q} \mu_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{P} X}} (x). $$

(5)

Likewise, a new Fuzzy dependence function could be evaluated as:

$$ \gamma_{P}^{\prime } (Q) = \frac{{|\mu_{{POS_{P} (Q)}} (x)|}}{|U|}. $$

(6)

RS theory as introduced by Pawlak regards the information subspaces in the sort of LA, UA, and boundary region, whereas the FRSs approximate the same subspaces as overlapping regions having certain membership values [25]. The FRSs’ concept was extended by Zhang et al. [26] and Chen et al. [27] for the cases embracing DM uncertainty. Hesitant FRSs have been utilized effectually in the literary works for handling hesitant DM.

Hesitant fuzzy sets: basic concepts

Definition 5

Consider X as a reference set and, here, the HFSs A on the X set defined in respect of function $h_{A} (x)$. While it is employed to X, it returns a sub set A as $A = \{ \langle x,h_{A} (x)\rangle |x \in X\}$, where $h_{A} (x)$ could be called hesitant fuzzy elements (HFE) [10, 28] and it indicates the set of possible membership degrees of $x \in X$ element to A.

Definition 6

For a given HFE (h), the lower bound as well as upper bound as per [29] are,

$$ \begin{aligned}& h^{ - } (x) = \hbox{min} h(x) \hfill \\& h^{ + } (x) = \hbox{max} h(x). \hfill \\ \end{aligned} $$

(7)

Definition 7

The score function of the HFSs $s(h_{A} (x))$ as per [29] is:

$$ \begin{aligned} s(h_{A} (x)) = \frac{{\sum\nolimits_{i = 1}^{{l(h_{A} (x))}} {h_{A}^{\sigma (j)} (x)} }}{{l(h_{A} (x))}} \hfill \\ {\text{where}}\;s(h_{A} (x)) \in [(0,1)]. \hfill \\ \end{aligned} $$

(8)

However, the normalized score function could be proffered as:

$$ s_{{n_{ij} }} = \frac{{s_{ij} }}{{\sum\nolimits_{i = 1}^{m} {s_{ij} } }}. $$

(9)

Definition 8

If X, Y are the ‘2’ non-empty finite universes and as well R signifies “X to Y” hesitant fuzzy relationship, then (X, Y, R) is called Hesitant fuzzy rough approximations (HFRA) space. For any $P \in {\text{HF}}(Y)$, the LA and UA are indicated by $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{R} (P)$ and $\bar{R}(P)$ respectively [26],

$$ \begin{aligned} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{R} (P) = \{ \langle y,h_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{R} (P)}} (y)\rangle |y \in Y\} \hfill \\ \bar{R}(P) = \{ \langle y,h_{{\bar{R}(P)}} (y)\rangle |y \in Y\} , \hfill \\ \end{aligned} $$

(10)

where

$$ \begin{aligned} h_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{R} (P)}} (y) = \left\{ {\mathop \wedge \limits_{y \in Y} h_{{R^{c} }}^{\sigma (k)} (x,y) \vee h_{A}^{\sigma (k)} (y)|k = 1,2 \ldots l} \right\},x \in X \hfill \\ h_{{\bar{R}(P)}} (y) = \left\{ {\mathop \wedge \limits_{y \in Y} h_{R}^{\sigma (k)} (x,y) \vee h_{A}^{\sigma (k)} (y)|k = 1,2 \ldots l} \right\},x \in X, \hfill \\ \end{aligned} $$

(11)

where

$$ l = \hbox{max} \{ l(h_{R} (x,y)),l(h_{A} (x,y))\} . $$

(12)

Definition 9

As X stands as a finite universe of discourse, Torra et al. [9] offered the succeeding operations on hesitant FRSs. For any $P,Q \in {\text{HF}}(X)$, then for all $x \in X$:

• 1. The union of HFSs A and B is

  $$ h_{P \cup Q} (x) = h_{P} (x) \vee h_{Q} (x) = \bigcup\limits_{{\xi_{1} \in h_{P} (x),\xi_{2} \in h_{Q} (x)}} {\hbox{max} (\xi_{1} ,\xi_{2} )} . $$

  (13)

• 2. The intersection of HFSs A and B is

  $$ h_{P \cap Q} (x) = h_{P} (x) \wedge h_{Q} (x) = \bigcup\limits_{{\xi_{1} \in h_{P} (x),\xi_{2} \in h_{Q} (x)}} {\hbox{min} (\xi_{1} ,\xi_{2} )} $$

  (14)

• 3. The complement of A is

  $$ h_{{P^{c} }} (x) = \sim h_{P} (x) = \bigcup\limits_{{\xi \in h_{P} (x)}} {\{ 1 - \xi \} } . $$

  (15)

Definition 10

For HFSs A and B on $X = \{ x_{1} ,x_{2} \ldots x_{3} \}$, their weights are provided as weight vector $w = \{ w_{1} ,w_{2} \ldots w_{n} \}^{\text{T}}$ with $w_{i} \ge 1$ and $\sum\nolimits_{i = 1}^{n} {w_{i} = 1}$. The proposed correlation grounded on entropy-centric ordered weighted approach for HFRS is proffered as:

$$ \begin{aligned} \delta_{m} (A,B) & = \frac{{\kappa_{\text{HFRS}} (A,B)}}{{[\kappa_{\text{HFRS}} (A,A)]^{1/2} [\kappa_{\text{HFRS}} (B,B)]^{1/2} }} \\ & = \frac{{\left[ {\sum\nolimits_{i = 1}^{n} {w_{mi} \left( {\frac{1}{{l_{i} }}\left( {\sum\limits_{j = 1}^{{l_{i} }} {h_{A\sigma (j)}^{'} (x_{i} )*h_{B\sigma (j)}^{'} (x_{i} )} } \right)} \right)} } \right]^{{}} }}{{\left[ {\sum\nolimits_{i = 1}^{n} {w_{mi} \left( {\frac{1}{{l_{i} }}\left( {\sum\limits_{j = 1}^{{l_{i} }} {h_{A\sigma (j)}^{'} (x_{i} )*h_{A\sigma (j)}^{'} (x_{i} )} } \right)} \right)} } \right]^{1/2} \left[ {\sum\nolimits_{i = 1}^{n} {w_{mi} \left( {\frac{1}{{l_{i} }}\left( {\sum\limits_{j = 1}^{{l_{i} }} {h_{B\sigma (j)}^{'} (x_{i} )*h_{B\sigma (j)}^{'} (x_{i} )} } \right)} \right)} } \right]^{1/2} }}, \\ \end{aligned} $$

(16)

where $\delta_{m} (A,B)$ satisfies the below properties

$$ \begin{aligned} &(1)\quad \delta_{m} (A,B) = \delta_{m} (B,A) \hfill \\& (2)\quad 0 \le \delta_{m} (A,B) \le 1; \hfill \\& (3)\quad \delta_{m} (A,B) = 1\;{\text{if}}\;A = B. \hfill \\ \end{aligned} $$

(17)

Proof

• 1. It is highly straight forward.

• 2. The inequality $\delta_{m} (A,B)$ > 0 is obvious and to prove $\delta_{m} (A,B) \le 1$:

  $$ \begin{aligned} \kappa_{\text{HFRS}} (A,B) & = \sum\limits_{i = 1}^{n} {w_{mi} \left( {\frac{1}{{l_{i} }}\left( {\sum\limits_{j = 1}^{{l_{i} }} {h_{A\sigma (j)}^{'} (x_{i} )*h_{B\sigma (j)}^{'} (x_{i} )} } \right)} \right)} \\ & = w_{m1} \left( {\frac{1}{{l_{1} }}\left( {\sum\limits_{j = 1}^{{l_{i} }} {h_{A\sigma (j)}^{'} (x_{i} )*h_{B\sigma (j)}^{'} (x_{i} )} } \right)} \right) + w_{m2} \left( {\frac{1}{{l_{2} }}\left( {\sum\limits_{j = 1}^{{l_{i} }} {h_{A\sigma (j)}^{'} (x_{i} )*h_{B\sigma (j)}^{'} (x_{i} )} } \right)} \right) \\ & \quad \cdots w_{mn} \left( {\frac{1}{{l_{n} }}\left( {\sum\limits_{j = 1}^{{l_{i} }} {h_{A\sigma (j)}^{'} (x_{i} )*h_{B\sigma (j)}^{'} (x_{i} )} } \right)} \right) \\ \end{aligned} $$

  (18)
  $$ = w_{m1} \sum\limits_{j = 1}^{{l_{1} }} {\frac{{h_{A\sigma (j)}^{'} (x_{i} )}}{{\sqrt {l_{1} } }}} *\frac{{h_{B\sigma (j)}^{'} (x_{i} )}}{{\sqrt {l_{1} } }} + w_{m2} \sum\limits_{j = 1}^{{l_{1} }} {\frac{{h_{A\sigma (j)}^{'} (x_{i} )}}{{\sqrt {l_{2} } }}} *\frac{{h_{B\sigma (j)}^{'} (x_{i} )}}{{\sqrt {l_{2} } }} + \cdots + w_{mn} \sum\limits_{j = 1}^{{l_{1} }} {\frac{{h_{A\sigma (j)}^{'} (x_{i} )}}{{\sqrt {l_{n} } }}} *\frac{{h_{B\sigma (j)}^{'} (x_{i} )}}{{\sqrt {l_{n} } }}. $$

  (19)

By utilizing Cauchy’s Schwarz inequality, the above equation becomes:

$$ \begin{aligned} \kappa_{\text{HFRS}} (A,B)^{2} & = \left[ \begin{aligned} w_{m1} \left( {\frac{1}{{l_{1} }}\left( {\sum\limits_{j = 1}^{{l_{i} }} {h_{A\sigma (j)}^{2} (x_{1} )} } \right)} \right) + w_{m2} \left( {\frac{1}{{l_{2} }}\left( {\sum\limits_{j = 1}^{{l_{i} }} {h_{A\sigma (j)}^{2} (x_{2} )} } \right)} \right) \hfill \\ + \cdots + w_{mn} \left( {\frac{1}{{l_{n} }}\left( {\sum\limits_{j = 1}^{{l_{i} }} {h_{A\sigma (j)}^{2} (x_{i} )} } \right)} \right) \hfill \\ \end{aligned} \right] \\ & \quad \times \left[ \begin{aligned} w_{m1} \left( {\frac{1}{{l_{1} }}\left( {\sum\limits_{j = 1}^{{l_{i} }} {h_{B\sigma (j)}^{2} (x_{1} )} } \right)} \right) + w_{m2} \left( {\frac{1}{{l_{2} }}\left( {\sum\limits_{j = 1}^{{l_{i} }} {h_{B\sigma (j)}^{2} (x_{2} )} } \right)} \right) \hfill \\ + \cdots + w_{mn} \left( {\frac{1}{{l_{n} }}\left( {\sum\limits_{j = 1}^{{l_{i} }} {h_{B\sigma (j)}^{2} (x_{i} )} } \right)} \right) \hfill \\ \end{aligned} \right] \\ & = \left[ {\sum\limits_{i = 1}^{n} {w_{mi} \left( {\frac{1}{{l_{i} }}\left( {\sum\limits_{j = 1}^{{l_{i} }} {h_{A\sigma (j)}^{2} (x_{i} )} } \right)} \right)} } \right]*\left[ {\sum\limits_{i = 1}^{n} {w_{mi} \left( {\frac{1}{{l_{i} }}\left( {\sum\limits_{j = 1}^{{l_{i} }} {h_{B\sigma (j)}^{2} (x_{i} )} } \right)} \right)} } \right] \\ \end{aligned} $$

(20)

$$ = \kappa_{\text{HFRS}} (A,A)\quad \kappa_{\text{HFRS}} (B,B). $$

(21)

Therefore:

$$ \kappa_{\text{HFRS}} (A,B) \le \kappa_{\text{HFRS}} (A,A)^{1/2} .\kappa_{\text{HFRS}} (B,B)^{1/2} . $$

(22)

When A = B, then:

$$ h_{A\sigma (j)}^{'} (x_{i} ) = h_{B\sigma (j)}^{'} (x_{i} ),\quad \kappa_{\text{HFRS}} (A,B) = 1. $$

(23)

Definition 11

[30] Information entropy H(X) of knowledge X proffers the uncertainty measure about knowledge X and is evaluated as

$$ H(X) = - \sum\limits_{i = 1}^{n} {p(X_{i} )\log } p(X_{i} ). $$

(24)

Methodology

Here, a detailed and systematic description on the proposed mathematical design for DM in HFR framework is proffered. The novelty exists in rendering weighted entropy centered optimum attribute selection method for assessing correlation of the input alternatives with the output class in HFR domain. Entropy weight approach gauges value dispersion in DM and is the common weighting methodology. If the degree of dispersion is greater, then its degree of differentiations will be greater, and can derive more information. Moreover, the maximal weight must be provided to the index and vice versa. This entropy weighting approach always gives reliable and effective results. As per [9], the DM uncertainty could be best expounded with the employment of HFSs. The relevant attributes could be specified for further processing utilizing entropy centered evaluation of weights for the attributes. MCDM in HFS was extensively studied by [10, 16]. Nevertheless, the performance indicators employed by Zhang et al. [29] render ambiguous outcomes on the dataset utilized in this work. Hence, these performance indicators are re-framed in the proposed model. As the fifth parameter, the FTOPSIS centered performance indicator is utilized to assess the alternatives appropriately. A detailed clarification of the approach is proffered below:

• 1. Consider an attribute set of {${\text{A}}_{1} , {\text{A}}_{2} , {\text{A}}_{3} \ldots {\text{A}}_{n}$} for an HFS in $X = \{ x_{1} ,x_{2} ,x_{3} \ldots x_{n} \}$. The hesitant fuzzy decision matrix (HFDM) is

  $$ D = \left[ {\begin{array}{*{20}c} {h_{11} } & {h_{12} } & \ldots & {h_{1n} } \\ {h_{21} } & {h_{21} } & \ldots & \ldots \\ . & \ldots & \ldots & \ldots \\ {h_{m1} } & \ldots & \ldots & {h_{mn} } \\ \end{array} } \right]. $$

  (25)

  Also consider $R(x_{i} ,y_{j} )$ as the relational matrix which shows the fuzzy relation from $X \to Y$ where input is $x{}_{i}(x_{i} \in X)$ and output is $y_{j} (y \in Y)$

• 2. This step finds $S_{n}$ which is the normalized score matrix (NSM), where S indicates a score matrix as per Definition 3

• 3. As provided in Definition 8, the entropy-based determination of weights of attributes is

  $$ E_{j} = - \frac{1}{\ln m}\sum\limits_{i = 1}^{m} {\bar{s}_{ij} } \ln \bar{s}_{ij} \;{\text{where}}\; \, j = 1 \ldots n, $$

  (26)

  where $\bar{s}_{ij}$ signifies the NSM. Attribute weights are given is

  $$ w_{mj} = \frac{{1 - E_{j} }}{{\sum\nolimits_{j = 1}^{n} {(1 - E_{j} )} }}. $$

  (27)

• 4. Calculation of correlation coefficient for every alternative $A_{i}$ and the output $y_{j}$ is given in step 7.

• 5. Calculation of LA and UA spaces in respect of (X, Y, R) is symbolized as $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{R} (P)$ and $\bar{R}(P)$ which are the ‘2’ approximate hesitant FRS.

• 6. Computation of the performance indices (${\text{PI}}_{i}$) [29] is detailed below:

  $$ {\text{PI}}_{1} = \mathop {\hbox{max} }\limits_{{y_{i} \in Y}} \{ s(h_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{R} (P)}} (y_{i} ))\} $$

  (28)
  $$ {\text{PI}}_{2} = \mathop {\hbox{max} }\limits_{{y_{i} \in Y}} \{ s(h_{{\bar{R}(P)}} (y_{i} ))\} $$

  (29)
  $$ {\text{PI}}_{3} = \hbox{max} (s(h_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{R} (P)}} (y_{i} )),s(h_{{\bar{R}(P)}} (y_{i} ))) $$

  (30)
  $$ {\text{PI}}_{4} = \mathop {\hbox{max} }\limits_{{y_{i} \in Y}} \{ \delta_{m} (P,R(x,y)\} . $$

  (31)

  The applied decision rules are:

  • 1. If ${\text{PI}}_{1} \cap {\text{PI}}_{2} \cap {\text{PI}}_{3} \cap {\text{PI}}_{4} \ne \emptyset$, and then, the optimal output will be $y_{k}$ where k = ${\text{PI}}_{1} \cap {\text{PI}}_{2} \cap {\text{PI}}_{3} \cap {\text{PI}}_{4}$.

  • 2. If ${\text{PI}}_{1} \cap {\text{PI}}_{2} \cap {\text{PI}}_{3} \cap {\text{PI}}_{4} = \emptyset$, then optimal output would be $y_{k}$ where k = ${\text{PI}}_{1} \cap {\text{PI}}_{2} \cap {\text{PI}}_{3} .$,

  • 3. If ${\text{PI}}_{1} \cap {\text{PI}}_{2} \cap {\text{PI}}_{3} = \emptyset$, then optimal output will be $y_{k}$ where k = ${\text{PI}}_{i} \cap {\text{PI}}_{j}$, $i \ne j{\kern 1pt} {\text{ and }}{\kern 1pt} i,j = 2,3,4$

  • 4. The decision for optimal output shall be provided by ${\text{PI}}_{1}$ when 1 and 2 are false

• 7. This work proposed the application of FTOPSIS to evaluate the degree of closeness ($\delta$) as performance indicator (${\text{PI}}_{5}$). A novel integration of FTOPSIS with the FRS centered MCDM renders an accurate and robust optimal DM system. The proposed performance indicator (${\text{PI}}_{5}$) could be computed as follows:

  • (a) Consider the correlation matrix between $A_{i}$ and $y_{j} .$

  • (b) Evaluate normalized correlation score matrix $r_{ij}$

    $$ r_{ij} = \frac{{x_{ij} }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {x_{ij}^{2} } } }}. $$

    (32)

  • (c) Multiply each column with the weights decided by the experts to evaluate the weighted decision matrix $v_{ij}$

    $$ v_{ij} = w_{ij} r_{ij} . $$

    (33)

  • (d) The maximum value of each column vector is determined and is the ideal positive solution $v_{j}^{*}$. Also, the ideal negative solution $v_{j}^{ - }$ is determined.

  • (e) Evaluate the Euclidean distance (ED) from $v_{j}^{*}$ to each alternative as,

    $$ D^{ + } (x_{j} ) = \sqrt {\sum\limits_{j = 1}^{n} {(v_{j}^{*} - v_{ij} )^{2} } } . $$

    (34)

  • (f) Compute the ED between $v_{j}^{ - }$ and each alternative as,

    $$ D^{ - } (x_{j} ) = \sqrt {\sum\limits_{j = 1}^{n} {(v_{j}^{ - } - v_{ij} )^{2} } } . $$

    (35)

  • (g) The $\delta$ renders a rational solution to the problem of ascertaining optimum attributes for a specific dataset. Find $\delta$ for every alternative as:

    $$ \delta (x_{j} ) = \frac{{D^{ - } (x_{j} )}}{{D^{ - } (x_{j} ) + D^{ + } (x_{j} )}}. $$

    (36)

This work proposes $\delta$ as the ${\text{PI}}_{5}$, an additional performance indicator in fuzzy rough approach. The decision rules are also enhanced accordingly to have rules which assist in choosing input samples having maximal correlation with the class and $\delta$ regarding the output parameters. The rules are re-framed as:

• 1. If ${\text{PI}}_{1} \cap {\text{PI}}_{2} \cap {\text{PI}}_{3} \cap {\text{PI}}_{4} \cap {\text{PI}}_{5} \ne \emptyset$, then optimal output will be $y_{k}$ where k =  ${\text{PI}}_{1} \cap {\text{PI}}_{2} \cap {\text{PI}}_{3} \cap {\text{PI}}_{4} \cap {\text{PI}}_{5} .$

• 2. If ${\text{PI}}_{1} \cap {\text{PI}}_{2} \cap {\text{PI}}_{3} \cap {\text{PI}}_{4} \cap {\text{PI}}_{5} = \emptyset$, then optimal output would be $y_{k}$ where k =  $({\text{PI}}_{1} \cap {\text{PI}}_{2} \cap {\text{PI}}_{3} ) \cup ({\text{PI}}_{4} \cup {\text{PI}}_{5} ).$

• 3. If ${\text{PI}}_{1} \cap {\text{PI}}_{2} \cap {\text{PI}}_{3} = \emptyset$, then optimal output will be $y_{k}$ with k =  $({\text{PI}}_{1} \cap {\text{PI}}_{2} ) \cup ({\text{PI}}_{4} \cup {\text{PI}}_{5} ).$

• 4. If ${\text{PI}}_{1} \cap {\text{PI}}_{2} = \emptyset$, then optimal output would be $y_{k}$; here, k =  $({\text{PI}}_{4} \cup {\text{PI}}_{5} ).$

• 5. If $({\text{PI}}_{4} \cup {\text{PI}}_{5} ) = \emptyset$, then optimal output will be ${\text{PI}}_{5} .$

Experimentation and implementation

Experimentation is made on two datasets. A medical diagnosis dataset which is utilized by [6, 31, 32] is proffered as Table 1. Medical diagnosis dataset has patients $A = \{ A_{1} ,A_{2} ,A_{3} ,A_{4} \}$ who show the symptoms are evinced as $x = \{ x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} \}$ where $x_{1}$ indicates “temperature”,$x_{2}$ stands for “headache”,$x_{3}$ stands for “stomach pain”,$x_{4}$ stands for “cough”, and $x_{5}$ stands for “chest pain”. The probable diseases are evinced as $Y = \{ y_{1} ,y_{2} ,y_{3} ,y_{4} \}$ where $y_{1}$ stands for “Viral fever”,$y_{2}$ stands for “Malaria”,$y_{3}$ stands for “Typhoid”, and $y_{4}$ stands for “Chest problem”. Table 2 indicates the values that are possible as per the expert information. Grounded on the steps described in methodology, correlation matrix is proffered as Fig. 1 and is calculated. It is followed by the evaluation of LA and UA sets. The proposed performance indicator (${\text{PI}}_{5}$) is evaluated utilizing the FTOPSIS technique as elucidated in Step 7. Finally, the rules stated in the proposed work are applied for diagnosis of the disease. Table 3 evinces the calculations for ideal positive and negative solutions, and $\delta$. Performance indicator ${\text{PI}}_{5}$ provides $\delta$ between the input samples and the outputs. Hence, for the medical diagnosis problem,$y_{1}$ exhibits greater $\delta$ to the input samples, i.e., patients. This result is completely consistent with the outcomes acquired utilizing the performance indicators proposed by [16]

Table 1 HFS for symptoms shown by the patients

Table 2 Diagnosis of the patient according to symptoms

Fig. 1

Correlation matrix between the input alternative (patients) and the outputs (diseases)

Table 3 Calculations for degree of closeness according to fuzzy TOPSIS technique

However, the below example clearly emphasizes the necessity of the proposed performance indicator i.e.${\text{PI}}_{5}$ as ${\text{PI}}_{1}$ to ${\text{PI}}_{4}$ performance indicators produced ambiguous results. Consider the following HFS in $X = \{ x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} \}$ which indicates the decision given by the risk evaluation committee. Let $A = \{ A_{1} ,A_{2} \ldots A_{10} \}$ be the ten firms to be evaluated on the basis of criteria { $x_{1}$:managers’ work experience, $x_{2}$:profitability, $x_{3}$:operating capacity, $x_{4}$: ability of paying debt, and $x_{5}$: market competition}. The outcome is also provided as imprecise membership values as evaluated by the risk evaluation committee in the form of FS which is a special form of hesitant set [1]. The corresponding HFDM is proffered as Table 4. $Y = \{ y_{1} ,y_{2} ,y_{3} \}$ where $y_{1}$: corporate stability index, $y_{2}$: survival index and $y_{3}$:long-term economical growth. Let the correlation between the criteria $x_{i}$ and Y is provided by the risk evaluation committee as indicated in Tables 4 and 5.

Table 4 Hesitant fuzzy input decision matrix

Table 5 Hesitant fuzzy output decision matrix

The algorithm commences with the evaluation of score matrix for Table 6 as expounded in Definition 7. The evaluated score matrix is proffered in Table 6.

Table 6 Score matrix for HFS

The NSM given in Table 7 facilitates the evaluation of entropy and weights (as in Definition 8) to have optimal attributes.

Table 7 Normalized score matrix

The NSM given in Table 8 facilitates the evaluation of entropy and weights (as in Definition 8) for the computation of optimal attributes:

Table 8 HFDM with repetition in required membership values

$$ E_{j} = [\begin{array}{*{20}c} {0.978} & {0.978} & {0.975} & {0.944} & {0.976} \\ \end{array} ] $$

(37)

$$ w_{j} = [\begin{array}{*{20}c} {0.146} & {0.150} & {0.167} & {0.373} & {0.164} \\ \end{array} ]. $$

(38)

The weight vector w_j symbolizes the significance of the attributes. Therefore, further steps involve the computation of the weighted decision matrix proffered as Table 9 which is attained by multiplying the elements of Table 8 with their respective column weights given by $w_{j}$. Table 9 is same as Table 1, but the only difference is that the length of all sequences is made the same by extending the higher membership value for a specific sequence as stated by [1]. This updation in the HFDM is needed for the evaluation of the correlation matrix.

Table 9 Weighted hesitant fuzzy decision matrix

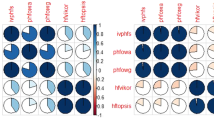
Table 9 is then utilized to evaluate the correlation coefficient $\kappa_{\text{HFRS}} (A_{i} ,y_{i} )$ utilizing Definition 10. This further enables the calculation of $\delta_{m} (A_{i} ,y_{i} )$ as evinced in Fig. 2

Fig. 2

Correlation between input samples and output space

Figure 2 signifies the correlation of the ten firms $A_{i}$ which were to be evaluated centered on the criteria {$x_{1}$:managers’ work experience, $x_{2}$:profitability, $x_{3}$:operating capacity, $x_{4}$: ability of paying debt, and $x_{5}$:market competition with $Y = \{ y_{1} ,y_{2} ,y_{3} \}$, where {$y_{1}$: corporate stability index, $y_{2}$: survival index as well as $y_{3}$: long-term economical growth. The output $y_{1}$ has a maximal degree of correlation (0.213) to the input samples $A_{8}$, while the output $y_{2}$ has 0.205 (higher) to the input samples $A_{5}$, and the output $y_{3}$ has 0.219 (higher) to the input samples $A_{1} \;{\text{and}}\;A_{7}$. As given in the methodology, the upper HFRA and lower HFRA are evaluated utilizing Definition 8. The outcomes are proffered as Tables 10 and 11

Table 10 The lower HFRA

Table 11 The upper HFRA

For calculating the performance indices, the equivalent score matrices of LA and UA hesitant FRSs are needed. These sets are evaluated and even tabulated as Table 12 and 13.

Table 12 Score function of lower hesitant fuzzy RS

Table 13 Score function of upper hesitant fuzzy RS

Calculation for ${\text{PI}}_{5}$ grounded on FTOPSIS approach is then carried out. The correlation matrix which is the input matrix for FTOPSIS is evaluated. Figure 2 details those correlation matrices between input samples and output samples. The weights for $y_{i}$ for the further calculations are presumed to be 1 as all the outputs $y_{i}$ are equally significant. Figure 3 indicates the ideal positive solution and ideal negative solution as expounded in step 7. This follows the ED calculation which is evinced in Tables 14 and 15. Finally, Fig. 4 indicates $\delta$ calculation.

Fig. 3

Ideal positive and negative solutions

Table 14 Calculation of ED for an ideal positive solution

Table 15 Calculation of ED for ideal negative solution

Fig. 4

Degree of closeness between input and output samples

Figure 4 evinces $\delta$ of the ‘Y’ output in respect of the input samples. The output $y_{1}$ has higher $\delta$ (0.58) to the input samples $A{}_{i}$ which means that the ten firms could provide a better corporate stability as contrasted to long-term economical growth and survival index. That means the output of the survival index ($y_{2}$) as well as long-term economical growth ($y_{3}$) gives $\delta$ of 0.44 and 0.51 to the input samples which are lower on considering the output $y_{1}$. Tables 10, 11, 12, 13, 14, and 15 finally help in $(PI_{i} )$ calculation of as proffered in Table 16

Table 16 Performance indicator table

Table 16 implies that the entire alternatives cannot be estimated utilizing an algorithm that is recommended in [16]. Column 6 has a letter I written for alternatives $A_{3} ,A_{4} ,A_{9}$ and $A_{10}$.Those alternatives have ${\text{PI}}_{2}$ carrying two values. Zhang et al.’s algorithm [29] does not render a solution for these cases. Nevertheless, the proposed algorithm incorporated an additional performance indicator ${\text{PI}}_{5}$ that is centered on FTOPSIS, and this is capable of having a solution to the aforesaid ambiguity. The $\delta$ betwixt the input alternatives and output aids the fuzzy rough centered MCDM in making a suitable decision. Therefore, the proposed work exclusively renders correlations betwixt the input alternatives and the output in line with the evaluation criterion. It is concluded as of the aforesaid outcomes that the proposed DM can be properly employed to resolve the manifold and DM issues with completely unidentified attribute weights. The proposed work renders a helpful means for managing multicriteria fuzzy DM issues within attribute weights. An appropriate entropy weighting methodology derives the attribute weights as per alternative, and it picks the best alternative as per them.

Conclusion

The proposed work methodically modeled the MCDM for hesitant FRSs. An additional performance parameter “FTOPSIS centered $\delta$” is also proposed here to resolve ambiguous cases effectively. And, this is confirmed via implementations on multiple datasets. Correlation matrix which shows the correlation of input alternatives with the output class grounded on a certain set of criteria eventually assists in computing the proposed FTOPSIS centered performance index. Entropy-centric weighing of the attribute aids in selecting the relevant as well as non-redundant attributes. Grounded on the volume of information, this entropy approach finds the index’s weight for the attributes, which is the objective fixed weight methodology. The disorder degrees of the attributes and their utility in the system information are ascertained by Entropy. Finally, the evaluations of upper HFRA and lower approximate HFRA further facilitate the selection of optimum attributes. Thus, a generic approach which is hybrid entropy-centric optimal attribute selector, i.e., RSs and HFSs, shall effectually assist the researchers in vagueness and uncertain DM problems without an ambiguity. Utilizing this proposed entropy weight centric approach, the weights of the attributes are found and the appropriate attributes are selected which eradicates the disturbances (caused by man) and makes outcomes as per facts. The entropy weight together with FTOPSIS method is clear, simple, and reasonable when contrasted to fuzzy synthetic assessment and other evaluation approaches. Nevertheless, the entropy weighting approach merely regards the numerical discrimination degrees of the attribute index and disregards rank discrimination. These shortcomings signify that the entropy approach could not exactly reflect the significance of the index weight, thus causing distorted DM results. This problem can well be tackled in future.

In addition, knowledge reduction is the notable content for the research of RS theory. Therefore, in the future, the proposed algorithm can be extended grounded on interval-valued FRSs and type 2 FSs for knowledge reduction under complete information systems.