Introduction

The fuzzy transportation problem is one of the most well-known optimization problems in the field of fuzzy set and system. This problem appears in many real-life applications, e.g., computer networks, routing, shortest path problems [1,2,3,4,5,6,7,8], communication, etc. It has been researched extensively in many engineering fields such as electronics engineering, electrical engineering, and computer science in terms of effective algorithms.

The supply and demand costs are considered as real numbers, i.e., crisp numbers in classical transportation problems. It computes a solution on the base of demand and supply. It has been applied in many fields, including optimal control, inventory, logistics management, and supply chain management. Many researchers have used fuzzy variables/numbers (especially triangular fuzzy number and trapezoidal fuzzy number) to express the approximate intervals, linguistic terms, and unequally possible data set. Zimmermann [9] has introduced a fuzzy linear programming model. It has applied to solve different fuzzy transportation problem (FTP) [10,11,12,13,14]. Chanas et al. [15] proposed a fuzzy linear programming model to determine the solution of an FTP with fuzzy supply and demand, but transportation costs are in real number. Dinagar and Palanivel [16] described an FTP where demand, supply, and transportation costs are trapezoidal fuzzy numbers. Kaur and Kumar [17] have introduced an algorithmic for solving the fuzzy transportation problem. Some researchers used the rough set to handle the uncertainty of transportation problems. Liu [18] has initiated the concept of rough variables to manage the uncertainty of the problem. Xu and Yao [19] have proposed an algorithmic approach for solving the two-person zero-sum matrix games with payoffs as rough variables. Kundu et al. [20] introduced a solid transportation model with crisp and rough costs. Some other researchers [21,22,23,24,25,26,27,28,29,30] also have studied this transportation problem in a fuzzy environment.

Usually, human perception [31, 32] is used to evaluate the degree of membership of an ordinary fuzzy set, which is a crisp value. However, it may not be possible to find an exact membership degree using a type-1 (ordinary) fuzzy set, i.e., fuzzy variable/number because of various types of complications, insufficient information, noises, multiple sources of available data. The type 2 fuzzy set is an extension of a fuzzy set, and it can be used to solve them. Type 2 fuzzy set (T2FS) [33, 34] has also been proposed by Zadeh [33] as an extension of type 1 fuzzy set (T1FS), about 10 years after he has introduced T1FS. Zadeh [33] has described the T2FS as the fuzzy set, which is a mapping from U to [0, 1] with the membership function of this set, classified as type 1. The uncertainty associated with the linguistic description of information [35,36,37,38,39] is not represented properly by T1FS due to incorrectness of human perception in the evaluation of membership degrees having crisp values. Mendel and Karnik [40] have enhanced the number of degrees of freedom for fuzzy sets. They have described the idea to add at least one higher degree to T1FSs. It provides a measurement of dispersion for a certain membership degree of T1FS. Hence, T2FS is the extension of the T1FS to a higher degree. T2FSs have a degree of membership that is itself determined by T1FSs. The membership function of T2FS is known as secondary membership functions. T2FS enhances the number of degrees of immunity to handle the ambiguity of the problem T2FS and has a better ability to cover inexact information is logically appropriate behavior. Since the generalized T2FSs are demanding for computation, most of the researchers use interval type-2 fuzzy set (IT2FS) in practical fields [41,42,43,44,45,46,47,48]. Computation in IT2FS is more manageable compared to generalize T2FS. Both IT2F membership function and generalized fuzzy membership function are three dimensions, but the secondary membership value of the IT2F membership function is all-time equal to 1.

Fig. 1
figure 1

Crisp grades of membership for type-1 fuzzy set (T1FS) A

Full size image
Fig. 2
figure 2

Fuzzy grades of membership for IT2FS \({\widetilde{A}}\) (color figure online)

Full size image

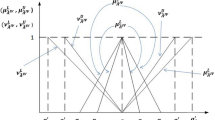
Let A is a type-1 fuzzy set and \({\widetilde{A}}\) is an interval type-two fuzzy set as displayed in Figs. 1 and 2, respectively. For a certain value of x, say \(x_i\), a single membership value \(r_1\) is obtained in A. However, there is an interval of membership degree between \(r_1\) and \(r_2\) in \({\widetilde{A}}\) for the same value of \(x_i\).

The motivation of this paper is to present an algorithmic approach for the transportation problem, which will be simple enough and efficient in real-world situations. In transportation problems, transportation parameters (e.g., demands, supplies, transportation costs) are not always crisp, and that parameters could be uncertain due to several reasons. Therefore, computing the exact parameters in such scenarios could be challenging. Fuzzy can be used in transportation problems to handle this type of uncertainty, and many researchers have described this transportation problem with type 1 fuzzy variables. T2FS extends the degrees of freedom to present uncertainties, and it increases the capacity to deal uncertain/fuzzy/inexact information of any real-life problem in a logically appropriate manner. The main objective of this paper is to consider transportation problems with T2FSs. In this paper, we have mainly investigated the following things:

  1. 1.

    We propose an algorithm to solve the fuzzy transportation problem based on Modified Vogel‘s approximation method (MVAM), where the costs are trapezoidal IT2FSs.

  2. 2.

    We introduce a linear programming problem (LPP) method for solving this problem.

The rest of our paper is arranged as follows.

In Sect. 2, we briefly describe some ideas about the fuzzy set, T1FS, T2FS, IT2FS and centroid-based ranking method [49]. In Sect. 3, we introduce the interval type 2 fuzzy transportation problems and some algorithms with flowcharts to solve this problem. In Sect. 4, the two numerical examples are illustrated to describe our proposed algorithm. We present the conclusion in Sect. 5.

Preliminaries

Definition 1

Modification form of classical set is called the fuzzy set, where the elements have various degrees of membership. In the classical set, the logic is based on two truth values, either it will be true or it will be false. It is sometimes insufficient when relating human thoughts. Fuzzy logic can use the whole interval between 1 (true) and 0 (false) for better result. A fuzzy set accommodate its members with different membership degrees in the interval [0, 1]. Let x be an element of X, then a fuzzy set \({\tilde{A}}\) in X is a set of ordered pairs in which the value of \(\mu _{{\widetilde{A}}}\left( x,u\right) \) lies between 0 and 1. Here, x is primary variable, \(T_x\) is primary membership function of x, u is the secondary variable and \(\mu _{{\widetilde{A}}}\left( x,u\right) \) is the secondary member function of x.

$$\begin{aligned} {\tilde{A}}=\left\{ x,\mu _{{\tilde{A}}}\left( x\right) | x\in X\right\} . \end{aligned}$$
(1)

Definition 2

[50]. A T2FS, represented as \({\widetilde{A}}\), is described by a type-2 membership function \(\mu _{{\widetilde{A}}}\left( x,u\right) \), where u \(\in \) \(T_x\) \(\subseteq \) [ 0, 1 ] and x \(\in \) X, i.e.,

$$\begin{aligned} {\widetilde{A}}=\left\{ \left( \left( x,u\right) ,\mu _{{\widetilde{A}}}\left( x,u\right) \right) \mid \forall x \in X,\forall u \in T_{x}\subseteq \left[ 0,1\right] \right\} \end{aligned}$$
(2)
$$\begin{aligned} {\int }_{x \in X}{\int }_{u \in T_x} \mu _{{\widetilde{A}}}\left( x,u\right) \big /\left( x, u\right) , \end{aligned}$$
(3)

where \(\int \int \) describes union over all primary variable x and secondary variable u and \(T_{x}\subseteq \left[ 0,1\right] \). For discrete universes of discourse, \(\int \int \) is changed by \(\sum \).

Fig. 3
figure 3

Trapezoidal interval type 2 fuzzy set (IT2FS) \(\widetilde{A_i}\) with footprint of uncertainty (FOU) (color figure online)

Full size image

Definition 3

[50] : IT2FS is a simpler version of T2FS. IT2FS has uniform shading over the footprint of uncertainty (FOU). A T2FS with all \(\mu _{{\widetilde{A}}}\left( x,u\right) \) =1 is named an IT2FS. Let \({\widetilde{A}}\) represent an IT2FS, then it is described as

$$\begin{aligned} {\int }_{x \in X}{\int }_{u \in T_x}1 \big /\left( x, u\right) ={\int }_{x \in X}\left[ {\int }_{u \in T_x} 1 \big / u\right] \bigg / x, \end{aligned}$$
(4)

where primary variable is x,the primary membership of x is \(T_{x}\) an interval in [0,1], the secondary variable is u and the secondary membership function at x is \(\int _{u \in T_x} 1/u\).

In this paper, we initiate an algorithmic problem for solving Transportation problem using IT2FS. Heights of the lower and upper membership functions of IT2FS represent an IT2FS of a reference point. We consider trapezoidal IT2FS in our algorithm. A trapezoidal IT2FS \({\widetilde{A}}\) is shown in Fig. 3. The shaded region is the FOU. It is bounded by a lower membership function (LMF) \(\underline{\mu _{i}}\left( x_{i}\right) \) and an upper membership function (UMF) \(\overline{\mu _{i}}\left( x_{i}\right) \). The LMF and UMF have represented type-1 fuzzy sets.

Definition 4

[51]: Let us consider two trapezoidal IT2FSs \({\widetilde{A}}_{1}\) and \({\widetilde{A}}_{2}\), where

\({\widetilde{A}}_{1} = \left( {\widetilde{A}}_{1}^{U},{\widetilde{A}}_{1}^{L}\right) = \left( a_{11}^{U},a_{12}^{U},a_{13}^{U},a_{14}^{U};H_{1}\left( {\widetilde{A}}_{1}^{U}\right) ,H_{2}\left( {\widetilde{A}}_{1}^{U}\right) \right) \)

\(\left( a_{11}^{L},a_{12}^{L},a_{13}^{L},a_{14}^{L};H_{1}\left( {\widetilde{A}}_{1}^{L}\right) ,H_{2}\left( {\widetilde{A}}_{1}^{L}\right) \right) \)

\({\widetilde{A}}_{2}=\left( {\widetilde{A}}_{2}^{U},{\widetilde{A}}_{2}^{L}\right) =\left( a_{21}^{U},a_{22}^{U},a_{23}^{U},a_{24}^{U};H_{1}\left( {\widetilde{A}}_{2}^{U}\right) ,H_{2}\left( {\widetilde{A}}_{2}^{U}\right) \right) \)

\(\left( a_{21}^{L},a_{22}^{L},a_{23}^{L},a_{24}^{L};H_{1}\left( {\widetilde{A}}_{2}^{L}\right) ,H_{2}\left( {\widetilde{A}}_{2}^{L}\right) \right) \).

Addition [51] operation (\(\oplus \)) among the two trapezoidal IT2FSs \(\widetilde{A_{2}}\) and \(\widetilde{A_{1}}\) is defined in (5) as follows.

$$\begin{aligned} \widetilde{A}_{1} = &(\widetilde{A}_{1}^{U},\widetilde{A}_{1}^{L}) \\ = &((a_{11}^{U},a_{12}^{U},a_{13}^{U},a_{14}^{U};H_{1}(\widetilde{A}_{1}^{U}),H_{2}(\widetilde{A}_{1}^{U})) \\ &(a_{11}^{L},a_{12}^{L},a_{13}^{L},a_{14}^{L};H_{1} \widetilde{A}_{1}^{L}),H_{2}(\widetilde{A}_{1}^{L}))) \end{aligned}$$
(5)

The result of Addition is also a IT2FS. Multiplication [51] operation (\(\otimes \)) between the two trapezoidal IT2FSs \(\widetilde{A_{1}}\) and \(\widetilde{A_{2}}\) is defined in (6) as follows.

$$\begin{aligned} \widetilde{A}_{2}=&(\widetilde{A}_{2}^{U},\widetilde{A}_{2}^{L}) \\ =&((a_{21}^{U},a_{22}^{U},a_{23}^{U},a_{24}^{U};H_{1}(\widetilde{A}_{2}^{U}),H_{2} (\widetilde{A}_{2}^{U}))\\&(a_{21}^{L},a_{22}^{L},a_{23}^{L},a_{24}^{L};H_{1}(\widetilde{A}_{2}^{L}),H_{2} (\widetilde{A}_{2}^{L})))\end{aligned}$$
(6)

The result of Multiplication is also a IT2FS.

Definition 5

[52]: The centroid value,i.e., \(C({\widetilde{B}})\) of an IT2FS \({\widetilde{B}}\) is the union of the centroid values of all its embedded type 1 fuzzy set \(B_{e}\) as follows.

$$\begin{aligned} C\left( {\widetilde{B}}\right) =\bigcup _{\forall B_{e}}c\left( B_e\right) =\left[ c_{l}\left( {\widetilde{B}}\right) ,c_{r}\left( {\widetilde{B}}\right) \right] . \end{aligned}$$
(7)

Here \(\cup \) represents the union operation and

$$\begin{aligned}&c_{l}\left( {\widetilde{B}}\right) =\min _{\forall {B_e}}\left( c\left( B_{e}\right) \right) \end{aligned}$$
(8)
$$\begin{aligned}&c_{r}\left( {\widetilde{B}}\right) =\max _{\forall {B_e}}\left( c\left( B_{e}\right) \right) \end{aligned}$$
(9)
$$\begin{aligned}&c\left( B_e\right) =\frac{\sum _{i=1}^{N}x_{i}\mu \left( x_{i}\right) }{\sum _{i=1}^{N} \mu \left( x_{i}\right) }. \end{aligned}$$
(10)

It is expressed in [40, 52,53,54] that \(c_l\left( {\widetilde{B}}\right) \) and \(c_r\left( {\widetilde{B}}\right) \) can be described as follows:

$$\begin{aligned}&c_l\left( {\widetilde{B}}\right) =\frac{\sum _{i=1}^L x^{i}\overline{\mu _{i}}\left( x_i\right) + \sum _{i=L+1}^{N} x^{i}\underline{\mu _{i}}\left( x_{i}\right) }{\sum _{i=1}^{L }\overline{\mu _{i}}\left( x_i\right) +\sum _{i=L+1}^{N} \underline{\mu _{i}}\left( x_i\right) } \end{aligned}$$
(11)
$$\begin{aligned}&c_r\left( {\widetilde{B}}\right) =\frac{\sum _{i=1}^R x^{i}\underline{\mu _{i}}\left( x_i\right) + \sum _{i=R+1}^{N} x^{i}\overline{\mu _{i}}\left( x_{i}\right) }{\sum _{i=1}^{R }\underline{\mu _{i}}\left( x_i\right) +\sum _{i=R+1}^{N} \overline{\mu _{i}}\left( x_i\right) }. \end{aligned}$$
(12)

Here R and L are right and left switch points. First, we calculate the centroids for IT2FS \({\widetilde{B}}\), then we find out the average centroid

$$\begin{aligned} C\left( {\widetilde{B}}\right) =\frac{c_{l}\left( {\widetilde{B}}\right) +c_{r}\left( {\widetilde{B}}\right) }{2}. \end{aligned}$$
(13)

Here centroid-based ranking value [49] of IT2FS \({\widetilde{B}}\) is \(C({\widetilde{B}})\).

Definition 6

[55]: Let \({\widetilde{B}}_{1}\) and \({\widetilde{B}}_{2}\) be considered two interval type 2 fuzzy sets (IT2FSs). Then

The value of IT2FS \({\widetilde{B}}_{1}\) is greater than \({\widetilde{B}}_{2}\) if \(c({\widetilde{B}}_{1})\) > \(c({\widetilde{B}}_{2})\).

The value of IT2FS \({\widetilde{B}}_{1}\) is less than \({\widetilde{B}}_{2}\) if \(c({\widetilde{B}}_{1})\) < \(c({\widetilde{B}}_{2})\).

The value of IT2FS \({\widetilde{B}}_{1}\) is equal to \({\widetilde{B}}_{2}\) if \(c({\widetilde{B}}_{1})\) \(=\) \(c({\widetilde{B}}_{2})\).

Proposed algorithm for fuzzy interval type 2 transportation problem

Mathematical statement

Suppose that there are p numbers of sources and q destination. Let \({\tilde{s}}_{i}\) represent the fuzzy numbers of sources i (\(i = 1,2,3,\ldots ,p\)) and let \({\tilde{d}}_{j}\) represent the fuzzy numbers of destinations j (\(j = 1,2,3,\ldots ,q\)).

Mathematical model of fuzzy transportation problem is given below:

$$\begin{aligned} \text {Minimize}~~ {\tilde{Z}} = \sum _{i=1}^{p}\sum _{j=1}^{q} {\tilde{c}}_{ij} {\tilde{z}}_{ij}, \end{aligned}$$
(14)

subject to

$$\begin{aligned}&\sum _{j=1}^{q} {\tilde{z}}_{ij} = {\tilde{s}}_{i}, \quad i=1,2,\ldots ,p \end{aligned}$$
(15)
$$\begin{aligned}&\sum _{i=1}^{p} {\tilde{z}}_{ij} = {\tilde{d}}_{j}, \quad j=1,2,\ldots ,q \end{aligned}$$
(16)
$$\begin{aligned}&{\tilde{z}}_{ij} \ge 0 ~~~~ \forall i,j, \end{aligned}$$
(17)

where \({\tilde{c}}_{ij}\) is the interval type 2 fuzzy set that represents the transportation cost for one unit from source node i to the destination node j and \({\tilde{z}}_{ij}\) is the interval type 2 fuzzy set of units transported from source i to destination j. \({\tilde{s}}_{i}\) is the supply at source i and \({\tilde{d}}_{j}\) is the demand at destination j.

Proposed algorithm 1

The Vogel’s approximation method algorithm is a well-known algorithm to compute the transportation problem. In this article, we modify the VAM algorithm to handle the transportation problem in a fuzzy environment. Most of the cases, researches use T1FS or fuzzy number as transportation cost value. T1FS is unable to handle the ambiguity due to the inaccuracy of human conception. An interval type-2 fuzzy set (IT2FS) is an extension of the type 1 fuzzy set. IT2FS can handle this ambiguity. The flowchart of modified Vogel’s approximation method is shown in Fig. 4.

Fig. 4
figure 4

Flowchart of modified Vogel’s approximation method (color figure online)

Full size image
  1. Step 1 :

    In this problem, the cell cost, demand, and supply are considered as trapezoidal IT2FSs. The centroid value of IT2FS, i.e., the real values of each cell, demand, and supply have computed using Eq. (13). These are used for computation purposes.

  2. Step 2:

    For the given transportation table, determine the cost of the penalty, distinction between minimum cost and next minimum cost of every column and rows.

  3. Step 3:

    Select the largest penalty value from all column and row difference, which is found out in Step 2 and select the corresponding row or column.

  4. Step 4:

    In this step, select the least cost in row or column which is identified in Step 3.

  5. Step 5:

    This step allocates minimum value corresponding row and column value which is select in Step 4.

  6. Step 6:

    Depending upon this cell which column or row has adjusted, this column or row has removed.

  7. Step 7:

    Same methodology from Step 2 to Step 6 has been applied to the rest of all the unallocated cells until all demands and supplies have been adjusted.

Proposed Algorithm 2

Fig. 5
figure 5

Flowchart of proposed LPP method

Full size image
  1. Step 1 :

    Formulate the given transportation problem into linear programming method using Eqs. (14) and (17).

  2. Step 2 :

    Using definition of centroid ranking (Definitions 5 and 6), write the standard linear model as given below.

    $$\begin{aligned} \text {Minimize}~~ {\tilde{Z}} = \sum _{i=1}^{m}\sum _{j=1}^{n} {\tilde{c}}_{ij}^R {\tilde{z}}_{ij}, \end{aligned}$$
    (18)

    subject to

    $$\begin{aligned}&\sum _{j=1}^{n} {\tilde{z}}_{ij} = {\tilde{a}}_{i}^R, \quad i=1,2,\ldots ,m \end{aligned}$$
    (19)
    $$\begin{aligned}&\sum _{i=1}^{m} {\tilde{z}}_{ij} = {\tilde{b}}_{j}^R, \quad j=1,2,\ldots ,n \end{aligned}$$
    (20)
    $$\begin{aligned}&{\tilde{z}}_{ij} \ge 0 ~~~~ \forall i,j, \end{aligned}$$
    (21)

    where \({\tilde{c}}_{ij}^R = C({\tilde{c}}_{ij})\), \({\tilde{a}}_{i}^R = C({\tilde{a}}_{i})\), \({\tilde{b}}_{j}^R = C({\tilde{b}}_{i})\), C is the centroid rank.

  3. Step 3:

    We use Definition 4 in Eq. (19) and find out the crisp standard model.

  4. Step 4:

    Solve the given problem using the standard linear programming technique and find out the optimal value and objective value.

  5. Step 5:

    We get the fuzzy optimal cost to use this value in Eq. (14).

  6. Step 6:

    End.

The flowchart of the proposed LPP method is shown in Fig. 5.

Modified MODI method

Optimality tests always conduct depend upon the initial basic feasible solution of a transportation problem, where the value of \(m+n-1\) is equal to the number of non-negative unoccupied cells and n is the number of columns and m is the number of row. These all allocated cells stay in an independent position. This type of method always uses for better solutions than the initial basic feasible solution. The flowchart of the modified MODI (MMODI) method is shown in Fig. 6.

Fig. 6
figure 6

Flowchart of modified MODI method

Full size image
  1. Step 1:

    Calculate \({u}_{i}\) and \({v}_{j}\) with the expression \({u}_{i} + {v}_{j}={c}_{ij}\) for each occupied cell.

  2. Step 2:

    Consider the value of \({u}_{i}\) or \({v}_{j}\) equal to 0 to any row or column, respectively, with having maximum no of allocation. If it is more than one then choose any one of them arbitrarily and calculate rest of all \({u}_{i}\) and \({v}_{j}\) for all rows and columns, respectively.

  3. Step 3:

    Compute the value of every unoccupied cell with the equation \({\widetilde{x}}_{ij}\) = \({c}_{ij}\) − (\({u}_{i}\) + \({v}_{j}\)).

  4. Case I:

    Have an unique solution and it is an optimal solution if all \({\widetilde{x}}_{ij} > 0\).

  5. Case II:

    Have an alternative solution and it is optimal if all \({\widetilde{x}}_{ij} >= 0\).

  6. Case III:

    It has no optimal solution if \({\widetilde{x}}_{ij} < 0\). For that type, the case considers the next step for the optimal solution.

  7. Step 4:

    If case III occurs, then select the maximum negative value of \({\widetilde{x}}_{ij}\) and form a close loop with occupied cell and assign “+” and “−” sign alternately. Find out the minimum allocation with a negative sign. It will be added to the positive allocation cell and subtract from the negative allocation cell.

  8. Step 5:

    Compute and reallocate the occupied cell for finding the new set of basic feasible solutions.

  9. Step 6:

    Repeat Step 1 to Step 5 until optimal basic feasible solution occurs.

Numerical illustration

We have used two examples for demonstrating our modified Vogel’s approximation method to solve FTP with IT2FS cost, i.e., transporting each unit from source to destination.

Numerical Example I

Now we are consider first example with three supply and four demand base problem and solve it using our proposed modified Vogel’s approximation method.

Example 1

We have taken IT2FSs from [56] and which are indexed in Tables 1 and 2. In Table 1, IT2FSs transportation cost is indexed, and in Table 2 IT2FSs supply and demand are indexed.

Solution: We calculate the centroid based rank of cell cost, demand, and supply using Definitions 5 and 6.

Table 1 The cell costs of the transportation problem represented as IT2FSs for Example I
Full size table

In Table 3, the costs of transportation, supplies, and demands represent as centroid-based ranking values and Table 4 represents the final allocation table of Example I, respectively.

Table 2 The supplies and demands of the transportation problem represented as IT2FSs for Example I
Full size table
Table 3 Initial allocation table of the IT2F transportation problem for Example I
Full size table
  1. Step 1:

    Select the first row \({\widetilde{S}}_{1}\) in Table 3 and calculate the value of the difference between the lowest cost and the next lowest cost, which is 2.87. Using the same procedure, calculate the value of every corresponding column and row.

  2. Step 2:

    Select the highest value of these column difference and row difference values say 2.87.

  3. Step 3:

    Select minimum cost cell say \({\widetilde{C}}_{11}\) and allocate the value of the corresponding minimum value of supply and demand say 2.19.

  4. Step 4:

    Since demand value adjusts with cell allocation value, eliminate the first column say \({\widetilde{D}}_{1}\)

  5. Step 5:

    For creating a new table, we should be use above steps.

  6. Step 6:

    The same procedure is used in the rest of the table for finding BFS using the proposed algorithm.

Table 4 Final allocation table of the IT2F transportation problem for Example I
Full size table

In Table 4, the total number of source (m) is 3, the total number of destination (n) is 4, and total number of non-negative allocation 6 is equal to \(m + n - 1\) = 3 + 4 − 1 = 6.

So, it has a basic feasible solution. The total cost can be computed by multiplying the units assigned to the allocated value of each cell with the concerned transportation cost of respective cell.

Therefore, basic feasible solution of the problem = \(2.32*2.19\) + \(7.25*3.22\) + \(5.19*2.19\) + \(8.12*1.91\) + \(2.13*3.91\) + \(2.13*2.59\) \(=\) 69.1461.

Compute optimal value of Example I using MMODI method

Table 5 Initial allocation table for MMODI method
Full size table

To calculate the optimal value, we use the MMODI method. Tables 5 and 6 represent the initial and final allocation table of MMODI method, respectively. In Table 5, \({\widetilde{C}}_{21} = {\widetilde{S}}_{2}{\widetilde{D}}_{1} - ({\widetilde{S}}_{2} + {\widetilde{D}}_{1})\) is negative and \({\widetilde{C}}_{31} = {\widetilde{S}}_{3}{\widetilde{D}}_{1} - ({\widetilde{S}}_{3} + {\widetilde{D}}_{1})\) is Negative. Hence, does not have any optimal solution here. Proceed to next step until all \({\widetilde{C}}_{ij}\) are positive.

Table 6 Final allocation table of MMODI method
Full size table

In Table 6, all \({\widetilde{C}}_{ij}\) are positive. So, there is an optimal solution and this optimal solution is displayed in Table 7. Required optimal solution \(= 5.19*0.28 + 7.25*5.13 + 2.13*2.19 + 5.19*1.91 + 2.13*3.91 + 2.13*2.59 = 67.0683\), which is more better than the initial basic feasible solution 69.1461.

Solution of Example 1 using LINGO is 67.0683, which is exactly equal to the optimal solution of proposed algorithm.

Corresponding type 2 fuzzy optimization solution is:

= 0.28 * \({\widetilde{C}}_{12}\) + 5.13 * \({\widetilde{C}}_{13}\) + 2.19 * \({\widetilde{C}}_{21}\) + 1.91 * \({\widetilde{C}}_{22}\) + 3.91 * \({\widetilde{C}}_{24}\) + 2.59 * \({\widetilde{C}}_{34}\) = ( ( 33.6337, 56.7825, 76.0925, 104.6313 ), ( 57.002, 65.8038, 65.8038, 72.5788, 0.27 ) ).

Table 7 Optimal solution of Example I
Full size table

Numerical Example II

We considered another example with six supply and eight demand base problems and solve it modified Vogel’s approximation algorithm same as the first one.

Example 2

We have taken IT2FSs as transportation cost which are indexed in Tables 8 and 9, assigned to the IT2FSs supply and demand. Table 10 represents the corresponding ranking values and Table 11 represents the required optimal solution of Example II.

Table 8 The cell costs of the transportation problem represented as IT2FSs for Example II
Full size table
Table 9 The supplies and demands of the transportation problem represented as IT2FSs for Example II
Full size table

Solution: We have calculated the centroid based rank of cost value, demand and supply using Definitions 5 and 6.

Fig. 7
figure 7

Comparison chart of our proposed algorithms for Numerical Example I

Full size image
Table 10 The cell cost, supply and demand of the IT2F transportation problem for Example II, represented as centroid base ranking value
Full size table
Table 11 Optimal solution of Example II
Full size table

Required optimal solution = 378.2358.

Hence type 2 fuzzy optimization solution is =

((124.3066, 285.530, 440.0125, 674.5364), (351.9588, 353.8824, 399.6022, 0.27)).

Results and discussion

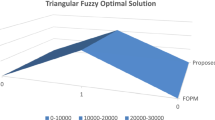
In this study, we have worked on two transportation problems. In the first problem, there are three sources and four destination nodes. We have used IT2FSs to represent those costs. The Lingo software is used to solve this problem. In Example 1, we get IT2FSTP cost is ((33.6337, 56.7825, 76.0925, 104.6313), (57.002, 65.8038, 65.8038, 72.5788, 0.27)) and the predicted optimal transportation cost is 67.0683. Here, it is clear that our predicted cost is within the IT2FS fuzzy. The efficiency of our proposed algorithm is shown in Fig. 7.

Conclusion

The VAM algorithm is a common algorithm to solve the transportation problem. In this paper, the classical VAM algorithm is modified to solve the fuzzy transportation problem fuzzy. We represent all the demand, supply, and transportation costs as IT2FSs. The idea of our proposed algorithm is elementary and effective to apply for real-world scenarios, e.g., management, transportation system, and many other network optimization problems. Here, we present two small numerical examples to demonstrate our proposed algorithm. Therefore, as future research, we have to solve a large scale practical transportation problem using the proposed algorithm. Furthermore, we will try to modify our proposed algorithm for the Pythagorean fuzzy set [57] and interval type-2 intuitionistic fuzzy sets [58,59,60,61].