Analysis of watermarking framework for color image through a neural network-based approach

Abstract

In the research presented here, the general idea of watermarking framework is analyzed to deal with color image under a set of attacks through a neural network-based approach. It is realized in the area of transformation, especially with a focus on contourlet transform to address the proposed technique, as long as the bands of the suitable coefficients are accurately chosen. In summary, there is the logo information that is embedded in the edge of color image, while the Zenzo edge detector is correspondingly realized to handle the approach. In fact, the edge of the second subband is acquired, and subsequently, the capability of the above-referenced edge is calculated. A number of techniques are discussed to cope with the above-captioned watermarking framework through the new integration of contourlet transform in association with the multilayer perceptron to extract the logo information, appropriately. The approaches of the embedding and the de-embedding in case of learning algorithm of the aforementioned neural network through individual training data set are considered in the present research to carry out a series of experiments with different scenarios for the purpose of verifying the effectiveness of the proposed approach, obviously.

Introduction

The subject behind the present research is to analyze a new robust image watermarking utilizing contourlet transform (CT) in line with the Zenzo edge detector that are organized to deal with the proposed framework to choose the bands of coefficients. The logo information is embedded in the edge of color image, as long as the Zenzo edge detector is realized. There is the second subband that is acquired. The subbands of $C1$ and $C24$ are chosen based on the color channels.

There is a focus on the realizations of the CT in connection with the Zenzo edge detector to present the research with respect to state-of-the-art, appropriately. It is to note that the main idea of the proposed watermarking framework is suggested in this research via the embedding and de-embedding techniques, while a series of attacks are applied to the outcomes for the purpose of presenting an applicable and efficient approach to be useful in real environments. In a word, the approach is an integration of new embedding and de-embedding approaches, as long as the efficiencies of the CT in association with the Zenzo edge detector are directly used to generate watermarked image and the corresponding extracted logo image with high accuracy. It is to note that there is a technique of analyzing the performance to present both watermarked image and also the corresponding extracted logo image, as well. Prior to considering the contourlet-based watermarking framework proposed, in details, it is important to survey the recent potential investigations with respect to state-of-the-art, where the integration of watermarking framework and contourlet representation are exactly researched. In one such case, Inoue et al. consider the digital watermark based on the wavelet transform and its robustness on image compression, where Liu et al. suggest the SVD-based watermarking scheme for protecting rightful ownership [1, 2]. It should be noted that the novelty of the Liu et al.'s approach is to use the SVD and also inserting the logo in “S” matrix, whilst the original image is constantly needed to extract the aforementioned logo. There is no efficient method to optimize the watermarking intensity and also the quality of logo extraction is not nearly suitable, where the verification process cannot automatically be finalized and human interactions are truly needed. Makbol et al. work is to deal with the robust blind image watermarking scheme based on redundant discrete wavelet transform and singular value decomposition and Reyes et al. work is to cope with digital video watermarking in DWT domain using chaotic mixtures [3, 4]. Abdallah et al. explore the homomorphic image watermarking with a singular value decomposition algorithm [5]. Anurag Mishra et al. propose gray-scale image watermarking. Here, the singular values of a binary watermark are all embedded in singular values regarding the subband coefficients related to the host image using multiple scaling factors [6]. Makbol et al. focus on a robust and secure digital image watermarking scheme, since the integer wavelet transform and singular value decomposition are realized that can be used for copyright protection [7]. The investigations given in the entire above-referenced materials can be taken into consideration as the extended version of the Liu et al.'s approach, where the process of using original image is eliminated to extract the logo information. They have in fact tried to improve the robustness in the image attacks. Lei et al. propose reversible watermarking scheme in the area of medical image in line with differential evolution. The presentation indicates that signature information and textual data are used to be inserted into the original medical images in association with recursive dither modulation algorithm, since the wavelet transform and singular value decomposition are realized [8]. One of the applicabilities of the watermarking is to process the medical images, where the researchers found a number of transformations to improve the performance of the watermarking. The results of using them in improving the watermarked image quality and also its extracted logo are now considered in the following investigations.

Chen et al. suggest full quaternion discrete Fourier transform in association with watermarking in color images. It is to establish the links, which exist between the DFT regarding the three RGB color channels and the corresponding components regarding the QDFT coefficients, as long as a general unit pure quaternion is considered [9]. In considering the other corresponding potential investigations in this area, NianCai et al. present difference angle quantization index modulation scheme in image watermarking, while Wang et al. propose a robust color image watermarking through local quaternion exponent moments [10, 11]. Yang et al. explain a geometric correction-based robust color image watermarking scheme using quaternion exponent moments [12].

Now, in the proposed approach, a comprehensive idea is in fact investigated for the purpose of finding an improved results, in this area, regarding the watermarked image and its logo extraction. With this goal, the contourlet transform that has the best signal-to-noise ratio is first chosen with respect to other related ones. In this way, the directional coefficients are produced and Zenzo edge detector is also used to provide the edge of image, simultaneously. In fact, the integration of the mentioned Zenzo edge detector and the contourlet transform is useful to improve the quality of the same watermarked image. Furthermore, the genetic algorithm is used to handle watermarking intensity to insert the logo information, appropriately, and also two methods including differential one and the multilayer perceptron (MLP) are used to extract the logo information. Regarding the above-captioned differential one, it aims us to reach low computational process, in its minimum time, although the computational process in case of the second one is high that is not important factor in watermarking domain, generally, due to the fact that the above-referenced computational process is directly related to the training time to produce the coefficients as first-order key that can be suitable to handle the extraction process.

The rest of the research is organized as follows: The proposed watermarking framework is presented in the section “The proposed watermarking framework”. The experimental results are given in the section “The experimental results”. Finally, the results conclude the investigated outcomes in “Conclusion”, item by item.

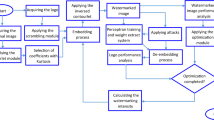
The proposed watermarking framework

The CT in connection with the Zenzo edge detector is applied to each color channel of the covering image in the process of embedding approach, while the outcomes of the subband of transformation are chosen to be suitable band of coefficients. It is to note that the logo information should be embedded in the edge of color image, as long as the Zenzo edge detector is realized. There is the second subband that is acquired, while the subbands of $C1$ and $C24$ are chosen based upon the color channels and the Zenzo edge detector is applied to $C1$, which is related to the three color channels and also $C24$ is applied to the same three color channels, so that the positions of inserting the logo can correspondingly be determined. The information of the logo with the appropriate watermarking intensity through the genetic algorithm can be calculated to insert in the chosen subband of transformation. Differential and the MLP are designed to extract logo that the aforementioned MLP based on the training data set is realized to provide the appropriate weights, which are useful to deal with the extraction of the information of the logo image through de-embedding approach. To calculate the watermarking intensity through the aforementioned neural network in association with training data set generation, a number of predefined attacks to watermarking image are applied to be able to calculate the optimum value of the watermarking intensity. In these algorithms including the first and the second ones, the training data set is provided based upon the subband coefficients of the chosen transformed coefficients of the image by the following instruction:

(a) The covering image without logo and the watermarked logo, (b) the covering image without logo and with logo under 5 × 5 median filtering, and (c) the covering image without logo and with logo under 30%, 40%, 70%, and 80% jpeg compression attacks, respectively. The main parts of the proposed first algorithm including the embedding and de-embedding approaches are considered in the proceeding sub-sections. The main reason to choose contourlet transform is related to its peak-signal-to-noise (PSNR) that is better than wavelet transform [13]. With a focus on the best locations of inserting the logo information that are given in the edge of image and also considering contourlet transform as a time–frequency representation, the present integration aims us to increase the probability of reaching the improved quality of the same watermarked image. It can also be shown that the genetic algorithm is realized to find the optimized quality of the watermarked image and also its extracted logo information. The Zenzo edge detector is applied to color images that are working based on the maximum of pixel intensities in each channel as presented in [14]. The aforementioned Zenzo edge detector to be suitable to deal with the contourlet coefficients is amended that is fully mentioned in “The embedding approach”, item 4. It should be noted that for the purpose of applying the Zenzo edge detector to the whole of $C1R$, $C1G$, and $C1B$, the first position of the insertion is determined to be able to apply this one to the whole of $C24R$, $C24G$, and $C24B$, respectively, and the second position of the insertion is determined as is mentioned in “The embedding approach”, item 5. In one such case, it is noticeable to use these positions as the key in extracting the logo and the Zenzo edge detector is not used again for the watermarked images.

The embedding approach

The embedding approach in the present research is organized by the following:

• 1. Acquiring the cover image to be embedded. The image of this stage that is given in the size of 512 × 512 is initially titled as ‘COV’.

• 2. The image acquiring in the previous stage is splitted in the three channels of R, G, and B:

  $$ {\text{COV}} = {\bigcup }\left( {{\text{COV}}^{R} ,{\text{COV}}^{G} ,{\text{COV}}^{B} } \right). $$

• 3. Applying CT in two levels to color image, independently.

  The coefficients at this stage are taken as C1, C21, C22, C23, C24, C31, C32, C33, C34 and C34 by the following:

  $$ \begin{aligned} {\bigcup }\left( {C1^{R} , \mathop {\bigcup }\limits_{i = 2}^{3} \mathop {\bigcup }\limits_{j = 1}^{4} \left( { Cij^{R} } \right)} \right) & = {\text{CT}}\left( {{\text{COV}}^{R} } \right) \\ {\bigcup }\left( {C1^{G} , \mathop {\bigcup }\limits_{i = 2}^{3} \mathop {\bigcup }\limits_{j = 1}^{4} \left( { Cij^{G} } \right)} \right) & = {\text{CT}}\left( {{\text{COV}}^{G} } \right) \\ {\bigcup }\left( {C1^{B} , \mathop {\bigcup }\limits_{i = 2}^{3} \mathop {\bigcup }\limits_{j = 1}^{4} \left( { Cij^{B} } \right)} \right) & = {\text{CT}}\left( {{\text{COV}}^{B} } \right). \\ \end{aligned} $$

• 4. To determine the logo position, the maximum angular variation is calculated by:

  $$ \begin{gathered} \theta_{H} \left( {i,j} \right) = {\tan}^{ - 1} \left[ {\frac{{2C24^{B} \left( {i,j} \right)}}{{C24^{G} \left( {i,j} \right) - C24^{R} \left( {i,j} \right)}}} \right] \hfill \\ \theta_{L} \left( {i,j} \right) = {\tan}^{ - 1} \left[ {\frac{{2C1^{B} \left( {i,j} \right)}}{{C1^{G} \left( {i,j} \right) - C1^{R} \left( {i,j} \right)}}} \right]. \hfill \\ \end{gathered} $$

  Now, the variation rate of (i, j) at $\theta \left( {i,j} \right)$ is resulted by:

  $$ \begin{aligned} F_{H} \left( {i,j} \right) & = \left[ {\left( {C24^{G} \left( {i,j} \right) + C24^{R} \left( {i,j} \right)} \right) + \left( {C24^{G} \left( {i,j} \right) - C24^{R} \left( {i,j} \right)} \right)\cos \left( {2\theta_{H} \left( {i,j} \right)} \right) + 2C24^{B} \left( {i,j} \right){\sin}\left( {2\theta_{H} \left( {i,j} \right)} \right)} \right] \\ F_{L} \left( {i,j} \right) & = \left[ {\left( {C1^{G} \left( {i,j} \right) + C1^{R} \left( {i,j} \right)} \right) + \left( {C1^{G} \left( {i,j} \right) - C1^{R} \left( {i,j} \right)} \right)\cos \left( {2\theta_{L} \left( {i,j} \right)} \right) + 2C1^{B} \left( {i,j} \right){\sin}\left( {2\theta_{L} \left( {i,j} \right)} \right)} \right]. \\ \end{aligned} $$

• 5. The positions of positive variations for inserting the logo are initiated as:

  $$ \left[ {{\text{row}}_{H} ,{\text{col}}_{H} } \right] = {\text{find}}(F_{H} > 0) $$

  To choose the positions of inserting the logo in low frequency of CT is provided through the following stages:

  • (a) Calculating the minimum value of low-frequency coefficients of the CT is represented as min_L.

  • (b) Calculating the mean value of low-frequency coefficients of the CT is represented as mean_L.

  • (c) The positions, which F are greater than min_L + mean_L/2 are calculated, that is:

    $$ \left[ {{\text{row}}_{l} ,{\text{col}}_{l} } \right] = {\text{find}}\left( {F_{L} > \min_{L} + {\text{mean}}_{L} } \right). $$

• 6. The positions that are the same as logo size should be determined as (a) determining the number of rows for directional items and low-frequency ${\text{size}}_{{{\text{row}}H}} = {\text{size}}\left( {{\text{row}}_{H} } \right)$ and ${\text{size}}_{{{\text{row}}H}} = {\text{size}}\left( {{\text{row}}_{H} } \right)$, (b) calculating the step of inserting in row ${\text{step}}_{H} = {\text{floor}}\left( {\frac{{{\text{size}}_{{{\text{row}}H}} }}{{{\text{size}}\left( {{\text{logo}}} \right)}}} \right)$ and ${\text{step}}_{L} = {\text{floor}}\left( {\frac{{{\text{size}}_{{{\text{row}}L}} }}{{{\text{size}}\left( {{\text{logo}}} \right)}}} \right).$

• 7. Defining the genetic algorithm parameters including the population of 50 chromosomes and the crossover of 50%, the mutation of 14%, and the generation rate of 36%.

• 8. Embedding the logo into the contourlet transformation coefficients by the following. The logo is presented to 1-D matrix and then the logo is inserting in the directional coefficients in low frequency:

  $$ \begin{aligned} & c24^{R} \left( {{\text{row}}_{H} \left( {i \times {\text{step}}_{H} ),{\text{col}}_{H} (i \times {\text{step}}_{H} } \right)} \right) = c24^{R} \left( {{\text{row}}_{H} \left( {i \times {\text{step}}_{H} ),{\text{col}}_{H} (i \times {\text{step}}_{H} } \right)} \right) + alfa_{H} \times arnold\_logo\left( i \right) \\ & c24^{G} \left( {{\text{row}}_{H} \left( {i \times {\text{step}}_{H} ),{\text{col}}_{H} (i \times {\text{step}}_{H} } \right)} \right) = c24^{G} \left( {{\text{row}}_{H} \left( {i \times {\text{step}}_{H} ),{\text{col}}_{H} (i \times {\text{step}}_{H} } \right)} \right) + alfa_{H} \times arnold\_logo\left( i \right) \\ & c24^{B} \left( {{\text{row}}_{H} \left( {i \times {\text{step}}_{H} ),{\text{col}}_{H} (i \times {\text{step}}_{H} } \right)} \right) = c24^{B} \left( {{\text{row}}_{H} \left( {i \times {\text{step}}_{H} ),{\text{col}}_{H} (i \times {\text{step}}_{H} } \right)} \right) + alfa_{H} \times arnold\_logo\left( i \right) \\ & c1^{R} \left( {{\text{row}}_{L} \left( {i \times {\text{step}}_{L} ),{\text{col}}_{L} (i \times {\text{step}}_{L} } \right)} \right) = c1^{R} \left( {{\text{row}}_{L} \left( {i \times {\text{step}}_{L} ),{\text{col}}_{L} (i \times {\text{step}}_{L} } \right)} \right) + alfa_{H} \times arnold\_logo\left( i \right) \\ & c1^{G} \left( {{\text{row}}_{L} \left( {i \times {\text{step}}_{L} ),{\text{col}}_{L} (i \times {\text{step}}_{L} } \right)} \right) = c1^{G} \left( {{\text{row}}_{L} \left( {i \times {\text{step}}_{L} ),{\text{col}}_{L} (i \times {\text{step}}_{L} } \right)} \right) + alfa_{H} \times arnold\_logo\left( i \right) \\ & c1^{B} \left( {{\text{row}}_{L} \left( {i \times {\text{step}}_{L} ),{\text{col}}_{L} (i \times {\text{step}}_{L} } \right)} \right) = c1^{B} \left( {{\text{row}}_{L} \left( {i \times {\text{step}}_{L} ),{\text{col}}_{L} (i \times {\text{step}}_{L} } \right)} \right) + alfa_{H} \times arnold\_logo\left( i \right). \\ \end{aligned} $$

• 9. Applying the inverse transformation for each one by the following:

  $$ \begin{aligned} {\text{WAT}}^{R} & = {\text{ICT}}\left( {{\bigcup }\left( {C1^{R} ,\mathop {\bigcup }\limits_{i = 2}^{3} \mathop {\bigcup }\limits_{j = 1}^{4} \left( { Cij^{R} } \right)} \right)} \right) \\ {\text{WAT}}^{G} & = {\text{ICT}}\left( {{\bigcup }\left( {C1^{G} ,\mathop {\bigcup }\limits_{i = 2}^{3} \mathop {\bigcup }\limits_{j = 1}^{4} \left( { Cij^{G} } \right)} \right)} \right) \\ {\text{WAT}}^{B} & = {\text{ICT}}\left( {{\bigcup }\left( {C1^{B} ,\mathop {\bigcup }\limits_{i = 2}^{3} \mathop {\bigcup }\limits_{j = 1}^{4} \left( { Cij^{B} } \right)} \right)} \right). \\ \end{aligned} $$

• 10. Providing the color image as:

  $$ {\text{WAT}} = {\bigcup }\left( {{\text{WAT}}^{R} ,{\text{WAT}}^{G} ,{\text{WAT}}^{B} } \right) . $$

• 11. Preparing further attacks to optimize the extraction of logo in difference method using NSGA algorithm.

• 12. Calculation of the performance index by the following:

  $$ \begin{aligned} f1 & = {\text{SF}}1*\left| {\left( {\frac{1}{4}\mathop \sum \limits_{i = 1}^{4} {\text{NC}}_{{{\text{Attack}},H}} \left( i \right)} \right) - {\text{NC}}\left| { + {\text{SF}}2*} \right|52 - {\text{PSNR}}} \right| \\ f2 & = {\text{SF}}1*\left| {\left( {\frac{1}{4}\mathop \sum \limits_{i = 1}^{4} {\text{NC}}_{{{\text{Attack}},L}} \left( i \right)} \right) - {\text{NC}}\left| { + {\text{SF}}2*} \right|52 - {\text{PSNR}}} \right|. \\ \end{aligned} $$

  where SF1 and SF2 are taken as the scaling factor.

• 13. Updating the parameter of alfaH and alfaL via the NSGA with ten populations through stages 9–13.

• 14. Choosing the parameter of alfaH and alfaL through the performance index.

The de-embedding approach

The de-embedding approach is organized at the following stages:

• 1. Acquiring the watermarked image that is taken WAT.

• 2. The image is splitted in three channels of R, G and B. Each channel represents ${\text{WAT}}^{R}$,${\text{WAT}}^{G}$, and ${\text{WAT}}^{B}$ by the following:

  $$ {\text{WAT}} = {\bigcup }\left( {{\text{WAT}}^{R} ,{\text{WAT}}^{G} ,{\text{WAT}}^{B} } \right). $$

• 3. Applying the CT transformation in the four levels to color watermarked image, independently:

  $$ \begin{aligned} {\bigcup }\left( {C1^{R} , \mathop {\bigcup }\limits_{i = 2}^{3} \mathop {\bigcup }\limits_{j = 1}^{4} \left( { Cij^{R} } \right)} \right) & = {\text{CT}}\left( {{\text{COV}}^{R0} } \right) \\ {\bigcup }\left( {C1^{G} , \mathop {\bigcup }\limits_{i = 2}^{3} \mathop {\bigcup }\limits_{j = 1}^{4} \left( { Cij^{G} } \right)} \right) & = {\text{CT}}\left( {{\text{COV}}^{G} } \right) \\ {\bigcup }\left( {C1^{B} , \mathop {\bigcup }\limits_{i = 2}^{3} \mathop {\bigcup }\limits_{j = 1}^{4} \left( { Cij^{B} } \right)} \right) & = {\text{CT}}\left( {{\text{COV}}^{B} } \right). \\ \end{aligned} $$

• 4. Using the following relations, the pixels of the disarranged logo are calculated for each colour channel by:

  $$ \begin{aligned} L_{{{\text{Arn}}}}^{R,L} \left( i \right) & = C1_{w}^{R} \left( {{\text{row}}_{L} \left( {i \times {\text{step}}_{L} ),{\text{col}}_{L} (i \times {\text{step}}_{L} } \right)} \right) - C1_{w}^{R} \left( {{\text{row}}_{L} \left( {i \times {\text{step}}_{L} ),{\text{col}}_{L} (i \times {\text{step}}_{L} } \right)} \right) \\ L_{{{\text{Arn}}}}^{G,L} \left( i \right) & = C1_{w}^{G} \left( {{\text{row}}_{L} \left( {i \times {\text{step}}_{L} ),{\text{col}}_{L} (i \times {\text{step}}_{L} } \right)} \right) - C1_{w}^{G} \left( {{\text{row}}_{L} \left( {i \times {\text{step}}_{L} ),{\text{col}}_{L} (i \times {\text{step}}_{L} } \right)} \right) \\ L_{{{\text{Arn}}}}^{B,L} \left( i \right) & = C1_{w}^{B} \left( {{\text{row}}_{L} \left( {i \times {\text{step}}_{L} ),{\text{col}}_{L} (i \times {\text{step}}_{L} } \right)} \right) - C1_{w}^{B} \left( {{\text{row}}_{L} \left( {i \times {\text{step}}_{L} ),{\text{col}}_{L} (i \times {\text{step}}_{L} } \right)} \right) \\ L_{{{\text{Arn}}}}^{R,H} \left( i \right) & = C24_{w}^{R} \left( {{\text{row}}_{H} \left( {i \times {\text{step}}_{H} ),{\text{col}}_{H} (i \times {\text{step}}_{H} } \right)} \right) - C24_{w}^{R} \left( {{\text{row}}_{H} \left( {i \times {\text{step}}_{H} ),{\text{col}}_{L} (i \times {\text{step}}_{H} } \right)} \right) \\ L_{{{\text{Arn}}}}^{G,H} \left( i \right) & = C24_{w}^{G} \left( {{\text{row}}_{H} \left( {i \times {\text{step}}_{H} ),{\text{col}}_{H} (i \times {\text{step}}_{H} } \right)} \right) - C24_{w}^{G} \left( {{\text{row}}_{H} \left( {i \times {\text{step}}_{H} ),{\text{col}}_{L} (i \times {\text{step}}_{H} } \right)} \right) \\ L_{{{\text{Arn}}}}^{B,H} \left( i \right) & = C24_{w}^{B} \left( {{\text{row}}_{H} \left( {i \times {\text{step}}_{H} ),{\text{col}}_{H} (i \times {\text{step}}_{H} } \right)} \right) - C24_{w}^{B} \left( {{\text{row}}_{H} \left( {i \times {\text{step}}_{H} ),{\text{col}}_{L} (i \times {\text{step}}_{H} } \right)} \right), \\ \end{aligned} $$

  where R, G, and B are used to represent red, green, and blue, respectively. Also, H and L are using to represent the low-frequency coefficients and directional one, as long as Arn is using to represent Arnold transformation. Hereinafter, Cw and Ch denote to contourlet coefficient of watermarked image and contourlet coefficient of host image, respectively.

• 5. The disarranged logo regarding each channel is summed as:

  $$ L_{{{\text{Arn}}}} \left( i \right) = L_{{{\text{Arn}}}}^{R,L} \left( i \right) + L_{{{\text{Arn}}}}^{G,L} \left( i \right) + L_{{{\text{Arn}}}}^{B,L} \left( i \right) + L_{{{\text{Arn}}}}^{R,H} \left( i \right) + L_{{{\text{Arn}}}}^{G,H} \left( i \right) + L_{{{\text{Arn}}}}^{B,H} \left( i \right). $$

• 6. The values of each pixels are mapped into − 1, 1 via:

  $$ L_{{{\text{Arn}}}} \left( i \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill &\quad {{\text{if}}\;\left( {L_{{{\text{Arn}}}} \left( i \right)} \right) > 0} \hfill \\ { - 1} \hfill &\quad {{\text{else}}} \hfill \\ \end{array} } \right.. $$

• 7. The one-dimensional matrix regarding the disarranged logo is provided in its two-dimensional one by:

  $$ {\text{L2D}}_{{{\text{Arn}}}} \left( i \right) = {\text{reshape}}\left( {L_{{{\text{Arn}}}} \left( i \right),m,n} \right). $$

• 8. Applying the inverse Arnold to extract the logo

The experimental results

The procedure of the experiments considered in the present research is carried. Regarding the first one, the information of the logo image for the CT is illustrated in Fig. 1.

Fig. 1

The information of the logo image

The proposed algorithm for image watermarking against various attacks is presented in Fig. 2. These attacks include compression 50%, median filter 3 × 3, Gaussian noise with a variance of 0.005 and 0.015, and cropping 6% of image, respectively.

Fig. 2

The proposed algorithm for image watermarking against various attacks

The performance analysis

There are a number of methods to measure the approach performance in the area of watermarking framework. It is important to analyze the results. Because in the process of de-embedding approach that is correspondingly appeared after that embedding approach, the errors are unintentionally provided. With this goal, the mean square error (MSE) and the PSNR are presented by the following:

$$ {\text{MSE}}(x,y) = \frac{1}{N}\sum\limits_{i = 1}^{N} {(x_{i} - y_{i} )^{2} } $$

(1)

$$ {\text{PSNR}} = 10\log \frac{{{\text{L}}^{{2}} }}{{\text{MSE }}}, $$

(2)

where y_i is related to the transform and its inverse and also x_i is related to the original image. With a focus on the proposed framework, in the process of optimization, the watermarking intensity is calculated for covering image. After that the NC is illustrated under a number of jpeg compression attacks through CT transformations in Fig. 3.

Fig. 3

The robustness of the difference method under jpeg compression attacks

The performance analysis of the covering image is tabulated in Table 1 through CT in connection with the Zenzo edge detector via the SSIM and the PSNR, while the outcomes are all tabulated in Table 1 for a number of separated covering images, as well.

Table 1 The performance analysis

The attacks results analysis in inserting the logo in some different directions for Lena is tabulated in Table 2. As tabulated in this table, the insertion process in a number of different directions of contourlet coefficients is affected in the NC parameter. It is to note that the most of attacks are of the stochastic behavior, and therefore, this one is carried out ten times, randomly, for one image and the results are tabulated, averagely. The results of contourlet in a number of different directions for a set of separated images are totally different, correspondingly. Based on the image context, some of them are taken in some directions including 21, 22, 23, and 24 to be inserted, but if the average of 16 is supposed to use, it is the nearly same as the different directions. The attacks results analysis of logo extraction for a separated number of cover images is correspondingly tabulated in Table 3.

Table 2 The attacks results analysis in inserting the logo in some different directions for Lena

Table 3 The attacks results analysis in inserting the logo in some different directions for a separated number of cover images

Conclusion

The applicability of the new image watermarking framework is considered to deal with the embedding and de-embedding approaches in the unique area of analyzing the contourlet transform in connection with the canny edge detector. It is to note that the investigated results are taken into real consideration with a focus on the realizations of the contourlet transform, while the effectiveness of the canny edge detector is considered to be able to address the research with respect to state-of-the-art, appropriately. The key subject behind the investigation is to provide the watermarked image and the corresponding extracted logo image with the high accuracy to be reached. The proposed framework is of significance with respect to the integration of modules realized in the unique form to be competitive in case of acquired investigated outcomes. The investigated outcomes that are carried out through a series of experiments are considered to present that there is an indication of novelty with regard to state-of-the-art materials available to use in this area. Subsequently, the analysis of the proposed watermarking framework is organized in line with the peak signal-to-noise ratio, as long as the normal correlation is taken into consideration, as well.