Introduction

Neutrosophic set is the generalization of classical set, fuzzy set [1], intuitionistic fuzzy set [2, 3], and so on which highlights the origin and nature of neutralities in different fields. This multifaceted logic was introduced by F. Smarandache [4,5,6] which imports the term indeterminacy and carries more information than fuzzy logic. This leads to give the better performance than fuzzy logic. In neutrosophic logic, a proposition has a degree of truth (T), a degree of indeterminacy (I), and a degree of falsity (F), where T, I, and F are standard or non-standard subsets of ] \(-0\), \(1+\)[. However it is difficult to handle data with non-standard interval, and hence, the [7] single-valued neutrosophic set was introduced which takes the values in the standard interval [0, 1].

The notion of neutrosophic measure, neutrosophic integral, and neutrosophic probability were introduced by Smarandache [8]. Many practical examples are presented in neutrosophic measure, and consequently, the neutrosophic integral and neutrosophic probability are also defined in many ways, because there are various types of indeterminacies, depending on the problem. Many researchers have applied the neutrosophic logic in various fields.

Single-valued neutrosophic numbers, triangular neutrosophic numbers and trapezoidal neutrosophic numbers, and their application in decision-making are explored in [9,10,11]. The neutrosophic number from different view points are introduced [12] and the different types of linear and non-linear generalized triangular neutrosophic numbers which are very important for uncertainty theory and de-neutrosophication concept for neutrosophic number for triangular neutrosophic numbers are discussed that helps to convert a neutrosophic number into a crisp number. This has been applied in imprecise project evaluation review technique and route selection problem. Abdel-Basset et al. [13] introduced a advanced type of neutrosophic technique, called type 2 neutrosophic numbers(T2NN), and a real case dealing with a decision-making problem based on T2NN-TOPSIS (Technique for order preference by similarity to ideal solution) methodology to prove the efficiency and the applicability of the type 2 neutrosophic number were illustrated. The triangular neutrosophic numbers (TriNs) were used to present the linguistic variables based on opinions of experts and decision-makers. The problem of supplier selection in sustainable supplier chain management (SSCM) is also incorporated in [14]. The multicriteria decision-making (MCDM) methodology is one of the keys for solving complicated and complex decision problems. In [15], bipolar neutrosophic number was defined and Group Decision-Making based on Neutrosophic TOPSIS approach has been applied for Smart Medical Device Selection. Neutrosophic logic helps in preventing the loss of data, and hence, it has been applied in many decision-making problems [16,17,18,19,20].

The Internet of Things (IoT) is the network of physical devices and the network connectivity enables these objects to collect and exchange data. The IoT allows objects to be sensed or controlled remotely across existing network infrastructure, creating opportunities for more direct integration of the physical world into computer-based systems, and resulting in improved efficiency, accuracy, and economic benefit in addition to reduced human intervention. The IoT has the potential to add a new dimension by enabling communications with and among smart objects, thus leading to the vision of “anytime, anywhere, anymedia, anything” communications. IoT is one of the challenging and emerging fields of research in science and engineering. Nabeeh et al. [21] presented a neutrosophic analytical hierarchy process (AHP) of the IoT in enterprises to help decision-makers to estimate the influential factors.

Differentiation plays an important role in the field of science and engineering. Many problems arise with uncertain or imprecise parameters. To model this uncertainty, we develop the differential equation with imprecise parameters. Fuzzy differential equation [22,23,24,25,26,27,28,29,30] has been introduced to model this uncertainty. However, it considers only the membership value. Later, intuitionistic fuzzy differential equation [31,32,33,34,35,36] was emerged with degree of membership and non-membership. However, these two logic does not have the term indeterminacy. Hence, neutrosophic differential equation was developed to model the indeterminacy. Smarandache [37] initiated the concept of neutrosophic function such as exponential function, neutrosophic logarithmic function, and neutrosophic inverse function. Also he introduced, neutrosophic calculus, which studies the neutrosophic limits, neutrosophic derivatives, and neutrosophic integrals. Differential equation with uncertainty in a growing area.The differential equations with neutrosophic numbers is studied in [38]. The multifaceted factors of neutrosophic numbers have been exemplified in higher order differential equation. The structure of the paper is organized as follows. In Preliminary section, the pre-requisite concepts are given and the conditions for strong solution are defined for solving the second-order differential equations. Followed by preliminaries, the solution of second-order differential equation with trapezoidal neutrosophic number as boundary condition is derived. Finally, the numerical example is illustrated and its graphical interpretations are also shown. In the conclusion part, the future research scope is discussed.

Preliminaries

Definition 1

[4] Let X be a universe set. A neutrosophic set A on X is defined as \(A = \{\left\langle T_{A}(x),I_{A}(x),F_{A}(x)\right\rangle :x \in X\}\), where \(T_{A}(x),I_{A}(x),F_{A}(x): X \rightarrow ^{-}]0,1[^{+}\) represents the degree of membership, degree of indeterministic, and degree of non-membership respectively of the element x \(\in \)X, such that \(^{-}0 \le T_{A}(x)+I_{A}(x)+F_{A}(x)\le 3^{+}\).

Definition 2

[7] Let X be a universe set. A single-valued neutrosophic set A on X is defined as \(A =\{\left\langle T_{A}(x),I_{A}(x),F_{A}(x)\right\rangle :x \in X\}\), where \(T_{A}(x)\), \(I_{A}(x)\), \(F_{A}(x):\)\(X \rightarrow [0,1]\) represents the degree of membership, degree of indeterministic, and degree of non-membership, respectively, of the element x \(\in \) X, such that \(0 \le T_{A}(x)+I_{A}(x)+F_{A}(x)\le 3\).

Definition 3

\((\alpha , \beta , \gamma )\)-cut: The \((\alpha , \beta , \gamma )\)-cut neutrosophic set is denoted by \(F_{(\alpha , \beta , \gamma )}\), where \(\alpha , \beta , \gamma \in [0,1\) and are fixed numbers, such that \(\alpha +\beta +\gamma \le 3\) is defined as \(F_{\alpha , \beta , \gamma }= \{\left\langle T_{A}(x),I_{A}(x),F_{A}(x)\right\rangle :x \in X, T_{A}(x)\ge \alpha , I_{A}(x)\le \beta , F_{A}(x)\le \gamma \}\).

Definition 4

A neutrosophic set A defined on the universal set of real numbers R is said to be neutrosophic number if it has the following properties.

  1. (i)

    A is normal if there exist \(x_{0} \in R\), such that \(T_{A}(x_{0}) = 1\)(\(I_{A}(x_{0})=F_{A}(x_{0})=0\)).

  2. (ii)

    A is convex set for the truth function \(T_{A}(x)\), i.e.,

    \(T_{A}(\mu x_{1}+(1-\mu )x_{2})\ge min(T_{A}(x_{1}), T_{A}(x_{2})) \forall x_{1}, x_{2} \in R, \mu \in [0,1]\).

  3. (iii)

    A is concave set for the indeterministic function and false function \(I_{A}(x)\) and \(F_{A}(x)\), i.e.,

    \(I_{A}(\mu x_{1}+(1-\mu )x_{2})\ge \max (I_{A}(x_{1}), I_{A}(x_{2})) \forall x_{1}, x_{2} \in R, \mu \in [0,1]\).

    \(F_{A}(\mu x_{1}+(1-\mu )x_{2})\ge \max (F_{A}(x_{1}), F_{A}(x_{2})) \forall x_{1}, x_{2} \in R, \mu \in [0,1]\).

Definition 5

[37] A trapezoidal neutrosophic number A is a subset of neutrosophic number in R with the following truth function, indeterministic function, and falsity function which is given by the following:

$$\begin{aligned} T_{A}(x)= & {} {\left\{ \begin{array}{ll}\left( \dfrac{x-a}{b-a}\right) \vartheta _{A} &{}\text {for } a \le x \le b\\ \,\, \,\, \,\, \,\,\vartheta _{A} &{}\text {for } b \le x \le c \\ \left( \dfrac{d-x}{d-c}\right) \vartheta _{A} &{}\text {for } c \le x \le d \\ \,\, \,\, \,\, \,\, 0 &{}\text {otherwise } \end{array}\right. }, \\ I_{A}(x)= & {} {\left\{ \begin{array}{ll}\left( \dfrac{b-x}{b-a}\right) \nu _{A} &{}\text {for } a \le x \le b\\ \,\, \,\, \,\, \,\,\nu _{A} &{}\text {for } b \le x \le c \\ \left( \dfrac{d-x}{d-c}\right) \nu _{A} &{}\text {for } c \le x \le d \\ \,\, \,\, \,\, \,\, 1 &{}\text {otherwise } \end{array}\right. } \hbox {and} \\ F_{A}(x)= & {} {\left\{ \begin{array}{ll}\left( \dfrac{b-x}{b-a}\right) \kappa _{A} &{}\text {for } a \le x \le b\\ \,\, \,\, \,\, \,\,\kappa _{A} &{}\text {for } b \le x \le c \\ \left( \dfrac{d-x}{d-c}\right) \kappa _{A} &{}\text {for } c \le x \le d \\ \,\, \,\, \,\, \,\, 1 &{}\text {otherwise }, \end{array}\right. } \end{aligned}$$

where \(a \le b \le c\le d\) and a trapezoidal neutrosophic number is denoted by \(A_{TRN}=\left\langle (a,b,c,d);\vartheta _{A}, \nu _{A}, \kappa _{A} \right\rangle \).

Note 1: Here, \(T_{A}(x)\) increases with constant rate for \(x \in [a,b]\) and decreases for \(x \in [c,d]\), but \(I_{A}(x)\) and \(F_{A}(x)\) decreases with constant rate for \(x \in [a,b]\) and increases for \(x \in [c,d]\)

Definition 6

\((\alpha ,\beta ,\gamma )\)-cut of a trapezoidal neutrosophic number \(A_{TRN}=\left\langle (a,b,c,d);\vartheta _{A}, \nu _{A}, \kappa _{A} \right\rangle \) is defined as follows:

\(A_{\alpha ,\beta ,\gamma }={[A_{1}(\alpha ),A_{2}(\alpha )];[A'_{1}(\beta ),A'_{2}(\beta )];[A''_{1}(\gamma ),A''_{2}(\gamma )]}\), \(0\le \alpha +\beta +\gamma \le 3\), where

$$\begin{aligned} {[}A_{1}(\alpha ),A_{2}(\alpha )]= & {} [(a+\alpha (b-a))\vartheta _{A}, (d-\alpha (d-c))\vartheta _{A}]\\ {[}A'_{1}(\beta ),A'_{2}(\beta )]= & {} [(b-\beta (b-a))\nu _{A}, (c+\beta (d-c))\nu _{A}], \\ {[}A''_{1}(\gamma ),A''_{2}(\gamma )]= & {} [(b-\gamma (b-a))\kappa _{A}, (c+\gamma (d-c))\kappa _{A}] \end{aligned}$$

Definition 7

[28] The derivative of a fuzzy valued function \(f:(a,b)\rightarrow R\) at \(x_{0}\) is defined as follows:

$$\begin{aligned} f'(x_{0})=\mathrm{lim}_{h\rightarrow 0}\frac{f(x_{0}+h)-f(x_{0})}{h} \hbox { and} \end{aligned}$$

\(f'(x_{0})\) is \(\mathscr {D}^{1}\)-differentiable at \(x_{0}\) if

$$\begin{aligned}{}[f'(x_{0})]_{\alpha } = [f'_{1}(x_{0}, \alpha ), f'_{2}(x_{0}, \alpha )] \hbox { and} \end{aligned}$$

\(f'(x_{0})\) is \(\mathscr {D}^{2}\)-differentiable at \(x_{0}\) if

$$\begin{aligned}{}[f'(x_{0})]_{\alpha } = [f'_{2}(x_{0}, \alpha ), f'_{1}(x_{0}, \alpha )] \end{aligned}$$

for all \(\alpha \in [0,1]\).

Definition 8

[27] The second-order derivative of a fuzzy valued function \(f:(a,b)\rightarrow R\) at \(x_{0}\) is defined as follows:

\(f''(x_{0})=\mathrm{lim} _{h\rightarrow 0}\frac{f'(x_{0}+h)-f'(x_{0})}{h}\) and

\(f'(x_{0})\) is \(\mathscr {D}^{1}\)-differentiable at \(x_{0}\) if

for all \(\alpha \in [0,1]\) and \(f'(x_{0})\) is \(\mathscr {D}^{2}\)-differentiable at \(x_{0}\) if

for all \(\alpha \in [0,1]\).

Definition 9

Let the solution of the neutrosophic differential equation be y(x) and its \((\alpha ,\beta ,\gamma )\)-cut be \([y(x,\alpha ,\beta ,\gamma )\) = \([(y_{1}(x,\alpha ),y_{2}(x,\alpha ),(y'_{1}(x,\beta ),y'_{2}(x,\beta ),(y''_{1}(x,\gamma ),\)\(y''_{2}(x,\gamma )]\) The solution is a strong solution if

$$\begin{aligned}&\mathrm{(i)}\,\dfrac{\mathrm{d}y_{1}(x,\alpha )}{\mathrm{d}\alpha }>0, \dfrac{\mathrm{d}y_{2}(x,\alpha )}{\mathrm{d}\alpha }<0 \forall \alpha \in [0,1], y_{1}(x,1)\le y_{2}(x,1).\\&\mathrm{(ii)}\,\dfrac{\mathrm{d}y'_{1}(x,\beta )}{\mathrm{d}\beta }<0, \dfrac{\mathrm{d}y'_{2}(x,\beta )}{\mathrm{d}\beta }>0\forall \beta \in [0,1], y'_{1}(x,0)\le y'_{2}(x,0).\\&\mathrm{(iii)}\,\dfrac{\mathrm{d}y''_{1}(x,\gamma )}{\mathrm{d}\gamma }<0, \dfrac{\mathrm{d}y''_{2}(x,\gamma )}{\mathrm{d}\gamma }>0 \forall \gamma {\in } [0,1], y''_{1}(x,0)\le y''_{2}(x,0). \end{aligned}$$

Solution of second-order neutrosophic differential equation

Consider the differential equation \(\frac{\mathrm{d}_{2}y(x)}{\mathrm{d}x_{2}}= py(x)\) with the boundary condition \(y(0)= \tilde{u}\) and \(y(l)=\tilde{v}\), where \(\tilde{u},\tilde{v}\) are trapezoidal neutrosophic number.

Let \(\tilde{u}=\{(u_{1},u_{2},u_{3},u_{4});\vartheta _{1}, \nu _{1}, \kappa _{1}\}\) and \(\tilde{v}=\{(v_{1},v_{2},v_{3},v_{4});\vartheta _{2}, \nu _{2}, \kappa _{2}\}\).

  1. 1.

    When p is positive constant, i.e., \(p>0\). then two cases are possible.

Case 1:y(x) and \(\frac{\mathrm{d}y(x)}{\mathrm{d}x}\) are \(\mathscr {D}^{1}\)-differentiable or \(\mathscr {D}^{2}\)-differentiable, and then, we have the following:

$$\begin{aligned}&\begin{array}{ll} \frac{\mathrm{d}^{2}y_{1}(x,\alpha )}{\mathrm{d}x^{2}}=py_{1}(x,\alpha );&\quad \frac{\mathrm{d}^{2}y_{2}(x,\alpha )}{\mathrm{d}x^{2}}=py_{2}(x,\alpha )\end{array}\\&\begin{array}{ll} \frac{\mathrm{d}^{2}y'_{1}(x,\beta )}{\mathrm{d}x^{2}}=py'_{1}(x,\beta );&\quad \frac{\mathrm{d}^{2}y'_{2}(x,\beta )}{\mathrm{d}x^{2}}=py'_{2}(x,\beta )\end{array}\\&\begin{array}{ll} \frac{\mathrm{d}^{2}y''_{1}(x,\gamma )}{\mathrm{d}x^{2}}=py''_{1}(x,\gamma );&\quad \frac{\mathrm{d}^{2}y''_{2}(x,\gamma )}{\mathrm{d}x^{2}}=py''_{2}(x,\gamma ) \end{array} \end{aligned}$$

with the boundary conditions:

$$\begin{aligned} y_{1}(0, \alpha )= & {} (u_{1}+\alpha (u_{2}-u_{1}))\vartheta _{1}, \nonumber \\ y_{2}(0, \alpha )= & {} (u_{4}-\alpha (u_{4}-u_{3}))\vartheta _{1},\nonumber \\ y'_{1}(0, \beta )= & {} (u_{2}-\beta (u_{2}-u_{1}))\nu _{1}, \nonumber \\ y'_{2}(0, \beta )= & {} (u_{3}+\beta (u_{4}-u_{3}))\nu _{1},\nonumber \\ y''_{1}(0, \gamma )= & {} (u_{2}-\gamma (u_{2}-u_{1}))\kappa _{1}, \nonumber \\ y''_{2}(0, \gamma )= & {} (u_{3}+\gamma (u_{4}-u_{3}))\kappa _{1} \nonumber \\ y_{1}(l, \alpha )= & {} (v_{1}+\alpha (v_{2}-v_{1}))\vartheta _{2},\nonumber \\ y_{2}(l, \alpha )= & {} (v_{4}-\alpha (v_{4}-v_{3}))\vartheta _{2},\nonumber \\ y'_{1}(l, \beta )= & {} (v_{2}-\beta (v_{2}-v_{1}))\nu _{2}, \nonumber \\ y'_{2}(l, \beta )= & {} (v_{3}+\beta (v_{4}-v_{3}))\nu _{2},\nonumber \\ y''_{1}(l, \gamma )= & {} (v_{2}-\gamma (v_{2}-v_{1}))\kappa _{2}, \nonumber \\ y''_{2}(l, \gamma )= & {} (v_{3}+\gamma (v_{4}-v_{3}))\kappa _{2}. \end{aligned}$$
(1)

Solution

The general solution of the first equation is as follows:

$$\begin{aligned} y_{1}(x, \alpha )= k_{1}e^{\sqrt{p}x} + k_{2}e^{-\sqrt{p}x}. \end{aligned}$$

Applying the boundary conditions, we get \(k_{1}+k_{2}= (u_{1}+\alpha (u_{2}-u_{1}))\vartheta _{1}\) and \( k_{1}e^{\sqrt{p}l} + k_{2}e^{-\sqrt{p}l}=(v_{1}+\alpha (v_{2}-v_{1}))\vartheta _{2} \), and solving the above, we have the following:

$$\begin{aligned} k_{1}&= \frac{1}{e^{\sqrt{p}l} - e^{-\sqrt{p}l}} \lbrace \left[ (v_{1}+\alpha (v_{2}-v_{1}))\vartheta _{2}\right] \\&\quad - \left[ (u_{1}+\alpha (u_{2}-u_{1}))\vartheta _{1}\right] e^{-\sqrt{p}l} \rbrace \end{aligned}$$

and

$$\begin{aligned} k_{2}&= -\frac{1}{e^{\sqrt{p}l} - e^{-\sqrt{p}l}} \lbrace \left[ (v_{1}+\alpha (v_{2}-v_{1}))\vartheta _{2}\right] \\&\quad -\left[ (u_{1}+\alpha (u_{2}-u_{1}))\vartheta _{1}\right] e^{\sqrt{p}l}\rbrace . \end{aligned}$$

Therefore, the general solution is as follows:

$$\begin{aligned} y_{1}(x,\alpha )&= \frac{1}{e^{\sqrt{p}l} - e^{-\sqrt{p}l}}\{ ( [(v_{1}+\alpha (v_{2}-v_{1}))\vartheta _{2}] \\&\quad -[(u_{1}+\alpha (u_{2}-u_{1}))\vartheta _{1}]e^{-\sqrt{p}l})e^{\sqrt{p}x} \\&\quad -([ (v_{1}+\alpha (v_{2}-v_{1}))\vartheta _{2}] \\&\quad -[(u_{1}+\alpha (u_{2}-u_{1}))\vartheta _{1}]e^{\sqrt{p}l})e^{-\sqrt{p}x}\}. \end{aligned}$$

Similarly

$$\begin{aligned} y_{2}(x,\alpha )&= \frac{1}{e^{\sqrt{p}l} - e^{-\sqrt{p}l}}\{([(v_{4}-\alpha (v_{4}-v_{3}))\vartheta _{2}] \\&\quad -[(u_{4}-\alpha (u_{4}-u_{3}))\vartheta _{1}]e^{-\sqrt{p}l})e^{\sqrt{p}x}\\&\quad -([ (v_{4}-\alpha (v_{4}-v_{3}))\vartheta _{2}] \\&\quad -[(u_{4}-\alpha (u_{4}-u_{3}))\vartheta _{1}]e^{\sqrt{p}l})e^{-\sqrt{p}x}\}\\ y'_{1}(x,\beta )&= \frac{1}{e^{\sqrt{p}l} - e^{-\sqrt{p}l}}\{ ([(v_{2}-\beta (v_{2}-v_{1}))\nu _{2}] \\&\quad -[(u_{2}-\beta (u_{2}-u_{1}))\nu _{1}]e^{-\sqrt{p}l})e^{\sqrt{p}x} \\&\quad -([ (v_{2}-\beta (v_{2}-v_{1}))\nu _{2}] \\&\quad -[(u_{2}-\beta (u_{2}-u_{1}))\nu _{1}]e^{\sqrt{p}l})e^{-\sqrt{p}x}\}\\ y'_{2}(x,\beta )&= \frac{1}{e^{\sqrt{p}l} - e^{-\sqrt{p}l}}\{([(v_{3}+\beta (v_{4}-v_{3}))\nu _{2}] \\&\quad -[(u_{3}+\beta (u_{4}-u_{3}))\nu _{1}]e^{-\sqrt{p}l})e^{\sqrt{p}x} \\&\quad -([ (v_{3}+\beta (v_{4}-v_{3}))\nu _{2}] \\&\quad -[(u_{3}+\beta (u_{4}-u_{3}))\nu _{1}]e^{\sqrt{p}l})e^{-\sqrt{p}x}\}\\ y''_{1}(x,\gamma )&= \frac{1}{e^{\sqrt{p}l} - e^{-\sqrt{p}l}}\{([(v_{2}-\gamma (v_{2}-v_{1}))\kappa _{2}] \\&\quad -[(u_{2}-\gamma (u_{2}-u_{1}))\kappa _{1}]e^{-\sqrt{p}l})e^{\sqrt{p}x}\\&\quad -([ (v_{2}-\gamma (v_{2}-v_{1}))\kappa _{2}] \\&\quad -[(u_{2}-\gamma (u_{2}-u_{1}))\kappa _{1}]e^{\sqrt{p}l})e^{-\sqrt{p}x}\}\\ y''_{2}(x,\gamma )&= \frac{1}{e^{\sqrt{p}l} - e^{-\sqrt{p}l}}\{([(v_{3}+\gamma (v_{4}-v_{3}))\kappa _{2}] \\&\quad -[(u_{3}+\gamma (u_{4}-u_{3}))\kappa _{1}]e^{-\sqrt{p}l})e^{\sqrt{p}x}\\&\quad -([ (v_{3}+\gamma (v_{4}-v_{3}))\kappa _{2}] \\&\quad -[(u_{3}+\gamma (u_{4}-u_{3}))\kappa _{1}]e^{\sqrt{p}l})e^{-\sqrt{p}x}\}. \end{aligned}$$

Case 2:y(x) is \(\mathscr {D}^{2}\)-differentiable and \(\frac{\mathrm{d}y(x)}{\mathrm{d}x}\) is \(\mathscr {D}^{1}\)-differentiable or y(x) is \(\mathscr {D}^{1}\)-differentiable and \(\frac{\mathrm{d}y(x)}{\mathrm{d}x}\) is \(\mathscr {D}^{1}\)-differentiable, and then, we have the following:

$$\begin{aligned}&\begin{array}{ll} \frac{\mathrm{d}^{2}y_{1}(x,\alpha )}{\mathrm{d}x^{2}}=py_{2}(x,\alpha );&\quad \frac{\mathrm{d}^{2}y_{2}(x,\alpha )}{\mathrm{d}x^{2}}=py_{1}(x,\alpha )\end{array}\\&\begin{array}{ll} \frac{\mathrm{d}^{2}y'_{1}(x,\beta )}{\mathrm{d}x^{2}}=py'_{2}(x,\beta );&\quad \frac{\mathrm{d}^{2}y'_{2}(x,\beta )}{\mathrm{d}x^{2}}=py'_{1}(x,\alpha )\end{array}\\&\begin{array}{ll} \frac{\mathrm{d}^{2}y''_{1}(x,\gamma )}{\mathrm{d}x^{2}}=py''_{2}(x,\gamma );&\quad \frac{\mathrm{d}^{2}y''_{2}(x,\gamma )}{\mathrm{d}x^{2}}=py''_{1}(x,\gamma ) \end{array} \end{aligned}$$

with the boundary conditions (1).

The general solution is as follows:

$$\begin{aligned} y_{1}(x,\alpha )= & {} k_{1}e^{\sqrt{p}x}+k_{2}e^{-\sqrt{p}x}+k_{3} \cos \sqrt{p}x+k_{4} \sin \sqrt{p}x\\ y_{2}(x,\alpha )= & {} k_{1}e^{\sqrt{p}x}+k_{2}e^{-\sqrt{p}x}-k_{3} \cos \sqrt{p}x-k_{4} \sin \sqrt{p}x\\ y'_{1}(x,\beta )= & {} k_{5}e^{\sqrt{p}x}+k_{6}e^{-\sqrt{p}x}+k_{7} \cos \sqrt{p}x+k_{8} \sin \sqrt{p}x\\ y'_{2}(x,\beta )= & {} k_{5}e^{\sqrt{p}x}+k_{6}e^{-\sqrt{p}x}-k_{7} \cos \sqrt{p}x-k_{8} \sin \sqrt{p}x\\ y''_{1}(x,\gamma )= & {} k_{9}e^{\sqrt{p}x}{+}k_{10}e^{-\sqrt{p}x}{+}k_{11} \cos \sqrt{p}x{+}k_{12} \sin \sqrt{p}x\\ y''_{2}(x,\gamma )= & {} k_{9}e^{\sqrt{p}x}{+}k_{10}e^{-\sqrt{p}x}{-}k_{11} \cos \sqrt{p}x{-}k_{12} \sin \sqrt{p}x, \end{aligned}$$

where

$$\begin{aligned} k_{1} =&\frac{1}{e^{\sqrt{p}l} - e^{-\sqrt{p}l}} \left\{ \left[ \left( \frac{(v_{1}+v_{4})+\alpha ((v_{2}-v_{1}) -(v_{4}-v_{3}))}{2}\right) \vartheta _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{1}+u_{4})+\alpha ((u_{2}-u_{1})-(u_{4}-u_{3}))}{2}\right) \vartheta _{1}\right] e^{-\sqrt{p}l}\right\} \\ k_{2} =&\frac{-1}{e^{\sqrt{p}l} - e^{-\sqrt{p}l}} \left\{ \left[ \left( \frac{(v_{1}+v_{4})+\alpha ((v_{2}-v_{1})-(v_{4}-v_{3}))}{2}\right) \vartheta _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{1}+u_{4})+\alpha ((u_{2}-u_{1})-(u_{4}-u_{3}))}{2}\right) \vartheta _{1}\right] e^{\sqrt{p}l}\right\} \\ k_{3} =&\left[ \frac{(u_{1}-u_{4})}{2}+\left( \frac{\alpha ((v_{2}-v_{1})+(v_{4}-v_{3}))}{2}\right) \vartheta _{2}\right] \\ k_{4} =&\frac{1}{\sin {\sqrt{p}l}} \left\{ \left[ \left( \frac{(v_{1}+v_{4})+\alpha ((v_{2}-v_{1})-(v_{4}-v_{3}))}{2}\right) \vartheta _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{1}+u_{4})+\alpha ((u_{2}-u_{1})-(u_{4}-u_{3}))}{2}\right) \vartheta _{1}\right] \cos {\sqrt{p}l}\right\} \\ k_{5} =&\frac{1}{e^{\sqrt{p}l} - e^{-\sqrt{p}l}} \left\{ \left[ \left( \frac{(v_{2}+v_{3})-\beta ((v_{2}-v_{1})-(v_{4}-v_{3}))}{2}\right) \nu _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{2}+u_{3})-\beta ((u_{2}-u_{1})-(u_{4}-u_{3}))}{2}\right) \nu _{1}\right] e^{-\sqrt{p}l}\right\} \\ k_{6} =&\frac{-1}{e^{\sqrt{p}l} - e^{-\sqrt{p}l}} \left\{ \left[ \left( \frac{(v_{2}+v_{3})-\beta ((v_{2}-v_{1})-(v_{4}-v_{3}))}{2}\right) \nu _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{2}+u_{3})-\beta ((u_{2}-u_{1})-(u_{4}-u_{3}))}{2}\right) \nu _{1}\right] e^{\sqrt{p}l}\right\} \\ k_{7} =&\left[ \frac{(u_{2}-u_{3})}{2}-\left( \frac{\beta ((v_{2}-v_{1})+(v_{4}-v_{3}))}{2}\right) \nu _{2}\right] \\ k_{8} =&\frac{1}{\sin {\sqrt{p}l}} \left\{ \left[ \left( \frac{(v_{2}-v_{3})-\beta ((v_{2}-v_{1})-(v_{4}-v_{3}))}{2}\right) \nu _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{2}-u_{3})-\beta ((u_{2}-u_{1})+(u_{4}-u_{3}))}{2}\right) \nu _{1}\right] \cos {\sqrt{p}l}\right\} \\ k_{9} =&\frac{1}{e^{\sqrt{p}l} - e^{-\sqrt{p}l}} \left\{ \left[ \left( \frac{(v_{2}+v_{3})-\gamma ((v_{2}-v_{1})-(v_{4}-v_{3}))}{2}\right) \kappa _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{2}+u_{3})-\gamma ((u_{2}-u_{1})-(u_{4}-u_{3}))}{2}\right) \kappa _{1}\right] e^{-\sqrt{p}l}\right\} \\ k_{10} =&\frac{-1}{e^{\sqrt{p}l} - e^{-\sqrt{p}l}} \left\{ \left[ \left( \frac{(v_{2}+v_{3})-\gamma ((v_{2}-v_{1})-(v_{4}-v_{3}))}{2}\right) \kappa _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{2}+u_{3})-\gamma ((u_{2}-u_{1})-(u_{4}-u_{3}))}{2}\right) \kappa _{1}\right] e^{\sqrt{p}l}\right\} \\ k_{11} =&\left[ \frac{(u_{2}-u_{3})}{2}-\left( \frac{\gamma ((v_{2}-v_{1})+(v_{4}-v_{3}))}{2}\right) \kappa _{2}\right] \\ k_{12} =&\frac{1}{\sin {\sqrt{p}l}} \left\{ \left[ \left( \frac{(v_{2}-v_{3})-\gamma ((v_{2}-v_{1})-(v_{4}-v_{3}))}{2}\right) \kappa _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{2}-u_{3})-\gamma ((u_{2}-u_{1})+(u_{4}-u_{3}))}{2}\right) \kappa _{1}\right] \cos {\sqrt{p}l}\right\} . \end{aligned}$$
  1. 2.

    When p is negative constant, i.e., \(p<0\) , let \(p =-q\) and \(q>0\), then two cases are possible.

Case 1:y(x) and \(\frac{\mathrm{d}y(x)}{\mathrm{d}x}\) are \(\mathscr {D}^{1}\)-differentiable or \(\mathscr {D}^{2}\)-differentiable, and then, we have the following:

$$\begin{aligned}&\begin{array}{ll} \frac{\mathrm{d}^{2}y_{1}(x,\alpha )}{\mathrm{d}x^{2}}=-qy_{1}(x,\alpha );&\quad \frac{\mathrm{d}^{2}y_{2}(x,\alpha )}{\mathrm{d}x^{2}}=-qy_{2}(x,\alpha )\end{array}\\&\begin{array}{ll} \frac{\mathrm{d}^{2}y'_{1}(x,\beta )}{\mathrm{d}x^{2}}=-qy'_{1}(x,\beta );&\quad \frac{\mathrm{d}^{2}y'_{2}(x,\beta )}{\mathrm{d}x^{2}}=-qy'_{2}(x,\beta )\end{array}\\&\begin{array}{ll} \frac{\mathrm{d}^{2}y''_{1}(x,\gamma )}{\mathrm{d}x^{2}}=-qy''_{1}(x,\gamma );&\quad \frac{\mathrm{d}^{2}y''_{2}(x,\gamma )}{\mathrm{d}x^{2}}=-qy''_{2}(x,\gamma ) \end{array} \end{aligned}$$

with the boundary conditions (1).

Table 1 Solution for \({x}=1\)
Full size table

The general solution of the above equations are as follows:

$$\begin{aligned} y_{1}(x,\alpha )= & {} k_{1}e^{\sqrt{q}x}+k_{2}e^{-\sqrt{q}x}+k_{3} \cos \sqrt{q}x+k_{4} \sin \sqrt{q}x\\ y_{2}(x,\alpha )= & {} -k_{1}e^{\sqrt{q}x}-k_{2}e^{-\sqrt{q}x}{+}k_{3} \cos \sqrt{q}x{+}k_{4} \sin \sqrt{q}x\\ y'_{1}(x,\beta )= & {} k_{5}e^{\sqrt{q}x}+k_{6}e^{-\sqrt{q}x}+k_{7} \cos \sqrt{q}x+k_{8} \sin \sqrt{q}x\\ y'_{2}(x,\beta )= & {} -k_{5}e^{\sqrt{q}x}{-}k_{6}e^{-\sqrt{q}x}{+}k_{7} \cos \sqrt{q}x{+}k_{8} \sin \sqrt{q}x\\ y''_{1}(x,\gamma )= & {} k_{9}e^{\sqrt{q}x}{+}k_{10}e^{-\sqrt{q}x}{+}k_{11} \cos \sqrt{q}x+k_{12} \sin \sqrt{q}x\\ y''_{2}(x,\gamma )= & {} -k_{9}e^{\sqrt{q}x}{-}k_{10}e^{-\sqrt{q}x}{+}k_{11} \cos \sqrt{q}x{+}k_{12} \sin \sqrt{q}x, \end{aligned}$$

where

$$\begin{aligned} k_{1} =&\frac{1}{e^{\sqrt{q}l} - e^{-\sqrt{q}l}}\left\{ \left[ \left( \frac{(v_{1}-v_{4})+\alpha ((v_{2}-v_{1})+(v_{4}-v_{3}))}{2}\right) \vartheta _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{1}-u_{4})+\alpha ((u_{2}-u_{1})+(u_{4}-u_{3}))}{2}\right) \vartheta _{1}\right] e^{-\sqrt{q}l}\right\} \\ k_{2} =&\frac{-1}{e^{\sqrt{q}l} - e^{-\sqrt{q}l}}\left\{ \left[ \left( \frac{(v_{1}-v_{4})+\alpha ((v_{2}-v_{1})+(v_{4}-v_{3}))}{2}\right) \vartheta _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{1}-u_{4})+\alpha ((u_{2}-u_{1})+(u_{4}-u_{3}))}{2}\right) \vartheta _{1}\right] e^{\sqrt{q}l}\right\} \\ k_{3} =&\left[ \frac{(u_{1}+u_{4})}{2}+\left( \frac{\alpha ((v_{2}-v_{1})-(v_{4}-v_{3}))}{2}\right) \vartheta _{2}\right] \\ k_{4} =&\frac{1}{\sin {\sqrt{q}l}}\left\{ \left[ \left( \frac{(v_{1}+v_{4})+\alpha ((v_{2}-v_{1})-(v_{4}-v_{3}))}{2}\right) \vartheta _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{1}+u_{4})+\alpha ((u_{2}-u_{1})-(u_{4}-u_{3}))}{2}\right) \vartheta _{1}\right] \cos {\sqrt{q}l}\right\} \\ k_{5} =&\frac{1}{e^{\sqrt{q}l} - e^{-\sqrt{q}l}}\left\{ \left[ \left( \frac{(v_{2}-v_{3})-\beta ((v_{2}-v_{1})+(v_{4}-v_{3}))}{2}\right) \nu _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{2}-u_{3})-\beta ((u_{2}-u_{1})+(u_{4}-u_{3}))}{2}\right) \nu _{1}\right] e^{-\sqrt{q}l}\right\} \\ k_{6} =&\frac{-1}{e^{\sqrt{q}l} - e^{-\sqrt{q}l}}\left\{ \left[ \left( \frac{(v_{2}-v_{3})-\beta ((v_{2}-v_{1})+(v_{4}-v_{3}))}{2}\right) \nu _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{2}-u_{3})-\beta ((u_{2}-u_{1})+(u_{4}-u_{3}))}{2}\right) \nu _{1}\right] e^{\sqrt{q}l}\right\} \\ k_{7} =&\left[ \frac{(u_{2}+u_{3})}{2}-\left( \frac{\beta ((v_{2}-v_{1})-(v_{4}-v_{3}))}{2}\right) \nu _{2}\right] \\ k_{8} =&\frac{1}{\sin {\sqrt{q}l}}\left\{ \left[ \left( \frac{(v_{2}+v_{3})-\beta ((v_{2}-v_{1})-(v_{4}-v_{3}))}{2}\right) \nu _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{2}+u_{3})-\beta ((u_{2}-u_{1})-(u_{4}-u_{3}))}{2}\right) \nu _{1}\right] \cos {\sqrt{q}l}\right\} \\ k_{9} =&\frac{1}{e^{\sqrt{q}l} - e^{-\sqrt{q}l}}\left\{ \left[ \left( \frac{(v_{2}-v_{3})-\gamma ((v_{2}-v_{1})+(v_{4}-v_{3}))}{2}\right) \kappa _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{2}-u_{3})-\gamma ((u_{2}-u_{1})+(u_{4}-u_{3}))}{2}\right) \kappa _{1}\right] e^{-\sqrt{q}l}\right\} \\ k_{10} =&\frac{-1}{e^{\sqrt{q}l} - e^{-\sqrt{q}l}}\left\{ \left[ \left( \frac{(v_{2}-v_{3})-\gamma ((v_{2}-v_{1})+(v_{4}-v_{3}))}{2}\right) \kappa _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{2}-u_{3})-\gamma ((u_{2}-u_{1})+(u_{4}-u_{3}))}{2}\right) \kappa _{1}\right] e^{\sqrt{q}l}\right\} \\ k_{11} =&[\frac{(u_{2}+u_{3})}{2}-\left( \frac{\gamma ((v_{2}-v_{1})-(v_{4}-v_{3}))}{2}\right) \kappa _{2}]\\ k_{12} =&\frac{1}{\sin {\sqrt{q}l}}\left\{ \left[ \left( \frac{(v_{2}+v_{3})-\gamma ((v_{2}-v_{1})-(v_{4}-v_{3}))}{2}\right) \kappa _{2}\right] \right. \\&\left. -\left[ \left( \frac{(u_{2}+u_{3})-\gamma ((u_{2}-u_{1})-(u_{4}-u_{3}))}{2}\right) \kappa _{1}\right] \cos {\sqrt{q}l}\right\} . \end{aligned}$$

Case 2:y(x) is \(\mathscr {D}^{1}\)-differentiable and \(\frac{\mathrm{d}y(x)}{\mathrm{d}x}\) is \(\mathscr {D}^{2}\)-differentiable or y(x) is \(\mathscr {D}^{2}\)-differentiable and \(\frac{\mathrm{d}y(x)}{\mathrm{d}x}\) is \(\mathscr {D}^{1}\)-differentiable

$$\begin{aligned}&\begin{array}{ll} \frac{\mathrm{d}^{2}y_{1}(x,\alpha )}{\mathrm{d}x^{2}}=-qy_{2}(x,\alpha );&\quad \frac{\mathrm{d}^{2}y_{2}(x,\alpha )}{\mathrm{d}x^{2}}=-qy_{1}(x,\alpha )\end{array}\\&\begin{array}{ll} \frac{\mathrm{d}^{2}y'_{1}(x,\beta )}{\mathrm{d}x^{2}}=-qy'_{2}(x,\beta );&\quad \frac{\mathrm{d}^{2}y'_{2}(x,\beta )}{\mathrm{d}x^{2}}=-qy'_{1}(x,\beta )\end{array}\\&\begin{array}{ll} \frac{\mathrm{d}^{2}y''_{1}(x,\gamma )}{\mathrm{d}x^{2}}=-qy''_{2}(x,\gamma );&\quad \frac{\mathrm{d}^{2}y''_{2}(x,\gamma )}{\mathrm{d}x^{2}}=-qy''_{1}(x,\gamma ) \end{array} \end{aligned}$$

with the boundary conditions (1), and then, the solution is as follows:

$$\begin{aligned} y_{1}(x,\alpha )&= [(u_{1}+\alpha (u_{2}-u_{1}))\vartheta _{1}]\cos \sqrt{q}l\\&\quad +\frac{1}{\sin \sqrt{q}l}\{[(v_{1}+\alpha (v_{2}-v_{1}))\vartheta _{2}] \\&\quad -[(u_{1}+\alpha (u_{2}-u_{1}))\vartheta _{1}]\cos \sqrt{q}l\} \sin \sqrt{q}x\\ y_{2}(x,\alpha )&= [(u_{4}-\alpha (u_{4}-u_{3}))\vartheta _{1}]\cos \sqrt{q}l\\&\quad +\frac{1}{\sin \sqrt{q}l}\{[(v_{4}-\alpha (v_{4}-v_{3}))\vartheta _{2}] \\&\quad - [(u_{4}-\alpha (u_{4}-u_{3}))\vartheta _{1}]\cos \sqrt{q}l\} \sin \sqrt{q}x\\ y'_{1}(x,\beta )&= [(u_{3}+\beta (u_{4}-u_{3}))\nu _{1}] \cos \sqrt{q}l\\&\quad +\frac{1}{\sin \sqrt{q}l}\{[(v_{2}-\beta (v_{2}-v_{1}))\nu _{2}] \\&\quad -[(u_{3}+\beta (u_{4}-u_{3}))\nu _{1}] \cos \sqrt{q}l\} \sin \sqrt{q}x\\ y'_{2}(x,\beta )&= [(u_{2}-\beta (u_{2}-u_{1}))\nu _{1}] \cos \sqrt{q}l\\&\quad +\frac{1}{ \sin \sqrt{q}l}\{[(v_{3}+\beta (v_{4}-v_{3}))\nu _{2}] \\&\quad -[(u_{2}-\beta (u_{2}-u_{1}))\nu _{1}] \cos \sqrt{q}l\} \sin \sqrt{q}x\\ y''_{1}(x,\gamma )&= [(u_{3}+\gamma (u_{4}-u_{3}))\kappa _{1}] \cos \sqrt{q}l\\&\quad +\frac{1}{ \sin \sqrt{q}l}\{[(v_{2}-\gamma (v_{2}-v_{1}))\kappa _{2}] \\&\quad -[(u_{3}+\gamma (u_{4}-u_{3}))\kappa _{1}] \cos \sqrt{q}l\} \sin \sqrt{q}x\\ y''_{2}(x,\gamma )&= [(u_{2}-\gamma (u_{2}-u_{1}))\kappa _{1}] \cos \sqrt{q}l\\&\quad +\frac{1}{ \sin \sqrt{q}l}\{[(v_{3}+\gamma (v_{4}-v_{3}))\kappa _{2}] \\&\quad -[(u_{2}-\gamma (u_{2}-u_{1}))\kappa _{1}] \cos \sqrt{q}l\} \sin \sqrt{q}x. \end{aligned}$$

Analytic example

Let us consider the differential equation \(\frac{\mathrm{d}^{2}y(x)}{\mathrm{d}x^{2}}=y(x)\) with the boundary conditions \(y(0)=((3,4,5,6);0.7,0.6,0.4)\) and \(y(2)=((7,8,9,10);0.4,0.5,0.6)\), and let y(x) and \(\frac{\mathrm{d}y(x)}{\mathrm{d}x}\) is \(\mathscr {D}^{1}\)-differentiable.

Solution

$$\begin{aligned} y_{1}(x,\alpha )&= \frac{1}{e^{2}-e^{-2}}\{[(7+0.4\alpha )-(3+0.7\alpha )e^{-2}]e\\&\quad -[(7+0.4\alpha )-(3+0.7\alpha )e^{2}]e^{-1}\}\\ y_{2}(x,\alpha )&= \frac{1}{e^{2}-e^{-2}}\{[(10-0.4\alpha )-(6-0.7\alpha )e^{-2}]e\\&\quad -[(10-0.4\alpha )-(6-0.7\alpha )e^{2}]e^{-1}\}\\ y'_{1}(x,\beta )&= \frac{1}{e^{2}-e^{-2}}\{[(8-0.5\beta )-(4-0.6\beta )e^{-2}]e\\&\quad -[(8-0.5\beta )-(4-0.6\beta )e^{2}]e^{-1}\}\\ y'_{2}(x,\beta )&= \frac{1}{e^{2}-e^{-2}}\{[(9+0.5\beta )-(5+0.6\beta )e^{-2}]e\\&\quad -[(9+0.5\beta )-(5+0.6\beta )e^{2}]e^{-1}\}\\ y''_{1}(x,\gamma )&= \frac{1}{e^{2}-e^{-2}}\{[(8-0.6\gamma )-(4-0.4\gamma )e^{-2}]e\\&\quad -[(8-0.6\gamma )-(4-0.4\gamma )e^{2}]e^{-1}\}\\ y''_{2}(x,\gamma )&= \frac{1}{e^{2}-e^{-2}}\{[(9+0.6\gamma )-(5+0.4\gamma )e^{-2}]e\\&\quad -[(9+0.6\gamma )-(5+0.4\gamma )e^{2}]e^{-1}\}. \end{aligned}$$

When we take \({x} = 1\) and for different values of \(\alpha , \beta , \gamma \), the solution is given in Table 1.

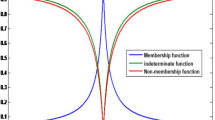
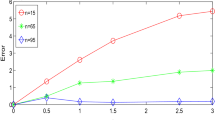
The graphical interpretation of the above table is shown in the following.

figure a
figure b
figure c

From the table values and graph, we see that \(y_{1}(x,\alpha )\) is increasing function and \(y_{2}(x,\alpha )\) decreasing function, whereas \(y'_{1}(x,\beta )\) and \(y''_{1}(x,\gamma )\) are decreasing function and \(y'_{2}(x,\beta )\) and \(y''_{2}(x,\gamma )\) are increasing function. Hence, the solution is strong solution.

Conclusion

In this paper, we have derived the solution of second-order differential equation in neutrosophic environment. An example is given to demonstrate the strong solution of the same. For future research work, we use this approach to solve higher order differential equations and we can explore this method to solve linear and non-linear differential equations, simultaneous differential equations, and so on. Also the numerical techniques can be applied to solve the neutrosophic differential equations. Neutrosophic integration can be developed to solve the problems involving neutrosophic numbers in real-world applications. Internet of things is one of the developing areas in recent times. In [21], neutrosophic AHP (Analytical hierarchy process) of the IoT in enterprises has been effectively presented in decision-making criteria. Neutrosophic logic in IoT may be employed to handle inconsistent data.