Extension of a coupled mooring–viscous flow solver to account for mooring–joint–multibody interaction in waves

Abstract

To account for nonlinear wave–structure interaction, mooring dynamics and the associated viscous flow effects, a coupled mooring–viscous flow solver was formerly developed and validated (Jiang et al. in Mar Struct 72:783, 2020a, Validation of a dynamic mooring model coupled with a RANS solver). This paper presents an extension of the coupled mooring–viscous flow solver to solve mooring dynamics interacting with an articulated multibody offshore system. The presently extended solver is verified by comparing the predicted motions of and loads on a moored floating box to those obtained from the formerly validated solver, which was aimed for solving mooring dynamics interacting with a single floating body. The almost identical results obtained from both solvers verify the presently developed multi-module coupling technique for solving the mooring dynamics and articulated multibody dynamics in a coupled manner. Apart from the code comparison and verification, the numerical predictions are also validated against experimental tank measurements both for a single body and an articulated multibody. The good agreements between the numerical predictions and the experimental measurements validate the presently extended solver, where wave-induced body motions together with loads acting on mooring lines and joint connections were examined. Developed as an open-source tool, the extended solver shows a potential of the coupled methodology for analyzing an articulated multibody offshore system, moored with various mooring configurations in extreme sea states, which goes beyond the state of the art.

1 Introduction

Within the Space@Sea project (Flikkema and Waals 2019), an innovative hinged multibody floating offshore module was developed to be employed for various functions of artificial islands. By following the analogy of standardization to enlarge a floating structure using a multitude of smaller structures, this project intended to significantly reduce building and installation costs and to provide the desired flexibility of additional deck space at sea (Flikkema et al. 2021). Compared to a conventional very large floating structure (VLFS), which generally endures large shear force and bending moment due to its sizeable dimension, a modular floating structure (MFS) could be built not only to withstand large internal forces, but also to benefit from lower construction, transportation and installation costs, and the potential expansion of an existing VLFS (Ren et al. 2019).

Fig. 1

Examples of various mooring configurations: standard catenary cables (left), configuration consisting of cables and floaters (right) from Jiang et al. (2021)

The complexity inherent in a moored and coupled multibody offshore system requires accounting for not only the fluid-multibody interaction, but also the dynamics of its mechanical coupling system and mooring system. Depending on the purpose of a MFS, various articulation techniques, such as hinge, prismatic, cylindrical and screw joints, can be applied (Featherstone 2014). To calculate the motions of simply connected floating bodies, a linear frequency-domain technique using a mode expansion method was introduced by Newman (1994). For a floating multibody system coupled in different degrees of complexity, a two-step strategy, where the hydrodynamic coefficients and wave forces were first calculated by a diffraction–radiation model in the frequency domain and then the motion equations of multibody system were solved in the time domain, has been documented in numerous publications, e.g., Diamantoulaki and Angelides (2010), for hinged wave energy converters; Rogne (2014), for hinged floating breakwaters; Zhu et al. (2017), for a floating offshore wind turbine with hinged structures; Ghesmi et al. (2019), for articulated ships.

Apart from the fluid–multibody interaction, a MFS must maintain station; that is, its mooring system must withstand the environmental loads over its long asset life, while operating under various sea conditions. To assess the hydrodynamics of a moored multibody offshore system, various mathematical models of mooring system (Davidson and Ringwood 2017) can be coupled to the hydrodynamic analysis techniques, which are generally classified as potential and viscous flow solvers. Although potential flow solvers are unable to implicitly consider viscous effects nor accurately predict oscillatory motions of a floating structure at its resonant region (Jonkman 2010), they are widely used in marine hydrodynamics due to their robustness and computational efficiency. For instance, van Rij et al. (2019) evaluated and compared extreme wave loads on the moored, multibody wave energy converter using both a potential flow model and a viscous flow model. In general, potential flow-based methods can be used for the analysis under operational conditions, albeit with a carefully selected approach to account for viscous damping. They are challenging to consider a number of key situations, where nonlinearities and complex free surface effects are prevalent (Jiang et al. 2020d). On other hand, a potential flow solver is challenging to fully reproduce the hydrodynamic process of wave interaction for a mechanically coupled multibody system. This is not only because the inherent inaccuracies of the potential flow solver arise from lacking viscous effects, but also the hydrodynamic coefficients obtained from the linear frequency-domain computations are required for the time-domain computations.

On the other hand, a viscous flow method has to be used over the potential flow method, to consider nonlinear viscous effects, wave–structure interaction as well as complex fluid dynamics, such as green water on deck, gap flow resonance between structures. Palm et al. (2013) coupled analyzed the dynamics of a floating wave energy converter(WEC) using the Navier–Stokes equations for fluid dynamics and a high-order finite-element solver for cable dynamics. Relying on the Reynolds-averaged Navier–Stokes equations, a similar coupled analysis was reported by Nicholls-Lee et al. (2013), where the mooring dynamics was, however, solved via OrcaFlex. To fully account for the nonlinear viscous flow effects, wave-structure interaction and the dynamics of attached mooring system, inspired by the work of Palm et al. (2016), an open-source dynamic mooring model namely MoorDyn (Hall 2015) was implemented into a viscous flow solver to predict the hydrodynamic damping of a moored floating structure (Jiang et al. 2019). MoorDyn is a lumped-mass model that has been successfully validated against wave tank measurements by coupling it to a potential flow solver (Hall and Goupee 2015), to a meshless smoothed particle hydrodynamics (SPH) approach (Domínguez et al. 2019), and to a mesh-based viscous flow method (Jiang et al. 2020a), respectively. The benefits of the coupled mooring–viscous flow solver for solving highly nonlinear rigid-body motions interacting with its mooring dynamics were demonstrated by comparing it to a coupled mooring–potential flow solver (Jiang et al. 2020a), and to a coupled quasi-static mooring–viscous flow solver (Jiang et al. 2020b). In addition, the implemented mooring model supports various mooring configurations by adding floaters and/or clump-weights on the mooring lines (Vissio et al. 2015; Hall 2020; Jiang et al. 2020c, 2021), as exemplarily shown in Fig. 1. To more accurately calculate the hydrodynamic loads on mooring cables, de Lataillade (2019) used the fluid velocity and acceleration directly from the solution of the Navier–Stokes model at each node of a cable. To further include the influence of bending stiffness on snap loads in marine cables, Palm and Eskilsson (2020) implemented bending stiffness as a rotation-free, nested local discontinuous Galerkin (DG) method into an existing hp-adaptive DG method. The effects of bending and shearing on mooring dynamics were also studied by Martin and Bihs (2021), using a geometrically exact beam model. A literature review shows that wave-induced motions of an articulated multibody offshore system moored with linear spring have been studied using a commercial viscous flow tool (Seithe and el Moctar 2019), but discussions of an articulated multibody offshore system interacting with its mooring dynamics are still few. Using smoothed particle hydrodynamics (SPH), Moreno et al. (2020) analyzed the response of a multi-float wave energy converter M4 in focused waves, where complex multi-floats were coupled with mechanical constraint and mooring.

This paper presents an extension of coupled mooring–viscous flow solver to consider the mooring dynamics interacting with a multibody offshore system in waves, where the equations governing the fluid dynamics, multibody dynamics, and mooring dynamics are solved via an implicitly coupling approach (namely the mooring-rigidBodyDynamics solver). This coupling technique is verified by comparing the predicted motions of and loads on a moored floating box to those obtained from a formerly validated solver (Jiang et al. 2020a), which was aimed to solve the mooring dynamics coupled with the six degree-of-freedom motions of a single body (namely the mooring-sixDoFRigidBodyMotion solver). Except for the code comparison and verification, the numerically predicted motions and loads are validated against experimental tank measurements both for a single body and an articulated multibody. The almost identical results of wave-induced body motions and mooring loads obtained from the two coupled solvers verify the coupling technique used for the presently developed mooring-rigidBodyDynamics solver. The good agreement between the numerical predictions and the experimental measurements validates the presently coupled solver. Apart from the validation for a single body, validation was also performed for a moored and articulated multibody in waves. The good agreements between the numerical predictions and the experimental measurements validate the presently extended solver, where wave-induced body motions together with loads acting on mooring lines and joint connections were examined. To demonstrate the potential of the extended mooring–viscous flow solver for solving an articulated multibody offshore system interacting with its mooring dynamics, the floating box, moored with four symmetric catenary cables, is extended by coupling a second box at its rear via a mechanical hinge joint. The highly nonlinear behaviors arising from catenary moorings, hinged bodies, waves, flow viscosity, and complex free surface topologies, such as green water and gap flow effects are well represented.

2 Numerical method

The extended mooring–viscous flow coupling scheme is implemented in the open-source CFD library OpenFOAM-v2012 (Weller et al. 1998). This section starts with a brief overview of the governing equations for incompressible two-phase flow, following which the rigid-body dynamics is derived. Coming after the introductions of numerical models for solving fluid and rigid-body dynamics, the implemented dynamic mooring model is explained. This section ends with the presentation of a multi-module coupling approach.

2.1 Fluid flow governing equations

The governing equations for the incompressible Newtonian fluids are based on the continuity and the momentum conservation equations. The mass conservation equation is given by

$$\begin{aligned} \nabla \cdot {{\mathbf {v}}} = 0 \end{aligned}$$

(1)

where ${{\mathbf {v}}}$ denotes the fluid velocity filed vector in the global coordinate system. The conservation of momentum is governed by

$$\begin{aligned} \frac{\partial {\left( \rho \mathbf {v}\right) }}{\partial t} +\nabla \cdot \left( \rho {{\mathbf {v}}}{{\mathbf {v}}}\right) =\nabla \cdot {\varvec{\sigma }} + \rho {{\mathbf {f}}}_b - \nabla p \end{aligned}$$

(2)

where ${\varvec{\sigma }}$ is the deviatoric viscous stress tensor:

$$\begin{aligned} {\varvec{\sigma }}=\mu \left[ \nabla {{\mathbf {v}}} + \left( \nabla {{\mathbf {v}}}\right) ^T\right] - \frac{2}{3}\mu {{\mathbf {I}}}\left( \nabla \cdot {{\mathbf {v}}}\right) \end{aligned}$$

(3)

with the identify tensor ${{\mathbf {I}}}\equiv \delta _{ij}$. $\mathbf {\rho }$ and $\mathbf {\mu }$ are the effective density and the effective dynamic viscosity, respectively. For free surface hydrodynamic applications, the effective density and kinematic viscosity can be expressed in terms of water volume fraction $\alpha$ as follows:

$$\begin{aligned}&\rho = \alpha \rho _w + \rho _a\left( 1-\alpha \right) \end{aligned}$$

(4)

$$\begin{aligned}&\mu = \alpha \mu _w + \mu _a\left( 1-\alpha \right) \end{aligned}$$

(5)

where subscripts w and a represent the two immiscible fluids, water and air, respectively. The volume fraction $\alpha$ stands for a fraction of the volume occupied by water inside an arbitrary closed volume, i.e., Volume-Of-Fluid (VOF) method (Hirt and Nichols 1981). At each time step, the existing velocity field convects phase fractions, and the distribution and development of the free surface is estimated using the following equation:

$$\begin{aligned} \frac{\partial \alpha }{\partial t} + \nabla \cdot \left( {{\mathbf {v}}}\alpha \right) + \nabla \cdot \left[ {{\mathbf {v}}}_r\alpha \left( 1-\alpha \right) \right] =0 \end{aligned}$$

(6)

where ${{\mathbf {v}}}_r$ is a velocity field normal to the interface, standing for the artificial compression on the free surface, and its magnitude is proportional to the instantaneous velocity. Equation 6 is an extended VOF formulation following the work of Rusche (2003), and its boundedness is insured using the MULES (Multidimensional Universal Limiter with Explicit Solution) algorithm (Berberović et al. 2009).

The solution domain is discretized into a finite number of control volumes, which may be of arbitrary shape. The mass conservation is ensured using a pressure correction equation based on the hybrid PIMPLE approach (Patankar and Spalding 1983), which combines the Semi-Implicit Pressure Linked Equations (SIMPLE) algorithm with the Pressure Implicit with Splitting of Operators (PISO) algorithm.

2.2 Rigid body dynamics

The rigid-body dynamics addressed in this study includes not only the dynamics of a single body, but also the dynamics of an articulated multibody system.

2.2.1 Dynamics of a single body

The dynamics of a single rigid body is solved via the sixDoFRigidBodyMotion solver in OpenFOAM package. This means that the body can translate along and rotate about three axes, defining an inertial Cartesian coordinate system (o-xyz), as sketched in Fig. 2.

Fig. 2

Coordinate systems and notations used to describe rigid-body dynamics

The time-invariant moment of inertia $\mathbf {I'}$, defined in the local reference frame ($o'-x'y'z'$), has to be transformed to the inertial reference frame by means of transformation matrix ${{\mathbf {S}}}$. The transformation matrix consists of three consecutive Euler rotations $\phi$, $\theta$ and $\psi$ as follows:

$$\begin{aligned} {{\mathbf {S}}} = {{\mathbf {S}}}_\phi {{\mathbf {S}}}_\theta {{\mathbf {S}}}_\psi \end{aligned}$$

(7)

Applying the linear and angular momentum laws of Newton–Euler dynamics, the equation of motion for a single rigid body in the inertial coordinate system is given by Dullweber et al. (1997):

$$\begin{aligned} \left[ \begin{array}{cc} m{{\mathbf {E}}} &{} {{\mathbf {0}}} \\ {{\mathbf {0}}} &{} {{\mathbf {S}}}\mathbf {I'}{{\mathbf {S}}}^T \end{array}\right] \left[ \begin{array}{c} \ddot{{{\mathbf {r}}}} \\ \dot{{\varvec{\omega }}} \end{array}\right] + \left[ \begin{array}{cc} {{\mathbf {0}}} &{} {{\mathbf {0}}} \\ {{\mathbf {0}}} &{} {\varvec{\omega }}\times {{\mathbf {S}}}\mathbf {I'}{{\mathbf {S}}}^T \end{array}\right] \left[ \begin{array}{c} \dot{{{\mathbf {r}}}} \\ {\varvec{\omega }} \end{array}\right] = \left[ \begin{array}{c} {{\mathbf {F}}} \\ {{\mathbf {M}}} \end{array}\right] \end{aligned}$$

(8)

where m is body mass and ${{\mathbf {E}}}$ is an identity matrix. ${{\mathbf {r}}}$ and ${\varvec{\omega }}$ are the body position and angular velocity vectors with respect to its center of gravity. ${{\mathbf {F}}}$ and ${{\mathbf {M}}}$ are the force and moment, respectively.

Fig. 3

Sample of the discretized dynamic mooring model

2.2.2 Dynamics of a multibody system

For the dynamics of multiple bodies without internal connections, their equations of motion are straightforward extensions of the equation of motion for a single body. Each body can be treated separately in six degree-of-freedoms, and their interactions are governed by the fluids surrounding them. For convenience, the notation ${{\mathbf {q}}}$ is defined to denote a generalized coordinate of the body reference:

$$\begin{aligned} {{\mathbf {q}}} = \left[ \begin{array}{cccccc} x&y&z&\phi&\theta&\psi \end{array} \right] ^T \end{aligned}$$

(9)

The motion of equation expressed in Eq. 8 can be then recast as

$$\begin{aligned} \left[ \begin{array}{cc} m{{\mathbf {E}}} &{} {{\mathbf {0}}} \\ {{\mathbf {0}}} &{} {{\mathbf {S}}}\mathbf {I'}{{\mathbf {S}}}^T{{\mathbf {J}}}_\alpha \end{array}\right] \ddot{{{\mathbf {q}}}} +\left[ \begin{array}{cc} {{\mathbf {0}}} &{} {{\mathbf {0}}} \\ {{\mathbf {0}}} &{} {{\mathbf {S}}}{{\mathbf {I}}}{{\mathbf {S}}}^T{{\mathbf {J}}}_\omega + \dot{{{\mathbf {S}}}}{{\mathbf {S}}}\mathbf {I'}{{\mathbf {S}}}^T{{\mathbf {J}}}_\alpha \end{array}\right] \dot{{{\mathbf {q}}}} = \left[ \begin{array}{c} {{\mathbf {F}}} \\ {{\mathbf {M}}} \end{array}\right] \nonumber \\ \end{aligned}$$

(10)

where ${{\mathbf {J}}}_\alpha$ and ${{\mathbf {J}}}_\omega$ are Jacobins related to rotation and angular velocity, respectively. The final motion of equation given by Eq. 10 can be simplified as follows:

$$\begin{aligned} {{\mathbf {H}}}\left( {{\mathbf {q}}}\right) \ddot{{{\mathbf {q}}}} +{{\mathbf {C}}}\left( {{\mathbf {q}}},\dot{{{\mathbf {q}}}}\right) \dot{{{\mathbf {q}}}}={\varvec{\tau }} \end{aligned}$$

(11)

where ${{\mathbf {H}}}$ is the matrix containing the mass and moment of inertia, and it is a function of ${{\mathbf {q}}}$. ${{\mathbf {C}}}$ is the body’s Coriolis and centripetal matrix, depending on both ${{\mathbf {q}}}$ and $\dot{{{\mathbf {q}}}}$. ${\varvec{\tau }}$ is the force vector containing forces and moments. Provided that kinematic constraints are applied, the equation of motion becomes

$$\begin{aligned} {{\mathbf {H}}}\left( {{\mathbf {q}}}\right) \ddot{{{\mathbf {q}}}} +{{\mathbf {C}}}\left( {{\mathbf {q}}},\dot{{{\mathbf {q}}}}\right) \dot{{{\mathbf {q}}}}={\varvec{\tau }} + {\varvec{\tau }}_c \end{aligned}$$

(12)

Here, ${\varvec{\tau }}_c$ is the constraint force. This force is unknown, but it has the important property that allows us to either calculate its value, or to eliminate it from the equation (Featherstone 2014).

In many engineering fields, articulating the bodies into a multibody system is equivalent to imposing dynamic constraints on the bodies. For a multibody system, its dynamic behavior is described by the equations of motion of the bodies and the constraint equations at the joints. In OpenFOAM, an articulated multibody system is solved via the rigidBodyDynamics solver, using the forward-dynamics algorithm from Featherstone (2014). In a forward-dynamics problem, ${\varvec{\tau }}$ is given, the task is to calculate $\ddot{{{\mathbf {q}}}}$ by the following procedure:

• determine ${{\mathbf {C}}}$

• calculate ${{\mathbf {H}}}$

• solve ${{\mathbf {H}}}\ddot{{{\mathbf {q}}}}={\varvec{\tau }}-{{\mathbf {C}}}\dot{{{\mathbf {q}}}}$ for $\ddot{{{\mathbf {q}}}}$

2.3 Mooring dynamics

Mooring cables used in marine applications are slender structures with characteristic length-to-diameter ratio of several thousands. Bending stresses are several orders of magnitude smaller than axial stresses, and generally can be neglected for catenary chains. The lumped-mass approach involves lumping effects of mass, external forces, and inertial reactions at a finite number of nodes along the cable’s length, as depicted in Fig. 3.

The behavior of a continuous mooring cable is modeled as a set of concentrated masses connected by massless springs. A right-handed inertial reference frame defines the z-axis, pointing positive upwards from the calm water plane. Cable masses are lumped at nodes together with gravitational and buoyancy forces, hydrodynamic loads, and reactions from contact with the seabed. Hydrodynamic drag and added mass are calculated based on Morison’s equation. A cable’s axial stiffness is modeled by specifying a linear stiffness for each cable segment, albeit in tension only. A damping term is also specified for each segment to dampen nonphysical resonances caused by the lumped-mass discretization. Bending and torsional stiffness are neglected. Bottom contact is represented by vertical stiffness and damping forces when nodes pass below the seabed. For further details, see Hall (2015) and Hall and Goupee (2015).

2.3.1 Internal forces

A cable is represented as a cylinder of equivalent diameter d, unstretched length L, and density $\rho _c$. The stiffness is then calculated from Young’s modulus E. For a cable with N segments connecting $N+1$ nodes including the bottom anchor node and the top fairlead node, the unstretched length of each cable segment is $l=\frac{L}{N}$, and its net buoyancy is

$$\begin{aligned} W=\frac{\pi }{4}d^2l\left( \rho _w-\rho _c\right) g \end{aligned}$$

(13)

where $\rho _w$ is water density, and g is acceleration of gravity. Assuming the force is evenly divided among two connecting nodes, the net buoyancy at node i is described in vector form as

$$\begin{aligned} {{\mathbf {W}}}_i=\frac{1}{2}\left( W_{i-\frac{1}{2}}+W_{i+\frac{1}{2}}\right) {\hat{{{\mathbf {e}}}}}_z \end{aligned}$$

(14)

where ${\hat{{{\mathbf {e}}}}}_z$ is a unit vector in the positive z-direction. The tension in cable segment $i+\frac{1}{2}$ is

$$\begin{aligned} {{\mathbf {T}}}_{i+\frac{1}{2}}=E\frac{\pi }{4}d^2\left( \frac{|{{\mathbf {r}}}_{i+1}-{{\mathbf {r}}}_i|}{l}-1\right) \left( \frac{{{\mathbf {r}}}_{i+1}-{{\mathbf {r}}}_i}{|{{\mathbf {r}}}_{i+1}-{{\mathbf {r}}}_i|}\right) \end{aligned}$$

(15)

where the direction of the tension is defined as pointing from node i to node $i+1$. The calculations assume that cable tensions are always positive (i.e., $|{{\mathbf {r}}}_{i+1}-{{\mathbf {r}}}_i|\ge l$), and compressive cable forces are not allowed. To improve numerically stability, a numerical internal damping force is included as

$$\begin{aligned} {{\mathbf {C}}}_{i+\left( \frac{1}{2}\right) }=C_{in}\frac{\pi }{4}d^2 \frac{\partial }{\partial t}\left( \frac{|{{\mathbf {r}}}_{i+1}-{{\mathbf {r}}}_i|}{l}\right) \left( \frac{{{\mathbf {r}}}_{i+1}-{{\mathbf {r}}}_i}{|{{\mathbf {r}}}_{i+1}-{{\mathbf {r}}}_i|}\right) \end{aligned}$$

(16)

where $C_{in}$ is the numerical internal damping coefficient.

2.3.2 External forces

The transverse and tangential cable hydrodynamic forces, including drag and added mass, are calculated at each node via Morison’s equation. The direction of a line passing between two adjacent nodes is approximated by the tangential direction ${\hat{{{\mathbf {q}}}}}_i$:

$$\begin{aligned} {\hat{{{\mathbf {q}}}}}_i=\frac{{{\mathbf {r}}}_{i+1}-{{\mathbf {r}}}_{i-1}}{|{{\mathbf {r}}}_{i+1}-{{\mathbf {r}}}_{i-1}|} \end{aligned}$$

(17)

Correspondingly, the transverse direction $\hat{{{\mathbf {p}}}}_i$ is defined as perpendicular to $\hat{{{\mathbf {q}}}}_i$ and aligned with the direction of the relative water velocity over the cable. Using the transverse drag coefficient ${C}_{dn}$ and the tangential drag coefficient $C_{dt}$, transverse and tangential drag forces are calculated as

$$\begin{aligned}&{{\mathbf {D}}}_{{{\mathbf {p}}}i}=\frac{1}{2}\rho _wC_{dn}dl|\left( {\dot{{{\mathbf {r}}}}}_i\cdot {\hat{{{\mathbf {q}}}}}_i\right) {\hat{{{\mathbf {q}}}}}_i-{\dot{{{\mathbf {r}}}}}_i|\left[ \left( {\dot{{{\mathbf {r}}}}}_i\cdot {\hat{{{\mathbf {q}}}}}_i\right) {\hat{{{\mathbf {q}}}}}_i-{\dot{{{\mathbf {r}}}}}_i\right] \end{aligned}$$

(18)

$$\begin{aligned}&{{\mathbf {D}}}_{{{\mathbf {q}}}i}=\frac{1}{2}\rho _wC_{dt}dl|\left( -{\dot{{{\mathbf {r}}}}}_i\cdot {\hat{{{\mathbf {q}}}}}_i\right) {\hat{{{\mathbf {q}}}}}_i|\left[ \left( -{\dot{{{\mathbf {r}}}}}_i\cdot {\hat{{{\mathbf {q}}}}}_i\right) {\hat{{{\mathbf {q}}}}}_i\right] \end{aligned}$$

(19)

Similarly, the transverse added mass forces for each node are computed as

$$\begin{aligned}&{{\mathbf {A}}}_{{{\mathbf {p}}}i}={{\mathbf {a}}}_{{{\mathbf {p}}}i}{\ddot{{{\mathbf {r}}}}}_i=\rho _wC_{an}\frac{\pi }{4}d^2l\left[ \left( {\ddot{{{\mathbf {r}}}}}_i\cdot {\hat{{{\mathbf {q}}}}}_i\right) {\hat{{{\mathbf {q}}}}}_i-{\ddot{{{\mathbf {r}}}}}_i\right] \end{aligned}$$

(20)

$$\begin{aligned}&{{\mathbf {A}}}_{{{\mathbf {q}}}i}={{\mathbf {a}}}_{{{\mathbf {q}}}i}{\ddot{{{\mathbf {r}}}}}_i=\rho _wC_{at}\frac{\pi }{4}d^2l\left( -{\ddot{{{\mathbf {r}}}}}_i\cdot {\hat{{{\mathbf {q}}}}}_i\right) {\hat{{{\mathbf {q}}}}}_i \end{aligned}$$

(21)

where ${{\mathbf {a}}}_{{{\mathbf {p}}}i}$ and ${{\mathbf {a}}}_{{{\mathbf {q}}}i}$ are the corresponding transverse added mass and tangential added mass, respectively. The interaction with seabed is modeled by a linear spring–damper model:

$$\begin{aligned} {{\mathbf {B}}}_i=dl\left[ \left( z_{bot}-z_i\right) k_b-{{\dot{z}}}_ic_b\right] {\hat{{{\mathbf {e}}}}}_z \end{aligned}$$

(22)

where $k_b$ is the seabed stiffness coefficient, and $c_b$ is the seabed damping coefficient. If a node contacts the seabed ($z_i\le z_{bot}$), this model is activated. Note that horizontal friction from the seabed and Froude-Krylov forces caused by wave kinematics are not considered in present version. Different from the work of de Lataillade (2019), the fluid velocity and acceleration at the nodes of mooring lines are not included in the present study, i.e., drag and inertia forces on the mooring lines were computed in still water. In certain conditions these missing components from the fluid flow may only have very limited effects.

2.3.3 Integration of motion equations

The equation of motion for each node is expressed as

$$\begin{aligned} \left( {{\mathbf {m}}}_i+{{\mathbf {a}}}_{i}\right) {\ddot{{{\mathbf {r}}}}}_i={{\mathbf {T}}}_i+{{\mathbf {C}}}_i+{{\mathbf {W}}}_i+{{\mathbf {B}}}_i+{{\mathbf {D}}}_{i} \end{aligned}$$

(23)

where ${{\mathbf {m}}}_i$ is the mass matrix for node i, which is defined by assigning each node half the combined mass of the two adjacent cable segments:

$$\begin{aligned} {{\mathbf {m}}}_i=\frac{\pi }{4}d^2l\rho _c{{\mathbf {E}}} \end{aligned}$$

(24)

where ${{\mathbf {E}}}$ denotes an identity matrix; ${{\mathbf {a}}}_i$ and ${{\mathbf {D}}}_i$ are the final added mass and drag force via combining their tangential and transverse components; ${{\mathbf {T}}}_i$ and ${{\mathbf {C}}}_i$, the final internal stiffness and damping via combining the two adjacent segments. The second-order system of ordinary differential equation represented in Eq. 23 can be reduced to a system of first-order differential equation, and then solved using a second-order Runge–Kutta integration scheme with a constant time step.

2.4 Multi-module coupling approach

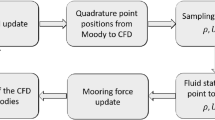
The implemented coupling approach comprises a mooring model to consider the mooring dynamics, and a mechanical model to represent an articulated multibody system, as shown in Fig. 4. The multi-module coupling technique is achieved by coupling each solver module with the module of rigid-body motions. Mooring-induced forces and joint-induced kinematic constraints directly affect the equations of rigid body motions, while flow dynamics is coupled with rigid body motions in an iterative manner.

Fig. 4

The developed multi-module coupling scheme

The equation of motion for an articulated multibody system given by Eq. 11 is numerically stiff and demands relatively small time steps. The temporal discretization of this equation is solved using the second-order Crank–Nicholson method in the present study. The forces and moments acting on a rigid body are given in the inertial coordinate system:

$$\begin{aligned}&{{\mathbf {F}}} = {{\mathbf {F}}}_p + {{\mathbf {F}}}_v + {{\mathbf {F}}}_c + {{\mathbf {F}}}_m + m {{\mathbf {g}}} \end{aligned}$$

(25)

$$\begin{aligned}&{{\mathbf {M}}} = {{\mathbf {M}}}_p + {{\mathbf {M}}}_v + {{\mathbf {M}}}_c + {{\mathbf {M}}}_m \end{aligned}$$

(26)

where subscripts p and v denote the pressure and viscous component of the fluid-induced force and moment. Subscripts m and c denote the mooring-induced and constraint-induced forces and moments, respectively. Pressure and viscous fluid forces and moments are obtained based on the pressure and velocity fields:

$$\begin{aligned}&{{\mathbf {F}}}_p = \int _S{{\mathbf {n}}} p~dS \end{aligned}$$

(27)

$$\begin{aligned}&{{\mathbf {F}}}_v = \int _{S}\rho _e \nu _{e} {{\mathbf {n}}} \cdot {\varvec{\sigma }}^*dS \end{aligned}$$

(28)

$$\begin{aligned}&{{\mathbf {M}}}_p = \int _{S}{{\mathbf {r}}}_c\times {{\mathbf {n}}} p~dS \end{aligned}$$

(29)

$$\begin{aligned}&{{\mathbf {M}}}_v = \int _{S}{{\mathbf {r}}}_c\times \left( \rho _e\nu _{e} {{\mathbf {n}}} \cdot {\varvec{\sigma }}^*\right) ~dS \end{aligned}$$

(30)

where p is the fluid pressure, ${{\mathbf {n}}}$ stands for surface normal vector of the body surface S. ${\varvec{\sigma }}^*$ denotes the deviatoric component of stress tensor, and ${{\mathbf {r}}}_c$ is the distance vector from current boundary surface to the body’s center of gravity.

The constraint-induced forces and moments (i.e., ${{\mathbf {F}}}_c$ and ${{\mathbf {M}}}_c$) are calculated via the forward-dynamic algorithm given in Sect. 2.2. According to Jourdain’s principle of virtual power, the constraint forces deliver zero power along every direction of velocity freedom that is compatible with the motion constraints (Featherstone 2014):

$$\begin{aligned} \left[ \begin{array}{c} {{\mathbf {F}}}_c \\ {{\mathbf {M}}}_c \end{array}\right] \cdot \dot{{{\mathbf {q}}}}=0 \end{aligned}$$

(31)

Based on the property of Eq. 31, the constraint forces can either be calculated or eliminated from the equations of motion.

The mooring-induced forces and moments (i.e., ${{\mathbf {F}}}_m$ and ${{\mathbf {M}}}_m$) are obtained from the implemented dynamic mooring model described in Sect. 2.3. The mooring is implemented to restrain the moving boundary surfaces of the rigid body. For the two solvers of rigidBodyDynamics ($\Omega$) and MoorDyn ($\Pi$), they exchange information between vector spaces ${{\mathbf {X}}}_\Omega$ (i.e., positions and velocities of the attached points) and ${{\mathbf {X}}}_\Pi$ (i.e., mooring-induced forces and moments) a number of times within each time step. The solver $\Pi$ uses the boundary values ${{\mathbf {X}}}_\Omega$ from previous time step or iteration, whichever is applicable, to compute ${{\mathbf {X}}}_\Pi$ for the next time step or iteration:

$$\begin{aligned} {{\mathbf {X}}}_\Pi ^{n+1,\;i+1}= \Pi \left( {{\mathbf {X}}}_{\Omega }^{n+1,\; i} \right) \end{aligned}$$

(32)

where n stands for time steps and i for iterations. The updated ${{\mathbf {X}}}_\Pi$ is then used to calculate ${{\mathbf {X}}}_\Omega$ for the next time step or iteration:

$$\begin{aligned} {{\mathbf {X}}}_\Omega ^{n+1,\;i+1}= \Omega \left( {{\mathbf {X}}}_{\Pi }^{n+1,\; i+1} \right) \end{aligned}$$

(33)

The coupling time step is identical to the time step used in the leading solver $\Omega$. The equations governing the mooring dynamics are solved using a sub-stepping approach with interpolated boundary conditions from the initial value of ${{\mathbf {X}}}_\Omega$. For each internal $\Pi$ time step, the velocity of the attached point is assumed constant, and the intermediate position is adjusted accordingly at each sub-step. Palm (2017) found that numerical instabilities occurred when interpolating the velocity boundary conditions from given positions. In the present study, both position and velocity boundary conditions were provided during the coupling and the velocity changes between each iteration were assumed to be small.

Note that, in Eq. 11, the translational motions of articulated rigid bodies are solved in the global reference frame. Hence, external forces acting on the body can be directly applied, without a transformation to calculate the corresponding translational accelerations. However, to calculate the rotational motions, the moments of inertia need to be reformulated using the rotational inertias of bodies in their local reference frames. In terms of an articulated multibody, its inertia is the sum of the inertias of its multiple parts. Articulated-body inertia depends not only on the inertias of the member of bodies, but also the constraints imposed by the member joints, i.e., they are functions of the joint position variables. In the present study, the assembly method was used to calculate articulated-body inertia, in which the articulated body was assembled step-by-step from its component parts and a sequence of articulated-body inertia was computed along the way (Featherstone 2014).

3 Test case description

To validate the extended solver, a moored floating box in waves experimentally tested by Wu et al. (2019) is adopted in the present study. The wave flume experiments studied the motion and mooring performance of a floating box in waves, where a database for numerical validation was provided. After describing the experimental setup, the corresponding numerical setup is outlined in this section.

3.1 Experimental setup

Table 1 lists the geometric characteristics of the box model. The box is made of light material with a constant density, and its center of gravity is located in its geometric center.

Table 1 Geometric characteristics of the experimentally tested box model, summarized from Wu et al. (2019)

Fig. 5

Sketch and dimensions of the box model equipped with a tracking plate

A high plate of 0.324 m was attached to the front face of the box, on which reflective markers were installed to be used by the motion tracking system, as sketched in Fig. 5. The floating box was symmetrically moored to the bottom of wave flume via four catenary chains. The anchor of each mooring cable is connected to a load-cell fixed to the bottom of wave flume. The parameters of mooring cables are listed in Table 2. An overview of the experimental setup is given in Fig. 6. For further details, see Wu et al. (2019).

Table 2 The parameters of mooring cables used in the experimental test, summarized from Wu et al. (2019)

Fig. 6

An overview sketch of the experimental setup

3.2 Numerical setup

To reduce the computational cost, a two-dimensional numerical wave tank is designed in present study, as specified in Table 3. Figure 7 gives an overview of the numerical domain and its boundary conditions. The domain consists of three layers, namely, a uniform high-resolution middle layer extending above and below the calm water level to enclose the minimum and maximum surface elevation, and two layers extending from the middle layer to the top and bottom of the domain. The inlet and outlet boundaries are more than one wave length away from the floating box. The Stokes 2nd-order wave theory is used in the inlet boundary, while a wave absorption technique is applied for the outlet boundary to eliminate reflected waves (Higuera et al. 2013). The water depth is identical to the experimental setup. The breadth of the numerical tank is equivalent to the breadth of the box, but keeping only one cell in the breadth direction. Correspondingly, the front and rear sides of the numerical tank are modeled as empty type boundary conditions.

Table 3 Properties of the considered regular wave and the corresponding computational domain

Fig. 7

An overview of the numerical domain and its boundary conditions

Table 4 Parameters of the box and mooring cables used in present simulations

Note that the properties of the floating box listed in Table 1 did not consider the weights of attached mooring connections and tracking plate. Following the work of Domínguez et al. (2019), the relevant parameters adopted in present study are summarized in Table 4.

4 Numerical error and uncertainty

A refinement factor of $r=2$ is specified both in temporal and spatial directions to conduct the time-step and grid-spacing study. The resulting grids and time steps are listed in Table 5. For the two-dimensional computational domain, the ratios specifying the number of cells for the coarse grid $G_1$, the medium grid $G_2$, and the fine grid $G_3$ are adequately matched with a factor of $r^2$. The time-step sizes are defined based on the wave period T, with $\Delta t_1=\frac{T}{800}$, $\Delta t_2=\frac{T}{1600}$, $\Delta t_3=\frac{T}{3200}$. Grid-spacing and time-step convergence studies are conducted with a testing matrix of five solutions, using systematically refined time-step and grid sizes.

Table 5 Grid and time-step definitions for the wave characteristics study ($N_H$ denotes the number of cells per wave height; $N_\lambda$, the number of cells per wave length; $N_{total}$, the total number of cells for each grid)

To study the time-step and grid-spacing sizes in terms of wave generations, numerically recorded results from wave gauge 2 (WG2) are used, and its location is specified in Fig. 6. Figure 8 presents the wave elevations of time-step study; Fig. 9, the wave elevations of grid-spacing study. We applied a ramp function to ensure a smooth transition at the beginning of simulations. We see that simulations using three time steps $\Delta t_1$, $\Delta t_2$, and $\Delta t_3$ with a constant medium grid $G_2$, give almost identical results to each other. While in terms of the grid-spacing study using three grids $G_1$, $G_2$, and $G_3$ with the selected medium time step $\Delta t_2$, small discrepancies are observed between these grids, especially for the coarse grid $G_1$. The corresponding error and uncertainty of spatial discretization are quantified below. We neglected to determine the iterative errors, as a residual convergence criterion of $10^{-4}$ was applied in the PIMPLE algorithm for the simulations, where a residual level of two orders of magnitude below the discretization error is expected (Eça and Hoekstra , 2014).

Fig. 8

Comparative time histories of regular wave elevation obtained on time steps $\Delta t_1$, $\Delta t_2$, and $\Delta t_3$ with a constant grid $G_2$ for the time-step study

Fig. 9

Comparative time histories of regular wave elevation obtained on grids $G_1$, $G_2$, and $G_3$ with a constant time step $\Delta t_2$ for the grid-spacing study

For the grid study, the convergence ratio R is defined as the ratio of the difference between solutions obtained on the fine ($\phi _3$) and medium ($\phi _2$) grids, and the difference between solutions obtained with the medium and coarse ($\phi _1$) grids:

$$\begin{aligned} R= \frac{\phi _3 - \phi _2 }{\phi _2 - \phi _1} \end{aligned}$$

(34)

For results with monotonic convergence (i.e., $0< R < 1$), the Richardson extrapolation is applied, where the estimated numerical error $\delta _{RE}$ and the observed order of accuracy $p_{RE}$ can be derived. With three solutions, only the leading term can be estimated, which provides the following one-term estimates:

$$\begin{aligned}&p = \frac{\ln {\left( 1/R\right) }}{\ln {r}} \end{aligned}$$

(35)

$$\begin{aligned}&\delta _{RE} = \frac{\phi _3 - \phi _2}{1-r^{p}} \end{aligned}$$

(36)

Table 6 Estimated results of the discretization error and uncertainty. $\varepsilon _i$ corresponds the solution error in percentage of $\phi _\infty$

To better estimate the uncertainties of solutions far from the asymptotic range, a correction factor $C_F$ was proposed by Stern et al. (2001) as a measure to define the distance of solutions from the asymptotic range:

$$\begin{aligned} C_F = \frac{1-r^p}{1-r^{p_0}} \end{aligned}$$

(37)

where $p_0$ is an estimate for the limiting order of accuracy as the grid-spacing approaches zero, and $p_0=2$ is adopted here for a second-order accuracy method. The numerical error $\delta _{D}$ and the numerical benchmark result $\phi _\infty$ of grid size are obtained as

$$\begin{aligned}&\delta _{D} = C_F \delta _{RE} \end{aligned}$$

(38)

$$\begin{aligned}&\phi _\infty = \phi _3 - \delta _{D} \end{aligned}$$

(39)

For solutions close to the asymptotic range (i.e., $C_F$ is close to 1), the uncertainty $U_{D}$ is estimated by (Wilson et al. 2004)

$$\begin{aligned} U_{D} = \left\{ \begin{array}{ll} \left[ 2.4\left( 1-C_F\right) ^2+0.1\right] |\delta _{RE}|, &{} |1-C_F |< 0.25\\ |1-C_F||\delta _{RE}|,&{} |1-C_F |> 0.25 \end{array} \right. \end{aligned}$$

(40)

For $C_F$ significantly less than or greater than unity, the solutions are far away from the asymptotic range, and $U_D$ is then calculated by

$$\begin{aligned} U_{D} = \left\{ \begin{array}{ll} \left[ 9.6\left( 1-C_F\right) ^2+1.1\right] |\delta _{RE}|, &{} |1-C_F |< 0.125\\ \left[ 2|1-C_F|+1\right] |\delta _{RE}|,&{} |1-C_F |> 0.125 \end{array} \right. \nonumber \\ \end{aligned}$$

(41)

Table 6 lists the estimated error and uncertainty, based on the mean wave height $H_{m}$. We see that the numerical benchmark value of $\phi _\infty =0.1209$ m is very close to the input wave height of $H=0.120$ m. The discretization uncertainty of $U_D=0.41\%$ is less than $1\%$. The similar errors $\varepsilon _2$ and $\varepsilon _3$ indicate that decreasing the grid size from medium to fine did not significantly improve the results. We chose the medium grid size $G_2$ with time step $\Delta t_2$ for subsequent simulations.

Fig. 10

Comparative time histories of regular wave elevation (WG2) for a single moored box

Fig. 11

Time histories of the moored box’s surge (top), heave (center), and pitch (bottom) responses in a regular wave, where k is wave number

Fig. 12

Comparative time histories of tensile forces acting on the mooring cables, where front denotes the side close to wave maker and rear denotes the side far away from the wave maker. d is the breadth of the floating box

5 Results

Two validation cases, namely a single floating box with moorings and an articulated multibody offshore system with moorings, are presented in this section. The verification and validation of the extended solver are accomplished via the former case. While the latter aims to validate the capability of the extended solver for solving mooring–joint–multibody interaction in waves. Apart from the two validation cases, an additional test case is designed based on validation of the single body, aiming to further demonstrate the capability of the extended solver.

5.1 Verification and validation for a single body

To verify the coupling between the equations governing the mooring dynamics and the rigid body dynamics, a moored floating box in waves is numerically simulated using both the formerly validated solver mooring-sixDoFRigidBodyMotion and the presently extended solver mooring-rigidBodyDynamics. The associated results obtained from both codes are compared with each other. Apart from the code comparison and verification, experimentally measured results from Wu et al. (2019) are adopted as validation purpose.

The considered regular wave condition is specified in Table 3. Simulations were started with the moored floating box at rest in calm water. Figure 10 presents time histories of wave elevation obtained from numerical simulations together with experimental measurements, where results are normalized against wave amplitude ($\zeta =H/2$) and wave period (T). Note that compared to experimental setup, a relatively shorter domain is adopted in simulations. A ramp time of 27 s is truncated from the experimental measurements to achieve a better comparison. As see, the results obtained from the former solver (dotted line in red) and the present solver (dashed line in black) are nearly identical to each other. Their differences are plotted in dotted blue line as well. The good agreements between the numerical predictions and experimental measurement (point in black) verify the wave’s accurate generation and propagation in the numerical wave tank, ensuring that the computational domain complies with the experimental setup.

Figure 11 presents a comparison between numerical and experimental time series of box’s motions in surge, heave and pitch. Results show that surge, heave and pitch motions oscillate at wave frequency, and low-frequency horizontal motions are hardly observed. Predictions obtained from the former and present solvers are nearly identical to each other for translational motions (i.e., surge and heave). In terms of rotational motions (i.e., pitch), very small discrepancies are observed between the numerically predicted results. The reason lies in the discrepancies that the equations of motion are solved in different reference frames; that is, Eq. 8 is solved in a global reference frame in the former solver, while Eq. 10 is solved in a generalized body reference frame in the present solver. Recall that in the former solver for solving the six degree-of-freedom motions of a single body, a body’s center of gravity is defined in the global reference frame. However, in the present solver, a local frame has to be defined to determine a generalized body reference frame, where the body’s center of gravity is given relative to the generalized body frame. Kinematic constraints were applied in our simulations to restrict the floating box to moving in three degrees of freedom (i.e., motions in surge, heave and pitch). The differences in implementation of kinematic constraints are believed to be the reason leading to a marginal discrepancy in rotational motions of the two solvers. Although small discrepancies are observed in some local motion amplitudes, overall, the motion responses predicted by both solvers agree reasonably well with experimental measurements.

Figure 12 plots the time histories of tensile forces acting on the mooring cables. We see that the transient behaviors of these tensile forces correspond to the box’s motion behaviors, indicating that the cable tensions are dominated by the body’s lateral motion (i.e., surge in this case). Highly dynamic cable tensions are noticeable for mooring cables in both front and rear sides of the box. Again, the numerical predictions from the two solvers are almost identical to each other, except some small local high-frequency vibrations. Compared to the experimental measurements, in general, the tensile forces acting on the front mooring cables are overpredicted, while the tensile forces acting on the rear mooring cables are underpredicted. The discrepancies might be allocated to the unconsidered differences between the numerical and experimental setups. For instance, the mooring chains are simplified as equivalent solid core cables in simulations. Some dynamic behaviors of the chain, e.g., relative motions between each chain segment, are not represented in the mooring model. In addition, the connections between the mooring cables and the floating box are not considered in simulations, where running-through and/or end-connection behaviors might happen between the chains and screw eyes during the experiment. On the other hand, three-dimension effects are not taken into account in present simulations as well.

Generally, the reasonable agreements between the numerical predictions and the experimental measurements validate the coupling between the mooring model and the rigidBodyDynamics model for solving a floating box with moorings in a regular wave condition. In addition, the almost identical results obtained from the former solver, which has been successfully validated, verify the coupling technique used for the presently extended solver as well.

Fig. 13

An overview of the experimental setup within Space@Sea project

5.2 Validation for an articulated multibody

Table 7 Particulars of the floating module designed within Space@Sea project

To validate the adopted numerical model for predicting wave-induced motions of and loads on an articulated multibody system, the experimental measurements from Space@Sea project are used. Figure 13 sketches the location of the used wave probe in the tank, with a water depth of 2.5 m. Table 7 lists particulars of the floating box, including the location of its CoG above keel. The two floating modules were connected by a hinged joint and moored by four horizontal linear spring-like moorings. The mooring lines were guided through pulleys mounted on the tank wall, and these pulleys were located at the same height as the body-fixed fairleads, i.e., 0.02 m above the water surface. The applied pretension was 6.81 N, with a stiffness of 13.1 N/m. The model test report of Thill and Raghu (2018) contains additional details.

Fig. 14

Comparative time histories of regular wave elevation for an articulated multibody

Fig. 15

Time histories of the moored multibody’s surge (top), heave (center), and pitch (bottom) responses in a regular wave, where k denotes wave number

The numerical setup of Sect. 5.1 was adapted into this hinged multibody case, i.e., the computational domain, time-step and grid sizes were chosen based on the considered wave condition (wave amplitude $\zeta$ = 0.021 m, wave period $T=1.81$ s). The hinge joint does not permit relative translations, but allows relative rotational movement between bodies. It is worth mentioning that the joint connection is numerically represented by a massless body. Figure 14 plots time histories of wave elevation of WG2 obtained from our numerical simulation together with experimental measurement. Computed and measured wave elevations are nearly identical, which confirms that we adopted an appropriate wave generation for our study. Figure 15 presents a comparison between numerical and experimental time series of multibody’s motions in surge, heave and pitch. Results show that the restrictive action of the hinge joint causes relative surge motions between the two hinged boxes to be negligibly small. Although the computed heave of box2 differes somewhat from measured values, the predicted translational motions (surge and heave) generally compare favorably to experimental measurements.

However, discrepancies are observed between the computed and measured pitch motions, that is, the computed pitch motions of both box1 and box2 are larger than the measurements. The reason lies in the deviation that the hinged joint used during the experiment is not well represented in our simulations. On one hand, the experimental joint is much more complex than the numerical one, because it has to incorporate with load cells, see Fig. 16. Therefore, its actual position during the physical experiment is different from that in our simulations. On the other hand, the designed joint within the experimental model test was found to be relatively inflexible. The rotational hinge damping that existed in the experiments is not considered in our simulations.

Fig. 16

Experimental setup for hinge force and moment measurements during model test (left)  (Thill and Raghu 2018), and the simplified joint used in simulations (right)

Figure 17 plots time series of the corresponding longitudinal ($F_x$) and vertical ($F_z$) forces acting on the hinged joint. As seen, longitudinal hinge forces, in general, are much larger than vertical hinge forces. Our computed longitudinal hinge force agree fairly well with measurements, whereas our computed vertical hinge force differ from measurements, albeit a relatively larger phase difference. In addition, we observe strong nonlinearities in associated with the computed vertical hinge forces. In general, numerically predicted and experimentally measured hinge forces compare favorably. This is so because the forces acting on the hinge joint are dominated by surge and heave motions, which are reasonably well predicted by our simulations

5.3 Mooring–multibody interaction

To consider the mooring dynamics interacting with a multibody system, the moored floating box in waves studied in Sect. 5.1 is articulated to another floating box at its rear via a hinge joint (the same connection joint as used in Sect. 5.2). The rear mooring cables are attached to the second box, and all the other setups are remained the same as the single body case. The width of gap between the two floating boxes is equivalent to the box’s length. The hinge joint does not permit relative translations, but allows relative rotational movement between bodies. Again, the joint connection is represented by a massless body in the rigidBodyDynamics solver.

To demonstrate the mooring dynamics interacting with the articulated multibody system, the associated predictions are compared to those of the single floating box. Figure 18 presents time histories of wave elevation obtained from the single-body case (dotted line in red), and from the multibody case (dashed line in black). The almost identical wave elevations confirm that the same wave condition is investigated. Compared to the wave elevation of the single-body case, the peaks of wave elevation from the multibody case become slightly sharper while the associated troughs become flatter. Moreover, for the multibody case, stronger reflected waves are observed due to the presence of the second body, which are exhibited by local vibrations of the wave troughs.

Fig. 17

Comparative time histories of longitudinal (top) and vertical (bottom) forces acting on the hinged joint, where d is the breadth of the floating module

Fig. 18

Time histories of wave elevation of WG2 obtained the single-body case, and from the multibody case

Fig. 19

Time histories of motion responses in surge (top), heave (center), and pitch (bottom) of the single-body and multibody cases

Fig. 20

Tensile forces acting on the front cables (top), and the rear cables (bottom) at anchor and fairlead positions, where initial tensions were excluded

Figure 19 plots the associated motion responses of the single-body and multibody cases in the same incident wave. Note that the initial position of floating box was given at its equilibrium without attaching mooring lines. Its draft was adapted accordingly in the very beginning of simulations, where mooring-induced forces were included. Again, the floating box close to the wave maker is denoted as front and the one far away from the wave maker is denoted as rear. The same definition holds for the mooring cables. We see that, attaching a second body at rear suppresses the system’s motion response in surge. While the mean drift of the multibody increases, compared to the mean drift of the single body. In addition to this, due to the restriction from the hinge joint, the surge motions of the articulated two bodies are nearly identical to each other.

In terms of heave motions, the influence of applied joint is not evident. The heave motion of front body in the multibody system is similar to the heave motion of the single-body case. For a floating body moored with a soft mooring system, for instance catenary layout for present study, its heave motion is generally dominated by the body’s hydrostatic stiffness and inertia (Jiang 2021). The attached soft mooring system has limited effects on the body’s heave motion, which principally remains in the wave frequency domain. With regard to the heave motion of rear body, its heave amplitudes are much the same as the heave amplitudes of front body. While the mean value of rear body’s heave motion moves downwards a little bit, whose incident wave is scattered by the front body.

In consideration of the fact that the applied joint allows relative pitch motions between the hinged two bodies, highly dynamic responses are observed in the bottom graph of Fig. 19. As seen, the hinged two bodies rotate in opposite pitch directions with comparable amplitudes, which are much larger than the pitch amplitudes of the single-body case. Examining the pitch motions of the multibody case, we find that the pitch amplitudes of front body is somewhat larger than the pitch amplitudes of rear body. This is so because the front body encounters the unaltered incident waves. The strong interactions between the hinged bodies are substantially revealed via the relative pitch motions.

Fig. 21

Screenshot of wave–mooring–structure interaction of a moored and articulated multibody system

To study the mooring–multibody interaction, the tensile forces acting on the mooring cables of the multibody together with the associated results of the single body are plotted in Fig. 20. For mooring cables configured as catenary, due to the gravity, tensile forces acting on the fairleads are basically larger than tensile forces acting on the anchors. Their differences are clearly observed in Fig. 20, where dotted and dashed lines denote the tensile forces at anchor positions; circle and cross symbols, the tensile forces at fairlead positions. On account of the fact that front cables provide forces acting in the opposite direction to the wave propagation, one can see that they bear larger tensile forces than the rear cables, both at the anchor and fairlead positions.

For the tensile forces acting on the front cables, no large discrepancies are seen between the single-body and multibody cases. When it comes to the mean cable tension, the value from the multibody simulation slightly exceeds that from the single-body simulation. It is clearly revealed by the relative larger values of tension troughs in the multibody. The increment of mean cable tension is in agreement with the increment of the multibody’s mean drift in surge motion, as shown in the top graph of Fig. 19. As for the mooring cables configured as catenary layout, their dynamics is dominated by the body’s lateral motions (i.e., surge motions for the present study).

Concerning the tensile forces acting on the rear cables, however, the results from the multibody simulation are somewhat less than those from the single-body simulation, especially for the tension peaks. Recall that, compared to the single-body, the surge motion of the multibody is suppressed because of the hinge joint. Meanwhile, its mean surge position is shifted towards the rear direction due to the increased wave drift force. Apart from these, the slightly downwards mean heave position, as revealed in the center graph of Fig. 19, can be partly attributed to the reduction of the tensile forces acting on the rear cables of the multibody case. Figure 21 depicts an exemplary screenshot of the mooring cables interacting with the articulated multibody in a regular wave. The legend of the free surface, p_rgh, stands for the magnitude of hydrodynamic pressure. Free surface elevations and motion responses together with mooring dynamics are displayed.

6 Concluding remarks

This paper presents an extension of a coupled mooring–viscous flow solver to consider mooring dynamics interacting with an articulated multibody offshore system, where a dynamic mooring model was coupled with the rigidBodyDynamics solver in OpenFOAM.

The coupling technique was verified by comparing the predicted motions of and loads on a moored floating box, obtained from a formerly validated solver to those obtained from the presently developed solver. The nearly identical results obtained from both coupled solvers verified the coupling technique used for the presently developed solver. Apart from the code comparison and verification, the numerical predictions obtained from both codes were validated against experimental measurements as well. The good agreements between the numerical predictions and the experimental measurements validated the presently coupled solver.

To further validate the presently coupled solver for solving the dynamics of an articulated multibody, simulations were performed for a moored and articulated multibody offshore modules proposed within the Space@Sea project. Generally, the numerically predicted motions in surge and heave agreed favorably to experimental measurements. Nevertheless, discrepancies between numerically predicted and experimentally measured pitch motions were observed. This was because a relatively inflexible hinge joint was used in the experiment, and the rotational hinge damping that existed in the experiments was not considered in our simulations. Another uncertainty might come from the differences of the joint’s positions. Overall, numerically predicted and experimentally measured hinge forces compared favorably. This was so because the forces acting on the hinge joint were dominated by surge and heave motions, which were reasonably well predicted by our simulations.

To study the mooring dynamics interacting with an articulated multibody offshore system, the considered single body case with four symmetric catenary moorings was extended by articulating another body at its rear via a mechanical hinge joint. The hinge joint was modeled as a massless body. By comparing the associated results of the multibody case to the single-body case, the influences of the articulated body on the motions of and loads on the coupled system were discussed. The results showed that hinging a second body to an existing body suppresses their surge motions. While the effects of the hinged body on the system’s heave motions are limited. Strong interactions between the hinged bodies are revealed in terms of the highly pitch responses.

As discrepancies were observed between the results obtained from the sixDoFRigidBodyMotion solver and the rigidBodyDynamic solver, more fundamental tests are required to clarify their difference and resolve the problems of kinematic constrains. Physical tank tests have to be conducted in order to formally validate the presently developed solver for solving the mooring dynamics interacting with an articulated multibody system. Additional sea states would have to be considered to draw general conclusions. Here, the primary intention is to demonstrate the capability of the presently developed technique to analyze a moored and articulated multibody offshore system in a regular wave condition.