1 Introduction

Additive manufacturing, broadly known as “3D printing”, is a process used to fabricate 3D objects layer by layer based on a digital model. It is a type of green technology due to very little waste materials compared to traditional manufacturing technologies [1, 2]. Powder-bed fusion additive manufacturing technologies show great potential to fabricate metallic components with complicated geometry and high accuracy [3, 4]. Metallic thin channels, which play an important role in many fields including aerospace, automotive, energy, medical, etc., can be obtained by selective laser melting (SLM) and electron beam melting (EBM) technologies [5].

However, for thin channels, geometric accuracy is of great importance, and even a slight deviation from standard geometry, which can be caused by powder overmelting or surface roughness, cannot be tolerated in certain circumstances [6,7,8]. In some cooling systems, i.e., microelectronics, air conditioning or cutting tools, etc., the quality of thin channels strongly influences the efficiency of cooling and poor quality can induce unexpected pressure loss [9,10,11,12]. Thin channel is commonly used in gas turbines which is the key component in an electrical power generating system. Improving the quality of thin channels can improve the heat transfer efficiency and thus the power generation efficiency [11]. In medical applications, the dimensional deviation of implants may lead to overdose or under release of drugs. The surface structure of implants has a strong influence on the healing and integration of surrounding tissues. Thin channels can also be used in chemical reactors for process intensification. High dimensional accuracy of the thin channels is required for the chemical reaction process [13, 14].

Compared with vertical or inclined channels, horizontal channels experience the largest dimensional deviation from target dimensions [11, 15,16,17,18]. Hence, improving processing accuracy is critical for the manufacturing of horizontal thin channels. Some studies revealed that the dimensional deviations of horizontal thin channels were mainly caused by overmelting, dross formation, and distortion, especially in the down-skin region [16, 19, 20]. Since the contour data points of a 3D digital model display the centers of laser spots not the border of melting pools, ignoring laser/beam spot diameter will lead to overmelting. It is generally accepted that the size of the overmelting zone is also related to the precision of the control system and processing parameters (i.e., layer thickness, particle diameter, processing orientation, energy density, and scanning direction, scanning speed, scanning pattern, etc.) [19, 21]. When scanning in the channel’s down-skin region, melting pools sink into the loose powder material and result in dross formation. The dross is irregular in shape, and its amount is dependent on the base material and the applied process parameters. Hence, it is difficult to predict the resulting geometric error. The distortion related to the residual stress, deposition pattern and processing parameters, etc. [22,23,24], is another factor that affects the dimensional deviations of the channel. Since the effect of the distortion on the final geometry of thin channels is minor and difficult to evaluate, it is not considered generally.

In order to prevent excessive melting of powder particles and dross formation, adjusting processing parameters is commonly suggested [16, 25, 26]. Several studies lowered the energy density in the down-skin region [15, 18, 27] and identified the optimum conditions in the SLM process, e.g., a low laser velocity and power (65 W for aluminum [27] and 35 W for titanium [18]). So far, optimized SLM processing can accurately manufacture horizontally-oriented channels as small as 1 mm in diameter [18, 27]. Hassanin et al. revealed that decreasing energy density reduced geometric errors, but roughened the surface [18]. Khan et al. found that the number of layers processed with down-skin parameters affects the dross formation and 5 layers could achieve the least dross [27]. Franchitti et al. studied the effect of particle size distribution on the part dimensional accuracy and concluded that the finer the powder is, the better the surface quality of the thin hole will be [28]. Although adjusting processing parameters can significantly improve the product precision, it is constrained by the availability of the existing manufacturing technology, the size of laser spot precision, and the properties of used materials. Besides, the optimized parameters vary with process and materials. Hence, it cannot provide universal guidance for improving the dimensional accuracy of channels.

Another method for improving the dimensional accuracy of horizontal thin channels is to optimize the channel design. The offsets and compensation parameters are applied to balance the aforementioned dimensional deviation. The existing simple compensation designs are shapes of enlarged circle, diamond, and teardrop, etc. [17, 18, 29]. Among all the alternative shapes, the teardrop type allows the channel to retain an approximately cylindrical form in the horizontal direction. But it remains a challenge for the teardrop to achieve high-precision horizontal thin channels. In order to further improve the dimensional accuracy, Paggi et al. experimentally studied the distribution of geometric errors of the channel and found that the geometric errors were proportional to the down-skin angle. They further studied the corresponding compensation evolving with the scanning layers which reduced the deviations of microchannels [19]. Solyaev et al. proposed a finite element model that could predict and evaluate the final cross-section geometry of the channels. Based on this model, a compensated design, which made the final shape more consistent with the predefined cylindrical shape than the teardrop design, was obtained through a series of simulations [20]. However, the approaches of Paggi et al. and Solyaev et al. cannot provide an optimal compensated design for channel geometry directly, and a set of simulations or experiments have to be performed.

In short, the existing compensated shapes do not enable the channel to achieve high accuracy, and the existing methods including parameter optimization and compensated design require expensive and time-consuming trial and error experiments or simulations. A simple and effective method for improving the dimensional accuracy of horizontal thin channels is greatly needed. This work aims to establish a new compensated design method. In Sect. 2, a so-called “melting cell” concept is proposed to describe and quantify the dimensional deviation. Based on the geometric relationship between the melting cell and target channel, a method for predicting and optimizing the geometric shape of thin channels is proposed. In Sect. 3, the experimental verification of this method and the compensated design of a thin channel is presented. The results are discussed in Sect. 4. The main conclusions are summarized in Sect. 5.

2 Methodology

2.1 The Origin of Geometric Error

The thin horizontal channel is produced by SLM technology. As mentioned in the introduction, the geometric error of thin horizontal channels results from overmelting and dross formation and varies with the down-skin angle [19, 21]. In the powder bed fusion process, the dross is inevitably induced due to the melting pools around the melted zone sinking into the loose powder material. In order to understand the shape and distribution characteristics of the geometric error region, the origins of the overmelting are further analyzed below:

  1. 1.

    Intrinsic size of laser spot: in the SLM process, the laser spot size is 50–500 μm, and the layer thickness usually ranges from 20 to 100 μm. The resulting resolution of the printed part is about 150 μm [30]. For thin channels (radius < 1.5 mm), the ratio between the resolution and the radius of the thin channel is larger than 10%. The low resolution will lead to overmelting which can influence the dimensional deviation of thin channels significantly.

  2. 2.

    Low heat capacity of loose powder: the melting area around the channel is exposed to the loose powder inside the thin channel while the normal melting pool is attached to the solid part. The heat capacity of loose powder is lower than that of solid metal. Therefore, the melting pool exposed to the loose powder is larger than that attached to the solid part, which will contribute to the overmelting area [20].

  3. 3.

    Excessive energy: The heat input can be easily excessive at the start and end positions of passes, which will result in overmelting around the channel. The extent of the excess depends on printing technology.

  4. 4.

    Resolution of the control system: the precision of the control system also affects the geometric error. It is constrained by the availability of existing manufacturing technology.

2.2 The Concept of Melting Cell

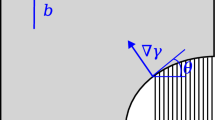
From the above analysis, it is concluded that the geometric error is caused by the intrinsic size of the laser spot, exposed to the loose powder, excessive energy, resolution of the control system, and dross formation. It is important to note that, under the same material and process condition, all of these factors are independent of scanning layers and can be considered constant during the printing process. The only variable affecting the melting area around the channel (ignoring the heat accumulation with the number of layers) is the ratio of powder to solid metal which increases with the surface angle (φ, the angle between the tangent of a point on a circle and the horizontal axis), as shown in Fig. 1. Since the heat capacities of metal powder and metal solid are different, the melting area next to the target channel varies with the φ.

Fig. 1
figure 1

a Printed sample with a horizontal thin channel; b schematic plot of the geometric relationship between the melting cell, the melting pool, and the target channel. The predefined channel is located in Z direction. The layers are built from bottom to top in Y direction. For each layer, the laser scans from left to right in X direction

Full size image

In order to evaluate the geometric error, a concept of melting cell is proposed, referring to the melting area that is completely exposed to the loose powder (φ = 180°). In contrast, the melting zone is a normal melting pool when it is completely in contact with solid metal (φ = 0°). The melting cell is larger than a normal melting pool due to the inclusion of overmelting zone and dross. Since the normal melting zone is generally considered to be elliptical and the factors affecting the overmelting are constant during the printing process, we assume that the melting cell is also elliptical and the size of the melting cell does not change with the number of layers.

In order to show the geometric relationship between the melting cell and the predefined channel, the schematic plots of a printed sample with a horizontal thin channel (without compensated design) are presented in Fig. 1. The 3D view of the printed sample with horizontal thin channel is shown in Fig. 1a and the corresponding 2D cross-section of a printed part with a thin internal circle channel is presented in Fig. 1b. In the manufacturing process, no support is used. The predefined channel is located in Z direction. The material around the channel is melted layer by layer in Y direction. For each layer, the laser scans from left to right in X direction and skips over the channel area. The profile of the target channel defines the laser spot centers at the start and stop positions (the purple points in Fig. 1b). When φ is between 0° and 180°, the melting area close to the target channel can be divided into two parts by the predefined channel profile: (1) the melted area attached to the solid part (outside of the channel) could be regarded as a part of normal melting pool; (2) the melted area exposed to the loose powder (inside of the channel) can be considered as a part of a melting cell. In this regard, the geometric error (the melted area inside the channel) is the overlapping part between the melting cell and the target channel. The area of the overlapping part is a function of φ. The dimensional error can be predicted by the geometrical relationship between the melting cells and the target channel.

As shown in Fig. 1, when φ are 0°, 90°, and 180°, the corresponding geometric errors are zero, half melting cell, and whole melting cell, respectively. Therefore, the width and depth of the melting cell can be calculated backward by the geometric error at φ of 90° and 180°. Besides, the melting cell size is independent of the sizes of the sample and channel, and only related to the processing parameters and material. It can be easily estimated through the measurement of the melting area at the end of a single scanning pass.

2.3 Predicting the Final Geometry of Thin Channels Based on the Melting Cell Concept

As aforementioned, for conventional printing, the size of the melting cell is not considered into the channel design. The overlapping area between this melting cell outline and the target channel profile defines the quality of the manufactured channel and is a function of φ, as shown in Fig. 2a. In order to obtain a mathematical expression of the final channel contour, the geometrical relationship between the melting cell and the target channel, as illustrated in Fig. 2b, is studied. It should be noted that the melting cell instead of the normal melting pool is associated with the final channel contour, therefore only the complete melting cells are plotted around the target channel, as shown in the blue ellipse. It is assumed that the centers of the melting cell follow the path of the target channel contour. The melting cell inside the target channel is the overmelting area, which determines the final contour of the channel. As analyzed above, the final geometry of the channel without compensation can be predicted once the geometries of the melting cell and the target channel are known. Hereby, the centers of the melting cell \(\left( {x_{0} ,y_{0} } \right)\) are on the target channel contour which is described as,

$$ \begin{aligned} x_{0} & = r\cos \theta \\ y_{0} & = r\sin \theta \quad (0 \le \theta \le 2\pi ) \\ \end{aligned} $$
(1)
Fig. 2
figure 2

Prediction of the final geometry of the thin channel. a Schematic diagram of the channel without compensation; b the geometric relationship between melting cells, target channel in the coordinate system. The black circle with radius r shows the target channel. The center of the circle (point O) is the origin of the coordinates. The blue area shows the melting cell which is assumed to be elliptical. The red points (x0, y0) on the black circle are the centers of the melting cells

Full size image

r is the channel radius and \(\theta\) is the parametric angel in the range of 0 to 2π.

The shape of the elliptical melting cell \(\left( {x_{1} ,y_{1} } \right)\) is defined as,

$$ \left( {\frac{{x_{1} - x_{0} }}{a}} \right)^{2} + \left( {\frac{{y_{1} - y_{0} }}{b}} \right)^{2} = 1 $$
(2)

a and b are the radius and depth of the melting cell, respectively.

Based on Eq. (1) and (2), the final geometries of the channels can be predicted.

2.4 Compensated Design of Thin Channels Based on the Melting Cell Concept

As analyzed above, the profile of melting cells inside the target channel determines the final contour of the channel. In order to eliminate the geometrical error caused by the melting cell, one possible way is to develop a compensated design. Hereby, the channel profile is adjusted: the outline of the target channel serves as the envelope line of all melting cells. Consequently, the target channel is tangent to the edge of upper melting cells and next to the tips of the lower melting cells, as shown in Fig. 3. The overlapping area between the melting cell and the target channel is offset. The trajectory of the melting cells’ centers, as shown in the red line in Fig. 3b, is the compensated design.

Fig. 3
figure 3

Method of compensated design based on the melting cell concept; a schematic diagram of the channel with compensation; b geometric relationship among melting cells, target channel, and final channel contour in the coordinate system. The blue area and black circle show the melting cell and target channel, respectively

Full size image

In order to obtain a mathematical expression of the compensated design, the relationship between the melting cell and the target channel is represented in the coordinate system, as shown in Fig. 3b. Similar to Sect. 2.3, the coordinates of the points on the target channel and the melting cell are expressed as \((x,y)\) and \((x_{1} ,y_{1} )\), respectively. The coordinates of the center points of the melting cell are \((x_{0} ,y_{0} )\). The round edge of the target channel and the melting cell’s shape can also be described by the circle Eq. (1) and the elliptic Eq. (2), respectively.

For the upper semi-circle, the edge of the melting cell should be tangent to the outline of the target channel. Since the ellipse and the circle have an intersection, like point A in Fig. 3b, there's at least one point on the ellipse that satisfies the following equation,

$$ \begin{gathered} x_{1} = x \hfill \\ y_{1} = y \hfill \\ \end{gathered} $$
(3)

Moreover, the circle is tangent to the half-elliptical. The circle and ellipse share a common tangent line as shown in Fig. 3b, which can be described as:

$$ - \frac{{b{}^{2}(x_{1} - x_{0} )}}{{a{}^{2}(y_{1} - y_{0} )}} = - \frac{x}{y} $$
(4)

a and b are the radius and depth of the melting cell, respectively. By solving Eq. (1–4), the path of the center \((x_{0} ,y_{0} )\) of the overmelting area for the upper semicircle is obtained,

$$ \begin{aligned} x_{0} & = \frac{{r\cos \theta a^{2} }}{{\sqrt {a^{2} r^{2} \cos^{2} \theta + b^{2} r^{2} \sin^{2} \theta } }} + r\cos \theta \\ y_{0} & = \frac{{r\sin \theta b^{2} }}{{\sqrt {a^{2} r^{2} \cos^{2} \theta + b^{2} r^{2} \sin^{2} \theta } }} + r\sin \theta \quad (0 \le \theta \le \pi ) \\ \end{aligned} $$
(5)

For the lower semicircle \((\left| {x_{0} } \right| \ge a)\), the tips of the melting cells must follow the path of the half-circle, like point B in Fig. 3b. The distance between the center and the intersection is half the radius of the melting cell (a). Combined with the circle Eq. (1), the coordinate \((x_{0} ,y_{0} )\) of the melting cell centers can be expressed as,

$$ \begin{aligned} x_{0} & = r\cos \theta + a \\ y_{0} & = r\sin \theta \quad (\pi \le \theta \le 2\pi ,\left| {x_{0} } \right| \ge a) \\ \end{aligned} $$
(6)

For the lower semicircle (\(\left| {x_{0} } \right| < a\)), the top surface line (length = 2a) of the melting cell, as plotted in orange in Fig. 3b, is in contact with the target channel. The expression is:

$$ y_{0} = - r\quad (\pi \le \theta \le 2\pi ,\left| {x_{0} } \right| < a) $$
(7)

Based on the above analysis, a mathematical description of the laser spot’s moving path can be obtained. This provides a quantitative guide for determining the compensated approach. Figure 3a shows the schematic diagram of the channel with compensation. The final geometry of the channel is much closer to the target circle than that in Fig. 2a.

3 Verification with Experimental Results

In order to verify our proposed methodology, the melting cell size, predicted channel geometry, and the compensated design are studied and compared with the experimental results by Solyaev et al. [20]. In their study, the cuboid AlSi10Mg samples (\(5 \times 50 \times 10\;{\text{mm}}^{3}\)) with thin horizontal cylindrical channels (radius = [0.2, 0.4, 0.6, 1, 1.6, 2] mm) were fabricated using SLM technology. The channels’ boundaries were obtained through the X-ray computed tomography method and image processing. In this section, the proposed method will be verified against the published experiments. First, the melting cell size will be identified. Then the identified melting cell size will be used to predict the final geometrical of thin channels with various radius and compare the predicting results with the experimental results. Finally, a compensated design based on the melting cell concept was proposed to achieve the best quality of a thin channel.

3.1 Identification of the Melting Cell Size

According to the relationship between the melting cell and the target channel analyzed above, the radius (a) and depth (b) of the melting cell are equal to the half short and long axis of the semi-ellipse, respectively. The layer thickness (0.03 mm) [20] is so small that it is ignored in this work. All the melting cell centers are assumed on the target channel, as illustrated in Fig. 4a.

Fig. 4
figure 4

Determination of melting cell size a the geometrical relationship between the melting cell (blue area) and the target circle (black curve); b elliptical melting cell size determined from the printed channel with the diameter r = 0.5 mm. The results are from Solyaev et al.’s study [20]. The black circle and the colored curves indicate the target channel and experimental results, respectively

Full size image

It should be noted that the depth and width of the melting cell can be calculated backward by the geometric error of printed channel samples at φ of 90° and 180°. The printed channel with the diameter r = 0.5 mm is taken as an example to determine the radius (a) and depth (b) of the melting cell. As shown in Fig. 4 (b), the average value (0.18 mm) of the distances between the black ideal circular curve (target geometry of the channel) and the colored curves (final geometry of the channel) on the positive Y-axis is equal to the depth of the melting cell. On the X-axis, the average values of the distances between the black ideal circular curve and the colored curves on the left and right sides are \({\text{a}}_{1}\) and \({\text{a}}_{2}\), respectively. The mean value ((\({\text{a}}_{1}\) + \({\text{a}}_{2}\))/2 = 0.068 mm) is equal to the radius of the melting cell (a).

Figure 5 shows the computed tomography results of the final cross-sections of the channels with different radius (r) [14]. The black circles and the colored curves represent the target channel and experimental results, respectively. It can be observed that the overmelting occurs on the entire channel surface, and the dimensional deviation also increases with the number of layers, which is consistent with our reasoning about the melting cell. The larger the channel size is, the smaller the relative dimensional error will be. This is due to that, the overmelting area, which increases with the number of layers, is almost independent of channel size.

Fig. 5
figure 5

Computed tomography results for channels with different radius a r = 0.2 mm, b r = 0.3 mm, c r = 0.5 mm, d r = 0.8 mm, and e r = 1 mm. The results are from Solyaev et al.’s study [20]. The black circle represents the target channel with different radii and the colored curves show the experimental results of different cross-sections at several different positions along the channel length

Full size image

Table 1 presents a and b of the melting cells obtained for all the channels in Fig. 5. Both the a and b values show very minor variance with the channel radius, and thus it can be concluded that the a and b are independent of the size of channels. This is in good agreement with our hypothesis that the melting cell can be used to quantify the overmelting area and its size is independent of the channel size. The mean value of a (0.0672 mm) and b (0.175 mm) are used as the radius and depth of the melting cell in the following analysis.

Table. 1 Channels and melting cell sizes
Full size table

3.2 Prediction of the Final Geometry of the Thin Channels

In order to further verify the concept of melting cell and the proposed predicting strategy, the final shapes of the channels with radius [0.2, 0.4, 0.6, 1, 1.6, 2] mm are predicted according to the Eqs. (1) and (2). The values of a and b in Eq. (2) are 0.0672 mm and 0.175 mm, as defined in Table 1. In Fig. 6a–f, the target channel is shown in black curves and the predicted results are presented as the white region inside the channel. The experimentally manufactured channel tomography from Solyaev et al.’s study [20] is denoted as three colored curves (measured at different cross-section positions in Z directions). It can be seen that the predicted results have a good agreement with the experimental results at all surface angles. In general, the predicted channel contour is slightly smaller than the experimentally manufactured channel contour. This is because the layer thickness is assumed infinitely small in the proposed method. The melting cells are distributed continuously around the target channel and thus the area between the layers is over-covered, as illustrated in Fig. 7.

Fig. 6
figure 6

Comparison between the predicted and experimental shapes of the channels with different target channel radii a r = 0.1 mm, b r = 0.2 mm, c r = 0.3 mm, d r = 0.5 mm, e r = 0.8 mm, and f r = 1 mm. The colored curves show the measured channel tomography. The outmost black circle line represents the target channel and the blue region is the overmelting area

Full size image
Fig. 7
figure 7

The comparison between the prediction results under certain layer thickness and infinitely small layer thickness

Full size image

It can also be observed that the relative error between the predicted and experimental results increases with the decrease of the channel radius. In addition, the channel with a radius of 0.1 mm shown in Fig. 6a is completely closed because the radius of the channel is smaller than that of the melting cell. The result is also consistent with the experimental observation, while the finite element numerical model used by Solyaev et al. was not able to properly predict the geometry of the channel with a radius of 0.1 mm.

3.3 Compensated Design of a Thin Channel

Both the final geometry prediction and the compensated design are based on the concept of the melting cell and the relationship between the melting cell and the target channel. Therefore, the successful verification of the predicted profiles of the thin channels also indicates that the proposed compensated design method can be used to optimize the channel shape.

Solyaev et al. proposed a finite element based compensated design, which can produce a nearly circular channel close to the target channels. However, this process is tedious and time-consuming. The compensated design can also be carried out by the proposed melting cell concept in a much efficient manner. Herein, in order to compare with the compensated method in Solyaev et al.’s work, the channel with a radius (r) of 0.3 mm is taken as an example to develop the compensated design. According to Eqs. (5–7), the compensated design is plotted in red as shown in Fig. 8. The results based on the thermal finite element analysis from Solyaev et al.’s work are plotted in blue.

Fig. 8
figure 8

Comparison of different compensated designs (“enlarged teardrop” and “egg”). The black dash shows the target channel with diameter r = 0.3 mm. The blue and red lines show the corresponding compensated designs based on finite element simulation results in Solyaev’s work and the proposed method in this work, respectively

Full size image

It can be observed that the proposed new compensated design exhibiting an egg-shape is close to the Solyaev et al.’s compensated design which is a type of enlarged teardrop shape. Along the X direction and Y direction of the target channel, these two compensated designs are very close, while the egg-shaped design is slightly larger than the enlarged teardrop design on the XY diagonal direction. This is because the layer thickness is ignored in the proposed method and the area between the layers is over-covered by the continuously distributed melting cells, as shown in Fig. 7. In order to offset the “larger overlapping area”, the relatively larger compensated design is applied. This comparison result demonstrates the proposed compensated design method can achieve high-precision horizontal thin channels.

4 Discussion

From the above results, it can be concluded that the melting cell can physically explain the geometric error of thin channels. For a channel of a given radius, a decrease in melting cell size could reduce the area of the overmelting zone and improve fabrication precision. In addition to optimizing the channel design, the excessive melting of powder can be prevented by reducing the size of the melting cell. This also explains why lower energy density, especially in the down-skin region, could contribute to diminishing the overmelting area in some studies [8, 9, 12]. However, parameter optimization for reducing the melting cell size is limited by the availability of the existing laser sintering technology. In this work, a simple and very effective method is proposed based on the origin of dimension deviation. The geometry prediction and compensated design can be obtained without the need for extensive experiments and simulations. The mathematical description of the compensated design can be derived by the geometries of the target channel and the melting cell, which makes it easier to build a 3D digital model of optimal design compared with the discrete points in Solyaev et al.’s design. The new finding may inspire future research to shift emphasis from optimizing processing parameters to compensated design considering the melting cell area resulted from the intrinsic size of the laser spot, overmelting, and dross. Although no new experiments were carried out to verify the proposed compensated method, this work is fully verified by Solyaev et al.’s experimental results of different channel radii in raegards to the melting cell and prediction results, and numerical results of the “enlarged teardrop” compensated design. Both the prediction method and the compensated design are based on the concept of the melting cell and the relationship between the melting cell and the target channel. Hence, the proposed compensated design is promising to improve the dimensional accuracy of thin horizontal circular channels.

The existing design approaches [20] cannot be easily extended to the processing of thin channels with various shapes, orientations, materials, sizes of the channel, and different powder bed fusion processes, since the optimized channel design was determined based on a series of preliminary thermal finite-element simulations or experiments. However, the proposed method in this work can be conveniently extended to other scenarios, once the melting cell size is identified. The melting cell size can be obtained through the measurement of a single scanning pass.

It should be noted that the method proposed was based on two assumptions about the melting cell: the cross-section of a melting cell is semi-elliptical and the melting cell size is constant in different layers. According to heat accumulation with layer building, the whole manufacturing process can be divided into two stages: non-steady stage and quasi-steady stage. This initial non-steady stage is detrimental to the printing stability and the melting area varies much with layers. After a few layers are deposited, a quasi-steady stage is obtained. In the quasi-steady stage, the melting cell size will be stable. Since the channel is very small, it is considered to be located in quasi-steady layers and the effect of heat accumulation on the melting cell size is ignored. In addition, the printing direction could also affect the geometrical deviation because the width of the melting cell in different directions is different. In this work, we assume that the printing direction is constant around the target channel. Based on all these reasons, it is reasonable to assume the geometry of the melting cell to be constant in different layers and different positions around the channel.

In practice, an ellipse cannot accurately describe the shape of the melting cell. The geometry of the melting cell will vary slightly from layer to layer. In future work, the cross-section of a melting cell and its statistical variation can be experimentally studied to improve the prediction and optimization. Another solution is controlling the size of the melting cell unchanged by optimizing the process parameter. In this regard, combining the proposed method and parameter optimization is an alternative approach to obtain perfect channels. Besides, the layer thickness is ignored in this work, which results that the predicted final geometry of thin channels is smaller than the experimental results and the compensation design is slightly larger than the finite element based compensated designs in Solyaev et al.’s work. The method can be improved to further enhance dimensional accuracy by considering the layer thickness into the compensated design of thin channels.

5 Concluding Remarks

The thin channel’s dimensional deviation, which varies with the surface angles (φ), is mainly caused by the overmelting and dross formation in additive manufacturing. In the literature, the existing optimized processing parameters and several compensated designs require extensive simulations or experiments, and a simple yet effective method for predicting and optimizing the final geometry of a thin channel is missing. In this work, the overmelting of a printed thin channel is ascribed to the intrinsic size of the laser spot, exposure to the loose powder, excessive energy, and resolution of the control system. The concept of “melting cell” is proposed to predict the cross section of the final channel according to the geometrical relationship between the melting cell and the target channel. Surprisingly, it is found that the proposed method can correctly explain the geometric error distribution, and the predicted results have a good agreement with the existing experimental results.

The geometric precision of the channel depends on the size of the melting cell. Reducing the size of the melting cell by adjusting the processing parameters can significantly improve product precision, but this is limited by the availability of the existing laser sintering technology. Instead, a novel compensated design of thin channels is proposed. The envelope line of the melting cells determining the final surface shape of the thin channel is defined as the target channel line, and the mathematical description is derived. The compensated design of thin channels is close to the reported work which obtains the thin horizontal channel with the least dimensional deviation. This method can serve as a common guideline for the manufacturing of the products in many scenarios, i.e. different product shapes, processing parameters, and materials, etc.