1 Introduction

Many existing NHPP software reliability models [1–28] have been used through the fault intensity rate function and the mean value functions m(t) within a controlled testing environment to estimate reliability metrics such as the number of residual faults, failure rate, and reliability of the software. Generally, these models are applied to the software testing data and then used to make predictions on the software failures and reliability in the field. In other words, the underlying common assumption of such models is that the operating environment and the developing environment are about the same [21, 27]. The operating environments in the field for the software, in reality, are quite different. The randomness of the operating environments will affect software failure and software reliability in an unpredictable way.

Estimating software reliability in the field is important, yet a difficult task. Usually, software reliability models are applied to system test data with the hope of estimating the failure rate of the software in user environments. Teng and Pham [3] discussed a generalized model that captures the uncertainty of the environment and its effects upon the software failure rate. Other researchers [8, 19–21, 24, 28] have also developed reliability and cost models incorporating both testing phase and operating phase in the software development cycle for estimating the reliability of software systems in the field. Pham et al. [26] recently discussed a new logistic software reliability model where the fault-detection rate per unit time follows a three-parameter logistic function. They did not take into consideration of the uncertainty of operating environment. Pham [27] recently also developed a software reliability model with Vtub-shaped fault-detection rate subject to the uncertainty of operating environments.

In this paper, we discuss a new generalized software reliability model subject to the uncertainty of operating environments. The explicit solution of the generalized model and a specific model with a logistic fault-detection rate function IS derived in Sect. 2. Model analysis and results are discussed in Sect. 3 to illustrate the performance of THE proposed model and compare it to several common existing NHPP models based on three existing criteria such as mean square error, predictive power and predictive ratio risk from a set of software failure data. Section 4 concludes the paper.

Notation

m(t):

Expected number of software failures detected by time t.

N :

Expected number of faults that exist in the software before testing.

b(t):

Time-dependent fault-detection rate per unit of time.

2 A generalized NHPP model with random operating environments

Many existing NHPP models assume that failure intensity is proportional to the residual fault content. A generalized mean value function m(t) with the uncertainty of operating environments [27] can be obtained by solving the following defined differential equation:

$$\begin{aligned} \frac{\mathrm{d}m(t)}{\mathrm{d}t}=\eta b(t)[N-m(t)], \end{aligned}$$
(1)

where \(\eta \) is a random variable that represents the uncertainty of the system detection rate in the operating environments with a probability density function g. The solution for the mean value function m(t), where the initial condition \(m(0) = 0,\) is given by [27]:

$$\begin{aligned} m(t)=\int \limits _\eta {N\left( {1-\mathrm{e}^{-\eta \int \limits _0^t {b(x)\mathrm{d}x} }}\right) }\mathrm{d}g(\eta ). \end{aligned}$$
(2)

Based on the above equation, in this study we assume that the random variable \(\eta \) has a generalized probability density function g with two parameters \(\alpha \ge 0\hbox { and }\beta \ge 0,\) so that the mean value function from Eq. (2) can be obtained in the general form below:

$$\begin{aligned} m(t)=N\left( {1-\frac{\beta }{\beta +\int \limits _0^t {b} (s)~\mathrm{d}s}}\right) ^{\alpha }, \end{aligned}$$
(3)

where b(t) is the fault-detection rate per fault per unit of time.

Depending on how elaborate a model one wishes to obtain, one can use b(t) to yield more complex or less complex analytic solutions for the function m(t). Various b(t) reflects various assumptions of the growth processes. In this paper, we use the time-dependent three-parameter logistic function (or “S-shaped” curve) below to describe the fault-detection rate per fault per unit of time in the software system:

$$\begin{aligned} b(t)=\frac{c}{1+a\mathrm{e}^{-bt}}\quad \hbox {for }a\ge 0, b\ge 0, c > 0. \end{aligned}$$
(4)

The characteristic “S-shaped” curve of a logistic function shows that the initial exponential growth is followed by a period in which growth slows, then increases rapidly, and eventually levels off, approaching (but never attaining) a maximum upper limit. Substituting the three-parameter logistic function b(t) from Eq. (4) into Eq. (3), we can obtain the expected number of software failures detected by time t subject to the uncertainty of the environments as follows:

$$\begin{aligned} m(t)=N\left( {1 - \frac{\beta }{\beta +\left( {\frac{c}{b}}\right) \ln \left( {\frac{a+\mathrm{e}^{bt}}{1+a}}\right) }}\right) ^\alpha . \end{aligned}$$
(5)

Table 1 summarizes the proposed model and several existing well-known NHPP models with different mean value functions.

Table 1 A summary of new and existing software reliability models
Full size table

3 Model analysis and results

3.1 Some existing criteria

There are several existing goodness-of-fit criteria. In this study, we apply three common criteria for model performance and comparisons. They are: the mean square error, the predictive ratio risk, and the predictive power. Below is a brief description of the criteria.

The mean square error (MSE) measures the deviation between the predicted values with the actual observation and is defined as:

$$\begin{aligned} \mathrm{MSE}=\frac{\sum \nolimits _{i=1}^n {( {\hat{m}(t_i )-y_i })} ^2}{n-k}, \end{aligned}$$
(6)

where n and k are the number of observations and number of parameters in the model, respectively.

The predictive ratio risk (PRR) measures the distance of model estimates from the actual data against the model estimate and is defined as [17]:

$$\begin{aligned} \hbox {PRR}=\sum \limits _{i=1}^n {\left( {\frac{\hat{m}(t_i )-y_i }{\hat{m}(t_i )}}\right) ^2}, \end{aligned}$$
(7)

where \( y_{i}\) is the total number of failures observed at time \(t_{i}\) according to the actual data and \(\hat{m}(t_i )\) is the estimated cumulative number of failures at time \(t_{i}\) for \(i =1,2,\ldots ,n.\)

The predictive power (PP) measures the distance of model estimates from the actual data against the actual data, is as follows:

$$\begin{aligned} \hbox {PP}=\sum \limits _{i=1}^n {\left( {\frac{\hat{m}(t_i )-y_i }{y_i }}\right) ^2}. \end{aligned}$$
(8)

For all these three criteria—MSE, PRR, and PP—the smaller the value, the better the model fits, relative to other models run on the same data set.

3.2 Software failure data

A set of system test data were provided in [2, page 149] which is referred to as Phase 2 data set and is given in Table 2. In this data set, the number of faults detected in each week of testing is found and the cumulative number of faults since the start of testing is recorded for each week. This data set provides the cumulative number of faults by each week up to 21 weeks. We use a Matlab software to perform the calculations for LSE parameter estimates.

Table 2 Phase 2 system test data [2]
Full size table
Table 3 Model parameter estimation and comparison criteria
Full size table
Fig. 1
figure 1

A three-dimensional (X, Y, Z) represents (MSE, PP, model), respectively

Full size image
Fig. 2
figure 2

A three-dimensional (X, Y, Z) represents (MSE, PRR, PP), respectively

Full size image

3.3 Model results and comparison

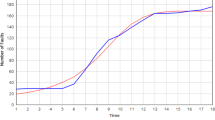
Table 3 summarizes the result of the estimated parameters of all 11 models as shown in Table 1 using the least square estimation (LSE) technique and their criteria (MSE, PRR and PP) values. The coordinates X, Y and Z represent the MSE, PP, and the model, respectively, as shown in Fig. 1. Figure 2 shows the MSE, PRR and PP values of all the models. As we can see from Table 3, the new model has the smallest MSE, PP and PRR values. The plots in Fig. 3 illustrate the expected number of failures detected versus testing time t. Table 4 includes the rank of each model based on each criteria.

Fig. 3
figure 3

Number of failures vs. testing time for all models based on Phase 2 data

Full size image
Table 4 Parameter estimation and model comparison
Full size table

The new model (model 11) as shown in Fig. 2 and Table 4 provides the best fit based on the MSE, PRR and PP criteria. Obviously, further work in broader validation of this conclusion is needed using other data sets as well as considering other comparison criteria.

4 Conclusion

In this paper, we present a new general software reliability model incorporating the uncertainty of the operating environments. The explicit mean value function solution of the proposed model for a logistic fault-detection rate is presented. The results of the estimated parameters of the proposed model and several NHPP models are discussed. The results show that the proposed logistic fault-detection model fits significantly better than all the existing NHPP models studied in this paper based on all MSE, PRR and PP criteria. Obviously, further work in broader validation of this conclusion is needed using other data sets as well as considering other comparison criteria.