An efficient method for mining association rules based on minimum single constraints

Abstract

Mining association rules with constraints allow us to concentrate on discovering a useful subset instead of the complete set of association rules. With the aim of satisfying the needs of users and improving the efficiency and effectiveness of mining task, many various constraints and mining algorithms have been proposed. In practice, finding rules regarding specific itemsets is of interest. Thus, this paper considers the problem of mining association rules whose left-hand and right-hand sides contain two given itemsets, respectively. In addition, they also have to satisfy two given maximum support and confidence constraints. Applying previous algorithms to solve this problem may encounter disadvantages, such as the generation of many redundant candidates, time-consuming constraint check and the repeated reading of the database when the constraints are changed. The paper proposes an equivalence relation using the closure of itemset to partition the solution set into disjoint equivalence classes and a new, efficient representation of the rules in each class based on the lattice of closed itemsets and their generators. The paper also develops a new algorithm, called MAR-MINSC, to rapidly mine all constrained rules from the lattice instead of mining them directly from the database. Theoretical results are proven to be reliable. Because MAR-MINSC does not meet drawbacks above, in extensive experiments on many databases it obtains the outstanding performance in comparison with some of existing algorithms in mining association rules with the constraints mentioned.

1 Introduction

For the aim of not only reducing the burden of storage and execution time but also rapidly responding to the demand of users, constraint-based data mining has attracted much interest and attention from researchers. At the beginning, they have designed algorithms to mine data with primitive constraints. A typical example is the one of the frequent itemset discoveries in a transaction database where the primitive constraint is a minimum frequency constraint. Based on frequent itemsets, association rules are mined, where the minimum confidence constraint is other primitive one. More concretely, let $\mathcal {T} = (\mathcal {O}, \mathcal {A}, \mathcal {R})$ be a binary database, where $\mathcal {O}$ is a non-empty set that contains objects (or transactions), $\mathcal {A}$ is a set of attributes (or items) appearing in these objects and $\mathcal {R}$ is a binary relation on $\mathcal {O}\times \mathcal {A}$. The cardinalities of $\mathcal {A}$ and $\mathcal {O}$ are denoted as ${m}=\vert \mathcal {A}\vert$ and ${n}=\vert {\mathcal {O}}\vert$, respectively ($m$ and $n$ are often very large). Let us denote $s_0$ as the minimum support threshold and $c_{0}$ as minimum confidence threshold, where $s_{0}, c_{0} \in (0; 1]$. The task is to mine frequent itemsets and association rules from ${\mathcal {T}}$. A basic problem, named (${P}_{1}$), is that the cardinalities of frequent itemset class $FS({s_{0}})$ and association rule set $\mathrm{ARS}(s_{0},c_{0})$ in the worst case are of exponent, i.e., $\mathrm{Max}(\#{FS}({s}_{0}))=2^m-1=O({2^m})$ and $\mathrm{Max}(\#{\mathrm{ARS}}({s}_0, {c}_0))=3^m-2^{m+1}+1=O(3^m)$. Therefore, extant algorithms remain riddled with limitations regarding the mining time and the main memory in case the size of ${\mathcal {T}}$ is quite large. Moreover, for rules that were discovered, it is difficult for users to quickly find the quite small subset of interest if there only have the constraints about support and confidence. To solve this problem (${P}_{1})$, many more complicated constraints have been introduced into algorithms to only generate association rules related directly to the user’s true needs, and to reduce the cost of the mining. Monotonic and anti-monotonic constraints, denoted as ${\mathcal {C}}_{\mathrm{m}}$ and ${\mathcal {C}}_{\mathrm{am}}$ respectively, are considered by Nguyen et al. [25]. They are pushed into an Apriori-like algorithm, named CAP, to reduce the frequent itemsets computation. In [7], the problem is restricted in two constraints that are the consequent and the minimum improvement. Srikant et al. [30] present the problem of mining association rules that include the given items in their two sides. A three-phase algorithm is proposed for mining those rules. First, the constraint is integrated into the Apriori-like candidate generation procedure to find only candidates that contain the selected items. Second, an additional scanning of the database is executed to count the support of the subsets of each mined frequent itemset. Finally, an algorithm based on Apriori principle is applied to generate rules. The concept of convertible constraint is introduced and pushed within the mining process of an FP-growth based algorithm [28]. The authors show that, since frequent itemset mining is based on the concept of prefix-itemsets, it is very easy to integrate convertible constraints into FP-growth-like algorithms. They also state that pushing these constraints into Apriori-like algorithms is not possible. Due to huge input databases, Bonchi et al. [8] propose data reduction techniques and they have been proven to be quite effective in cases of pushing convertible constraints into a level-wise computation. The authors in [21] design the algorithms for discovering association rules with multi-dimension constraints.

By combining the power of the condensed representation (closed itemsets and generators) of frequent itemsets with the properties of ${\mathcal {C}}_{\mathrm{m}}$ and ${\mathcal {C}}_{\mathrm{am}}$ constraints, in [2, 3, 16, 17], we consider some different item constraints and propose efficient algorithms to mine-constrained frequent itemsets. In detail, the work in [2] is to mine all frequent itemsets contained in a specific itemset. An algorithm, called MINE_FS_CONS, has been proposed to do this task. In [3], the efficient algorithms MFS-CC and MFS-IC for mining frequent itemsets with the dualistic constraints are presented. They are built based on the explicit structure of frequent itemset class. The class is split into two sub-classes. Each sub-class is found by applying the efficient representation of itemsets to the suitable generators. And in [16, 17], we consider the problem of mining frequent itemsets that (i) include a given subset and (ii) contain no items of another specific subset, or only satisfy the condition (i). Mining frequent itemsets that satisfy both (i) and (ii) is quite complicated because there is a tradeoff among these constraints. However, with a suitable approach, the papers propose efficient algorithms, named MFS-Contain-IC and MFS_DoubleCons, for discovering frequent itemsets with the constraints mentioned.

It is noted that, our results above only relate directly to frequent itemsets. We, in this paper, are interested in extending the result presented in [16] to association rule mining with many different constraints. The approach based on frequent closed itemset and their generators is still used but the problem is much more complicated. Firstly, let us state our problem as in sub-section below.

1.1 Problem statement

Before stating the problem of our study, we present some common concepts and related notations. Given ${\mathcal {T}} = ({\mathcal {O}}, {\mathcal {A}}, {\mathcal {R}})$, a set ${X}\subseteq {\mathcal {A}}$ is called an itemset. The support of an itemset X, denoted by supp(X), is the ratio of the number of transactions containing X and N, the number of transactions in ${\mathcal {T}}$. Let ${s}_{0}, {s}_{1}$ be the minimum and maximum support thresholds, respectively, where $0<1/{n}\le s_{0} \le s_1 \le 1$ and ${n} = \vert {\mathcal {O}}\vert$. A non-empty itemset $A$ is called frequent iff¹ ${s}_0 \le \mathrm{supp}({A})\le {s}_1$ (if ${s}_1$ is equal to 1, then the traditional frequent itemset concept is obtained). For any frequent itemset $S{^\prime }$, we take a non-empty, proper subset $L{^\prime }$ from $S{^\prime }$ $(\varnothing \ne$ $L{^\prime }$ $\subset$ $S{^\prime }$) and $R{^\prime }$ $\equiv$ $S{^\prime }\backslash L{^\prime }$. Then, $r:L{^\prime }$ $\rightarrow$ $R{^\prime }$ is a rule created by $L{^\prime }$, $R{^\prime }$ (or by $L{^\prime }$, $S{^\prime }$) and its support and confidence are determined by supp(r) $\equiv$ supp($S{^\prime }$) and conf(r) $\equiv$ supp($S{^\prime }$)/supp($L{^\prime }$), respectively. The minimum and maximum confidence thresholds are denoted by $c_{0}$ and $c_{1}$, respectively, where $0<c_0 \le c_1 \le 1$. The rule r is called an association rule in the traditional manner iff ${c}_{{0}}\le$ conf(r) and ${s}_{{0}}\le$ supp(r) and the set of all association rules is denoted by ${\mathrm{ARS}}({{s}_{{0}},{c}_{{0}}})\equiv$ {$r:L{^\prime }$ $\rightarrow$ $R{^\prime }$ $\vert \varnothing \ne$ $L{^\prime }$, $R{^\prime }$ $\subseteq _{\mathcal {A}},$ $L{^\prime }$ $\cap$ $R{^\prime }$ = $\varnothing$, $S{^\prime }$ $\equiv$ $L{^\prime }$ + $R{^\prime }$, $s_{0} \le$ supp(r), $c_0 \le$ conf(r)}

The present study considers the problems that comprise many constraints about support, confidence and sub-items. Such a problem is stated as follows. For additional constraints on two sides of rule, $L_{0}, R_{0} \subseteq {\mathcal {A}}$, the goal is to discover all association rules $r:L{^\prime }$ $\rightarrow$ $R{^\prime }$ so that their supports and confidences meet the conditions, $s_{0} \le \hbox {supp}({ r}) \le s_{1}, c_{0} \le \hbox {conf}({ r})\le c_1$, and their two sides contain the item constraints, $L{^\prime }$ $\supseteq L_{0},$ $R{^\prime }$ $\supseteq R_{0}$, called minimum single constraints. The problem can be described formally as follows.

$$\begin{aligned}&\mathrm{ARS}_{\supseteq L_0, \supseteq R_0} (s_0, s_1, c_0, c_1) \equiv \{{{r:L}}' \rightarrow {{R}}' \in \nonumber \\&\quad \mathrm{ARS}(s_0, s_1, c_0, c_1 ) \vert {{L}}' \supseteq {L}_0, {{R}}' \supseteq {R}_0\} \quad \hbox {(ARS}\_ \hbox {MinSC)}, \end{aligned}$$

where $\mathrm{ARS}(s_0, s_1, c_0, c_1) \equiv$ {$r:L{^\prime }$ $\rightarrow$ $R{^\prime }$ $\in \mathrm{ARS}(s_0, c_0)\vert \hbox {supp}({ r}) \le s_1, \hbox {conf}({ r}) \le c_1\}.$

For discussing about the constraints of the problem, it is noted that if $s_1 =c_1 =1$ and $L_0 =R_0 =\varnothing$, we obtain the problem of mining association rule set $\mathrm{ARS}({s_0, c_0})$ in the traditional meaning. Otherwise, the mined rules may be significant in different application domains such as market-basket analysis, network traffic domain and so on. For instance, the managers or leaders want to increase the turnover of their supermarket based on high valuable items such as gold and iPad. To this aim, a solution is to find an interesting association among two of these items. The proposed problem may help them to answer the question if there is an association or not by setting the constraints L ₀ = {gold} and R ₀ = {iPad}. If there has at least a found rule, it means that the association is existent. Then, it can be used to support for attaining the aim such as showing two of these items on close places which may encourage the sale of the items together and do discount strategies. At the beginning, the confidences of mined rules may be not high because such exceptional rules only have a few their instances. If the mining task received the high value of the maximum confidence threshold, it may generate a large number of rules. This makes it easy to miss the low confidence rules but they are of potential significance. Thus, in order to realize and monitor them easily, we should use the small value of maximum confidence threshold. After a time, if these rules have higher confidences and become more important, then foreseeing these associations of the items at the early period of the rules may bring about the higher profits for the supermarket.

In the other meaning, using a maximum confidence threshold is more general than the fixed value that is always equal to 1. For the maximum support threshold, when the value of $s_1$ is quite low and that of $c_0$ is very high, ${\mathrm{ARS}}({s}_{{0}},{s}_{{1}},{c}_{{0}},{c}_{{1}})$ comprises association rules with the high confidences, discovered from low frequent itemsets. This problem is of importance and practical significance. For instance, we want to detect fairly accurate rules from new, abnormal yet significant phenomena despite their low frequency.

Extant algorithms to mine rules with minimum single constraints might encounter problem, named (${P}_{2})$, such as the generation of many redundant candidate rules and the duplicates of solutions that are then eliminated. The current interest is to find an appropriate approach for mining-constrained association rule set (the rules satisfy minimum single constraints) without (${P}_{2}$).

1.2 Paper contribution

The contributions of the paper are as follows. First, we present an approach based on the lattice [26, 34, 37] of closed itemsets and their generators to efficiently mine association rules satisfying the minimum single constraints and the maximum support and confidence thresholds mentioned above. To this approach, we propose a equivalence relation on constrained rule set based on the closure operator [26]. It helps to partition the set of constrained rules, ${\mathrm{ARS}}_{\supseteq {{L}_{{0}},\supseteq {R}_{{0}}}}({s}_{{0}},{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}})$, into disjoint equivalence rule classes. Thus, each class is discovered independently and the duplication of the solution may be reduced considerably. Moreover, the partition also helps to decrease the burden of saving the supports and confidences of all rules in the same class and be a reliable theoretical basis for developing parallel algorithms in distributed environments. Second, we point out the necessary and sufficient conditions so that the solution of the problem or a certain rule class is existent. If the conditions are not satisfied, the mining process does not need to uselessly take up time for finding the solution. This makes an important contribution to the efficiency of the approach. Third, a new representation of constrained rules in each class is proposed with many advantages as follows: (1) it helps us to have a clear sight about the structure of constrained rule set; (2) the duplication is completely eliminated; (3) all constrained rules are rapidly extracted without doing any direct check on the constraints, ${{L}}'\supseteq L_0$ and ${R}'\supseteq R_0$. Finally, according to the proposed theoretical results, we design a new, efficient algorithm, named MAR_MinSC (Mining all Association Rules with Minimum Single Constraints) and related procedures to completely, quickly and distinctly generate all association rules satisfying the given constraints.

1.3 Preliminary concepts and notations

Prior to presenting an appropriate approach to discover the rules with minimum single constraints without (${P}_{2})$, let us recall some of the following basic concepts about the lattice of closed itemsets and the task of association rule mining.

Given ${\mathcal {T}} = ({\mathcal {O}}, {\mathcal {A}}, {\mathcal {R}})$, we consider two Galois connection operators $\lambda : 2^{\circ } \rightarrow 2^{{\mathcal {A}}}$ and $\rho : 2^{\mathcal {A}} \rightarrow 2^{\circ }$ defined as follows: $\forall {O}, {A}: \varnothing \ne {O}\subseteq \mathcal {O}, \varnothing \ne {A}\subseteq \mathcal {A}, \lambda ({O}) \equiv \left\{ {{a}\in \mathcal{A}\vert ({{o,a}})\in \mathcal{R}, \forall {o}\in {O}} \right\} , \rho ({A})\equiv \left\{ {{o}\in \mathcal{O}\vert ( {{o,a}})\in \mathcal{R},\,\forall {a}\in {A}} \right\}$ and, as convention, $\lambda (\varnothing )=\mathcal{A}, \rho ({\varnothing =\mathcal {O}})$. We denote h(A) $\equiv \lambda (\rho$(A)) as the closure of A (h is called the closure operation in 2$^{{\mathcal {A}}})$. An itemset A is called closed itemset iff h(A) = A [26]. We only consider non-trivial items in $\mathcal{A}^{{F}}\equiv \left\{ {{a}\in \mathcal{A}:\hbox {supp}({ \{{a} \} }) \ge s_0} \right\}$. Let ${\mathcal {CS}}$ be the class of all closed itemsets together with their supports. With normal order relation “$\supseteq$” over subsets of ${\mathcal {A}}$, the lattice of all closed itemsets that is organized by Hass diagram is denoted by ${{\mathcal {LC}}}\equiv ({{\mathcal {CS}}},\supseteq )$. Briefly, we use ${\mathrm{FS}}({s}_{{0}},{s}_{{1}})\equiv$ {$L'$:$\varnothing \ne$ $L'$ $\subseteq \mathcal{A}, s_{{0}} \le$ supp($L'$)$\le {s}_{{1}} \}$ to denote the class of all frequent itemsets and ${\mathrm{FCS}}({s}_{{0}},{s}_{{1}})\equiv {\mathrm{FS}}({s}_{{0}},{s}_{{1}})\cap {\mathcal {CS}}$ to denote the class of all frequent closed itemsets. For any two non-empty itemsets G and A, where $\varnothing \ne {G} \subseteq {A} \subseteq {{\mathcal {A}}}$, G is called a generator [23] of A iff h(G) = h(A) and $(h(G'$) $\subset {{ h}({ G})}, \forall$ $G'$: $\varnothing \ne$ $G'$ $\subset G$ ). The class of all generators of A is denoted by ${\mathcal {G}}$(A). Since ${\mathcal {G}}$(A) is non-empty and finite [5], $\vert {\mathcal {G}}{(A)}\vert = {k},$ all generators of A could be indexed as ${\mathcal {G}}{(A)}=\{A_1,A_2,\ldots ,A_k\}$. Let ${\mathcal {L}}{\mathcal {C}}{\mathcal {G}}\equiv \{({S}, {\mathrm{supp}(S)}, {\mathcal {G}}{(S)}) \vert ({S}, {\mathrm{supp}(S)}) \in {\mathcal {L}}{\mathcal {C}}\}$ be the lattice ${\mathcal {L}}{\mathcal {C}}$ of closed itemsets together their generators and ${\mathcal {F}}{\mathcal {L}}{\mathcal {C}}{\mathcal {G}}({s}_{{0}},{s}_{{1}})\equiv$ $\{({S}, {\mathrm{supp}(S)}, {\mathcal {G}}({S}))\in {\mathcal {L}}{\mathcal {C}}{\mathcal {G}} \vert {S} \in {\mathrm{FS}}({s}_{{0}}, {s}_{{1}})\}$ be the lattice of frequent closed itemsets and their generators.

From now on, we shall assume that the following conditions are satisfied, $0 <{s}_0 \le {s}_1 \le 1, 0 < {c}_0 \le {c}_1 \le 1, {L}_0 , {R}_0 \subseteq {\mathcal {A}}. \quad ({H}_{0}).$

Paper organization The rest of this paper is organized as follows. In Sect. 2, we present some approaches to the problem (ARS_MinSC) and the related works. Section 3 shows a partition and a unique representation of constrained association rule set based on closed itemsets and their generators. An efficient algorithm MAR_MinSC to generate all association rules with minimum single constraints is also proposed in this section. Experimental results are discussed in Sect. 4. Finally, conclusions and future works are presented in Sect. 5.

2 Approaches to the problem and related works

2.1 Approaches

Post-processing approaches To find association rule set with minimum single constraints ${\mathrm{ARS}}_{\supseteq L_0, \supseteq R_0} (s_0, s_1, c_0, c_1)$, the approaches often perform two phases: (1) association rule set ${\mathrm{ARS}}(s_0, c_0)$ without the constraints is discovered; (2) the procedures for checking and selecting rules $r:L'$ $\rightarrow$ $R'$ that satisfy the constraint

$\equiv {\hbox {supp}}({ r}) \le s_1 , \hbox {conf}({ r}) \le c_1$ and $L'$ $\supseteq L_0,$ $R'$ $\supseteq R_0\}$ are executed. In the phase (1), the rule set, $\mathrm{ARS}(s_0, c_0)$, is able to be mined based on the following simple two methods. One is that it is found by definition, i.e., the class of frequent itemsets $\mathrm{FS}(s_0)$ with the threshold $s_{0}$ needs to be mined by a well-known algorithm, such as Apriori [1, 23] or Declat [37]. Then, for $\forall$ $S'$ $\in \mathrm{FS}(s_0)$, all rules $r:L'$ $\rightarrow$ $R'$ $\in \mathrm{ARS}(s_0, c_0)$, where $\varnothing \ne$ $L'$ $\subset$ $S'$, $R'$ $\equiv$ $S'$ $\backslash$ $L'$ are discovered by an algorithm based on the Apriori principle, such as Gen-Rules [26]. The time for finding ${\mathrm{ARS}}({s}_{{0}}, {c}_{{0}})$ is often quite long because of the reasons as follows: (i) the phase of finding frequent itemsets may generate too many candidates and/or scan the database many times; (ii) the association rule extracting phase often produces many candidates and takes time a lot to calculate the confidences (since the supports of the left-hand sides of the rules may be undetermined). Let us call this post-processing algorithm PP-MAR-MinSC-1 (Post Processing-Mining Association Rule with Minimum Single Constraints-1). The other is to find $\mathrm{ARS}(s_0 ,c_0)$ based on the lattice ${\mathcal {FLCG}}$ of frequent closed itemsets and the partition of ${\mathrm{ARS}}({s}_{{0}}, {c}_{{0}})$ as presented in cotemoh4. Instead of exploiting all frequent itemsets, we only need to extract frequent closed itemsets and partition ${\mathrm{ARS}}({s}_{{0}}, {c}_{{0}})$ into equivalence classes. The rules in each class have the same support and confidence that are calculated only once (see in Sect. 3.1.1 for more details). We name PP-MAR-MinSC-2 for the algorithm of the second method. PP-MAR-MinSC-2 seems to be more efficient than PP-MAR-MinSC-1 because it is more suitable in cases support and confidence thresholds are often changed.

Post-processing approaches have the advantage of being simple, but they also have several disadvantages. Due to the enormous cardinality of ${\mathrm{ARS}}({s}_{{0}}, {c}_{{0}})$, the algorithms take a long time to search, but then there might be only a few or even no association rules in $\mathrm{ARS}(s_0, c_0)$ which are of ${\mathrm{ARS}}_{\supseteq {L}_{{0}}, \supseteq {R}_{{0}}} ({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}} )$ (the cardinality of ${\mathrm{ARS}}_{\supseteq {L}_{{0}} ,\supseteq {R}_{{0}}} ({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}})$ is often quite small compared to that of ${\mathrm{ARS}}({s}_{{0}} ,{c}_{{0}}))$. Moreover, after finding ${\mathrm{ARS}}({s}_{{0}} ,{c}_{{0}})$ is completed, post-processing algorithms have to do direct checks on the constraints, $L'$ $\supseteq L_0$, $R'$ $\supseteq R_0$. This might be time-consuming. In addition, when the constraints are changed based on the demands of online users, recalculating $\mathrm{ARS}(s_0, c_0)$ will uselessly take up time. If, at the beginning, we mine and store ${\mathrm{ARS}}({s}_{{0}}, {c}_{{0}})$ with ${s}_{{0}} ={c}_{{0}} = 1/\vert {\mathcal {O}} \vert$, then the computational and memory costs will be very high.

Paper approach To avoid the disadvantages of post-processing approaches and to solve the problem (${P}_{2})$, the paper proposes a new approach based on three key factors as follows. The first is the lattice ${\mathcal {LCG}}$ of closed itemsets, their generators and supports. Using ${\mathcal {LCG}}$ has three advantages: (1) the size of ${\mathcal {LCG}}$ is often very small in comparison with that of ${\mathrm{FS}}({s}_{{0}} )$; (2) ${\mathcal {LCG}}$ is calculated just once by one of the efficient algorithms such as CHARM-L and MinimalGegenators [36, 37], Touch [31] or GenClose [5]; (3) from the lattice ${\mathcal {LCG}}$, we can quickly derive the lattice

of frequent closed itemsets satisfying the constraint

together with the corresponding generators whenever

appears or changes. The second is the equivalence relation based on the closure of two sides of rules (L $\equiv$ h($L'$) $\subseteq$ S $\equiv$ h ($L'$+$R'$)). The third is the explicitly unique representation of rules in the same equivalence class $\mathrm{AR}$(L, S) upon the generators and their closures, (L, ${\mathcal {G}}$ (L)) and (S, ${\mathcal {G}}$ (S)). In each class, this representation helps us to have a clear sight of the rule structure and to completely eliminate the duplication. An important note is that our method does not need to directly check the generated rules on the constraints, $L'$ $\supseteq L_0$, $R'$ $\supseteq {R}_0$.

2.2 Related works

To solve the problem (P ₁) and improve the efficiency of existing mining algorithms, various constraints have been integrated during the mining process to only generate association rules of interest. The algorithms are mainly based on either the Apriori principle [1] or the FP-growth [18] in combination with the properties of ${\mathcal {C}}_{\mathrm{am}}$ and ${\mathcal {C}}_{\mathrm{m}}$ constraints. FP-bonsai [9] uses both ${\mathcal {C}}_{\mathrm{am}}$ and ${\mathcal {C}}_{\mathrm{m}}$ to mine frequent patterns. The advantage of FP-bonsai is that it utilizes ${\mathcal {C}}_{\mathrm{m}}$ to support the process of pruning candidate itemsets and the database upon ${\mathcal {C}}_{\mathrm{am}}$. It is efficient on dense databases but not on sparse ones. Fold-Growth [29, 35] is an improvement of FP-tree using a pre-processing tree structure, named SOTrielT. The first strength of SOTrielT is its ability to quickly find frequent 1-itemsets and 2-itemsets with a given support threshold. The second one is that it does not have to reconstruct the tree when the support is changed. A primary drawback of the FP-growth based algorithms is to require the large size of main memory for saving the original database and intermediate projected databases. Thus, if the main memory is not enough, the algorithms cannot be used. Another important limitation of this approach is that it is hard to take full advantage of a combination of different constraints, since each constraint has different properties. For instance, minimum single constraints above regarding support, confidence and item subsets include both ${\mathcal {C}}_{\mathrm{am}}$ and ${\mathcal {C}}_{\mathrm{m}}$ constraints whose properties are opposite. Moreover, the approach could take cost a lot to reconstruct FP-tree when mining frequent itemsets and association rules with different constraints. On the contrary, ExAMiner [8] is an Apriori-like algorithm. It uses input data reduction techniques to reduce the problem dimensions as well as the search space. It is good at huge input data. However, ExAMiner is not suitable with the problem stated in the paper because when the minimum single constraints are changed, the process of reducing input data needs to be started from the original database and generating rules may have time-consuming, direct checks on the constraints. Moreover, the authors in [20] show that the integration of ${\mathcal {C}}_{\mathrm{m}}$ can lead to a reduction in the pruning of ${\mathcal {C}}_{\mathrm{am}}$. Therefore, there is a tradeoff between ${\mathcal {C}}_{\mathrm{am}}$ and ${\mathcal {C}}_{\mathrm{m}}$ pruning.

For other related results, a constraint, named maximum constraint, is used by [19] to discover association rules with many minimum support thresholds. Each 1-itemset has a minimum support threshold of its own. The authors propose an Apriori-like algorithm for mining large-itemsets and rules with this constraint. Lee et al. [21] design an algorithm to mine association rules with multi-dimensional constraints. An example, max(S.cost) $<$6 and 200 $<$min(S.price), is the one of the multi-dimensional constraints, where S is an itemset, and each item of S has two attributes, cost and price. In [14], the CoGAR framework to mine generalized association rules with constraints is presented. Besides the traditional minimum support and confidence, two new constraints, schema and opportunistic confidence, are considered. The schema constraint is similar to that shown in [2] but the approach to solve the problem is different. An algorithm is proposed to discover generalized rules satisfying both these constraints in three phases: (1) the algorithm CI-Miner is used to extract schema constrained itemsets; (2) the generalized association rules are exploited by the Apriori-like rule mining algorithm, RuleGen; (3) a post-processing filtering algorithm, named CR-Filter, is designed to get the rules satisfying the opportunistic confidence constraint. The concept of periodic constraints is given in [32, 33] and new algorithms for mining association rules with this constraint are mentioned. The mining task, firstly, abstracts the variable and then eliminates the solutions falling outside at axiom constraints. The authors in [24] consider the problem of discovering multi-level frequent itemsets with the existent constraints that are represented as a Boolean expression in disjunctive normal form. A technique to model the constraints in the context of use of concept hierarchies is proposed and the efficient algorithms are developed to gain the aim.

Note that most of the previously proposed algorithms for mining association rules with constraints were designed to work on their own constraints. Thus, using them to discover rules based on minimum single constraints may be inefficient. In addition, these algorithms could encounter two important shortcomings; one is to generate many redundant candidates and duplicates of the solution that are then eliminated (the problem (P ₂)); the other is that the algorithms need to be rerun from the initial database whenever the constraints are changed. This reduces the mining speed for users.

While the results above seem to be not suitable with the stated problem, an approach that is based on the condensed representation of frequent itemsets might be more efficient. Instead of mining all frequent itemsets, only the condensed ones are extracted. Using condensed frequent itemsets has three primary advantages. First, it is easier to store because its cardinality is much smaller than the size of the class of all frequent itemsets, especially for dense databases. Second, they are mined only once from the database even when the constraints are changed. Third, they can be used to completely generate all frequent itemsets without having to access the database. There are two types of condensed representation. The first type is maximal frequent itemsets [13, 22]. Since their cardinality is very small, they can be discovered quickly. All frequent itemsets can be generated from the maximal ones. However, the generation often produces duplicates. In addition, the frequent itemsets generated can lose information about their supports. Therefore, the supports need to be recomputed when mining association rules. The second type is closed frequent itemsets, called maximal ones, and their generators, called minimal ones [10–12, 27]. Each closed frequent itemset represents a class of frequent itemsets. Thus, together with its generators, it can be used to uniquely determine all frequent itemsets in the same class without losing information about their supports.

Among two types of the condensed representation above, the second one is probably better and has been proven to be efficient in our previous works. Therefore, in this paper, we propose a new structure and an efficient representation of constrained association rule set based on closed itemsets and their generators. A new corresponding algorithm, named MAR_MinSC, is also developed for mining association rules satisfying the minimum single constraint and the maximum support and confidence thresholds.

3 Mining association rules with minimum single constraints

3.1 Partition of association rule set with minimum single constraints

3.1.1 Rough partition

To considerably reduce the duplication of candidates for the solution, we should partition the rule set into disjoint classes based on a suitable equivalence relation. Because the closure operator h of ${\mathcal {LCG}}$ has some good features, based on it, we propose the following two equivalence relations on ${\mathrm{FS}}({{s}_{{0}} ,{s}_{{1}}})$ and ${\mathrm{ARS}}({s}_{{0}} ,{s}_{{1}},{c}_{{0}} ,{c}_{{1}})$.

Definition 1

(Two equivalence relations on ${\mathrm{FS}}({s}_{{0}}, {s}_{{1}})$ and ${\mathrm{ARS}}({s}_{{0}},{s}_{{1}} ,{c}_{{0}},{c}_{{1}})$).

• (a) $\forall$ $A, B \in {\mathrm{FS}}({s}_{{0}}, {s}_{{1}})$, $A\sim _{{\mathcal {A}}}$ B $\Leftrightarrow$ h(A) = h(B).

• (b) $\forall {r}_{\mathrm{k}}: {L}_{\mathrm{k}}\rightarrow {R}_{\mathrm{k}} \in {\mathrm{ARS}}({s}_{{0}}, {s}_{{1}} ,{c}_{{0}},{c}_{{1}}), {k}=1,2,$

$$\begin{aligned}&{r}_{1}\sim _{\mathrm{r}} {r}_{2} \Leftrightarrow [{h}({L}_{1})= {h}({L}_{2}) \hbox { and } {h}({L}_{1}+{R}_{1})\\&\quad = {h}({L}_{2}+{R}_{2})]. \end{aligned}$$

Obviously, these are equivalence relations. For any ${L}\in {\mathrm{FCS}}({s}_{{0}}, {s}_{{1}})$, we use $[{L}]_{{\mathcal {A}}} \equiv$ {$L'$ $\subseteq$ L: $L'$ $\ne \varnothing$, h($L'$) = L} to denote the equivalence class of all frequent itemsets with the same closure L. For two arbitrary sets L, S $\in {\mathrm{FCS}}({s}_{{0}} ,{s}_{{1}})$ such that $\varnothing \ne L \subseteq$ S, supp(S)/supp(L)$\in [c_0 ; c_1]$, the equivalence class of all rules $r:L'$ $\rightarrow$ $R'$ so that h($L'$) = L, h($L'$+$R'$) = S is denoted by ${\mathrm{AR}}({L, S}) \equiv$ {$r:L'$ $\rightarrow$ $R'$ $\in {\mathrm{ARS}}({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}}) \vert$ $L'$ $\in [L]_{{\mathcal {A}}},$ $S'$ $\equiv$ $L'$+$R'$ $\in [{S}]_{{\mathcal {A}}}\}$.

Remark 1

• (a) Due to the features of $h, \forall L \in {\mathrm{FCS}}({s}_{{0}}, {s}_{{1}}),$ supp($L'$) = supp(L), $\forall$ $L'$ $\in [{L}]_{{{\mathcal {A}}}}$, i.e., all frequent itemsets in the same equivalence class [L]$_{{{\mathcal {A}}}}$ have the same support, supp(L).

• (b) With $\forall$ $r:L'$ $\rightarrow$ $R'$ $\in {\mathrm{ARS}}({s}_{{0}}, {s}_{{1}}, {c}_{{0}}, {c}_{{1}})$, let us set L $\equiv$ $h(L')$, $S'$ $\equiv$ $L'$+$R'$, S $\equiv$ $h(S'$), then we have $\varnothing \ne {L} \subseteq {S},$ supp($S'$) = supp(S) $\in [s_0, s_1],$ conf(r) $\equiv$ supp($S'$)/supp($L'$) = supp(S)/supp(L)$\in [c_0 , c_1]$ and $({L}, {S}) \in {\mathrm{NFCS}}({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}})$, where

  $$\begin{aligned}&{\mathrm{NFCS}}({s}_{{0}},{s}_{{1}} ,{c}_{{0}},{c}_{{1}})\\&\quad \equiv \{({L}, {S})\in {\mathcal {CS}}^{2} \vert {S} \in {\mathrm{FCS}}({s}_{{0}}, {s}_{{1}}),\\&\quad \varnothing \ne {L} \subseteq {S}, {\hbox {supp}}(S)/ {\hbox {supp}}(L) \in [c_0, c_1 ]\}. \end{aligned}$$

  Thus, for $\forall (L, S)\in {\mathrm{NFCS}}({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}}, {c}_{{1}})$, all rules in the same equivalence class $\mathrm{AR}(L, S)$ have the same support supp(S) and confidence supp(S)/supp(L). This helps to considerably reduce storage needed for the supports of the frequent itemsets and the confidences of association rules.

• (c) From (a) and (b), we have the partition of rule set ${\mathrm{ARS}}({s}_{{0}},{s}_{{1}} ,{c}_{{0}},{c}_{{1}})$ without the item constraints as follows.

  $$\begin{aligned}&{\mathrm{ARS}}({s}_{{0}},{s}_{{1}} ,{c}_{0},{c}_{{1}})\\&\quad =\sum \nolimits _{({L,S}) \in {\mathrm{NFCS}}({s}_{{0}},{s}_{{1}} ,{c}_{{0}},{c}_{{1}})}{\mathrm{AR}}({L,S}). \end{aligned}$$

  Since ${\mathrm{ARS}}_{\supseteq {L}_{{0}},\supseteq {R}_{{0}}}({s}_{{0}}, {s}_{{1}},{c}_{{0}} ,{c}_{{1}})\subseteq {\mathrm{ARS}}({s}_{{0}},{s}_{{1}}, {c}_{{0}},{c}_{{1}})$, the following rough partition of constrained rule set ${\mathrm{ARS}}_{\supseteq {L}_{{0}}, \supseteq {R}_{{0}}} ({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}})$ is derived.

Proposition 1

(The rough partition of constrained rule set). We have:

$$\begin{aligned}&{\mathrm{ARS}}_{\supseteq L_0 ,\supseteq R_0}({s}_{{0}}, {s}_{{1}}, {c}_{{0}}, {c}_{{1}}) \\&\quad =\sum \nolimits _{(L,S)\in {\mathrm{NFCS}}({s}_{{0}}, {s}_{{1}} ,{c}_{{0}},{c}_{{1}})} \mathrm{AR}_{\supseteq L_0 ,\supseteq R_0} (L,S), \end{aligned}$$

where ${\mathrm{AR}}_{\supseteq L_0, \supseteq R_0} (L,S) \equiv$ $\{$r:$L'$ $\rightarrow$ $R'$ $\in \mathrm{AR}({L, S}) \vert$ $L'$ $\supseteq L_0,$ $R'$ $\supseteq R_0^{(t)}\}$.

Based on Proposition 1, we can derive the simple post-processing algorithm PP-MAR-MinSC-2 to generate ${\mathrm{ARS}}_{\supseteq L_0, \supseteq R_0} ({s}_{{0}}, {s}_{{1}}, {c}_{{0}}, {c}_{{1}})$. However, we find that, on many values of the constraints, ${\mathrm{ARS}}_{\supseteq L_0 ,\supseteq R_0} ({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}})$ can be empty. Or there are many pairs of closed frequent itemsets $(L, S)\in {\mathrm{NFCS}}({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}})$ for which the subclasses ${\mathrm{AR}}_{\supseteq L_0 ,\supseteq R_0}(L,S)$ are empty. When $\varnothing \ne {\mathrm{AR}}_{\supseteq L_0 ,\supseteq R_0}({L,S})\subseteq \mathrm{AR}({L}, {S})$, the cardinality of ${\mathrm{AR}}({L}, {S})$ might still be too large and still has many redundant rules as can be seen in the following example.

Example 1

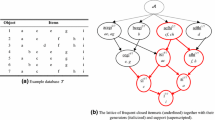
(Illustrating some disadvantages of PP-MAR-MinSC-2). The rest of this paper considers database ${\mathcal {T}}$ shown in Fig. 1a. For the minimum support threshold $s_0= 0.28$, Charm-L [37] and MinimalGenerators [36] are used to mine a lattice of all closed frequent itemsets and their generators. The result is shown in Fig. 1b. Let us choose the maximum support threshold $s_1= 0.5$ and the minimum and maximum confidence thresholds ${c}_0 = 0.4$ and ${c}_1$ = 0.9, respectively.

Fig. 1

a Example dataset and b the corresponding lattice of closed itemsets

• (a) Let us consider the constraints $L_0$= c and $R_0 = {f}$. The PP-MAR-MinSC-2 algorithm first generates $\vert {\mathrm{ARS}}({s}_{{0}},{s}_{{1}} ,{c}_{{0}},{c}_{{1}})\vert$ = 134 rules. But after testing them on constraints ${L}_{0}$ and ${R}_{0}$, we obtain ${\mathrm{AR}}_{\supseteq L_0, \supseteq R_0} (L,S) =\varnothing$ given any rule class of ${\mathrm{NFCS}}({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}} )$ for the 15 classes. Thus, ${\mathrm{ARS}}_{\supseteq L_0 ,\supseteq R_0 } ({s}_0 ,{s}_{{1}},{c}_{{0}} ,{c}_{{1}}) = \varnothing$.

• (b) For another set of constraints $L_0= {h}$ and $R_0 = {b}$, by using PP-MAR-MinSC-2 to generate 134 rules and to then check them on the constraints, we obtain $\vert {\mathrm{ARS}}_{\supseteq L_0 ,\supseteq R_0} ({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}} \vert =19$ rules of 4 rule classes (L, S) of ${\mathrm{NFCS}}({s}_{{0}}, {s}_{{1}}, {c}_{{0}}, {c}_{{1}})$, (egh, bcegh), (h,bcegh), (fh,bfh) and (h,bh). The algorithm generates $\vert {\mathrm{ARS}}({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}}) \backslash {\mathrm{AR}}_{\supseteq L_0 ,\supseteq R_0 } ({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}})\vert =115$ redundant candidate rules corresponding to $\vert {\mathrm{NFCS}}({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}})\vert -4$ = 11 rule classes (L, S) of ${\mathrm{NFCS}}({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}})$ so that $\mathrm{AR}_{\supseteq L_0 ,\supseteq R_0 } (L,S) = \varnothing$. Consider the class $( {bc, bcegh}) \in {\mathrm{NFCS}}({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}})$, there are 21 candidate rules in $\mathrm{AR}({bc, bcegh})$ enumerated by PP-MAR-MinSC-2. However, after they are tested on the conditions $L_0 \subseteq$ $L'$ and $R_0 \subseteq$ $R'$, the solution subset is empty, ${\mathrm{AR}}_{\supseteq L_0 ,\supseteq R_0} (bc,bcegh)= \varnothing$.

• (c) For $L_0= {f}$ and $R_0$ = h, the algorithm PP-MAR-MinSC-2 generates $\vert {\mathrm{ARS}}({s}_{{0}},{s}_{{1}} ,{c}_{{0}},{c}_{{1}} )\vert = 134$ rules of 15 pairs (L, S)$\in {\mathrm{NFCS}}({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}} )$, but there are only 4 rules corresponding to two pairs, (L ¹ = fh, S ¹ = efgh) and (L ² = fh, S ² = bfh) $\in {\mathrm{NFCS}}({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}})$ so that $\mathrm{AR}_{\supseteq L_0,\supseteq R_0} (L^i ,S^i)\ne \varnothing , i=1, 2$. For (L ¹ = fh, S ¹ = efgh), it is noted that the number of candidate rules generated in ${\mathrm{AR}}({L}^{1} ,{S}^{1})$ is 9. But there are only 3 rules satisfying the constraints $L_{0}$ and $R_{0}, {\mathrm{AR}}_{\supseteq L_0 ,\supseteq R_0}({L}^{1} ,{S}^{1} )$ = {f $\rightarrow$ eh, f $\rightarrow$ egh, f $\rightarrow$ gh}. Thus, there exist 6 redundant candidate rules generated in ${\mathrm{AR}}({L}^{1},{S}^{1}) \backslash \mathrm{AR}_{\supseteq {L}_0, \supseteq {R}_0} ({L}^{1} ,{S}^{1})$.

With the aim of overcoming these disadvantages, we need to find the necessary conditions for the constraint set

and the pairs $(L, S)$ so that ${\mathrm{ARS}}_{\supseteq {L}_{{0}} ,\supseteq {R}_{{0}}} ({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}})$ is not empty. As such, we have another representation ${\mathrm{AR}}_{\supseteq {L}_{{0}} ,\supseteq {R}_{{0}}}^{+} (L,S)$ of ${\mathrm{AR}}_{\supseteq {L}_{{0}} ,\supseteq {R}_{{0}}} (L,S)$ and then obtain a better partition of ${\mathrm{ARS}}_{\supseteq {L}_{{0}} ,\supseteq {R}_{{0}}}({s}_{{0}} ,{s}_{{1}} ,{c}_{{0}} ,{c}_{{1}})$.

3.1.2 Necessary conditions for the non-emptiness of ${\mathrm{ARS}}_{\supseteq {L}_{{0}}, \supseteq {R}_{{0}}}({s}_{{0}}, {s}_{{1}} ,{c}_{{0}} ,{c}_{{1}})$ and ${\mathrm{AR}}_{\supseteq {L}_{{0}}, \supseteq {R}_{{0}}} (L,S)$

Before presenting necessary conditions so that $\hbox {ARS}_{\supseteq {L}_0, \supseteq {R}_0} ({s}_0 ,{s}_1 ,{c}_0 ,{c}_1)$ and ${AR}_{{L}_0 ,{R}_0} ({L}, {S})$ are not empty, let us use some additional notations as follows. Assign that

• $.S_0^*\equiv L_0 +R_0 , C_0 \equiv L_0 , C_1 \equiv {\mathcal {A}}\backslash R_0 , \quad s_0^*\equiv \mathrm{max}(s_0 ; c_0 .\hbox {supp}(C_1)), s_1^*\equiv \mathrm{min}(s_1 ; c_1 .\hbox {supp}(L_0));$

• $.{{S}}'\equiv {{L}}' + {{R}}', {S} \equiv {h}({{S}}'),\quad \mathrm{FCS}_{\supseteq S_0^*} ({s_0^*, s_1^*}) \equiv \{{S}\in \mathrm{FCS}( {s_0^*,s_1^*}) \vert {S} \supseteq S_0^*\};$

• $.s_{0}^{\prime } \equiv s_{0}^{\prime } ({S})\equiv \hbox {supp}(S)/c_1,\quad s_1^{\prime } \equiv s_1^{\prime } ({S}) \equiv \mathrm{min}(1;\hbox {supp}(S)/c_0 ),$ ${L} \equiv {h}({{L}}'), \quad L_{C_1} \equiv {L}\cap C_1 = {L}\backslash R_0, G_{C_1} (L)\equiv \{L_i \in {{G}}({L})\quad \vert L_i \subseteq C_1\}, \mathrm{FCS}_{C_0 \subseteq C_1} ( {s_0^{\prime } ,s_1^{\prime }})\equiv \{L_{C_1} \equiv {L} \cap C_1 \vert {L}\in \mathrm{FCS}({s_0^{\prime }, s_1^{\prime }}), L\subseteq C_0, G_{C_1} (L) \ne \varnothing \}, \mathrm{FS}_{C_0 \subseteq L_{C1}} \equiv \{{{L}}'\subseteq L_{C_1} \vert C_0 \subseteq {{L}}', {{L}}'\ne \varnothing , {h}({{L}}') = {h}(L_{C_1})\};$

• $.R_0^*\equiv R_0, R_1^*\equiv R_1^*({{L}}')\equiv {S} \backslash {{L}}', \mathrm{FS}(S \backslash L')_{L^{\prime }, R_0^*\subseteq R_1^*} \equiv \{{{R}}' \supseteq R_0^*\vert \varnothing \ne {{R}}'\subseteq R_1^*, {h}({{L}}' + {{R}}') = {S}\};$

• $.\mathrm{NFCS}_{\supseteq L_0, \supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1 ) \equiv \{{(L,S)} \in {\mathcal {CS}}^{2} \vert {S} \in \mathrm{FCS}_{\supseteq S_0^*} ({s_0^*,s_1^*}), \varnothing \ne {L}\subseteq {S}, L_{C_1} \in \mathrm{FCS}_{C_0 \subseteq C_1} ({s_0^{\prime } ,s_1^{\prime }})\}.$

Then, $\forall$(L, S) $\in \mathrm{NFCS}_{\supseteq L_0,\supseteq R_0 } ( {s_0 ,s_1 ,c_0 ,c_1})$, we have

$$\begin{aligned}&\!\!\!\mathrm{AR}_{\supseteq L_0, R_0}^{+} (L,S)\\&\quad \equiv \{{r}:{{L}}'\rightarrow {{R}}'\vert {{L}}' \in \mathrm{FS}_{C_0 \subseteq L_{C1} }, {{R}}' \in \mathrm{FS}(S\backslash L')_{L^{\prime }, R_0^*\subseteq R_1^*} \}. \end{aligned}$$

We obtain the following proposition.

Proposition 2

(Necessary conditions for the non-emptiness of $\mathrm{ARS}_{\supseteq L_0, \supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1 )$ and $\mathrm{AR}_{\supseteq L_0, \supseteq R_0} (L,S)$, and an another representation of $\mathrm{AR}_{\supseteq L_0, \supseteq R_0} (L,S))$.

• (a) (Necessary conditions for $\mathrm{ARS}_{\supseteq L_0, \supseteq R_0} (s_0, s_1, c_0, c_1) \ne \varnothing )$

  If $r:L'\rightarrow$ R$'\in \mathrm{ARS}_{\supseteq L_0,\supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1)\ne \varnothing$, then

  $$\begin{aligned}&(L, S)\in \mathrm{NFCS}(s_0 ,s_1 ,c_0 ,c_1 ), \quad {r}\in \mathrm{AR}_{\supseteq L_0,\supseteq R_0 } (L,S)\\&\quad \ne \varnothing ,\quad {\mathrm{where} {L} = {h}({L}'),\quad {S} = {h}({L}'+ {R}')} \end{aligned}$$

  and the following necessary conditions are satisfied:

  $$\begin{aligned} L_0 \cap R_0&= \varnothing , s_0^*\le s_1^*, {{\mathrm{supp}}}(S_0^*)\\&\ge s_0^*, {{\mathrm{supp}}}({\mathcal {A}}) \le s_1^*. \qquad (H_{1}) \end{aligned}$$

  Thus, from now on, it is always assumed that (H₁) is satisfied.

• (b) (Necessary conditions for $\mathrm{AR}_{\supseteq L_0,\supseteq R_0} (L,S)\ne \varnothing )$. For each pair (L, S) $\in \mathrm{NFCS}({s}_0, {s}_1, {c}_0, {c}_1)$, then for any rule $r:L'\rightarrow$ R$'\in \mathrm{AR}_{\supseteq L_0 ,\supseteq R_0 } (L,S) \ne \varnothing$, the following necessary conditions are satisfied:

  $$\begin{aligned} S&\in \mathrm{FCS}_{S\supseteq S_0^*} ( {s_0^*,s_1^*}), \quad L_{C_1 } \in \mathrm{FCS}_{C_0 \subseteq C_1 } ( {s_0^{\prime }, s_1^{\prime }}),\\&{{L}}' \in \mathrm{FS}_{C_0 \subseteq L_{C1}},\quad {{R}}' \in \mathrm{FS}(S\backslash L')_{L^{\prime },R_0^*\subseteq R_1^*}. \end{aligned}$$

  Thus, $(L, S)\in \mathrm{NFCS}_{\supseteq L_0,\supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1 )\ne \varnothing$ and $\mathrm{AR}_{\supseteq L_0 ,\supseteq R_0 } (L,S)\subseteq \mathrm{AR}_{\supseteq L_0 ,\supseteq R_0 }^+ (L,S)$.

  And we have the result, $\mathrm{AR}_{\supseteq L_0 ,\supseteq R_0 } (L,S)\subseteq \mathrm{ARS}_{\supseteq L_0 ,\supseteq R_0} ({s_0 ,s_1 ,c_0 ,c_1})$.

• (c) (Another representation of $\mathrm{AR}_{\supseteq L_0 ,\supseteq R_0 } (L,S))$. For each $(L, S) \in \mathrm{NFCS}_{\supseteq L_0 ,\supseteq R_0 } (s_0 ,s_1 ,c_0 ,c_1 )\ne \varnothing$, then $\mathrm{FS}_{C_0 \subseteq L_{C_1 } } \ne \varnothing$ and

  $$\begin{aligned} \mathrm{AR}_{\supseteq L_0 ,\supseteq R_0 }^+ (L,S)= \mathrm{AR}_{\supseteq L_0 ,\supseteq R_0 } (L,S). \end{aligned}$$

Corollary 1

(Necessary and sufficient conditions for the non-emptiness of $\mathrm{ARS}_{\supseteq L_0 ,\supseteq R_0 } (s_0 ,s_1 ,c_0 ,c_1 ))$.

• (a) If one or more conditions in $(H_{1})$ are not satisfied, then $\mathrm{ARS}_{\supseteq L_0 ,\supseteq R_0 } (s_0 ,s_1 ,c_0 ,c_1 )=\varnothing$ .

• (b) $r:L'\rightarrow$R$'\in \mathrm{ARS}_{\supseteq L_0 ,\supseteq R_0 } ( {s_0 ,s_1 ,c_0 ,c_1 })\ne \varnothing \Leftrightarrow$ there exist $(L, S)\in \mathrm{NFCS}_{\supseteq L_0 ,\supseteq R_0 } (s_0 ,s_1 ,c_0 ,c_1 )$, $L'\in \mathrm{FS}_{C_0 \subseteq L_{C1} }$, R$'\in \mathrm{FS}(S\backslash L')_{L',R_0^*\subseteq R_1^*}$ and $r:L'\rightarrow$R$'\in \mathrm{AR}_{\supseteq L_0 ,\supseteq R_0 }^+ (L,S)\ne \varnothing$.

Proof

The assertion (a) and the dimension “$\Rightarrow$” of (b) are the obvious consequences of Proposition 2(a) and (b). The reverse dimension “$\Leftarrow$” of (b) is derived from $\mathrm{AR}_{\supseteq L_0 ,\supseteq R_0 }^+ (L,S)\subseteq \mathrm{AR}_{\supseteq L_0 ,\supseteq R_0 } (L,S) \subseteq \mathrm{ARS}_{\supseteq L_0 ,\supseteq R_0 } ({s_0 ,s_1 ,c_0 ,c_1 })$. $\square$

From Proposition 2 and Corollary 1, we have the following smooth partition of the constrained rule set $\mathrm{ARS}_{ \supseteq L_0, \supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1 ).$

3.1.3 Smooth partition of association rule set with minimum single constraints

Theorem 1

(Smooth partition of constrained rule set) Assume that the conditions of (H$_{1})$ are satisfied, then we have:

$$\begin{aligned}&\!\!\!\mathrm{ARS}_{\supseteq L_0 ,\supseteq R_0 } (s_0 ,s_1 ,c_0 ,c_1 )\\&\quad = \sum \nolimits _{(L,S) \in \mathrm{NFCS}_{\supseteq L_0 ,\supseteq R_0 } (s_0 ,s_1 ,c_0 ,c_1 )} \mathrm{AR}_{\supseteq L_0 ,\supseteq R_0 }^+ (L,S). \end{aligned}$$

This partition is the theoretical basis for the parallel algorithms that independently mine each rule class $\varvec{AR}_{\supseteq L_0 ,\supseteq R_0 }^+ (\varvec{L,S})$ in the distributed environments. This is an interesting feature when we apply the suitable equivalence relations of mathematics into computer science, a simple yet efficient application of the principle “divide and conquer”.

Example 2

(Illustrating the emptiness of $\mathrm{ARS}_{\supseteq L_0 ,\supseteq R_0 } (s_0 ,s_1 ,c_0 ,c_1 )$ or $\mathrm{AR}_{\supseteq L_0 ,\supseteq R_0 } (L,S)$ when one of the necessary conditions in (H$_{1}$ ) is not satisfied or (L, S) $\notin \mathrm{NFCS}_{\supseteq L_0 ,\supseteq R_0 } (s_0 ,s_1 ,c_0 ,c_1 ))$.

• (a) If one of the necessary conditions in (H$_{1})$ is not satisfied, we immediately obtain $\mathrm{ARS}_{\supseteq L_0 ,\supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1 )= \varnothing$. For instant, in Example 1a, we have $S_0^*$ = cf, $C_1$ = abcdegh, supp($S_0^*)$ = 1/7 $\thickapprox$ 0.14 and $s_{0}^*$ = 0.28, the necessary condition supp(${S}_{0}^{*}) \ge {s}_{0}^{*}$ is not satisfied. Thus, $\mathrm{ARS}_{\supseteq L_0 ,\supseteq R_0 } (s_0 ,s_1 ,c_0 ,c_1 ) = \varnothing$ and we do not need to generate $\vert \mathrm{ARS}(0.28, 0.5, 0.4, 0.9)\vert = 134$ candidate rules in $\mathrm{ARS}(s_0 ,s_1 ,c_0 ,c_1 )$, if only to discard them all afterwards. Another example, for $L_0 =$ d, $R_0 =$ g, then $C_0 =$d, $C_1 =$ abcdefh, $s_0^*= 0.28$, $s_1^*= 0.26$, we find that the necessary condition $s_0^*\le s_1^*$ is not satisfied. Thus, $\mathrm{ARS}_{\supseteq L_0 ,\supseteq R_0 } (s_0 ,s_1 ,c_0 ,c_1 ) = \varnothing$ and 134 redundant candidate rules are not generated.

• (b) If (L, S)$\in \mathrm{NFCS}(s_0 ,s_1 ,c_0 ,c_1 ) \backslash \mathrm{NFCS}_{\supseteq L_0 ,\supseteq R_0 } (s_0 ,s_1 ,c_0 ,c_1 )$, the result $\mathrm{AR}_{\supseteq L_0 ,\supseteq R_0} (L,S) = \varnothing$ is derived immediately and the pair (L, S) is discarded. In Example 1(b), consider the class $({L=\mathrm{bc}, S=\mathrm{bcegh}})$, we have $S_0^*$ = bh, $C_0$ = h, $C_1$ = acdefgh, ${\mathcal {G}}$(L)={c} and ($G_{C_1 } (L)\ne \varnothing$ and $C_0\nsubseteq L$). The condition $L_{C_1 } \in \mathrm{FCS}_{C_0 \subseteq C_1 } ( {s_0^{\prime }, s_1^{\prime }})$ is not satisfied, so (bc,bcegh) $\notin \mathrm{NFCS}_{\supseteq L_0 ,\supseteq R_0 } (s_0 ,s_1 ,c_0, c_1 )$. Thus, we have $\mathrm{AR}_{\supseteq L_0 ,\supseteq R_0} (L,S)=\varnothing$. Moreover, we also have 10 other redundant candidate classes ($L'$, $S'$) $\in \mathrm{NFCS}(s_0 ,s_1 ,c_0 ,c_1)\backslash \mathrm{NFCS}_{\supseteq L_0 ,\supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1 )$ so that $\mathrm{AR}_{\supseteq L_0, \supseteq R_0} ({L', S'})= \varnothing$.

We realize that the number of candidate classes (L, S) in $\mathrm{NFCS}( {s_0 ,s_1 ,c_0 ,c_1 }) (\supseteq \mathrm{NFCS}_{\supseteq L_0 ,\supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1 ))$ can still be quite large and there remain many redundant candidates that do not satisfy the constraints.

The algorithm MFCS_FromLattice (${\mathcal {LCG}}^{S}$, $C_0, C_1, s_0^{\prime }, s_1^{\prime })$ shown in Fig. 2 aims to find frequent closed itemsets $\mathrm{FCS}_{C_0 \subseteq C_1 } ( {s_0^{\prime }, s_1^{\prime }})$ satisfying the constraints from the lattice ${\mathcal {LCG}}^{S}$ (the restricted sub-lattice of ${\mathcal {LCG}}$ with the root node S). And, especially, we have $\mathrm{FCS}_{\supseteq S_0^*} ({s_0^*,s_1^*})$ = MFCS_FromLattice(${\mathcal {LCG}}, S_0^*, {\mathcal {A}}, s_0^*, s_1^*)$.

It is important to note that, from the Hass diagram on the lattice $\mathcal {LCG}$, if the concepts of positive and negative borders [23], concerning the anti-monotonic and monotonic properties of the support and item constraints, are added to the algorithm, then the sub-lattices whose closed itemsets satisfy the corresponding constraints will be generated quickly. For instance, with the monotonic property (supp(L) $\le {s}_1^{\prime }$ and L $\supseteq {C}_0 )^{({M})}$, we illustrate the creation of negative border in the algorithm as follows. At line 3, with the movement from up to down in the lattice, starting at node S, when considering a node N for which one of the conditions in $^{({M})}$ has been violated, we eliminate all sub-branches of N and supplement N into the negative border of the sub-lattice containing the class $\mathrm{FCS}_{C_0 \subseteq C_1 } ( {s_0^{\prime } ,s_1^{\prime }})$. More specifically, in example 1, we have S = bfg, supp(S) = 2/7, $s_0$ = 2/7, $s_1$ = 1, $c_0$ = 3/4, $c_1$ = 1, and $C_0 = L_0 = e$ in the sub-lattice ${\mathcal {LCG}}^{S}$. S has two direct sub-nodes $L\in${bh, fh}; consider the sub-node $L=bh$, then $s(L)=4/7$ $> s_1^{\prime }$ = min(1; (2/7)/(3/4))=8/21, thus, we eliminate all sub-branches that started at $L$; consider the sub-node $L=$fh, then $C_0 \nsubseteq$ $L$; therefore, we also do this. Hence, $\mathrm{FCS}_{C_0 \subseteq C_1} ( {s_0^{\prime } ,s_1^{\prime } })$ = {bfg} (only one frequent closed itemset S).

Fig. 2

MFCS_FromLattice algorithm

For $\forall$($L, S$)$\in \mathrm{NFCS}_{\supseteq L_0, \supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1 )$, each rule $r:L'\rightarrow$ $R'$ in the rule class $\mathrm{AR}_{\supseteq L_0, \supseteq R_0}^+ (L,S) = \{r:L'\rightarrow R'\vert L'\in \mathrm{FS}_{C_0 \subseteq L_{C1}}$, $R'\subseteq \mathrm{FS}(S\backslash L')_{L', R_0^*\subseteq R_1^*}\}$ has the left-hand and right-hand sides that do not have an explicit representation, and mining them might still generate many redundant candidates.

3.2 Distinctly generating all association rules in each equivalence class $\mathrm{AR}_{\supseteq L_0, \supseteq R_0}^+ (L,S)$

To completely eliminate the generation of duplicate candidates for the solution, based on each class $(L, S) \in \mathrm{NFCS}_{\supseteq L_0, \supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1 )$ and the generators ${\mathcal {G}}$(L), ${\mathcal {G}}$(S), we will propose an explicitly unique representation of rules in $\mathrm{AR}_{\supseteq L_0, \supseteq R_0}^+ (L,S)$. It will also demonstrate how to completely and distinctly generate all rules in each class.

For that, first of all, we need to show a structure and a unique representation for an extended class of frequent itemsets that are restricted by X and contain an item constraint. Thereby, explicitly unique representations and structures of the right-hand side $R'\in \mathrm{FS}(S\backslash L')_{L', R_0^*\subseteq R_1^*}$ and the left-hand side $L'\in \mathrm{FS}_{C_0 \subseteq L_{C1}}$ of rules $r: L' \rightarrow R'$ in each equivalence class $\mathrm{AR}_{\supseteq L_0, \supseteq R_0} ( {L,S})$ are derived.

3.2.1 The explicitly unique representation and the structure of an extended class

To briefly present the results regarding the representation of the rule sides, we first consider a fairly general representation of frequent sub-items of Y that are restricted on X with minimum single constraint.

Let $Y$, $X$, $Z_0 \subseteq {\mathcal {A}}$: $Y$ $\ne \varnothing$, $Y$ $\cap$ $X$ = $\varnothing$, $Z_0 \subseteq$ $Y$, we denote $\mathrm{FS}(Y)_{X, \supseteq Z_0} \equiv$ {$R'\supseteq Z_0 \vert \varnothing \ne$ $R'\subseteq$ $Y, h(X+R') = h(X+Y)\}$,

$R_{\mathrm{min}} \equiv$ Minimal{$R_k \equiv S_k \backslash ({X}+Z_0)$, $S_k \in G({X}+{Y})$}, $R_U^k \!\equiv \! \mathop {\bigcup }\nolimits _{R_j \in R_{\mathrm{min}}, {j} \le {k}} R_j$,    and $R_{U,k} \!\equiv \! {\left\{ \begin{array}{ll} R_U^{k-1} \backslash R_k, &{}\! if\,k \!\ge \! 1\\ \varnothing , &{}\! if\,k\!=\!0\\ \end{array}\right. }$, where $R_k \in R_{\mathrm{min}}$ and $R_{-,k} \equiv {Y} \backslash (Z_0 +R_U^k)$.

Note that if $Y$ = $\varnothing$ or $X$ $\cap Z_0 \ne \varnothing$, then $\mathrm{FS}(Y)_{X, \supseteq Z_0}\ne \varnothing$. Otherwise, let us set

$$\begin{aligned}&\mathrm{FS}^*(Y)_{X, \supseteq Z_0} \equiv \{{{R}}' \equiv Z_0 + R_k + R_k^{\prime } +R_k^{\sim } \vert R_k \in R_{\mathrm{min}},\\&\quad R_k^{\prime } \subseteq R_{U,k}, R_k^\sim \subseteq R_{-,k}, (R_j {\not \!\!{\subset }} R_k +R_k^{\prime }, \forall R_j \in R_{\mathrm{min}}\!:\\&\quad 1 \le j < k)^{(*)}, {{R}}' \ne \varnothing \}. \end{aligned}$$

Proposition 3

(The unique representation of sets in $\mathrm{FS}(Y)_{X, \supseteq Z_0})$ $\forall$ $X$, $Y$, $Z_0 \subseteq {\mathcal {A}}$: $Y$ $\ne \varnothing$, $Y$ $\cap$ $X=\varnothing$, $Z_0 \cap X = \varnothing , Z_0 \subseteq Y$, then

• (a) The elements of $\mathrm{FS}^*(Y)_{X, \supseteq Z_0}$ are generated distinctly.

• (b) $\mathrm{FS}(Y)_{X,\supseteq Z_0} = \mathrm{FS}^*(Y)_{X, \supseteq Z_0}.$

• (c) $\mathrm{FS}^*(Y)_{X,\supseteq Z_0} \ne \varnothing .$ (H$_{2}$)

Remark 2

See in ”Appendix”.

For special values of $Y, X$ and $Z_0$ in $\mathrm{FS}(Y)_{X, \supseteq Z_0}$, we obtain the structures of $\mathrm{FS}_{C_0 \subseteq L_{C1}}$ and $\mathrm{FS}(S\backslash L')_{L', R_0^*\subseteq R_1^*}$ as they are presented in the following section.

3.2.2 Structure and unique representation of sets in $\mathrm{FS}_{C_0 \subseteq L_{C1}}$ and $\mathrm{FS}(S\backslash L')_{L', R_0^*\subseteq R_1^*}$

Assume that the class (L, S) $\in \mathrm{NFCS}_{\supseteq L_0, \supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1 )$, S $\in \mathrm{FCS}_{\supseteq S_0^*} ({s_0^*, s_1^*})$, $L_{C_1} \in \mathrm{FCS}_{C_0 \subseteq C_1} ({s_0^{\prime } ,s_1^{\prime }})$ and $L'$ $\in \mathrm{FS}_{C_0 \subseteq L_{C1} }$, since $L_{C_1} \in \mathrm{FCS}_{C_0 \subseteq C_1 } ( {s_0^{\prime } ,s_1^{\prime } })$, we have $G_{C_1 }$(L) $\ne \varnothing$ and $\exists L_i \in G$(L) so that $\varnothing \subset L_i \subseteq L_{C_1}$ and $L_{C_1} \ne \varnothing$.

Lemma 1

$\forall$ L, $C_1 \subseteq {\mathcal {A}}$, if $L_{C_1} \equiv$ L $\cap C_1 \ne \varnothing$ and $G_{C_1} (L)\ne \varnothing$, then $G(L_{C_1 } )=G_{C_1 } (L)$.

Proof

• .“$\Leftarrow$”: $\forall L_k \in G_{C_1} (L)$: $L_k \in G(L), L_k \subseteq C_1$, then $L_k \subseteq L_{C_1} \subseteq$ L, L $= h(L_k) = h$($L_{C_1}$), thus $L_k \in G(L_{C_1})$.

• .“$\Rightarrow$”: Otherwise, $\forall L_k \in G(L_{C_1})$, then $L_k \subseteq L_{C_1 } \subseteq C_1$, $h(L_k$) = $h(L_{C_1}$), since $G_{C_1 }$(L)$\ne \varnothing$, so $\exists L_i \in G(L)$: $L_i \subseteq C_1$, $L_i \subseteq L_{C_1} \subseteq$ L and L = $h(L_i$) = $h(L_{C_1}$) = $h(L_k$), i.e., $L_k \in G(L)$ and $L_k \subseteq C_1$ or $L_k \in G_{C_1} (L)$.

$\square$

• (a) When Y $\equiv L_{C_1}$, X $\equiv \varnothing$ and $Z_0 \equiv C_0$. As $L_{C_1 } \in \mathrm{FCS}_{C_0 \subseteq C_1 } ( {s_0^{\prime } ,s_1^{\prime }})$, $C_0 \subseteq C_1$, then L $\supseteq C_0, C_0 \subseteq L_{C_1}$, and $L_{C_1}\ne \varnothing$. We have:

  $$\begin{aligned}&\mathrm{FS}(L_{C_1})_{\varnothing , \supseteq C_0} = \{{{L}}' \supseteq C_0 \vert \varnothing \ne {{L}}' \subseteq L_{C_1}, {{h}}({{L}}') \\&\quad = {h}(L_{C_1})\}\equiv \mathrm{FS}_{C_0 \subseteq L_{C1}}. \end{aligned}$$

  Based on the representation of $R_{\mathrm{min}}$ in $\mathrm{FS}^*(Y)_{X,\supseteq Z_0}$ and Lemma 1, we set $K_{\mathrm{min}} \equiv$ Minimal {$K_i \equiv L_i \backslash C_0$, $L_i \in G_{C_1}$(L)}, $K_U^i \equiv \mathop {\bigcup }\nolimits _{K_k \in K_{\mathrm{min}}, {k} \le {i}} K_k$, $K_{U,i} \equiv \small {\left\{ \begin{array}{ll} K_U^{i-1} \backslash K_i, &{} if\,i \le 1\\ \varnothing , &{} if\,i=0\\ \end{array}\right. }$ and $K_{-,i} \equiv L_{C_1} \backslash (C_0+K_U^i)$, and obtain the result as follows.

  $$\begin{aligned}&\mathrm{FS}_{C_0 \subseteq L_{C1}}^*\equiv \{{{L}}'\equiv C_0 + K_i +K_i^\prime +K_i^\sim \vert K_i \in K_{\mathrm{min}},\nonumber \\&\quad K_i^\prime \subseteq K_{U,i}, K_i^\sim \subseteq K_{-,i}\hbox { and }(K_k \not \!\!{\subset } K_i + K_i^\prime , \forall K_k\nonumber \\&\quad \in K_{\mathrm{min}}: 1 \le k<i)^{(**)}, {{L}}'\ne \varnothing \}. \end{aligned}$$

  (1)

  Since $L_{C_1}\ne \varnothing$ and Proposition 3(c), we have $\mathrm{FS}_{C_0\subseteq L_{C1}}^* \ne \varnothing$.

• (b) When Y$\equiv {R}_1^{*}$ $= {S}{\backslash }L'$, X $\equiv$ $L'$, $Z_0 \equiv {R}_0^{*} = R_0$, and assume that ${S} \backslash L'$ $\ne \varnothing$. Since S $\in \mathrm{FCS}_{\supseteq S_0^*} ({s_0^*, s_1^*})$ and $L'$ $\in \mathrm{FS}_{C_0 \subseteq L_{C1}}$, then S $\supseteq {S}_0^{*} \supseteq R_0$, $L'$ $\subseteq L_{C_1} \subseteq C_1 \equiv {\mathcal {A}}\backslash R_0$ and $R_0 \subseteq$ ${S}\backslash L'$. We have

  $$\begin{aligned}&\mathrm{FS}(S\backslash L')_{L', \supseteq R_0^*} \equiv \mathrm{FS}(S \backslash L')_{L', R_0^*\subseteq R_1^*} \nonumber \\&\quad =\{{{R}}' \supseteq {R}_0^{*}\vert \varnothing \ne {{R}}' \subseteq {R}_1^{*}, {{h}}({{L}}'+{{R}}') = S\}. \end{aligned}$$

  We assign $R_{\mathrm{min}} \equiv$ Minimal $\{R_k \equiv S_k \backslash$ ($L'$+$R_0^*), S_k \in G (S)\}, R_U^k \equiv \mathop {\bigcup }\nolimits _{R_j \in R_{\mathrm{min}}, {j} \le {k}} R_j$ and $R_{U,k} \equiv {\left\{ \begin{array}{ll} R_U^{k-1} \backslash R_k, &{} if\,k \ge 1\\ \varnothing , &{}if\,k=0\\ \end{array}\right. }$, where $R_k \in R_{\mathrm{min}}$, and $R_{-,k} \equiv { S}\backslash$($L'$+$R_0^*+ R_U^k)$, we derive the following result.

  $$\begin{aligned}&\mathrm{FS}^*(S\backslash L')_{L', R_0^*\subseteq R_1^*} \equiv \{{{R}}' \equiv R_0^*+R_k +R_k^{\prime } + R_k^{\sim } \vert R_k \nonumber \\&\quad \in R_{\mathrm{min}}, R_k^\prime \subseteq R_{U,k}, R_k^\sim \subseteq R_{-,k}, (R_j \not \!\!{\subset } R_k +R_k^\prime , \forall R_j \nonumber \\&\quad \in R_{\mathrm{min}}: 1 \le j<k)^{(*)}, R'\ne \varnothing \} \end{aligned}$$

  (2)

  As S $\backslash$L$'\ne \varnothing$ and Proposition 3(c), we obtain $\mathrm{FS}^* (S\backslash L')_{L', R_0^*\subseteq R_1^*}\ne \varnothing$.

The general procedure MFS-ExtendedMinSC (mining frequent itemsets—Extended Minimum Single Constraints), shown in Fig. 3, distinctly generate the elements of $\mathrm{FS}^* (Y)_{X, \supseteq Z_0}$:

$$\begin{aligned} \mathrm{FS}^*(Y)_{X, \supseteq Z_0} = \textit{MFS-ExtendedMinSC} ({Y, X}, Z_0, G({X} + {Y})). \end{aligned}$$

When using Remark 2, we add lines 4–10 and 25 to the procedure.

Fig. 3

MFS-ExtendedMinSC algorithm

In each equivalence class, two cases, $\mathrm{FS}_{C_0 \subseteq L_{C1}}^*$ = MFS-ExtendedMinSC ($L_{C1}, \varnothing , C_0, G(L_{C1}))$ and $\mathrm{FS}^* (S\backslash L')_{L', R_0^*\subseteq R_1^*}$ = MFS-ExtendedMinSC(S $\backslash$ $L'$, $L'$, $R_0^*, G(S))$, are to distinctly generate the left-hand sides $L'$ and the right-hand sides $R'$ of constrained rules, respectively. In addition, two cases, $\mathrm{FS}^*(L)$= MFS-ExtendedMinSC(L, $\varnothing$, $\varnothing$, $G(L))$ and $\mathrm{FS}^*(S\backslash L')_{L'}$ = MFS-ExtendedMinSC(S $\backslash$ $L'$, $L'$,$\varnothing , G(S))$, are used to produce the sets $L'$ $\in \mathrm{FS}^*(L)$ and $R'$ $\in \mathrm{FS}^*(S\backslash L')_{L'}$ in each class $\mathrm{AR}({L,S})$ without the item constraints, as the post-processing algorithm PP-MAR-MinSC-2 presented in Sect. 3.1.1.

According to Proposition 3, we have the following result.

Corollary 2

(Uniquely representing and distinctly generating two sides of rules in each equivalence class ${\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0}^{+} ({L,S})$). $\forall \mathrm{(L,S)} \in {\mathrm{NFCS}}_{\supseteq {L}_0 ,\supseteq {R}_0} ({s}_0 ,{s}_1 ,{c}_0 ,{c}_1 )$, then

• (a) The elements of ${\mathrm{FS}}^*({S}\backslash {L}^{\prime })_{{L}^{\prime },{R}_0^*\subseteq {R}_1^*}$ and ${\mathrm{FS}}_{{C0} \subseteq {L}_{{C1}}}^{*}$ are generated distinctly.

• (b) ${\mathrm{FS}}({S}\backslash {L}^{\prime })_{{L}^{\prime },{R}_0^*\subseteq {R}_1^*} = {\mathrm{FS}}^*({S}\backslash {L}^{\prime })_{{L}^{\prime },{R}_0^*\subseteq {R}_1^*}, {\mathrm{FS}}_{{C}_0 \subseteq {L}_{{C}1}} = {\mathrm{FS}}_{{C0} \subseteq {L}_{{C1}}}^{*}$.

• (c) ${\mathrm{FS}}_{{C}_0\subseteq {L}_{{C}1} }^*\ne \varnothing$

• (d) $\forall \mathrm{L}^{\prime } \in {\mathrm{FS}}_{{C}_0\subseteq {L}_{{C}1} }^*$, then ${\mathrm{FS}}^*({S}\backslash {L}^{\prime })_{{L}^{\prime },{R}_0^*\subseteq {R}_1^*}\ne \varnothing \Leftrightarrow \ {S/L^{\prime }}\ne \varnothing$.

3.2.3 Structure and unique representation of rules in ${\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0 }^+ ({L,S})$

For $\forall {(L, S)}\in {\mathrm{NFCS}}_{\supseteq {L}_0 ,\supseteq {R}_0 } ({s}_0 ,{s}_1 ,{c}_0 ,{c}_1 )$, let us denote

$$\begin{aligned}&{\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0}^*({L,S})\equiv \{{r:L^{\prime }\rightarrow R^{\prime }\vert L^{\prime }} \\&\quad \in {\mathrm{FS}}_{{C}_0\subseteq {L}_{{C}1}}^*, {R}^{\prime }\in {\mathrm{FS}}^*({S}\backslash {L}^{\prime })_{{L}^{\prime },{R}_0^*\subseteq {R}_1^*} \}\\&\quad \mathrm{and \, Suff}{\_}{\mathrm{FS}}_{{{C}}_0 \subseteq {{L}}_{{{C}}1}}^{*} ({S}) \equiv \{{L}^{\prime }\in {\mathrm{FS}}_{{C}_0\subseteq {L}_{{C}1} }^{*} \vert {S}\backslash {L}^{\prime } \ne \varnothing \}. \end{aligned}$$

From Corollary 2, we have the following corollary.

Corollary 3

(Necessary and sufficient conditions for the non-emptiness of ${\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0 }^+ ( {{L,S}}$ and its representation). For $\forall {(L, S)} \in {\mathrm{NFCS}}_{\supseteq {L}_0 ,\supseteq {R}_0 } ({s}_0 ,{s}_1 ,{c}_0 ,{c}_1 )$, then

• (a) The rules of ${\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0 }^*({L,S})$ are generated distinctly.

• (b) ${\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0 }^+ ({L,S})= {\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0 }^*({L,S}).$

• (c) ${\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0 }^*({L,S})\ne \varnothing \Leftrightarrow \mathrm{Suff}{\_} {\mathrm{FS}}_{{C}_0\subseteq {L}_{{C}1} }^{*} \mathrm{(S)}\ne \varnothing .$

• (d) ${\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0}^*({{L,S}})= \sum \nolimits _{{L}^{\prime }\in \,{\mathrm{Suff}}\_{\mathrm{FS}}_{{{C}}_0 \subseteq {\mathrm{L}}_{{{C}}1}}^{*} ({S})} \{{r}:{L}^{\prime }{R}^{\prime }:{R}^{\prime } \in {\mathrm{FS}}^*({{S}\backslash {L}^{\prime }})_{{L}^{\prime },{R}_0^*\subseteq {R}_1^*}\}.$

Remark 3

• (a) The result (1) is an improvement from our previous one (see Theorem $2^{(+)}$ in [17]). Since ${K}_{{U,i}}$ (that is used to check the condition ${K}_{i}^{\prime }\subseteq {K}_{{U,i}})$ is smaller than ${K}_{{U},{C}_0 ,{C}_1,{i}}$ and ${K}_{-,{i}}$ is larger than ${K}_{-,{C}_0 ,{C}_1 }$ in $^{(+)}$, checking the condition $^{(**) }$ in (1) is simpler.

• (b) When considering ${\mathrm{FS}}^*({S}\backslash {L}')_{{L}{\prime },{R}_0^*\subseteq {R}_1^*},$ if $S\equiv L\in {G}({L})$, then $\exists !L^{\prime }\equiv \in [L]$ and ${S}\backslash {L}^{\prime }={L}\backslash {L}^{\prime } = \varnothing .$ Thus, ${\mathrm{FS}}^*({L}\backslash {L}^{\prime })_{{L}^{\prime },{R}_0^*\subseteq {R}_1^*} =\varnothing$ and ${\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0 }^*{(L,L)}=\varnothing .$ Hence, if $L\equiv S$, we always assume that $L\notin {G}({L}).$

The algorithm MAR-MinSC-OneClass, shown in Fig. 4, distinctly generates all constrained rules in each class ${\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0 }^*({L,S})$ based on each pair ${(L, S)}\in {\mathrm{NFCS}}_{\supseteq {L}_0 ,\supseteq {R}_0} ({s}_0 ,{s}_1 ,{c}_0 ,c_1)$.

Fig. 4

MAR-MinSC-OneClass algorithm

Fig. 5

MAR-MinSC algorithm

Example 3

Illustrating the advantages of the algorithm MAR-MinSC-OneClass for distinctly generating rules in each equivalence class ${\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0 }^*({L,S}))$.

• (a) For the constraints ${L}_0, {R}_0$ in Example 1(b), we consider the rule class $(L, S) = \mathrm{(egh, bcegh)} \in {\mathcal {NFCS}}({s}_0 ,{s}_1, {c}_0, {c}_1 ),{\mathcal {G}}\mathrm{(L)=\{e,g\}}$ and ${\mathcal {G}}(S) = \mathrm{\{be, bg, ce, cg, ch\}}.$ We have ${S}_0^*= \mathrm{bh}, {C}_0 = {h}, {C}_1 = \mathrm{acdefgh}, {S}\supseteq {S}_0^*,{s}_0^*=0.28, {s}_1^*=0.5, {s}_0^*\le \, \mathrm{supp}(S) = 2/7\le {s}_1^*$. Thus, ${S} {\mathrm{FCS}}_{\supseteq {s}_0^*} ( {{s}_0^*,{s}_1^*})$. On the other hand, since ${L}\supseteq {C}_0$ and $\exists \mathrm{e}\in {\mathcal {G}}{(L)}$ so that ${e}\subseteq {C}_1$, then ${s}_0^{\prime } =0.32, {s}_1^{\prime } =0.71$ and ${s}_0^{\prime } \le \mathrm{supp}(L)=4/7 \le {s}_1^{\prime }$. Therefore, ${L}_{{C}_1} = \mathrm{egh}\in {\mathrm{FCS}}_{{C}_0 \subseteq {C}_1 } ( {{s}_0^{\prime } ,{s}_1^{\prime } })$ and ${G}_{{C}_1 } ({L})=\{\mathrm{e,g}\}.$ First is to generate the left-hand sides of rules, ${\mathrm{FS}}_{{C}_0 \subseteq {L}_{{C}1}}^*$. We have the result, ${K}_{\mathrm{min}} =\{{K}_1 = {e}, {K}_2 = {g}\}$. For ${K}_1 = {e}$, since ${K}_{U}^1 ={e}, {K}_{{U},1} =\varnothing$, and ${K}_{-,1} ={g}$, we obtain the left-hand sides: ${h}+{e}+\varnothing +\varnothing$ and ${h}+{e}+\varnothing +{g}$. For ${K}_2 = {g}$, as ${K}_{U}^2 =\mathrm{eg}, {K}_{{U},2} ={e}$, and ${K}_{-,2} =\varnothing$, then, an additional left-hand side is derived, ${h}+{g}+\varnothing +\varnothing$. Note that, without checking the condition ${K}_1\subset g+e$, the left-hand side, $h+g+e+\varnothing ,$ making a duplicate will be generated. Thus, ${\mathrm{FS}}_{{C}_0 \subseteq {L}_{{C}1} }^*\equiv \{\mathrm{he}, {heg}, {hg}\}$. Second is to generate the right-hand sides of rules based on (2) as follows. For ${L}^{\prime }=\mathrm{he}$, since ${S}\backslash {L}^{\prime }=\mathrm{bcg}\ne \varnothing \Leftrightarrow {\mathrm{FS}}^*( {{S}\backslash {L}^{\prime }})_{L^{\prime },R_0^*\subseteq R_1^*}\ne \varnothing$, where ${R}_0^*={b}$ and ${R}_1^*=\mathrm{bcg}$, we have ${R}_{\mathrm{min}} =\{{R}_1 \equiv \varnothing \}, {R}_{U}^1 ={R}_{{U},1} =\varnothing$ and ${R}_{-,1} =\{\mathrm{bcegh}\}\backslash \{\mathrm{he+b}\}=\mathrm{cg}$. Therefore, ${\mathrm{FS}}^*( {{S}\backslash {L}^{\prime }})_{{L}^{\prime },{R}_0^*\subseteq {R}_1^*} \equiv \{{R}^{\prime }={R}_0^*+{R}_i +{R}_i^{\prime } +R^{\prime \prime }\vert \quad {R}_i \in {R}_{\mathrm{min}} , {R}_i^{\prime } \subseteq {R}_{{U},{i}} , R^{\prime \prime }\subseteq R_{-,i}\} = \{\mathrm{b, bc, bg, bcg}\}$ and the constrained rules are derived: $\{\mathrm{he\rightarrow b, he\rightarrow bc, he\rightarrow bg, he\rightarrow bcg}\}$. Similarly, for ${L}^{\prime }=\mathrm{heg}$ and ${L}^{\prime }=\mathrm{gh}$, we obtain the rules $\{\mathrm{heg\rightarrow b, heg\rightarrow bc}\}$ and $\{\mathrm{hg\rightarrow b, hg\rightarrow bc, hg\rightarrow be,} \mathrm{hg\rightarrow bce}\}$, respectively. Finally, using Corollary 3, the rules that satisfy minimum single constraints are found: ${\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0}^*( {{L,S}})= \{\mathrm{he\rightarrow b, he\rightarrow bc, he\rightarrow bg, he}\mathrm{\rightarrow bcg, heg\rightarrow b, heg\rightarrow bc, hg\rightarrow b, hg\rightarrow bc, hg\rightarrow }\mathrm{be, hg\rightarrow bce}\}$.

• (b) For the constraints ${L}_0 , {R}_0$ in Example 1(c), we consider the rule class ${(L = \mathrm{fh}, S = \mathrm{efgh})}$, where ${\mathcal {G}}({L}) = \{{f}\}, {\mathcal {G}}({S}) = \{\mathrm{ef, fg}\}, {C}_0 = {f}, {C}_1 = \mathrm{abcdefg}$ and ${L}_{{C}_1 }= f$. Then, ${\mathrm{FS}}_{{C}_0 \subseteq {L}_{{C}1}}^*=\{f\}$. For $L^{\prime } = {f}$, then $\mathrm{S}\backslash {L}^{\prime } = \mathrm{egh}, {R}_0^*={h}$ and ${R}_1^*=\mathrm{egh}$, we obtain ${R}_{\mathrm{min}} =\{{R}_1 ={e}, {R}_2 ={g}\}$. With ${R}_1 ={e}$, since ${R}_{U}^1 ={e}, {R}_{{U},1} =\varnothing$ and ${R}_{-,1} =\{\mathrm{efgh}\}\backslash \{\mathrm{f+h+e}\}=\mathrm{g}$, the following right-hand sides are derived: $\mathrm{h+e}+\varnothing +\varnothing$ and $\mathrm{h+e}+\varnothing +{g}$. For ${R}_2 ={g}$, as ${R}_{U}^2 =\mathrm{eg}, {R}_{{U},2} = {e}$ and ${R}_{-,1} =\{\mathrm{efgh}\}\backslash \{\mathrm{f+h+eg}\}=\varnothing$, an additional right-hand side is derived, $\mathrm{h+g}+\varnothing +\varnothing$. The subset $h+g+e+\varnothing$ is not generated due to ${K}_1 \subset g+e$. Hence, ${\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0 }^*( {{L,S}}) = \{\mathrm{f\rightarrow he, f\rightarrow heg, f\rightarrow hg}\}$.

It is important to note that MAR-MinSC-OneClass completely and exactly discovers constrained rule set ${\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0 }^* ( {{L,S}})$ without generating any the redundancy of candidate rules as well as the duplication of the solution. Thus, MAR-MinSC-OneClass is much more efficient than PP-MAR-MinSC-2 and PP-MAR-MinSC-1.

3.3 Completely and distinctly generating all association rules in ${\mathrm{ARS}}_{\supseteq {L}_0 ,\supseteq {R}_0} ({s}_0 ,{s}_1 ,{c}_0 ,{c}_1 )$

From Theorem 1 and Proposition 3, we obtain the Theorem 2 below.

Theorem 2

(Generating all rules of ${\mathrm{ARS}}_{\supseteq {L}_0 ,\supseteq {R}_0 } ( {s}_0 ,{s}_1 ,{c}_0 ,{c}_1 )$ completely and distinctly) Assume that ($\mathrm{H}_{1})$ is satisfied, we derive the result

$$\begin{aligned}&{\mathrm{ARS}}_{\supseteq {L}_0 ,\supseteq {R}_0 } ({s}_0 ,{s}_1 ,{c}_0 ,{c}_1 )\\&\quad = \mathop \sum \nolimits _{({L,S})\in {\mathrm{NFCS}}_{\supseteq {L}_0 ,\supseteq {R}_0 } ({s}_0 ,{s}_1 ,{c}_0 ,{c}_1 )} {\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0}^*({L,S}), \end{aligned}$$

where ${\mathrm{AR}}_{\supseteq {L}_0 ,\supseteq {R}_0}^*( {{L,S}})=\quad \sum \nolimits _{{L}^{\prime }Suff\_{\mathrm{FS}}_{{C}_0\subseteq {L}_{{C}1} }^*({S})} \{{r}\!:{L}^{\prime } \rightarrow {R}^{\prime }:{R}^{\prime } \in {\mathrm{FS}}^*( {{S}\backslash {L}^{\prime }})_{{L}^{\prime },{R}_0^*{R}_1^*} \}$.

Then, we design an algorithm, named MAR-MinSC, shown in Fig. 5, to distinctly generate all rules in ${\mathrm{ARS}}_{\supseteq {L}_0 ,\supseteq {R}_0 } ({s}_0 ,{s}_1 ,{c}_0 ,{c}_1 )$ without producing any candidate.

Table 1 Dataset characteristics

Fig. 6

Performance of MAR-MinSC, PP-MAR-MinSC-2 and PP-MAR-MinSC-1 on Chess and T10I4D100K

4 Experimental results

We implemented the PP-MAR-MinSC-1, PP-MAR-MinSC-2 and MAR-MinSC algorithms in C# on Windows platforms. Experiments were performed on a PC with an i5-2400 CPU, 3.10 GHz@ 3.09 GHz PC and 3.16 GB of main memory. The source code for Charm-L, MinimalGenerators and dEclat algorithms [6] was converted to C#. Charm-L and MinimalGenerators were used to mine the lattice of the closed itemsets and their generators. dEclat was used to exploit all frequent itemsets. To evaluate the proposed algorithm, we compare its performance to those of PP-MAR-MinSC-2 and PP-MAR-MinSC-1 algorithms. PP-MAR-MinSC-1 includes three phases: (1) executing dEclat to mine frequent itemsets; (2) integrating the constraints satisfying the monotone and anti-monotone properties into Gen-Rules [26] (using Apriori principle [1]) to generate candidate rules; (3) filtering the ones satisfying the remained constraints in a post-processing step. PP-MAR-MinSC-2 also includes three phases as PP-MAR-MinSC-1. But, in phase 2, PP-MAR-MinSC-2 uses MFS-ExtendedMinSC $(\mathrm{L}, \varnothing , \varnothing , {G(L)})$ and MFS-ExtendedMinSC(${S} \backslash {L}^{\prime }, {L}^{\prime }, \varnothing , {G(S)})$ to generate the left-hand and right-hand sides of rules, respectively, without the item constraints.

For the performance test, five benchmark datasets in FIMDR [15] were chosen. Connect, Mushroom, Pumsb and Chess are real and dense datasets, i.e., they produce many long frequent itemsets even for very high support values. T10I4D100K is synthetic and sparse. Table 1 shows their characteristics.

Fig. 7

Performance of MAR-MinSC, PP-MAR-MinSC-1 and PP-MAR-MinSC-2 on Mushroom and Pumsb

For each tested dataset, the thresholds of $s_{1 }$ and $c_{1}$ are fixed at $0.9$ and $0.95$, respectively. With a pair of minimum confidence (MC) and minimum support (MS), the size of $\mathrm{L}_{0}$ and ${R}_{0}$ constraints ranges from 4 to 22 % of $\vert {\mathcal {A}}^{{\mathcal {F}}}\vert$ (step 2 %). For a pair of ${L}_{0}^{\prime }{s}$ size and ${R}_{0}^{\prime }{s}$ size, we choose 10 values of $({L}_{0},{R}_{0})$ (each $({L}_{0},{R}_{0})$ comprises of items taken randomly from ${\mathcal {A}}^{{\mathcal {F}}})$. Let T-MAR-MinSC, T-PP-MAR-MinSC-2 and T-PP-MAR-MinSC-1 be the average execution times of MAR-MinSC, PP-MAR-MinSC-2, and PP-MAR-MinSC-1 , respectively, for 100 constraint pairs $({L}_{0},{R}_{0})$. For each tested dataset together with two minimum thresholds of support and confidence, we execute three algorithms and find that their outputs are the same. The average running times of the algorithms are shown in Figs. 6, 7 and 8.

As can be seen from the figures, MAR-MinSC outperforms PP-MAR-MinSC-2 and PP-MAR-MinSC-1, especially for the lower values of minimum support and confidence.

To explain the efficiency of MAR-MinSC in comparison with those of PP-MAR-MinSC-2 and PP-MAR-MinSC-1, we also take into account the percent ratio of the number of redundant candidate rules (not satisfying the constraints) to the total of all generated rules after executing PP-MAR-MinSC-2 and PP-MAR-MinSC-1 on a given triple of dataset, minimum support and minimum confidence, called DS-MS-MC. The results are shown in Table 2.

Table 2 shows the average execution times of MAR-MinSC, PP-MAR-MinSC-2, and PP-MAR-MinSC-1, where columns R-OvPP2 and R-OvPP1 represent the ratios of T-MAR-MinSC to T-PP-MAR-MinSC-2 and T-PP-MAR-MinSC-1, respectively, and columns RR-PP2 and RR-PP1 show the ratios of the number of redundant rules, which do not satisfy the constraints, to the total of generated rules when PP-MAR-MinSC-2 and PP-MAR-MinSC-1 are used, respectively. Compared to PP-MAR-MinSC-2 and PP-MAR-MinSC-1, MAR-MinSC is faster for all tested datasets. The time is reduced by 48.23 to 17.77 % in column R-OvPP2 and by 6.86 to 0.12 % in column R-OvPP1. The reason for the reduction is that there are a large number of generated redundant rules (RR-PP2 and RR-PP1 range from 94.5 to 99.96 % and from 98.7 to 99.98 %, respectively) that fail the last test of PP-MAR-MinSC-2 and PP-MAR-MinSC-1, leading to lower performance.

Fig. 8

Performance of MAR-MinSC, PP-MAR-MinSC-1 and PP-MAR-MinSC-2 on Connect

Table 2 The time reduction of MAR-MinSC

5 Conclusions and future works

The paper proposed a new, efficient algorithm called MAR-MinSC for mining association rules with minimum single constraints. It uses the lattice of closed itemsets and their generators as the input data. MAR-MinSC neither leads to the redundancy of generated rules nor directly checks rules with the constraints. Thus, it obtains the high performance. Our method that is based on the lattice and suitable equivalence relations reveals many significant implications in theory and practice.

In theory, the method demonstrates the explicit structure and unique representation of the solution set based on essentially basic factors such as closed itemset, support and generator. Therefore, this is the representation without losing information. The correctness of the theoretical results was proven.

In practice, the method is a basis to design parallel algorithms for efficiently mining the solution set in distributed environments. Moreover, the efficiency of the algorithm is minimally affected by the frequent change of the constraints in online systems.

In the future, we will use this method to study problems with other extended constraints.

Appendix: Proofs and Remarks

Proposition 4

Proof

Since $\mathrm{ARS}_{\supseteq L_0, \supseteq R_0} (s_0, s_1, c_0, c_1) \subseteq \mathrm{ARS}(s_0 ,s_1 ,c_0 ,c_1)$, we obtain $\mathrm{ARS}_{\supseteq L_0, \supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1 )=\sum \nolimits _{({L,S})\mathrm{NFCS}(s_0 ,s_1 ,c_0 ,c_1 )} \mathrm{AR}_{\supseteq L_0, \supseteq R_0} (L,S)$, where $\mathrm{AR}_{\supseteq L_0, \supseteq R_0} (L,S)=\mathrm{ARS}_{\supseteq L_0, \supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1 ) \cap \mathrm{AR}(L, S)$ = {$r:L'$ $\rightarrow$ $R'$ $\in \mathrm{AR}(L, S)$ $\vert$ $L'$ $\supseteq L_0$, $R'$ $\supseteq R_0$}. Moreover, with $S'$ $\equiv$ $L'$+$R'$, since $(L,S)\in \mathrm{NFCS}(s_0 ,s_1 ,c_0 ,c_1 )$, so $s_0\le$ supp($S'$)=supp(S)$\le s_1, c_0\le$ supp($S'$)/supp($L'$)=supp(S)/supp(L)$\le c_1$.

Proposition 5

Proof

• (a) Since $r: L'$ $\rightarrow$ $R'$ $\in \mathrm{ARS}_{\supseteq L_0, \supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1 )$, we have $L'$, $R'$ $\ne \varnothing$, $L'$ $\cap$ $R'$ = $\varnothing$, $S'$ $\equiv$ $L'$+$R'$, $L_0 \subseteq$ $L'$, $R_0 \subseteq$ $R'$. Let L $\equiv$ $h(L'$), S $\equiv$ $h(L'$+$R'$), since $L'$ $\ne \varnothing$, so $\varnothing \ne$ L $\subseteq$ S (if L = $\varnothing$, then $\varnothing \subset$ $L'$ $\subseteq$ $h(L'$) $\subseteq$ $h(L) = \varnothing$!), supp(S) = supp($S'$) $\in$ [$s_0$, $s_1$], supp(S)/supp(L) = supp($S'$)/supp($L'$) = $c(r)$ $\in$ [$c_0$, $c_1$]. Thus, ($L, S$) $\in \mathrm{NFCS}(s_0 ,s_1 ,c_0 ,c_1 )$ and $r$ $\in \mathrm{AR}_{\supseteq L_0, \supseteq R_0} (L,S)$. Due to $L_0 \subseteq$ $L'$, $R_0 \subseteq$ $R'$, $L'$ $\cap$ $R'$=$\varnothing$, so $L_0 \cap R_0 =\varnothing , S_0^*\subseteq$ $S'$ $\subseteq$ ${\mathcal {A}}$, $L'$ = $S'$ $\backslash$ $R'$ $\subseteq {\mathcal {A}} \backslash R_0$, $L'$ $\subseteq$ L, therefore, $L_0 \subseteq$ $L'$ $\subseteq$ L $\backslash R_0 =L_{C_1} \subseteq C_1$, supp($C_1$) $\le$ supp($L'$)$\le$ supp($L_0 )$, supp($C_1).c_0 \le$ supp($L'$).$c_0$ $\le$ supp($S'$) $\le$ supp($L'$).$c_1$ $\le$ supp($L_0).c_1$ và $s_0^*$ $\le$ supp($S'$) = supp(S) $\le$ $s_1^*$. Thus, $s_0^*\le s_1^*$ and supp($S_0^*$) $\le$ supp($S'$) $\le$ $s_0^*$, supp(${\mathcal {A}}$) $\le$ supp($S'$) $\le$ $s_1^*$.

• (b) With $\forall$(L,S)$\in \mathrm{NFCS}(s_0,s_1 ,c_0 ,c_1 )$, $\forall$ $r:L'$ $\rightarrow$ $R'$ $\in \mathrm{AR}_{\supseteq L_0, \supseteq R_0} (L,S)$, we have $\varnothing \ne$ $L\subseteq$ S, $L'$, $R'$ $\ne \varnothing$, $L'$ $\cap$ $R'$ = $\varnothing$, $h(L'$) = $L, h(S'$) = S, $s_0\le$ supp($S'$) = supp(S) $\le s_1$, $c_0\le$ supp(S)/supp(L) $\le c_1$, $R_0 \subseteq$ $R'$, $L_0 \subseteq$ $L'$. Since $L'$ = $S'$ $\backslash$ $R'$ $\subseteq {\mathcal {A}} \backslash R_0 =C_1$, $L_0 \subseteq$ $L'$ $\subseteq L_{C_1}\subseteq$ L, L = $h(L'$)  =  $h(L_{C_1})$, so $L'$ $\in \mathrm{FS}_{C_0 \subseteq L_{C1}}$. On the other hand, since supp(S)/$c_1 \le$ supp($L'$) = supp(L) $\le$ supp(S)/$c_0$, $s_0^{\prime } \le$ supp($L'$) $\le s_1^{\prime }$, S $\supseteq$ $S'$ $\equiv$ $L'$+$R'$ $\supseteq$ $S_0^*$, supp($C_1).c_0$ $\le$ supp($L'$).$c_0 \le$ supp($S'$) = supp(S) $\le$ supp($L'$).$c_1 \le$ supp($L_0)$.$c_1$, so $s_0^*\le$ supp(S) $\le s_1^*$. Due to ${\mathcal {G}}$($L'$)$\ne \varnothing$ [5], we take $L_i \in {\mathcal {G}}$($L'$)$\subseteq {\mathcal {G}}$ (L), then $L_i\subseteq$ $L'$ $\subseteq {C_1}$, thus ${\mathcal {G}}_{C_1} (L)$ $\ne \varnothing , {L}_{C_1}\in \mathrm{FCS}_{C_0 \subseteq C_1}\subseteq ( {s_0^{\prime } ,s_1^{\prime }})$, S $\in \mathrm{FCS}_{S_0^{*} \subseteq S_1^{*}} ( {s_0^*,s_1^*})$ or (L, S) $\in \mathrm{NFCS}_{\supseteq L_0, \supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1 )$. Since $R_0^*\equiv R_0 \subseteq$ $R'$=$S'$ $\backslash$ $L'$ $\subseteq$ S $\backslash$ $L'$=$R_1^*$, so $R'$ $\in \mathrm{FS}(S\backslash L')_{L^{\prime },R_0^*\subseteq R_1^*}$, r $\in$ $\mathrm{AR}_{\supseteq L_0, \supseteq R_0}^+ (L, S)$ and $\mathrm{AR}_{\supseteq L_0, \supseteq R_0} (L,S) \subseteq \mathrm{AR}_{\supseteq L_0, \supseteq R_0}^+ (L, S)$. Finally, due to $c_0 \le$ c(r) = supp($S'$)/supp($L'$) = supp(S)/supp(L) $\le c_1$, so r $\in \mathrm{ARS}_{\supseteq L_0, \supseteq R_0} ( {s_0 ,s_1 ,c_0 ,c_1})$. Hence, $\mathrm{AR}_{\supseteq L_0, \supseteq R_0} (L, S) \subseteq \mathrm{ARS}_{\supseteq L_0, \supseteq R_0} ( {s_0 ,s_1 ,c_0 ,c_1 })$.

• (c) As (L, S) $\in NFCS_{\supseteq L_0, \supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1)$, then $L_{C_1} \in \mathrm{FCS}_{C_0 \subseteq C_1} {s_0^{\prime } ,s_1^{\prime }}$, L $\supseteq L_0$ and $\exists L_i \in {\mathcal {G}}$(L): $L_i \subseteq C_1 \equiv {\mathcal {A}} \backslash R_0$. Set $L'$ $\equiv L_i \cup L_0$, we have $\varnothing \subset L_i \subseteq$ $L'$. Thus, we obtain $L_i \subseteq L_{C_1}$. Due to $L_0 \cap R_0 = \varnothing$, then $L_0 \subseteq C_1$ and $L_0 \subseteq L_{C_1 }$. Therefore, $C_0 \equiv L_0 \subseteq$ $L'$ $\subseteq L_{C_1 }$, $L_i\subseteq$ $L'$ $\subseteq L_{C_1}\subseteq L, L=h$($L_i )$=$h(L'$)$=h(L_{C_1})$. Hence, $L'$ $\in \mathrm{FS}_{C_0 \subseteq L_{C1} } \ne \varnothing$.

Since $(L, S) \in \mathrm{NFCS}_{\supseteq L_0, \supseteq R_0} (s_0 ,s_1 ,c_0 ,c_1 ) \subseteq \mathrm{NFCS}(s_0 ,s_1 ,c_0 ,c_1 )$ and b., we have $\mathrm{AR}_{\supseteq L_0, \supseteq R_0} (L, S) \subseteq \mathrm{AR}_{\supseteq L_0, \supseteq R_0}^+ (L, S)$. Therefore, we only need to prove the reverse dimension, “$\supseteq$”. With $\forall$r: $L'\rightarrow R$ $'\in \mathrm{AR}_{\supseteq L_0, \supseteq R_0}^{+} (L, S)$, $L'$, $R'$ $\ne \varnothing$, $L'$ $\in \quad \mathrm{FS}_{C_0 \subseteq L_{C1} }$, $R'$ $\in \quad \mathrm{FS}(S\backslash L')_{L^{\prime },R_0^{*} \subseteq R_1^*}$, we have $L_0 \subseteq$ $L'$ $\subseteq L_{C1} \subseteq C_1 \subseteq L_1$, $h(L'$) = $h(L_{C1})$, $R_0 \subseteq$ $R'$ $\subseteq R_1^*$ = $S\backslash$ $L'$, $L'$ $\cap$ $R'$ = $\varnothing$, $h(L'$+$R'$)=S. As $L_{C_1}\in \mathrm{FCS}_{C_0 \subseteq C_1} ({s_0^{\prime } ,s_1^{\prime }})$, so $\exists L_i \in {\mathcal {G}}$(L): $L_i \subseteq C_1$, thus, $L_i \subseteq L_{C1} \subseteq$ L, $L=h$($L_i)$ = $h(L_{C1})$ = $h(L'$). Therefore, r $\in \mathrm{AR}_{\supseteq L_0, \supseteq R_0} (L, S)$ and $\mathrm{AR}_{\supseteq L_0, \supseteq R_0}^+ (L,S) \subseteq \mathrm{AR}_{\supseteq L_0, \supseteq R_0} (L, S)$. Hence, $\mathrm{AR}_{\supseteq L_0, \supseteq R_0}^+ (L, S)=\mathrm{AR}_{\supseteq L_0, \supseteq R_0} (L, S)$. $\square$

Proposition 6

Proof

• (a) Assume that there exist two duplicate subsets $R^{{\prime } 1}$, $R^{{\prime } 2}$ in $\mathrm{FS}^*(Y)_{X,Z_0\subseteq Z_1}$, i.e., $\exists$k2$>$k1$\ge 1, R^{{\prime } j} {\equiv }{\mathbf Z}_{\mathbf 0} +R_{kj} +R_{kj}^{\prime } +R_{kj}^\sim$, $R_{kj} \in R_{\mathrm{min},} R_{kj}^{\prime } \subseteq R_{U,kj} , R_{kj}^\sim \subseteq R_{-,kj}$. , $\forall$j =1,2, such that $R^{{\prime }1}$. = $R^{{\prime }2}$. Thus, $R_{k1} \subseteq R_{k1} +R_{k1}^{\prime } +R_{k1}^\sim$ = $R_{k2} +R_{k2}^{\prime } +R_{k2}^\sim$. Since $R_{k1} \cap R_{k2}^\sim \subseteq R_{k1} \cap R_{-,k2} \subseteq R_{k1} \cap R_{-,k1}$= $\varnothing$ and $R_{k1}$, $R_{k2}$ are two different minimal sets in $R_{\mathrm{min}}$, so $R_{k1} \subset R_{k2} +R_{k2}^{\prime }$: it contradicts with the method for selecting $R_{k2}^{\prime }$ in $^{(*)}$.

• (b) . “$\subseteq$”: For any $R'$ $\in \mathrm{FS}(Y)_{X, \supseteq Z_0} \ne \varnothing$, we have $Z_0 \subseteq$ $R'$ $\subseteq$ Y, $R'$ $\ne \varnothing$, $S'$ $\equiv$ X + $R'$, $h(S') = h(X+Y)$. Since Y$\cap$X = $\varnothing$, so $R'$ $\cap$X = $\varnothing$, X+$Z_0 \subseteq$ $S'$ $\subseteq$ X+Y. Since $S'$ $\ne \varnothing$, let $S_k \in G$($S'$) $\subseteq G$(X+Y) (see[5]), $S_k \subseteq$ $S'$, so $R_k \equiv S_k \backslash$(X+$Z_0)\subseteq$ $S'$ $\backslash$(X+$Z_0 )$=$R'$ $\backslash Z_0 \subseteq$ $R'$. Set B$\equiv${$R_i\equiv S_i \backslash$(X+$Z_0 )$: $S_i \in G(S^{\prime })$}, C $\equiv${$R_i \equiv S_i \backslash$(X+$Z_0 )$: $S_i \in G(X+Y)$}, then $R_k \in$ B. Since B and C are finite sets and $\varnothing \ne$ B $\subseteq$ C, there exist the minimal sets $R_{\mathrm{min},S'} \equiv$ Minimal(B)$\ne \varnothing$, $R_{\mathrm{min}} \equiv$Minimal(C)$\ne \varnothing$. We always have the lowest index k of sets $R_i$ in $R_{\mathrm{min},S'} \equiv$ Minimal(B). Assume that $R_k \notin R_{\mathrm{min}}$, as $R_k \in R_{\mathrm{min},S'} ,R_k \in C$, so $\exists R_j \in R_{\mathrm{min}}$: $R_j \subset R_k$, where $R_j\equiv S_j \backslash$($X+Z_0 )$, $S_j \in G(X+Y)$ and $h(S_j)=h(X+Y)$, $S_j \subseteq$($X+Z_0)\cup S_j$= ($X+Z_0 )+R_j \subseteq$($X+Z_0 )+R_k \subseteq$ $X+R'$=$S'$ $\subseteq$ $X+Y, h(X+Y)=h(S_j )$=$h(S'$). Then, $S_j \in G(S^{\prime })$, $R_j \in$ B $\cap R_{\mathrm{min}}$. Thus $R_j \in R_{\mathrm{min},S'}$ and $R_j \subset R_k \in R_{\mathrm{min},S'}$: it is contradictory because $R_k$ is a minimal set in B, Hence, $R_k \in R_{\mathrm{min}} \ne \varnothing$. Then, it is realized that, if $R_{\mathrm{min}} =\varnothing$ then $\mathrm{FS}(Y)_{X, \supseteq Z_0} = \varnothing \ne \mathrm{FS}^*(Y)_{X, \supseteq Z_0}$. . We have $S'$ = $S_k +S_k^{\prime \prime }$, where $S_k^{\prime \prime } \equiv$ $S'$ $\backslash S_k$. Since $S'$ $\supseteq$ $X+Z_0$, so $S'$ = $X+Z_0 +R_k +R_k^{\prime } +R_k^\sim$. = $X+R'$, where $R'$ $\equiv Z_0 +R_k +R_k^{\prime } +R_k^\sim$, $R_k \equiv S_k \backslash$($X+Z_0)\in R_{\mathrm{min}}$, $R_k^{\prime } \equiv [S_k^{\prime \prime } \backslash$($X+Z_0)]\cap R_U^k$= [$S'$ $\backslash$($X+Z_0 )\backslash S_k ] \cap R_U^{k-1} \subseteq R_U^{k-1} \backslash S_k \subseteq R_U^{k-1} \backslash R_k \equiv R_{U,k}$ (since $R_k \cap$ [$S'$ $\backslash$($X+Z_0 )\backslash S_k ] \subseteq R_k \backslash S_k$=$\varnothing$), $R_k^\sim \equiv [ S_k^{\prime \prime } \backslash$($X+Z_0 )]\backslash R_U^k \subseteq$ ($S'$ $\backslash$ $X)\backslash (Z_0 +R_U^k )$ $\subseteq Y$ $\backslash (Z_0 +R_U^k ) \equiv R_{-,k}$. Assume that $\exists R_j \equiv S_j \backslash$($X+Z_0 ) \in R_{\mathrm{min}}$: 1 $\le$ $j < k$ and $R_j \subset R_k +R_k^{\prime }$, then $h(S_j ) = h(X+Y)$, ${S_j}\subseteq$ ($X+Z_0 ) \cup S_j$ = ($X+Z_0 )+R_j \subseteq$($X+Z_0 )+R_k +R_k^{\prime } \subseteq$ $X+R'$ $\equiv$ $S'$ $\subseteq X+Y, h(X+Y) =$ $h(S_j)$ = $h(S'$). Thus, $S_j \in G(S')$ and $R_j \in R_{\mathrm{min},S^{\prime }}$ but j $<k$: it is contradictory to the method for selecting the index $k$. Hence, $R'$ $\in \mathrm{FS}^*(Y)_{X, \supseteq Z_0}$. . “$\supseteq$”: For any $R'\in \mathrm{FS}^*(Y)_{X, \supseteq Z_0}$, we have $R'$ = $Z_0 +R_k +R_k^{\prime } +R_k^\sim$, where $R_k \equiv S_k \backslash$($X+Z_0 ) \in R_{\mathrm{min}}$ and $S_k \in G(X+Y)$, $h(S_k) = h(X+Y)$, $R'$ $\ne \varnothing$, $R_k \subseteq$ $(X+Y)$ $\backslash$($X+Z_0 )$ = $Y$ $\backslash Z_0 \subseteq$ $Y$. Moreover, $R_k^{\prime } \subseteq R_{U,k} \subseteq$ $Y$, $R_k^\sim \subseteq R_{-,k} \subseteq$ $Y$, $Z_0 \subseteq$ $R'$ $\subseteq$ $Y$ and $R'$ $\cap$ $X$ = $\varnothing$. On the other hand, since $X+Y$ $\supseteq$ $X+R'$ $\supseteq$ $X+Z_0 +R_k$= ($X+Z_0) \cup S_k \supseteq S_k$, so $h(S_k)$ = $h(X+R'$)=$h(X+Y)$. Therefore, $R'$ $\in \mathrm{FS}(Y)_{X, \supseteq Z_0}$.

• (c) Since $Y$ $\cap$ $X$ = $\varnothing$ and $Z_0 \subseteq$ $Y$, so $Z_0 \cup$ $X$ = $\varnothing$. Set $R^* \equiv$ Y and $\forall R_k \equiv S_k \backslash$($X+Z_0$)$\in R_{\mathrm{min}} \ne \varnothing$: $S_k \in$ G $(X+Y)$, $R_k \subseteq$ $(X+Y)$ $\backslash$($X+$ $Z_0)$ = $Y$ $\backslash Z_0 \subseteq$ $R^*$, then $R^*$ $\ne \varnothing$ and $Z_0 \subseteq R* \subseteq Y$, $S_k \subseteq S_k \cup$($X+Z_0)$ = $(X+Z_0)+R_k \subseteq$ $X+R$ $^*$ = $X+Y$. Therefore, $h(X+Y) = h(S_k)$ = $h(X+R*)$. Hence, $\exists$ $R^*$ $\in \mathrm{FS}(Y)_{X, \supseteq Z_0} =\mathrm{FS}^*(Y)_{X, \supseteq Z_0} \ne \varnothing$. $\square$

Remark 4

From the proof of Proposition 3, we have remark as follows.

• (a) For $\forall$ $R'$ $\in \mathrm{FS}^*(Y)_{X, \supseteq Z_0}$ with the representation $R' \equiv Z_0 +R_k +R_k^{\prime } +R_k^\sim$. If $\exists R' = \varnothing ,$ then $Z_0$ = $\varnothing$ and $\exists S_k \in G$ (X+Y) so that $R_k \equiv S_k \backslash$($X+Z_0)$ = $\varnothing$. Thus, $S_k \subseteq$ X $\subseteq$ $X+Y and h(X+Y) = h(X) =$ $h(S_k)$. Moreover, $R_{\mathrm{min}} \equiv$ { $R_1 \equiv \varnothing$}, $R_{U,1} = R_U^1 =\varnothing , R_{-,1} \equiv Y \ne \varnothing$ and $R^{\prime }=R_1^\sim \subseteq R_{-,1}$. Therefore, when representing $R^{\prime }$in $\mathrm{FS}^*(Y)_{X, \supseteq Z_0}$ based on the sets$R_k \in R_{\mathrm{min}} , R^{\prime }$is only empty in the cases $Z_0$ = $\varnothing$, $h(X+Y) = h(X)$ and $R_{\mathrm{min}}$ = {$\varnothing$}. Then, $R^{\prime } \in \mathrm{FS}^*(Y)_{X, \supseteq Z_0} \Leftrightarrow \varnothing \subset R^{\prime } \subseteq Y \ne \varnothing$. In practice, we consider three cases as follows.

  • $\cdot$ If $R_{\mathrm{min}}$ = {$\varnothing$} and $Z_0$ = $\varnothing$, then $R_{U,1} = R_U^1 = \varnothing , R_{-,1} \equiv Y\ne \varnothing$ and $\mathrm{FS}^*(Y)_{X, \supseteq Z_0} \equiv$ {R$'\vert \varnothing \ne$ R$'\equiv R_1^\sim$ , $R_1^\sim \subseteq Y$} ={$R'\vert \varnothing \subset$ $R'$ $\subseteq Y$}.

  • $\cdot$ If $R_{\mathrm{min}}$={ $\varnothing$} and $Z_0 \ne \varnothing$, then $R_{U,1} = R_U^1 = \varnothing , R_{-,1} \equiv$ Y $\backslash Z_0$ and $\mathrm{FS}^*(Y)_{X, \supseteq Z_0} \equiv$ {$R'$ $\vert$ $R'$ $\equiv Z_0 +R_1^\sim$, $R_1^\sim \subseteq$Y$\backslash Z_0$}={$R'$ $\vert \quad Z_0 \subseteq$ $R'$ $\subseteq$Y }.

  • $\cdot$ If $R_{\mathrm{min}} \ne$ { $\varnothing$}, then $\mathrm{FS}^*(Y)_{X, \supseteq Z_0} \equiv$ {R’ $\equiv Z_0 +R_k +R_k^{\prime } +R_k^\sim \vert \quad R_k \in R_{\mathrm{min}}$, $R_k^{\prime } \subseteq R_{U,k}$, $R_k^\sim \subseteq R_{-,k}$, ($R_j \not \!\!{\subset } R_k +R_k^{\prime }$, $\forall R_j \in R_{\mathrm{min}}$: 1$\le$ $j$ $<$ $k$)}.

  For the last two cases, we do not need to check the obvious condition $R^{\prime } \ne \varnothing$ when generating $R'$.

• (b) (The advantage of the condition $^{(*)}$ in decreasing redundant candidates accompanying exponential reduction). In the process of forming set $R'$, which originated from ${R}_0^{*} +R_k$, when finding growing subsets $R_k^{\prime } \subseteq R_{U,k}$ and then $R_k^\sim \subseteq R_{-,k}$ to supplement $R'$, if the condition $^{(*)}$ is violated, then we neither need to continue considering the supersets $R^{\prime \prime }$ (estimated$2^{\vert R_{U,k} \backslash R_k^{\prime } \vert }$ supersets) of $R_k^{\prime } (R_k^{\prime } \subset$ $R$” $\subseteq R_{U,k} )$ nor add all subsets $R_k^\sim$ (estimated $2^{\vert R_{-,k} \vert }$ subsets) of $R_{-,k}$ to $R'$ (i.e., there are ($2^{\vert R_{U,k} \backslash R_k^{\prime } \vert }-1)$*($2^{\vert R_{-,k} \vert })$ subsets eliminated because all of them are redundant candidates for $R'$). Then, we go on considering other $R_k^{\prime \prime }$ sets $(R_k^{\prime }\not \!\!{\subset } R_k^{\prime \prime } \subseteq R_{U,k} )$ or other $R_k$ sets of $R_{\mathrm{min}}$. The necessary and sufficient condition $^{(*)}_{ }$for distinctly generating the right-hand side $R'$ of rules helps to eliminate many redundant candidates for them. This condition also helps to completely eliminate the duplication of the solutions, and the checking process is only based on minimal sets or generators with small quantity and size. It makes an important contribution to explain the efficiency of the corresponding algorithms.

• c. (Improving the calculation of the border sets). It is realized that, for each $k > 1$, to calculate $R_U^{k-1} = R_U^{k-2} \cup R_{k-1} ,R_{U,k}\equiv R_U^{k-1} \backslash R_k$, $R_{-,k} \equiv R^{*}\backslash R_U^k$, where $R^*\equiv$ $Y$ $\backslash Z_0$, we must perform two subtractions and one union on the generators that cannot be disjoint. To decrease the calculation of the border sets $R_{U,k}$ and $R_{-,k}$, we note that

  $$\begin{aligned}&\cdot S_k , S_k^{\prime } , R_k \in R_{\mathrm{min}} , \,R_k^{\prime } , R_k^\sim , \,{{R}}' \equiv R_0^*+R_k +R_k^{\prime }\\&\qquad +R_k^\sim ; \\&R_U^k,\, R_{U,k},\, R_{-,k} , R^*\\&{R}_{{U},{k}} = [(R_U^{k-2} \backslash R_{k-1} )+R_{k-1} ]\backslash R_k\\&\quad = ({R}_{{U},{k}-1} +R_{k-1} ) \\&\backslash R_k , R_{-,k} =R_{-,k-1} \backslash R_k , \forall k \ge 1 \quad \hbox {and}\\&\quad R_0 \equiv {R}_{{U},0} \equiv \varnothing , R_{-,0} \equiv R^*. \end{aligned}$$

  Thus, $R_{U,k} \!=\! { \left\{ {{\begin{array}{lll} {(R_{U,k\!-\!1} \!+\!R_{k-1} )\backslash R_k,if k\ge 1} \\ {\varnothing , \quad if k=0} \\ \end{array}}}\right. } , R_{-,k} ={\left\{ {\begin{array}{l} {R_{-,k-1}\backslash R_{k},\quad if k\ge 1} \\ {Y\backslash Z_{0}, \quad if k=0} \\ \end{array}}\right. }$ and $R_0 \equiv \varnothing$. For each k$\ge$1, there remains only a disjoint union $R_{U,k} = R_{U,k-1} +R_{k-1}$ on two small sets in size (thus, its calculation is faster than that of normal union $R_U^{k-1} = R_U^{k-2} \cup R_{k-1}$ on two sets that may not be disjoint and have large sizes), and two subtractions, where one $R_{-,k} = R_{-,k-1} \backslash R_k$ is performed on two sets $R_{-,k-1} \subseteq R^*$ and $R_k \subseteq R_U^k$ that their sizes are less than those of sets in the subtraction $R_{-,k} \equiv R^*\backslash R_U^k$.