Skip to main content
SpringerLink
Log in

On a robust stability criterion in the subdiffusion equation with Caputo–Dzherbashian fractional derivative

  • Original Article
  • Published:
Boletín de la Sociedad Matemática Mexicana Aims and scope Submit manuscript

Abstract

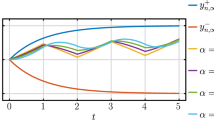
This paper presents a robust stability criterion for the subdiffusion equation with Caputo–Dzherbashian fractional derivative. The criterion is obtained by extending the concept of stability under constant-acting perturbations applied to systems of differential equations of integer order. It is assumed that the subdiffusion equation admits external sources that are represented by Fourier series. The robust stability criterion makes it possible to ensure that the solution of the subdiffusion equation, as well as its Caputo–Dzherbashian fractional derivative and its first partial derivative with respect to the longitudinal axis, are bounded.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data availability

Not applicable.

Code availability

Not applicable.

Notes

  1. In the literature, the fractional derivative of Caputo–Dzherbashian is also called the fractional derivative of Caputo–Djrbashian or fractional derivative of Caputo. In [9], some contributions of Dzherbashian to fractional calculus are presented.

References

  1. Oldham, K.B., Spanier, J.: The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order. Academic Press, New York (1974)

    MATH  Google Scholar 

  2. Capelas de Oliveira, E., Tenreiro Machado, J.A.: A review of definitions for fractional derivatives and integral. Math. Probl. Eng. 2014, 1–6 (2014). https://doi.org/10.1155/2014/238459

  3. Sales-Teodoro, G., Tenreiro-Machado, J.A., Capelas de Oliveira, E.: A review of definitions of fractional derivatives and other operators. J. Comput. Phys. 388, 195–208 (2019). https://doi.org/10.1016/j.jcp.2019.03.008

  4. Baleanu, D., Fernandez, A.: On fractional operators and their classifications. Mathematics 7(9) (2019). https://doi.org/10.3390/math7090830

  5. Atangana, A., Balenu, D.: New fractional derivatives with non-local and non-singular kernel: theory and application to heat transfer model. Therm. Sci. 20(2), 763–769 (2016). https://doi.org/10.2298/TSCI160111018A

    Article  Google Scholar 

  6. Cuahutenango-Barro, B., Taneco-Hernández, M.A., Gómez-Aguilar, J.F.: Application of fractional derivative with exponential law to bi-fractional-order wave equation with frictional memory kernel. Eur. Phys. J. Plus 132(12), 515 (2017). https://doi.org/10.1140/epjp/i2017-11796-9

    Article  Google Scholar 

  7. Cuahutenango-Barro, B., Taneco-Hernández, M.A., Gómez-Aguilar, J.F.: On the solutions of fractional-time wave equation with memory effect involving operators with regular kernel. Chaos Solitons Fract. 115, 283–299 (2018). https://doi.org/10.1016/j.chaos.2018.09.002

    Article  MathSciNet  MATH  Google Scholar 

  8. Cuahutenango-Barro, B., Taneco-Hernández, M.A., Yu-Pei, L., Gómez-Aguilar, J.F., Osman, M.S., Jahanshahi, H., Aly, A.A.: Analytical solutions of fractional wave equation with memory effect using the fractional derivative with exponential kernel. Results Phys. 25, 104148 (2021). https://doi.org/10.1016/j.rinp.2021.104148

    Article  Google Scholar 

  9. Rogosin, S., Dubatovskaya, M.: Mkhitar Djrbashian and his contribution to fractional calculus. Fract. Calc. Appl. Anal. 23(6), 1797–1809 (2020). https://doi.org/10.1515/fca-2020-0089

    Article  MathSciNet  MATH  Google Scholar 

  10. Diethelm, K.: The Analysis of Fractional Differential Equations. An Application-oriented Expositions Using Differential Operators of Caputo type. Lecture Notes in Mathematics, vol. 2004. Springer, Berlin (2010)

  11. Podlubny, I.: Fractional Differential Equations. Mathematics in Science and Engineering, vol. 198. Academic Press, California (1999)

  12. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies, vol. 204. Elsevier Science B. V., Amsterdam (2006)

  13. Elsgolts, L.: Differential Equations and the Calculus of Variations. Mir, Moscow (1977)

    Google Scholar 

  14. Mainardi, F.: Why the Mittag–Leffler function can be considered the Queen function of the fractional calculus? Entropy 22(12) (2020). https://doi.org/10.3390/e22121359

  15. Li, K., Peng, J., Gao, J.: On some properties of the \(\alpha \)-exponential function. Integral Transform. Spec. Funct. 24(7), 511–516 (2013). https://doi.org/10.1080/10652469.2012.713359

    Article  MathSciNet  MATH  Google Scholar 

  16. Dzherbashian, M.M.: Integral Transforms and Representation of Functions in a Complex Domain. Nauka, Moscow (1966) (in Russian)

  17. Gorenflo, R., Kilbas, A.A., Mainardi, F., Rogosin, S.: Mittag–Leffler Functions, Related Topics and Applications. Springer Monographs in Mathematics, 2nd edn. Springer, Berlin (2020)

    Book  MATH  Google Scholar 

  18. Caputo, M.: Elasticità e Dissipazione. Zanichelli, Bologna (1969). ((In Italian))

  19. Caputo, M., Mainardi, F.: A new dissipation model based on memory mechanism. Pure Appl. Geophys. 91(1), 134–147 (1971). https://doi.org/10.1007/BF00879562

    Article  MATH  Google Scholar 

  20. Caputo, M., Mainardi, F.: Linear models of dissipation in anelastic solids. Riv. del Nuovo Cim. 1(2), 161–198 (1971). https://doi.org/10.1007/bf02820620

    Article  Google Scholar 

  21. Dzherbashian, M.M., Nersesian, A.B.: Fractional derivatives and Cauchy problem for differential equations of fractional order. Fract. Calc. Appl. Anal. 23(6), 1810–1836 (2020). https://doi.org/10.1515/fca-2020-0090

    Article  MathSciNet  MATH  Google Scholar 

  22. Jin, B.: Fractional Differential Equations. An Approach Via Fractional Derivatives. Applied Mathematical Sciences, vol. 206. Springer, Cham (2021)

  23. Li, C., Qian, D., Chen, Y.: On Riemann–Liouville and Caputo derivatives. Discrete Dyn. Nat. Soc. 2011, 562494 (2011). https://doi.org/10.1155/2011/562494

    Article  MathSciNet  MATH  Google Scholar 

  24. Zhermolenko, V.N., Temoltzi-Ávila, R.: Bulgakov problem for a hyperbolic equation and robust stability. Mosc. Univ. Mech. Bull. 76(4), 95–104 (2021). https://doi.org/10.3103/S0027133021040051

    Article  MATH  Google Scholar 

  25. Temoltzi-Ávila, R.: Robust stability of the heat equation on a radial symmetric plate. Bol. Soc. Mat. Mex. 28(1), 14 (2022). https://doi.org/10.1007/s40590-021-00405-4

    Article  MathSciNet  MATH  Google Scholar 

  26. Abdeljawad, T.: On Riemann and Caputo fractional differences. Comput. Math. Appl. 62(3), 1602–1611 (2011). https://doi.org/10.1016/j.camwa.2011.03.036

    Article  MathSciNet  MATH  Google Scholar 

  27. Tavares, D., Almeida, R., Torres, D.F.M.: Caputo derivatives of fractional variable order: numerical approximations. Commun. Nonlinear Sci. Numer. Simul. 35, 69–87 (2016). https://doi.org/10.1016/j.cnsns.2015.10.027

    Article  MathSciNet  MATH  Google Scholar 

  28. Marin, A.M., Ortiz, R.D., Rodriguez-Ceballos, J.A.: A subdiffusion heat equations with Robin condition. Int. J. Pure Appl. Math. 94(4), 551–559 (2014). https://doi.org/10.12732/ijpam.v94i4.11

  29. Rodriguez-Ceballos, J.A., Marin, A.M., Ortiz, R.D.: A nonhomogeneous subdiffusion heat equation. Aust. J. Math. Anal. Appl. 11(1), 1–7 (2014)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The author thanks the referees for carefully reading the manuscript and for their helpful comments that helped improve this article.

Funding

Not applicable.

Author information

Authors and Affiliations

  1. Área Académica de Matemáticas y Física, Universidad Autónoma del Estado de Hidalgo, Pachuca-Tulancigo Km 4.5, 42184, Mineral de la Reforma, Hidalgo, Mexico

    R. Temoltzi-Ávila

Authors
  1. R. Temoltzi-Ávila
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Not applicable.

Corresponding author

Correspondence to R. Temoltzi-Ávila.

Ethics declarations

Conflict of interest

The author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Temoltzi-Ávila, R. On a robust stability criterion in the subdiffusion equation with Caputo–Dzherbashian fractional derivative. Bol. Soc. Mat. Mex. 29, 74 (2023). https://doi.org/10.1007/s40590-023-00548-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40590-023-00548-6

Keywords

Mathematics Subject Classification

Search

Navigation