1 Introduction

In recent years, ever-increasing energy demands and shortage of traditional fossil fuels seriously challenged the sustainable development of human society. At the same time, increasing concern about environment problems and carbon emissions of fossil fuels has provoked worldwide active research on the next-generation electric power system, which is known as the smart grid [1,2,3] and/or energy internet (EI) [4, 5]. It features renewable energy resources and intelligent energy management. The coming energy power generation system shifts from reliance on fossil fuels to various renewable energy resources, such as solar and wind power, etc. [6] However, the stochastic nature of some renewable resources also brings new challenges to the reliability and stability of existing power grids. Thus it is expected that using grid-connected energy storage system (ESS) for power buffering, peak shaving, load levelling and load frequency control, shall be important for modern electric power systems with large-scale renewable energy integration [7, 8]. Available energy storage technologies include batteries, super capacitors, flywheels, and pumped hydro storage, where batteries are generally considered as the dominant new solution for large-scale ESS due to its ability to supply power for periods of up to a few hours [9, 10]. The cost of batteries is descending rapidly and is expected to compete with pumped hydro in the near future [11].

To integrate battery energy storage system (BESS) installations to the grid, power converters should have the following features: (1) fault ride-through capability; (2) high redundancy and error correction capabilities. For megawatt-scale medium-voltage (MV) application, multilevel converters show significant advantages over conventional topologies [12]. Among them, the most promising concept for renewable energy integration and power transmission is the modular multilevel converter (MMC) [13,14,15]. Compared with conventional multilevel converters, MMCs provide advantages of high modularity, better harmonic spectra, lower switching frequency, higher efficiency, and reduced weight of the filtering components.

In the last decades, MMCs have attracted the interest of both academia and industry. The published literature mainly relates to their applications to high-voltage DC (HVDC) transmission [16,17,18], MV electric drives [19,20,21], and STATCOMs [22, 23]. MMCs used in BESSs for interfacing low- or medium-voltage batteries to medium- or high-voltage grids were reported in [24,25,26,27]. They enable a flexible scaling of power modules to integrate energy storage and power electronics to a wide range of operating voltages, output power and stored energy. However, existing MMC-based BESSs (MMC-BESSs) do not address DC fault handling capabilities, and special control issues arising in MMC-BESSs have not yet been fully overcome. Reverse blocking (RB) IGBTs have a symmetrical blocking voltage characteristic. Due to cancelling anti-parallel diodes, the conduction loss of RB-IGBTs is lower than that of normal IGBTs, so they are especially suitable for multilevel converters for low switching frequency application [28].

This paper proposes a reverse blocking MMC-BESS (RB-MMC-BESS) for enhancing the DC fault handling capability, which consists of new sub-modules (SMs) and distributed battery banks. Typical operating principles, detailed battery energy controls, and fault blocking mechanisms are thoroughly analyzed.

The paper is organized as follows. Section 2 describes the configuration and operating principles of RB-MMC-BESSs. Section 3 explores the battery energy and state of charge (SOC) balancing controls in detail. The DC fault blocking mechanism is analyzed in Section 4. To validate the feasibility and effectiveness of the proposed topology and theoretical analysis, extensive simulation results are discussed in Section 5. Finally, Section 6 reports the main conclusions.

2 Topologies and basic operations

2.1 Topologies for RB-MMC-based BESSs

A typical (n+1) level three-phase MMC-based BESS is shown in Fig. 1, comprised of three phase legs where each leg contains a stack of 2n identical sub-modules (SMs) and two inductors (L a).

Fig. 1
figure 1

General configuration of three-phase MMC-BESS

Full size image

For the convenience of discussion, the phase legs are further divided into an upper arm and a lower arm. Unlike conventional MMCs, the SMs integrate a battery storage bank BSM, which can also serve as an active power port. Fig. 1b illustrates one of the possible SM realizations proposed in [25], which consists of two IGBTs with antiparallel diodes and one capacitor that together form a typical bidirectional chopper. The distributed battery banks are directly connected across the SM capacitors. However, when a common DC link short-circuit fault happens, the diode D2 in each SM will create a fault current path. Large fault currents cause thermal overstress, which may result in severe damage to power electronic devices.

The proposed reverse blocking sub-module (RBSM) is illustrated in Fig. 1c. Unlike the abovementioned SM, two anti-parallel RB-IGBTs (T2 and T3) are used for the lower switch, and a bypass circuit consisting of auxiliary thyristor TS, auxiliary capacitor CS and varistor Rsr is connected in parallel with the RB-IGBTs. The distributed battery banks are directly connected across the RBSM capacitors CSM as before. A MMC-BESS employing RBSMs is hereafter called a RB-MMC-BESS.

Due to their high degree of modularity, RB-MMC-BESSs employ distributed battery banks with lower voltage ratings rather than centralized ones used with a conventional high-voltage common DC link. In case of battery faults, extra RBSMs can be placed in the phase leg to replace the damaged ones. RB-MMC-BESSs also have a fixed common DC link, which may be used to interconnect them with a MV DC network if desired. What is more, RB-MMC-BESSs may also transfer power from one phase leg to another using the controlled internal circulating current through this common DC link. This is the theoretical basis for SOC balancing control among phase legs.

2.2 Operating principles of RBSMs

Under normal operations, T2 and T1 operate with complementary switching states, while T3 is switched on all the time and acts as a free-wheeling diode. Once fault current is detected, the RBSMs go into fault protection mode by blocking the control signals of the IGBTs (T1, T2 and T3). Then the fault current starts to charge CS through TS, while Rsr is designed to prevent over-voltage across CS, thus it further avoids the potential threats to the main switching devices.

Generally, Rsr is not activated until the voltage of CS exceeds its threshold value. Thus the function of Rsr will not be considered in the following to simplify the analysis, but this does not affect the correctness of the theory. The switching states of the RBSM are listed in Table 1, where U B is the battery voltage of BSM and U clamp is the clamp voltage across T2 and T3.

Table 1 Switching states of a RBSM
Full size table

2.3 Operation principles of RB-MMC-BESS

As in [29] and without loss of generality, the following analysis assumes that the operating principles of the three phases are identical, and the conclusions are taken to apply to three-phase conditions. Phase-j is taken as an example to carry out the analysis, where j = a, b, c, and the following additional assumptions are made:

  1. 1)

    Three-phase AC voltages and currents are pure sinusoidal and symmetrical.

  2. 2)

    The common DC link voltage U DC is smooth.

  3. 3)

    The AC output current i sj is distributed equally between the upper and the lower legs.

  4. 4)

    Switching losses of the power devices are ignored.

These conditions are not exact for RB-MMC-BESSs but in general they are fulfilled to a good approximation. The AC terminals of an RB-MMC-BESS are connected to the grid U sj through a series connected filter L s. With reference direction shown in Fig. 1, the AC currents in normal operating mode are related by:

$$i_{{{\text{P}}j}} = \frac{1}{2}i_{{{\text{s}}j}} + i_{{{\text{Z}}j}}$$
(1)
$$i_{{{\text{N}}j}} = - \frac{1}{2}i_{{{\text{s}}j}} + i_{{{\text{Z}}j}}$$
(2)
$$i_{{{\text{s}}j}} = i_{{{\text{P}}j}} - i_{{{\text{N}}j}}$$
(3)
$$i_{{{\text{Z}}j}} = \frac{1}{2}\left( {i_{{{\text{P}}j}} + i_{{{\text{N}}j}} } \right)$$
(4)

where i Pj and i Nj denote the upper and lower arm currents, respectively. The arm currents flowing through both the upper and lower arms consist of half of the AC output current i sj and the common-mode circulating current i Zj . The role of the latter in balancing the SOC of batteries is discussed below in Section 3.2.

The resulting AC and DC voltages can be calculated as follows :

$$u_{{{\text{P}}j}} = \frac{{U_{\text{DC}} }}{2} - u_{j} - L_{\text{a}} \frac{{{\text{d}}i_{{{\text{P}}j}} }}{{{\text{d}}t}} - R_{\text{a}} i_{{{\text{P}}j}}$$
(5)
$$u_{{{\text{N}}j}} = \frac{{U_{\text{DC}} }}{2} + u_{j} - L_{\text{a}} \frac{{{\text{d}}i_{{{\text{N}}j}} }}{{{\text{d}}t}} - R_{\text{a}} i_{{{\text{N}}j}}$$
(6)
$$u_{j} = \frac{{u_{{{\text{N}}j}} - u_{{{\text{P}}j}} }}{2} - \frac{{L_{\text{a}} }}{2}\frac{{{\text{d}}i_{{{\text{s}}j}} }}{{{\text{d}}t}} - \frac{{R_{\text{a}} }}{2}i_{{{\text{s}}j}}$$
(7)
$$U_{\text{DC}} = u_{{{\text{P}}j}} + u_{{{\text{N}}j}} + 2L_{\text{a}} \frac{{{\text{d}}i_{{{\text{Z}}j}} }}{{{\text{d}}t}} + 2R_{\text{a}} i_{{{\text{Z}}j}}$$
(8)

where u Pj and u Nj denote the upper and lower arm voltages, respectively; u j is the AC output phase voltage; U DC is the rated common DC link voltage; and R a is the equivalent series arm resistor.

Under a DC link short-circuit fault condition, if the RB- MMC-BESS keeps running according to the above rules before system blocking, U DC will reduce to zero immediately. Then the inserted RBSMs’ capacitors CSM and battery banks BSM will be continuously discharged, and potentially over-discharged if the fault is not cleared quickly. Therefore some reasonable means for improving the DC fault ride-through capability of RB-MMC-BESSs should be found.

3 System controls

A RB-MMC-BESS operates differently to a regular MMC. Since each RBSM includes its own battery energy storage, which may act as the DC source, the power is not only delivered from the common DC link. As previously described, each arm conducts only half of the AC output current, thus reducing conduction loss in the converter. Unbalanced SOC of battery banks may cause premature failure after extended cycling due to overcharging or undercharging of batteries. The flat relationship of battery SOC as a function of their voltage, over a wide range of voltages, indicates the need for a SOC balancing algorithm that does not rely on the voltages [30, 31]. Thus SOC control in RB-MMC-BESSs is one of the main differences compared to conventional MMCs.

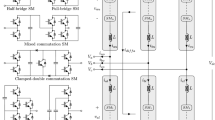
The controller of a RB-MMC-BESS has two main sections: the power control and SOC balancing control. Fig. 2 shows a block diagram of the system control structure.

Fig. 2
figure 2

Overview of system control structures

Full size image

3.1 Power control

Active and reactive power control of three-phase RB-MMC-BESSs is based on decoupled current control. Considering the sinusoidal output currents, proportional integration (PI) controllers K1 are adopted in a rotating frame synchronized with the output frequency. Fig. 3 shows the power control block diagram for a three-phase RB-MMC-BESS. Here, P * and Q * represent the power commands for the instantaneous active and reactive power at the AC side, respectively. The AC side active power P * causes charging and discharging of the RBSMs’ capacitors and battery banks, so the SOC and the DC link voltage are indirectly controlled. Finally, the upper and lower arm voltage references \(U_{{{\text{P}}j}}^{*}\) and \(U_{{{\text{N}}j}}^{*}\) are determined by the AC side power.

Fig. 3
figure 3

Block diagram of power control

Full size image

3.2 SOCs balancing control

The inherent circulating current among phases is required to charge the capacitors with the lowest SOC and discharge the ones with the highest SOC. Therefore, it is essential to control the circulating current of the converter to maximize the efficiency of the SOC controls. The SOC control structure of RB-MMC-BESS is illustrated in Fig. 4, where K2 to K5 refer to close-loop controllers such as PI controllers. SOC balancing control of the RB-MMC-BESS is divided into individual SM balancing, phase arm balancing, phase leg balancing, and inner circulating current control.

Fig. 4
figure 4

Block diagram of SOC control

Full size image

Figure 4a shows the block diagram for individual SOC balancing control; sign() denotes the signum function. This is responsible keeping all RBSMs in the same arm at the average arm SOC (i.e. \(\overline{SOC}_{{{\text{P}}j}}\), \(\overline{SOC}_{{{\text{N}}j}}\)) using a close-loop controller. The average arm SOC \(\overline{SOC}_{{{\text{P}}j}}\),\(\overline{SOC}_{{{\text{N}}j}}\) are given by:

$$\overline{SOC}_{{{\text{P}}j}} = \frac{1}{n}\sum\limits_{k = 1}^{n} {SOC_{jk} }$$
(9)
$$\overline{SOC}_{{{\text{N}}j}} = \frac{1}{n}\sum\limits_{k = n + 1}^{2n} {SOC_{jk} }$$
(10)

The arm SOC balancing control forces the SOC difference between the upper and lower arms (i.e. \(\overline{SOC}_{{{\text{P}}j}}\)−\(\overline{SOC}_{{{\text{N}}j}}\)) to be zero. The leg SOC control is designed to force the j-phase average SOC (\(\overline{SOC}_{{j , {\text{ave}}}}\)) to follow the average SOC of the three phases (\(\overline{SOC}_{\text{ave}}\)), where, \(\overline{SOC}_{{j , {\text{ave}}}}\) and \(\overline{SOC}_{\text{ave}}\) are given by:

$$\overline{SOC}_{{j , {\text{ave}}}} = \frac{1}{2n}\sum\limits_{k = 1}^{2n} {SOC_{jk} }$$
(11)
$$\overline{SOC}_{\text{ave}} = \frac{1}{3}\sum\limits_{j = a}^{c} {\overline{SOC}_{{j,{\text{ave}}}} }$$
(12)

These control objectives can be achieved using the circulating current. Therefore, the output signals of both leg and arm SOC balancing controllers are \(i_{{{\text{Z}}j1}}^{*}\) and \(i_{{{\text{Z}}j2}}^{*}\) respectively, from which the reference circulating current \(i_{{{\text{Z}}j}}^{*}\) is determined:

$$i_{{{\text{Z}}j}}^{*} = i_{{{\text{Z}}j1}}^{*} + i_{{{\text{Z}}j2}}^{*}$$
(13)

Together, the arm and leg SOC controls result in direct control of the circulating current in each phase leg, leading to good current regulation of the battery banks. The circulating current control loop is illustrated as Fig. 4. The current minor loop forces i zj to follow the command \(i_{{{\text{Z}}j}}^{*}\), which generates the voltage control command \(U_{{j,{\text{cir}}}}^{*}\).

Finally, the voltage reference for the upper and lower arm of phase-j is given by:

$$U_{{{\text{P}}jk}}^{*} = \frac{{U_{{{\text{P}}j}}^{*} }}{n} + U_{{{\text{P}}jk,{\text{ind}}}}^{*} + U_{{j,{\text{cir}}}}^{*} + \frac{{U_{\text{DC}}^{{}} }}{n}$$
(14)
$$U_{{{\text{N}}jk}}^{*} = \frac{{U_{{{\text{N}}j}}^{*} }}{n} + U_{{{\text{N}}jk,{\text{ind}}}}^{*} + U_{{j,{\text{cir}}}}^{*} + \frac{{U_{\text{DC}}^{{}} }}{n}$$
(15)

where the inputs are shown in Fig. 2.

4 DC fault blocking mechanism

A DC pole-to-pole fault is regarded as one of the most serious fault types. Therefore, the theory of the DC fault blocking mechanism will be studied under this condition. Fig. 5 shows the possible current paths after all IGBTs in a RBSM are blocked. When current i SM is positive as shown in Fig. 5a, the capacitor is charged through the anti-parallel diode D1 and the fault current is limited because the capacitor voltage U B provides an inverse voltage to switch off the diode. Otherwise, when current i SM is negative, the RBSM is bypassed as shown in Fig. 5b. The bypass circuit goes to work and Cs is charged by the fault current through the triggered TS. Cs is generally very small compared with the CSM. Thus u cs will increase quickly to provide the inverse voltage needed to cut off the arc path at the fault point.

Fig. 5
figure 5

Possible current paths of RBSMs in their blocking state

Full size image

Once a pole-to-pole DC short-circuit fault occurs, the common DC link voltage is collapsed to zero and a large inrush current would be induced. Then the RBSMs will enter their discharging stage immediately until system blocking is enabled by the central control system, which is the same behavior as the equivalent model presented in [32]. Rather than repeating the detailed explanation found there, this paper will focus on the fault mechanism in the blocking stage.

4.1 Modelling blocking mechanism

Once the RB-MMC-BESS goes into fault protection mode following a DC pole-to-pole fault, all IGBTs are blocked by the central control system, and the equivalent of a phase leg is illustrated in Fig. 6. The equivalent series capacitance of both the upper and lower arms is expressed as

$$C_{{{\text{seq}}1}} = C_{\text{seq2}} = \frac{{C_{\text{S}} }}{n}$$
(16)
Fig. 6
figure 6

Current path in the RB-MMC-BESS in the blocking state

Full size image

In this state, the fault current starts to charge the auxiliary capacitor Cs through Ts. Then u cs increases quickly to provide the inverse voltage u csI = 2n×u cs,which helps to extinguish the fault current. As shown in Fig. 6b, a second-order oscillating circuit is constructed with the equivalent series resistance R eq, equivalent inductance L eq and the equivalent capacitance C seq. This will govern the discharging of C seq which may be regarded as 2n auxiliary capacitors Cs in series. The following differential equation is deduced from Kirchhoff’s voltage law:

$$\frac{{{\text{d}}^{2} u_{\text{cs}} }}{{{\text{d}}t}} + \frac{{R_{\text{eq}} }}{{L_{\text{eq}} }}\frac{{{\text{d}}u_{\text{cs}} }}{{{\text{d}}t}} + \frac{1}{{L_{\text{eq}} C_{\text{seq}} }}u_{\text{cs}} = 0$$
(17)

The initial conditions and circuit parameters are:

$$\left\{ {\begin{array}{*{20}l} {u_{\text{cs}} (0_{ + } ) = u_{\text{cs}} (0_{ 1- } ) = 0} \hfill \\ {i_{\text{f}} (0_{ + } ) = i_{\text{f}} (0_{ - } ) = I_{0} } \hfill \\ \end{array} } \right.$$
(18)
$$\left\{ {\begin{array}{*{20}l} {R_{\text{eq}} = 2R_{\text{a}} + R_{\text{f}} } \hfill \\ {L_{\text{eq}} = 2L_{\text{a}} } \hfill \\ {C_{\text{seq}} = \frac{{C_{\text{s}} }}{2n}} \hfill \\ \end{array} } \right.$$
(19)

where I 0 is defined as the initial fault current at the blocking stage and R f is the short circuit resistance. Assuming for simplicity that the auxiliary capacitor voltages are equal, then the charging current and voltage of each auxiliary capacitor Cs is:

$$u_{\text{cs}} = e^{{ - \frac{t}{\tau }}} \frac{{2nI_{0} }}{{\omega C_{\text{s}} }}\sin (\omega t)$$
(20)
$$i_{\text{f}} = - e^{{ - \frac{t}{\tau }}} \frac{{\omega_{0} I_{0} }}{\omega }\sin \left( {\omega t - \beta } \right)$$
(21)

where τ is the fault current decay time constant, ω0 and ω are the natural angular frequency and system angular frequency, respectively, and β is the initial current phase angle. These four variables are defined as follows:

$$\left\{ {\begin{array}{*{20}l} {\tau = \frac{{4L_{\text{a}} }}{{2R_{\text{a}} + R_{\text{f}} }}} \hfill \\ {\omega = \sqrt {\frac{n}{{L_{\text{a}} C_{\text{s}} }} - \left( {\frac{{2R_{\text{a}} + R_{\text{f}} }}{{4L_{\text{a}} }}} \right)^{2} } } \hfill \\ {\omega_{0} = \sqrt {\frac{n}{{L_{\text{a}} C_{\text{s}} }}} } \hfill \\ {\beta = \arctan \sqrt {\frac{{16nL_{\text{a}} }}{{C_{\text{s}} \left( {2R_{\text{a}} + R_{\text{f}} } \right)_{{}}^{ 2} }} - 1} } \hfill \\ \end{array} } \right.$$
(22)

Equations (20) and (21) indicate that u cs and the fault current i f are affected by the initial fault current I 0; while u cs is approximately inverse proportional to the RBSM’s capacitance. In addition, the fault current i f is also influenced directly by the equivalent resistance R eq and inductance L eq.

4.2 Selecting parameters of auxiliary circuit

Without considering system redundancy, it is assumed for simplicity that the 2n RBSMs are series-connected in each phase leg. The voltage stress of the auxiliary capacitor always equals U SM under normal operating conditions. After system blocking is enabled, the auxiliary capacitors are charged in series by the fault current, and the auxiliary capacitor voltage will reach its peak value as the current decays to zero. From (20), the peak blocking voltage across T2 and T3 is

$$U_{\text{clamp}} = \frac{{u_{{{\text{cs}},{\text{peak}}}} }}{2n} = e^{{ - \frac{\beta }{\omega \tau }}} \frac{{I_{0} }}{{\omega C_{\text{s}} }}\sin (\beta )$$
(23)

The voltage stress across Cs is illustrated in Fig. 7, where the clamping voltage is related to both the auxiliary capacitance C s and leg inductance L a. A larger leg inductance value means that more inductive energy will be transformed to electric field energy, which results in higher capacitor voltage. The smaller the auxiliary capacitance and the larger the initial fault current I 0, the faster the capacitor voltage changes.

Fig. 7
figure 7

Voltage stress of C S in the bypass circuit

Full size image

Therefore the value of C s is determined by two parameters: the voltage limit for IGBTs (U T,max) and the optimized blocking voltage (U cs,min). The latter helps to eliminate the AC rectification feeding energy. Therefore, C s should satisfy:

$$U_{\text{cs,min}} \le u_{{{\text{Cs}},{\text{peak}}}} \le U_{\text{T,max}}$$
(24)

4.3 Fault management

Fig. 8 shows the DC fault protection flow chart for the RB-MMC-BESS. The operating state is monitored continuously, with both the DC link voltage and currents sent back to the central control system, so the DC fault state may be judged by comparing them with their threshold values.

Fig. 8
figure 8

Flow chart of DC fault protection in the RB-MMC-BESS

Full size image

Once a DC fault is detected, the system will immediately block all the trigger pulses in the RB-MMC- BESS to clear the fault currents. For non-permanent faults, it is expected that power transmission can be restarted quickly, so the IGBTs will be triggered to test which type of fault has occurred. If the fault is cleared then all the IGBTs are unblocked and the RB-MMC-BESS will be restarted. But if a permanent fault is identified, both the AC breakers and the DC breakers are tripped to achieve fault isolation after fault clearance.

Generally speaking, the fault clearance time achieved by the protection system is very short, perhaps less than 1ms, to protect the main power devices from thermal overstress.

5 Verification of RB-MMC-BESS by simulation

To verify the feasibility of the proposed RB-MMC- BESS and system control strategies, a fully switched simulation model has been developed as shown in Fig. 9, where PCC denotes the point of common coupling. The modulation method adopted in this simulation is the carrier phase-shifted sinusoidal pulse-width-modulation methods. Two simulated scenarios are considered in this section. The first simulation focuses on the system control algorithms under normal operating conditions, thus demonstrating control of SOC and power. The second simulation verifies the DC fault handling capabilities of the RB-MMC-BESS under a typical DC pole-to-pole fault.

Fig. 9
figure 9

Diagram of the simulated system

Full size image

5.1 Scenario 1: RB-MMC-BESS under normal operating conditions

In this scenario, all battery banks in phase a have been initialized with different SOC. After the RB-MMC-BESS starts, the power command P * = 2 MW is issued, and all battery banks in the RBSMs are discharging. The proposed power control and SOC balancing control algorithms have been tested and the results are illustrated in Fig. 10.

Fig. 10
figure 10

Convergence of SOC of the simulated battery banks

Full size image

The convergence SOC curves while discharging is shown as Fig. 10a. It is clear that the RBSMs with higher SOC discharge quicker, while some RBSMs with lower SOC are recharged for a period to bring the SOC closer together, before they convert to the same value. With the proposed controller, all the RBSMs’ battery banks are completely balanced after 9 s. From the power transmission point of view, the active and reactive power are not affected by the SOC balancing controls, as shown in Fig. 10b. Note that the battery parameters are adjusted to make the simulation time short for this demonstration.

5.2 Scenario 2: RB-MMC-BESS under typical DC fault condition

Since this paper mainly concerns the DC fault handling capability of the proposed topology, simulation of a nine-level RB-MMC-BESS is sufficient to demonstrate the functionality while maintaining simulation efficiency. Table 2 summarizes the simulation parameters. The fault scenario is a non-permanent DC pole-to-pole fault scenario that occurs at 0.3 s and is cleared at 0.4 s. The simulation results are shown in Fig. 11 and Fig. 12.

Table 2 Simulation parameters
Full size table
Fig. 11
figure 11

Simulation results for RB-MMC-BESS during a DC fault

Full size image
Fig. 12
figure 12

Simulation results for RBSMs during a DC fault

Full size image

From t = 0 s to 0.3 s, the RB-MMC-BESS operates at a power rating of 1 MW, supplied by battery banks in the RBSMs. When the DC pole-to-pole fault occurs at t = 0.3 s, the common DC link voltage U DC drops to zero immediately, shown in Fig. 11a. This is accompanied by an inrush DC short current in the fault point, as seen in Fig. 11b. It is further supposed that it takes 0.1 ms to block all the trigger pulses so the RB-MMC-BESS can clear the fault currents. According to the fault blocking mechanism theory in Section 4, the 2n series-connected auxiliary capacitor voltages u csI provide the inverse voltage that will help to extinguish the arc fault current in time. Fig. 11c and Fig. 11d illustrate the grid voltages and currents during the DC fault. The short circuit fault energy mainly comes from the DC fault loop shown in Fig. 6. Because the blocking measures are timely, the grid input currents reduce quickly to zero, while the grid voltages are not significantly affected. AC power transmission, shown in Fig. 11e, is interrupted by the DC fault and recovers very quickly after the non-permanent fault is cleared.

Fig. 12 illustrates the performance of RBSMs during the DC pole-to-pole short circuit fault. The SOC and capacitor voltage of each RBSM is shown in Fig. 12a and Fig. 12b. Since all IGBTs are blocked in time, the capacitor voltages remain almost constant at their value at the time of failure, resulting in the constant SOC of the battery banks. This maintains a reasonable condition for restarting the RB-MMC-BESS after the fault is cleared.

Section 3 found that the circulating current can be controlled according to the desired recharge current of the battery banks and the equalizing time. Fig. 12c shows the circulating current during the DC fault. As soon as the RBSMs go into fault protection mode, the fault current i f transfers to the bypass circuits and starts charging the auxiliary capacitors Cs through TS. Fig. 12d illustrates the voltage stress of RBSMs. It can be seen that u cs is directly applied to the lower switches T2 and T3 when fault protection mode is enabled.

Fig. 13 compares the simulated DC fault handling capabilities of a RB-MMC-BESS and a traditional MMC-BESS system. Once DC short circuit fault occurs in the RB-MMC-BESS and all IGBTs are blocked, the series-connected Cs voltage increases quickly to provide an inverse voltage to suppress the fault current. However, due to the lack of fault current suppression measures, the fault current in the traditional MMC-BESS increases dramatically. The peak value may reach nearly 18 times that of the RB-MMC-BESS under the same conditions. It is evident that the RB-MMC-BESS has better fault blocking capabilities, and this one of its salient merits.

Fig. 13
figure 13

Fault currents of a RB-MMC-BESS and a traditional MMC-BESS

Full size image

6 Conclusion

This paper has investigated the operation and control of a proposed reverse-blocking modular multilevel converter with a distributed battery energy storage system (RB-MMC-BESS) for interfacing low-voltage batteries to the medium or high voltage grids. Its theoretical performance has been analyzed and the findings have been confirmed through simulation.

Unlike conventional MMC-BESS designs, sub-modules with integrated battery banks use two anti-parallel RB-IGBTs and an additional bypass circuit. The proposed design can block fault currents effectively with reduced requirement for precise trigger pulses during fault conditions. This greatly enhances the ability of the BESS to respond to fault conditions and to ride through non-permanent faults.

The RB-MMC-BESS also employs direct management of state of charge (SOC) of battery banks, rather than sub-module voltages. Control algorithms combining power control and SOC control have been developed and demonstrated through simulation. The standard modulation strategies can be employed under the normal operating condition.