1 Introduction

Microgrids (MGs) are self-controlled entities which facilitate the penetration of renewable energy and distributed energy resources (DERs) for economic and reliability purposes. Generally, the MG can be operated in either the grid-connected or islanded mode [1]. With the development of MGs, a new concept of interconnected microgrids system (IMS) (or microgrid cluster) is introduced which considers several MGs exchanging energy with each other even when the MGs are isolated from the utility grid. By constituting the IMS, it is more flexible to ensure the full utilization of renewable energy sources (RESs), reduce the operation cost, and achieve high power supply reliability [2–4]. From the viewpoint of Transactive Energy, the MGs can be seen as prosumers with both attributes of sellers and buyers. During different time periods, the MG may act as a seller or buyer depending on real-time operating conditions and the net power profile. Therefore, in order to achieve the operation goal of IMS, the energy management is an important issue that should be addressed.

More recently, there were some studies focusing on the energy management of IMS, and the proposed method can be classified into two types: centralized optimization and distributed optimation. Generally, if all the MGs could share the information on their respective data on load, generation, and grid conditions, the optimal scheduling could be easily implemented based on the traditional centralized optimization, such as the optimal power flow (OPF). For instance, a method of joint optimization and distributed control for IMS was proposed in [5], which uses the minimum generation cost as the objective function. However, for security considerations, it is not desirable for each MG to do so because the shared information could compromise the privacy of each MG. Thus, this is the basic motivation for the deployment of distributed optimization. In this regard, more attention has been paid to the distributed optimizations for IMS energy management. A decentralized optimal control algorithm for distribution management systems was proposed in [6] by considering distribution network as coupled microgrids. The optimal control problem of IMS is modeled as a decentralized partially observable Markov decision process, which decreases the operating cost of distributed generation and improves the efficiency of distributed storages. Moreover, the alternating direction method of multipliers (ADMM) was applied in [7] and [8] for optimal generation scheduling of IMS. Only the expected exchanging power information needs to be shared among all the MGs during the iterative process to minimize the total operation cost. Similarily, a distributed convex optimization framework is developed for energy trading among islanded MGs in [9] and [10] with the objective of minimizing the total operation cost.

However, there are two common deficiencies in the existing methods: \(\textcircled {1}\) DERs of each MG are simply modeled as quadratic functions in most literature without considering the specific types; \(\textcircled {2}\) due to the limited regulation capacity of DERs, demand response (DR) [11] is an effective strategy to improve the cost-effectiveness and reliability, which are however not considered in the existing studies. Considering the energy usage for heating and cooling of many regions is a rigid demand for end users, it is believed that the combined heat and power (CHP) with microturbines has a great potential to be applied in the MGs [12]. For these reasons, this paper focuses on distributed energy management for enabling interconnected operation of CHP-based MGs with DR. The main contributions of this work are as follows.

  1. 1)

    Considering the power and heat demands and the possible energy trading among MGs, an hour-ahead optimal scheduling model is proposed. The system model considers the cost of DERs, the cost of DR, the network tariff, and the power loss of interconnected power lines.

  2. 2)

    A distributed iterative algorithm based on subgradient with dynamic search direction is proposed, in which the search direction is constructed by combining conjugacy and subgradient method.

2 System model

2.1 Distributed energy resource

Renewable energy resources play an important role in MG (i.e., wind turbine (WT) and photovoltaic (PV)) [13]. They are considered as uncontrollable distributed energy resources whose output power is related to the environment. During the scheduling, the output power of RESs \(P_{uc}\) should be fully used, and their operational costs can be ignored due to the zero fuel consumption.

$$\begin{aligned} \begin{aligned} P_{uc}=P_{PV}+P_{WT} \end{aligned} \end{aligned}$$
(1)

where \(P_{WT}\) and \(P_{PV}\) are the power forecasting results of WT and PV in the next scheduling time slot, respectively.

Diesel generation (DG) can act as a reserve power supply, and the fuel cost is expressed as follows [14]:

$$\begin{aligned} \begin{aligned} C_{dgi}=\alpha _{i}+\beta _{i}P_{dgi}+\gamma _{i}P_{dgi}^2 \end{aligned} \end{aligned}$$
(2)

where \(\alpha _{i}\), \(\beta _{i}\), \(\gamma _{i}\) are fuel cost coefficients of DG; and \(P_{dgi}\) is the output power of DG i.

CHP can provide electric and heat energy for MG, whose total cost can be formulated as follows [15]:

$$\begin{aligned} \begin{aligned} C_{chpj}&=\alpha _{j}+\beta _{j}P_{chpj}+\gamma _{j}P_{chpj}^2+\delta _{j}H_{chpj}\\&+\theta _{j}H_{chpj}^2+\xi _{j}H_{chpj}P_{chpj} \end{aligned} \end{aligned}$$
(3)

where \(\alpha _{j}\), \(\beta _{j}\), \(\gamma _{j}\), \(\delta _{j}\), \(\theta _{j}\) and \(\xi _{j}\) are fuel cost coefficients of CHP; \(P_{chpj}\) is power generation of CHP j; and \(H_{chpj}\) is heat generation of CHP j.

Heat-only unit only provides thermal energy for end users of MG, and its cost can be formulated as follows [14]:

$$\begin{aligned} \begin{aligned} C_{hk}=\alpha _{k}+\beta _{k}H_{hk}+\gamma _{k}H_{hk}^2 \end{aligned} \end{aligned}$$
(4)

where \(\alpha _{k}\), \(\beta _{k}\), \(\gamma _{k}\) are the fuel cost coefficients of heat-only units; and \(H_{hk}\) is the heat generation of the heat-only unit k.

2.2 Demand response

DR is one of the important solutions of demand side management (DSM). As the electricity price has a great effect on the power consumption of end users [16], in this paper the DR is treated as an equivalent virtual generation unit in order to reflect the sensitivity of load consumption demand to the change electricity price. According to [17], the power consumption of end users with DR utilization can be expressed as:

$$\begin{aligned} \begin{aligned} D=a^{lin}+b^{lin}P_{r} \end{aligned} \end{aligned}$$
(5)

where \(a^{lin}\) and \(b^{lin}\) are the coefficients of liner demand versus price expression; and \(P_{r}\) is the marginal cost of virtual generation.

Difference between the initial load and the responding load can be represented as the virtual power generation:

$$\begin{aligned} \begin{aligned} D=D_{0}- {\Delta } D \end{aligned} \end{aligned}$$
(6)

By substituting (6) in (5), we have marginal cost of the virtual generated power as:

$$\begin{aligned} \begin{aligned} P_{r}=\frac{-1}{b^{lin}} {\Delta } D+\frac{D_{0}-a^{lin}}{b^{lin}} \end{aligned} \end{aligned}$$
(7)

Furthermore, by multiplying \({\Delta } D\) in (7), we can obtain the cost function of the virtual generation unit:

$$\begin{aligned} \begin{aligned} C_{DR}=\frac{-1}{b^{lin}} {\Delta } D^2+\frac{D_{0}-a^{lin}}{b^{lin}} {\Delta } D \end{aligned} \end{aligned}$$
(8)

During the DR process, end users may have different responses to the incentive. According to (7), \(a^{lin}\) and \(|b^{lin}|\) are two important factors for the sensitiveness of loads in MG: \(\textcircled {1}\) the cost \(C_{DR}\) is increased with the increment of \(a^{lin}\), which means it is more difficult to curtail the load with a larger \(a^{lin}\); \(\textcircled {2}\) the cost \(C_{DR}\) is decreased with the increment of \(|b^{lin}|\), which means it is easier to curtail the load with a larger \(|b^{lin}|\). The load consumption demand in each MG may have a different sensitivity to the incentive of DR, which can be distinguished by \(a^{lin}\) and \(b^{lin}\).

2.3 Network cost

For network cost, many factors may have influence on the model, i.e., the investment and construction cost of the network, etc. For simplicity, we assume that the cost in all connection topologies of IMS is the same. According to [9], the cost of network tariff can be modeled as a cubic polynomial.

$$\begin{aligned} \begin{aligned} \gamma (x)=ax+bx^3 \end{aligned} \end{aligned}$$
(9)

where a and b are coefficients; and x is the trading energy.

2.4 Optimal scheduling model

Consider an IMS consisting of M interconnected MGs through a power interconnection infrastructure and a communication network. Let \(E_i^{(g)}\) and \(E_i^{(c)}\) be the generation and consumption of MG i during each scheduling time slot, respectively. MG i is allowed to sell energy \(E_{i,j}(E_{i,j}\ge 0)\) to MG j, \(j\ne i\), and can buy energy \(E_{k,i}(E_{k,i}\ge 0)\) from MG k, \(k\ne i\). In order to describe the connection between MGs, an adjacency matrix \({{\varvec{A}}}=[a_{i,j}]_{M\times M}\) is defined. If there exits a connection from MG i to MG j, element \(a_{i,j}\) is set as 1; otherwise, element \(a_{i,j}\) is set to be 0. Thus, \({{\varvec{A}}}\) may be nonsymmetric, meaning that at least two MGs are allowed to exchange energy in one direction only. Moreover, we choose \(a_{i,i}=0\), and if \(a_{i,j}=0\), we can directly have \(E_{i,j}=0\).

The design objective is to minimize the total operating cost of IMS, including the power generation cost, network cost, and power loss cost. This objective can be formulated as:

$$\begin{aligned} \begin{aligned} C^*=\min \limits _{\{E_{i,j}\}}\sum _{i=1}^M C_i(E_i^{(g)})+\sum _{i=1}{{\varvec{e}}}_i^{\rm T}{{\varvec{A}}}^{\rm T}\varvec{\gamma }({{\varvec{E}}}_i^{(b)}) \end{aligned} \end{aligned}$$
(10)

where \(C_i(E_i^{(g)})\) denotes the cost of generating \(E_i^{(g)}\) units of energy at MG i; \(\gamma (E_{i,j})\) is the cost of transferring \(E_{i,j}\) units of energy between MG i and MG j; \(\mathbf e _i\) is the ith column of the \(M\times M\) identity matrix; \({{\varvec{E}}}_i^{(b)}\) is the vector composed of the energy bought from other MGs by MG i; \(\varvec{\gamma }({{\varvec{E}}}_i^{(b)})=[\gamma (E_{1,i})\cdots \gamma (E_{M,i})]^{\rm T}\).

The coupled multiple MGs in one IMS, which have their set of possible actions, should be coordinated in order to achieve the common goal of the system and meet the power and heat demands.

As for MG i, its total operation cost \(C_i(E_i^{(g)})\) includes the cost of DG, CHP, heat-only unit and virtual generation unit.

$$\begin{aligned} \begin{aligned} C_i(E_i^{(g)})=\sum _{j=1}^{N_{dg}} C_{dgj}+\sum _{k=1}^{N_{chp}} C_{chpk}+\sum _{m=1}^{N_h} C_{hm}+C_{DRi} \end{aligned} \end{aligned}$$
(11)

where \(N_{dg}\) is the number of DGs in MG i; \(N_{chp}\) is the number of CHPs in MG i; \(N_h\) is the number of heat-only units in MG i; \(C_{dgj}\) is the cost function of DG j; \(C_{chpk}\) is the cost function of CHP k; \(C_{hm}\) is the cost function of heat-only unit m; and \(C_{DRi}\) is the cost function of the virtual generation unit of DR in MG i.

The optimal scheduling problem has several constraints, which can be classified as follows.

1) Power balance

This constraint guarantees that the generation plus the purchased energy equals the sum of the consumed power, the sold energy, and the power loss. Then the power balance of MG i requires:

$$\begin{aligned} \begin{aligned} E_i^{(g)}+{{\varvec{e}}}_i^{\rm T}{{\varvec{A}}}^{\rm T}{{\varvec{E}}}_i^{(b)}=E_i^{(c)}+{{\varvec{e}}}_i^{\rm T}{{\varvec{A}}}{{\varvec{E}}}_i^{(s)}+P_{j,i}^{loss} \end{aligned} \end{aligned}$$
(12)

where

$$\begin{aligned} \begin{aligned} E_i^{(c)}=D_{i0} \end{aligned} \end{aligned}$$
(13)
$$\begin{aligned} \left\{ \begin{aligned} {{\varvec{E}}}_i^{(b)}= \begin{bmatrix} E_{1,i}\\ \vdots \\ E_{M,i} \end{bmatrix} \\ {{\varvec{E}}}_i^{(s)}= \begin{bmatrix} E_{i,1}\\ \vdots \\ E_{i,M} \end{bmatrix} \end{aligned} \right. \end{aligned}$$
(14)
$$\begin{aligned} \begin{aligned} E_i^{(g)}=\sum _{j=1}^{N_{dg}} P_{dgj}+\sum _{k=1}^{N_{chp}} P_{chpk}+P_{uc}+ {\Delta } D_i \end{aligned} \end{aligned}$$
(15)
$$\begin{aligned} \begin{aligned} P_{j,i}^{loss}=\frac{P_{j,i}^{2}}{U^2}R_{ij} \end{aligned} \end{aligned}$$
(16)

where \({{\varvec{E}}}_i^{(b)}\) and \({{\varvec{E}}}_i^{(s)}\) are the vectors composed of quantities of purchased power and sold power, respectively; \(D_{i0}\) is the initial load during the current scheduling interval; \({\Delta } D_i\) denotes the curtailed load in this scheduling time slot; \(P_{j,i}^{loss}\) is the power loss [18] caused by buying energy from MG j by MG i; U is the voltage of interconnection lines; and \(R_{ij}\) is the resistance of the interconnection line between MG i and MG j.

Moreover, any power transfer between MGs is accompanied with a cost of power loss over the interconnection lines. We assume that the reactive power is compensated for by each MG individually. Also it is assumed here that the cost of the power loss between MGs is covered by the power purchaser.

2) DR constraint

According to the flexibility of user demands, the DR constraint can be specified as:

$$\begin{aligned} \begin{aligned} 0\le {\Delta } D\le D_0v \end{aligned} \end{aligned}$$
(17)

where v is the pre-specified portion of the nominal load, and thus (17) guarantees that the load curtailment is smaller than a pre-specified portion of the nominal load.

3) Power constraints

For ensuring stable operations, the power generation of DG and CHP should have the following constraints:

$$\begin{aligned}&P_{dg}^{{\rm min}}\le P_{dg}\le P_{dg}^{{\rm max}} \end{aligned}$$
(18)
$$\begin{aligned}&P_{chp}^{{\rm min}}\le P_{chp}\le P_{chp}^{{\rm max}} \end{aligned}$$
(19)

4) Heat power constraints

Heat generation of CHP and heat-only units also should have lower and upper bounds for providing the intended service.

$$\begin{aligned}&H_{chp}^{{\rm min}}\le H_{chp}\le H_{chp}^{{\rm max}} \end{aligned}$$
(20)
$$\begin{aligned}&H_{h}^{{\rm min}}\le H_{h}\le H_{h}^{{\rm max}} \end{aligned}$$
(21)

5) Heat power balance

The heat output by CHP and heat-only units must cover the heat demand of each MG.

$$\begin{aligned} \begin{aligned} H_{Di}=\sum _{k=1}^{N_{chp}} H_{chpk}+\sum _{j=1}^{N_h} H_{hj} \end{aligned} \end{aligned}$$
(22)

where \(H_{Di}\) is the heat demand in MG i.

3 Distributed model and algorithm

3.1 Distributed optimal scheduling model

Problem (10) is known to have a unique minimum point since both the objective function and the constraints are strictly convex. As discussed in Sect. 1, there are difficulties for centralized optimization applied to IMS. In this regard, we decide to propose a distributed optimal scheduling model by decomposing the problem (10) into M local subproblems, which can be implemented by the MGs in an autonoums and cooperative manner.

By using Lagrangian method and duality theorem, a multiplier mechanism is introduced as the exchanged information between MGs to solve the decoupled subproblem for each MG. Thus, problem (10) can be rewritten as the following equivalent form:

$$\begin{aligned} \begin{aligned} C^*=\min \limits _{\{\varepsilon _i^{(s)}\}\{E_{i,j}\}}\sum _{i=1}^M C_i(E_i^{(g)})+\sum _{i=1}{{\varvec{e}}}_i^{\rm T}{{\varvec{A}}}^{\rm T}\varvec{\gamma }({{\varvec{E}}}_i^{(b)}) \end{aligned} \end{aligned}$$
(23)

subject to

$$\begin{aligned} E_i^{(g)}+{{\varvec{e}}}_i^{\rm T}{{\varvec{A}}}^{\rm T}{{\varvec{E}}}_i^{(b)}=E_i^{(c)}+\varepsilon _i^{(s)}+P_{j,i}^{loss} \end{aligned}$$
(24)
$$\begin{aligned} \varepsilon _i^{(s)}={{\varvec{e}}}_i^{\rm T}{{\varvec{A}}}{{\varvec{E}}}_i^{(s)} \end{aligned}$$
(25)

and other constraints in (17)–(22).

In the above equations, \(\varepsilon _i^{(s)}\) denotes the total selling energy of MG i, which is forced to be equal to all the energy bought by other MGs from MG i. A coupling constraint is formed as follows: \(\varepsilon _i^{(s)}={{\varvec{e}}}_i^{\rm T}{{\varvec{A}}}{{\varvec{E}}}_i^{(s)}\).

Lagrangian multipliers are introduced to relax the coupling constraint. Then we can form the corresponding dual function as:

$$\begin{aligned} \begin{aligned} C^*=\max \limits _{\varvec{\lambda }}C(\varvec{\lambda }) \end{aligned} \end{aligned}$$
(26)

where \(C(\varvec{\lambda })=\sum _{i=1}^M C_i^{(l)}(\varvec{\lambda })\)

$$\begin{aligned} \left\{ \begin{aligned}&C_i^{(l)}(\varvec{\lambda })=\min \limits _{\{\varepsilon _i^{(s)}\}\{{{\varvec{E}}}_i^{(b)}\}}C_i(\varepsilon _i^{(s)},{{\varvec{E}}}_i^{(b)},\varvec{\lambda })\\&s.t. \quad (17)-(22)\\&{\varepsilon _i^{(s)}\ge 0}\quad {E_{j,i}\ge 0}\quad \forall j\\&E_i^{(g)}+{{\varvec{e}}}_i^{\rm T}{{\varvec{A}}}^{\rm T}{{\varvec{E}}}_i^{(b)}=E_i^{(c)}+\varepsilon _i^{(s)}+P_{j,i}^{loss} \end{aligned} \right. \end{aligned}$$
(27)

For each MG, we have:

$$\begin{aligned} \begin{aligned} C_i(\{\varepsilon _i^{(s)},{{\varvec{E}}}_i^{(b)},\varvec{\lambda })=&C_i(E_i^{(g)})+{{\varvec{e}}}_i^{\rm T}{{\varvec{A}}}^{\rm T}\varvec{\gamma }({{\varvec{E}}}_i^{(b)})\\&+{{\varvec{e}}}_i^{\rm T}{{\varvec{A}}}^{\rm T}{\rm diag}{\{\varvec{\lambda }\}}{{\varvec{E}}}_i^{(b)}-\lambda _i\varepsilon _i^{(s)} \end{aligned} \end{aligned}$$
(28)

that is the contribution of MG i to the Lagrangian function relative to (10). Based on the above analysis, each Lagrange multiplier \(\lambda _i\) can be interpreted as the marginal cost of MG i, namely the price that selling a unit of power to adjacent MGs. Thus Lagrange function (28) can be seen as the net expenditure. The expenditure of each MG consists of the following parts: \(\textcircled {1} \,C_i(E_i^{(g)})\) is the generating cost including various generation units; \(\textcircled {2}\) \({{\varvec{e}}}_i^{\rm T}{{\varvec{A}}}^{\rm T}\varvec{\gamma }({{\varvec{E}}}_i^{(b)})\) is the network cost resulted from transferring the energy purchased from other MGs; \(\textcircled {3}\) \({{\varvec{e}}}_i^{\rm T}{{\varvec{A}}}^{\rm T}{\rm diag}{\{\varvec{\lambda }\}}{{\varvec{\textit{E}}}}_i^{(b)}\) is the cost due to purchasing energy; and \(\textcircled {4}\) \(\lambda _i\varepsilon _i^{(s)}\) is the income by selling energy.

3.2 Distributed algorithm

Obviously, the problem is transformed to the maximum dual problem. To this end, the optimal Lagrangian multipliers which converge to the optimal point of the dual problem are necessary to be found, \(\varvec{\lambda }^*={\rm argmax}_{\varvec{\lambda }}C(\varvec{\lambda })\). For each point \(\varvec{\lambda }[k]\), each MG minimizes its contribution to the Lagrangian function by solving the local subproblem (27) and determining the minimum point. As subproblem (27) is a convex function, we use interior point method to obtain the optimal solution.

According to [19], the conjugate gradient method is used to solve for the minimum value of the function, which has the quadratic termination property. Combining conjugacy and subgradient method, it shows a better convergence performance. In the conjugate gradient method, the search direction is constructed by taking n steps as a round and taking the negative gradient direction for the initial search direction of each round. Thus, referring to the conjugate gradient method, a subgradient method considering the dynamic search direction is developed. In this paper, we aim to search for the maximum value of the dual problem (26). Therefore, during the iteration, the initial search direction of each round is a subgradient direction.

The subgradient of \(C(\varvec{\lambda })\) in \(\varvec{\lambda }=\varvec{\lambda }[k]\) can be described as \(\varvec{\varsigma }=[{{\varvec{e}}}_i^{\rm T}{{\varvec{A}}}{{\varvec{E}}}_i^{(s)}[k]-\varepsilon _i^{(s)}[k]]_{M\times 1}\). For \(\forall \varvec{\lambda }\), we have \(C(\varvec{\lambda })\le C(\varvec{\lambda }[k])+\varvec{\varsigma }_T(\varvec{\lambda }-\varvec{\lambda }[k])\).

First, we take n steps as a round, and the initial update function of the Lagrange multipliers in each round can be expressed as:

$$\begin{aligned} \begin{aligned} \varvec{\lambda }[k+1]=\varvec{\lambda }[k]+\alpha [k]\begin{bmatrix} {{\varvec{e}}}_1^{\rm T}{{\varvec{A}}}{{\varvec{E}}}_1^{(s)}[k]-\varepsilon _1^{(s)}[k]\\ \vdots \\ {{\varvec{e}}}_M^{\rm T}{{\varvec{A}}}{{\varvec{E}}}_M^{(s)}[k]-\varepsilon _M^{(s)}[k] \end{bmatrix} \end{aligned} \end{aligned}$$
(29)

Second,the Lagrange multipliers can be updated as:

$$\begin{aligned} \varvec{\lambda }[k+1]&= {} \varvec{\lambda }[k]+\alpha [k]\varvec{d}[k] \end{aligned}$$
(30)
$$\begin{aligned} \varvec{d}[k]&= {} \nabla C(\varvec{\lambda }[k])+\beta _{k-1}\varvec{d}[k-1] \end{aligned}$$
(31)
$$\begin{aligned} \beta _{k-1}&= {} \frac{\mid \mid \nabla C(\varvec{\lambda}[k]) \mid \mid ^2}{\mid \mid \nabla C(\varvec{\lambda} [k-1])\mid \mid ^2} \end{aligned}$$
(32)

where \(\alpha [k]\) is the positive step factor; \(\varvec{d}[k]\) is the search direction; and k is the iteration number.

Next, when the convergence condition is not satisfied and m ( m is the iteration variable of determining the search direction) is no longer less than n, we take the next round according to (29), (30), (31) and (32).

Algorithm 1 summarizes the steps of the proposed distributed iterative algorithm.

figure d

Having solved (27) in all MGs, each MG can be aware of \(\varepsilon _i^{(s)}[k]\) and \({{\varvec{E}}}_i^{(b)}[k]\), namely the total energy it sold and the vector composed of the energy bought from other MGs. Furthermore, we can obtain \({{\varvec{E}}}_i^{(s)}\) from \({{\varvec{E}}}_i^{(b)}\) according to (14). Combined with Algorithm 1, the Lagrangian multipliers can be updated. Therefore, all data we need can be calculated by each MG without a centralized controller. In addition, the information exchange between MGs is limited to Lagrange multipliers \({\lambda _i}\) and the expected purchasing energy \({E_{j,i}}\), which is only communicated to the corresponding MG j. Therefore, the privacy of MGs can be preserved.

According to Algorithm 1, the price \(\lambda _i\) would be modified constantly before the supply-demand balance. When the energy offered by MG is less than the requested energy from other MGs, the price will be increased as the demand exceeds supply; whereas the price will be decreased as the demand is less than supply. The price remains constant when the supply matches the demand.

4 Numerical results

4.1 Basic data

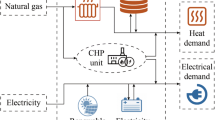
In the case study, we consider a testing IMS consisting of three different MGs, including PVs, WTs, DGs, CHPs and heat-only units. The interconnection topology of IMS is shown in Fig. 1. Fuel coefficients of DG, CHP and heat-only unit are shown in Table 1 and Table 2, respectively. The capacities of CHP and heat-only unit are listed in Table 3. The demand versus price coefficients are presented in Table 4. The parameters in the algorithm are set as follows: \(n=20,\varepsilon =10^{-5}, \alpha =100\).

Fig. 1
figure 1

Connection topology of IMS

Full size image
Table 1 Fuel coefficients and capacity of DGs
Full size table
Table 2 Fuel coefficients of CHP and heat-only units
Full size table
Table 3 Capacity of CHP and heat-only units
Full size table
Table 4 Demand versus price coefficients
Full size table

By using the method introduced in [20], the forecasting results in one time slot are obtained, which are shown in Table 5.

Table 5 Forecasting results in one time slot
Full size table

4.2 Results and analysis of distributed optimal scheduling

1) Trading prices

Figure 2 shows the iterative process of electricity price of each MG. The results show that the algorithm converges after 38 iterations. The prices of MG1, MG2 and MG3 are 317.5522 $/MWh, 324.8854 $/MWh and 237.2819 $/MWh, respectively. The prices of MGs converge to different values in spite of the same initial prices. Moreover, Fig. 2 also shows the final selling prices of MGs have the direct relationship with their own loads, that is, the MG that consumes more electricity has a higher selling price after the convergence is achieved. For instance, MG3 receives revenue by selling energy to other MGs with a lower price, since it has a lower level of power consumption.

Fig. 2
figure 2

Iterative process of the electricity price of each MG

Full size image

In fact, as for MG3, it only generates and sells energy, whose local cost function is:

$$\begin{aligned} C_3=C_{chp1}(P_{chp1})+C_{DR}(\Delta D_3)-\lambda _3\varepsilon _3 \end{aligned}$$
(33)

The optimal price \(\lambda _3=\lambda _3^*\) can be given in the form of the marginal cost:

$$\begin{aligned} \lambda _3^*=C_{chp1}^{\prime }(P_{chp1}) \end{aligned}$$
(34)

On the contrary, MG1 only generates and buys energy from MG3, and its local cost function can be expressed as:

$$\begin{aligned} C_1&=C_{dg1}(P_{dg1})+\gamma (E_{31})+C_{heat1}(P_{heat1})\nonumber \\&\quad +C_{DR}(\Delta D_1)+\lambda _3E_{31} \end{aligned}$$
(35)

Moreover, from the perspective of MG1, \(\lambda _3=\lambda _3^*\) can be expressed as:

$$\begin{aligned} \lambda _3^*=C_{dg1}^{\prime }(P_{dg1})-\gamma ^{\prime }(E_{31}) \end{aligned}$$
(36)

Therefore, MG1 should reduce its net expenditure by buying energy. The price of MG3 after convergence can be calculated according to (34) and (36), which is consistent with the result of algorithm 1.

2) Trading energy

The iterative process of the energy trading between MGs is shown in Figs. 3, 4 and 5.

Fig. 3
figure 3

Iterative process of the trading energy quantity of MG1

Full size image
Fig. 4
figure 4

Iterative process of the trading energy quantity of MG2

Full size image
Fig. 5
figure 5

Iterative process of the trading energy quantity of MG3

Full size image

The energy trading after convergence in the current time slot can be explained as follows: MG1 purchases 0.1675 MWh energy from MG3 including \(8.4\times 10^{-4}\) MWh as power loss; MG2 purchases 0.1587 MWh energy from MG3 including \(8\times 10^{-4}\) MWh power loss; MG3 sells 0.3261 MWh. As we can observe, the total energy sold is equal to the total energy bought in the IMS. The coupling constraint \(\varepsilon _i^{(s)}={{\varvec{e}}}_i^{\rm T}{{\varvec{A}}}{{\varvec{E}}}_i^{(s)}\) is satisfied after convergence, which proves that the algorithm performs well.

During the optimization, the cost of power loss caused by power transmission between MGs is covered by the energy buyer. In this regard, the power loss is also taken into consideration during the distributed optimal scheduling.

In this time slot, MG1 purchases energy from MG3 to meet its load demand, as the marginal cost of its own generation unit is higher than the sum of selling price and the network cost of MG3. Similarly, the marginal cost of DG2 in MG2 is not economical, thus it is better to work on the lower generation limit. The insufficient load demand of MG2 is supplied by the generation of CHP2, curtailing load through DR and purchasing power from MG3.

3) DR

During the scheduling, each MG can opt to curtail load with a comprehensive consideration of the resources of the supply side and the demand side. From the above analysis, the curtailed load of different MG varies with the following factors: \(\textcircled {1}\) the discrepant generation cost due to different generation units; \(\textcircled {2}\) trading price with other MG; \(\textcircled {3}\) load characteristic; and \(\textcircled {4}\) DR cost. Figure 6 shows the load comparison before and after the DR implementation.

Fig. 6
figure 6

Load comparison before and after DR

Full size image

By calculation, the ratios of curtailed load in MG1, MG2 and MG3 are 16.96\(\%\), 7.88\(\%\) and 21.73\(\%\), respectively. Compared to Table  4, the curtailed loads in different MGs have direct relationships with coefficients \(|b_{lin}|\). For example, the load demand of MG3 is most sensitive to the DR incentive, thus the ratio of curtailed load is much higher than other MGs. Moreover, The total costs with DR and without consideration DR are 924.6475 $ and 935.0376 $ respectively. The total operation cost can be reduced through DR under the premise of meeting the basic load demand of each MG.

4) Iterative process of variables

All optimal variables including the selling energy, buying energy, generation, and curtailed load can be solved by Algorithm 1. Taking MG1 as an example, Fig. 7 shows the iterative processes of variables in the decetralized model of MG1.

After convergence, MG1 purchases 0.1675 MWh energy from MG3 including \(8.4\times 10^{-4}\) MWh as power loss. The generation of DG1 is 0.2486 MWh and the curtailed load is 0.0848 MWh. According to power balance constraint, supplied power energy is consistent with the net power load. Moreover, supplied heat energy is 0.1 MWh, which is also equal to the forecast heat demand of MG1. Similarly, the power and heat energy can be satisfied in MG2 and MG3. The heat demand is supplied by the heat-only unit in MG1 whereas CHPs in MG2 and MG3 generate power and heat simultaneously. The utilization of CHP can improve energy efficiency and reduce cost, which is also beneficial to energy savings and emission reduction.

Fig. 7
figure 7

Iterative process of the variables of MG1

Full size image

Having gained insight into the iterative process, the decision of MG1 is affected by the trading prices with MG2 and MG3. Initially, MG1 intends to buy a large quantity of energy. However, as the selling prices of MG2 and MG3 are increased with iterations, the expected buying energy of MG1 has also been reduced, whereas the generation of DG and curtailed load in MG1 is increased. Finally, all the variables of MG1 have converged to consant values. From this result, we can find that each MG can decide to curtail load, adjust generation of DG, or trade with other MGs with a comprehensive consideration of the generation cost, trading price, load characteristic and DR cost, which eventually reduces operation costs and makes power usage flexible and interactive.

Table 6 Comparison with several related papers
Full size table

5) Benefits of interconnection

By using the same basic data, we assume that each MG can also be operated independently. Figure 8 shows the cost comparison of each MG between isolated and interconnected operation.

Fig. 8
figure 8

Cost comparison of each MG between isolated and interconnected operation

Full size image

The results show that trading not only reduces the total operation cost, but also cuts down the expenditure of each individual MG. This is because MG3 achieves revenue by selling energy whereas MG1 and MG2 decrease their cost by purchasing energy.

4.3 Comparison with the related work

In order to illustrate the benefits and advantages of the proposed model and algorithm, the results are compared to several related papers mentioned in the Introduction section, in terms of exchanged information, the type of DERs, DR, power loss, the number of MGs, solution algorithm and performances. The comparative results are shown in Table 6 where algorithm performance indicators including iteration number and iteration time are obtained based on the same test case. Note that the method in [7] can only be applied for two interconnected MGs. Thus, we only use part of the IMS (as shown in Fig. 1, MG1 and MG2) as the test case for method of [7].

The results show that the proposed method features advantages in several aspects, especially in system modeling and algorithm performance, as compared to the related studies. First, we have incorporated the CHP and DR into the model, which makes the optimal scheduling model more realistic with respect to the practical applications. Second, the proposed algorithm has shown a better convergence performance as compared with the algorithm proposed in [9]. Finally, the optimal operation cost obtained by Algorithm 1 is almost equal to the centralized method, which is shown in Table 7.

Table 7 Cost comparison between centralized optimization and distributed optimization of IMS
Full size table

As for the exchanged information, [5] which belongs to the centralized optimization requires all measured data of sources and load to be transmitted to the system control center, which results in more requirements on the overall communication cost. Besides, sharing information of load and sources can lead to serious privacy and business information leakage, since MGs may belong to different business owners. For [7], all the expected exchange power of MGs should be shared with each other in the IMS. In this paper, the method is developed based on the distributed optimization framework of [9], the information exchanged among MGs is limited to Lagrange multipliers and the expected purchasing energy quantities, which are only communicated with the trading MGs.

As for the convergence performance of algorithms, the results show that the proposed algorithm has an improved performance compared to the distributed subgradient algorithm of [9]. In order to find details of the convergence process, we have obtained the iterative process comparison of price in MG1 between this paper and [9] based on the same test case, as shown in Fig. 9.

Fig. 9
figure 9

Iterative process comparison of price in MG1 between this study and that in [9]

Full size image

The initial prices of MG1 in this paper and [9] are same before iteration. In this paper, the search direction of first iteration is the subgradient direction, which is same as initial search direction in [9]. Therefore, the prices of MG1 in this paper and [9] are same at the first iteration. Next, the algorithm based on subgradient with dynamic search direction has a faster iteration speed. Finally, the prices of MG1 in this paper and [9] converge to the same value. Obviously, the proposed algorithm has a better convergence performance. Considering that the MGs should be operated in a distributed manner, better convergence speed would finally lower the interaction time with less data exchanges.

Having gained insight into this result, the search routine of subgradient algorithm seems sawtooth shaped. In the local space, the subgradient is the fastest direction for the increasing of objective function value. Thereby, it should be a good choice to search on the subgradient direction. However, in the global space, the convergence speed would be slowed down due to the existence of sawtooth shaped routine. For this drawback, we have extended the subgradient algorithm with the dynamic search directions. During each round of iteration, the initial search direction is obtained by subgradient; after that, the following search directions are constructed based on the combination of conjugacy and subgradient methods. By using the dynamic search direction, the proposed algorithm has addressed the problem caused by the searching routine of sawtooth type, and eventually expedited the convergence.

5 Conclusion

In this paper, we present a distributed energy management method for interconnected operation of CHP-based MGs. An hour-ahead optimal scheduling model is built, and the objective function includes the operation cost of CHPs, DGs, DR and network tariff. Considering each MG is operated independently, the optimal scheduling problem is decentralized into n sub-problems in accordance with the number of the associated MGs. Moreover, a distributed iterative algorithm is proposed based on the subgradient method considering the dynamic search direction. From numerical simulations, we have shown that each MG can choose to curtail load, adjust generation of DGs or trade with other MGs with a comprehensive consideration of generation cost, trading price, load characteristic and DR cost, which eventually reduces operation costs and makes power utilization more flexible and more interactive. Compared with the related studies, we have also shown the advantageous features in the proposed method on modeling and algorithm performance.