Comprehensive comparison of the delta- and wye-connected autotransformer applied to 12-pulse rectifier

Abstract

12-pulse rectifier is extensively used in high power rectification, and the delta-connected autotransformer and wye-connected autotransformer are its two most popular phase-shift transformers. This paper compares the 12-pulse rectifiers using the two transformers via calculating the input line current, load voltage, kVA ratings of the two autotransformer, kVA ratings of the auxiliary magnetic devices. From the viewpoint of power quality of AC mains and DC side, the two 12-pulse rectifiers are the same. The kVA rating of the IPR in the two 12-pulse rectifiers are equal, and the kVA rating of the ZSBT in the two 12-pulse rectifier are also equal to each other, under the same load power. However, the kVA of the delta-connected autotransformer is less than that of the wye-connected autotransformer under the same load power. Some experimental results are shown to validate the correctness of the theoretical analysis.

1 Introduction

Because of its simple system configuration, low EMI at input ac mains and reduced voltage rippled dc side, multi-pulse rectifier (MPR) is widely used in adjustable speed drives, electro-chemical processes, aircraft converter systems and renewable energy conversion systems [1–6]. A MPR comprises a phase-shifting transformer and several three-phase diode bridge rectifiers, where the harmonics generated by one rectifier can be cancelled by other rectifiers [7]. The phase-shifting transformer produces a set of 3N-phase voltages with proper phase-shift angle to feed the three-phase diode bridge rectifiers [8]. Therefore, the phase-shifting transformer is the necessary device in MPR.

Generally, the phase-shifting transformer can be classified into two types. One is the isolated transformer, and another is the autotransformer [9–14]. Compared with the isolated transformer, the windings in auto-connected transformer are inter-connected. Therefore, the auto-connected transformer has lower kVA rating than that of the isolated transformer [13]. When the difference between the input and output voltages are not much, the auto-connected transformer is suitable to be a phase-shifting transformer in MPR. There are lots of different winding connections about auto-connected transformer, such as the delta-connection, wye-connection, polygon-connection, T-connection, and the fork-connection [1].

In MPRs, the phase-shifting transformer determines the power density of the rectifier. Among the auto-connected transformers, the transformer used in the 12-pulse rectifier has the highest power density. The six-phase delta- and wye-connected autotransformers are the most popular in 12-pulse rectifier. Therefore, it is meaningful to compare the delta- and wye-connected autotransformers. In this paper, we compare the two autotransformers from the input line current, load voltage, kVA rating under the same output power. Some simulations and experiments are carried out to validate the theoretical analysis.

2 Input line currents and load voltage of 12-pulse rectifier

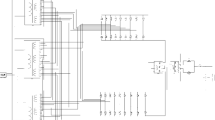
Figure 1 shows the 12-pulse rectifier using autotransformer. The autotransformer is used to produce two sets of three-phase voltages with 30^o phase-shift. The function of the IPR (IPR: Inter-phase Reactor) is to absorb the output voltage difference of two bridge rectifiers, which can ensure the independent operation of the two bridge rectifiers. The ZSBT (Zero-sequence Blocking Transformer) exhibits high impedance to zero-sequence currents, which is used to promote 120^o conduction for each rectifier diode [5].

Fig. 1

12-pulse rectifier using auto-connected transformer

Figure 2 shows the winding connection of delta-connected autotransformer and its phase diagram.

Fig. 2

Winding connection of delta-connected autotransformer and its phase diagram

In Fig. 2a, N _∆ is the turn numbers of the delta-connected winding, and N _q∆ is the turn numbers of the extended winding of the autotransformer.

Figure 3 illustrates the winding connection of wye-connected autotransformer and its phase diagram.

Fig. 3

Winding connection of wye-connected autotransformer and its phase diagram

In Fig. 3a, N _Y is the turn numbers of the wye-connected winding, and N _Y∆ is the turn numbers of the extended winding of the autotransformer.

From Fig. 2, the relation between the turn numbers of the delta-connected autotransformer meet

$$\frac{{N_{\Delta } }}{{N_{{{\text{q}}\Delta }} }} = \frac{\sqrt 3 }{2 - \sqrt 3 }$$

(1)

From Fig. 3, the relation between the turn numbers of the wye-connected autotransformer meet

$$\frac{{N_{\text{Y}} }}{{N_{\text{qY}} }} = 2 + \sqrt 3$$

(2)

Assume the three-phase input phase voltage as

$$\left\{ \begin{aligned} \begin{array}{lll}u_{\text{a}} = \sqrt 2 U_{\text{m}} \sin \omega t \hfill \\ u_{\text{b}} = \sqrt 2 U_{\text{m}} \sin (\omega t - 120^{ \circ } ) \hfill \\ u_{\text{c}} = \sqrt 2 U_{\text{m}} \sin (\omega t + 120^{ \circ } ) \hfill \\ \end{array} \end{aligned} \right.$$

(3)

From Fig. 2b, the two sets of three-phase output voltages of the delta-connected autotransformer are calculated as

$$\left\{ \begin{aligned} \begin{array}{lll}u_{{{\text{a1}}\Delta }} = \sqrt 2 U_{{{\text{n}}\Delta }} \sin (\omega t + 15^{\text{o}} )\hfill \\ u_{{{\text{b1}}\Delta }} = \sqrt 2 U_{{{\text{n}}\Delta }} \sin (\omega t - 105^{\text{o}} ) \hfill \\ u_{{{\text{c1}}\Delta }} = \sqrt 2 U_{{{\text{n}}\Delta }} \sin (\omega t + 135^{\text{o}} ) \hfill \\ u_{{{\text{a2}}\Delta }} = \sqrt 2 U_{{{\text{n}}\Delta }} \sin (\omega t - 15^{\text{o}} )\hfill \\ u_{{{\text{b2}}\Delta }} = \sqrt 2 U_{{{\text{n}}\Delta }} \sin (\omega t - 135^{\text{o}} ) \hfill \\ u_{{{\text{c2}}\Delta }} = \sqrt 2 U_{{{\text{n}}\Delta }} \sin (\omega t + 105^{\text{o}} ) \hfill \\ \end{array} \end{aligned} \right.$$

(4)

where $U_{{{\text{n}}\Delta }} = (\sqrt 6 - \sqrt 2 )U_{\text{m}}$.

From Fig. 3b, the two sets of three-phase output voltages of the wye-connected autotransformer are calculated as

$$\left\{ \begin{aligned} \begin{array}{lll} u_{\text{a1Y}} = \sqrt 2 U_{\text{nY}} \sin (\omega t + 15^{^\circ } )\hfill \\ u_{\text{b1Y}} = \sqrt 2 U_{\text{nY}} \sin (\omega t - 105^{^\circ } ) \hfill \\ u_{\text{c1Y}} = \sqrt 2 U_{\text{nY}} \sin (\omega t + 135^{^\circ } ) \hfill \\ u_{\text{a2Y}} = \sqrt 2 U_{\text{nY}} \sin (\omega t - 15^{^\circ } )\hfill \\ u_{\text{b2Y}} = \sqrt 2 U_{\text{nY}} \sin (\omega t - 135^{^\circ } ) \hfill \\ u_{\text{c2Y}} = \sqrt 2 U_{\text{nY}} \sin (\omega t + 105^{^\circ } ) \hfill \\ \end{array} \end{aligned} \right.$$

(5)

where $U_{\text{nY}} = \sqrt 6 (\sqrt 3 - 1 )U_{\text{m}} /2$.

From (4) and (5), it is obtained that the delta-connected autotransformer operating under step up condition, and the wye-connected autotransformer operating under step down condition.

In addition, from (4), (5) and Fig. 1, it is also obtained that the switching functions of the 12-pulse rectifier with delta-connected autotransformer are the same with that of the 12-pulse rectifier with wye-connected autotransformer, that is

$$\left\{ \begin{aligned} S_{{{\text{a1}}\Delta }} = S_{\text{a1Y}} \hfill \\ S_{{{\text{b1}}\Delta }} = S_{\text{b1Y}} \hfill \\ S_{{{\text{c1}}\Delta }} = S_{\text{c1Y}} \hfill \\ S_{{{\text{a2}}\Delta }} = S_{\text{a2Y}} \hfill \\ S_{{{\text{b2}}\Delta }} = S_{\text{b2Y}} \hfill \\ S_{{{\text{c2}}\Delta }} = S_{\text{c2Y}} \hfill \\ \end{aligned} \right.$$

(6)

where S _a1△, S _a2△, S _b1△, S _b2△, S _c1△, S _c2△ are the switching functions of phases a1, a2, b1, b2, c1, c2 in the 12-pulse rectifier with delta-connected autotransformer, respectively; S _a1Y, S _a2Y, S _b1Y, S _b2Y, S _c1Y, S _c2Y are the switching functions of phases a1, a2, b1, b2, c1, c2 in the 12-pulse rectifier with wye-connected autotransformer.

From (4), the switching function S _a1△ can be derived, as illustrated in Fig. 4.

Fig. 4

Switching function of S _a1△

The relation between the switching functions meets

$$\left\{ \begin{aligned} \begin{array}{lll} S_{{{\text{a1}}\Delta }} = S_{\text{a1Y}} \hfill \\ S_{{{\text{b1}}\Delta }} = S_{\text{b1Y}} = S_{{{\text{a1}}\Delta }} \angle \,{-}120^{^\circ } \hfill \\ S_{{{\text{c1}}\Delta }} = S_{\text{c1Y}} = S_{{{\text{a1}}\Delta }} \angle \,{+}120^{^\circ } \hfill \\ S_{{{\text{a2}}\Delta }} = S_{\text{a2Y}} = S_{{{\text{a1}}\Delta }} \angle \,{-}30^{^\circ } \hfill \\ S_{{{\text{b2}}\Delta }} = S_{\text{b2Y}} = S_{{{\text{b1}}\Delta }} \angle \,{-}30^{^\circ } \hfill \\ S_{{{\text{c2}}\Delta }} = S_{\text{c2Y}} = S_{{{\text{c1}}\Delta }} \angle \,{-}30^{^\circ } \hfill \\ \end{array} \end{aligned} \right.$$

2.1 Input line current

In Fig. 2a, when using the delta-connected autotransformer, from the ampere-turn balance law, the three-phase input line currents are expressed as

$$\left\{ \begin{aligned} i_{{{\text{a}}\Delta }} = i_{1\Delta } - i_{3\Delta } + i_{{{\text{a1}}\Delta }} + i_{{{\text{a2}}\Delta }} \hfill \\ i_{{{\text{b}}\Delta }} = i_{2\Delta } - i_{1\Delta } + i_{{{\text{b1}}\Delta }} + i_{{{\text{b2}}\Delta }} \hfill \\ i_{{{\text{c}}\Delta }} = i_{3\Delta } - i_{2\Delta } + i_{{{\text{c1}}\Delta }} + i_{{{\text{c2}}\Delta }} \hfill \\ \end{aligned} \right.$$

(7)

and from Kirchhoff’s current law, it is obtained that

$$\left\{ \begin{aligned} N_{\Delta } i_{1\Delta } = N_{{{\text{q}}\Delta }} \left( {i_{{{\text{c}}2\Delta }} - i_{{{\text{c}}1\Delta }} } \right) \hfill \\ N_{\Delta } i_{2\Delta } = N_{q\Delta } \left( {i_{{{\text{a}}2\Delta }} - i_{{{\text{a}}1\Delta }} } \right) \hfill \\ N_{\Delta } i_{3\Delta } = N_{q\Delta } \left( {i_{{{\text{b}}2\Delta }} - i_{{{\text{b}}1\Delta }} } \right) \hfill \\ \end{aligned} \right.$$

(8)

From (1), (7) and (8), the input line current is calculated as

$$\left\{ \begin{aligned} i_{{{\text{a}}\Delta }} = i_{{{\text{a1}}\Delta }} + i_{{{\text{a2}}\Delta }} + \frac{2 - \sqrt 3 }{\sqrt 3 }\left( {i_{{{\text{c2}}\Delta }} - i_{{{\text{b2}}\Delta }} + i_{{{\text{b1}}\Delta }} - i_{{{\text{c1}}\Delta }} } \right) \hfill \\ i_{{{\text{b}}\Delta }} = i_{{{\text{b1}}\Delta }} + i_{{{\text{b2}}\Delta }} + \frac{2 - \sqrt 3 }{\sqrt 3 }\left( {i_{{{\text{a2}}\Delta }} - i_{{{\text{c2}}\Delta }} + i_{{{\text{c1}}\Delta }} - i_{{{\text{a1}}\Delta }} } \right) \hfill \\ i_{{{\text{c}}\Delta }} = i_{{{\text{c1}}\Delta }} + i_{{{\text{c2}}\Delta }} + \frac{2 - \sqrt 3 }{\sqrt 3 }\left( {i_{{{\text{b2}}\Delta }} - i_{{{\text{a2}}\Delta }} + i_{{{\text{a1}}\Delta }} - i_{{{\text{b1}}\Delta }} } \right) \hfill \\ \end{aligned} \right.$$

(9)

When the load is large inductive, the load current is viewed to be constant. Therefore, the output currents of the two diode bridge rectifiers are calculated as

$$i_{\text{d1}} = i_{\text{d2}} = \frac{1}{2}I_{\text{d}}$$

(10)

From Fig. 1, the input currents of the two diode bridge rectifiers is calculated as

$$\left\{ \begin{aligned} \begin{array}{lll} i_{\text{a1}} = S_{{{\text{a1}}\Delta }} i_{\text{d1}} = S_{\text{a1Y}} i_{\text{d1}} \hfill \\ i_{\text{b1}} = S_{{{\text{b1}}\Delta }} i_{\text{d1}} = S_{\text{b1Y}} i_{\text{d1}} \hfill \\ i_{\text{c1}} = S_{{{\text{c1}}\Delta }} i_{\text{d1}} = S_{\text{c1Y}} i_{\text{d1}} \hfill \\ i_{\text{a2}} = S_{{{\text{a2}}\Delta }} i_{\text{d2}} = S_{\text{a2Y}} i_{\text{d2}} \hfill \\ i_{\text{b2}} = S_{{{\text{b2}}\Delta }} i_{\text{d2}} = S_{\text{b2Y}} i_{\text{d2}} \hfill \\ i_{\text{c2}} = S_{{{\text{c2}}\Delta }} i_{\text{d2}} = S_{\text{c2Y}} i_{\text{d2}} \hfill \\ \end{array} \end{aligned} \right.$$

(11)

Substituting (11) into (9) yields

$$\left\{ \begin{aligned} i_{{{\text{a}}\Delta }} = \frac{1}{2}I_{\text{d}} \left[ {S_{{{\text{a1}}\Delta }} + S_{{{\text{a2}}\Delta }} + \frac{2 - \sqrt 3 }{\sqrt 3 }\left( {S_{{{\text{c2}}\Delta }} - S_{{{\text{b2}}\Delta }} + S_{{{\text{b1}}\Delta }} - S_{{{\text{c1}}\Delta }} } \right)} \right] \hfill \\ i_{{{\text{b}}\Delta }} = \frac{1}{2}I_{\text{d}} \left[ {S_{{{\text{b1}}\Delta }} + S_{{{\text{b2}}\Delta }} + \frac{2 - \sqrt 3 }{\sqrt 3 }\left( {S_{{{\text{a2}}\Delta }} - S_{{{\text{c2}}\Delta }} + S_{{{\text{c1}}\Delta }} - S_{{{\text{a2}}\Delta }} } \right)} \right] \hfill \\ i_{{{\text{c}}\Delta }} = \frac{1}{2}I_{\text{d}} \left[ {S_{{{\text{c1}}\Delta }} + S_{{{\text{c2}}\Delta }} + \frac{2 - \sqrt 3 }{\sqrt 3 }\left( {S_{{{\text{b2}}\Delta }} - S_{{{\text{a2}}\Delta }} + S_{{{\text{a2}}\Delta }} - S_{{{\text{b1}}\Delta }} } \right)} \right] \hfill \\ \end{aligned} \right.$$

(12)

To set i _a∆ as an example, the Fourier series Expansion of i _a∆ can calculated as

$$i_{{{\text{a}}\Delta }} = \frac{ 2\sqrt 6 (\sqrt 3 - 1 )}{\pi }I_{\text{d}} \left[ {\sin (\omega t) - \sum\limits_{k = 1}^{\infty } {\frac{\sin (12k \pm 1)\omega t}{12k \pm 1}} } \right]$$

(13)

Similarly, in Fig. 3a, from the ampere-turn balance law, it is obtained that

$$\left\{ \begin{aligned} N_{\text{qY}} i_{\text{c2Y}} + N_{\text{qY}} i_{\text{b1Y}} = N_{\text{Y}} i_{{ 1 {\text{Y}}}} \hfill \\ N_{\text{qY}} i_{\text{a2Y}} + N_{\text{qY}} i_{\text{c1Y}} = N_{\text{Y}} i_{{ 2 {\text{Y}}}} \hfill \\ N_{\text{qY}} i_{\text{b2Y}} + N_{\text{qY}} i_{\text{a1Y}} = N_{\text{Y}} i_{{ 3 {\text{Y}}}} \hfill \\ \end{aligned} \right.$$

(14)

and from Kirchhoff’s current law, it is obtained that

$$\left\{ \begin{aligned} i_{\text{aY}} = i_{{ 1 {\text{Y}}}} + i_{\text{a1Y}} + i_{\text{a2Y}} \hfill \\ i_{\text{bY}} = i_{{ 2 {\text{Y}}}} + i_{\text{b1Y}} + i_{\text{b2Y}} \hfill \\ i_{\text{cY}} = i_{{ 3 {\text{Y}}}} + i_{\text{c1Y}} + i_{\text{c2Y}} \hfill \\ \end{aligned} \right.$$

(15)

From (2), (14) and (15), the input line currents are calculated as

$$\left\{ {\begin{array}{*{20}c} {i_{\text{aY}} = (2 - \sqrt 3 )\left( {i_{\text{b1Y}} + i_{\text{c2Y}} } \right) + i_{\text{a1Y}} + i_{\text{a2Y}} } \\ {i_{\text{bY}} = (2 - \sqrt 3 )\left( {i_{\text{c1Y}} + i_{\text{a2Y}} } \right) + i_{\text{b1Y}} + i_{\text{b2Y}} } \\ {i_{\text{cY}} = (2 - \sqrt 3 )\left( {i_{\text{a1Y}} + i_{\text{b2Y}} } \right) + i_{\text{c1Y}} + i_{\text{c2Y}} } \\ \end{array} } \right.$$

(16)

Substituting (10) and (11) into (16) yields

$$\left\{ {\begin{array}{*{20}c} {i_{\text{aY}} = \frac{1}{2}I_{\text{d}} \left[ { (2 - \sqrt 3 )\left( {S_{\text{b1Y}} + S_{\text{c2Y}} } \right) + S_{\text{a1Y}} + S_{\text{a2Y}} } \right]} \\ {i_{\text{bY}} = \frac{1}{2}I_{\text{d}} \left[ { (2 - \sqrt 3 )\left( {S_{\text{c1Y}} + S_{\text{a2Y}} } \right) + S_{\text{b1Y}} + S_{\text{b2Y}} } \right]} \\ {i_{\text{cY}} = \frac{1}{2}I_{\text{d}} \left[ { (2 - \sqrt 3 )\left( {S_{\text{a1Y}} + S_{\text{b2Y}} } \right) + S_{\text{c1Y}} + S_{\text{c2Y}} } \right]} \\ \end{array} } \right.$$

(17)

To set i _aY as an example, the Fourier series Expansion of i _aY can calculated as

$$i_{\text{aY}} = \frac{3\sqrt 6 (\sqrt 3 - 1 )}{2\pi }I_{\text{d}} \left[ {\sin (\omega t) - \sum\limits_{k = 1}^{\infty } {\frac{\sin (12k \pm 1)\omega t}{12k \pm 1}} } \right]$$

(18)

Figure 5a shows the input line current i _a∆, and Fig. 5b shows the input line current i _aY, and Fig. 5c shows their spectrum.

Fig. 5

Input line currents of the two 12-pulse rectifiers and their spectrum

From (13), (18), and Fig. 5, the following conclusions are obtained:

• 1) Under the same load current, when using the delta-connected autotransformer, the input line current is greater than that of using the wye-connected autotransformer, and the RMS ratio of the current i _a∆ to current i _aY is 4/3.

• 2) The THD values of the two currents are equal to each other, and the spectrums of the two currents are the same.

2.2 Load voltage

From Fig. 1, when using the delta-connected autotransformer, the load voltage can be presented as

$$\begin{aligned} u_{{{\text{d}}\Delta }} & = v_{{{\text{Mn}}\Delta }} - v_{{{\text{Nn}}\Delta }} = \frac{1}{2}\left( {v_{{{\text{m1n}}\Delta }} - v_{{{\text{m}}2{\text{n}}\Delta }} } \right) + \frac{1}{2}\left( {v_{{{\text{m3n}}\Delta }} - v_{{{\text{m}}4{\text{n}}\Delta }} } \right) \\ & = \frac{1}{2}\left( {u_{{{\text{d1}}\Delta }} + u_{{{\text{d2}}\Delta }} } \right) \\ \end{aligned}$$

(19)

The output voltages of the two diode bridge rectifiers can be derived from the modulation theory

$$\left\{ \begin{aligned} u_{{{\text{d1}}\Delta }} = S_{{{\text{a1}}\Delta }} u_{{{\text{a1}}\Delta }} + S_{{{\text{b1}}\Delta }} u_{{{\text{b1}}\Delta }} + S_{{{\text{c1}}\Delta }} u_{{{\text{c1}}\Delta }} \hfill \\ u_{{{\text{d2}}\Delta }} = S_{{{\text{a2}}\Delta }} u_{{{\text{a2}}\Delta }} + S_{{{\text{b2}}\Delta }} u_{{{\text{b2}}\Delta }} + S_{{{\text{c2}}\Delta }} u_{{{\text{c2}}\Delta }} \hfill \\ \end{aligned} \right.$$

(20)

From (3), (4) and (20), the load voltage u _d∆ is calculated as

$$u_{{{\text{d}}\Delta }} = \left\{ {\begin{array}{lll} {\sqrt 6 U_{\text{m}} \cos \left( {\omega t - \frac{k\pi }{6}} \right)} & {\left[ {\frac{k\pi }{6},\frac{k\pi }{6} + \frac{\pi }{12}} \right]} \\ {\sqrt 6 U_{\text{m}} \cos \left( {\omega t - \frac{\pi }{6} - \frac{k\pi }{6}} \right)} & {\left[ {\frac{k\pi }{6} + \frac{\pi }{12},\frac{k\pi }{6} + \frac{2\pi }{12}} \right]} \\ \end{array} } \right.$$

(21)

Similarly, when using the wye-connected autotransformer, the load voltage is calculated as

$$u_{{{\text{d}}Y}} = \left\{ {\begin{array}{lll} {\frac{3\sqrt 2 }{2}U_{\text{m}} \cos \left( {\omega t - \frac{k\pi }{6}} \right)} & {\left[ {\frac{k\pi }{6},\frac{k\pi }{6} + \frac{\pi }{12}} \right]} \\ {\frac{3\sqrt 2 }{2}U_{\text{m}} \cos \left( {\omega t - \frac{\pi }{6} - \frac{k\pi }{6}} \right)} & {\left[ {\frac{k\pi }{6} + \frac{\pi }{12},\frac{k\pi }{6} + \frac{2\pi }{12}} \right]} \\ \end{array} } \right.$$

(22)

Figure 6 shows the load voltages u _d∆ and u _dY.

Fig. 6

Load voltages when using different autotransformers

From (21), (22) and Fig. 6, when using the delta-connected autotransformer, the load voltage is greater than that of using the wye-connected autotransformer under the same input voltages.

3 kVA ratings of delta-connected autotransformer and wye-connected autotransformer

The phase-shifting transformer is the main magnetic device in a MPR, which determines the power density of the system. Therefore, it is meaningful to compare the kVA ratings of the two autotransformers under the same load power.

In order to calculate the kVA rating of the autotransformer, it is necessary to calculate the voltages across and currents through the windings of the autotransformer.

3.1 kVA rating of delta-connected autotransformer

From Fig. 2, the voltage across the delta-connected winding is equal to the input line-to-line voltage, and its RMS is $\sqrt 3$ U _m. From (1), the RMS of the voltage across the extended winding is equal to $(2 - \sqrt 3 )$ U _m.

From Fig. 4 and (11), the RMS of current through the extended winding is

$$I_{{{\text{a}}1\Delta }} = I_{{{\text{b}}1\Delta }} = I_{{{\text{c}}1\Delta }} = I_{{{\text{a}}2\Delta }} = I_{{{\text{b}}2\Delta }} = I_{{{\text{c}}2\Delta }} = \frac{\sqrt 6 }{6}I_{{{\text{d}}\Delta }}$$

(23)

where I _d∆ is the load current when using delta-connected autotransformer.

From Fig. 4, (1) and (8), the RMS of the current through the delta-connected winding is

$$I_{1\Delta } = I_{2\Delta } = I_{3\Delta } = \frac{2 - \sqrt 3 }{6}I_{{{\text{d}}\Delta }}$$

(24)

Therefore, the kVA rating of the delta-connected autotransformer is

$$\begin{aligned} S_{{\rm delta}{\text{-}}{\rm con}{\text{-}}{\rm tra}} & = \frac{1}{2}\left[ {6 (2 - \sqrt 3 )U_{\text{m}} \frac{\sqrt 6 }{6}I_{{{\text{d}}\Delta }} + 3\sqrt 3 U_{\text{m}} \frac{2 - \sqrt 3 }{6}I_{{{\text{d}}\Delta }} } \right] \\ & = \frac{1}{4} (2 - \sqrt 3 )\sqrt 3 (2\sqrt 2 + 1 )U_{\text{m}} I_{{{\text{d}}\Delta }} \\ \end{aligned}$$

(25)

From (21), the RMS value of the load voltage is calculated as

$$U_{{{\text{d}}\Delta }} = \frac{{\sqrt 3 \sqrt {\pi + 3} U_{\text{m}} }}{\sqrt \pi }$$

(26)

Substituting (26) into (25) yields

$$\begin{aligned} S_{{\rm delta}{\text{-}}{\rm con}{\text{-}}{\rm tran}} & = \frac{(2 - \sqrt 3 )(2\sqrt 2 + 1)\sqrt \pi }{{4\sqrt {\pi + 3} }}U_{{{\text{d}}\Delta }} I_{{{\text{d}}\Delta }} \\ & = 18.34\% \;U_{{{\text{d}}\Delta }} I_{{{\text{d}}\Delta }} \\ \end{aligned}$$

(27)

When using the delta-connected autotransformer, define the load power as

$$P_\Delta = U_{{\text{d}} \Delta} I_{{\text{d}}\Delta}$$

(28)

From (27) and (28), the kVA rating of the delta-connected autotransformer accounts for 18.34% of the load power.

3.2 kVA rating of wye-connected autotransformer

From Fig. 3, the voltage across the delta-connected winding is equal to the input phase voltage, and its RMS is U _m. From (2), the RMS value of the voltage across the extended winding is equal to $(2 - \sqrt 3 )$ U _m.

From Fig. 4 and expression (11), the RMS of current through the extended winding of the wye-connected autotransformer also meets (23), that is

$$I_{\text{a1Y}} = I_{\text{b1Y}} = I_{\text{c1Y}} = I_{\text{a2Y}} = I_{\text{b2Y}} = I_{\text{c2Y}} = \frac{\sqrt 6 }{6}I_{\text{dY}}$$

(29)

where I _dY is the load current when using wye-connected autotransformer.

From Fig. 4, expression (2) and (14), the RMS value of the current through the wye-connected winding is

$$I_{{ 1 {\text{Y}}}} = I_{{ 2 {\text{Y}}}} = I_{{ 3 {\text{Y}}}} = \frac{(2\sqrt 3 - 3)}{6}I_{\text{dY}}$$

(30)

Therefore, the kVA rating of the wye-connected autotransformer is

$$\begin{aligned} S_{{\text{wye}}{\text{-}}{\rm con}{\text{-}}{\rm tran}} & = \frac{1}{2}\left[ { 3U_{\text{m}} \frac{(2\sqrt 3 - 3)}{6}I_{\text{dY}} + 6 ( 2- \sqrt 3)U_{\text{m}} \frac{\sqrt 6 }{6}I_{\text{dY}} } \right] \\ & = \frac{1 + 2\sqrt 2 }{4} ( 2- \sqrt 3)\sqrt 3 U_{\text{m}} I_{\text{dY}} \\ \end{aligned}$$

(31)

From (22), the RMS of the load voltage is

$$U_{\text{dY}} = \frac{{3\sqrt {\pi + 3} U_{\text{m}} }}{2\sqrt \pi }$$

(32)

Substituting (32) into (31) yields

$$S_{{\text{wye}}{\text{-}}{\rm con}{\text{-}}{\rm tran}} = \frac{ ( 2- \sqrt 3) (1 + 2\sqrt 2 )\sqrt \pi }{{2\sqrt 3 \sqrt {\pi + 3} }}U_{\text{dY}} I_{\text{dY}} = 21.18\% \;U_{\text{dY}} I_{\text{dY}}$$

(33)

When using the wye-connected autotransformer, define the load power as

$$P_{\text{Y}} = U_{\text{dY}} I_{\text{dY}}$$

(34)

From (33) and (34), the kVA rating of the wye-connected autotransformer accounts for 21.28% of the load power.

From (23) and (29), under the same load current, the RMS of currents through the extended windings of the wye-connected autotransformer is larger than that of the delta-connected autotransformer. Therefore, under the same load power, the kVA rating of the wye-connected autotransformer is greater than that of the delta-connected autotransformer.

4 kVA rating of the auxiliary magnetic devices

IPR and ZSBT are the important auxiliary magnetic devices in MPR using auto-connected transformer. Therefore, it is necessary to calculate their kVA rating and compare it under the same load power.

In Fig. 1, the voltage across IPR can be expressed as

$$\begin{aligned} u_{\text{IPR}} & = v_{\text{m1n}} - v_{\text{m3n}} - \left( {v_{\text{m2n}} - v_{\text{m4n}} } \right) \\ & = v_{\text{m1n}} - v_{\text{m2n}} - \left( {v_{\text{m3n}} - v_{\text{m4n}} } \right) \\ & = u_{\text{d1}} - u_{\text{d2}} \\ \end{aligned}$$

(35)

where v _m1n, v _m2n, v _m3n, v _m4n are the potentials of points m1, m2, m3, m4, respectively.

Substituting (20) into (35), when using the delta-connected autotransformer, the RMS of the voltage across IPR is

$$U_{{{\text{IPR}}{\text{-}}\Delta }} = \frac{{2\sqrt 3 ( 2- \sqrt 3 )\sqrt {\pi - 3} }}{\sqrt \pi }U_{\text{m}}$$

(36)

Similarly, when using wye-connected autotransformer, the RMS of the voltage across IPR is calculated as

$$U_{{\text{IPR}}{\text{-}}{\rm Y}} = \frac{{3 ( 2- \sqrt 3 )\sqrt {\pi - 3} }}{\sqrt \pi }U_{\text{m}}$$

(37)

From Fig. 1, the voltage across ZSBT meets

$$u_{\text{ZSBT}} = \frac{1}{2}\left( {v_{{{\text{m}}2{\text{n}}}} - v_{\text{m4n}} } \right)$$

(38)

From Fig. 1, v _m2n and v _m4n meet

$$\left\{ \begin{aligned} v_{\text{m2n}} = S_{\text{a1}}^{{\prime \prime }} u_{\text{a1}} + S_{\text{b1}}^{{\prime \prime }} u_{\text{b1}} + S_{\text{c1}}^{{\prime \prime }} u_{\text{c1}} \hfill \\ v_{\text{m4n}} = S_{\text{a2}}^{{\prime \prime }} u_{\text{a2}} + S_{\text{b2}}^{{\prime \prime }} u_{\text{b2}} + S_{\text{c2}}^{{\prime \prime }} u_{\text{c2}} \hfill \\ \end{aligned} \right.$$

(39)

where $S_{\text{a1}}^{{\prime \prime }}$, $S_{\text{b1}}^{{\prime \prime }}$, $S_{\text{c1}}^{{\prime \prime }}$, $S_{\text{a2}}^{{\prime \prime }}$, $S_{\text{b2}}^{{\prime \prime }}$, $S_{\text{c2}}^{{\prime \prime }}$meet

$$S_{i 1}^{{\prime \prime }} = \frac{1}{2}\left( {\left| {S_{i 1} } \right| - S_{i 1} } \right)$$

(40)

where i = a, b, c.

Therefore, from (6), (38), (39) and Fig. 4, when using the delta-connected autotransformer, the RMS of the voltage across ZSBT is calculated as

$$U_{{{\text{ZSBT}}{\text{-}}\Delta }} = \sqrt {\frac{8 - 3\sqrt 3 }{2} - \frac{9 - 3\sqrt 3 }{\pi }} \frac{{U_{\text{m}} }}{(\sqrt 3 + 1)}$$

(41)

When using the wye-connected autotransformer, the RMS of the voltage across ZSBT is calculated as

$$U_{{\text{ZSBT}}{\text{-}}{\rm Y}} = \sqrt {\frac{8 - 3\sqrt 3 }{2} - \frac{9 - 3\sqrt 3 }{\pi }} \frac{\sqrt 3 }{ 2 (\sqrt 3 + 1 )}U_{\text{m}}$$

(42)

The currents through the IPR and ZSBT are equal to the output currents of the two bridge rectifiers. Therefore, the currents through IPR and ZSBT meet

$$\left\{ \begin{aligned} \begin{array}{lll} I_{{{\text{IPR}}{\text{-}}{\text{ZSBT}}{\text{-}}\Delta }} = \frac{1}{2}I_{{{\text{d}}\Delta }} \hfill \\ I_{{\text{IPR}}{\text{-}}{\rm ZSBT}{\text{-}}{\rm Y}} = \frac{1}{2}I_{\text{dY}} \hfill \\ \end{array} \end{aligned} \right.$$

(43)

Therefore, when using the delta-connected autotransformer, the kVA rating of IPR is calculated as

$$S_{{{\text{IPR}}{\text{-}}\Delta }} = \frac{{ ( 2- \sqrt 3 )\sqrt {\pi - 3} }}{{2\sqrt {\pi + 3} }}U_{{{\text{d}}\Delta }} I_{{{\text{d}}\Delta }} { = }2.03\%\;U_{{{\text{d}}\Delta }} I_{{{\text{d}}\Delta }}$$

(44)

and the kVA rating of IPR when using the wye-connected autotransformer is calculated as

$$\begin{aligned} S_{{\text{IPR}}{\text{-}}{\text{Y}}} & = \frac{{ ( 2- \sqrt 3 )\sqrt {\pi - 3} }}{{2\sqrt {\pi + 3} }}U_{\text{dY}} I_{\text{dY}} \\ & = 2.03\% \; U_{\text{dY}} I_{\text{dY}} \\ \end{aligned}$$

(45)

When using the delta-connected autotransformer, the kVA rating of ZSBT is calculated as

$$\begin{aligned} S_{{{\text{ZSBT}}{\text{-}}\Delta }} & = \sqrt {\frac{8 - 3\sqrt 3 }{2} - \frac{9 - 3\sqrt 3 }{\pi }} \frac{\sqrt \pi }{{\sqrt {\pi + 3} }}\frac{ (3 - \sqrt 3 )}{6}U_{{{\text{d}}\Delta }} I_{{{\text{d}}\Delta }} \\ & { = }6.61\%\;U_{{{\text{d}}\Delta }} I_{{{\text{d}}\Delta }} \\ \end{aligned}$$

(46)

and the kVA rating of ZSBT when using the wye-connected autotransformer is calculated as

$$\begin{aligned} S_{{\text{ZSBT}}{\text{-}}{\text{Y}}} & = \sqrt {\frac{8 - 3\sqrt 3 }{2} - \frac{9 - 3\sqrt 3 }{\pi }} \frac{\sqrt \pi }{{\sqrt {\pi + 3} }}\frac{ (3 - \sqrt 3 )}{6}U_{\text{dY}} I_{\text{dY}} \\ & = \,6.61\% \;U_{\text{dY}} I_{\text{dY}} \\ \end{aligned}$$

(47)

From (27), (44) and (46), when using the delta-connected autotransformer, the sum of the kVA rating of the magnetic devices is calculated as

$$S_{{{\text{kVA}}{\text{-}}\Delta }} = S_{{{\text{delta}}{\text{-}}{\rm con}{\text{-}}{\rm tran}}} + S_{{{\text{ZSBT}}{\text{-}}\Delta }} + S_{{{\text{IPR}}{\text{-}}\Delta }} = 26.98\%\;U_{{{\text{d}}\Delta }} I_{{{\text{d}}\Delta }}$$

(48)

From (33), (45) and (47), when using the wye-connected autotransformer, the sum of the kVA rating of the magnetic devices is calculated as

$$S_{{\text{kVA}}{\text{-}}{\text{Y}}} = S_{{\text{wye}}{\text{-}}{\rm con}{\text{-}}{\rm tran}} + S_{{\text{ZSBT}}{\text{-}}{\text{Y}}} + S_{{\text{IPR}}{\text{-}}{\text{Y}}} = 29.82\% \;U_{\text{dY}} I_{\text{dY}}$$

(49)

From (36), (37), (41), (42), (44)–(49), the following conclusions are obtained.

• 1) Under the same input voltages, when using the delta-connected autotransformer, the voltages across ZSBT and IPR are greater than that of using wye-connected autotransformer, respectively.

• 2) Under the load power, when using the delta-connected autotransformer, the kVA ratings of ZSBT and IPR are equal to that of using wye-connected autotransformer, respectively.

• 3) Under the same load power, when using the delta-connected autotransformer, the kVA rating of the magnetic devices is less that of using wye-connected autotransformer.

5 Experimental validation

In order to validate the aforementioned analysis, we designed two 12-pulse rectifiers using delta-connected autotransformer and wye-connected autotransformer, respectively, and carried out the corresponding experiments. The experimental conditions are listed as follows: (1) The RMS value of the three-phase input voltages is 220 V; (2) The load is resistive-inductive load, and the load resistance is 20 Ω in the 12-pulse rectifier using wye-connected autotransformer, and the load resistance is 30 Ω in the 12-pulse rectifier using delta-connected autotransformer, the load inductance is 15 mH.

5.1 Experimental results of delta-connected autotransformer

Figure 7 shows the input line current. In Fig. 7, the RMS of the three current are 14.547, 14.519, 14.550 A, respectively; and the THD values of the three currents are 12.81%, 12.76%, 12.71%, respectively. Because of the effect of the leakage inductance of autotransformer, the THD of the experimental results is less than that of the theoretical results.

Fig. 7

Input line currents when using the delta-connected autotransformer

Load current and load voltage are illustrated in Fig. 8, and their RMS values are 533 V and 17.9 A, respectively. Therefore, the load power is 9540.7 W.

Fig. 8

Load current and load voltage of 12-pulse rectifier using the delta-connected autotransformer

Figure 9a shows the currents through the delta-connected windings, and their RMS values are 0.911, 0.913, 0.906 A, respectively. Figure 9b shows the voltages across and currents through the extended windings, and the RMS values of the two voltages are 58.38, 59.09 V, respectively; the RMS values of the two currents are 7.088 A, 7.144 A, respectively.

Fig. 9

Voltages across and currents through the windings of the delta-connected autotransformer

Assume the winding configuration of autotransformer is symmetrical, the kVA rating of the delta-connected autotransformer can be calculated as

$$\begin{aligned} S_{{{\text{Auto}}{\text{-}}\Delta }} & = \frac{1}{2} \times 380 \times (0.911 + 0.913 + 0.906) \\ & \quad + \frac{1}{2} \times 3 \times 58.38 \times 7.088 + \frac{1}{2} \times 3 \times 59.09 \times 7.144 \\ & = 1772.6{\text{VA}} \\ \end{aligned}$$

(51)

Therefore, the kVA rating is about 18.57% of the load power.

Figure 10 shows the voltages across the IPR and ZSBT. The RMS values of the two voltages are 47.8, 35.8 V, respectively.

Fig. 10

Voltages across ZSBT and IPR when using the delta-connected autotransformer

Assume that the system is symmetrical, output currents of the two diode bridge rectifiers are equal. From Fig. 10, the kVA ratings of ZSBT and IPR are calculated as

$$S_{{{\text{ZSBT}}{\text{-}}\Delta }} = \frac{1}{2} \times 4 \times 35.8 \times 8.95 = 640.82\;{\text{VA}}$$

(52)

$$S_{{{\text{IPR}}{\text{-}}\Delta }} = \frac{1}{2} \times 47.8 \times 8.95 = 213.91\;{\text{VA}}$$

(53)

Therefore, the kVA rating of ZSBT is 6.72% of load power, and the kVA rating of IPR is 2.24% of load power.

From (51), (52) and (53), it is obtained that the sum of the kVA ratings of the magnetic devices are 2627.33 VA, which is account for 27.54% of load power.

5.2 The experimental results of the wye-connected autotransformer

Figure 11 shows the input line current. In Fig. 11, the RMS of the three current are 16.069, 16.053, 16.079 A, respectively; and the THD values of the three currents are 12.92%, 12.73%, 12.67%, respectively. Similarly, because of the effect of the leakage inductance of autotransformer, the THD of the experimental results is less than that of the theoretical results.

Fig. 11

Input line currents when using wye-connected autotransformer

Load current and load voltage are shown in Fig. 12, and their RMS values are 462 V and 22.4 A, respectively. Therefore, the load power is about 10348.8 W.

Fig. 12

Load voltage and load current of 12-pulse rectifier using the wye-connected autotransformer

Figure 13a shows the currents through the wye-connected windings, and the RMS values of the currents are 1.668, 1.678, 1.708 A, respectively. Figure 13b shows the voltages across and the currents through the extended windings, and their RMS values are 60.16 and 59.21 V, and the RMS values of the currents are 9.214 and 9.105 A.

Fig. 13

Voltage across and current through the winding of the wye-connected autotransformer

From Fig. 13, the kVA rating of the wye-connected autotransformer is

$$\begin{aligned} S_{{\text{Auto}}{\text{-}}{\text{Y}}} & = \frac{1}{2} \times 220 \times (1.668 + 1.678 + 1.708) \\ & \quad + \frac{1}{2} \times 3 \times 60.16 \times 9.214 + \frac{1}{2} \times 3 \times 59.21 \times 9.105 \\ & = 2196.072\;{\text{VA}} \\ \end{aligned}$$

(54)

The kVA rating of the autotransformer accounts for about 21.22% of the load power.

Figure 14 shows the voltages across the IPR and ZSBT. The RMS values of the two voltages are 42.4 and 30.3 V, respectively.

Fig. 14

Voltages across ZSBT and IPR when using the wye-connected autotransformer

From Figs. 13 and 14, the kVA ratings of ZSBT and IPR are calculated as

$$S_{{\text{ZSBT}}{\text{-}}{\text{Y}}} = \frac{1}{2} \times 4 \times 30.3 \times 11.2 = 678.72\;{\text{VA}}$$

(55)

$$S_{{\text{IPR}}{\text{-}}{\text{Y}}} = \frac{1}{2} \times 42.4 \times 11.2 = 153.4\;{\text{VA}}$$

(56)

Therefore, the kVA rating of ZSBT is 6.56% of load power, and the kVA rating of IPR is 2.29% of load power.

From (54), (55) and (56), it is obtained that the sum of the kVA ratings of the magnetic devices are 3028.192 VA, which is account for 29.26% of load power.

From above theoretical analysis and experimental results, the comprehensive comparison of the 12-pulse rectifier when using delta- and wye-connected autotransformer is listed in Table 1.

Table 1 Comprehensive comparison of the 12-pulse rectifier using delta- and wye- connected autotransformer

6 Conclusion

This paper compares the two 12-pulse rectifiers using delta-connected autotransformer and wye-connected autotransformer. From the theoretical analysis and experimental results, some conclusions are obtained as follows:

• 1) Both of the input line currents of the two 12-pulse rectifiers contains 12 steps, and both of the load voltage of the two 12-pulse rectifiers contains 12 pulses. Therefore, the two 12-pulse rectifiers are the same power quality.

• 2) Under the same load current, when using the delta-connected autotransformer, the input line current is greater than that of using the wye-connected autotransformer.

• 3) Because of the delta-connected autotransformer and wye-connected autotransformer operating under step-up and step-down condition, respectively, under the same input voltages, the load voltage when using the delta-connected autotransformer is greater than that of using the wye-connected autotransformer.

• 4) Under the same load power, the kVA rating of the delta-connected autotransformer is less than that of the wye-connected autotransformer.

• 5) Under the same input voltages, when using delta-connected autotransformer, the voltages across the ZSBT and IPR are greater than that of using wye-connected autotransformer, respectively.

• 6) Under the load power, when using delta-connected autotransformer, the kVA ratings of the ZSBT and IPR are equal to that of using the wye-connected autotransformer, respectively.

• 7) Under the same load power, when using delta-connected autotransformer, the kVA rating of the magnetic devices is less that of using wye-connected autotransformer.