1 Introduction

With the environmental degradation around the world, people are increasingly advocating and pursuing the green living concept, and electric vehicles (EVs) are being increasingly seen as eco-friendly vehicles. On the other hand, the oil and other traditional fossil fuel resources are being depleted, wind power and solar power are being widely studied and used as sustainable and clean energy. Wind, solar and other renewable energy naturally have the characteristics of intermittence and volatility, thus renewable energy generation will inevitably produce power fluctuations to the grid. When large-scale renewable energy connects to the grid, how to stabilize the fluctuation and improve the renewable energy integration ability of the grid becomes a serious problem. With the improvement in the EV technology and rapid rollout of EVs, EV charging is likely to have significant impact on the grid [1, 2]. Therefore, it is important to manage and influence EV charging behaviors in a controlled manner so as to reduce their impact. The controlled EV charging strategy can also improve the load characteristics of the grid, smooth the fluctuation of wind and solar power outputs, and optimize peak-valley of the grid load.

For the study of EV controlled charging and related fields, some results have been published. From the perspective of operation benefits of the charging station and by responding to the time-of-use (TOU) price of the grid, [3] uses the control methods of controlled charging to improve the economic benefits of charging stations, but it does not consider smoothing load fluctuations of the grid, it may result in an additional peak at night. Reference [4] proposes an optimized model for TOU price time-period. It uses the controlled charging of EVs to cut the peak and fill the valley of the power grid load curve, but it does not consider the value of peak-valley price and demand side response. Reference [5] considers reducing the peak-valley difference as the primary goal, taking into account the division of TOU periods and load fluctuations of the local distribution network. It does not consider the influence of the wind, solar and other new energy power on the grid load characteristics. Reference [6] establishes a mathematical model of dispatching EVs and wind power cooperatively, analyses the feasibility of dispatching the EV charging to smooth the load fluctuations and to consume the superfluous wind power at night. However, the paper does not propose specific solutions for controlled charging from the point of demand side response.

This paper develops a probabilistic model of wind and photovoltaic (PV) power outputs, and a method of assessing the peak-valley difference of the stochastic load curve is put forward. A two-stage peak-valley price model is constructed and is used to guide EV charging, an optimization model is built, in which genetic algorithms are used to determine the start and end time of the valley price, as well as the value of the peak-valley price.

2 Controlled EV charging based on demand side response

2.1 Two-stage model of peak-valley price

Firstly, the two-stage peak-valley price model is built for controlled EV charging as follows:

$$ f_{\text{p}} \left( t \right) = \left\{ {\begin{array}{*{20}l} {P_{\text{v}} } \hfill & {t_{1} <\, t < \,t_{2} } \hfill \\ {P_{\text{p}} } \hfill & {\text{else}} \hfill \\ \end{array} } \right. $$
(1)

where P v is the price of valley period; P p is the price of peak period; t 1 is the start time of valley period; t 2 is the end time of valley period.

In this paper, the peak-valley rate β is defined as:

$$ \beta = \frac{{P_{\text{p}} - P_{\text{v}} }}{{P_{0} }} $$
(2)

where P 0 is the grid original tariff when TOU pricing policies are not implemented.

2.2 Analysis of user response

With the increasing of β, the user response has three stages, as shown in Fig. 1. In the first stage, β is in the interval (0, a), users choosing to charge in valley period for tariff factor are very few. In the second stage, when β reaches a certain value, with the increasing of β, more and more users choose to charge in valley period for the price factor. In the third stage, the number of users choosing to charge in valley period stops increasing. In the figure, λ = n/N is the ratio of the responding EV users, in which n is the number of EVs charged in valley period and N is the total number of EVs.

Fig. 1
figure 1

Schematic diagram of user response

Full size image

The EV users’ responsiveness to the peak-valley rate β is also affected by the time.

$$ T_{\text{p}} + T_{\text{y}} + T_{\text{d}} = 24 $$
(3)

where T p is the period that users’ driving demand for EVs is urgent; T y is the period that users’ driving demand for EVs is common; and T d is the period that users’ driving demand for EVs is low.

In different periods, users’ response to peak-valley rate β is different, as shown in Fig. 2.

Fig. 2
figure 2

Responding curve considering driving demand factors

Full size image

So, EV users’ price response function should be a three-dimensional surface which contains peak-valley rate β and time, as shown in Fig. 3.

Fig. 3
figure 3

Response surface considering driving demand factors

Full size image

The responding users’ start time of charging is described by the formula:

$$ t_{\text{s}} = \left\{ {\begin{array}{*{20}l} {t_{1} + \alpha (t_{2} - t_{\text{c}} )} \hfill & {0 \le t_{\text{c}} <\, t_{2} - t_{1} } \hfill \\ {t_{1} } \hfill & {\text{else}} \hfill \\ \end{array} } \right. $$
(4)

where t s is the start time of charging; t c is the duration of charging; and α is a random number in interval (0,1).

When the charging time is shorter than the valley period, users will choose any time in the valley period that EV can be fully charged, and when the charging time is longer than the valley period, users will choose the start time of valley period to charge.

3 Probabilistic model of regional wind and PV power

3.1 Load curve transformation when renewable energy is superimposed on

If a area has n wind farms, the number of wind turbines in farm i is N i (i = 1,2,⋯,n) and the farm has m PV power stations, the number of PV modules in PV station j is M j (j = 1, 2,⋯, m), the following assumptions are made.

  1. 1)

    In the same wind farm, the relationship between the outputs of different wind turbines is strongly correlated, the correlation coefficient is 1; and the relationship between the outputs of different wind farms is mutually independent, the correlation coefficient is thus 0.

  2. 2)

    Similarly, in the same PV station, the relationship between the outputs of different PV modules has a correlation coefficient of 1; and the relationship between the outputs of different PV stations is mutually independent with correlation coefficient equal to 0.

  3. 3)

    The relationship between the outputs of PV stations and wind farms is mutually unrelated, the correlation coefficient is 0.

Then for wind farm i, its total output is \( P_{i} = N_{i} P_{\text{w} } \), in which P i is the total output of the wind farm i, P w is the output of a single wind turbine. Similar results could be obtained for PV stations.

According to the methods in [7], when wind speed meets the Weibull distribution, assuming the active power outputs of wind farms are random variables, based on the historical data, we can get their semi-invariants δ i , i = 1, 2,⋯,n. Similarly, when light intensity meets the Beta distribution, based on the historical data, the semi-invariant of the active power output of PV station j is ε j , j = 1, 2,⋯, m.

Since the active power outputs of n wind farms and m PV stations are mutually independent, based on the additivity of the semi-invariant, the semi-invariant of the regional total active power output is:

$$ \gamma = \sum\limits_{i = 1}^{n} {\delta_{i} } + \sum\limits_{j = 1}^{m} {\varepsilon_{j} } $$
(5)

where γ is the semi-invariant of the regional total active power output.

In this paper, we consider that the distribution of wind speed and light intensity are different at different times of the day. Based on the historical hourly data, we can divide one day into 24 parts, therefore, 24 pairs of expectation μ and standard deviation σ for wind speed and light intensity can be obtained, respectively, and we can get 24 Weibull distributions and 24 Beta distributions.

Therefore we can get 24 semi-invariants of the regional total power output:

$$ \gamma_{k} = \sum\limits_{i = 1}^{n} {\delta_{ki} } + \sum\limits_{j = 1}^{m} {\varepsilon_{kj} } $$
(6)

where γ k is the semi-invariant of the regional total active power output of the time k, k = 1,2,⋯,24.

In turn, by the Gram–Charlier expanding [8, 9], for the random variables of the regional total active power outputs, their probability density function f k (x) and cumulative distribution function F k (x) can be obtained, as shown in Fig. 4 (the semi-invariant of the curve is got from the historical data of wind speed and light intensity in the certain area).

Fig. 4
figure 4

Probability density function f k (x) and cumulative distribution function F k (x)

Full size image

Generally, the random variable falls inside the interval (μ k  − 3σ k , μ k  + 3σ k ), which can be considered, for the total active power outputs of wind farms and PV stations, the minimum is μ k  − 3σ k , and the maximum is μ k  + 3σ k , k = 1,2,⋯,24.

Figure 5 is a typical daily load curve of a certain area, when regional wind and PV power outputs are superimposed on it, the composite load curve is shown in Fig. 6. So the load curve is no longer deterministic, it is a random curve inside the ‘load belt’ and meets certain probabilistic rules, as shown in Fig. 7.

Fig. 5
figure 5

A typical daily load curve of a certain area

Full size image
Fig. 6
figure 6

Changing process of load curve

Full size image
Fig. 7
figure 7

The ‘load belt’ of area

Full size image

3.2 Impact of unordered charging

So when large-scale EVs get charged in an uncontrolled manner, using the Monte Carlo simulation method of [10], the load curve of uncontrolled charging can be obtained. When there are one million uncontrolled charging EVs in a certain city, its ‘load belt’ is shown in Fig. 8.

Fig. 8
figure 8

Impact of large-scale EV uncontrolled charging on original ‘load belt’

Full size image

It can be obtained from Fig. 8 that, the charging peak would appear near the peak of the original load, resulting in the lifting of the original ‘load belt’ peak, and the peak-valley difference gets bigger.

3.3 Probabilistic model of wind and PV power outputs

In every hour, the load is a random value between the minimum and the maximum, and its derivation process of the probability density function is as follows.

In Fig. 9, at time t, t = 1, 2,⋯,24, if the random variable of load is L t . L t is a random value between point b and c. Point a corresponds to the original load of the grid, its value L ta is determined; point b corresponds to the load when total outputs of wind farms and PV stations are maximum, its value is L tb ; point c corresponds to the load when total output is minimum, it is L tc . The relations among them are:

Fig. 9
figure 9

Range of load fluctuation at time t

Full size image
$$ \left\{ {\begin{array}{*{20}l} {L_{tc} = L_{ta} - (\mu_{t} - 3\sigma_{t} )} \hfill \\ {L_{tb} = L_{ta} - (\mu_{t} + 3\sigma_{t} )} \hfill \\ {L_{t} = L_{ta} - C_{t} } \hfill \\ \end{array} } \right. $$
(7)

where C t is the random variable of the total output of wind farms and PV stations at time t, probability density function of C t is f t (c) (the method of calculating f t (c) has been explained before), the probability density function of random variable L t is \( g_{t} (l) = f_{t} \left( {L_{ta} - l} \right) \), in which l is the value of L t .

In the above process, the probabilistic model of wind and PV power outputs is built, thus, for each of the 24 time points of the ‘load belt’, the probability density function of the random variable has been obtained [11–13].

4 Method of assessing peak-valley of uncertain load curve

When regional wind and PV power outputs are superimposed on, the load curve is no longer deterministic, it is a random curve inside the ‘load belt’ [14]. This paper proposes a probabilistic method to assess the peak-valley difference.

If the random variable of load at t 1 is L t1, its probability density function is g t1(l), and at t 2, the probability density function of L t2 is g t2(l), assume that \( \mu_{t2} > \mu_{t1} \), then:

$$ P\left( {\frac{{L_{t2} - L_{t1} }}{{L_{t2} }} \le \theta } \right) = P\left( {\left( {1 - \theta } \right)L_{t2} - L_{t1} \le 0} \right) $$
(8)

In this paper, we refer to θ as the peak-valley difference index. Therefore, assume that random variables L t1 and L t2 are mutually independent, and if \( L^{\prime} = \left( {1 - \theta } \right)L_{t2} - L_{t1} \), then by using the additivity of the semi-invariant, the cumulative distribution function of \( L^{\prime} \) can be obtained from g t1(l) and g t2(l), we write it F F(l), therefore:

$$ P\left( {\left( {1 - \theta } \right)L_{t2} - L_{t1} \le 0} \right) = P\left( {L^{\prime} \le 0} \right) = F_{\text{F} } \left( 0 \right) $$
(9)

Firstly, calculate the expectations of the 24 random variables at 24 time points, select the first three maximum points as the possible ‘peak’ time points and the last three minimum points as the possible ‘valley’ time points, then use \( P\left( {(L_{t2} - L_{t1} )/L_{t2} \le \theta } \right) \) to calculate the three pairs of time points above. Choose the minimum of the calculation results as the final value of P θ , P θ is the probability that peak-valley difference is less than or equal to the certain peak-valley difference index θ:

$$ P_{\theta } = P\left( {\frac{{L_{t{\rm p}} - L_{t{\rm v}} }}{{L_{t{\rm p}} }} \le \theta } \right) $$
(10)

where L tp is the random variable of load at ‘peak’ time; L tv is the random variable of load at ‘valley’ time. As the interval between random variables L tp and L tv is long, they can be considered mutually independent [15, 16].

To illustrate P θ can effectively reflect the value of the peak-valley difference, for the first graph in Fig. 10, \( P_{\theta }^{(1)} = P\left( {(L_{t{\rm p}} - L_{t{\rm v}} )/L_{t{\rm p}} \le \theta } \right) \), and the second graph \( P_{\theta }^{(2)} = P\left( {(L_{t{\rm p}} - L_{t{\rm v}} )/L_{t{\rm p}} \le \theta } \right) \), we can get the Table 1.

Fig. 10
figure 10

Two different ‘load belts’

Full size image
Table 1 P θ corresponding to different peak-valley difference indices of two load curves
Full size table

It can be seen from Table 1 that, for every peak-valley difference indices, \( P_{\theta }^{(1)} < P_{\theta }^{(2)} \) is right. Therefore it can be concluded that, there is a positive correlation between P θ and the peak-valley difference of the uncertain load curve, the bigger the value of P θ is, the smaller the peak-valley difference (peak-valley difference rate) is, and the flatter the load curve is.

5 Optimization model

Based on the ordered charging model, the power supply side guides the charging of EVs by formulating P p and P v, and delimiting the start and end time of valley period t 1 and t 2.

If the total number of EVs is N, corresponding to every (P p, P v, t 1, t 2), there are λN EVs choose ordered charging, its load curve is ζ o; (1 − λ)N EVs choose unordered charging, its load curve is ζ f; the ‘load belt’ superimposed on the regional wind and PV power outputs is ζ b, then corresponding to the (P p, P v, t 1, t 2), the ‘load belt’ is ζ = ζ b + ζ o + ζ f, it is meaningful and important to find the (P p, P v, t 1, t 2) that can make the peak-valley difference of the ζ minimum, that is to make the P θ of ζ maximum.

Through the above analysis, we know λ is a function and t 1, Δt, β are its independent variables, Δt is the duration of valley period, Δt = t 2 − t 1.

$$ \lambda = f(t_{1} ,\Delta t,\beta ) $$
(11)

Therefore, in order to optimize the peak-valley difference, the following optimization model is built:

$$ \begin{aligned} & \hbox{max} P_{\theta } \left( {t_{1} ,\Delta t,\beta } \right) \\ & \text{s.t.} \left\{ {\begin{array}{*{20}l} {0 \le t_{1} \le 24} \hfill \\ {0 < \Delta t < 12} \hfill \\ {0 < \beta < \beta_{\lim } } \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(12)

To take the maximum P θ as the target, and use genetic algorithms to determine the start time t 1 and the duration of valley period Δt, as well as the peak-valley rate β.

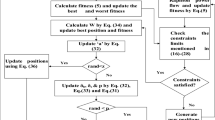
The flow chart of genetic algorithm optimization and objective function is shown in Fig. 11.

Fig. 11
figure 11

Flow chart of genetic algorithm optimization and objective function

Full size image

6 Case study

In this example, the typical daily load curve of a city is selected as the basis. By assuming the specific parameters of its wind farms and PV stations, and based on the historical data, we assume the city has one million EVs. EV constant charging power is P c = 2.5 kW.

In this example, when driving demand is different, users’ response to peak-valley rate β is shown in Fig. 12. When driving demand is common, the response curve is the average of the two curves. The maximum value is β lim = 1.5.

Fig. 12
figure 12

Response curves in different driving demands

Full size image

At different time, users’ driving demand for EVs is different in a day, so we divide one day into three periods according to EV users’ schedule of the city: ①T p: the period that users’ driving demand for EVs is urgent (7:00–10:00 and 16:00–20:00); ②T y: the period that users’ driving demand for EVs is common (22:00–7:00); ③T d: the period that users’ driving demand for EVs is low (10:00–16:00 and 20:00–22:00).

According to the above parameters, the genetic algorithm toolbox of MATLAB is used to achieve the simulation, the optimization results are shown in Table 2.

Table 2 Optimization results
Full size table

From the above results, it can be seen that, for different peak-valley difference indices, an optimization result (t 1, Δt, β) can be got corresponding to it, as shown in Fig. 13.

Fig. 13
figure 13

Optimization ‘load belts’ of different peak-valley difference indices

Full size image

Take the optimization result when θ = 35% as an example, (t 1, Δt, β) is (0.926, 6.4787, 1.1822).

After using the genetic algorithm to optimize P θ , the probability that the peak-valley difference is less than or equal to 35% is 79.69%, in the valley period of load, after guiding EV ordered charging, the load increases. It can be intuitively seen from Fig. 13b that, the optimized ‘load belt’ tends to be smooth. It can be obtained from the optimization results that, when considering the regional wind and PV power outputs, the method of ordered charging in this paper can effectively optimize the peak-valley difference.

7 Conclusion

Through the probabilistic model of regional wind and PV power outputs and the model of peak-valley price in two-stage, this paper solves the problem of large scale EV ordered charging. Furthermore, it achieves the goal of stabilizing the power fluctuations caused by the regional wind and PV outputs and optimizing the peak-valley difference in the gird. As analyzed above, the effectiveness and rationality of the models and methods have been proved.