1 Introduction

Traditional power distribution systems were principally passive because the networks only consumed power from the conventional generators through the transmission lines. However, the modern distribution networks have the ability to generate power through the use of distributed generators [1]. PV systems can be integrated into distribution networks as micro grids or standalone units, depend on the regulatory framework and constraints in the country.

A micro-grid is a cluster of distributed generators and loads operating under different conditions [2]. The micro-grids are typically designed for bi-mode of operations: the first mode is the grid connected mode and the other is the stand alone or islanded mode. When operating in the grid connected mode, the micro-grid interchangeably imports and exports power to the utility grid as per the operating criteria. The distribution networks, which are connected with embedded generators and active controls, are termed as an active distribution network (ADN).

There are different types of micro grids that are operated using different types of generating technologies. In the recent past years, the micro grids that are driven through PV systems evolved considerably [3]. Some of published literature reports that PV micro-grids improves the network reliability [4], however, such micro grids are not always economically viable. Some of the other published literature looked at economical deployment of micro-grids with improved reliability [5]. The PV micro-girds without energy storage mediums are capable of exporting power during the day and shut down during the night. Such situations can lead to bidirectional power flows and unwanted congestion of lines [6]. The rapid growth of PV micro-grids has been motivated by many factors including pollution reduction in the environment and reduced customer interruptions. This growth has brought many challenges and invoked significant researches [7]. The penetration of PV generation through micro-grids poses a number of challenges in the evaluation of reliability [8]. Integration of distributed generation also requires the capacity assessment of a distribution network incorporating uncertainties [9]. Distributed generation can be integrated into distribution networks by prioritizing different aspects, including their values [10].

This paper proposes a new mathematical model that captures intermittent effects, uncertain operating conditions, and component based operation of PV systems. The model can be incorporated for the reliability planning of an active distribution network. The major benefit of the proposed model is its adaptability and flexibility to capture the detailed effects of varying insolation levels through stochastic transitions.

2 Proposed model for a PV system

A PV system can be comprised of solar power conversion components (PV arrays), the energy storage units (batteries) and the power conditioning units (inverters) [11]. Figure 1 shows an abstract model of a PV system.

Fig. 1
figure 1

Abstract model of a PV system

Full size image

2.1 Stochastic model for the PV array

The output power of the PV generation is constantly changing with changes in insolation levels during a day [11], which results in operational complications such as bidirectional power flows, voltage rise effects, and congestion. A PV array subsystem can be accurately represented by a three state model. One state for fully operational or UP state, one for fully non-operational or DOWN state, and another for partially operational or DERATED state [12].

2.2 Stochastic model for storage (battery bank)

Figure 2 shows the stochastic model for the storage facility where λ and μ terms give failure and repair rates correspond to the transitions, respectively. The subscripts b and c denote battery storage and charger controller respectively.

Fig. 2
figure 2

Stochastic model for storage facility

Full size image

The storage facility has two important components, which are the battery bank and the charge controller. The effect of other components of this subsystem can be considered negligible for the reliability studies. Figure 2 shows the Markov model for the battery bank (B/Bank) and charge controller (C/C) with four states. Both the battery bank and the charge controller have two operational states: the up or fully operational state and the down or the fully non-operational states.

Since two components are connected in series, the storage system is only operational if both the battery bank and the charge controller are fully operational. Therefore, the system will operate if, and only if, it is in STATE1 otherwise it will be in ‘DOWN state’. Equation (1) gives the stochastic transitional probability matrix for the architecture shown in Fig. 2.

$$ \varvec{P}_{cb} = \left[ {\begin{array}{*{20}c} {1 - \lambda_{b} - \lambda_{c} } & {\lambda_{c} } & {\lambda_{b} } & - \\ {\mu_{c} } & {1 - \lambda_{b} - \mu_{c} } & - & {\lambda_{b} } \\ {\mu_{b} } & - & {1 - \mu_{b} - \lambda_{c} } & {\lambda_{c} } \\ - & {\mu_{b} } & {\mu_{c} } & {1 - \mu_{b} - \mu_{c} } \\ \end{array} } \right]. $$
(1)

The state probability matrix shows the probability of the system residing in one of the states shown in Fig. 2. As a series configuration, the subsystem is only operational if both components are operable. Therefore, STATES2, 3 and 4 (being failure states) can be represented by absorbing states which results (2) as a truncated matrix.

$$ \varvec{Q} = \left[ {1 - \lambda_{b} - \lambda_{c} } \right]. $$
(2)

The mean time to failure (MTTF) for this subsystem can be calculated as per the steps given in (3)–(4).

$$ t_{MTTF} = \left[ {\varvec{I} - \varvec{Q}} \right]^{ - 1} , $$
(3)

where I is the identity matrix. Therefore,

$$ t_{MTTF} = \left[ {1 - \left[ {1 - \lambda_{b} - \lambda_{c} } \right]} \right]^{ - 1} = \left[ {\lambda_{b} + \lambda_{c} } \right]^{ - 1} = \frac{1}{{\lambda_{b} + \lambda_{c} }}. $$
(4)

Thus, the composite failure rate for this subsystem is determined using (5).

$$ \lambda_{bc} = \frac{1}{{t_{MTTF} }} = \frac{1}{{1/(\lambda_{b} + \lambda_{c} )}} = \lambda_{b} + \lambda_{c} , $$
(5)

where λ bc is the composite failure rate of the storage subsystem.

The mean time to repair (MTTR) is obtained by truncating the original stochastic probability matrix and eliminating the operational state as per (6)–(8). Thus, the composite mean time to repair for this subsystem is determined using (9).

$$ t_{MTTR} = \left[ {\varvec{I} - \varvec{Q}_{t} } \right]^{ - 1} , $$
(6)

where

$$ \varvec{Q}_{t} = \left[ {\begin{array}{*{20}c} {1 - \lambda_{b} - \mu_{c} } & 0 & {\lambda_{b} } \\ 0 & {1 - \mu_{b} - \lambda_{c} } & {\lambda_{c} } \\ {\mu_{b} } & {\mu_{c} } & {1 - \mu_{b} - \mu_{c} } \\ \end{array} } \right], $$
$$ \varvec{t}_{MTTR} = \left[ {\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {1 - \lambda_{b} - \mu_{c} } & 0 & {\lambda_{b} } \\ 0 & {1 - \mu_{b} - \lambda_{c} } & {\lambda_{c} } \\ {\mu_{b} } & {\mu_{c} } & {1 - \mu_{b} - \mu_{c} } \\ \end{array} } \right]} \right]^{ - 1} . $$
(7)

Equation (7) reduces to the following:

$$ \varvec{t}_{MTTR} = \left[ {\begin{array}{*{20}c} {\lambda_{b} + \mu_{c} } & 0 & { - \lambda_{b} } \\ 0 & {\mu_{b} + \lambda_{c} } & { - \lambda_{c} } \\ { - \mu_{b} } & { - \mu_{c} } & {\mu_{b} + \mu_{c} } \\ \end{array} } \right]^{ - 1} , $$
(8)
$$ t_{MTTR} = \frac{{\lambda_{b} + \mu_{b} + \mu_{c} }}{{(\mu_{b} + \mu_{c} )^{2} }}. $$
(9)

Then, the composite storage system repair rate is determined using (10).

$$ \mu_{cb} = \frac{{(\mu_{b} + \mu_{c} )^{2} }}{{\left( {\lambda_{b} + \mu_{b} + \mu_{c} } \right)}}. $$
(10)

The battery bank and the charge controller can be modeled as a single component with a constant failure rate (λ bc ) and a constant repair rate (μ cb ).

2.3 Stochastic model for power conditioning unit

Figure 3 shows the Markov model for the power conditioning unit (PCU), where subscripts inv and CB give the inverter and disconnect switch respectively. The subsystem has an inverter and power disconnection switch (D/Switch) as the two most important components. Thus, its Markov model is similar to the storage subsystem. The resulting transitional probability matrix is given in (11).

$$ \varvec{P}_{inv} = \left[ {\begin{array}{*{20}c} {1 - \lambda_{inv} - \lambda_{CB} } & {\lambda_{CB} } & {\lambda_{inv} } & - \\ {\mu_{CB} } & {1 - \lambda_{inv} - \mu_{CB} } & - & {\lambda_{inv} } \\ {\mu_{inv} } & - & {1 - \mu_{inv} - \lambda_{CB} } & {\lambda_{CB} } \\ - & {\mu_{inv} } & {\mu_{CB} } & {1 - \mu_{inv} - \mu_{CB} } \\ \end{array} } \right]. $$
(11)
Fig. 3
figure 3

Stochastic model for power conditioning unit (PCU)

Full size image

From (11), the failure rate can be evaluated using (12).

$$ \lambda_{invCB} = \frac{1}{{t_{MTTR} }} = \frac{1}{{1/(\lambda_{inv} + \lambda_{CB} )}} = \lambda_{inv} + \lambda_{CB} , $$
(12)

and the repair rate is

$$ \mu_{invCB} = \frac{{(\mu_{inv} + \mu_{CB} )^{2} }}{{\lambda_{inv} + \mu_{inv} + \mu_{CB} }}. $$
(13)

2.4 Stochastic model for the entire PV system

Figure 4 shows the Markov model for the entire PV system. The composite failure and repair rates are defined as:

Fig. 4
figure 4

Stochastic model for the PV system

Full size image

  • PV array λ PV  = λ1, μ PV  = μ1;

  • Battery bank/charge controller λ cb  = λ2, μ cb  = μ2;

  • Inverter/disconnect switch λ invCB  = λ3, μ invCB  = μ3.

The probability transitional matrix derived from the above diagram is shown in (14).

$$ \varvec{P} = \left[ {\begin{array}{*{20}c} {(1 - \lambda_{1} - \lambda_{2} - \lambda_{3} )} & {\lambda_{1} } & {\lambda_{2} } & {\lambda_{3} } & 0 & 0 & 0 & 0 \\ {\mu_{1} } & {(1 - \mu_{1} - \lambda_{2} - \lambda_{3} )} & 0 & 0 & {\lambda_{2} } & 0 & {\lambda_{3} } & 0 \\ {\mu_{2} } & 0 & {(1 - \mu_{2} - \lambda_{1} - \lambda_{2} )} & 0 & {\lambda_{1} } & {\lambda_{3} } & 0 & 0 \\ {\mu_{3} } & 0 & 0 & {(1 - \mu_{3} - \lambda_{1} - \lambda_{2} )} & 0 & {\lambda_{2} } & {\lambda_{1} } & 0 \\ 0 & {\mu_{2} } & {\mu_{1} } & 0 & {(1 - \mu_{2} - \mu_{1} - \lambda_{3} )} & 0 & 0 & {\lambda_{3} } \\ 0 & 0 & {\mu_{3} } & {\mu_{2} } & 0 & {(1 - \mu_{2} - \mu_{3} - \lambda_{1} )} & 0 & {\lambda_{2} } \\ 0 & {\mu_{3} } & 0 & {\mu_{1} } & 0 & 0 & {(1 - \mu_{1} - \mu_{2} - \lambda_{2} )} & {\lambda_{1} } \\ 0 & 0 & 0 & 0 & {\mu_{3} } & {\mu_{1} } & {\mu_{2} } & {(1 - \mu_{1} - \mu_{2} - \mu_{3} )} \\ \end{array} } \right]. $$
(14)

This matrix reduces to a truncated matrix involving the operational states of the system as in (15).

$$ \varvec{Q}_{PV} = \left[ {\begin{array}{*{20}c} {1 - \lambda_{1} - \lambda_{2} - \lambda_{3} } & {\lambda_{1} } & {\lambda_{2} } \\ {\mu_{1} } & {1 - \mu_{1} - \lambda_{2} - \lambda_{3} } & 0 \\ {\mu_{2} } & 0 & {1 - \mu_{2} - \lambda_{1} - \lambda_{2} } \\ \end{array} } \right]. $$
(15)

Equation (15) is used for reliability analysis and to evaluate the reliability performance of an active distribution network.

The reliability assessment, which described in Sect. 3, incorporates de-rating of PV outputs into the calculations; however, it is not modelled within the Markov process of the PV system directly. The reason is that, unlike conventional power generating units, PVs are inherited with intermittent outputs and within the up-state of an intermittent output; the de-rating resulting through PV string failures can also be included. In this way, the size of the stochastic transitional matrix can be kept at a reasonable level. Alternatively, the Markov model given in Fig. 4 can also be extended to incorporate the de-rated state of the PV system; however; it will further complicate the stochastic transitional matrix, demanding an increased processing time for calculating the reliability indices. This is particularly the case with high penetration of dispersed PVs [13].

Stochastic generation output of the reliability calculation is modelled by using time series of intermittent power outputs, superimposed by de-rating effects of PV strings.

3 Calculation of reliability indices

The calculation of reliability indices involves the following steps.

  • Step 1: Model the distribution network base case.

  • Step 2: Define possible load demands or load forecast and growth scenarios.

  • Step 3: Characterise load points based on the type of customers (customer types include agricultural, domestic, commercial and industrial).

  • Step 4: Model component failures of buses, lines, cables, transformers, shunt devices, generators, protection/switch, and common mode as appropriate.

  • Step 5: Create the network condition with one or more simultaneous faults and specific load conditions.

  • Step 6: Establish the power balance with power flow analysis.

  • Step 7: Analyse the effects of failure of components through clearing faults by tripping of protection breakers or fuses, separating the faults by opening separating switches, restoring the power by closing normally open switches, alleviating overload by load transfer and load shedding, alleviating voltage constraint violations by load shedding at critical conditions. Thus, this step determines if system faults lead to load interruptions and if so, which loads are to be interrupted and how long. The loads can be shed in discrete blocks (e.g., 25%, 50%, 75%, and 100% of the base value), the minimum level considering priority, or the minimum level ignoring priority. The load shedding is attempted if the load transfer through switches of the distribution network is failed. The approach alleviates overload after power restoration with a minimum level of load shedding. It uses linear sensitivity indices to first select those loads with any contribution to overloading. A linear optimization is then used to find the best shedding option.

  • Step 8: Calculate load point reliability indices and then system level reliability indices. At first, the amount of load shedding is multiplied by the duration of the system state to calculate the energy not supplied. The system energy not supplied for all possible system states is calculated after the entire system reliability assessment process is completed. CAIDI (customer average interruption duration index) and CAIFI (customer average interruption frequency index) are calculated taking into account duration of customers affected and respective frequencies. Similarly, SAIDI (system average interruption duration index) and SAIFI (system average interruption frequency index) are also calculated taking into account duration of customer interruptions of the system and the frequency of the system [14, 15].

4 Application of the proposed model

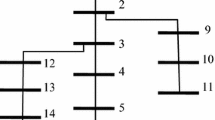
The proposed PV system model was applied to a modified RBTS (Roy Billinton Test System) model, shown in Fig. 5 [16]. This is a primary four radial feeders and secondary loop distribution network with a peak active power load of 20 MW. The network has a PV system maximum capacity of 5 MW. The reliability data of all the system equipment is obtained from the IEEE test system [17] and the RBTS test system [18–20]. However, the reliability data of the PV systems are obtained from [21]. Table 1 shows the definition of loads. The aggregate power production of each PV system and the reliability data is given in Table 2.

Fig. 5
figure 5

Modified RBTS model

Full size image
Table 1 Definition of loads
Full size table
Table 2 PV system data
Full size table

4.1 Case 1: varying load

The load is varied regardless of the integration of PV systems. It is varied from its base case level to 200% of the base case level. The results of SAIDI, SAIFI, and ENS (energy not supplied) are shown in Fig. 6a–c. Results suggest that the increase in load up to 40% does not affect the system reliability performance of this particular network considerably. However, after point A, a further increase in load results in a significant increase in the values of indices. This is due to the rapid increase in the total number of loads being shed off from the system coupled with a significant increase in the magnitude of the load.

Fig. 6
figure 6

Variation of index with load increases. a SAIDI variation with load increases, b SAIFI variation with load increases, c ENS variation with load increases

Full size image

In region L to K, there is a marked increase in ENS from 220 to 495 MWh/year. This represents a 125% increase in ENS for an increase of 100% in the load which is less than that obtained for the initial section. The increase in the load of the order of 175% of the base case load leads to overload system transformers and lines. This results in more loads being curtailed.

4.2 Case 2: varying PV generation output

The effect of hourly variation in the output of the PV generator on the network reliability is investigated and shown in Fig. 7a–d. Figure 7a shows active power output of the PV generators in the system in per unit on a 1 MVA base. The graph shows that how the power of the PV system varies during the day. The power production increases sharply to the maximum at 11 am and then drops steadily down to zero at around 9 pm.

Fig. 7
figure 7

Variation of power output and the indices of the PV system. a Power output variation of the PV system, b SAIDI against PV generation variation, c CAIDI against PV generation variation, d ENS against PV generation variation

Full size image

Figure 7b shows the variation of SAIDI during a particular day with the same PV output power variation as shown in Fig.7a. It is seen that the SAIDI value improves from the initial value of 3.48 h, for the initial condition in which the PV output power is zero, to 2.8 h at point B when the outputs of the PV generators increase. This represents a steep improvement of 19.5% within 30 min of PV outputs increase from 0 to 0.15 pu.

SAIDI continues to improve at point B to point C with reduced steepness. At point C, the PV output power is the highest and thus the SAIDI is also at the maximum value. Compared to the initial value, SAIDI at this point is improved to 2.15 h representing a 38% improvement.

Between C and D, SAIDI remains substantially constant because of the outputs of the PV generators are almost constant. SAIDI increases gradually from D to E and finally goes to the initial value at F when the insolation reduces to zero.

Figure 7c and d show the variation of CAIDI and ENS respectively with time of the day. The graphs are similar to that for SAIDI and as such follow the same trends as SAIDI.

4.3 Case 3: effect of cloud cover on reliability

Because of the power production capabilities of the PV generators are entirely dependent on the insolation in a particular area; the reliability of a distribution network with high PV penetration is heavily affected by insolation variations. The graph of Fig. 7a shows the output of the PV generators on a particular day, and it follows the insolation closely. One way in which the insolation is affected is by the clouds.

The results for the system under the influence of cloud cover are shown in Fig. 8a–c.

Fig. 8
figure 8

Variation of PV generation and the indices on a cloudy day. a PV generation variation on a cloudy day, b SAIFI against PV generation variation on a cloudy day, c SAIDI against PV generation variation on a cloudy day

Full size image

The entire results suggest that the reliability performance of an active distribution network can potentially be impacted by insolation variations, level of the stress of the network, and the level of penetration of PV generation. The proposed model is able to characterise the detailed transitions of states in a PV system that is a requirement for the assessment of true impacts in a distribution network.

5 Conclusions

A new mathematical model is proposed to assess the impacts on the reliability of an active distribution network with high penetration of PV power generation. The model, which is flexible, is able to capture intermittent outputs and uncertainties of PV power generating systems.

The study results suggest that PV systems impact less on the reliability performance of moderately loaded networks. In contrast, the highly stressed networks may have significant impacts from high penetration of PV systems. Cloudy effects resulting insolation variations can potentially impact the reliability performance in stressed networks that are high penetrated with PV power generation. The new model-based approach proposed in the paper can quantify the benefit thresholds in a distribution network with high penetration of PV power generation. Results also argue that PV systems can potentially improve the reliability of distribution networks if they are strategically integrated within thresholds.

The proposed model-based approach can be used as a benchmarking entity for the operational planning of a distribution network with high PV concentrations.