Vehicle–track–tunnel dynamic interaction: a finite/infinite element modelling method

Abstract

The aim of this study is to develop coupled matrix formulations to characterize the dynamic interaction between the vehicle, track, and tunnel. The vehicle–track coupled system is established in light of vehicle–track coupled dynamics theory. The physical characteristics and mechanical behavior of tunnel segments and rings are modeled by the finite element method, while the soil layers of the vehicle–track–tunnel (VTT) system are modeled as an assemblage of 3-D mapping infinite elements by satisfying the boundary conditions at the infinite area. With novelty, the tunnel components, such as rings and segments, have been coupled to the vehicle–track systems using a matrix coupling method for finite elements. The responses of sub-systems included in the VTT interaction are obtained simultaneously to guarantee the solution accuracy. To relieve the computer storage and save the CPU time for the large-scale VTT dynamics system with high degrees of freedoms, a cyclic calculation method is introduced. Apart from model validations, the necessity of considering the tunnel substructures such as rings and segments is demonstrated. In addition, the maximum number of elements in the tunnel segment is confirmed by numerical simulations.

1 Introduction

Railway tunnel, as a kind of underground passageway for moving vehicles, plays important roles in shortening the line, reducing the slope, improving the operating conditions, and promoting the traction capacity. It has been majorly and mostly applied in mountainous areas and urban transit. So far, abundant work has mainly been focused on the monitoring [1], risk evaluation [2] and construction [3], etc.

In the last decades, the track-tunnel dynamics subjected to moving vehicles has drawn attention worldwide, following an increasing interest on vibrations, noise, fatigue, and damage originated from the vehicle–track–tunnel (VTT) dynamic interaction. As an alternative solution to expensive and labor-consuming in situ or laboratory experiments, the simulation achieved by computer codes is more versatile and can also obtain practical results in design and performance evaluation. Much work has been done in the modelling of train–track–tunnel (or soil) interaction in recent years. For example, Wei et al. [4] paid special attention to the frequency-dependent characteristics of rail pads and investigated its dynamic influence on environmental vibrations. In their model, the tunnel and soil are simplified as beam and springs, respectively. To further clarify the importance of joints in lining of shield tunneling, Gharehdash and Barzegar [5] built a 3-D dynamic finite difference model to investigate the influence of metro train impacts on shield tunnel and its soil foundation, where the train dynamics is not considered by expressing the wheel-rail forces as the composition of static and harmonic forces.

Regarding the modelling of the tunnel dynamics, most research activities are concentrated on the characterization and discussion of soil vibration from the tunnel instead of the specific tunnel vibration. By applying the 2.5-D coupled finite element–boundary element (FE–BE) method, Sheng et al. [6] established a mathematical model for analyzing the ground vibration induced by trains, where the track, tunnel and ground are regarded as homogeneous and infinitely long layers in the longitudinal direction, and the model was formulated by x-direction wave numbers and yz-plane discretization. Zhou, Di and He et al. [7,8,9,10] established a series of models to calculate the soil vibration from the tunnel induced by moving loads, where the soil is generally assumed as a saturated porous medium at the poroelastic half-space and the tunnel is assumed as periodic joint cylinder rings. The solution for wave propagation in the soil is obtained by Biot's theory [11] and potential decomposition, or other theories such as the improved FE-BE method. Besides, Forrest and Hunt [12] proposed a well-established model for railway underground vibration analysis, known as the pipe-in-pipe (PiP) model. Hussein et al. [13] extended the PiP model and calculated the vibration from the tunnel embedded in layered half-space.

Undoubtedly, the literature on train-induced ground vibration is numerous [14,15,16,17,18]. However, the detailed modelling method specifically aimed at the VTT interaction from aspects of coupled dynamics is rarely reported. The issues to be solved lie in the following aspects:

• (1) Large modeling simplification. The detailed configurations of the tunnel, such as tunnel rings, segments and joints, are hardly considered in the VTT dynamics. In addition, the moving vehicles are mostly regarded as moving loads, ignoring the complex wheel-rail contact in geometries/forces.

• (2) Uncoupled solution. The train-induced vibrations of the tunnel or the tunnel-soil system are obtained by two-step method, in which the loads calculated by the vehicle–track interaction model are subsequently imposed into substructures or the layered soil, such as the work in [19].

• (3) Low computational efficiency. To model track-tunnel systems with consideration of the structural details, finite element method is practically the most useful tactics. However, it significantly increases the degrees of freedom (DOFs) of the dynamic system, thereby reducing the computational efficiency.

• (4) Soil boundary consideration. The soil is assumed to be elastic solid at the outer layer of the tunnel or spring-dashpots in VTT coupled system [4]. However, it is difficult to determine the parameter values such as the stiffness coefficients.

Aiming at the aforementioned issues, this work contributes to developing a more complex VTT dynamic model by coupling the vehicle, the track and the tunnel as an entire system, where the track-tunnel system is modeled by the finite element method (FEM) and the soil around the tunnel is modeled by the infinite element method (IEM). In this model, the detailed configuration of the tunnel is considered, and the solving method for obtaining the system response with improvement of the computational efficiency is also presented. The novelty lies in two aspects: one is that the discontinuity between the tunnel segments and rings is accounted for, and accordingly, their interactions can be elaborated in detail; and the other is that the sub-systems within a VTT interaction framework have been united by the vehicle–track coupled dynamics [20] for the first time, and consequently, the performance of subsystems within the VTT coupled system is evaluated by simultaneously considering their interaction.

The rest of the paper is organized as follows:

• (1) In Sect. 2, the method for modelling the VTT dynamic interaction is presented, where the vehicle, the track and the tunnel are coupled as an entire one.

• (2) In Sect. 3, the method for obtaining a numerical solution of VTT systems is developed, where the track-tunnel coupled matrices are truncated to reduce the number of DOFs, and accordingly, improving the computational efficiency. Besides, it allows the vehicle to move on the track-tunnel system with an infinite length, even though the length of the track-tunnel system modeled in the program can not cover the total moving distance of a train.

• (3) In Sect. 4, numerical examples are presented to validate the accuracy and efficiency of this model. Moreover, the influence of the tunnel type and the segment element number on VTT system performance is clarified.

• (4) In Sect. 5, conclusions are drawn from the studies.

2 Modelling of vehicle–track–tunnel dynamic interaction

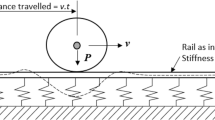
A vehicle–track–tunnel coupled dynamic model is established, as shown in Fig. 1, where the vehicle moves on the track structures supported by the tunnel. The vehicle is modelled as a multi-rigid-body system with one car body, two bogie frames and four wheelsets. Each body considers five DOFs including the lateral displacement, the vertical displacement, the yaw angle, the roll angle and the pitch angle. The track structures are modelled as a ballastless track including the rail (Euler–Bernoulli beams), the slab track (thin plates), the rail pads (spring-dashpot elements) and the concrete layer (spring-dashpot elements) supporting the track. The tunnel is assembled by tunnel rings, and each ring consists of several tunnel segments. The tunnel rings and segments are connected by joints.

Fig. 1

Vehicle–track–tunnel coupled interaction system

2.1 Dynamic equations of motion for the VTT interaction systems

In the VTT interaction model, vehicle–track coupled dynamics [20] and matrix coupling method in finite elements [21] are applied to construct the vehicle, track, and tunnel as an entire dynamic system. That is to say, the VTT systems are solved and obtained synchronously based on the following assumptions:

• (1) Only the motions at the centroid of the vehicle bodies are considered.

• (2) The elastic compression between the wheel and rail is ignored.

• (3) The track–tunnel interaction is considered as linear elastic interaction.

The dynamic equations of motion for the VTT interaction are assembled by matrix formulations as follows:

$$\left[ {\begin{array}{cccc} {{\varvec{M}}_{{{\text{vv}}}} } & {{\varvec{M}}_{{{\text{vr}}}} } & 0 & 0 \\ {{\varvec{M}}_{{{\text{rv}}}} } & {{\varvec{M}}_{{{\text{rr}}}} } & 0 & 0 \\ 0 & 0 & {{\varvec{M}}_{{{\text{tt}}}} } & 0 \\ 0 & 0 & 0 & {{\varvec{M}}_{{{\text{ss}}}} } \\ \end{array} } \right]\left\{ \begin{aligned} {\ddot{\varvec{X}}}_{{\text{v}}} \hfill \\ {\ddot{\varvec{X}}}_{{\text{r}}} \hfill \\ {\ddot{\varvec{X}}}_{{\text{t}}} \hfill \\ {\ddot{\varvec{X}}}_{{\text{s}}} \hfill \\ \end{aligned} \right\} + \left[ {\begin{array}{cccc} {{\varvec{C}}_{{{\text{vv}}}} } & {{\varvec{C}}_{{{\text{vr}}}} } & 0 & 0 \\ {{\varvec{C}}_{{{\text{rv}}}} } & {{\varvec{C}}_{{{\text{rr}}}} } & {{\varvec{C}}_{{{\text{rt}}}} } & 0 \\ 0 & {{\varvec{C}}_{{{\text{tr}}}} } & {{\varvec{C}}_{{{\text{tt}}}} } & {{\varvec{C}}_{{{\text{ts}}}} } \\ 0 & 0 & {{\varvec{C}}_{{{\text{st}}}} } & {{\varvec{C}}_{{{\text{ss}}}} } \\ \end{array} } \right]\left\{ \begin{aligned} {\dot{\varvec{X}}}_{{\text{v}}} \hfill \\ {\dot{\varvec{X}}}_{{\text{r}}} \hfill \\ {\dot{\varvec{X}}}_{{\text{t}}} \hfill \\ {\dot{\varvec{X}}}_{{\text{s}}} \hfill \\ \end{aligned} \right\} + \left[ {\begin{array}{cccc} {{\varvec{K}}_{{{\text{vv}}}} } & {{\varvec{K}}_{{{\text{vr}}}} } & 0 & 0 \\ {{\varvec{K}}_{{{\text{rv}}}} } & {{\varvec{K}}_{{{\text{rr}}}} } & {{\varvec{K}}_{{{\text{rt}}}} } & 0 \\ 0 & {{\varvec{K}}_{{{\text{tr}}}} } & {{\varvec{K}}_{{{\text{tt}}}} } & {{\varvec{K}}_{{{\text{ts}}}} } \\ 0 & 0 & {{\varvec{K}}_{{{\text{st}}}} } & {{\varvec{K}}_{{{\text{ss}}}} } \\ \end{array} } \right]\left\{ \begin{aligned} {\varvec{X}}_{{\text{v}}} \hfill \\ {\varvec{X}}_{{\text{r}}} \hfill \\ {\varvec{X}}_{{\text{t}}} \hfill \\ {\varvec{X}}_{{\text{s}}} \hfill \\ \end{aligned} \right\} = \left[ \begin{aligned} {\varvec{F}}_{{\text{v}}} \hfill \\ {\varvec{F}}_{{\text{r}}} \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{aligned} \right],$$

(1)

where ${\varvec{M}}$, ${\varvec{C}}$ and ${\varvec{K}}$ denote the mass, damping, and stiffness matrixes, respectively; ${\varvec{X}}$, ${\dot{\varvec{X}}}$ and ${\ddot{\varvec{X}}}$ denote the displacement, velocity and acceleration vector, respectively; ${\varvec{F}}$ denotes the loading vector; the subscripts “v”, “r”, “t” and “s” denote the vehicle, rail, track slab and tunnel sub-systems, respectively; the subscripts “vr” and “rv” denote the interaction between the vehicle and rail; the subscripts “rt” and “tr” denote the interaction between the rail and track slab; the subscripts “ts” and “st” denote the interaction between the track slab and tunnel; variables with subscripts “vv”, “rr”, “tt” and “ss” denote the self-matrices of the vehicle, rail, track slab and tunnel, respectively.

In Eq. (1), the matrices for the vehicle, rail and track slab, and the coupling matrices for the wheel–rail interaction, the rail–track slab interaction and the track slab–tunnel interaction have been illustrated in detail in [21, 22], and here not presented for brevity. In this work, an emphasis is put on the modelling formulations of the tunnel system.

2.2 Modelling of the tunnel system

For the modelling of the tunnel system, the 8-node iso-parametric finite element and a mapping infinite element are introduced to model the tunnel segments and the elastic half space of soil boundary.

2.2.1 Finite elemental matrix for tunnel segments

The 8-node iso-parametric element is applied to model the tunnel system, as shown in Fig. 2.

Fig. 2

Element for modelling the tunnel system

Before modelling of the tunnel, the following variables are defined:

• (1) The radius of the internal and external wall at the tunnel cross section: $r_{{{\text{t1}}}}$ and $r_{{{\text{t2}}}}$, respectively.

• (2) The number of segments for each tunnel ring: $n_{{\text{t}}}$.

• (3) The longitudinal length of the tunnel ring element: $l_{{\text{t}}}$.

• (4) The angles between the positive direction of the tunnel global X-coordinate and the sides of the i-th tunnel segment element: $\alpha_{{i,{1}}}$ and $\alpha_{i,2}$.

• (5) The elastic modulus and Poisson ratio of tunnel slab: $E_{{\text{t}}}$ and $u_{{\text{t}}}$, respectively.

• (6) The mass of tunnel per unit volume: $m_{{\text{t}}}$.

• (7) The longitudinal, lateral and vertical stiffness coefficients between tunnel segments: $k_{{{\text{tt,}}x}}$, $k_{{{\text{tt,}}y}}$ and $k_{{{\text{tt,}}z}}$, respectively.

• (8) The longitudinal, lateral and vertical damping coefficients between tunnel segments: $c_{{{\text{tt,}}x}}$, $c_{{{\text{tt,}}y}}$ and $c_{{{\text{tt,}}z}}$, respectively

• (9) The number of tunnel rings in a tunnel: $N_{{\text{t}}}$.

Following the principle of iso-parametric element, the first derivative of the shape function against local natural coordinate can be obtained by

$$\left\{ \begin{aligned} {\varvec{N}}_{\xi } = \left[ {\frac{{\partial N_{{{\text{s}}_{1} }} }}{\partial \xi } \; \; \; \frac{{\partial N_{{{\text{s}}_{2} }} }}{\partial \xi } \; \; \cdots \; \; \frac{{\partial N_{{{\text{s}}_{8} }} }}{\partial \xi }} \right] \hfill \\ {\varvec{N}}_{\eta } = \left[ {\frac{{\partial N_{{{\text{s}}_{1} }} }}{\partial \eta } \; \; \; \frac{{\partial N_{{{\text{s}}_{2} }} }}{\partial \eta } \; \; \cdots \; \; \frac{{\partial N_{{{\text{s}}_{8} }} }}{\partial \eta }} \right] \hfill \\ {\varvec{N}}_{\zeta } = \left[ {\frac{{\partial N_{{{\text{s}}_{1} }} }}{\partial \zeta } \; \; \; \frac{{\partial N_{{{\text{s}}_{2} }} }}{\partial \zeta } \; \; \cdots \; \; \frac{{\partial N_{{{\text{s}}_{8} }} }}{\partial \zeta }} \right] \hfill \\ \end{aligned} \right.,$$

(2)

with

$$N_{{{\text{s}}_{i} }} = \frac{{(1 + \xi_{i} \xi )(1 + \eta_{i} \eta )(1 + \zeta_{i} \zeta )}}{8},\quad i = 1,2,\ldots,8,$$

$$\xi_{1} = - 1,\xi_{2} = - 1,\xi_{3} = - 1,\xi_{4} = - 1,\xi_{5} = 1,\xi_{6} = 1,\xi_{7} = 1,\xi_{8} = 1,$$

$$\eta_{1} = - 1,\eta_{2} = 1,\eta_{3} = - 1,\eta_{4} = 1,\eta_{5} = - 1,\eta_{6} = 1,\eta_{7} = - 1,\eta_{8} = 1,$$

$$\zeta_{1} = - 1,\zeta_{2} = - 1,\zeta_{3} = 1,\zeta_{4} = 1,\zeta_{5} = - 1,\zeta_{6} = - 1,\zeta_{7} = 1,\zeta_{8} = 1.$$

Its corresponding Jacobian matrix can be calculated by

$${\varvec{J}} = \left[ {\begin{array}{ccc} {{\varvec{N}}_{\xi} {\varvec{X}}^{{\text{T}}} } & {{\varvec{N}}_{\xi } {\varvec{Y}}^{{\text{T}}} } & {{\varvec{N}}_{\xi } {\varvec{Z}}^{{\text{T}}} } \\ {{\varvec{N}}_{\eta } {\varvec{X}}^{{\text{T}}} } & {{\varvec{N}}_{\eta } {\varvec{Y}}^{{\text{T}}} } & {{\varvec{N}}_{\eta } {\varvec{Z}}^{{\text{T}}} } \\ {{\varvec{N}}_{\zeta } {\varvec{X}}^{{\text{T}}} } & {{\varvec{N}}_{\zeta } {\varvec{Y}}^{{\text{T}}} } & {{\varvec{N}}_{\zeta } {\varvec{Z}}^{{\text{T}}} } \\ \end{array} } \right],$$

(3)

with

$$\left\{ \begin{aligned} {\varvec{X}} = \left[ {\begin{array}{cccccccc} {X_{1} } & {X_{2} } & {X_{3} } & {X_{4} } & {X_{5} } & {X_{6} } & {X_{7} } & {X_{8} } \\ \end{array} } \right] \hfill \\ {\varvec{Y}} = \left[ {\begin{array}{cccccccc} {Y_{1} } & {Y_{2} } & {Y_{3} } & {Y_{4} } & {Y_{5} } & {Y_{6} } & {Y_{7} } & {Y_{8} } \\ \end{array} } \right] \hfill \\ {\varvec{Z}} = \left[ {\begin{array}{cccccccc} {Z_{1} } & {Z_{2} } & {Z_{3} } & {Z_{4} } & {Z_{5} } & {Z_{6} } & {Z_{7} } & {Z_{8} } \\ \end{array} } \right] \hfill \\ \end{aligned} \right.,\quad J_{\det } = \det \left| {\varvec{J}} \right|,$$

$$X_{1} = - \frac{{l_{{\text{t}}} }}{2}, \; X_{2} = - \frac{{l_{{\text{t}}} }}{2}, \; X_{3} = - \frac{{l_{{\text{t}}} }}{2}, \; X_{4} = - \frac{{l_{{\text{t}}} }}{2}, \; X_{5} = \frac{{l_{{\text{t}}} }}{2}, \; X_{6} = \frac{{l_{{\text{t}}} }}{2}, \; X_{7} = \frac{{l_{{\text{t}}} }}{2}, \; X_{8} = \frac{{l_{{\text{t}}} }}{2},$$

$$Y_{1} = Y_{5} = r_{{{\text{t}}1}} \cos \;\alpha_{i,1} , \; Y_{2} = Y_{6} = r_{{{\text{t}}1}} \cos \;\alpha_{i,2} , \; Y_{3} = Y_{7} = r_{{{\text{t}}2}} \cos \;\alpha_{i,1} , \; Y_{4} = Y_{8} = r_{{{\text{t}}2}} \cos \;\alpha_{i,2} ,$$

$$Z_{1} = Z_{5} = - r_{{{\text{t}}1}} \sin \;\alpha_{i,1} , \; Z_{2} = Z_{6} = - r_{{{\text{t}}1}} \sin \;\alpha_{i,2} , \; Z_{3} = Z_{7} = - r_{{{\text{t}}2}} \sin \;\alpha_{i,1} , \; Z_{4} = Z_{8} = - r_{{{\text{t}}2}} \sin \;\alpha_{i,2} ,$$

where ${\varvec{X}}$, ${\varvec{Y}}$ and ${\varvec{Z}}$ are global physical coordinate vectors.

Besides the first derivative of the space iso-parametric element shape function is given by

$${\varvec{N}}^{\prime} = {\varvec J}^{ - 1} {\varvec{N}},$$

(4)

in which ${\varvec{N}} = \left[ \begin{aligned} {\varvec N}_{\xi }\ {\varvec N}_{\eta } \ {\varvec N}_{\zeta } \end{aligned} \right]^{\text{T}}$, and the strain geometric matrix can be assembled by

$${\varvec{B}} = \left[ {\begin{array}{cccccccc} {{\overline{\varvec{B}}}_{1} } & {{\overline{\varvec{B}}}_{2} } & {{\overline{\varvec{B}}}_{3} } & {{\overline{\varvec{B}}}_{4} } & {{\overline{\varvec{B}}}_{5} } & {{\overline{\varvec{B}}}_{6} } & {{\overline{\varvec{B}}}_{7} } & {{\overline{\varvec{B}}}_{8} } \\ \end{array} } \right],$$

(5)

with

$${\overline{\varvec{B}}}_{i} = \left[ {\begin{array}{ccc} {{\varvec{N}}^{{\mathbf{^{\prime}}}}_{(1,i)} } & 0 & 0 \\ 0 & {{\varvec{N}}^{{\mathbf{^{\prime}}}}_{(2,i)} } & 0 \\ 0 & 0 & {{\varvec{N}}^{{\mathbf{^{\prime}}}}_{(3,i)} } \\ 0 & {{\varvec{N}}^{{\mathbf{^{\prime}}}}_{(3,i)} } & {{\varvec{N}}^{{\mathbf{^{\prime}}}}_{(2,i)} } \\ {{\varvec{N}}^{{\mathbf{^{\prime}}}}_{(3,i)} } & 0 & {{\varvec{N}}^{{\mathbf{^{\prime}}}}_{(1,i)} } \\ {{\varvec{N}}^{{\mathbf{^{\prime}}}}_{(2,i)} } & {{\varvec{N}}^{{\mathbf{^{\prime}}}}_{(1,i)} } & 0 \\ \end{array} } \right],i = 1,2, \ldots ,8.$$

Moreover, the elastic matrix can be expressed by

$${\varvec{D}} = e_{3} \left[ {\begin{array}{cccccc} 1 & {e_{1} } & {e_{1} } & 0 & 0 & 0 \\ {e_{1} } & 1 & {e_{1} } & 0 & 0 & 0 \\ {e_{1} } & {e_{1} } & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & {e_{2} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {e_{2} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {e_{2} } \\ \end{array} } \right],$$

(6)

with

$$e_{1} = \frac{{E_{{\text{t}}} }}{{1 - u_{{\text{t}}} }},$$

$$e_{2} = \frac{{1 - 2u_{{\text{t}}} }}{{2(1 - u_{{\text{t}}} )}},$$

$$e_{3} = E_{{\text{t}}} \frac{{(1 - u_{{\text{t}}} )}}{{(1 + u_{{\text{t}}} )(1 - 2u_{{\text{t}}} )}},$$

where ${\varvec{D}}$ is the elastic matrix.

According to the elastic strain energy of the iso-parametric element, the stiffness matrix of the tunnel system can be derived as

$${\varvec{K}}_{{\text{t}}} = \sum\limits_{{n_{{\text{t}}} }} {\sum\limits_{{N_{{\text{t}}} }} {\int_{ - 1}^{1} {\int_{ - 1}^{1} {\int_{ - 1}^{1} {{\varvec{B}}^{{\text{T}}} {\varvec{DB}}J_{\det } {\text{d}}\xi {\text{d}}\eta {\text{d}}} } } \zeta } } .$$

(7)

To solve the triple integral problem in Eq. (7), the Gaussian integral method can be applied.

Similarly, the mass matrix of the tunnel system can be derived by the negative value of the work done by inertial forces, namely

$${\varvec{M}}_{{\text{t}}} = \sum\limits_{{n_{{\text{t}}} }} {\sum\limits_{{N_{{\text{t}}} }} {m_{{\text{t}}} \int_{ - 1}^{1} {\int_{ - 1}^{1} {\int_{ - 1}^{1} {\left( {{\varvec{N}}_{{{\text{t}}\xi }}^{{\text{T}}} {\varvec{N}}_{{{\text{t}}\xi }} + {\varvec{N}}_{{{\text{t}}\eta }}^{{\text{T}}} {\varvec{N}}_{{{\text{t}}\eta }} + {\varvec{N}}_{{{\text{t}}\zeta }}^{{\text{T}}} {\varvec{N}}_{{{\text{t}}\zeta }} } \right)J_{\det } {\text{d}}\xi {\text{d}}\eta {\text{d}}} } } \zeta } },$$

(8)

with

$${\varvec{N}}_{{{\text{t}}\xi }} = \left[ {\begin{array}{cccccccc} {{\varvec{N}}_{{{\text{t}}\xi ,1}} } & {{\varvec{N}}_{{{\text{t}}\xi ,2}} } & {{\varvec{N}}_{{{\text{t}}\xi ,3}} } & {{\varvec{N}}_{{{\text{t}}\xi ,4}} } & {{\varvec{N}}_{{{\text{t}}\xi ,5}} } & {{\varvec{N}}_{{{\text{t}}\xi ,6}} } & {{\varvec{N}}_{{{\text{t}}\xi ,7}} } & {{\varvec{N}}_{{{\text{t}}\xi ,8}} } \\ \end{array} } \right],{\varvec{N}}_{{{\text{t}}\xi ,i}} = \left[ {\begin{array}{ccc} {N_{{{\text{s}}_{i} }} } & 0 & 0 \\ \end{array} } \right], $$

$${\varvec{N}}_{{{\text{t}}\eta }} = \left[ {\begin{array}{cccccccc} {{\varvec{N}}_{{{\text{t}}\eta ,1}} } & {{\varvec{N}}_{{{\text{t}}\eta ,2}} } & {{\varvec{N}}_{{{\text{t}}\eta ,3}} } & {{\varvec{N}}_{{{\text{t}}\eta ,4}} } & {{\varvec{N}}_{{{\text{t}}\eta ,5}} } & {{\varvec{N}}_{{{\text{t}}\eta ,6}} } & {{\varvec{N}}_{{{\text{t}}\eta ,7}} } & {{\varvec{N}}_{{{\text{t}}\eta ,8}} } \\ \end{array} } \right],{\varvec{N}}_{{{\text{t}}\eta ,i}} = \left[ {\begin{array}{ccc} 0 & {N_{{{\text{s}}_{i} }} } & 0 \\ \end{array} } \right],$$

$${\varvec{N}}_{{{\text{t}}\zeta }} = \left[ {\begin{array}{cccccccc} {{\varvec{N}}_{{{\text{t}}\zeta ,1}} } & {{\varvec{N}}_{{{\text{t}}\zeta ,2}} } & {{\varvec{N}}_{{{\text{t}}\zeta ,3}} } & {{\varvec{N}}_{{{\text{t}}\zeta ,4}} } & {{\varvec{N}}_{{{\text{t}}\zeta ,5}} } & {{\varvec{N}}_{{{\text{t}}\zeta ,6}} } & {{\varvec{N}}_{{{\text{t}}\zeta ,7}} } & {{\varvec{N}}_{{{\text{t}}\zeta ,8}} } \\ \end{array} } \right],{\varvec{N}}_{{{\text{t}}\zeta ,i}} = \left[ {\begin{array}{ccc} 0 & 0 & {N_{{{\text{s}}_{i} }} } \\ \end{array} } \right],i = 1,2, \ldots ,8.$$

2.2.2 Interaction matrices between tunnel segments

In this work, a tunnel ring consists of a set of tunnel segments; therefore, the interaction between the independent tunnel segments should be considered. As shown in Fig. 3, the stiffness matrix for the i-th and (i + 1)-th track segment can be given by

$${\varvec{K}}_{{{\text{tt}}}} = \sum\limits_{{{{\varOmega}}}} {k_{{{\text{tt}},{{{\varOmega}}}}} \int_{ - 1}^{1} {\int_{ - 1}^{1} {{\varvec{N}}_{{{\text{tt}},{{{\varOmega}}}}}^{{\text{T}}} {\varvec{N}}_{{{\text{tt}},{{{\varOmega}}}}} A{\text{d}}\xi {\text{d}}\zeta } } },$$

(9)

with

$${{{\varOmega}}} = \left( {x,y,z} \right),\;{\varvec{N}}_{{{\text{tt}},{{{\varOmega}}}}} = {\varvec{N}}_{{{\text{tt}},{{{\varOmega}}}}}^{i} - {\varvec{N}}_{{{\text{tt}},{{{\varOmega}}}}}^{i + 1} ,\;{\varvec{N}}_{{{\text{tt}},{{{\varOmega}}}}}^{i} = {\varvec{N}}_{{{\text{tt}},{{{\varOmega}}}}}^{i + 1} = \left\{ \begin{aligned} {\varvec{N}}_{{{\text{t}}\xi }}, {\text{when}}{{{\varOmega}}} = x \, \hfill \\ {\varvec{N}}_{{{\text{t}}\eta }}, {\text{when}}{{{\varOmega}}} = y \, \hfill \\ {\varvec{N}}_{{{\text{t}}\zeta }} , {\text{when }}{{{\varOmega}}} = z \, \hfill \\ \end{aligned} \right.,$$

$$A = \sqrt {\left( {J_{1,1} J_{3,2} - J_{1,2} J_{3,1} } \right)^{2} + \left( {J_{1,1} J_{3,3} - J_{1,3} J_{3,1} } \right)^{2} + \left( {J_{1,2} J_{3,3} - J_{1,3} J_{3,2} } \right)^{2} } ,$$

$$J_{1,1} = {\varvec{N}}_{\xi } {\varvec{X}}^{{\text{T}}} ,\;J_{1,2} = {\varvec{N}}_{\xi } {\varvec{Y}}^{{\text{T}}} ,\;J_{1,3} = {\varvec{N}}_{\xi } {\varvec{Z}}^{{\text{T}}} ,$$

$$J_{3,1} = {\varvec{N}}_{\zeta } {\varvec{X}}^{{\text{T}}} ,\;J_{3,2} = {\varvec{N}}_{\zeta } {\varvec{Y}}^{{\text{T}}} ,\;J_{3,3} = {\varvec{N}}_{\zeta } {\varvec{Z}}^{{\text{T}}} ,$$

where $\eta = 1$ and $- 1$ for ${\varvec{N}}_{{{\text{tt}},{{{\varOmega}}}}}^{i}$ and ${\varvec{N}}_{{{\text{tt}},{{{\varOmega}}}}}^{{i{ + }1}}$, respectively; $A$ is the area microelement.

Fig. 3

Interaction between track segments

The damping matrix for the interaction between tunnel segments can be obtained by almost the same approach as Eq. (9), just needing to substitute the stiffness coefficient $k_{{{\text{tt}},{{{\varOmega}}}}}$ with the damping coefficient $c_{{{\text{tt}},{{{\varOmega}}}}}$.

2.3 Modelling of the soil around the tunnel

The soil around the tunnel is regarded as an elastic half-space, and mapping infinite elements are introduced to model the external boundary of tunnels and the far field vibration of the soil space.

Between the global and local coordinates, a mapping infinite element is applied [23], where the mapping infinite element includes the mapping function to represent coordinate mapping relation and the shape function to characterize the displacement movement of the elements, as shown in Fig. 4.

Fig. 4

Infinite element for modelling the soil boundary of the tunnel system

(1) The mapping function of infinite elements can be expressed as

$${\varvec{M}} = \left[ {\begin{array}{cccccccc} {M_{1} } & {M_{2} } & {M_{3} } & {M_{4} } & {M_{5} } & {M_{6} } & {M_{7} } & {M_{8} } \\ \end{array} } \right],$$

(10)

with

$$M_{1} = \frac{(1 - \xi )(1 - \eta )( - \zeta )}{{2(1 - \zeta )}},M_{2} = \frac{(1 - \xi )(1 + \eta )( - \zeta )}{{2(1 - \zeta )}},M_{3} = \frac{(1 - \xi )(1 - \eta )(1 + \zeta )}{{4(1 - \zeta )}},M_{4} = \frac{(1 - \xi )(1 + \eta )(1 + \zeta )}{{4(1 - \zeta )}},$$

$$M_{5} = \frac{(1 + \xi )(1 - \eta )( - \zeta )}{{2(1 - \zeta )}},M_{6} = \frac{(1 + \xi )(1 + \eta )( - \zeta )}{{2(1 - \zeta )}},M_{7} = \frac{(1 + \xi )(1 - \eta )(1 + \zeta )}{{4(1 - \zeta )}},M_{8} = \frac{(1 + \xi )(1 + \eta )(1 + \zeta )}{{4(1 - \zeta )}}.$$

Accordingly, the geometric relation between the global coordinate ($x$, $y$ and $z$) and local coordinate ($\xi$, $\eta$ and $\zeta$) can be given by

$${\varvec{G}}_{\gamma } = {\varvec{ML}}_{\gamma },$$

(11)

with

$${\varvec{L}}_{\gamma} = \left[ {\begin{array}{cccccccc} {u_{\gamma ,1} } & {u_{\gamma ,2} } & {u_{\gamma ,3} } & {u_{\gamma ,4} } & {u_{\gamma ,5} } & {u_{\gamma ,6} } & {u_{\gamma ,7} } & {u_{\gamma ,8} } \\ \end{array} } \right],\gamma = \left( {X,Y,Z} \right),$$

where the subscript “$\gamma$” denotes the label of longitudinal coordinate (X-axis), lateral coordinate (Y-axis) and vertical coordinate (Z-axis); symbol “$u$” denotes the global coordinate of the infinite element node.

(2) The shape function of infinite elements can be expressed as

$${\varvec{N}} = \left[ {\begin{array}{cccccccc} {N_{1} } & {N_{2} } & {N_{3} } & {N_{4} } & {N_{5} } & {N_{6} } & {N_{7} } & {N_{8} } \\ \end{array} } \right],$$

(12)

with

$$N_{1} = \frac{{(1 - \xi )(1 - \eta )(\zeta^{2} - \zeta )}}{8},N_{2} = \frac{{(1 - \xi )(1 + \eta )(\zeta^{2} - \zeta )}}{8},$$

$$N_{3} = \frac{{(1 - \xi )(1 - \eta )(1 - \zeta^{2} )}}{4},N_{4} = \frac{{(1 - \xi )(1 + \eta )(1 - \zeta^{2} )}}{4},$$

$$N_{5} = \frac{{(1 + \xi )(1 - \eta )(\zeta^{2} - \zeta )}}{8},N_{6} = \frac{{(1 + \xi )(1 + \eta )(\zeta^{2} - \zeta )}}{8},$$

$$N_{7} = \frac{{(1 + \xi )(1 - \eta )(1 - \zeta^{2} )}}{4},N_{8} = \frac{{(1 + \xi )(1 + \eta )(1 - \zeta^{2} )}}{4}.$$

Like Eq. (7), the stiffness matrix of an infinite element can be given by

$${\varvec{K}}_{{\text{s}}} = \int_{ - 1}^{1} {\int_{ - 1}^{1} {\int_{ - 1}^{1} {{\varvec{B}}_{{\text{s}}}^{{\text{T}}} {\varvec{D}}_{{\text{s}}} {\varvec{B}}_{{\text{s}}} J_{{\det ,{\text{s}}}} {\text{d}}\xi {\text{d}}\eta {\text{d}}} } } \zeta,$$

(13)

with

$${\varvec{B}}_{i} = \left[ {\begin{array}{ccc} {\frac{{\partial N_{i} }}{\partial \xi }} & 0 & 0 \\ 0 & {\frac{{\partial N_{i} }}{\partial \eta }} & 0 \\ 0 & 0 & {\frac{{\partial N_{i} }}{\partial \zeta }} \\ 0 & {\frac{{\partial N_{i} }}{\partial \zeta }} & {\frac{{\partial N_{i} }}{\partial \eta }} \\ {\frac{{\partial N_{i} }}{\partial \zeta }} & 0 & {\frac{{\partial N_{i} }}{\partial \xi }} \\ {\frac{{\partial N_{i} }}{\partial \eta }} & {\frac{{\partial N_{i} }}{\partial \xi }} & 0 \\ \end{array} } \right],\quad \left( {i = 1,2,\ldots,8} \right),$$

$${\varvec{J}}_{{\det ,{\text{s}}}} = \left[ {\begin{array}{ccc} {\sum\limits_{i = 1}^{8} {\frac{{\partial M_{i} }}{\partial \xi }x_{i} } } & {\sum\limits_{i = 1}^{8} {\frac{{\partial M_{i} }}{\partial \xi }y_{i} } } & {\sum\limits_{i = 1}^{8} {\frac{{\partial M_{i} }}{\partial \xi }z_{i} } } \\ {\sum\limits_{i = 1}^{8} {\frac{{\partial M_{i} }}{\partial \eta }x_{i} } } & {\sum\limits_{i = 1}^{8} {\frac{{\partial M_{i} }}{\partial \eta }y_{i} } } & {\sum\limits_{i = 1}^{8} {\frac{{\partial M_{i} }}{\partial \eta }z_{i} } } \\ {\sum\limits_{i = 1}^{8} {\frac{{\partial M_{i} }}{\partial \zeta }x_{i} } } & {\sum\limits_{i = 1}^{8} {\frac{{\partial M_{i} }}{\partial \zeta }y_{i} } } & {\sum\limits_{i = 1}^{8} {\frac{{\partial M_{i} }}{\partial \zeta }z_{i} } } \\ \end{array} } \right],$$

where ${\varvec{B}}_{{\text{s}}}$ is the elemental geometry matrix, and ${\varvec{B}}_{{\text{s}}} = \left[ {B_{{1}} ,B_{2} ,\ldots,B_{8} } \right]$; ${\varvec{D}}_{{\text{s}}}$ has the same expression as ${\varvec{D}}$ in Eq. (6), only needing to substitute ‘$E_{{\text{t}}}$’ and ‘$\mu_{{\text{t}}}$’ in ${\varvec{D}}$ with corresponding parameters of the soil ‘$E_{{\text{s}}}$’ and ‘$\mu_{{\text{s}}}$’.

Similarly, the mass matrix of an infinite element can be obtained by

$${\varvec{M}}_{{\text{s}}} = \int_{ - 1}^{1} {\int_{ - 1}^{1} {\int_{ - 1}^{1} {m_{{\text{s}}} \left( {{\varvec{N}}_{{{\text{s}}\xi }}^{{\text{T}}} {\varvec{N}}_{{{\text{s}}\xi }} + {\varvec{N}}_{{{\text{s}}\eta }}^{{\text{T}}} {\varvec{N}}_{{{\text{s}}\eta }} + {\varvec{N}}_{{{\text{s}}\zeta }}^{{\text{T}}} {\varvec{N}}_{{{\text{s}}\zeta }} } \right){\varvec{J}}_{{\det ,{\text{s}}}} {\text{d}}\xi {\text{d}}\eta {\text{d}}} } } \zeta,$$

(14)

with

$${\varvec{N}}_{{{\text{s}}\xi }} = \left[ {\begin{array}{cccccccc} {{\varvec{N}}_{{{\text{s}}\xi ,1}} } & {{\varvec{N}}_{{{\text{s}}\xi ,{2}}} } & {{\varvec{N}}_{{{\text{s}}\xi ,{3}}} } & {{\varvec{N}}_{{{\text{s}}\xi ,{4}}} } & {{\varvec{N}}_{{{\text{s}}\xi ,{5}}} } & {{\varvec{N}}_{{{\text{s}}\xi ,{6}}} } & {{\varvec{N}}_{{{\text{s}}\xi ,{7}}} } & {{\varvec{N}}_{{{\text{s}}\xi ,{8}}} } \\ \end{array} } \right],{\varvec{N}}_{{{\text{s}}\xi {,}i}} = \left[ {\begin{array}{ccc} {{\varvec{N}}_{i} } & 0 & 0 \\ \end{array} } \right],$$

$${\varvec{N}}_{{{\text{s}}\eta }} = \left[ {\begin{array}{cccccccc} {{\varvec{N}}_{{{\text{s}}\eta ,1}} } & {{\varvec{N}}_{{{\text{s}}\eta ,{2}}} } & {{\varvec{N}}_{{{\text{s}}\eta ,{3}}} } & {{\varvec{N}}_{{{\text{s}}\eta ,{4}}} } & {{\varvec{N}}_{{{\text{s}}\eta ,{5}}} } & {{\varvec{N}}_{{{\text{s}}\eta ,{6}}} } & {{\varvec{N}}_{{{\text{s}}\eta ,{7}}} } & {{\varvec{N}}_{{{\text{s}}\eta ,{8}}} } \\ \end{array} } \right],{\varvec{N}}_{{{\text{s}}\eta {,}i}} = \left[ {\begin{array}{ccc} 0 & {{\varvec{N}}_{i} } & 0 \\ \end{array} } \right],$$

$${\varvec{N}}_{{{\text{s}}\zeta }} = \left[ {\begin{array}{cccccccc} {{\varvec{N}}_{{{\text{s}}\zeta ,1}} } & {{\varvec{N}}_{{{\text{s}}\zeta ,{2}}} } & {{\varvec{N}}_{{{\text{s}}\zeta ,{3}}} } & {{\varvec{N}}_{{{\text{s}}\zeta ,{4}}} } & {{\varvec{N}}_{{{\text{s}}\zeta ,{5}}} } & {{\varvec{N}}_{{{\text{s}}\zeta ,{6}}} } & {{\varvec{N}}_{{{\text{s}}\zeta ,{7}}} } & {{\varvec{N}}_{{{\text{s}}\zeta ,{8}}} } \\ \end{array} } \right],{\varvec{N}}_{{{\text{s}}\zeta {,}i}} = \left[ {\begin{array}{ccc} 0 & 0 & {{\varvec{N}}_{i} } \\ \end{array} } \right],$$

where $m_{{\text{s}}}$ is the mass of the soil per unit volume.

3 Solution for the VTT dynamic interaction

Considering the high DOFs of the tunnel system, the cyclic calculation method proposed in [24] is introduced, where the track-tunnel system is truncated to reduce the DOFs of VTT system in the numerical integral solutions and accordingly, to improve the computational efficiency.

3.1 Improved cyclic calculation method for VTT dynamic solutions

The steps to obtain the solution for the VTT system are as follows:

Step 1 Confirm the total DOFs for each subsystem (the rail, track slab and tunnel) in the initially constructed matrices, denoted as ${\varvec{D}}_{{\text{r}}}$, ${\varvec{D}}_{{\text{s}}}$ and ${\varvec{D}}_{{\text{t}}}$, respectively, and the total DOFs required in the realistic calculation are correspondingly $\overline{D}_{{\text{r}}}$, $\overline{D}_{{\text{s}}}$ and $\overline{D}_{{\text{t}}}$, the initial time label $n_{{0}} = 0$, the truncated boundary length $L_{{\text{b}}}$, and the cyclic calculation length $L_{{\text{c}}}$. The $L_{{\text{b}}}$ and $L_{{\text{c}}}$ are set to be integral multiple of rail pad spacing, namely $N_{{\text{b}}}$ and $N_{{\text{c}}}$, as shown in Fig. 5.

Step 2 Make the vehicle run a distance $L_{{\text{s}}}$ to finish the initial unsteady state.

Step 3 When $VT \ge L_{{\text{s}}}$, in which $V$ is the vehicle speed and $T$ is the total time of the vehicle moving on the tracks, it means that the VTT system runs into the cyclic calculation period, where the corresponding coordinate is represented as $X^{\prime} - O^{\prime} - Y^{\prime}$, and $n_{{0}} = n_{{0}} + 1$ for each increment of the time step.

Step 4 The moving distance of the vehicle after entering the cyclic calculation period is $L = V \cdot (n_{{0}} - 1)\Delta t$, and we determine the number of cycles by

$$N_{{\text{v}}} = \left[ {\frac{L}{{L_{{\text{c}}} }}} \right] + 1,$$

(15)

where $\left[ \cdot \right]$ denotes an operator rounding the element in it to the nearest integers.

Step 5 Calculate the DOFs of the sub-systems (rail, track slab, tunnel and soil) with respect to the coordinates of $X - O - Y$ and $X^{\prime} - O^{\prime} - Y^{\prime}$, respectively, as below:

• (1) Rail sub-system:

  $${{\varvec{\varPhi}}}_{XOY}^{{\text{r}}} = \left[ {{\varsigma}_{\text{r}} \left( {n_{\text{b}} - 1} \right) + 1,{\varsigma}_{{\text{r}}} \left( {n_{\text{f}} + 1} \right)} \right]$$

  ,

  $${{\varvec{\varPhi}}}_{{X^{\prime} O^{\prime} Y^{\prime} }}^{\text{r}} = \left[ {{\varsigma}_{\text{r}} \left( {n_{\text{b}}^{\prime} - 1} \right) + 1,{\varsigma}_{\text{r}} \left( {n_{\text{f}}^{\prime} + 1} \right)} \right]$$

  , where $\left\{ \begin{aligned} n_{{\text{b}}} = n_{4} - N_{{\text{b}}} n_{{\text{r}}} \hfill \\ n_{{\text{f}}} = n_{1} + N_{{\text{b}}} n_{{\text{r}}} \hfill \\ \end{aligned} \right.$, $\left\{ \begin{aligned} n_{{\text{b}}}^{\prime} = n_{4} - N_{{\text{b}}} n_{{\text{r}}} - \left( {N_{{\text{v}}} - 1} \right)N_{{\text{c}}} n_{{\text{r}}} \hfill \\ n_{{\text{f}}}^{\prime} = n_{1} + N_{{\text{b}}} n_{{\text{r}}} - \left( {N_{{\text{v}}} - 1} \right)N_{{\text{c}}} n_{{\text{r}}} \hfill \\ \end{aligned} \right.$;

  $n_{1}$ and $n_{4}$ denote rail element number contacting the first and the fourth wheelset, respectively; $n_{{\text{r}}}$ denotes the number of rail element within a rail pad spacing; ${\varsigma}_{{\text{r}}}$ denotes the half number of DOFs of a rail beam element.

• (2) Track slab sub-system:

  $${{\varvec{\varPhi}}}_{XOY}^{{\text{s}}} = \left[ {\overline{D}_{{\text{r}}} + {\varsigma}_{{\text{s}}} \left( {n_{{\text{b}}} - 1} \right) + 1,\;\overline{D}_{{\text{r}}} + {\varsigma}_{{\text{s}}} \left( {n_{{\text{f}}} + 1} \right)} \right],{{\varvec{\varPhi}}}_{{X^{\prime} O^{\prime} Y^{\prime} }}^{{\text{s}}} = \left[ {D_{{\text{r}}} + {\varsigma}_{{\text{s}}} \left( {n_{{\text{b}}}^{\prime} - 1} \right) + 1,\;D_{{\text{r}}} + {\varsigma}_{{\text{s}}} \left( {n_{{\text{f}}}^{\prime} + 1} \right)} \right],$$

  where $\varsigma_{{\text{s}}}$ denotes the half number of DOFs at a track slab cross section.

• (3) Tunnel sub-system:

  $${{\varvec{\varPhi}}}_{XOY}^{{\text{t}}} = \left[ {\overline{D}_{{\text{r}}} + \overline{D}_{{\text{s}}} + {\varsigma}_{{\text{t}}} \left( {n_{{\text{b}}} - 1} \right) + 1,\;\overline{D}_{{\text{r}}} + \overline{D}_{{\text{s}}} + {\varsigma}_{{\text{t}}} \left( {n_{{\text{f}}} + 1} \right)} \right],$$
  $${{\varvec{\varPhi}}}_{{X^{\prime} O^{\prime} Y^{\prime} }}^{{\text{t}}} = \left[ {D_{{\text{r}}} + D_{{\text{s}}} + {\varsigma}_{{\text{t}}} \left( {n_{{\text{b}}}^{\prime} - 1} \right) + 1,\;D_{{\text{r}}} + D_{{\text{s}}} + {\varsigma}_{{\text{t}}} \left( {n_{{\text{f}}}^{\prime} + 1} \right)} \right],$$

  where $\varsigma_{{\text{t}}}$ denotes the total number of DOF for a tunnel ring.

• (4) Soil infinite system:

  $${{\varvec{\varPhi}}}_{XOY}^{{\text{I}}} = \left[ {\overline{D}_{{\text{r}}} + \overline{D}_{{\text{s}}} + \overline{D}_{{\text{t}}} + d_{{\text{I}}}^{1} ,\;\overline{D}_{{\text{r}}} + \overline{D}_{{\text{s}}} + \overline{D}_{{\text{t}}} + d_{{\text{I}}}^{2} } \right],{{\varvec{\varPhi}}}_{{X^{\prime} O^{\prime} Y^{\prime} }}^{{\text{I}}} = \left[ {D_{{\text{r}}} + D_{{\text{s}}} + D_{{\text{t}}} + d_{{\text{I}}}^{1} ,\;D_{{\text{r}}} + D_{{\text{s}}} + D_{{\text{t}}} + d_{{\text{I}}}^{2} } \right],$$

  where $d_{{\text{I}}}^{1}$ and $d_{{\text{I}}}^{2}$ denote the start and end DOFs of the soil infinite element system.

Step 6 Introduce the direct integration method into the solution of the VTT matrix equations, where the mass, damping and stiffness matrices used in the integral scheme can be obtained by

$$\left\{ \begin{aligned} &{\varvec{M}}_{{\tilde{\text{t}}}} = {\varvec{M}}_{0} \left( {{{\varvec{\varPhi}}}_{{X^{\prime} O^{\prime} Y^{\prime} }} ,\;{{\varvec{\varPhi}}}_{{X^{\prime} O^{\prime} Y^{\prime} }} } \right) \hfill \\ &{\varvec{C}}_{{\tilde{\text{t}}}} = {\varvec{C}}_{0} \left( {{{\varvec{\varPhi}}}_{{X^{\prime} O^{\prime} Y^{\prime} }} ,\;{{\varvec{\varPhi}}}_{{X^{\prime} O^{\prime} Y^{\prime} }} } \right) \hfill \\ &{\varvec{K}}_{{\tilde{\text{t}}}} = {\varvec{K}}_{0} \left( {{{\varvec{\varPhi}}}_{{X^{\prime} O^{\prime} Y^{\prime} }} ,\;{{\varvec{\varPhi}}}_{{X^{\prime} O^{\prime} Y^{\prime} }} } \right) \hfill \\ \end{aligned} \right.,$$

(16)

with

$${{\varvec{\varPhi}}}_{{X^{\prime} O^{\prime} Y^{\prime} }} = \left( {{{\varvec{\varPhi}}}_{{X^{\prime} O^{\prime} Y^{\prime} }}^{{\text{r}}} ,\;{{\varvec{\varPhi}}}_{{X^{\prime} O^{\prime} Y^{\prime} }}^{{\text{s}}} ,\;{{\varvec{\varPhi}}}_{{X^{\prime} O^{\prime} Y^{\prime} }}^{{\text{t}}} ,\;{{\varvec{\varPhi}}}_{{X^{\prime} O^{\prime} Y^{\prime} }}^{{\text{I}}} } \right).$$

where the subscript “$\tilde{\text{t}}$” denotes the track-tunnel coupled system.

The equivalent stiffness matrix can be obtained by

$${\varvec{K}}_{{\rm e}} = {\frac{2}{\Delta {t^{2}} }}\left[ {\begin{array}{cc} {\varvec{M}}_{{\text{v}} } & {{\varvec{M}}_{{{\rm v}}{\tilde{{\rm t}}}} } \\ {\varvec{M}}_{\tilde{{\rm t}}{{\rm v}} } & {\varvec{M}}_{\tilde{{\rm t}} } \end{array} } \right] + {\frac{11}{6\Delta t}}\left[ {\begin{array}{cc} {{\varvec{C}}_{{\rm v}} } & {{\varvec{C}}_{{{\rm v}}{\tilde{{\rm t}}}} } \\ {{\varvec{C}}_{\tilde{{\rm t}}{{\rm v}}} } & {{\varvec{C}}_{\tilde{{\rm t}}} } \end{array} } \right] + \left[ {\begin{array}{cc} {{\varvec{K}}_{{\rm v}} } & {{\varvec{K}}_{{{\rm v}}{\tilde{{\rm t}}} }} \\ {{\varvec{K}}_{\tilde{{\rm t}}{{\rm v}}} } & {{\varvec{K}}_{\tilde{{\rm t}}} } \end{array} } \right],$$

(17)

where ${\varvec{M}}_{{\text{v}}}$, ${\varvec{C}}_{{\text{v}}}$ and ${\varvec{K}}_{{\text{v}}}$ denote the mass, damping and stiffness matrices of a vehicle; the matrices with subscripts “${\text{v}}{\tilde{\text{t}}}$” and “${\tilde{\text{t}}}{\text{v}}$” denote the interaction matrices between the vehicle and the track-tunnel system; and $\Delta t$ denotes the time step size.

The equivalent loading vector is obtained by

$$\begin{aligned} & {\varvec{F}}_{{\rm e}} = {\varvec{F}}_{t} + \left( {\frac{5}{\Delta t^{2} }\left[ {\begin{array}{cc} {{\varvec{M}}_{{\rm v}} } & {{\varvec{M}}_{{{\rm v}}\tilde{{\rm t}}} } \\ {{\varvec{M}}_{\tilde{{\rm t}}{{\rm v}}} } & {{\varvec{M}}_{\tilde{{\rm t}}} } \\ \end{array} } \right] + \frac{3}{\Delta t}\left[ {\begin{array}{*{20}c} {{\varvec{C}}_{{{\rm v}}} } & {{\varvec{C}}_{{\rm v}\tilde{{\rm t}}} } \\ {{\varvec{C}}_{\tilde{{\rm t}}{{\rm v}}} } & {{\varvec{C}}_{\tilde{{\rm t}}} } \\ \end{array} } \right]} \right){\varvec{X}}_{t - 3\Delta t}^{{\rm T}} \left( {\left[ {\varvec{\varPhi}_{XOY} \, {\varvec{\varPhi}}_{{\rm v}} } \right]} \right) + \hfill \\ & \left( {\frac{4}{{\Delta t^{2} }}\left[ {\begin{array}{cc} {{\varvec{M}}_{{\rm v}} } & {{\varvec{M}}_{{{\rm v}}\tilde{{\rm t}}}} \\ {{\varvec{M}}_{\tilde{{\rm t}}{{\rm v}}} } & {{\varvec{M}}_{\tilde{{\rm t}}} } \\ \end{array} } \right] + \frac{3}{2\Delta t}\left[ {\begin{array}{cc} {{{\varvec{C}}}_{{\rm v}} } & {{\varvec{C}}_{{{\rm v}}\tilde{{\rm t}}}} \\ {{\varvec{C}}_{\tilde{{\rm t}}{{\rm v}}} } & {{\varvec{C}}_{\tilde{{\rm t}}} } \\ \end{array} } \right]} \right){\varvec{X}}_{t - 2\Delta t}^{{\rm T}} \left( {\left[ {\varvec{\varPhi}_{XOY} \, {\varvec{\varPhi}}_{{\rm v}} } \right]} \right) + \hfill \\ & \left( {\frac{1}{{\Delta t^{2} }}\left[ {\begin{array}{cc} {{{\varvec{M}}}_{{\rm v}} } & {{\varvec{M}}_{{{\rm v}}\tilde{{\rm t}}}} \\ {{\varvec{M}}_{\tilde{{\rm t}}{{\rm v}}} } & {{\varvec{M}}_{\tilde{{\rm t}}} } \\ \end{array} } \right] + \frac{1}{3\Delta t}\left[ {\begin{array}{cc} {{{\varvec{C}}}_{{\rm v}} } & {{\varvec{C}}_{{{\rm v}}\tilde{{\rm t}}}} \\ {{\varvec{C}}_{\tilde{{\rm t}}{{\rm v}}} } & {{\varvec{C}}_{\tilde{{\rm t}}} } \\ \end{array} } \right]} \right){\varvec{X}}_{t - \Delta t}^{{\rm T}} \left( {\left[ {\varvec{\varPhi}_{XOY} \, {\varvec{\varPhi}}_{{\rm v}}} \right]} \right) \hfill \\ \end{aligned}$$

(18)

with

$${{\varvec{\varPhi}}}_{XOY} = \left( {{{\varvec{\varPhi}}}_{XOY}^{{\text{r}}} ,{\varvec{\varPhi}}_{XOY}^{{\text{s}}} ,{\varvec{\varPhi}}_{XOY}^{{\text{t}}} ,{{\varvec{\varPhi}}}_{XOY}^{{\text{I}}} } \right),$$

where $\varPhi_{{\text{v}}}$ denotes the DOFs of the vehicle; the subscript “$t$” denote the current time step, and the superscript “T” denotes the transpose of a vector or a matrix.

The displacement, acceleration, and velocity response of VTT system are obtained by

$${\varvec{X}}_{t} \left( {\left[ {{\varvec{\varPhi}}_{XOY} \, {\varvec{\varPhi}}_{{\text{v}}} } \right]} \right) = {\varvec{K}}_{{\text{e}}}^{ - 1} {\varvec{F}}_{{\text{e}}},$$

(19)

$${\ddot{\varvec{X}}}_{t} \left( {\left[ {{\varvec{\varPhi}}_{XOY} \, {\varvec{\varPhi}}_{{\text{v}}} } \right]} \right) = \frac{1}{{\Delta t^{2} }}\left( {2{\varvec{X}}_{t} \left( {\left[ {{\varvec{\varPhi}}_{XOY} \, {\varvec{\varPhi}}_{{\text{v}}} } \right]} \right) - 5{\varvec{X}}_{t - 3\Delta t} \left( {\left[ {{\varvec{\varPhi}}_{XOY} \, {\varvec{\varPhi}}_{{\text{v}}} } \right]} \right) + 4{\varvec{X}}_{t - 2\Delta t} \left( {\left[ {{\varvec{\varPhi}}_{XOY} \, {\varvec{\varPhi}}_{{\text{v}}} } \right]} \right) - {\varvec{X}}_{t - \Delta t} \left( {\left[ {{\varvec{\varPhi}}_{XOY} \, {\varvec{\varPhi}}_{{\text{v}}} } \right]} \right)} \right), $$

(20)

$$ {\dot{\varvec{X}}}_{t} \left( {\left[ {{{\varvec{\varPhi}}}_{XOY} \, {{\varvec{\varPhi}}}_{{\text{v}}} } \right]} \right) = \frac{1}{6\Delta t}\left( {11{\varvec{X}}_{t} \left( {\left[ {{{\varvec{\varPhi}}}_{XOY} \, {{\varvec{\varPhi}}}_{{\text{v}}}} \right]} \right) - 18{\varvec{X}}_{t - 3\Delta t} \left( {\left[ {{{\varvec{\varPhi}}}_{XOY} \, {{\varvec{\varPhi}}}_{{\text{v}}} } \right]} \right) + 9{\varvec{X}}_{t - 2\Delta t} \left( {\left[ {{{\varvec{\varPhi}}}_{XOY} \, {{\varvec{\varPhi}}}_{{\text{v}}} } \right]} \right) - 2{\varvec{X}}_{t - \Delta t} \left( {\left[ {{{\varvec{\varPhi}}}_{XOY} \, {{\varvec{\varPhi}}}_{{\text{v}}} } \right]} \right)} \right). $$

(21)

Step 7 Update the displacement vector: ${\varvec{X}}_{t - 3\Delta t} = {\varvec{X}}_{t - 2\Delta t}$, ${\varvec{X}}_{t - 2\Delta t} = {\varvec{X}}_{t - \Delta t}$ and ${\varvec{X}}_{t - \Delta t} = {\varvec{X}}_{t}$, and go to step 3.

Fig. 5

Solution procedure for VTT dynamic interaction

3.2 Modeling framework for the VTT dynamic interaction

Based on the above demonstration, it is known that the vibrational systems, consisting of the vehicle, the rail, the track slab, and the tunnel components, have been entirely coupled into VTT dynamic interaction matrices. By applying the infinite elements and the cyclic calculation method, the radiation condition of the soil is satisfied, and the high DOFs of track-tunnel finite element systems have been reduced.

The modeling framework can be expressed as Fig. 6.

Fig. 6

The modeling framework for characterizing vehicle–track–tunnel dynamic interaction

4 Numerical study

In the numerical studies, the vehicle speed is set as 80 km/h. The vehicle and track parameters are taken from those of metro car A-type and monolithic track bed. Besides, track irregularities measured from a metro line are treated as the system excitations. The numerical examples are presented to validate the proposed model in accuracy and efficiency. Moreover, examples are conducted to demonstrate the necessity of considering tunnel configuration in VTT interaction and to confirm the maximum number of the tunnel segmental element for guaranteeing the solution precision.

4.1 Model validation

To validate the accuracy and efficiency of the proposed model, we first validate the cyclic calculation solution, and the then show the practicality of the model by comparing it to other model solutions.

4.1.1 Validation of the cyclic calculation solution

To validate the effectiveness of this model, comparisons are made between the cyclic calculation and the full matrix calculation, where the full matrix calculation indicates that the track-tunnel system matrices are totally considered in the direct integral scheme without boundary truncation.

Figure 7 shows the comparisons on tunnel vertical and lateral displacements at the bottom layer of the track slab, wheel-rail lateral force and car body lateral acceleration. It can be clearly observed from Fig. 7 that the results obtained by the cyclic calculation coincide well with those obtained by full matrix calculation from aspects of both wheel-rail forces and rail vibrations with very slight deviations. However, the application of cyclic calculation method possesses high computational efficiency. In a computer with Intel (R) Core (TM) i7-10700 K CPU @ 3.80 GHz, the time consumed by the cyclic calculation and full matrix calculation is, respectively, 2,430 and 7,890 s; that is, the computational efficiency has been significantly improved nearly without loss of precision.

Fig. 7

Comparisons between cyclic calculation and full matrix calculation: a tunnel vertical displacement; b tunnel lateral displacement; c wheel-rail lateral force; d car body lateral acceleration

4.1.2 Comparisons with the wheel-rail elastic contact solution

To further validate the accuracy and efficiency of this model, the wheel-rail contact model proposed in [20] is also introduced for comparison. Unlike the wheel-rail rigid contact of the present model, Hertzian contact is applied in [20] to consider the wheel-rail normal elastic contact.

In Figs. 8 and 9, comparisons are made on tunnel vertical displacement and acceleration, wheel-rail vertical force and car body vertical acceleration. It can be observed from Fig. 8 that the tunnel displacements derived by these two models agree well with each other from aspects of both amplitude and curve distribution characteristics. For example, the maximum tunnel vertical displacements of this model and the model in Ref. [20] are 0.076 and 0.074 mm, respectively, with a relatively small deviation of 2.7%. Moreover, Fig. 9 compares the wheel–rail interaction force and car body vibration. It can also be noticed that the results approach each other rather well, especially for the car body accelerations. As to the wheel-rail vertical force, the differences are also very slight between these two models though the dealing methods for wheel-rail vertical contacts are totally different. Generally, the response curves of the two models are basically approachable, only with a maximum deviation of 6.2%, which is generally acceptable in engineering.

Fig. 8

Comparison on tunnel vertical displacement and acceleration: a vertical displacement; b vertical acceleration

Fig. 9

Comparisons on wheel-rail force and car body acceleration: a wheel-rail vertical force; b car body vertical acceleration

In addition, comparisons are made in the frequency domain to show the effectiveness of this model. As illustrated in Fig. 10, the power spectral density (PSD) distributions of the tunnel and car body vertical acceleration have been compared between this model and the model in [20]. It can be clearly observed that the frequency responses agree well with each other at the coincident frequency range, especially at frequencies lower than 60 Hz. The system responses at the high-frequency domain are possibly underestimated in the wheel-rail rigid contact model.

Fig. 10

Comparisons on the tunnel and car body vertical accelerations from frequency domain: a vertical acceleration of the tunnel segment under track structures; b car body vertical acceleration

The time step size in the wheel-rail elastic contact model should be strictly small enough to guarantee the solution convergence, generally $\Delta t$ ≤ 10^–4 s, due to the nonlinear consideration in elastic contacts. While the present model possesses high computational stability, the solution can be obtained even at a large time step size such as 0.001 s or larger. In this example, the time consumed by this model and the mode of Ref. [20] is, respectively, 4,687 and 63,811 s. Obviously, this model also demonstrates significantly higher efficiency.

4.2 Influence of segment element number on VTT system performance

The element number in a tunnel segment, closely correlated to the iso-parametric element size, will greatly affect the efficiency and precision of the numerical solutions. For investigating the minimum element number to reach a balance between solution efficiency and precision in this study, the element number is set in the range of 3–17.

Figure 11 shows the maximum responses of wheel-rail force and track slab acceleration with respect to various element number, from which it can be observed that the maximum responses of different indices show slight deviations against different element numbers of tunnel segment. The maximum deviations are 0.6%, 0.09%, 2.5% and 2.7%, respectively, for wheel-rail vertical force, wheel-rail lateral force, track slab vertical acceleration and track slab lateral acceleration. That is, the response differences are relatively small for various element size of tunnel segment when a vehicle runs with a low speed of 80 km/h. For evaluating the macroscopic responses of track structures such as displacements, the tunnel element size can be relatively large without noticeable loss of precision.

Fig. 11

Maximum responses with respect to various elemental number: a wheel-rail vertical force; b wheel-rail lateral force; c track slab vertical acceleration; d track slab lateral acceleration

As to the tunnel system, it is known that the elemental stress/strain is significantly affected by the elemental size. Figure 12 shows the maximum vertical stress of the iso-parametric elements with respect to various element numbers in a tunnel segment. It can be observed from Fig. 12 that the maximum vertical stress gradually becomes steady when the element number reaches 13 or above.

Fig. 12

Maximum vertical stress against the element number in a tunnel segment

4.3 Influence of the tunnel configuration on vehicle–track interaction

In the VTT interaction system, the necessity of considering the full configuration of the tunnel system should be investigated. Here, three kinds of tunnel systems are considered as follows:

• (1) The first one, denoted by C₁, a tunnel ring consists of 6 tunnel segments which are connected by radius joints, as shown in Fig. 13a.

• (2) The second one, denoted by C₂, only the tunnel segment at the bottom of the track slab is considered, as shown in Fig. 13b.

• (3) The third one, denoted by C₃, a tunnel ring is continuous without radius joints and segments, as shown in Fig. 13c.

Fig. 13

Different types of tunnel ring representations: a C₁; b C₂; c C₃

The joint stiffness coefficients between tunnel segments are listed in Table 1.

Table 1 The joint stiffness coefficients between tunnel segments

Figure 14 shows the tunnel displacement and acceleration with respect to various types of tunnel systems. It can be seen from Fig. 14 that significant differences exist in the tunnel segment’s vibration in both vertical and lateral directions. Generally, the responses under tunnel ring of type C₂ are the most violent, C₁ the middle and the tunnel responses are the smallest if treating the tunnel ring as an whole without the decomposition of tunnel segments (C₃). As illustrated in Fig. 14a, the maximum tunnel vertical displacements are, respectively, 0.072, 0.081, and 0.049 mm. That is to say, the vibration will be overestimated if not accounting for the participation of the entire tunnel system in the VTT interaction, and it will be underestimated if only considering the tunnel ring as a united one without segments.

Fig. 14

Comparisons on tunnel segment centroid vibration at the bottom of the track slab: a vertical displacement; b lateral displacement; c vertical acceleration; d lateral acceleration

Besides, the comparisons on wheel–rail interaction force and car body acceleration are also investigated. As shown in Fig. 15, the influence law of tunnel types on wheel–rail interaction and vehicle vibration is generally similar to its influence on tunnel vibrations, but with smaller effects. Especially, the influence of types of tunnel system on car body vibrations can be ignored. As to the wheel-rail vertical force, a maximum difference of 0.9 kN is found between the response curves of the three types of tunnel systems.

Fig. 15

Comparisons on wheel–rail interaction and car body vibration: a wheel-rail vertical force; b car body vertical acceleration

Moreover, the tunnel response at the circumference can also be obtained only in conditions with full consideration of the segments in a tunnel ring. As Fig. 16 shows, the measurement points can be selected at the tunnel segmental centroid, and Fig. 17 shows the tunnel displacement and acceleration at these tunnel segmental measurement points. It can be observed from Fig. 17 that the tunnel responses show obvious symmetrical characteristics. The vertical displacement and acceleration of the tunnel segment at the bottom segment are the maxima because it directly bears the vehicle dynamic loads.

Fig. 16

The measurement points in a tunnel ring

Fig. 17

Tunnel vibrations at different measurement points: a vertical displacement; b lateral displacement; c vertical acceleration; d lateral acceleration

To further clarify the influence of joint stiffness between tunnel segments on tunnel responses, the longitudinal, lateral, and vertical joint stiffness are, respectively, set to be varied from 10⁷ to 10¹⁰ N/m. The tunnel points at the tunnel bottom segment and sidewall are selected as the response recording points, i.e., the points ‘a’ and ‘c_r’ in Fig. 16. Figures 18, 19, 20 and 21, respectively, show the tunnel vertical acceleration and displacement, and tunnel lateral acceleration and displacement at the recording points.

Fig. 18

Influence of tunnel segmental joint stiffness on tunnel vertical acceleration: a tunnel bottom segment; b tunnel sidewall

Fig. 19

Influence of tunnel segmental joint stiffness on tunnel vertical displacement: a tunnel bottom segment; b tunnel sidewall

Fig. 20

Influence of tunnel segmental joint stiffness on tunnel lateral acceleration: a tunnel bottom segment; b tunnel sidewall

Fig. 21

Influence of tunnel segmental joint stiffness on tunnel lateral displacement: a tunnel bottom segment; b tunnel sidewall

It can be observed from Figs. 18 and 19 that the longitudinal joint stiffness shows little influence on tunnel vertical vibrations. However, the vertical and lateral stiffness display significant influence on tunnel vertical displacement and acceleration. The tunnel vertical displacement and acceleration at the tunnel bottom gradually decrease with an increase in the vertical and lateral joint stiffness, whereas the tunnel vertical displacement at the tunnel sidewall increases with the vertical joint stiffness increasing.

From the lateral responses of the tunnel shown in Figs. 20 and 21, it can be seen that the tunnel lateral displacement and acceleration at the bottom segment gradually decrease with an increase in the joint stiffness, and the lateral joint stiffness exerts larger effects on lateral vibrations of the tunnel bottom segment compared with other forms of joint stiffness. However, the vertical joint stiffness also shows great influence on the lateral displacement and acceleration of the tunnel sidewall, attributed to the circular configuration of the tunnel (Figs. 20b and 21b).

4.4 Influence of VTT coupling effects on system responses

To quantify the influence of VTT coupling effects on system response evaluations, comparisons are made between this coupled model and the two-step model [19] in terms of vehicle-related response indices, i.e., wheel-rail vertical force and car body vertical acceleration. As the time-domain response curves in Fig. 22 show, the two models generate approachable results with a slight deviation, indicating that taking into consideration the coupling effects or not have little influence on vehicle responses.

Fig. 22

Comparisons on vehicle-related response indices: a wheel-rail vertical force; b car body vertical acceleration

Figures 23 and 24 further present the tunnel responses of the two models. Comparison on the tunnel displacements (Fig. 23) illustrates that there exist noticeable differences between the two models in tunnel vertical and lateral displacements. Especially at local positions, the responses of the coupled model fluctuate more violently than those of the two-step model. For revealing the difference clearer, Fig. 24 demonstrates the comparisons on tunnel accelerations. It can be clearly seen from Fig. 24a, b that the tunnel acceleration derived from the coupled model is significantly larger than that derived from the two-step model. Additionally, Fig. 24c, d display comparisons in frequency domain by PSD evaluations. Obviously, the two-step model can only reveal the system performance in the low frequency range. As to the tunnel vertical acceleration, the results of the two model agree well with each other at frequencies below 15 Hz; above it, large deviations start to emerge. It indicates that the two-step model might underestimate tunnel responses in engineering applications.

Fig. 23

Comparisons on tunnel displacement: a vertical displacement; b lateral displacement

Fig. 24

Comparisons on tunnel acceleration in time and frequency domains: a time-domain vertical acceleration; b time-domain lateral acceleration; c PSD of vertical acceleration; d PSD of lateral acceleration

5 Conclusions

In this work, matrix formulations for revealing vehicle–track–tunnel dynamic interaction mechanisms are presented in light of the methodology of vehicle–track coupled dynamics [20]. In this model, specific issues on the modeling of the tunnel system with infinite boundaries and the development of highly efficient solution programs are paid close attention to and have been solved with detailed schemes, and consequently, it becomes a possibility to efficiently evaluate the dynamic performance of a fully configurated vehicle–track–tunnel coupled system in engineering practices for the first time.

Apart from numerical validations, several conclusions can be drawn as follows:

• (1) The method of truncating the system matrices can significantly improve the computational efficiency and obtain approachable results to those of full matrix solutions.

• (2) It is significantly important to consider the detailed structural configuration of the tunnel in the dynamic evaluation of VTT systems; otherwise, the vibrational behavior of the tunnel can not be revealed accurately.

• (3) It is important to confirm the maximum size of finite elements. The iso-parametric element number contained in a track segment should reach at least 13 to guarantee the precision of the stress.

• (4) The two-step solutions or non-coupling solutions might underestimate the tunnel vibrations, especially in high frequency ranges.