1 Introduction

Extruded aluminium panels are key structural components for high-speed train frame structures and airplane fuselage due to their significant advantages of light weight, high static stiffness and great fatigue resistance. However, they are also found to be rather poor noise barriers owning to their high flexural stiffness, extended coincidence frequency ranges, and local resonances [1, 2]. In order to improve the structural characteristics of a vehicle for greater noise insulation and less noise radiation, vibro-acoustic modelling of extruded aluminium panels has received significant attention from both academia and industry in the past decades, e.g. Refs. [3–14].

It has been found [7–14] that the vibrational and sound transmission behaviours of such kinds of stiffened panel structures can be very difficult to predict by either conventional deterministic methods, such as finite element methods (FEM) and/or boundary element methods (BEM), or conventional statistical methods, such as statistical energy analysis (SEA). This is mainly because the extruded train panel structures are built up by beam-like stiffeners and thin flat panels. Since the stiffeners are generally much stiffer than the panels, under external/internal/acoustic loadings, the dynamic response of the stiffened panels as a whole can contain deformations of both long- and short-wavelength, generated by the stiff and flexible components, respectively, for quite a large frequency region. In this case, neither a single deterministic nor a single statistical modelling technique is suitable [15]. In addition, parameter uncertainties are unavoidable due to manufacturing variations, tolerances, ageing, imperfections in joints and material properties, and so on. As the dynamic behaviour of a structure becomes increasingly sensitive to the exact details of the structure with frequency increasing, the short-wavelength components tend to be more significantly affected than the long-wavelength ones by the system parameter uncertainties [16]. Consequently, the long-wavelength deformations tend to behave “deterministically” whereas the short-wavelength ones behave “randomly” [17]. As a result, neither deterministic FEM/BEM nor high-frequency statistical methods are suitable [18]. This problem is generally termed as “mid-frequency vibro-acoustic issues” [19, 20].

In the past decades, extensive research effort has been put into the mid-frequency vibro-acoustic modelling of stiffened-panel-like structures and resulted in a large number of publications. Several special issues of journal publications and conferences on mid-frequency vibro-acoustic modelling problems are also available. The most influential ones include the Journal of Sound and Vibration Vol. 288, Issue 3 (2005) and Vol. 332 Issues 8–10 (2013), the International Conference of Noise and Vibration: Emerging Methods (NOVEM) which was started in 2004, and the International Conference of Uncertainty in Structural Dynamics which was started in 2007. Major reviews on the relevant developments can be found in [20], [21], and [22] (2013, Chapter 1). However, despite the rapid development of the mid-frequency theories in recent years, it is true to say that there are still many questions remained to be answered [23, 24].

With the above in mind, the current review focuses on the most recent developments on the mid-frequency vibro-acoustic modelling techniques as well as the state-of-the-art of industrial application to extruded aluminium train floor structures. First, the major mid-frequency vibro-acoustic characteristics associated with stiffened panel structures are briefly introduced in Sect. 2, together with an illustration of the locally resonant behaviours of an extruded aluminium section which dominate the mid-frequency region and have significantly effects on the vibration and sound transmission of the structure. Then in Sect. 3, the main principle and theoretical predicting procedures for a few of major hybrid techniques are recapitulated and compared, and their advantages and disadvantages are discussed. Two recently developed hybrid models are particularly introduced in Sect. 4 for their great potentials on predicting the mid-frequency issues of stiffened panel structures. Finally in Sect. 5, as the end of the paper, future developments and remaining challenges are highlighted.

2 Mid-frequency vibro-acoustics of extruded aluminium panels

A section of extruded aluminium panel used for high-speed train floor structure is shown in Fig. 1. Geometrically, it belongs to rib-stiffened panel structures. Vibro-acoustics of extruded aluminium panels are characterized by mid-frequency behaviours for quite a large frequency range [9–12].

Fig. 1
figure 1

A section of extruded aluminium train floor structure (Fig. 8 in Ref. [14])

Full size image

For a generic rib-stiffened panel structure it is generally known [1, 2] that, when frequency is far below a certain value, it behaves vibro-acoustically like an orthotropic thin plate; when frequency is far above that value, the structure simply behaves as a diffuse reverberant field. Between the low- and high-frequency ranges, there is a so-called mid-frequency region, in which the stiffened panel starts to develop structural waves of quite different wavelengths, and in particular individual corrugations start to exhibit localized behaviours. Due to the complex dynamic couplings between the stiffeners and the plates, these structural waves are found to interact with each other via a rather complex mechanism [9–11].

A local resonance of the plate strip in Fig. 1 and its influences on the vibration response of the structure section has been illustrated in Fig. 2 (which was originally given in Ref. [14] as Fig. 9). In Fig. 2, the input powers predicted by two different hybrid approaches are compared with the measurement results with a shaker excitation first at a point on the rib position and then in the centre of a plate strip closet to the rib position. It is seen from Fig. 2 that, below about 250 Hz, differences between these two loading positions are quit small. However, as frequency goes higher, the power input for the strip-located forcing case exhibits a sharp rise, and becomes more than 10 times that of the rib-located forcing case. The sharp rise is actually due to the cut-on frequency of the first local modes of the plate strip. (The 1st local mode shape was also illustrated in Fig. 2 which occurs at about 447 Hz). One may thus conclude that the vibration and sound transmissions of the extruded aluminium structure in the mid-frequency regime can be significantly affected by the local resonances, and hence one may expect that a successful hybrid model should be able to capture the local resonances as well as their influences on the vibro-acoustics of extruded panel structures.

Fig. 2
figure 2

Power input from point force excitation (Fig. 9 in Ref [14]). Rib-located: predicted, black line; measured, black dot. Strip-located: predicted, grey line; measured, grey cross. The fundamental modal shape of the strips with natural frequency at 447 Hz is also shown

Full size image

In fact, such dynamic behaviours of extruded aluminium section is typical for stiffened panel structures, for which the dynamic response from a point load is global and uniform at low frequencies and tends to localize at higher frequencies where the point mobility increases substantially. Because of the differences in dominant vibro-acoustic characteristics at different frequency ranges for stiffened panel structures, different vibration and acoustic modelling approaches should be applied accordingly. In principle, the choice for appropriate techniques should follow the two criteria below: (1) the adopted technique should be able to effectively reflect the critical design changes for the vibro-acoustic performance of the product, and (2) the predicting procedure should be computationally robust and efficient.

3 Major mid-frequency vibro-acoustic modelling techniques

Vibro-acoustic modelling techniques can be generally categorized into deterministic and statistical approaches [16]. The former, such as the conventional FEM/BEM methods, are more suitable for deterministic predictions at low frequencies [20], while the latter, such as the standard SEA, are more convenient at higher frequencies [21]. Moreover, it is generally recognized that deterministic approaches are more useful for solving structure-borne sound transmission problems while statistical methods are mainly for air-borne sound transmissions [24]. In terms of the prediction principles, deterministic approaches can be further divided into analytical and numerical modelling. Analytical models are commonly based on wave propagations and/or modal analysis, while the numerical ones are mainly based on the element-solutions, such as the standard FEM and/or BEM. Consequently, an analytical model has the advantages of providing insights into the physical parameters that govern the response of the system, but may generally have much limited range of applicability than numerical approaches. On the other hand, a numerical model can account for arbitrarily geometric complexity of the structures, but tends to be very much computationally expensive, especially for large-scaled structures.

As far as the extruded train floor structure concerned, element-based deterministic methods, such as FEM/BEM, are often used to predict the vibro-acoustic response at low frequencies [4, 5]; while at high frequencies, SEA is more likely to be used [6, 7]. At mid-frequencies, however, due to the limitations of conventional deterministic FEM/BEM models and standard SEA models, the main methodologies currently adopted are hybrid approaches which are formed by combinations of two or more different standard modelling techniques into one procedure [20, 21].

Typical hybrid approaches for mid-frequency vibro-acoustic modelling of generic complex structures, by the prediction nature of the combined techniques, can be roughly divided as [24]: (1) enhanced deterministic methods, (2) enhanced statistical methods, and (3) hybrid deterministic/statistical methods. A common advantage of these hybrid methods is that the hybrid procedure allows the main mid-frequency vibration behaviours of a built-up structure to be predicted at a reasonable computational cost but still with an acceptable accuracy [20–24].

3.1 Enhanced deterministic methods

An enhanced deterministic method is actually a combination of different types of conventional deterministic methods with improved computational efficiency so that the upper bound of the applicable frequency range can be extended to be higher [24].

It is known that element-based deterministic approaches are only suitable for the frequency range where the wavelength in the dynamic response of the structure is much longer than the characteristic wavelength of the structure, i.e. when the response of the system is determined by well-separated modes [20]. Since wavelengths get shorter as frequency increases, the number of elements required for describing the problem domain can become very large at higher frequencies and hence may result in huge computational cost as well as significant dispersion and pollution errors [24]. Contrary to the element-based numerical solutions, wave-based analytical method (WBM), as an indirect Trefftz approach, approximates the field variable by a weighted sum of so-called “wave functions”, each of which is an exact solution of the governing differential equation of the problem domain [24]. These wave functions comprise propagating as well as evanescent waves with the associated wave numbers relying on the dimensions of the problem domain. As a result, model refinement can be easily done by increasing the number of wave functions in the problem domain rather than increasing the number of elements. Consequently, wave-based methods can be much more efficient for large problem domains with a simple geometry when compared with the conventional element-based models.

Alternative approaches for long extruded structures are to use a wave analysis in the axial direction and a FE/BE approach in the cross-section, known as waveguide finite elements (WFE) [25, 26], or to use FE models of a periodic segment of the structure and to derive wave properties from this, known as the wave and FEM [27].

For example, in Ref. [14], two different deterministic approaches were used to predict the sound transmission of a section of extruded aluminium train floor structure. One was a model based on the periodicity of the structure, i.e. the so-called periodic cell method (PCM), and the other was the waveguide FE method (WFEM) which requires a wave guiding geometry in at least one direction of the structure. The sound transmission loss of the extruded floor panel was calculated by both methods and then compared against the experimental measurement as shown in Fig. 3 (i.e. Fig. 11 of Ref. [14]). The advantages and disadvantages of these two approaches were then illustrated.

Fig. 3
figure 3

Sound transmission loss of extruded floor panel (Fig. 11 in Ref. [14]). Measured, black dot; PCM calculated, solid line; WFEM calculated, dashed line

Full size image

It is seen from Fig. 3 that both the PCM and WFEM approaches can predict the sound transmission of the floor section reasonably well for the mid-frequency region (e.g. from 500 to 4,000 Hz). However, the WFEM was found computationally much cheaper than the PCM modelling. Moreover, WFEM technique was found more accurate than the PCM approach at low frequencies. However, WFEM is not applicable for structures with moderate geometrical complexity, although the WFEM has obviously more advantages than the PCM for extruded aluminium structures.

Having said that, however, one should bear in mind that the enhanced determinist approaches, in nature, are based on analytical modelling of wave propagations and numerical modelling (element-meshing) of dynamic deformations. Therefore, despite the significant advantages of relieving efficiently the severe frequency limitations of pure element-based methods, such enhanced deterministic models may become quite problematic when dealing with system models which involve component parts with large parameter uncertainties and/or complex geometries [18, 19]. In this case, enhanced statistical methods and/or hybrid deterministic-statistical methods tend to be more appropriate [21–24].

3.2 Enhanced statistical methods

It is known that SEA is computationally very efficient but relies on quite a few assumptions, such as that each subsystem is of diffuse field and/or that waves are uncorrelated. Since these major assumptions tend to be met only above a certain frequency limit, the method is restricted to the high-frequency range. Enhanced statistical methods therefore try to extend the statistical approaches towards lower frequencies [14].

The currently existing enhanced statistical methods can be mainly divided into two categories: (1) by improving the conventional SEA predicting procedure so that the validity range of the SEA results can be extended to lower frequencies compared to standard SEA models, e.g. in Refs. [6, 7]; and (2) by setting up new statistical models according to new statistical theories, which are similar in form to, but different in nature from, the conventional SEA, so that a better accuracy than standard SEA models can be achieved, e.g. in Refs. [28–30].

For the improved SEA models, the main techniques involved were usually by getting a better estimation of SEA parameters and/or by relaxing one or more key assumptions imposed by SEA. For example, in Ref. [6] a SEA subsystem formulation based on a combination of FEM, component mode synthesis (CMS) [31], and periodic structure theory [31–33] was developed. The approach focused on the problematic subsystems which are often encountered in industry but not well represented by existing analytical formulations of standard SEA. Examples of such subsystems include composite fuselages, isogrid fairings, complex ribbed panels, and extruded train floors, as shown in Fig. 4 (i.e. Fig. 1 of Ref. [6]).

Fig. 4
figure 4

Typical panel constructions (Fig. 1 in Ref. [6]). a Simple uniform panel. b Laminated panel. c Skin-stringer fuselage. d Corrugated composite fuselage. e Isogrid launch vehicle fairing. f Extruded aluminium train floor

Full size image

With the approach described in Ref. [6], any general panel structure can be treated as a single SEA subsystem, whose key SEA parameters, such as modal density, damping loss factor, and acoustic transmission loss (and hence the coupling loss factors with the acoustical domain) can all be formulated as explicit expressions so as to compute efficiently and more accurately.

Although the technique presented in Ref. [6] enables the SEA parameters to be computed with better accuracy for general structural panels, it can still be quite time consuming for applications on train floor-like structures due to the large dimensions of each “cell”, e.g. three bays of triangular extrusions in case of the extruded panel structure shown in Fig. 1. Meanwhile, it was found to be more suitable to predict the transmission through the structures (i.e. air-borne transmission) but tends to have limitations in predicting the transmission along the structures (i.e. structure-borne transmission) [14].

Most recently, a new statistical approach called “Dynamic Energy Analysis” (DEA) was developed in Ref. [28], which extends SEA towards non-diffusive wave fields, and thus can provide a better resolution than the conventional SEA. In principle, DEA takes into account the full directionality of the wave field. Coupling of subsystems at interfaces is described in terms of scattering matrices by solving the wave equation locally with the help of full wave solution methods. This technique was then further extended to mid-frequency structures which admit short- and long-wavelength components [29, 30]. This was mainly achieved by treating the short-wavelength part of a structure by DEA and the long-wavelength component by constructing a corresponding scattering matrix using FEM with appropriate boundary conditions. Hence a so-called hybrid DEA/FEM model can be constructed. It has been shown that DEA can handle multi-mode wave propagation effectively taking into account mode conversion between shear, pressure, and bending waves.

3.3 Hybrid deterministic-statistical methods

Hybrid deterministic-statistical models are generated by combining deterministic and statistical modelling techniques into one predicting procedure, e.g. in Refs. [17–22, 34–43], in which the long-wavelength, stiff components are usually described deterministically whereas the short-wavelength, flexible components are described statistically so as to account properly for the effects of system parameter variability [23, 44, 45]. Consequently, such combined hybrid models can provide more representative solutions than purely deterministic models for the vibro-acoustic response of an ensemble of products [20–22].

According to different deterministic modelling approaches employed in the combination procedure, hybrid FE-SEA [21] and WBM-SEA [24] approaches are among the most promising recently developed mid-frequency modelling techniques. For both types of hybrid modelling, the dynamic response of the deterministic components and statistical energy response (i.e. time- and space-averaged subsystem energies) of the statistical components are usually predicted (Detailed theoretical principles of these two hybrid models will be introduced in Sect. 4). The major differences between them lie in that the former describes the deterministic subsystem by conventional FEM, while the latter substitutes the FE part of the hybrid model by the WBM in order to achieve an increased efficiency. Of course, the FE-SEA models are obviously more generic than the WBM-SEA ones due to the general limitations of wave methods on modelling complex geometries.

Although present applications of both types of hybrid models for industry examples have been demonstrated in a few of publications by predicting successfully the mid-frequency vibrational responses and sound transmissions, e.g. in Refs. [46–49], direct applications of these approaches to vibro-acoustic modelling of extruded aluminium panel structures are still quite problematic because of the complex dynamic nature of extruded panel structures [50, 51]. It is true to say that mature and adequate prediction techniques are still very much needed for solving sound transmission through, and radiation from, extruded aluminium panels used for high-speed train structures.

Having said this, however, the deterministic-statistical methods have exhibited a great potential in predicting the mid-frequency-related vibro-acoustic issues of rib-stiffened panel structures. It is worthwhile to explore further the possible extension of these two hybrid techniques in solving the vibro-acoustics of extruded train floor structures. For this purpose, therefore, the main theoretical principles of hybrid FE-SEA and WBM-SEA approaches are introduced in the section below.

4 Main principles of hybrid deterministic-statistical methods

For simplicity, the reviews of both the hybrid FE-SEA and the WBM-SEA approaches are based on a general deterministic-statistical hybrid model shown in Fig. 5. In both hybrid approaches, the whole system is divided into a deterministic and many statistical subsystems [38, 49], of which, the boundary \(\varGamma_{\text{S}}\) of a statistical subsystem can be divided into a deterministic boundary \(\varGamma_{\text{Sd}}\) (in thick solid line) which is known precisely and has a deterministic behaviour, and a boundary \(\varGamma_{\text{Ss}}\) (in dashed line) which has a statistical behaviour so that the average responses of the statistical subsystem can be treated as independent of the exact boundary conditions of \(\varGamma_{\text{Ss}}\) [38]. Obviously, all the subsystem interfaces (including those between the SEA subsystems) should be treated as parts of the deterministic model.

Fig. 5
figure 5

A general deterministic-statistical hybrid model

Full size image

For such a hybrid model, only the displacement-based response of the deterministic part of the model and statistical energy response of each SEA subsystem are of interest.

4.1 Hybrid FE-SEA method

In Ref. [49], the energy balance relation between two coupled SEA subsystems was illustrated as Fig. 6, where the input power into each subsystem simply equals to the power dissipated by the subsystem itself and the power transmitted to the other subsystem through their couplings.

Fig. 6
figure 6

Energy balance for two coupled SEA subsystems

Full size image

In Ref. [38], the response of each statistical subsystem can be written as a superposition of a “direct-field” and a “reverberant field”, as shown in Fig. 7. Here, the direct field is defined as the outgoing field through the deterministic boundary in the absence of the statistical boundary (i.e. by ignoring the existence of the statistical boundary so that the SEA subsystem can be treated as semi-infinite) while the reverberant field satisfies blocked boundary conditions across the deterministic boundary and the prescribed boundary conditions across the statistical boundary, when added to the direct field. Consequently, a power balance equation for each individual SEA subsystem of the built-up system can then be set up by equating the power input into the direct field of subsystem with the power output from its reverberant field.

Fig. 7
figure 7

Response of statistical subsystem

Full size image

Hence in Ref. [38], for the \(j{\text{th}}\) SEA subsystem, for example, the power balance equation is given by

$$\omega \eta_{j} E_{j} + \omega \eta_{{{\text{d}},j}} E_{j} + \sum\limits_{k = 1}^{N} {\omega \eta_{jk} n_{j} \left( {\frac{{E_{j} }}{{n_{j} }} - \frac{{E_{k} }}{{n_{k} }}} \right) = P_{{{\text{in}},j}}^{\text{ext}} } ,$$
(1)

where \(N\) is the total number of SEA subsystems; \(E_{j}\) and \(n_{j}\) are, respectively, the ensemble-averaged vibrational energy and the modal density of SEA subsystem \(j\); and, \(\eta_{{{\text{d}},j}}\) and \(\eta_{jk}\) are, respectively, the effective coupling loss factor between subsystem \(j\) and the FE subsystem and that between SEA subsystem \(j\) and SEA subsystem \(k\). Thus the four terms on the left side of Eq. (1) represent, respectively, the power dissipated within SEA subsystem \(j\), the power transmitted from the reverberant field of subsystem \(j\) to the FE model, the power transmitted from the reverberant field of subsystem \(j\) to the direct field of other SEA subsystems, and the power injected into the reverberant field of subsystem \(j\) from other SEA subsystems.

The effective coupling loss factors \(\eta_{{{\text{d}},j}}\) and \(\eta_{jk}\) in Eq. (1) can be determined by [38]

$$\omega \eta_{{{\text{d}},j}} = \left( {\frac{2}{{\uppi n_{j} }}} \right)\sum\limits_{rs} {\text{Im} \left( {D_{{{\text{d}},rs}} } \right)\left( {\varvec{D}_{\text{tot}}^{ - 1} \text{Im} \left( {\varvec{D}_{\text{dir}}^{ (j )} } \right)\left( {\varvec{D}_{\text{tot}}^{ - 1} } \right)^{\text{H}} } \right)_{rs} } ,$$
(2)
$$\omega \eta_{jk} n_{j} = \frac{2}{\uppi }\sum\limits_{rs} {\text{Im} \left( {D_{{{\text{dir}},rs}}^{(j)} } \right)\left( {\varvec{D}_{\text{tot}}^{ - 1} \text{Im} \left( {\varvec{D}_{\text{dir}}^{ (k )} } \right)\left( {\varvec{D}_{\text{tot}}^{ - 1} } \right)^{\text{H}} } \right)_{rs} } ,$$
(3)

where the superscript H represents conjugate transpose, and

$$\varvec{D}_{\text{tot}} = \varvec{D}_{\text{d}} + \sum\limits_{k} {\varvec{D}_{\text{dir}}^{(k)} } .$$
(4)

In Eq. (4), \(\varvec{D}_{\text{d}}\) and \(\varvec{D}_{\text{dir}}^{(k)}\) are, respectively, the dynamic stiffness matrix of the FE model and the direct field dynamic stiffness matrix of subsystem k.

On the right side of Eq. (1), \(P_{{{\text{in}},j}}^{\text{ext}}\) is simply the power input into the direct field of subsystem \(j\) by the external force loading on the FE model of the system, which is given by [38]

$$P_{{{\text{in}},j}}^{\text{ext}} = \frac{\omega }{2}\sum\limits_{rs} {\left[ {\text{Im} \left( {D_{{{\text{dir}},rs}}^{(j)} } \right)\left( {\varvec{D}_{\text{tot}}^{ - 1} \varvec{S}_{ff} \left( {\varvec{D}_{\text{tot}}^{ - 1} } \right)^{\text{H}} } \right)_{rs} } \right]} ,$$
(5)

where \(\varvec{S}_{ff}\) is the ensemble-averaged cross-spectral matrix of the external force loadings \(\varvec{f}\) with \(\varvec{S}_{ff} = {\text{E}}[\varvec{ff}^{\text{H}} ]\), of which, \({\text{E}}[ \cdot ]\) represents ensemble average.

Substituting Eqs. (2)–(5) into Eq. (1), the power balance equation for each individual SEA subsystem can be completed. Combining these power balance equations, the energy response for each individual SEA subsystem can then be obtained.

Following the solutions of the energy responses of all SEA subsystems, a specified procedure is adopted in the hybrid FE-SEA theory to set up the relations between the displacement of the FE model and the SEA subsystems, i.e. the so-called “diffuse field reciprocity relation”: If the subsystem is assumed to be sufficiently random (which generally requires a statistical overlap factor to be larger than unity [48]), the reverberant force loadings of each SEA subsystem on its deterministic boundaries (i.e. the coupling interfaces either between SEA subsystems and/or between FE and SEA subsystems) are statistically related to the energy response of the subsystem, as [38]

$$\varvec{S}_{{ff , {\text{rev}}}}^{ (j )} = {\text{E}}\left[ {\varvec{f}_{\text{rev}}^{(j)} \varvec{f}_{\text{rev}}^{{(j){\text{H}}}} } \right] = \left( {\frac{{4E_{j} }}{{\omega \uppi n_{j} }}} \right)\text{Im} \left( {\varvec{D}_{\text{dir}}^{(j)} } \right) .$$
(6)

Equation (6) thus allows a statistical formulation to be established between the displacement response of the FE model and the energy responses of the SEA subsystems, as [38]

$$\varvec{S}_{qq} = {\text{E}}(\varvec{qq}^{\text{H}} ) = \varvec{D}_{\text{tot}}^{ - 1} \left[ {\varvec{S}_{ff} + \sum\limits_{j = 1}^{N} {\left( {\frac{{4E_{j} }}{{\omega \uppi n_{j} }}} \right)\text{Im} \left( {\varvec{D}_{\text{dir}}^{(j)} } \right)} } \right]\left( {\varvec{D}_{\text{tot}}^{ - 1} } \right)^{\text{H}} ,$$
(7)

where q is the displacement vector of degrees of freedom (DOFs) of the FE structure, and \(\varvec{S}_{qq}\) is the ensemble-averaged cross-spectral matrix of the displacement response q.

So far the vibration responses of both the FE and SEA subsystems can be predicted in a statistical way. The only main assumption involved in the hybrid FE/SEA theory is that the non-deterministic boundaries of each SEA subsystem are sufficiently random [38, 39] such that the diffuse field reciprocity relation [Eq. (6)] can hold to be valid. Although it generally requires each SEA subsystem to be of high modal density, this “sufficient randomness condition” may be relaxed if the FE and the SEA subsystems are of large dynamic mismatch [51].

Very recently, the hybrid FE-SEA approach has been further extended to allow the FE components to possess a low level of parameter uncertainties [40, 41], of which two ensembles of uncertainty have been considered: a non-parametric one (SEA subsystems) and a parametric one (FE components). At the first stage, e.g. in Ref. [40], the SEA subsystem ensemble was dealt with analytically, while the FE components ensemble was dealt with numerically, i.e. by Monte Carlo Simulations. However, this treatment was found to be quite computationally intensive when applied to complex engineering systems having many uncertain parameters. To solve this problem, in Ref. [41], two different strategies were proposed: (1) the combination of the hybrid FE-SEA method with the first order reliability method [41, 52] which allows the probability of the non-parametric ensemble average of a response variable exceeding a barrier to be calculated, and (2) the combination of the hybrid FE-SEA method with Laplace’s method [41, 53] which allows the evaluation of the probability of a response variable exceeding a limit value. However, the validity of the proposed approaches has only been illustrated using simple built-up plate systems in Ref. [41].

From the above theoretical procedure of the hybrid FE-SEA method, it is seen that, although the Hybrid FE-SEA approach has set up a deterministic-statistical framework which can well combine FEM and SEA models, this method can be very limited in use due to the computational load of the FEM models [49, 50] when the size of the FE model is quite large, for example, when there exists a large number of interface DOFs between the connected subsystems [24]. Therefore, the hybrid FE-SEA model faces a great challenge of model reduction so as to improve the computational efficiency.

4.2 Hybrid WBM-SEA method

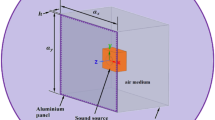
With the above in mind, a framework for coupling Trefftz-based deterministic models with statistical SEA models was set up in Ref. [49]. Instead of the FEM, the computationally more efficient wave-based method (WBM) is being used, and hence a hybrid WBM-SEA method can be achieved [50]. In this subsection, the major theoretical procedure developed in [49] is briefly reviewed in which WBM for acoustics is combined with SEA for structural vibrations in order to tackle the vibro-acoustic problems.

The concept of the hybrid WBM-SEA method is illustrated in Fig. 8, in which a 3-D deterministic acoustic cavity \({\varvec{A}}\) is coupled to a 2-D elastic plate with statistical properties. In Fig. 8, \(\varvec{q}_{\text{f}}\) is the displacement vector at the DOF on the interface between the deterministic and statistical subsystem, and w is the displacement vector at the DOF of deterministic cavity \({\varvec{A}}\), and \(\varvec{C}_{\text{as}}\) and \(\varvec{C}_{\text{sa}}\) are the associated acoustic–structural coupling matrices between the interface DOFs, \(\varvec{q}_{\text{f}}\) and the internal DOFs, w. Here, the employment of discretized interface frame is mainly to make use of the diffuse field reciprocity relationship [i.e. Eq. (6)] so that a hybrid methodology similar to those described in Sect. 4.1 can be adopted.

Fig. 8
figure 8

The vibro-acoustic WBM-SEA (Fig. 5 in Ref. [49])

Full size image

In case of Fig. 8, therefore, the coupled matrix equation for the deterministic-statistical model can be written as [49]

$$\left[ {\begin{array}{*{20}l} \varvec{A} \hfill & {\varvec{C}_{\text{as}} } \hfill \\ {\varvec{C}_{\text{sa}} } \hfill & {\varvec{D}_{\text{dir}} } \hfill \\ \end{array} } \right]\left\{ \begin{aligned} \varvec{w} \hfill \\ \varvec{q}_{\text{f}} \hfill \\ \end{aligned} \right\} = \left\{ \begin{aligned} \varvec{b} \hfill \\ \varvec{f} \hfill \\ \end{aligned} \right\} + \left\{ \begin{aligned} 0\;\;\; \hfill \\ \varvec{f}_{\text{rev,s}} \hfill \\ \end{aligned} \right\} ,$$
(8)

where b is the load vector of the deterministic subsystem, f is the generalized interface force vector, and \(\varvec{f}_{\text{rev,s}}\) is the blocked reverberant force on the interface DOFs.

Based on the WBM theory, in [49], the structural–acoustic coupling matrix \(\varvec{C}_{\text{as}}\) and the acoustic-structure coupling matrix \(\varvec{C}_{\text{sa}}\) are found, respectively, as

$$\varvec{C}_{\text{as}} = \int\limits_{\varGamma } {{\text{i}}\omega\varvec{\varPhi}(\varvec{r})\varvec{N}(\varvec{r}){\text{d}}\varGamma } ,$$
(9)
$$\varvec{C}_{\text{sa}} = - \varvec{D}_{\text{dir}} \int\limits_{\varGamma } {G\left( {d(\varvec{r}_{\text{f}} ,\varvec{r})} \right)\varvec{\varPhi}(\varvec{r}){\text{d}}\varGamma } ,$$
(10)

where r is an arbitrary point of acoustic cavity and \(\varvec{r}_{\text{f}}\) is the local vector of the interface points, \(\varvec{\varPhi}(\varvec{r})\) represents the basis wave functions which can exactly satisfy the homogeneous Helmholtz of the acoustic cavity (deterministic model), while \(G\left( d \right)\) is the Green’s function of an infinite plate to the acoustic pressure, \(d(\varvec{r}_{\text{f}} ,\varvec{r})\) is the distance between the points \(\varvec{r}_{\text{f}}\) and r, and \(\varvec{N}(\varvec{r}_{\text{f}} )\) is a vector containing shape functions interpolating the nodal displacements \(\varvec{q}_{\text{f}}\).

By modifying the terms in the power balance relation of Eq. (1) according to the specified coupling matrices \(\varvec{C}_{\text{as}}\) and \(\varvec{C}_{\text{sa}}\) [Eqs. (9)–(10)], the hybrid WBM-SEA predicting procedure can then be formed which possesses a better computing efficiency than the hybrid FE-SEA model [49, 50].

However, due to the geometrical limitations of WBM, the hybrid WBM-SEA model can be less general than the FE-SEA model [50, 51]. Research towards reducing the geometrical limitations of the WBM for structural problems, e.g. by allowing local in-homogeneities, holes or inclusions, is still in progress, e.g. in [50].

5 Concluding remarks

A brief review is given in the present paper to the vibro-acoustic modelling of extruded aluminium train floor structures including the state-of-the-art of industrial applications, as well as the most recent developments on mid-frequency modelling techniques in general. These methods are all heavily relying on certain types of hybrid modelling which can be roughly divided as: (1) enhanced deterministic modelling, (2) enhanced statistical modelling, and (3) combined deterministic/statistical modelling. A common advantage of these hybrid methods is that the hybrid procedure allows the main mid-frequency vibration behaviours of a built-up structure to be predicted at a reasonable computational cost but still with an acceptable accuracy. Two most promising recently developed hybrid modelling techniques, i.e. the hybrid FE-SEA and hybrid WBM-SEA approaches, are particularly addressed, due to their great potential in predicting the mid-frequency vibro-acoustics of stiffened panel structures.

Although the recent development of mid-frequency vibro-acoustic modelling techniques has led to a significant step forward in the applicability in solving the sound transmission and radiation of extruded aluminium panels for high-speed train structures, in fact, as pointed in Refs. [24, 54], there are currently still no mature and adequate prediction techniques available. Efforts must be continuously excised to improve existing techniques and/or develop new ones to meet the need of the high-speed railway industry.