1 Introduction

In order to evaluate the ride quality of a railway vehicle, the vertical and lateral contact forces have to be measured. In the reference frame as shown in Fig. 1, the three components of the measured contact force are indicated: the longitudinal force X, directed along the x-axle in the longitudinal direction of rail, the lateral force Y, directed along the y-axle, and the vertical force denoted by Q.

Fig. 1
figure 1

Wheel–rail reference system

Full size image

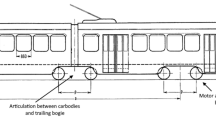
A dynamic behavior analysis in the norm UIC518 [1, 2] prescribes the experimental measurement of Y-force and Q-force with a minimum bandwidth of 20 Hz. The X-force is also scientifically interesting to the identification and modeling of wheel–rail adhesion phenomena in the testing and homologation of safety relevant subsystems like the odometry for on-board wheel-slide protection system (WSP). In this article, we propose a benchmark test bogie for the three components of contact force, designed to be equipped with sensor and control systems. In order to reduce the negative influence of braking forces, the bogie layout as shown in Fig. 2 is designed, which has a standard H-shaped steel frame, inspired by a widely diffused design adopted also on coaches of ETR500 High Speed Train. To diminish the disturbances on measurements caused by braking, the disks are flanged over an auxiliary shaft connected through a suspended gearbox to the axle. This mechanical solution is usually adopted on some well-diffused locomotive like Siemens E190, typically running with a maximum service speed of about 200 km/h and a 22.5 t of axle weight. Hence, this layout is considered as reliable and feasible even in the cases of augmented bogie with unsuspended masses/inertia.

Fig. 2
figure 2

Bogie layout

Full size image

This article is organized as follows: In Sect. 2, the layout for the contact force measurement is introduced; Sect. 3 describes the FEM model and the relative calculation; in Sect. 4, the error sensitivity analysis is conducted: the longitudinal and vertical forces with a mathematical model, and the lateral force with a FEM model. Moreover, in Sect. 5, a study of dynamic bogie behavior is carried out in terms of frequency response functions.

2 Contact force measurement

The solution proposed in Fig. 2 insures enough space on the axle to place sensor and other telemetry devices on the shaft. Here, a classical layout in which the three contact force components are acquired independently on its own sensor system is supposed:

  • Longitudinal forces X are reconstructed in terms of the torque exchanged along the axle [3];

  • Lateral force Y measurements are performed by instrumenting the lateral deformation of the wheel using the methods in Ref. [4];

  • Vertical forces Q are measured by the estimation of the shear stress in different sections of the axle; the shear stress is evaluated by comparing bending stresses on adjacent instrumented sections [4].

2.1 Longitudinal force

Longitudinal forces X are estimated from torque measurements on two instrumented sections on the axle. Both sections are located between wheels, and the torque load is applied by braking or traction system (see Fig. 3). Torque is measured using the Wheatstone bridge [4, 5]. The strain gauge layout assures the rejection of disturbances such as spurious load due to axial forces, bending, and thermal-induced deformations. The longitudinal force X i of the i-th wheel is calculated by

$$ X_{i} \; = \; - \frac{{M_{\text{tor}}^{i} }}{{r_{\text{w}} }}, $$
(1)

where rw is the rolling radius, adopted as a constant, and \( M_{\text{tor}}^{i} \) is the torque load applied by braking or traction system on the i-th section. The torque load is calculated with traditional expression for a hollow shaft:

$$ M_{\text{tor}} \; = \;\frac{{\uppi G\varepsilon_{{45^{ \circ }}} \left( {d_{\text{est}}^{4} - d_{\text{int}}^{4} }\right)}}{{8d_{\text{est}} }} , $$
(2)

where \( \varepsilon_{{45^{^\circ } }} \) is the strain gauge deformation taken on a 45° helix and its polar moment of inertia is \( J_{\text{p}} \; = \;{{{{\uppi}}\left( {d_{\text{est}}^{4} - d_{\text{int}}^{4} } \right)} \mathord{\left/ {\vphantom {{{{\uppi}}\left( {d_{\text{est}}^{4} - d_{\text{int}}^{4} } \right)} {32}}} \right. \kern-0pt} {32}} \) dest and dint are the external and internal diameters of the axle, respectively, and G is shear modulus.

Fig. 3
figure 3

Strain gauge layout for the measurement of X

Full size image

2.2 Vertical force

The vertical contact force on each wheel was obtained by measuring the axle bending torque with strain gauges through the compression of primary suspension. The vertical component Q i of the contact force on the i-th wheel is evaluated by imposing the corresponding equilibrium relation calculated according to the simplified scheme of Figs. 4 and 5:

$$ \left. {\begin{array}{*{20}c} {Q_{1} \; = \;T_{3} - V_{1} \; + \;m_{3} g,} \hfill \\ {Q_{2} \; = \;T_{6} - V_{2} \; + \;m_{6} g,} \hfill \\ \end{array} } \right\} $$
(3)

where m3g and m6g are the weights of the corresponding axle and bogie parts which are delimited by sections 3 and 6, respectively; T3 and T6 are the shear loads, respectively, applied in sections 3 and 6. Shear is defined as the derivative of the bending effort M along the axle; hence, it can be measured according to (4) as the ratio between the measured increment of the bending \( \Updelta M_{fi} \) along the axle to a known length \( \Updelta x_{i} \):

$$ T_{i} \; = \;\frac{{\text{d}}{M}}{\text{d}{x}}\; = \;\frac{{\Updelta M_{fi} }}{{\Updelta x_{i} }}; $$
(4)

v1 and v2 are the vertical forces transmitted by primary suspension as shown in Fig. 4, which can be also measured by a load cell.

Fig. 4
figure 4

Strain gauge positioning on suspension (simplified scheme)

Full size image
Fig. 5
figure 5

Measurament sections for Q-force

Full size image

This solution should be preferred especially to reduce encumbrances of the measurement system. In this case, toroidal load cells can be inserted under the springs of the primary suspension system. The bending torque is expressed with the function of longitudinal deformation ε f :

$$ M_{f} = \frac{{\uppi E\varepsilon_{f} (d_{\text{est}}^{4} -d_{\text{int}}^{4} )}}{{32d_{\text{est}} }}, $$
(5)

where E is Young’s modulus.

2.3 Lateral force

Lateral forces are estimated trough the bending moment by an array of strain-gauges on two different circular arrays as shown in Fig. 6. The lateral force Y1 on a wheel is calculated by

$$ Y_{1} = \frac{{M_{I} - M_{II} }}{{r_{11} - r_{12} }}, $$
(6)

where MI and MII are the bending moments on two measurement radius. The radii of the two circumferences on which strain gauges are placed have to be optimized to increase the sensitivity of the sensors to the lateral forces and to eliminate cross-sensitivity effects against spurious forces:

$$ \begin{gathered} M_{\text{I}} \, = \,Y_{1} \cdot r{}_{11}\, \pm \,Q_{1} \cdot \Updelta b_{1}, \hfill \\ M_{\text{II}} \, = \,Y_{1} \cdot r{}_{12}\, \pm \,Q_{1} \cdot \Updelta b_{1}. \hfill \\ \end{gathered} $$
(7)
Fig. 6
figure 6

Strain gauge layout for Y-force

Full size image

2.4 Contact point position

With the complete sensor layout used to calculate vertical and lateral components of the wheel rail contact forces (Q and Y), it is also possible to estimate the contact point position by imposing static equilibrium of the forces applied on the axle.

3 FEM model

In order to evaluate the influence of strain gauge position on measurement, a complete FEM model of the axle and bogie is developed using MSC Nastran–Patran™. Preliminary simulations for a complete wheelset with two braking disks are performed to evaluate the stress–strain distribution, and consequently, to find an optimal strain gauge layout for the measurement of lateral forces Y. The strain gauges have to be placed on two concentric circumferences with radii r1 and r2 as shown in Fig. 7.

Fig. 7
figure 7

Radial strain on wheels (referred to the loading condition of N2)

Full size image

Values of r1 and r2 are optimized to improve the sensitivity of the measurement system to Y and to minimize the influences of other forces applied to the wheels such as vertical and lateral forces.

In particular, the optimization is performed with three different loading conditions, N1, N2, and N3, and three different positions A, B, and C for a single contact point (see Fig. 8). As a consequence, in the optimization of r1 and r2, nine FEM simulations have to be performed, in which both the applied forces and the position of a single contact point are changed. Values of applied forces X, Y, and Q in the three loading conditions N1, N2, and N3 are chosen according to realistic operating conditions [6–8].Tables 1, 2 shows the values of the relative percentage error of Y measurements e ij , which is defined as

$$ e_{ij} = 100\frac{{\Updelta Y_{ij} }}{{Y_{ij} }}, $$
(8)

where Y ij denotes the value of the Y force considering the i-th contact point and the j-th loading condition; for instance, YB2 represents the nominal condition in which the measurement system is calibrated: contact point position corresponding to case B and loading conditions corresponding to case 2. \( \Updelta Y_{ij} \) is the absolute estimation error between measured and real values of Y ij .

Fig. 8
figure 8

Contact point positions corresponding to the three differrent loading conditions N1, N2, and N3

Full size image
Table 1 Vertical (Q), lateral (Y), and longitudinal (X) forces corresponding to the three loading conditions
Full size table
Table 2 Evaluation of indexes e ij under different applied loadings and with different positions of the contact point
Full size table

In Table 2, values of e ij corresponding to the optimal strain gauge layout (r1 = 0.189 and r2 = 0.402 mm) are shown. It is interesting to notice that the values of the relative error e ij of Y force estimation are slightly disturbed by a change of the loading conditions (N 1 , N 2 , and N 3 ). On the other hand, the proposed measure layout is more influenced by the equivalent contact point position which might cause relative estimation errors more than 10 %.

4 Uncertainty analysis

Uncertainty analysis was performed according to the standard UNI CEI ENV 1300 [9] and the nomenclature definitions in UNI CEI 70099 [10].

In particular, the X-force and Q-force are evaluated with explicit functions in subsect. 2.1 and 2.2. As it is not possible to evaluate an explicit relationship between the applied Y values and the corresponding measurement, the sensitivity analysis is performed by a numerical approach, by means of which the results of FEM model simulations are used to evaluate how disturbances and parametric uncertainties of the system affect the reliability and the precision of the measurement.

4.1 Uncertainty analysis of longitudinal force measurement

The X-force and Q-force as measurands are defined by the explicit relationships with a known set of independent quantities x i . We define X and Q by considering the axle as a Bernoulli beam:

$$ \begin{gathered} X = f_{X} (x_{1} ,x_{2} , \ldots .x_{N} ), \hfill \\ Q = f_{Q} (x_{1} ,x_{2} , \ldots .x_{N} ). \hfill \\ \end{gathered} $$
(9)

Each quantity x i is subjected to a standard uncertainty deriving from measurement errors or by natural tolerances when assuming system parameters as constants. The combined standard measurement uncertainty u of a generic quantity y is defined as

$$ u = \sqrt {\sum\nolimits_{i = 1}^{N} {\left[ {\left( {\frac{\partial y}{{\partial x_{i} }}} \right) \cdot u_{i} } \right]^{2} } }, $$
(10)

where u i is uncertainty of the i-th parameter. Supposing that independent variables are affected by a Gaussian distribution of uncertainties with a coverage factor equal to 2, the following relation is applied to calculate the expanded measurement uncertainty:

$$ U = k \cdot u = \sqrt {\sum\nolimits_{i = 1}^{N} {\left[ {\left( {\frac{\partial y}{{\partial x_{i} }}} \right)ku_{i} } \right]^{2} } } = \sqrt {\sum\nolimits_{i = 1}^{N} {\left[ {\left( {\frac{\partial y}{{\partial x_{i} }}} \right)k_{i} u_{i} } \right]^{2} } }, $$
(11)
$$ U = \sqrt {\sum\nolimits_{i = 1}^{N} {\left[ {\left( {\frac{\partial y}{{\partial x_{i} }}} \right)U_{i} } \right]^{2} } }.$$
(12)

Table 3 shows the results for the X-force during a braking maneuver with a deceleration of about 1–1.2 m/s2 and a tangential force on each axle of about 10–15 kN. The measurements of longitudinal forces X are affected by errors which are strongly influenced by wheel–rail adhesion factor μ:

$$ \mu = \frac{X}{Q}. $$
(13)

From a physical point of view, the vehicle adhesion coefficient should be the minimum wheel–rail friction factor that assures the transmission of the tangential force X if the contribution of rotating inertias is neglected. As Fig. 9 shows, the relative precisions of the X measurements rapidly decrease in the degraded adhesion conditions or when small longitudinal forces X between wheel and rails are exchanged.

Table 3 Estimated uncertainty in the X-force measurement
Full size table
Fig. 9
figure 9

Relative uncertainty on longitudinal force with respect to adhesion behavior

Full size image

The reason for the unacceptable precision performances for low values of the wheel–rail friction factor lies in the high torsional stiffness of the axle compared with the applied torques and X. For low μ values, longitudinal forces are quite low, and consequently, axle deformations are quite negligible and affected by heavy errors.

In order to measure small longitudinal forces in degraded adhesion tests, brakes or the auxiliary shaft in Fig. 2 is equipped with sensors to measure applied braking torques. In this way, it is possible to accurately estimate the total force of X exchanged between both wheels and rails. For low adhesion tests that are usually performed on straight lines, these kinds of results/measurements of the total X force are valuable. In particular, degraded adhesion tests are often performed to verify performances of Wheel Slide Protection (WSP) systems installed on passenger coaches [11].

4.2 Uncertainty analysis of vertical force measurement

Also for the measurement of vertical forces Q, a sensitivity analysis is performed. The sensitivity analysis is conducted by introducing a symmetric vertical load discharge factor ΔQ r , which is defined as a ratio between the absolute vertical load variation and the vertical load on wheel:

$$ \Updelta Q_{r} = \Updelta Q_{{r_{ 1} }} = \Updelta Q_{ 1} /Q_{i } = - \Updelta Q_{{r_{ 2} }} = \Updelta Q_{ 2} /Q_{i }. $$
(14)

In Fig. 10, the graphical behavior of the estimated maximum uncertainty between the two wheels, as a function of ΔQ r , is shown. Note that with more load transfer between wheels, the uncertainty increases. The sensitivity analysis results of the vertical force Q are shown in Table 4, where i and j correspond to the two measurements sections (numbered as section numbers 3 and 6) according the scheme of Fig. 5. The analysis is performed with some known uncertainties such as errors on strain measurements, geometric tolerances, and partially known material properties.

Fig. 10
figure 10

Relative uncertainty in the function of ΔQr

Full size image
Table 4 Estimated uncertainty of Q-force measurements
Full size table

4.3 Uncertainty analysis of lateral force

For the measurement of Y, it is not possible to apply an analytic expression. Thus, the uncertainty analysis is performed using the FEM model. In particular, the analysis is performed considering linear and angular errors of strain gauge positioning as shown in Fig. 11, where Δr = ±1 mm, Δθ = ±1°, Δα = ±2°.

Fig. 11
figure 11

Placement errors of strain gauge

Full size image

FEM model produces strain results which are defined over a discrete population of nodes. In order to perform a sensitivity analysis, continuous derivatives of strain with respect to strain gauge's positioning have to be performed. As a consequence, techniques to obtain a smart interpolation of calculated stress and strain along the wheel surface have to be applied. With a polar reference system centered on the rotation axis of the wheel, strain results have to be interpolated over a grid of 936 nodes corresponding to 26 radial distances r and 36 angular positions .

Two different interpolation techniques are used:

  • Standard triangular interpolation: the generic properties y p for a point p is calculated as the weighted sum of the calculated \( y_{{p_{1} }} \), \( y_{{p_{2} }} \), and \( y_{{p_{0} }} \) on the three nearest nodes p0, p1, and p2. The simplified scheme is shown in Fig. 12.

    Fig. 12
    figure 12

    Standard triangular interpolation

    Full size image

  • Inverse distance weighted interpolation (IDWI) [12]: the interpolation is performed on a subset of the complete population of nodes, with a weighting function which is inversely proportional to the squared distance between the interpolation point p and the corresponding node pi. The subset population is chosen among the n nearest nodes with respect to p where n is the size of the chosen subset population. Figure 13 demonstrates how the IDWI interpolation gradually converges to a very high precision with the increase of size n.

    Fig. 13
    figure 13

    IDWI interpolation of Radial microstrain FEM results

    Full size image

After several tests, IDWI is chosen since it produces desirable results on the polar grid used for the FEM model of the bogie. As clearly shown in Fig. 13, the precision of the IDWI interpolation gradually improve as the number of nodes n used for interpolation increases.

Using the interpolated results of the FEM model, it is possible to calculate how predicted tolerances on strain gauge position affect the precision of Y measurements as shown in Table 5.

Table 5 Relative uncertainty on Y measurements due to placement tolerances of strain gauges
Full size table

5 Frequency response estimation

Using the FEM model of the bogie, it is possible to approximately evaluate the bandwidth of the proposed measurement system in terms of transfer functions. In Figs. 14 and 15, the calculated transfer functions P Y (ω) and P Q (ω) between Y and Q forces and the corresponding measurements performed by the proposed system are shown. Notice that for both Y and Q measurements, the bandwidth is limited to about 20 Hz. This bandwidth limitation is mainly caused by a structural mode-eigenfrequency of the bogie located at about 22.5 Hz. The modal shape of the bogie vibrating at 22.5 Hz is shown in Fig. 16.

Fig. 14
figure 14

The transfer function between Y force and corresponding strain measurement

Full size image
Fig. 15
figure 15

The transfer function between Q force and corresponding strain measurement

Full size image
Fig. 16
figure 16

Modal response of the bogie at 22.5 Hz

Full size image

6 Conclusions and future developments

In this study, a railway bogie model was proposed for the contact force measurements, and its performance has been evaluated.

The proposed model has the following features:

  • Disturbances introduced by braking (both thermally and mechanically induced deformations) are not considered.

  • The proposed approach is based on a static FEM model of the bogie, and the most accurate results are obtained by introducing mixed flexible-multibody models of vehicles and railway line.

  • The influence of strain gauge position on the measurement of contact force was evaluated based on a synergy between FEM model bogie and sensitivity analysis of contact force measurements against several uncertainty factors. Among the various factors, the position of the contact point is one of the most important factors. Calculation of contact point positions is directly estimated in the case of a single wheel–rail contact point. For the identification of multiple contact points, an undirect approach should be applied. We are also considering different approaches such as the inverse identification approach [13] and investigating the feasibility of using an estimator based on a modal approach [14].

  • From the calculation of the frequency response of the system, a strong coupling between the flexible behaviors of rails and vehicle is clearly recognized. As a consequence, the real bandwidth of the contact force measurement system has to be verified taking into account the dynamic response of both systems.

Research activities will be further extended to introducing a more accurate model of the flexible three-dimensional contact between rail and wheels using FEM. In particular, attention needs to be directed to the possibility of identifying some typical disturbance pattern associated with known singularities or failure that should be identified such as sleeper voids [15] or wheel flats [16]. Moreover, neural networks, fuzzy, or other approaches such as wavelet analysis should be applied to identify separately different kinds of defects [17–19].

Also further studies need to be performed to identify in a fast and smart manner the noise introduced in the acquisition of measurements by the process of analog-to-digital conversion, to accord with the approach proposed by Balestrieri [20].