Revealed cardinal preference

Abstract

I prove that as long as we allow the marginal utility for money ($\lambda$) to vary between purchases (similarly to the budget), then the quasi-linear and the ordinal budget-constrained models rationalize the same data on consumer purchases. However, in the short run, $\lambda$ is approximately constant. I provide a simple constructive proof for the necessary and sufficient condition for the constant $\lambda$ rationalization, which I argue should replace the Generalized Axiom of Revealed Preference in empirical studies of consumer behavior.

“Go Cardinals!”

It is the minimal requirement of any scientific theory to be consistent with the data it attempts to explain. In the case of (Hicksian) consumer theory, it was revealed preference—introduced by Samuelson (1938, 1948)—that provided the empirical test to satisfy this need. At that time, most of economic reasoning was done in terms of a competitive general equilibrium, a concept abstract enough to be built on the ordinal preferences over baskets of goods—even if the extremely specialized ones of Arrow and Debreu. However, starting in the 1960s, economics has moved beyond the “invisible hand” explanation of how—even competitive—markets operate. A seemingly unavoidable step of this “revolution” was that ever since, most economic research has been carried out in a partial equilibrium context. Of course, the partial equilibrium approach does not mean that the rest of the markets are ignored, rather that they are held constant (ceteris paribus...). In other words, there is a special commodity—call it money—that reflects the trade-off of moving purchasing power across markets. As a result, the basic building block of consumer behavior in partial equilibrium is no longer the consumer’s preferences over goods, rather her valuation of them, in terms of money. This new paradigm necessitates a new theory of revealed preference.

1 A motivating example

Assume that there are two discrete goods, A and B, and two observations: when the price vector is $(p_{A}^{1}=1,p_{B}^{1}=3)$, the consumer chooses B, when the price vector is $(p_{A}^{2}=1,p_{B}^{2}=2)$ she chooses A. Intuitively, this does not seem to be rational behavior: a decrease in the price of B has made the consumer switch away from it. However, according to the accepted theory of revealed preference (for a synopsis, see Varian 2006), these choices are consistent with the consumer maximizing a(n ordinal) utility function subject to a budget constraint: any utility function that assigns a higher value to B than to A is acceptable.¹ How come? The reason is implicit in the definition of the hypothesis we are testing. As each observation corresponds to a different decision, even if the preferences are assumed constant, the budgets are allowed to vary. Consequently, there seem to be “ too many” degrees of freedom: as we cannot reject the possibility that in the second experiment the consumer had a budget less than 2, the second observation is effectively discarded.

To resolve this problem, I suggest that we should discard the notion that the consumer is budget constrained, instead. To replace the budget constraint—following Marshall (1890)—assume that the consumer is endowed with a marginal utility for money, $\lambda .$ Now both observations count and we have two inequalities that need to be satisfied for the data to be consistent with our new definition of rationality:

$$\begin{aligned} u(B)-\lambda _{1}(p_{B}^{1}-p_{A}^{1})\ge u(A)\ge u(B)+\lambda _{2}(p_{A}^{2}-p_{B}^{2}). \end{aligned}$$

Substituting in

$$\begin{aligned} u(B)-2\lambda _{1}\ge u(A)\ge u(B)-\lambda _{2}. \end{aligned}$$

It is immediate that, despite having an additional constraint, consistency can be assured: as long as $\lambda _{2}\ge 2\lambda _{1},$ there exist (cardinal) utility levels such that both inequalities are satisfied.² That is, if (and only if) we cannot reject the possibility that the consumer values money at least twice as much in the second experiment, the data continue to be reconciled with the—modified—theory.

So far it seems that the two modeling assumptions are operationally equivalent. Not quite so! Unlike budgets, the marginal utility of money is not mercurial: barring significant shocks to lifetime(!) wealth occurring between the experiments, $\lambda$—understood as the value of an extra dollar to the consumer in the rest of her life—should be (at least, approximately) constant across the observations. Taking this on board, our consistency conditions become

$$\begin{aligned} u(B)-2\lambda \ge u(A)\ge u(B)-\lambda , \end{aligned}$$

which obviously cannot be satisifed for any $\lambda >0.$

Consequently, appealing to the “stickiness” of marginal utility of money, we can refine GARP, so that the result of the test agrees with our intuition. At the same time, we have surreptitiously introduced a “partial equilibrium” model of consumer choice as the paradigm of rationality. In the next section, we show that the example generalizes.

2 The general model

We have $T<\infty$ observations of a consumer’s chosen bundles, $x^{t}\in \mathfrak R _{+}^{L},$ at price vectors, $p^{t}\in \mathfrak R _{++}^{L}$. The $L$ goods in the choice set are assumed to be a small subset of the ones comprising the consumers’ full, lifetime optimization problem, but for simplicity the choice set is not further restricted.

Let $a_{tj}=p^{t}\cdot (x^{j}-x^{t})$ denote the pecuniary advantage of the (chosen) bundle $x^{t}$ relative to an arbitrary bundle $x^{j}$ in observation $t.$ Afriat (1967) has shown³ that the following axiom is necessary and sufficient for the data to be consistent with the Hicksian theory of a budget constrained consumer:

Generalized Axiom of Revealed Preference (GARP)⁴ For every ordered subset ${i,j,k,\ldots ,s}\subseteq {1,2,\ldots ,T}$

$$\begin{aligned} \text{ if } a_{ij},a_{jk},\ldots ,a._s \le 0 \text{ then } a_{si}\ge 0. \end{aligned}$$

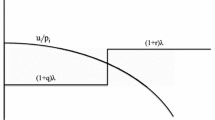
The heart of Afriat’s argument is that the existence of positive numbers $u_{k}$ and $\lambda _{k},k\in \{1,\ldots ,T\}$ that satisfy the following set of inequalities

$$\begin{aligned} u_{i}\le u_{j}+\lambda _{j}a_{ji}\quad \text{ for } \text{ all } i,j\text{, } \end{aligned}$$

(1)

is equivalent both to GARP and to consistency with the Hicksian theory.⁵ Paradoxically, Afriat’s inequalities—developed to buttress the Hicksian model—seem more conducive to a quasi-linear representation than to the Hicksian one! Using Afriat’s Theorem, it is immediate from (1) that

Proposition 1

If and only if the choices are consistent with the consumer maximizing a standard utility function subject to a variable budget constraint, they are consistent with the consumer maximizing a quasi-linear utility function with a variable marginal utility for money.

Based on the example above, the quasi-linear representation seems to impose more constraints on the data, rendering Proposition 1 somewhat counter-intuitive. To see what is happening, first note that because on the left-hand side each inequality appears twice:

$$\begin{aligned} u_{j}-\lambda _{i}a_{ij}\le u_{i}\le u_{j}+\lambda _{j}a_{ji} \text{ for } \text{ all } i,j\Longleftrightarrow u_{i}\le u_{j}+\lambda _{j}a_{ji}\quad \text{ for } \text{ all } \,i,j. \end{aligned}$$

(2)

Now observe that the trick in Afriat’s Theorem is that the observations with positive $a_{ij}$ are not actually discarded, rather they can always be accommodated by a judiciously chosen $\lambda$ vector⁶ and hence they never refute consistency.

A hasty conclusion from Proposition 1 could be that GARP continues to be the litmus test of rationality even if in the definition of the latter the budget constraint (plus an ordinal utility function) is replaced by a quasi-linear utility function. Such an interpretation would be based on mistaking the formal equivalence of variable budgets and variable $\lambda$s for real equivalence. The Hicksian theory does not explain the procedence of the budget. As it is just an arbitrary (and unobservable!) exogenous amount, we have no basis to rule out that it takes all kinds of values during the period of observation of the consumer’s behavior. This is what leads to the characterization via GARP—and to the counter-intuitive classification as rational behavior of the one in the example above. $\lambda$, on the other hand, can be backed up by a robust theory both as the slope of the indirect utility function of the continuation and as a rule of thumb (see Friedman and Sákovics (2011), for a developed treatment). Both justifications coincide in that in the short run $\lambda$ is approximately constant.⁷ As we will see, the constancy of $\lambda$ has major implications.

We wish to check when the choice behavior is consistent with the following alternative theory of the consumer: she is endowed with a shadow utility for money, $\lambda ,$ and a quasi-linear utility function $U(x;p,\lambda )=u(x)-\lambda p\cdot x:\mathfrak R _{+}^{L}\times \mathfrak R _{++}^{L}\times \mathfrak R _{++}\rightarrow \mathfrak R ,$ such that she strictly (weakly) prefers consuming $x$ at expense $p\cdot x$ to consuming $x^{\prime }$ at expense $p\cdot x^{\prime }$ if and only if $U(x;p,\lambda )>(\ge )\,U(x^{\prime };p,\lambda ).$ ⁸ Moreover, she chooses her most preferred bundle without any constraint.⁹

Definition 1

The cardinal utility function $u(x)$ rationalizes the observed choices iff there exists $\lambda >0$ such that for all $t\in \{1,2,\ldots ,T\}$

$$\begin{aligned} u(x^{t})-\lambda p^{t}\cdot x^{t}\ge u(x)-\lambda p^{t}\cdot x \text{ for } \text{ all } x\in \mathfrak R _{+}^{L}. \end{aligned}$$

(3)

It is immediate that $u(.)$ and $\lambda$ are only fixed up to a (jointly applied) positive affine transformation (just as von Neumann-Morgenstern utility).¹⁰ Therefore, we can normalize the utility function by setting $\lambda =1.$ Unsurprisingly, (3) also implies that $u(.)$ must be concave.

Replacing GARP, the following axiom will play the key role in the proceedings:

Axiom of Revealed Valuation (ARV)¹¹ For every ordered subset $\{i,j,k,\ldots ,s\}$ $\subseteq \{1,2,\ldots ,T\}$

$$\begin{aligned} a_{ij}+a_{jk}+\cdots +a_{si}\ge 0. \end{aligned}$$

(4)

Note that ARV is a stricter condition than GARP.

In proving the representation theorem, the following object will play a key role:

Definition 2

When ARV holds, let the indirect cost advantage be defined as $b_{ij}$ $=\min \{a_{ik}+a_{kt}+\cdots +a_{sj}\},$ where the minimum is taken over all ordered subsets of $\{1,2,\ldots ,T\}$ that start at $i$ and finish at $j.$

This definition is only meaningful if adding extra cycles does not decrease the value of $b_{ij}$. However, ARV implies that $b_{ii}=\min _{j} \{b_{ij}+a_{ji}\}\ge 0$ ensuring that the $b_{ij}$ are well defined. The interpretation of the $b_{ij}$ is that they impose a bound on the difference between the utility values of $x^{i}$ and $x^{j}:u(x^{j})-u(x^{i})\le b_{ij}$. It is easy to see why. Consider the case of three observations; $i,j$ and $k$. There are two different ways of going from $i$ to $j$ : one is directly, imposing the standard (cf. (3)) constraint $u(x^{j})-u(x^{i})\le a_{ij}$; the other via $k$, imposing two constraints $u(x^{k})-u(x^{i})\le a_{ik}$ and $u(x^{j})-u(x^{k})\le a_{kj}.$ Summing the latter two we have $u(x^{j})-u(x^{i})\le a_{ik}+a_{kj}$; implying that $u(x^{j})-u(x^{i})\le \min \{a_{ij},a_{ik}+a_{kj}\}=b_{ij}$. The argument generalizes trivially.

With this last observation, we are ready to present the representation theorem:

Theorem 1

If and only if the choices satisfy ARV, they are rationalizable by a cardinal utility function.

Proof

As $u(.)$ rationalizes the choices, by (3) we have that for all $i,j\in \{1,2,\ldots ,T\}$

$$\begin{aligned} u(x^{j})-u(x^{i})\le a_{ij}. \end{aligned}$$

(5)

Take any ordered subset $\{i,j,k,\ldots ,s\}\subseteq \{1,2,\ldots ,T\}.\$ Summing up the inequalities corresponding to each consecutive pairing $(i,j),\left( j,k\right) ,\ldots (s,i)$, the terms on the left-hand side cancel out and we obtain (4). To show the converse, we will construct a utility function that rationalizes the choices when they satisfy ARV. We set the utility values for the chosen bundles at $u(x^{i})=b_{1i}\$and extend the utility function to arbitrary bundles via $u(x)=\min _{t}\{u(x^{t})+p^{t} \cdot \left( x-x^{t}\right) \}.$ The two steps are consistent: $\min _{t}\{u(x^{t})+p^{t}\cdot \left( x^{r}-x^{t}\right) \}=\min _{t}\{b_{1t}+a_{tr}\}=b_{1r}=u(x^{r}),$ where the second equality follows in two steps: first, the minimizer could be $r$ and thus $\min _{t}\{b_{1t}+a_{tr}\}\le b_{1r}+a_{rr}=b_{1r},$ second, $\min _{t}\{b_{1t}+a_{tr}\}\ge \min _{t}\{b_{1r}\}=b_{1r},$ as $b_{1t}+a_{tr}\ge b_{1r}$ for any $t.$ It is straightforward to verify that the utility function that we have constructed satisfies (3), with $\lambda =1$. $\square$

For easier referencing, we state the recovered utility function in a corollary:

Corollary 1

When ARV is satisfied, the choices can be rationalized by $u(x)=\min _{t}\{b_{1t}+p^{t}\cdot \left( x-x^{t}\right) \},$ $t\in \{1,2,\ldots ,T\}.$

3 Liquidity constraints and mistakes

The example above points to a clear procedure for relaxing the constancy-of-lambda constraint. Instead of keeping $\lambda$ constant across all experiments, we could accept a small variation across the sample. For example, if we think of credit card debt (one of the most expensive forms of borrowing) and bound the borrowing period at 1 year, we get an upper bound of 20 % interest, which corresponds to a 20 % allowed variation in $\lambda$. In the example, this would mean that for $p_{B}^{2}\ge 2.6$ we would accept the behavior of our consumer as “rational”.

Even without thinking of credit, it is customary to allow for errors. Afriat (1972), for example, proposes the Critical Cost Efficiency Index to measure the size of deviation from rationality. Allowing $\lambda$ to vary within a range as above can also be interpreted as allowing for errors. Note, however, that by Proposition 1 this correction mechanism is only useful for data that satisfy GARP.

4 Related literature

This is not the right place to provide an overview of the extensive literature on revealed preference. I will only discuss the two papers I know that have previously derived a cardinal/quasi-linear version of revealed preference.

Richter and Wong (2005) look at infinite (linear) inequality systems and provide a solvability criterion for them. One of their applications is how to rationalize the choices of a consumer with a quasi-linear utility subject to a budget constraint. They claim that the finite version of their Strong Axiom of Solvability—which is an extension of ARV to include strict inequalities—rationalizes choices. Of course, in the context of observing actual consumer choices, the ability to consider infinitely many of them is of scant value: the consumer may have to do that but not the econometrician. In between their quests for generality both in terms of applications and in terms of the number and strictness of inequalities, they fail to emphasize the importance of cardinal revealed preference—in fact, they also apply their machinery for ordinal revealed preference.

Brown and Calsamiglia (2007) address the finite observation case directly (though still including a budget constraint). They claim that—a condition equivalent to—ARV is equivalent to rationalizability, by referring to a result in convex analysis for the characterization of the subgradient correspondence of a concave function.

Both papers have identified the correct necessary and sufficient axiom for cardinal/quasi-linear rationalizability. Nonetheless, their proofs are less than straightforward and they have not argued why quasi-linear rationalizability should be the preferred requirement in empirical analysis.

5 Conclusion

State-of-the-art empirical contributions still use GARP as the litmus test of consumer rationality (cf. Blundell et al. 2003; Cherchye et al. 2009; Choi et al. 2011,¹² Echenique et al. 2011. This should change.