Skip to main content

Advertisement

SpringerLink
Log in

Analysis of a mathematical model of periodically pulsed chemotherapy treatment

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

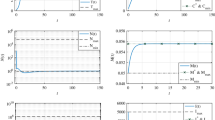
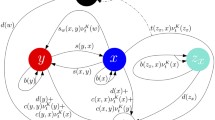
In this paper, we have considered competition models describing tumor–normal–immune cell interaction with the added effects of periodically pulsed chemotherapy. The parametric conditions needed to prevent relapse following attempts to remove the tumor or tumor metastasis are obtained. The effects of resistant tumor sub-populations are also investigated and recurrence prevention strategies are discussed. Our analytical findings are explained through numerical simulation which show the reliability of our models from the epidemiological point of view.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Knolle H (1988) Cell kinetic modelling and the chemotherapy of cancer. Lecture notes in biomathematics, Vol 75. Springer, New York

  2. Miller FR, Medina D, Heppner GH (1981) Preferential growth of mammary tumors in intact mammary fatpads. Cancer Res 41:3863–3867

    Google Scholar 

  3. Aroesty J, Lincoln T, Shapiro N, Boccia G (1973) Tumor growth and chemotherapy: mathematical methods, computer simulations, and experimental foundations. Math Biosci 17:243–300

    Article  MATH  Google Scholar 

  4. Berenbaum MC (1969) Dose–response curves for agents that impair cell reproductive integrity. Br J Cancer 23:434–445

    Article  Google Scholar 

  5. Murray JM (1990) Some optimal control problems in cancer chemotherapy with a toxicity limit. Math Biosci 100:49–67

    Article  MathSciNet  MATH  Google Scholar 

  6. Panetta JC (1996) A mathematical model of periodically pulsed chemotherapy tumor recurrence and metastasis in a competitive environment. Bull Math Biol 58(3):425–447

    Article  MATH  Google Scholar 

  7. Kuznetsov V, Makalkin I (1992) Bifurcation analysis of mathematical model of interactions between cytotoxic lymphocytes and tumor cells—effect of immunological amplification of tumor growth and its connection with other phenomena of oncoimmunology. Biofizika 37(6):1063–1070

    Google Scholar 

  8. Kuznetsov V, Knott GD (2001) Modeling tumor regrowth and immunotherapy. Math Comput Model 33:1275–1287

    Article  MathSciNet  MATH  Google Scholar 

  9. Kuznetsov V, Makalkin I, Taylor M, Perelson A (1994) Nonlinear dynamics of immunogenic tumors: parameter estimation and global bifurcation analysis. Bull Math Biol 56(2):295–321

    Article  MATH  Google Scholar 

  10. Kirschner D, panetta J (1998) Modelling immunotherapy of the tumor–immune interaction. J Math Biol 37:235–252

  11. Kolev M (2003) Mathematical modelling of the competition between tumors and immune system considering the role of the antibodies. Math Comput Model 37:1143–1152

    Article  MATH  Google Scholar 

  12. de Pillis LG, Gu W, Radunskaya AE (2006) Mixed immunotherapy and chemotherapy of tumors: modeling, applications and biological interpretations. J Theor Biol 238:841–862

    Article  MathSciNet  Google Scholar 

  13. de Pillis LG, Radunskaya AE (2001) A mathematical tumor model with immune resistance and drug therapy: an optimal control approach. J Theor Med 3:79–100

    Article  MATH  Google Scholar 

  14. Arciero JC, Jackson TL, Kirschner DE (2004) A mathematical model of tumor-immune evasion and siRNA treatment. Discret Contin Dyn Syst Ser B 4(1):39–58

    MathSciNet  MATH  Google Scholar 

  15. Bellomo N, Bellouquid A, Delitala M (2004) Mathematical topics on the modelling of multicellular systems in competition between tumor and immune cells. Math Models Methods Appl Sci 14:1683–1733

    Article  MathSciNet  MATH  Google Scholar 

  16. Bellomo N, Preziosi L (2000) Modelling and mathematical problems related to tumor evolution and its interaction with the immune system. Math Comput Model 32:413–452

    Article  MathSciNet  MATH  Google Scholar 

  17. Chan BS, Yu P (2012) Bifurcation analysis in a model of cytotoxic T-lymphocyte response to viral infections. Nonlinear Anal: Real World Appl 13:64–77

    Article  MathSciNet  MATH  Google Scholar 

  18. de Pillis LG, Radunskaya AE, Wiseman CL (2005) A validatted mathematical model of cell-mediated immune response to tumor growth. Cancer Res 61(17):7950–7958

    Article  Google Scholar 

  19. Derbel L (2004) Analysis of a new model for tumor-immune system competition including long time scale effects. Math Models Methods Appl Sci 14:1657–1682

    Article  MathSciNet  MATH  Google Scholar 

  20. d’Onofrio A (2005) A general framework for modeling tumor-immune system competition and immunotherapy: mathematical analysis and biomedical references. Phys D 208:220–235

    Article  MathSciNet  MATH  Google Scholar 

  21. Nani F, Freedman HI (2000) A mathematical model of cancer treatment by immunotherapy. Math Biosci 163:159–199

    Article  MathSciNet  MATH  Google Scholar 

  22. Pinho STR, Bacelar FS, Andrade RFS, Freedman HI (2013) A mathematical model for the effect of anti-angiogenic therapy in the treatment of cancer tumors by chemotherapy. Nonlinear Anal: Real World Appl 14:815–828

    Article  MathSciNet  MATH  Google Scholar 

  23. Siu H, Vitetta ES, May RD, Uhr IW (1986) Tumor dormancy. I. Regression of bcl tumor and induction of a dormant tumor state in mice chimeric at the major histocompatibility complex. J Immunol 137:1376–1382

    Google Scholar 

  24. Takayanagi T, Ohuchi A (2001) A mathematical analysis of the interactions between immunogenic tumor cells and cytotoxic T lymphocytes. Microbiol Immunol 45:709–715

    Article  Google Scholar 

  25. Yafia R (2006) Dynamics analysis and limit cycle in a delayed model for tumor growth with quiescene. Nonlinear Anal: Model Control 11:95–110

    MathSciNet  MATH  Google Scholar 

  26. de Pillis LG, Gu W, Fister KR, Head T, Maples K, Murugan A, Neal T, Yoshida K (2007) Chemotherapy for tumors: an analysis of the dynamics and a study od quadratic and linear optimal controls. Math Biosci 209:292–315

    Article  MathSciNet  MATH  Google Scholar 

  27. de Pillis LG, Radunskaya AE (2003) The dynamics of an optimally controlled tumor model: a case study. Math Comput Model 37:1221–1244

    Article  MATH  Google Scholar 

  28. Engelhart M, Lebiedz D, Sager S (2011) Optimal control for selected cancer chemotherapy ODE models: a view on the potential of optimal schedules and choice of objective function. Math Biosci 229:123–134

    Article  MathSciNet  MATH  Google Scholar 

  29. Fister KR, Donnelly J (2005) Immunotherapy: an optimal control theory approach. Math Biosci Eng 2(3):499–510

    Article  MathSciNet  MATH  Google Scholar 

  30. Fister KR, Panetta JC (2000) Optimal control applied to cell-cycle specific cancer chemotherapy. SIAM J Appl Math 60(3):1059–1072

    Article  MathSciNet  MATH  Google Scholar 

  31. Fister KR, Panetta JC (2003) Optimal control applied to competing chemotherapeutic cell-kill strategies. SIAM J Appl Math 63(6):1954–1971

    Article  MathSciNet  MATH  Google Scholar 

  32. Matveev A, Savkin A (2002) Application of optimal control theory to analysis of cancer chemotherapy regimens. Syst Cont Lett 46:311–321

    Article  MathSciNet  MATH  Google Scholar 

  33. Swarnali S, Samanta GP (2013) Dynamical behaviour of a tumor-immune system with chemotherapy and optimal control. J Nonlinear Dyn. doi:10.1155/2013/608598

    MATH  Google Scholar 

  34. Swarnali S, Samanta GP (2015) Analysis of the dynamics of a tumor-immune system with chemotherapy and immunotherapy and quadratic optimal control. Differ Equ Dyn Syst. doi:10.1007/s12591-015-0250-1

    MATH  Google Scholar 

  35. Elmouki I, Saadi S (2014) BCG immunotherapy optimization on an isoperimetric optimal control problem for the treatment of superficial bladder cancer. Int J Dyn Control. doi:10.1007/s40435-014-0106-5

    MATH  Google Scholar 

  36. Gyori I, Michelson S, Leith JT (1988) Time-dependent subpopulation induction in heterogeneous tumors. Bull Math Biol 50:681–696

    Article  MathSciNet  MATH  Google Scholar 

  37. Michelson S, Leith JT (1995) Interlocking triads of growth control in tumors. Bull Math Biol 57:345–366

    Article  MATH  Google Scholar 

  38. Michelson S, Leith JT (1988) Unexpected equilibria resulting from differing growth rates of subpopulations within heterogeneous tumors. Math Biosci 91:119–129

  39. Michelson S, Leith JT (1993) Tumor heterogeneity: a review of the theory. Drug News Perspect 6:655–661

    Google Scholar 

  40. Burger RA, Grosen EA, Ioli GR, Van Eden ME, Brightbill HD, Gatanaga M, DiSaia PJ, Granger GA, Gatanaga T (1994) Host-tumor interaction in ovarian cancer spontaneous release of tumor necrosis factor and interleukin-1 inhibitors by purified cell populations from human ovarian carcinoma in vitro. Gynecol Oncol 55:294–303

    Article  Google Scholar 

  41. Dotto GP, Weinberg A, Ariza A (1988) Malignant transformation of mouse primary keratinocytes by Harvey sarcoma virus and its modulation by surrounding normal cells. Proc Natl Acad Sci USA 85:6389–6393

    Article  Google Scholar 

  42. La Rocca SA, Grossi M, Falcone G, Alema S, Tato F (1989) Interaction with normal cells suppresses the transformed phenotype of v-myc-transformed quail muscle cells. Cell 58:123–131

    Article  Google Scholar 

  43. Cornil I, Theodorescu D, Man S, Herlyn M, Jambrosic J, Kerbel RS (1991) Fibroblast cell interactions with human melanoma cells affect tumor cell growth as a function of tumor progression. Proc Natl Acad Sci USA 88:6028–6032

    Article  Google Scholar 

  44. Hale JK (1977) Theory of functional differential equations. Springer, New York

    Book  MATH  Google Scholar 

  45. Goldie JH, Coldman AJ (1979) A mathematical model for relating the drug sensitivity of tumors to their spontaneous mutation rate. Cancer Treat Rep 63:1727–1733

    Google Scholar 

  46. Michelson S, Miller BE, Glicksman AS, Leith JT (1987) Tumor micro-ecology and competitive interactions. J Theor Biol 128:233–246

    Article  MathSciNet  Google Scholar 

  47. Schimke RT (1984) Gene amplification, drug resistance, and cancer. Cancer Res 44:1735–1742

    Google Scholar 

  48. Schimke RT (1988) Gene amplification in cultured cells. J Biol Chem 263:5989–5992

    Google Scholar 

  49. Souhami RL, Gregory WM, Birkhead BG (1988) Mathematical models in high-dose chemotherapy. Antibiot Chemother 41:21–28

    Article  Google Scholar 

  50. Birkhead BG, Gregory WM (1984) A mathematical model of the effects of drug resistance in cancer chemotherapy. Math Biosci 72:59–69

    Article  MATH  Google Scholar 

  51. Martin RB, Fisher ME, Michin RF, Teo KL (1992) Optimal control of tumor size used to maximize survival time when cells are resistant to chemotherapy. Math Biosci 110:201–219

    Article  MATH  Google Scholar 

  52. Costa MIS, Boldrini JL, Bassanezi RC (1995) Drug kinetics and drug resistance in optimal chemotherapy. Math Biosci 125:191–209

    Article  MATH  Google Scholar 

Download references

Acknowledgments

The authors are grateful to the anonymous referees and the Editor-in-Chief (Prof. Jian-Qiao Sun) for their careful reading, valuable comments and helpful suggestions, which have helped them to improve the presentation of this work significantly. The first author likes to thank TWAS, UNESCO and National Autonomous University of Mexico (UNAM) for financial support. He is grateful to Prof. José Antonio Seade Kuri and Prof. Marcelo Aguilar, Institute of Mathematics, National Autonomous University of Mexico for their helps and encouragements.

Author information

Author notes

  1. G. P. Samanta

    Present address: Department of Mathematics, Indian Institute of Engineering Science and Technology, Shibpur, Howrah, 711103, India

Authors and Affiliations

  1. Institute of Mathematics, National Autonomous University of Mexico, C.P. 04510, Mexico, D.F., Mexico

    G. P. Samanta & Ricardo Gómez Aíza

  2. Department of Mathematics, Heritage Institute of Technology, Kolkata, 700107, India

    Swarnali Sharma

Authors
  1. G. P. Samanta
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ricardo Gómez Aíza
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Swarnali Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. P. Samanta.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Samanta, G.P., Aíza, R.G. & Sharma, S. Analysis of a mathematical model of periodically pulsed chemotherapy treatment. Int. J. Dynam. Control 5, 842–857 (2017). https://doi.org/10.1007/s40435-015-0204-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-015-0204-z

Keywords

Search

Navigation