Skip to main content
SpringerLink
Log in

Optimization of three-element tuned mass damper based on minimization of the acceleration transfer function for seismically excited structures

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

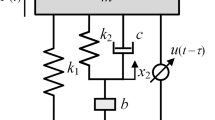
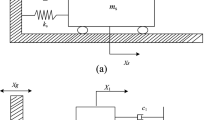
The three-element tuned mass damper (T-TMD) is an effective passive control device for single-degree of freedom structures due to harmonic external force. Unlike previous studies, this study aims at proposing a methodology for optimization of T-TMD positioned at the top floor of multi-degree of freedom structures under seismic loads. The equations of motion for a multi-story building controlled by a T-TMD are derived, and the T-TMD is then optimized using an advanced firefly algorithm (AFA) in the frequency domain. The aim of the optimization is to minimize the amplitude of the acceleration transfer function of the top floor of the building. The proposed methodology is implemented in two different shear buildings, and the optimum parameters are then verified by using benchmark earthquakes with different frequency components. The comparisons with the available works illustrate the availability of the AFA. The effect of the mass ratio on the optimum parameters of the T-TMD is also discussed in detail. Numerical results show that the use of the optimum T-TMD is an effective strategy to minimize the maximum structural responses of the multi-story buildings under seismic excitations. In particular, the optimum T-TMD is very effective when the maximum story responses (i.e., displacement and acceleration) occur at the top floor of the building.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  1. Frahm H (1911) Device for damping of bodies. US Patent 989, 958

  2. Ormondroyd J, Den Hartog JP (1928) The theory of dynamic vibration absorber. Trans Am Soc Mech Eng 50:9–22

    Google Scholar 

  3. Den Hartog JP (1956) Mechanical vibrations. McGraw-Hill, New York

    MATH  Google Scholar 

  4. Tsai HC, Lin GC (1993) Optimum tuned-mass dampers for minimizing steady-state response of support-excited and damped systems. Earthq Eng Struct Dyn 22(11):957–973

    Article  Google Scholar 

  5. Hadi MN, Arfiadi Y (1998) Optimum design of absorber for MDOF structures. J Struct Eng 124:1272–1280

    Article  Google Scholar 

  6. Lee CL, Chen YT, Chung LL, Wang YP (2006) Optimal design theories and applications of tuned mass dampers. Eng Struct 28(1):43–53

    Article  Google Scholar 

  7. Lavan O, Daniel Y (2013) Full resources utilization seismic design of irregular structures using multiple tuned mass dampers. Struct Multidisc Optim 48(3):517–532

    Article  Google Scholar 

  8. Venanzi I (2015) Robust optimal design of tuned mass dampers for tall buildings with uncertain parameters. Struct Multidisc Optim 51(1):239–250

    Article  Google Scholar 

  9. Salvi J, Rizzi E (2016) Closed-form optimum tuning formulas for passive tuned mass dampers under benchmark excitations. Smart Struct Syst 17(2):231–256

    Article  Google Scholar 

  10. Miranda JC (2016) Discussion of system intrinsic parameters of tuned mass dampers used for seismic response reduction. Struct Control Health 23(2):349–368

    Article  Google Scholar 

  11. Araz O, Kahya V (2018) Effects of manufacturing type on control performance of multiple tuned mass dampers under harmonic excitation. J Struct Eng Appl Mech 1(3):117–127

    Article  Google Scholar 

  12. Djerouni S, Ounis A, Elias S, Abdeddaim M, Rupakhety R (2022) Optimization and performance assessment of tuned mass damper inerter systems for control of buildings subjected to pulse-like ground motions. Structures 38:139156

    Article  Google Scholar 

  13. Lee BH, Chen CC, Chen TW, Shiao SY, Jiang CR, Yeh FY (2022) Enhancement of structural seismic performance of low-rise buildings using displacement-dependent tuned mass damper. Structures 37:11191128

    Article  Google Scholar 

  14. Araz O (2020) Effect of detuning conditions on the performance of non-traditional tuned mass dampers under external excitation. Arch Appl Mech 90:523–532

    Article  Google Scholar 

  15. Sadek F, Mohraz B, Taylor AW, Chung RM (1997) A method of estimating the parameters of tuned mass dampers for seismic applications. Earth Eng Struct Dyn 26:617–635

    Article  Google Scholar 

  16. Liu MY, Chiang WL, Hwang JH, Chu CR (2008) Wind-induced vibration of high-rise building with tuned mass damper including soil-structure interaction. J Wind Eng Ind Aerodyn 96:1092–1102

    Article  Google Scholar 

  17. Lu X, Chen J (2011) Mitigation of wind-induced response of Shanghai center tower by tuned mass damper. Struct Des Tall Spec Build 20:435–452

    Article  Google Scholar 

  18. Alkmim MH, Fabro AT, Morais MVG (2018) Optimization of a tuned liquid column damper subject to an arbitrary stochastic wind. J Braz Soc Mech Sci Eng 40:551

    Article  Google Scholar 

  19. Ghassempour M, Failla G, Arena F (2019) Vibration mitigation in offshore wind turbines via tuned mass damper. Eng Struct 183:610–636

    Article  Google Scholar 

  20. Kahya V, Araz O (2017) Series tuned mass dampers in train-induced vibration control of railway bridges. Struct Eng Mech 61(4):453–461

    Article  Google Scholar 

  21. Araz O, Kahya V (2020) Series tuned mass dampers in vibration control of continuous railway bridges. Struct Eng Mech 73(2):133–141

    Google Scholar 

  22. Araz O, Kahya V (2022) Optimization of multiple tuned mass dampers for a two-span continuous railway bridge via differential evolution algorithm. Structures 39:29–38

    Article  Google Scholar 

  23. Bekdas G, Nigdeli SM (2011) Estimating optimum parameters of tuned mass dampers using harmony search. Eng Struct 33(9):2716–2723

    Article  Google Scholar 

  24. Zhang HY, Zhang LJ (2017) Tuned mass damper system of high-rise intake towers optimized by improved harmony search algorithm. Eng Struct 138:270–282

    Article  Google Scholar 

  25. Kaveh A, Javadi SM, Moghanni RM (2020) Optimal structural control of tall buildings using tuned mass dampers via chaotic optimization algorithm. Structures 28:2704–2713

    Article  Google Scholar 

  26. Caicedo D, Lara-Valencia L, Blandon J, Graciano C (2021) Seismic response of high-rise buildings through metaheuristic-based optimization using tuned mass dampers and tuned mass dampers inerter. J Build Eng 34:101927

    Article  Google Scholar 

  27. Farshidianfar A, Soheili S (2013) Ant colony optimization of tuned mass dampers for earthquake oscillations of high-rise structures including soil–structure interaction. Soil Dyn Earthq Eng 51:14–22

    Article  Google Scholar 

  28. Leung AYT, Zhang H (2009) Particle swarm optimization of tuned mass dampers. Eng Struct 31:715–728

    Article  Google Scholar 

  29. Araz O, Kahya V (2021) Design of series tuned mass dampers for seismic control of structures using simulated annealing algorithm. Arch Appl Mech 91:4343–4359

    Article  Google Scholar 

  30. Lara-Valencia L, Caicedo D, Valencia-Gonzalez Y (2021) A novel whale optimization algorithm for the design of tuned mass dampers under earthquake excitations. Appl Sci 11(13):6172

    Article  Google Scholar 

  31. Asami T, Nishihara O (1999) Analytical and experimental evaluation of an air damped dynamic vibration absorber: design optimizations of the three-element type model. J Vib Acoust 121:334–342

    Article  Google Scholar 

  32. Asami T, Nishihara O (2002) H2 optimization of the three-element type dynamic vibration absorbers. J Vib Acoust 124:583–592

    Article  Google Scholar 

  33. Anh ND, Nguyen NX, Hoa LT (2013) Design of three-element dynamic vibration absorber for damped linear structures. J Sound Vib 332:4482–4495

    Article  Google Scholar 

  34. Javidialesaadi A, Wierschem NE (2018) Three-element vibration absorber–inerter for passive control of single-degree-of-freedom structures. J Vib Acoust 140(6):1–11

    Article  Google Scholar 

  35. Nishihara O (2019) Exact optimization of a three-element dynamic vibration absorber: minimization of the maximum amplitude magnification factor. J Vib Acoust 141:011001

    Article  Google Scholar 

  36. Yang Y, Gao H, Ma W, Liu Q (2020) Design of a turning cutting tool with large length–diameter ratio based on three-element type vibration absorber. Proc Inst Mech E Part B J Eng Manuf 234:1–12

    Google Scholar 

  37. Wang L, Shi W, Li X, Zhang Q, Zhou Y (2019) An adaptive-passive retuning device for a pendulum tuned mass damper considering mass uncertainty and optimum frequency. Struct Control Health Monit 26(7):e2377

    Article  Google Scholar 

  38. Wang L, Shi W, Li X, Zhang Q, Zhou Y (2020) Study on adaptive-passive multiple tuned mass damper with variable mass for a large-span floor structure. Eng Struct 209:110010

    Article  Google Scholar 

  39. Wang L, Nagarajaiah S, Shi W, Zhou Y (2021) Semi-active control of walking-induced vibrations in bridges using adaptive tuned mass damper considering human-structure-interaction. Eng Struct 244:112743

    Article  Google Scholar 

  40. Wang L, Shi W, Zhou Y (2022) Adaptive-passive tuned mass damper for structural aseismic protection including soil-structure interaction. Soil Dyn Earthq Eng 158:107298

    Article  Google Scholar 

  41. Wang L, Shi W, Zhou Y (2019) Study on self-adjustable variable pendulum tuned mass damper. Struct Des Tall Special Build 28(1):e1561

    Article  Google Scholar 

  42. Wang L, Nagarajaiah S, Shi W, Zhou Y (2020) Study on adaptive-passive eddy current pendulum tuned mass damper for wind-induced vibration control. Struct Des Tall Special Build 29(15):e1793

    Article  Google Scholar 

  43. Wang L, Shi W, Zhou Y, Zhang Q (2020) Semi-active eddy current pendulum tuned mass damper with variable frequency and damping. Smart Struct Syst 25(1):65–80

    Google Scholar 

  44. Yang XS (2010) Nature-inspired metaheuristic algorithms. Luniver Press, United Kingdom

    Google Scholar 

  45. Tighzert L, Fonlupt C, Mendil B (2018) A set of new compact firefly algorithms. Swarm Evol Comp 40:92–115

    Article  Google Scholar 

  46. Osaba E, Yang XS, Diaz F, Onieva E, Masegosa AD, Perallos A (2017) A discrete firefly algorithm to solve a rich vehicle routing problem modelling a newspaper distribution system with recycling policy. Soft Comp 21:5295–5308

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Gümüşhane University, Gümüşhane, Turkey

    Onur Araz

Authors
  1. Onur Araz
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Onur Araz.

Additional information

Technical Editor: Pedro Manuel Calas Lopes Pacheco.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Araz, O. Optimization of three-element tuned mass damper based on minimization of the acceleration transfer function for seismically excited structures. J Braz. Soc. Mech. Sci. Eng. 44, 459 (2022). https://doi.org/10.1007/s40430-022-03743-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-022-03743-0

Keywords

Search

Navigation