Skip to main content

Advertisement

SpringerLink
Log in

Numerical and experimental investigation of the dynamic behavior of a cantilever beam driven by two non-ideal sources

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

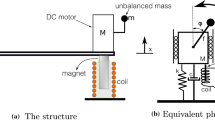
Non-ideal energy sources are present in several engineering applications where the power source interacts with the dynamics of the structure to which it is coupled. The systems driven by this kind of source present a rich dynamic behavior and some phenomena that can only be observed under non-ideal consideration. The modeling of such systems becomes much more complex due to the interaction between the system and the energy source, requiring an additional equation. The present work proposes a continuous vibration model of a cantilever beam with two unbalanced DC motors. The motors are considered non-ideal energy sources. The advantage of the continuous approach is that the position of the motors can be easily varied. In addition, time–frequency methods are performed in order to characterize and identify the occurrence of the Sommerfeld effect on the non-stationary operation. In order to validate the model, experimental measurements were performed and, subsequently, compared with the numerical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Mereles A, Varanis M, Silva AL, Balthazar JM, Lopes EMO, Bavastri CA (2019) Mathematical modelling of a cantilever beam driven by two unbalanced electric motors. In: Proceedings of the 25th international congress of mechanical engineering, ABCM

  2. Balthazar JM, Mook DT, Weber HI, Brasil RM, Fenili A, Belato D, Felix J (2003) An overview on non-ideal vibrations. Meccanica 38(6):613–621

    MATH  Google Scholar 

  3. Kononenko VO (1969) Vibrating systems with a limited power supply. Iliffe, London

    Google Scholar 

  4. Sommerfeld A (1902) Beiträge zum dynamischen ausbau der festigkeitslehe. Physikal Zeitschr 3:266–286

    MATH  Google Scholar 

  5. Felix JLP, Balthazar JM, Brasil RM (2005) On saturation control of a non-ideal vibrating portal frame foundation type shear-building. J Vib Control 11(1):121–136

    MATH  Google Scholar 

  6. Zhang X, Wen B, Zhao C (2014) Experimental investigation on synchronization of three co-rotating non-identical coupled exciters driven by three motors. J Sound Vib 333(13):2898–2908

    Google Scholar 

  7. Samantaray A, Dasgupta S, Bhattacharyya R (2010) Sommerfeld effect in rotationally symmetric planar dynamical systems. Int J Eng Sci 48(1):21–36

    Google Scholar 

  8. Dimentberg MF (1988) Statistical dynamics of nonlinear and time-varying systems, vol 5. Research Studies Press, Baldock

    MATH  Google Scholar 

  9. Evan-Iwanowski R (1976) Resonance oscillations in mechanical systems. North-Holland, Amsterdam

    MATH  Google Scholar 

  10. Nayfeh AH, Mook DT (2008) Nonlinear oscillations. Wiley, Hoboken

    MATH  Google Scholar 

  11. Cveticanin L, Zukovic M, Balthazar JM (2018) Dynamics of mechanical systems with non-ideal excitation. Springer, Berlin

    MATH  Google Scholar 

  12. El-Badawy AA (2007) Behavioral investigation of a nonlinear nonideal vibrating system. J Vib Control 13(2):203–217

    MathSciNet  MATH  Google Scholar 

  13. Gonçalves P, Silveira M, Junior BP, Balthazar J (2014) The dynamic behavior of a cantilever beam coupled to a non-ideal unbalanced motor through numerical and experimental analysis. J Sound Vib 333(20):5115–5129

    Google Scholar 

  14. Varanis M, Balthazar J, Silva A, Mereles A, Pederiva R (2018) Remarks on the Sommerfeld effect characterization in the wavelet domain. J Vib Control 25:98–108

    MathSciNet  Google Scholar 

  15. Brasil R, Balthazar JM (2000) Nonlinear oscillations of a portal frame structure excited by a nonideal motor. In: Proceedings of 2000 2nd international conference on control of oscillations and chaos vol. 2. IEEE, pp 275–278

  16. Tusset AM, Bueno ÁM, dos Santos JPM, Tsuchida M, Balthazar JM (2016) A non-ideally excited pendulum controlled by SDRE technique. J Braz Soc Mech Sci Eng 38(8):2459–2472

    Google Scholar 

  17. Arbex HC, Balthazar JM, de Pontes Junior BR, da Fonseca RMLR, Felix JLP, Tusset AM, Bueno ÁM et al (2015) On nonlinear dynamics behavior and control of a new model of a magnetically levitated vibrating system, excited by an unbalanced dc motor of limited power supply. J Braz Soc Mech Sci Eng 37(4):1139–1150

    Google Scholar 

  18. Hu W-H, Thöns S, Rohrmann RG, Said S, Rücker W (2015) Vibration-based structural health monitoring of a wind turbine system. Part i: resonance phenomenon. Eng Struct 89:260–272

    Google Scholar 

  19. Balthazar JM, Cheshankov BI, Ruschev D, Barbanti L, Weber H (2001) Remarks on the passage through resonance of a vibrating system with two degrees of freedom, excited by a non-ideal energy source. J Sound Vib 239(5):1075–1085

    MATH  Google Scholar 

  20. Wauer J, Suherman S (1998) Vibration suppression of rotating shafts passing through resonances by switching shaft stiffness. J Vib Acoust 120(1):170–180

    Google Scholar 

  21. De Souza S, Caldas IL, Viana R, Balthazar JM, Brasil R (2005) Impact dampers for controlling chaos in systems with limited power supply. J Sound Vib 279(3–5):955–967

    Google Scholar 

  22. Felix J, Balthazar JM, Brasil R (2009) A short note on transverse vibrations of a shaft carrying two (or one) disk excited by a nonideal motor. J Comput Nonlinear Dyn 4(1):014501

    Google Scholar 

  23. Balthazar JM, Felix J, Brasil R, Krasnopolskaya T, Shvets AY (2009) Nonlinear interactions in a piezoceramic bar transducer powered by a vacuum tube generated by a nonideal source. J Comput Nonlinear Dyn 4(1):011013

    Google Scholar 

  24. Piccirillo V, Tusset AM, Balthazar JM (2014) Dynamical jump attenuation in a non-ideal system through a magnetorheological damper. J Theor Appl Mech 52(3):595–604

    Google Scholar 

  25. Felix JL, Balthazar JM, Brasil RM (2005) On tuned liquid column dampers mounted on a structural frame under a non-ideal excitation. J Sound Vib 282:1285–1292

    Google Scholar 

  26. de Castro Silva FE, Bavastri CA (2019) A methodology for an optimal design of physical parameters, positions, and viscoelastic materials of simple dynamic absorbers for passive vibration control. J Vib Control 25(6):1133–1147

    MathSciNet  Google Scholar 

  27. Bronkhorst KB, Febbo M, Lopes EM, Bavastri CA (2018) Experimental implementation of an optimum viscoelastic vibration absorber for cubic nonlinear systems. Eng Struct 163:323–331

    Google Scholar 

  28. Addison PS (2017) The illustrated wavelet transform handbook: introductory theory and applications in science, engineering, medicine and finance. CRC Press, Boca Raton

    MATH  Google Scholar 

  29. Varanis M, Pederiva R (2018) Statements on wavelet packet energy-entropy signatures and filter influence in fault diagnosis of induction motor in non-stationary operations. J Braz Soc Mech Sci Eng 40(2):98

    Google Scholar 

  30. Daubechies I, Lu J, Wu H-T (2011) Synchrosqueezed wavelet transforms: an empirical mode decomposition-like tool. Appl Comput Harmon Anal 30(2):243–261

    MathSciNet  MATH  Google Scholar 

  31. Zhigang C, Xu X, Xiaolei D, Junling Z, Nan Z (2019) Leakage detection in pipelines based on synchrosqueezed wavelet transform. In: 2019 Chinese control and decision conference (CCDC). IEEE, pp 2679–2684

  32. Auger F, Flandrin P, Lin Y-T, McLaughlin S, Meignen S, Oberlin T, Wu H-T (2013) Time-frequency reassignment and synchrosqueezing: an overview. IEEE Signal Process Mag 30(6):32–41

    Google Scholar 

  33. Varanis M, Norenberg JPC, Rocha RT, Oliveira C, Balthazar JM, Tusset ÂM (2020) A comparison of time-frequency methods for nonlinear dynamics and chaos analysis in an energy harvesting model. Braz J Phys 1–10

  34. Wang S, Chen X, Selesnick IW, Guo Y, Tong C, Zhang X (2018) Matching synchrosqueezing transform: a useful tool for characterizing signals with fast varying instantaneous frequency and application to machine fault diagnosis. Mech Syst Signal Process 100:242–288

    Google Scholar 

  35. Mihalec M, Slavič J, Boltežar M (2016) Synchrosqueezed wavelet transform for damping identification. Mech Syst Signal Process 80:324–334

    Google Scholar 

  36. Cao H, Xi S, Chen X, Wang S (2016) Zoom synchrosqueezing transform and iterative demodulation: methods with application. Mech Syst Signal Process 72–73:695–711

    Google Scholar 

  37. Feng Z, Chen X, Liang M (2015) Iterative generalized synchrosqueezing transform for fault diagnosis of wind turbine planetary gearbox under nonstationary conditions. Mech Syst Signal Process 52–53:360–375

    Google Scholar 

  38. Hibbeler RC, Fan SC (2002) Engineering mechanics: dynamics. Prentice Hall, Upper Saddle River

    Google Scholar 

  39. Bisoi A, Samantaray A, Bhattacharyya R (2017) Control strategies for DC motors driving rotor dynamic systems through resonance. J Sound Vib 411:304–327

    Google Scholar 

  40. Wu H-T, Flandrin P, Daubechies I (2011) One or two frequencies? The synchrosqueezing answers. Advn Adapt Data Anal 3(01n02):29–39

    MathSciNet  MATH  Google Scholar 

  41. Mihalec M, Slavič J, Boltežar M (2016) Synchrosqueezed wavelet transform for damping identification. Mech Syst Signal Process 80:324–334

    Google Scholar 

  42. Perez-Ramirez CA, Amezquita-Sanchez JP, Adeli H, Valtierra-Rodriguez M, Camarena-Martinez D, Romero-Troncoso RJ (2016) New methodology for modal parameters identification of smart civil structures using ambient vibrations and synchrosqueezed wavelet transform. Eng Appl Artif Intell 48:1–12

    Google Scholar 

  43. Oberlin T, Meignen S, Perrier V (2014) The fourier-based synchrosqueezing transform. In: 2014 IEEE international conference on acoustics speech and signal processing (ICASSP). IEEE, pp 315–319

  44. Oliynik P (2016) Development of wireless vibration transducer based on MEMS accelerometer. East Eur J Enterp Technol 3(9):18–24

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Engineering, Federal University of Grande Dourados (UFGD), Dourados, MS, Brazil

    Marcus Varanis

  2. Faculty of Mechanical Engineering, University of Campinas (UNICAMP), Campinas, SP, Brazil

    Arthur Mereles

  3. Department of Mechanical Engineering (UFPR), Federal University of Paraná, Curitiba, PR, Brazil

    Anderson L. Silva, Maurizio Radloff Barghouthi, Eduardo M. O. Lopes & Carlos Alberto Bavastri

  4. Federal University of Technology - Paraná (UTFPR), Ponta Grossa, PR, Brazil

    José Manoel Balthazar

Authors
  1. Marcus Varanis
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Arthur Mereles
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Anderson L. Silva
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Maurizio Radloff Barghouthi
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. José Manoel Balthazar
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Eduardo M. O. Lopes
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Carlos Alberto Bavastri
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marcus Varanis.

Additional information

Technical Editor: Thiago Ritto.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Varanis, M., Mereles, A., Silva, A.L. et al. Numerical and experimental investigation of the dynamic behavior of a cantilever beam driven by two non-ideal sources. J Braz. Soc. Mech. Sci. Eng. 42, 516 (2020). https://doi.org/10.1007/s40430-020-02589-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-020-02589-8

Keywords

Search

Navigation