Triangular Ratio Metric Under Quasiconformal Mappings in Sector Domains

Abstract

The hyperbolic metric and different hyperbolic type metrics are studied in open sector domains of the complex plane. Several sharp inequalities are proven for them. Our main result describes the behavior of the triangular ratio metric under quasiconformal maps from one sector onto another one.

1 Introduction

Geometric function theory studies families of functions such as conformal maps and analytic functions as well as quasiconformal and quasiregular mappings defined in subdomains G of $\mathbb {R}^n, n\ge 2\,.$ In this research, a key notion is an intrinsic distance, which is a distance between two points in the domain, specific to the domain itself and, in particular, its boundary [6, 7]. In the planar case $n=2$, such a distance is the hyperbolic distance that can be readily defined by use of a conformal mapping for a simply connected domain, but this does not generalize to higher dimensions. It is natural therefore to look for various extensions and generalizations of hyperbolic metrics. Twelve metrics recurrent in geometric function theory are listed by Papadopoulos [13, pp. 42–48].

Many people have studied generalizations of hyperbolic metrics to subdomains of $\mathbb {R}^n$, $n\ge 3$, and found hyperbolic type metrics, which share some but not all properties of the hyperbolic metric. In their study of quasidisks, Gehring and Hag [6] apply the hyperbolic, quasihyperbolic, distance ratio, and Apollonian metrics. Very recently, the geometry of the quasihyperbolic metric has been studied by Herron and Julian [12], Rasila et al. [17], Buckley and Herron [3]. Another hyperbolic type metric is the triangular ratio metric introduced by Hästö [9] and most recently studied by Fujimura et al. [5]. The interrelations between these metrics have been investigated by Hästö et al. [10]. See also Herron et al. [11] and Aksoy et al. [1].

Our work is motivated by the recent progress of the study of the intrinsic geometry of domains, of which the above papers and the monographs [6, 7, 13] are examples. First, in Sect. 3, we find new inequalities between three different hyperbolic type metrics in sector domains of the complex plane and establish sharp forms of some earlier results in [4, 8]. In Sect. 4, we apply a rotation method involving Möbius transformations to obtain a sharp inequality between the triangular ratio metric and the hyperbolic metric in a sector with a fixed angle. Finally, in Sect. 5, we present our main result that provides a sharp distortion theorem for the triangular ratio metric under quasiconformal maps between two planar sector domains.

2 Preliminary Facts

Suppose that G is a proper domain in $\mathbb {R}^n$. In other words, choose a subset $G\subsetneq \mathbb {R}^n$ so that it is non-empty, open and connected. Denote the Euclidean distance dist$(x,\partial G)=\inf \{|x-z|\text { }|\text { }z\in \partial G\}$ between the point x and the boundary of G by $d_G(x)$. Define then the following hyperbolic type metrics: The triangular ratio metric $s_G:G\times G\rightarrow [0,1]$,

$$\begin{aligned} s_G(x,y)=\frac{|x-y|}{\inf _{z\in \partial G}(|x-z|+|z-y|)}, \end{aligned}$$

the $j^*_G$-metric $j^*_G:G\times G\rightarrow [0,1),$

$$\begin{aligned} j^*_G(x,y)=\frac{|x-y|}{|x-y|+2\min \{d_G(x),d_G(y)\}}, \end{aligned}$$

and the point pair function $p_G:G\times G\rightarrow [0,1),$

$$\begin{aligned} p_G(x,y)=\frac{|x-y|}{\sqrt{|x-y|^2+4d_G(x)d_G(y)}}, \end{aligned}$$

Note that the point pair function is not a metric in some domains G [4,   Rmk. 3.1 p. 689], and see [4, 8, 14,15,16] for more details about these functions.

In this paper, we focus on the case where the domain G is an open sector $S_\theta =\{x\in \mathbb {C}\text { }\backslash \{0\}|\text { }0<\arg (x)<\theta \}$ with an angle $\theta \in (0,2\pi )$. In the limiting case $\theta =0$, we consider the strip domain $S_0=\{x\in \mathbb {C}\text { }|\text { }0<\text {Im}(x)<\pi \}$. Other common domains are the upper half-space $\mathbb {H}^n=\{(x_1,\ldots ,x_n)\in \mathbb {R}^n\text { }|\text { }x_n>0\}$ and the unit ball $\mathbb {B}^n=B^n(0,1)$. Here, $B^n(x,r)$ is the open ball with the Euclidean metric, $\overline{B}^n(x,r)$ is its closure and $S^{n-1}(x,r)$ is the boundary $\partial B^n(x,r)$. For two distinct points x, y, L(x, y) is the Euclidean line passing through them and [x, y] is the Euclidean line segment between them.

With the notations presented above, we can also write formulas for the hyperbolic metric $\rho _G$ in these domains $G\in \{\mathbb {H}^n,\mathbb {B}^n,S_\theta \}$ as [7,  (4.8), p. 52 & (4.14), p. 55]

$$\begin{aligned} \text {ch}\rho _{\mathbb {H}^n}(x,y)&=1+\frac{|x-y|^2}{2d_{\mathbb {H}^n}(x)d_{\mathbb {H}^n}(y)},\quad x,y\in \mathbb {H}^n,\\ \text {sh}^2\frac{\rho _{\mathbb {B}^n}(x,y)}{2}&=\frac{|x-y|^2}{(1-|x|^2)(1-|y|^2)},\quad x,y\in \mathbb {B}^n,\\ \rho _{S_\theta }(x,y)&=\rho _{\mathbb {H}^2}(x^{\pi /\theta },y^{\pi /\theta }),\quad x,y\in S_\theta , \end{aligned}$$

Note that the third formula above follows from the conformal invariance of the hyperbolic metric: If G is a domain and $f:G\rightarrow G'=f(G)$ is a conformal mapping, then

$$\begin{aligned} \rho _G(x,y)=\rho _{G'}(f(x),f(y)). \end{aligned}$$

Thus, the hyperbolic metric $\rho _G$ can be defined in any planar simply connected domain in terms of a conformal mapping of the domain onto the unit disk [2,  Thm. 6.3 p. 26]. Furthermore, the hyperbolic metric is invariant under Möbius transformations, see [7, Def. 3.6, p. 27] for the definition, because Möbius transformations are a subclass of conformal mappings. In the two-dimensional plane, the definitions of hyperbolic metric can be simplified to

$$\begin{aligned} \text {th}\frac{\rho _{\mathbb {H}^2}(x,y)}{2}&=\text {th}\left( \frac{1}{2}\log \left( \frac{|x-\overline{y}|+|x-y|}{|x-\overline{y}|-|x-y|}\right) \right) =\left| \frac{x-y}{x-\overline{y}}\right| ,\\ \text {th}\frac{\rho _{\mathbb {B}^2}(x,y)}{2}&=\text {th}\left( \frac{1}{2}\log \left( \frac{|1-x\overline{y}|+|x-y|}{|1-x\overline{y}|-|x-y|}\right) \right) =\left| \frac{x-y}{1-x\overline{y}}\right| , \end{aligned}$$

where $\overline{y}$ is the complex conjugate of y.

The following inequalities between hyperbolic type metrics are already known:

Theorem 2.1

[8, Lem. 2.3, p. 1125]. For a proper subdomain G of $\mathbb {R}^n$, the inequality $j^*_G(x,y)\le p_G(x,y)\le \sqrt{2}j^*_G(x,y)$ holds for all $x,y\in G$.

Theorem 2.2

[8, Lem. 2.1, p. 1124 and Lemma 2.2, p. 1125]. For a proper subdomain G of $\mathbb {R}^n$, the inequality $j^*_G(x,y)\le s_G(x,y)\le 2j^*_G(x,y)$ holds for all $x,y\in G$.

Theorem 2.3

[8, Lem. 2.8 and Thm 2.9(1), p. 1129]. If $G\subsetneq \mathbb {R}^n$ is convex, $j^*_G(x,y)\le s_G(x,y)\le \sqrt{2}j^*_G(x,y)$ holds for all $x,y\in G$.

The following results are useful when calculating the value of $s_G(x,y)$:

Lemma 2.4

(Heron’s shortest distance problem) Given $x,y\in \mathbb {H}^2$, the Heron point $w=L(\overline{x},y)\cap \mathbb {R}$ minimizes the sum $|x-z|+|z-y|$ where $z\in \mathbb {R}$, and therefore $\inf _{z\in \mathbb {R}}(|x-z|+|z-y|)=|\overline{x}-y|$.

It follows from Lemma 2.4 that for all $x,y\in \mathbb {H}^2$,

$$\begin{aligned} s_{\mathbb {H}^2}(x,y)=\left| \frac{x-y}{\overline{x}-y}\right| . \end{aligned}$$

Theorem 2.5

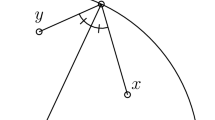
For all $\theta \in (0,2\pi )$ and $x,y\in S_\theta$, there is an analytical solution to the value of $s_{S_\theta }(x,y)$.

Proof

Consider a line $l\subset \mathbb {R}^2$, a half-line $l_0\subset l$ and two points $x,y\in \mathbb {R}^2$. If $[x,y]\cap l_0\ne \varnothing$, $\inf _{z\in l_0}(|x-z|+|z-y|)=|x-y|$. Let $x'$ be the point x reflected over the line l. If $[x,y]\cap l_0=\varnothing$ and $[y,x']\cap l_0\ne \varnothing$, then, by Lemma 2.4, $\inf _{z\in l_0}(|x-z|+|z-y|)=|x'-y|$. Otherwise, $\inf _{z\in l_0}(|x-z|+|z-y|)=|x-z_0|+|z_0-y|$ where $z_0$ is the endpoint of $l_0$. Clearly,

$$\begin{aligned} \inf _{z\in \partial S_\theta }(|x-z|+|z-y|)=\min \{\inf _{z\in l_j}(|x-z|+|z-y|)\text { }|\text { }j=1,2\}, \end{aligned}$$

where $l_1,l_2$ are the half-lines forming the sector $S_\theta$. See Fig. 1. $\square$

Fig. 1

The point z giving the infimum $\inf _{z\in \partial S_\theta }(|x-z|+|z-y|)$ in the sector $S_\theta$ with an angle $\theta =3\pi /4$

2.6

Some computed values of $s_{S_{\theta }}(x,y).$ In Table 1, there are some values of the triangular ratio metric $s_{S_{\theta }}(x,y)$ in a sector $S_\theta$ for a few different choices of x, y and $\theta$. These values have been computed by applying the above theorem and some formulas for the geometry of the complex plane such as reflection over line from [7,  (B.3) and (B.11), pp. 458-460]. In Fig. 1, the points are $x=1+7i/10$ and $y=(1+14i)/10$, and the angle $\theta =3\pi /4$, so the triangular ratio distance $s_{S_{\theta }}(x,y)$ is $\sqrt{65/29}/3$ in this case.

Table 1 Values of triangular ratio metric $s_{S_{\theta }}(x,y)$ in a sector $S_\theta$ for certain choices of x, y and $\theta$

3 Hyperbolic Type Metrics

In this section, our main result is Theorem 3.23. This theorem provides sharp inequalities between the hyperbolic type metrics in a sector domain. First, we will show that certain equalities are possible.

Lemma 3.1

For any fixed domain $G\subsetneq \mathbb {R}^n$, there are distinct points $x,y\in G$ such that $s_G(x,y)=j^*_G(x,y)=p_G(x,y)$.

Proof

Fix $x\in G$ and choose a ball $B^n(x,r)\subset G$ with $S^{n-1}(x,r)\cap \partial G\ne \varnothing$ where $r>0$. Fix $z\in S^{n-1}(x,r)\cap \partial G$ and $y\in [x,z]$ so that $|x-y|=kr$ with $k\in (0,1)$. From $d_G(x)=r$ and $d_G(y)=(1-k)r$, it follows that $j^*_G(x,y)=p_G(x,y)=k/(2-k)$. By [7,  11.2.1(1), p. 205],

$$\begin{aligned} s_G(x,y)\le s_{B^n(x,r)}(x,y)=s_{\mathbb {B}^n}(0,k)=\frac{k}{2-k}=\frac{|x-y|}{|x-z|+|z-y|}\le s_G(x,y) \end{aligned}$$

so that $s_G(x,y)=k/(2-k)$, too. $\square$

Lemma 3.2

For any fixed Jordan domain $G\subsetneq \mathbb {R}^2$, if there exists a line segment $[u,v]\subset \partial G$, then there are distinct points $x,y\in G$ such that $p_G(x,y)=\sqrt{2}j^*_G(x,y)$.

Proof

First, note that the equality $p_G(x,y)=\sqrt{2}j^*_G(x,y)$ holds non-trivially when $x\ne y$ and $|x-y|/2=d_G(x)=d_G(y)$. If $[u,v]\subset \partial G$, we can fix a segment $[x,y]\subset G$ so that it is parallel to the segment [u, v], has the same perpendicular bisector as [u, v] and fulfills $d_G(x)=d_G(y)=d([x,y],[u,v])=|x-y|/2$. The equality $p_G(x,y)=\sqrt{2}j^*_G(x,y)$ follows. $\square$

Remark 3.3

The metrics $s_G$ and $j^*_G$, and the point pair function $p_G$ are all invariant under the stretching $z\mapsto rz$ by a factor $r>0$ and the reflection by the symmetry axis of the domain G, if G is, for instance, $\mathbb {H}^2$, $S_\theta$ or $\mathbb {R}^n\backslash \{0\}$.

Theorem 3.4

For a fixed angle $\theta \in (\pi ,2\pi )$ and for all $x,y\in S_\theta$, the sharp inequality $s_{S_\theta }(x,y)\le 2\sin (\theta /4)j^*_{S_\theta }(x,y)$ holds.

Proof

Consider the quotient

$$\begin{aligned} \frac{s_{S_\theta }(x,y)}{j^*_{S_\theta }(x,y)}=\frac{|x-y|+2\min \{d_{S_\theta }(x),d_{S_\theta }(y)\}}{\inf _{z\in \partial S_\theta }(|x-z|+|z-y|)}. \end{aligned}$$

(3.5)

We clearly need to find the maximal value of this quotient for each $\theta \in (\pi ,2\pi )$. First, fix the point z so that it gives the infimum $\inf _{z\in \partial S_\theta }(|x-z|+|z-y|)$. Since clearly $d_{S_\theta }(x)\le |x-z|$ and $d_{S_\theta }(y)\le |z-y|$, the sum $d_{S_\theta }(x)+d_{S_\theta }(y)$ has an upper limit $|x-z|+|z-y|$. If we set $r=d_{S_\theta }(x)+d_{S_\theta }(y)$, it follows that $\min \{d_{S_\theta }(x),d_{S_\theta }(y)\}\le \min \{d_{S_\theta }(x),r-d_{S_\theta }(x)\}$. To find the maximum of $\min \{d_{S_\theta }(x),d_{S_\theta }(y)\}$, we need to choose $d_{S_\theta }(x)=r/2=d_{S_\theta }(y)$.

Now, we need to minimize the value of $\inf _{z\in \partial S_\theta }(|x-z|+|z-y|)$ compared to the numerator $|x-y|+r$ of the quotient (3.5). This happens when the point z in the infimum is fixed to the origin, and x and y are on different sides of the bisector of the sector $S_\theta$. It follows that $\inf _{z\in \partial S_\theta }(|x-z|+|z-y|)=|x|+|y|$.

Let us next consider the distance $|x-y|$ compared to the infimum in the quotient (3.5). Suppose $\inf _{z\in \partial S_\theta }(|x-z|+|z-y|)=|x|+|y|$ is fixed. By Pythagoras’ theorem, $|x-y|=\sqrt{|x|^2-l^2}+\sqrt{|y|^2-l^2}$, where $l=d([x,y],\{0\})$ so we see that, for a fixed sum $|x|+|y|$, the value of $|x-y|$ is at maximum when $|x|=|y|$.

Because of these observations and by Remark 3.3, we can fix $x=e^{hi}$ and $y=e^{(\theta -h)i}$ with some $(\theta -\pi )/2<h<\theta /2$. It follows that

$$\begin{aligned}&|x-y|=2\sin \left( \frac{\theta }{2}-h\right) ,\\&d_{S_\theta }(x)=d_{S_\theta }(y)= {\left\{ \begin{array}{ll} \sin (h) &{} \text { if }h<\frac{\pi }{2},\\ 1 &{} \text {otherwise,} \end{array}\right. }\quad \text {and}\\&\inf _{z\in \partial S_\theta }(|x-z|+|z-y|)=2. \end{aligned}$$

If $h<\pi /2$, the quotient (3.5) is $\sin (\theta /2-h)+\sin (h)$, which attains a maximum when $h=\theta /4$. Clearly, $(\theta -\pi )/2<\theta /4<\pi /2$ for all $\theta \in (\pi ,2\pi )$. Thus, the maximum value of the quotient (3.5) with limitation $h<\pi /2$ is $2\sin (\theta /4)$.

If $h\ge \pi /2$ instead, the quotient (3.5) is $\sin (\theta /2-h)+1$. Within the limitation $h\ge \pi /2$, this quotient attains its maximum $1-\cos (\theta /2)$ when $h=\pi /2$. Since, for all $\theta \in (\pi ,2\pi )$, $1-\cos (\theta /2)<2\sin (\theta /4)$, the true maximum value of the quotient is $2\sin (\theta /4)$ and the theorem follows. $\square$

Theorem 3.6

For a domain $G\subsetneq \mathbb {R}^n$, the sharp inequality

$$\begin{aligned} \frac{1}{\sqrt{2}}p_G(x,y)\le s_G(x,y)\le \sqrt{2}p_G(x,y) \end{aligned}$$

holds for all $x,y\in G$.

Proof

According to [7,  11.16(1), p. 203], the inequality $p_G(x,y)/\sqrt{2}\le s_G(x,y)$ holds for all $x,y\in G$ and this is sharp for $p_G(x,y)/\sqrt{2}=s_G(x,y)$ if $G=\{z\in \mathbb {C}\text { }|\text { }0<\text {Im}(z)<1\}$, $x=i/4$ and $y=3i/4$.

If we fix $z\in \partial G$ so that it gives the infimum $\inf _{z\in \partial G}(|x-z|+|z-y|)$,

$$\begin{aligned} \frac{s_G(x,y)}{p_G(x,y)}&=\frac{\sqrt{|x-y|^2+4d_G(x)d_G(y)}}{|x-z|+|z-y|} \le \frac{\sqrt{|x-y|^2+4|x-z||z-y|}}{|x-z|+|z-y|}\\&\le \frac{\sqrt{(|x-z|+|z-y|)^2+4|x-z||z-y|}}{|x-z|+|z-y|} =\sqrt{1+\frac{4|x-z||z-y|}{(|x-z|+|z-y|)^2}}. \end{aligned}$$

It can be shown by the inequality of arithmetic and geometric means that the quotient above attains its maximum value $\sqrt{2}$, when $|x-z|=|z-y|$. This proves the inequality $s_G(x,y)\le \sqrt{2}p_G(x,y)$. Here, the equality holds for $G=\mathbb {R}^2\backslash \{0\}$, $x=-1$ and $y=1$, since now $s_G(x,y)=\sqrt{2}p_G(x,y)=1$. $\square$

Remark 3.7

Theorem 3.6 improves the upper bound of [8,  Lem. 2.5(1), p. 1126].

Theorem 3.8

A domain $G\subsetneq \mathbb {R}^n$ is convex if and only if the inequality $s_G(x,y)\le p_G(x,y)$ holds for all $x,y\in G$.

Proof

By [7,  Lem. 11.6(1), p. 197], $s_G(x,y)\le p_G(x,y)$ holds for all $x,y\in G$ if G is convex. Suppose now that G is non-convex and fix $x,y\in G$ so that $[x,y]\cap \partial G\ne \varnothing$. Clearly, $s_G(x,y)\ge p_G(x,y)$ because

$$\begin{aligned} \inf _{z\in \partial G}(|x-z|+|z-y|)=|x-y|<\sqrt{|x-y|^2+4d_G(x)d_G(y)}. \end{aligned}$$

Consequently, if $s_G(x,y)\le p_G(x,y)$ holds for all $x,y\in G$, then G must be convex. $\square$

Theorem 3.9

For a fixed angle $\theta \in (0,\pi )$ and for all $x,y\in S_\theta$, the sharp inequality

$$\begin{aligned} \frac{p_{S_\theta }(x,y)}{\sqrt{2}\cos (\frac{\theta }{4})}\le s_{S_\theta }(x,y) \end{aligned}$$

holds.

Proof

Consider the quotient

$$\begin{aligned} \frac{s_{S_\theta }(x,y)}{p_{S_\theta }(x,y)}=\frac{\sqrt{|x-y|^2+4d_{S_\theta }(x)d_{S_\theta }(y)}}{\inf _{z\in \partial S_\theta }(|x-z|+|z-y|)}. \end{aligned}$$

(3.10)

Suppose without loss of generality that $x=e^{hi}$ and $y=re^{ki}$ with $0<h\le k<\theta$ and $r>0$. If $k\le \theta /2$, then the closest boundary points of $\partial S_\theta$ to x, y are on the positive real axis, as is the point z in the infimum of the triangular ratio metric. Consequently, $s_{S_\theta }(x,y)=s_{\mathbb {H}^2}(x,y)$ and $p_{S_\theta }(x,y)=p_{\mathbb {H}^2}(x,y)$ and, because $s_{\mathbb {H}^2}(x,y)=p_{\mathbb {H}^2}(x,y)$ by [7,  p. 460], we will have $p_{S_\theta }(x,y)=s_{S_\theta }(x,y)$. By symmetry, $p_{S_\theta }(x,y)=s_{S_\theta }(x,y)$ also when $h\ge \theta /2$.

Next, assume that $h<\theta /2<k$. Now, the infimum in the quotient (3.10) is $\min \{|\overline{x}-y|,|x-y'|\}$, where $\overline{x}$ is the complex conjugate of x and $y'$ is the point y reflected over the line $L(0,e^{\theta i})$. Clearly, $|\overline{x}-y|=|1-re^{(k+h)i}|$ and $|x-y'|=|1-re^{(2\theta -k-h)i}|$. Let $u=k+h$, so that $k=u-h$. Note that $\theta /2<u<3\theta /2$. By the law of cosines, the quotient (3.10) can be written as

$$\begin{aligned} \sqrt{\frac{1+r^2+2r(-\cos (u-2h)+2\sin (h)\sin (\theta -u+h))}{1+r^2-2r\max \{\cos (u),\cos (2\theta -u)\}}}, \end{aligned}$$

(3.11)

where $\theta /2<u<3\theta /2$ and $\max \{0,u-\theta \}<h<\min \{u/2,u-\theta /2,\theta /2\}$. By differentiation and the addition formula of the sine function, we will have

$$\begin{aligned} \begin{aligned}&\frac{d}{dh}(-\cos (u-2h){+}2\sin (h)\sin (\theta -u+h)) {=}2(\sin (\theta -u+2h){-}\sin (u-2h)){\le }0\\&\Leftrightarrow \quad h\le \frac{u}{2}-\frac{\theta }{4}. \end{aligned} \end{aligned}$$

(3.12)

Because

$$\begin{aligned} \max \{0,u-\theta \}<\frac{u}{2}-\frac{\theta }{4}<\min \left\{ \frac{u}{2},u-\frac{\theta }{2},\frac{\theta }{2}\right\} \end{aligned}$$

for all $\theta /2<u<3\theta /2$, the quotient (3.11) is always at minimum with respect to h at $h\le u/2-\theta /4$. Consequently, the quotient (3.10) is therefore bounded below by

$$\begin{aligned} \sqrt{\frac{1+r^2+2r(-\cos (\frac{\theta }{2})+2\sin (\frac{u}{2}-\frac{\theta }{4})\sin (\frac{3\theta }{4}-\frac{u}{2}))}{1+r^2-2r\max \{\cos (u),\cos (2\theta -u)\}}}, \end{aligned}$$

where $\theta /2<u<3\theta /2$. Because the values of this quotient are the same at $u=v$ and $u=2\theta -v$ for all $\theta /2<v<3\theta /2$, we can suppose without loss of generality that $\theta /2<u\le \theta$. By differentiation, it can be proved that the quotient

$$\begin{aligned} \frac{1+r^2+2r(-\cos (\frac{\theta }{2})+2\sin (\frac{u}{2}-\frac{\theta }{4})\sin (\frac{3\theta }{4}-\frac{u}{2}))}{1+r^2-2r\cos (u)} \end{aligned}$$

is decreasing with respect to $u\in (\theta /2,\theta ]$ and therefore bounded below by

$$\begin{aligned} \frac{1+r^2+2r(2\sin ^2(\frac{\theta }{4})-\cos (\frac{\theta }{2}))}{1+r^2-2r\cos (\theta )} =\frac{1+2r+r^2-4r\cos (\frac{\theta }{2})}{1+r^2-2r\cos (\theta )}. \end{aligned}$$

By using differentiation again, we can show that the expression above attains its minimum value with $r=1$. Thus, the minimum value of the quotient (3.10) is

$$\begin{aligned} \sqrt{\frac{2-2\cos (\frac{\theta }{2})}{1-\cos (\theta )}}=\frac{1}{\sqrt{2}\cos (\frac{\theta }{4})}. \end{aligned}$$

$\square$

Theorem 3.13

For a fixed angle $\theta \in [\pi ,2\pi )$ and for all $x,y\in S_\theta$, the sharp inequality $p_{S_\theta }(x,y)\le s_{S_\theta }(x,y)$ holds.

Proof

Fix $x=e^{hi}$ and $y=re^{ki}$ with $0<h\le k<\theta$ and $r>0$. Denote $u=h+k$ and $q=\inf _{z\in \partial S_\theta }(|x-z|+|z-y|)$. By symmetry, suppose that $u\le \theta$. Namely, if $u>\theta$, we could reflect the points x and y over the line $L(0,e^{\theta i/2})$ so that $u<\theta$ for the new points, see Remark 3.3. If $u\le \pi$, then $q=|\overline{x}-y|=|1-re^{ui}|$; if $\pi <u\le \min \{\theta ,\pi +2h\}$, $q=|x|+|y|=1+r$, and if $u\ge \pi +2h$, $[x,y]\cap \partial S_\theta \ne \varnothing$ and $q=|x-y|$. Furthermore, $d_{S_\theta }(x)=\sin (h)$ for $h\le \pi /2$ and $d_{S_\theta }(x)=1$ for $\pi /2<h<\theta /2$. Similarly, $d_{S_\theta }(y)=r\sin (k)$ for $k\le \pi /2$, $d_{S_\theta }(y)=r$ for $\pi /2<k<\theta -\pi /2$ and $d_{S_0}(y)=r \sin (\theta -k)$ for $k\ge \theta -\pi /2$.

It follows from this that there are seven different options for the value of the quotient $s_{S_\theta }(x,y)/p_{S_\theta }(x,y)$:

$$\begin{aligned}&\frac{s_{S_\theta }(x,y)}{p_{S_\theta }(x,y)} =\sqrt{\frac{1+r^2-2r\cos (k-h)+4r\sin (h)\sin (k)}{1+r^2-2r\cos (h+k)}} =1, \quad \text {if}\quad k\le \frac{\pi }{2}, \end{aligned}$$

(3.14)

$$\begin{aligned}&\frac{s_{S_\theta }(x,y)}{p_{S_\theta }(x,y)} =\sqrt{\frac{1+r^2-2r\cos (u-2h)+4r\sin (h)}{1+r^2-2r\cos (u)}}, \end{aligned}$$

(3.15)

$$\begin{aligned}&\text {if}\quad h\le \frac{\pi }{2},\,\frac{\pi }{2}+h<u\le \min \left\{ \theta -\frac{\pi }{2}+h,\pi \right\} ,\nonumber \\&\frac{s_{S_\theta }(x,y)}{p_{S_\theta }(x,y)} =\frac{\sqrt{1+r^2-2r\cos (u-2h)+4r\sin (h)}}{1+r}, \end{aligned}$$

(3.16)

$$\begin{aligned}&\text {if}\quad h\le \frac{\pi }{2},\,\pi<u<\min \left\{ \theta -\frac{\pi }{2}+h,\pi +2h\right\} \nonumber \\&\frac{s_{S_\theta }(x,y)}{p_{S_\theta }(x,y)} =\frac{\sqrt{1+r^2-2r\cos (u-2h)+4r}}{1+r}, \quad \text {if}\quad h\ge \frac{\pi }{2},\,\pi <u\le \theta \end{aligned}$$

(3.17)

$$\begin{aligned}&\frac{s_{S_\theta }(x,y)}{p_{S_\theta }(x,y)} =\frac{\sqrt{1+r^2-2r\cos (k-h)+4r\sin (h)\sin (\theta -k)}}{1+r}, \end{aligned}$$

(3.18)

$$\begin{aligned}&\text {if}\quad h\le \frac{\pi }{2},\,\max \left\{ \theta -\frac{\pi }{2},\pi -h\right\} \le k<\min \{\theta -h,\pi +h\},\nonumber \\&\frac{s_{S_\theta }(x,y)}{p_{S_\theta }(x,y)} =\sqrt{\frac{1+r^2-2r\cos (k-h)+4r\sin (h)\sin (\theta -k)}{1+r^2-2r\cos (k+h)}}, \end{aligned}$$

(3.19)

$$\begin{aligned}&\text {if}\quad h\le \frac{\pi }{2},\,\theta -\frac{\pi }{2}\le k<\pi -h,\nonumber \\&\frac{s_{S_\theta }(x,y)}{p_{S_\theta }(x,y)}=\frac{1}{p_{S_\theta }(x,y)}\ge 1, \quad \text {if}\quad k-h\ge \pi . \end{aligned}$$

(3.20)

The situation of the third quotient (3.16) is shown in Fig. 2.

The conditions $0<h\le \pi /2$ and $\pi /2+h<u\le \min \{\theta -\pi /2+h,\pi \}$ of the quotient (3.15) are equivalent to $\pi /2<u\le \pi$ $\max \{u-\theta + \pi /2,0\}\le h<u-\pi /2$.By differentiation,

$$\begin{aligned} \frac{d}{dh}(-2r\cos (u-2h){+}4r\sin (h)) {=}4r(\cos (h)-\sin (u-2h)){\ge }0 \quad \Leftrightarrow \quad h{\le }\frac{u}{3}{-}\frac{\pi }{6}. \end{aligned}$$

(3.21)

It follows that to minimize the quotient (3.15) with respect to h, we need to choose one of the endpoints of h’s interval: either $h=\max (u-\theta +\pi /2,0)$ or $h=u-\pi /2$. With these choices of h, we see that the quotient (3.15) either has the value of 1 or, if $\max \{\pi /2,\theta -\pi /2\}\le u\le \pi$, it can also become the following quotient instead:

$$\begin{aligned}&\sqrt{\frac{1+r^2+2r\cos (2\theta -u)+4r\cos (u-\theta )}{1+r^2-2r\cos (u)}}\ge 1\\&\quad \Leftrightarrow \cos (2\theta -u)+2\cos (u-\theta )+\cos (u)\ge 0. \end{aligned}$$

Since it can be proved that the inequality above holds with $\max \{\pi /2,\theta -\pi /2\}\le u\le \pi$, it follows that the quotient (3.15) is greater than or equal to 1.

Clearly, the quotient (3.16) is greater than or equal to 1 if and only if

$$\begin{aligned} -\cos (u-2h)+2\sin (h)\ge 1. \end{aligned}$$

Clearly, the left side of the inequality is increasing with respect to u when $h\le \pi /2$ and $\pi<u<\min \{\theta -\pi /2+h,\pi +2h\}$. Consequently, we will have

$$\begin{aligned} -\cos (u-2h)+2\sin (h) \ge -\cos (\pi -2h)+2\sin (h) =\cos (2h)+2\sin (h) \ge 1, \end{aligned}$$

so the value of the quotient (3.16) is at least 1.

Furthermore, the quotient (3.17) is greater than or equal to 1, because trivially $-\cos (u-2h)+2\ge 1$ for all choices of h, u. The quotient (3.18) is at least 1, too, because it can be shown by differentiation with respect to k that

$$\begin{aligned} -\cos (k-h)+2\sin (h)\sin (\theta -k)\ge 1 \end{aligned}$$

with $h\le \pi /2,\,\max \{\theta -\pi /2,\pi -h\}\le k<\min \{\theta -h,\pi +h\}$. Furthermore, if $\theta -k\le \pi /2$,

$$\begin{aligned} -\cos (k{-}h){+}2\sin (h)\sin (\theta -k){>} {-}\cos (k-h){+}2\sin (h)\sin (\pi -k){=} {-}\cos (k{+}h), \end{aligned}$$

from which it follows that the quotient (3.19) is also at least 1. Consequently, we have now checked all the possible cases and the theorem is proved. $\square$

Fig. 2

The distances needed to compute the quotient $s_{S_\theta }(x,y)/p_{S_\theta }(x,y)$, when $x=e^{hi}$ and $y=re^{ki}$ are in the sector $S_\theta$ with an angle $\theta =7\pi /4$

Theorem 3.22

For a fixed angle $\theta \in (\pi ,2\pi )$ and for all $x,y\in S_\theta$, the sharp inequality

$$\begin{aligned} s_{S_\theta }(x,y)\le \sqrt{2}\sin \left( \frac{\theta }{4}\right) p_{S_\theta }(x,y) \end{aligned}$$

holds.

Proof

Just like in the proof of Theorem 3.13, let us fix $x=e^{hi}$ and $y=re^{ki}$ with $0<h\le k<\theta$ and $r>0$, denote $u=h+k$ and let $u\le \theta$ by symmetry. Let us now go through again all the seven options in the proof of Theorem 3.13, and find their maximum values. Note that $\sqrt{2}\sin (\theta /4)\ge 1$ for all $\theta \ge \pi$, so the quotient (3.14) fulfills this inequality trivially.

Recall the differentiation in (3.21). Note that the value $u/3-\pi /6$ of h is possible within the conditions of the quotient (3.15) if

$$\begin{aligned} u-\theta +\frac{\pi }{2}\le \frac{u}{3}-\frac{\pi }{6} \quad \Leftrightarrow \quad u\le \frac{3\theta }{2}-\pi . \end{aligned}$$

So to maximize the quotient (3.15), we need to choose $h=u/3-\pi /6$ if $\pi /2<u\le \min \{3\theta /2-\pi ,\pi \}$, and $h=u-\theta +\pi /2>0$ if $3\theta /2-\pi <u\le \pi$ and $\theta <4\pi /3$. Since it can be proved by differentiation that both the quotients

$$\begin{aligned}&\sqrt{\frac{1+r^2-2r\cos (\frac{u}{3}+\frac{\pi }{3})+4r\sin (\frac{u}{3}-\frac{\pi }{6})}{1+r^2-2r\cos (u)}}, \quad \frac{\pi }{2}<u\le \min \left\{ \frac{3\theta }{2}-\pi ,\pi \right\} \\&\sqrt{\frac{1+r^2+2r\cos (2\theta -u)+4r\cos (u-\theta )}{1+r^2-2r\cos (u)}}, \quad \frac{3\theta }{2}-\pi<u\le \pi ,\,\theta <\frac{4\pi }{3} \end{aligned}$$

are increasing with respect to u and the inequalities

$$\begin{aligned}&\frac{\sqrt{1+3r+r^2}}{1+r}\le \frac{\sqrt{5}}{2} \le \sqrt{2}\sin \left( \frac{\theta }{4}\right) , \text { if }\frac{4\pi }{3}\le \theta<2\pi ,\\&\sqrt{\frac{1+r^2-6r\cos (\frac{\theta }{2})}{1+r^2+2r\cos (\frac{3\theta }{2})}} \le \sqrt{\frac{1-3\cos (\frac{\theta }{2})}{1+\cos (\frac{3\theta }{2})}} \le \sqrt{2}\sin \left( \frac{\theta }{4}\right) , \text { if }\pi<\theta<\frac{4\pi }{3}\\&\frac{\sqrt{1+r^2-2r\cos (2\theta )-4r\cos (\theta )}}{1+r} \le \sqrt{\frac{1-\cos (2\theta )-2\cos (\theta )}{2}} \le \sqrt{2}\sin \left( \frac{\theta }{4}\right) ,\\&\text { if }\pi<\theta <\frac{4\pi }{3} \end{aligned}$$

hold, it follows that the quotient (3.15) is at most $\sqrt{2}\sin (\theta /4)$.

Let us assume that $0<h<\pi /2$ and that $\pi<u<\min \{\theta -\pi /2+h,\pi +2h\}$. If $\pi<\theta -\pi /2+h<\pi +2h$, then $\max \{3\pi /2-\theta ,\theta 3-\pi /2\}<h<\pi /2$ and the quotient (3.16) is

$$\begin{aligned} \frac{\sqrt{1+r^2-2r\cos (u-2h)+4r\sin (h)}}{1+r}&\le \frac{\sqrt{1+r^2-2r\sin (\theta -h)+4r\sin (h)}}{1+r}\\ \le \sqrt{\frac{1-\sin (\theta -h)+2\sin (h)}{2}}&\le \sqrt{2}\sin \left( \frac{\theta }{4}\right) . \end{aligned}$$

If $\pi <\pi +2h\le \theta -\pi /2+h$ instead, then $0<h<\theta -3\pi /2$ and

$$\begin{aligned}&\frac{\sqrt{1+r^2-2r\cos (u-2h)+4r\sin (h)}}{1+r} \le \frac{\sqrt{1+r^2+2r+4r\sin (h)}}{1+r}\\&\qquad \le \frac{\sqrt{1+r^2+2r+4r\sin (\theta -\frac{3\pi }{2})}}{1+r} \le \sqrt{1+\sin \left( \theta -\frac{3\pi }{2}\right) } \le \sqrt{2}\sin \left( \frac{\theta }{4}\right) . \end{aligned}$$

Consequently, the quotient (3.16) is less than or equal to $\sqrt{2}\sin (\theta /4)$.

If $h\ge \pi /2$ and $\pi <u\le \min \{\theta ,\pi +2h\}$, then $0<u-2h\le \min \{\theta -2h,\pi \}\le \theta -\pi$, and the quotient (3.17) is

$$\begin{aligned}&\frac{\sqrt{1+r^2-2r\cos (u-2h)+4r}}{1+r} \le \frac{\sqrt{1+r^2-2r\cos (\theta -\pi )+4r}}{1+r}\\&\quad =\frac{\sqrt{1+r^2+2r(2+\cos (\theta ))}}{1+r} \le \sqrt{\frac{3+\cos (\theta ))}{2}} \le \sqrt{2}\sin \left( \frac{\theta }{4}\right) . \end{aligned}$$

Denote now $v=k-h$ so that

$$\begin{aligned} -\cos (k-h)+2\sin (h)\sin (\theta -k) =-\cos (v)+2\sin (h)\sin (\theta -v-h). \end{aligned}$$

The bounds $h\le \pi /2$, $\max \{\theta -\pi /2,\pi -h\}\le k<\min \{\theta -h,\pi +h\}$ can be now written as $\theta -\pi<v<\pi$ and $\max \{\theta -\pi /2-v,\pi /2-v/2\}\le h\le \theta /2-v/2$. By differentiation,

$$\begin{aligned}&\frac{d}{dh}(\sin (h)\sin (\theta -v-h)){=}\sin (\theta -v-2h){\ge }0\\ \Rightarrow \quad&\qquad \sin (h)\sin (\theta -v-h) {\le }\sin ^2\left( \frac{\theta }{2}{-}\frac{v}{2}\right) \end{aligned}$$

and

$$\begin{aligned}&\frac{d}{dv}\left( -\cos (v)+2\sin ^2\left( \frac{\theta }{2}-\frac{v}{2}\right) \right) =\sin (v)-\sin (\theta -v)\ge 0 \quad \Leftrightarrow \quad v\ge \frac{\theta }{2}\\&\qquad \Rightarrow -\cos (v)+2\sin ^2\left( \frac{\theta }{2}-\frac{v}{2}\right) \le \cos \left( \frac{\theta }{2}\right) +2\sin ^2\left( \frac{\theta }{4}\right) =1-2\cos \left( \frac{\theta }{2}\right) . \end{aligned}$$

It follows that the quotient (3.18) fulfills

$$\begin{aligned}&\frac{\sqrt{1+r^2-2r\cos (k-h)+4r\sin (h)\sin (\theta -k)}}{1+r} \le \frac{\sqrt{1+r^2+2r(1-2\cos (\frac{\theta }{2}))}}{1+r}\\&\qquad \le \sqrt{1-\cos \left( \frac{\theta }{2}\right) } =\sqrt{2}\sin \left( \frac{\theta }{4}\right) . \end{aligned}$$

Furthermore, we can see that the inequality in the theorem cannot have a better constant by considering the quotient (3.18) when $r=1$, $h=\theta /4$ and $k\rightarrow 3\theta /4^-$.

By denoting $u=h+k$, the quotient (3.19) can be written as

$$\begin{aligned} \sqrt{\frac{1+r^2-2r\cos (u-2h)+4r\sin (h)\sin (\theta -u+h)}{1+r^2-2r\cos (u)}}, \end{aligned}$$

where $\pi<\theta <3\pi /2$, $\theta -\pi /2<u<\pi$ and $0<h<u-\theta +\pi /2$. With the same differentiation as in (3.12), we can see that

$$\begin{aligned} \frac{d}{dh}(-\cos (u-2h)+2\sin (h)\sin (\theta -u+h))=0 \quad \Leftrightarrow \quad h=\frac{u}{2}-\frac{\theta }{4} \end{aligned}$$

but, unlike in (3.12), this value of h is the location of a maximum and it is not always included in the values of $h\in (0,u-\theta +\pi /2)$. Consequently, to maximize the quotient (3.19) with respect to h, we need to choose $h=\min \{u/2-\theta /4,u-\theta +\pi /2\}$. If $\pi <\theta \le 4\pi /3$ and $3\theta /2-\pi \le u\le \pi$, then $u/2-\theta /4\le u-\theta +\pi /2$ and the quotient (3.19) is majorized by

$$\begin{aligned}&\sqrt{\frac{1+r^2-2r\cos (\frac{\theta }{2})+4r\sin (\frac{u}{2}-\frac{\theta }{4})\sin (\frac{3\theta }{4}-\frac{u}{2})}{1+r^2-2r\cos (u)}}\\&\le \frac{\sqrt{1+r^2-2r\cos (\frac{\theta }{2})-4r\cos (\frac{\theta }{4})\cos (\frac{3\theta }{4})}}{1+r}\\&\le \sqrt{\frac{1-\cos (\frac{\theta }{2})-2\cos (\frac{\theta }{4})\cos \left( \frac{3\theta }{4}\right) }{2}} \le \sqrt{2}\sin \left( \frac{\theta }{4}\right) . \end{aligned}$$

If $\pi<\theta <3\pi /2$ and $\theta -\pi /2<u<\pi$ still but we choose $h=u-\theta +\pi /2$ instead, then the quotient (3.19) is

$$\begin{aligned}&\sqrt{\frac{1+r^2+2r\cos (2\theta -u)+4r\cos (u-\theta )}{1+r^2-2r\cos (u)}} \le \frac{\sqrt{1+r^2-2r\cos (2\theta )-4r\cos (\theta )}}{1+r}\\&\qquad \le \sqrt{\frac{1-\cos (2\theta )-2\cos (\theta )}{2}} \le \sqrt{2}\sin \left( \frac{\theta }{4}\right) . \end{aligned}$$

Thus, the value of the quotient (3.19) is at most $\sqrt{2}\sin (\theta /4)$.

Finally, for $0<h<(\theta -\pi )/$ and $\pi +h<k<\theta$, the quotient (3.20) fulfills

$$\begin{aligned} \frac{1}{p_{S_\theta }(x,y)}&{=}\sqrt{1+\frac{4d_{S_\theta }(x)d_{S_\theta }(y)}{|x-y|^2}} {=}\sqrt{1+\frac{4r\sin (h)\sin (\theta -k)}{1+r^2-2r\cos (k-h)}} {\le }\sqrt{1+\cos ^2\left( \frac{\theta }{2}\right) }\\&\le \sqrt{2}\sin \left( \frac{\theta }{4}\right) , \end{aligned}$$

so our proof is complete. $\square$

Theorem 3.23

For a fixed angle $\theta \in (0,2\pi )$, the following inequalities hold:

• (1) $j^*_{S_\theta }(x,y)\le p_{S_\theta }(x,y)\le \sqrt{2}j^*_{S_\theta }(x,y)$ if $\theta \in (0,2\pi )$,

• (2) $j^*_{S_\theta }(x,y)\le s_{S_\theta }(x,y)\le \sqrt{2}j^*_{S_\theta }(x,y)$ if $\theta \in (0,\pi ]$,

• (3) $j^*_{S_\theta }(x,y)\le s_{S_\theta }(x,y)\le 2\sin (\theta /4)j^*_{S_\theta }(x,y)$ if $\theta \in (\pi ,2\pi )$,

• (4) $(\sqrt{2}\cos (\theta /4))^{-1}p_{S_\theta }(x,y)\le s_{S_\theta }(x,y)\le p_{S_\theta }(x,y)$ if $\theta \in (0,\pi ]$,

• (5) $p_{S_\theta }(x,y)\le s_{S_\theta }(x,y)\le \sqrt{2}\sin (\theta /4)p_{S_\theta }(x,y)$ if $\theta \in (\pi ,2\pi )$.

Furthermore, the constants are sharp in each case.

Proof

Inequality (1) and its sharpness follow from Theorem 2.1 and Lemmas 3.1 and 3.2. Inequality (2) holds by Theorems 2.3 and its sharpness follows from Lemma 3.1 and the fact that, for $k=\sin (\min \{\theta /2,\pi /4\})$, $x=1+ki$ and $y=1+2k+ki$, the equality $s_{S_\theta }(x,y)=\sqrt{2}j^*_{S_\theta }(x,y)$ holds. By Theorem 2.2, Lemma 3.1 and Theorem 3.4, the inequality (3) holds and is sharp. The inequality (4) and its sharpness follow from Theorem 3.8, Lemma 3.1 and Theorem 3.9. Finally, the inequality (5) holds and is sharp by Theorems 3.13 and 3.22. $\square$

In the limiting case, where $\theta \rightarrow 0^+$, we obtain the following results for the strip domain $S_0$.

Theorem 3.24

The following inequalities hold for all $x,y\in S_0$:

• (1) $j^*_{S_0}(x,y)\le p_{S_0}(x,y)\le \sqrt{2}j^*_{S_0}(x,y)$,

• (2) $j^*_{S_0}(x,y)\le s_{S_0}(x,y)\le \sqrt{2}j^*_{S_0}(x,y)$,

• (3) $p_{S_0}(x,y)/\sqrt{2}\le s_{S_0}(x,y)\le p_{S_0}(x,y)$.

Furthermore, in each case the constants are sharp.

Proof

The inequality (1) and its sharpness follow from Theorem 2.1 and Lemmas 3.1 and 3.2. The inequalities (2) and (3) hold by Theorems 2.3, 3.6 and 3.8. They are sharp, too: For $x=1+i$ and $y=3+i$, $s_{S_0}(x,y)=p_{S_0}(x,y)=\sqrt{2}j^*_{S_0}(x,y)$ and, for $x=(\pi /4)i$ and $y=(3\pi /4)i$, $s_{S_0}(x,y)=j^*_{S_0}(x,y)=p_{S_0}(x,y)/\sqrt{2}$. $\square$

4 Hyperbolic Metric in a Sector

The main result of this section is Corollary 4.9 which compares the triangular ratio metric and the hyperbolic metric of a sector domain. To prove it, we construct a conformal self-map of the sector, mapping two points in a general position to a pair of points, symmetric with respect to the bisector of the sector angle. Because conformal maps preserve the hyperbolic distance, under this mapping the hyperbolic distance remains invariant whereas the triangular ratio distance may change. This enables us to reduce the comparison of these two metrics to the case where the points are symmetric with respect to the bisector.

Proposition 4.1

Let $x,y\in \mathbb {H}^2$ be two distinct points, let L(x, y) be the line through them, and let the angle of intersection between L(x, y) and the real axis be $\alpha$ and suppose that $\alpha \in (0,\pi /2)$. Then there are two circles $S^1(c_1,r_1)$ and $S^1(c_2,r_2)$, centered at the real axis and orthogonal to each other, such that $x,y\in S^1(c_1,r_1)$ and $c_2=L(x,y)\cap \mathbb {R}$.

Proof

First, fix $\beta =\pi /2+\arg (x-y)$ so that $[x,y]\perp [0,e^{\beta i}]$. Choose now

$$\begin{aligned} c_1=L(0,1)\cap L\left( \frac{x+y}{2},\frac{x+y}{2}+e^{\beta i}\right) ,\quad c_2=L(0,1)\cap L(x,y),\quad r_1=|x-c_1|. \end{aligned}$$

Let $r_2$ be such that $r_1^2+r_2^2=(c_1-c_2)^2$, so that the two circles are orthogonal. $\square$

Lemma 4.2

For given two distinct points $x\,, y \in \mathbb {H}^2$, there exists a Möbius transformation $g:\mathbb {H}^2\rightarrow \mathbb {H}^2$ such that $|g(x)|=|g(y)| =1$ and $\mathrm{Im}(g(x)) = \mathrm{Im}(g(y))\,.$

• (1) If $\mathrm{Im}(x) = \mathrm{Im}(y)\,,$ then $g(z)=(z-a)/r$ where $a= \mathrm{Re}((x+y)/2)$ and $r =|x-a|\,.$

• (2) If $\mathrm{Re}(x) = \mathrm{Re}(y) =a\,$ and $r=\sqrt{\mathrm{Im}(x) \mathrm{Im}(y)}$, then g is the Möbius transformation fulfilling $g(a-r)=0$, $g(a)=1$ and $g(a+r) =\infty$.

• (3) In the remaining case, the angle $\alpha =\measuredangle (L(x,y),\mathbb {R})$ belongs to $(0,\pi /2)$. Let $S^1(c_1,r_1)$ and $S^1(c_2,r_2)$ be as in Proposition 4.1. Then g is determined by $g(B^2(c_1,r_1)\cap \mathbb {H}^2)=\mathbb {B}^2\cap \mathbb {H}^2\,,$ $g(c_1-r_1)=-1$, $g(c_1+r_1)=1$ and $g(S^1(c_2,r_2)\cap \mathbb {H}^2)=\{yi\text { }|\text { }y>0\}$.

Proof

• (1) This case is obvious.

• (2) Since $g(S^1(a,r))$ is the imaginary axis, $g(\{z\text { }|\text { }\mathrm{Re}(z)=a\})=S^1(0,1)$ and, because $S^1(a,r)$ passes through the hyperbolic midpoint of the segment J[x, y] [7, pp. 52-53], it follows that the required conditions hold.

• (3) There are two possible cases. If $c_1-r_1<c_2-r_2<c_1+r_1$, the transformation g fulfills $g(u)=0$ for $u=c_2-r_2$ and is given by

  $$\begin{aligned} g(z)=\frac{r_1(z+r_2-c_2)}{(c_1+r_2-c_2)z+r_1^2+c_1c_2-c_1^2-c_1r_2}. \end{aligned}$$

  (4.3)

  See Fig. 3. Otherwise $c_1-r_1<c_2+r_2<c_1+r_1$, g is given by the formula (4.3), substituting $r_2$ with $-r_2$, and it holds that $g(c_2+r_2)=0$. $\square$

Fig. 3

Circles $S^1(c_1,r_1)$ and $S^1(c_2,r_2)$ before and after the transformation g of Lemma 4.2

Remark 4.4

The proof of Lemma 4.2 shows that the circle $S^1(c_2,r_2)$ bisects the hyperbolic segment J[x, y] joining x and y in $\mathbb {H}^2$.

Lemma 4.5

For all $\theta \in (0,2\pi )$ and $x,y\in S_\theta$, there exists a conformal mapping $f:S_\theta \rightarrow S_\theta$ such that $f(x)=e^{(1-k)\theta i/2}$ and $f(y)=e^{(1+k)\theta i/2}$ for some $k\in (0,1)$. Furthermore,

$$\begin{aligned} \inf _{0<k<1}Q(f(x),f(y))\le Q(x,y)\equiv \frac{\mathrm{th}\left( \frac{\rho _{S_\theta }(x,y)}{2}\right) }{s_{S_\theta }(x,y)}\le \sup _{0<k<1}Q(f(x),f(y)). \end{aligned}$$

Proof

Let $h:S_\theta \rightarrow \mathbb {H}^2$ be the conformal map $h(z)=z^{\pi /\theta }$ for all $z\in S_\theta$. By Lemma 4.2, we find a Möbius transformation $g:\mathbb {H}^2\rightarrow \mathbb {H}^2$ such that $|g(h(x))|=|g(h(y))|=1$ and Im$(g(h(x)))=$Im(g(h(y))). It follows that the points $h^{-1}(g(h(x)))$ and $h^{-1}(g(h(y)))$ are $e^{(1-k)\theta i/2}$ and $e^{(1+k)\theta i/2}$, respectively, for some $k\in (0,1)$. Thus, we can always form a suitable conformal map $f=h^{-1}\circ g\circ h$, and the latter part of the assertion follows from the conformal invariance of the hyperbolic metric. $\square$

Theorem 4.6

For a fixed angle $\theta \in (0,\pi )$ and for all $x,y\in S_\theta$, the sharp inequality $s_{S_\theta }(x,y)\le \mathrm{th}(\rho _{S_\theta }(x,y)/2)\le (\pi /\theta )\sin (\theta /2) s_{S_\theta }(x,y)$ holds.

Proof

Consider the quotient

$$\begin{aligned} \frac{\text {th}\left( \frac{\rho _{S_\theta }(x,y)}{2}\right) }{s_{S_\theta }(x,y)}=\frac{|x^{\pi /\theta }-y^{\pi /\theta }|\inf _{z\in \partial S_\theta }(|x-z|+|z-y|)}{|x^{\pi /\theta }-\overline{(y^{\pi /\theta })}||x-y|}. \end{aligned}$$

(4.7)

By Lemma 4.5, we can choose points so that $x=e^{(1-k)\theta i/2}$ and $y=e^{(1+k)\theta i/2}$, where $k\in (0,1)$ without loss of generality. It follows that the quotient (4.7) is

$$\begin{aligned} \frac{\sin (\frac{k\pi }{2})\sin \left( \frac{\theta }{2}\right) }{\sin \left( \frac{k\theta }{2}\right) }, \end{aligned}$$

which is decreasing with respect to k. Thus, the extreme values of the quotient are

$$\begin{aligned} \lim _{k\rightarrow 1^-} \left( \frac{\sin (\frac{k\pi }{2})\sin (\frac{\theta }{2})}{\sin (\frac{k\theta }{2})}\right) =1 \quad \text {and}\quad \lim _{k\rightarrow 0^+} \left( \frac{\sin (\frac{k\pi }{2})\sin (\frac{\theta }{2})}{\sin (\frac{k\theta }{2})}\right) =\frac{\pi }{\theta }\sin \left( \frac{\theta }{2}\right) . \end{aligned}$$

$\square$

Theorem 4.8

For a fixed angle $\theta \in (\pi ,2\pi )$ and for all $x,y\in S_\theta$, the sharp inequality

$$\begin{aligned} (\pi /\theta )s_{S_\theta }(x,y)\le \mathrm{th}(\rho _{S_\theta }(x,y)/2)\le s_{S_\theta }(x,y) \end{aligned}$$

holds.

Proof

Just like in the proof of Theorem 4.6, we can fix $x=e^{(1-k)\theta i/2}$ and $y=e^{(1+k)\theta i/2}$ with $0<k<1$. The quotient (4.7) is

$$\begin{aligned} \frac{\text {th}\left( \frac{\rho _{S_\theta }(x,y)}{2}\right) }{s_{S_\theta }(x,y)}=\frac{\sin \left( \frac{k\pi }{2}\right) }{\sin \left( \frac{k\theta }{2}\right) }\quad \text {or}\quad \sin \left( \frac{k\pi }{2}\right) , \end{aligned}$$

depending on if $k<\pi /\theta$ or not. It has a minimum value

$$\begin{aligned} \lim _{k\rightarrow 0^+} \left( \frac{\sin (\frac{k\pi }{2})}{\sin (\frac{k\theta }{2})}\right) =\frac{\pi }{\theta }, \end{aligned}$$

and a maximum value $\lim _{k\rightarrow 1^-}\sin (k\pi /2)=1$. $\square$

Corollary 4.9

For a fixed angle $\theta \in (0,2\pi )$ and for all $x,y\in S_\theta$, the following results hold:

• (1) $s_{S_\theta }(x,y)\le \mathrm{th}(\rho _{S_\theta }(x,y)/2)\le (\pi /\theta )\sin (\theta /2) s_{S_\theta }(x,y)$ if $\theta \in (0,\pi )$,

• (2) $s_{S_\theta }(x,y)=\mathrm{th}(\rho _{S_\theta }(x,y)/2)$ if $\theta =\pi$,

• (3) $(\pi /\theta )s_{S_\theta }(x,y)\le \mathrm{th}(\rho _{S_\theta }(x,y)/2)\le s_{S_\theta }(x,y)$ if $\theta \in (\pi ,2\pi )$.

Furthermore, these bounds are also sharp.

Proof

Follows from Theorems 4.6 and 4.8, and from [4,  Rmk. 2.9 p. 687]. $\square$

Corollary 4.10

For a fixed angle $\theta \in (0,2\pi )$ and for all $x,y\in S_\theta$, the following results hold:

• (1) $j^*_{S_\theta }(x,y)\le \mathrm{th}(\rho _{S_\theta }(x,y)/2)\le \sqrt{2}(\pi /\theta )\sin (\theta /2) j^*_{S_\theta }(x,y)$ if $\theta \in (0,\pi )$,

• (2) $j^*_{S_\theta }(x,y)\le \mathrm{th}(\rho _{S_\theta }(x,y)/2)\le \sqrt{2}j^*_{S_\theta }(x,y)$ if $\theta =\pi$,

• (3) $(\pi /\theta )j^*_{S_\theta }(x,y){\le } \mathrm{th}(\rho _{S_\theta }(x,y)/2){\le }2\sin (\theta /4) j^*_{S_\theta }(x,y)$ if $\theta {\in }(\pi ,2\pi )$.

Proof

Follows from Theorem 3.23 and Corollary 4.9. $\square$

Corollary 4.11

For a fixed angle $\theta \in (0,2\pi )$ and for all $x,y\in S_\theta$, the following results hold:

• (1) $p_{S_\theta }(x,y)/(\sqrt{2}\cos (\theta /4))\le \mathrm{th}(\rho _{S_\theta }(x,y)/2)\le (\pi /\theta )\sin (\theta /2) p_{S_\theta }(x,y)$ if $\theta \in (0,\pi )$,

• (2) $p_{S_\theta }(x,y)=\mathrm{th}(\rho _{S_\theta }(x,y)/2)$ if $\theta =\pi$,

• (3) $(\pi /\theta )p_{S_\theta }(x,y)\le \mathrm{th}(\rho _{S_\theta }(x,y)/2)\le \sqrt{2}\sin (\theta /4) p_{S_\theta }(x,y)$ if $\theta \in (\pi ,2\pi )$.

Proof

Follows from Theorem 3.23, Corollary 4.9 and [4,  Rmk. 2.9 p. 687]. $\square$

Theorem 4.12

For all $x,y\in S_0$, the sharp inequality

$$\begin{aligned} s_{S_0}(x,y)\le \mathrm{th}\left( \frac{\rho _{S_0}(x,y)}{2}\right) \le \frac{\pi }{2}s_{S_0}(x,y) \end{aligned}$$

holds.

Proof

First, note that there is a conformal mapping $h:S_0\rightarrow \mathbb {H}^2$, $h(z)=e^z$. By using the Möbius transformation g of Lemma 4.2, we can create a conformal mapping $f=h^{-1}\circ g\circ h:S_0\rightarrow S_0$ such that $f(x)=(1-k)\pi i/2$ and $f(y)=(1+k)\pi i/2$ for some $k\in (0,1)$. Just like in the proof of Lemma 4.5, it follows that

$$\begin{aligned} \inf _{0<k<1}Q(f(x),f(y))\le Q(x,y)\equiv \frac{\text {th}\left( \frac{\rho _{S_0}(x,y)}{2}\right) }{s_{S_0}(x,y)}\le \sup _{0<k<1}Q(f(x),f(y)). \end{aligned}$$

Consider now the quotient

$$\begin{aligned} Q(f(x),f(y))=\frac{\text {th}\left( \rho _{S_0}(f(x),\frac{f(y))}{2}\right) }{s_{S_0}(f(x),f(y))}. \end{aligned}$$

(4.13)

Clearly, $s_{S_0}(f(x),f(y))=s_{S_0}((1-k)\pi i/2,(1+k)\pi i/2)=k$. Furthermore,

$$\begin{aligned} \text {th}\left( \frac{\rho _{S_0}(f(x),f(y))}{2}\right) = \text {th}\left( \frac{\rho _{\mathbb {H}^2}(h(f(x)),h(f(y)))}{2}\right) = \sin \left( \frac{k\pi }{2}\right) . \end{aligned}$$

The quotient on the right hand side of (4.13) is therefore $\sin (k\pi /2)/k$. By differentiation, it can be shown that this result is decreasing with regards to k, so its minimum value is $\lim _{k\rightarrow 1^-}(\sin (k\pi /2)/k)=1$ and its maximum value $\lim _{k\rightarrow 0^+}(\sin (k\pi /2)/k)=\pi /2$. $\square$

Corollary 4.14

For all $x,y\in S_0$, the following inequalities hold:

• (1) $j^*_{S_0}(x,y)\le \mathrm{th}(\rho _{S_0}(x,y)/2)\le (\pi /\sqrt{2})j^*_{S_0}(x,y)$,

• (2) $p_{S_0}(x,y)/\sqrt{2}\le \mathrm{th}(\rho _{S_0}(x,y)/2)\le (\pi /2)p_{S_0}(x,y)$.

Proof

Follows from Theorems 3.24(2), 3.24(3) and 4.12. $\square$

Remark 4.15

The inequalities of Theorem 4.12 and Corollary 4.14 are the same as the inequalities of Corollaries 4.9, 4.10 and 4.11 when $\theta \rightarrow 0^+$.

5 Triangular Ratio Metric in Quasiconformal Mappings

The main result of this section and the whole paper is Corollary 5.11. First, we introduce a general result related to the triangular ratio metric under quasiconformal mappings and then we develop it further with the inequalities of Corollary 4.9. At the end of this section, we also consider the triangular ratio metric under a conformal mapping between sectors. The behaviour of the triangular ratio metric under Möbius transformations and quasiconformal mappings has been studied earlier; see [4,  Thms. 1.2 & 1.3 p. 684; Cor. 3.30 & Thm. 3.31 p. 697], [8,  Thm. 4.7 p. 1144; Thm. 4.9 p. 1146].

For the definition and basic properties of K-quasiconformal homeomorphisms, the reader is referred to [18,  Ch. 2]. We start with two preliminary results.

Lemma 5.1

For all $t\in (0,1)$ and $d\ge 1$, the inequality $\mathrm{th}(d\mathrm{arth}(t))\le dt$ holds.

Proof

For all $t>0$, $\text {th}(t)/t$ is decreasing. This is because, by differentiation,

$$\begin{aligned} \frac{d}{dt}\left( \frac{\text {th}(t)}{t}\right) =\frac{1}{t\text {ch}^2(t)}-\frac{\text {th}(t)}{t^2} =\frac{1}{t\text {ch}(t)}\left( \frac{1}{\text {ch}(t)}-\frac{\text {sh}(t)}{t}\right) \le 0\quad \Leftrightarrow \quad t\le \text {sh}(t)\text {ch}(t), \end{aligned}$$

which clearly holds since $\text {ch}(t)\ge \text {sh}(t)\ge t$ for $t>0$. It follows from this that

$$\begin{aligned} \frac{\text {th}(d\text {arth}(t))}{d\text {arth}(t)}\le \frac{\text {th}(\text {arth}(t))}{\text {arth}(t)}= \frac{t}{\text {arth}(t)} \quad \Leftrightarrow \quad \text {th}(d\text {arth}(t))\le dt. \end{aligned}$$

$\square$

Lemma 5.2

For all $t\in (0,1)$ and $c\ge K\ge 1$,

$$\begin{aligned} w(t)\le \max \{1,d^{1/K}\}t^{1/K}, \quad w(t)\equiv \mathrm{th}\left( \frac{c}{2}(2\mathrm{arth}(t))^{1/K}\right) , \end{aligned}$$

where $d=2(c /2)^K$.

Proof

The function $h(\alpha )=\text {th}(u^\alpha )^{1/\alpha }$, where $u>0$ is fixed, is increasing for $\alpha >0$ because, by differentiation,

$$\begin{aligned} \frac{d}{d\alpha }\log (h(\alpha ))&= \frac{u^\alpha \log (u)}{\alpha ^2\text {th}(u^\alpha )\text {ch}^2(u^\alpha )} -\frac{\log (\text {th}(u^\alpha ))}{\alpha ^3} -\frac{\log (\text {th}(u^\alpha )^{1/\alpha })}{\alpha ^2}\\&=\frac{u^\alpha \log (u))}{\alpha \text {th}(u^\alpha )\text {ch}^2(u^\alpha )} -\frac{\log (\text {th}(u^\alpha ))}{\alpha ^2}>0. \end{aligned}$$

It follows that

$$\begin{aligned} w(t)^K=\text {th}((d\text {arth}(t))^{1/K})^K\le \text {th}(d\text {arth}(t)) \quad \Rightarrow \quad w(t)\le \text {th}(d\text {arth}(t))^{1/K}\equiv A. \end{aligned}$$

Clearly, $A\le \text {th}(\text {arth}(t))^{1/K}=t^{1/K}$ if $d\in (0,1]$. If $d>1$ instead, by Lemma 5.1, $A\le d^{1/K}t^{1/K}$. $\square$

Theorem 5.3

The function

$$\begin{aligned} H(t)=\mathrm{th}\left( \frac{C}{2}\max \left\{ 2\mathrm{arth}(t),(2\mathrm{arth}(t))^{1/K}\right\} \right) , \end{aligned}$$

where $t\in (0,1)$, $K\ge 1$ and $C\ge 1$, fulfills $H(t)\le Ct^{1/K}$ and is thus Hölder continuous with exponent $1/K$.

Proof

Observe first that

$$\begin{aligned} 2\text {arth}(t)\ge (2\text {arth}(t))^{1/K} \quad \Leftrightarrow \quad 2\text {arth}(t)\ge 1 \quad \Leftrightarrow \quad t\ge \text {th}\left( \frac{1}{2}\right) =\frac{e-1}{e+1}\equiv t_1. \end{aligned}$$

If $t\in (0,t_1)$, by Lemma 5.2,

$$\begin{aligned} H(t)&=\text {th}\left( \frac{C}{2}(2\text {arth}(t))^{1/K}\right) \le \max \{1,\frac{C}{2^{1-1/K}}\}t^{1/K} \le Ct^{1/K}. \end{aligned}$$

If $t\in [t_1,1)$ instead, by Lemma 5.1,

$$\begin{aligned} H(t)=\text {th}(C\text {arth}(t))\le Ct\le Ct^{1/K}. \end{aligned}$$

Thus, the inequality $H(t)\le Ct^{1/K}$ holds for all $t\in (0,1)$. $\square$

In order to understand the following results, consider the definition of a quasiregular mapping.

5.4

K-quasiregular mappings. [7,  pp. 288–289] Choose a domain $G\subset \mathbb {R}^n$, and suppose that a function $f:G\rightarrow \mathbb {R}^n$ is $\mathrm{ACL}^n$, which is defined, for instance, in [7, p. 150]. Denote the Jacobian determinant of f at point $x\in G$ by $J_f(x)$. The function f is called quasiregular, if there exists a constant $K\ge 1$ such that f fulfills

$$\begin{aligned} |f'(x)|^n\le KJ_f(x),\quad |f'(x)|=\max _{|h|=1}|f'(x)h| \end{aligned}$$

(5.5)

a.e in G. Furthermore, the smallest constant $K\ge 1$ for which the inequality (5.5) holds, is the outer dilatation of f, denoted by $K_O(f)$. Similarly, the inner dilatation of f, denoted by $K_I(f)$, is the smallest constant $K\ge 1$ such that the inequality

$$\begin{aligned} J_f(x)\le K\ell (f'(x))^n,\quad \ell (f'(x))=\min _{|h|=1}|f'(x)h|, \end{aligned}$$

holds a.e in G. The function f is now K-quasiregular, if $\max \{K_I(f),K_O(f)\}\le K$.

Define a decreasing homeomorphism $\gamma _2:(1,\infty )\rightarrow (0,\infty )$ with the following formulas [7,  (7.18), p. 122]

$$\begin{aligned} \gamma _2\left( \frac{1}{r}\right) =\frac{2\pi }{\mu (r)},\quad \mu (r)=\frac{\pi }{2}\frac{\mathcal {K}(\sqrt{1-r^2})}{\mathcal {K}(r)},\quad \mathcal {K}(r)=\int ^1_0 \frac{dx}{\sqrt{(1-x^2)(1-r^2x^2)}}. \end{aligned}$$

Define then an increasing homeomorphism $\varphi _{K,2}:[0,1]\rightarrow [0,1]$, [7, (9.13), p. 167]

$$\begin{aligned} \varphi _{K,2}(r)=\frac{1}{\gamma _2^{-1}(K\gamma _2(\frac{1}{r}))},\quad 0<r<1,\,K>0. \end{aligned}$$

Now, we can denote

$$\begin{aligned} c(K)=2\mathrm{arth}\left( \varphi _{K,2}\left( \mathrm{th}\left( \frac{1}{2}\right) \right) \right) \end{aligned}$$

(5.6)

as in [7,  Thm. 16.39, p. 313].

Remark 5.7

By [7,  Thm. 16.39, p. 313],

$$\begin{aligned} K\le c(K)\le (K-1)\log \left( 2\left( 1+\sqrt{1-\frac{1}{e^2}}\right) \right) +K \end{aligned}$$

and, in particular, $c(K)\rightarrow 1$, when $K\rightarrow 1$.

The main results of this section are based on the following recent form of the quasiregular Schwarz lemma:

Theorem 5.8

[7,  Thm. 16.39, p. 313], [19] If $f:\mathbb {B}^2\rightarrow \mathbb {B}^2$ is a K-quasiregular and non-constant mapping, then

$$\begin{aligned} \rho _{\mathbb {B}^2}(f(x),f(y))\le c(K)\max \{\rho _{\mathbb {B}^2}(x,y),\rho _{\mathbb {B}^2}(x,y)^{1/K}\} \end{aligned}$$

for all $x,y\in \mathbb {B}^2$ where c(K) is as in (5.6).

Note that Theorem 5.8 trivially holds also if we replace the unit disks by two simply connected planar domains $G_1,G_2\subsetneq \mathbb {R}^2$. Namely, by Riemann’s mapping theorem, there exists a conformal mapping $h:G\rightarrow \mathbb {B}^2=h(G)$ for any simply connected planar domain G and the inverse mapping of any conformal mapping is conformal, too. Since the hyperbolic metric is conformally invariant, using these mappings to map some simply connected planar domain onto the unit disk and vice versa does not change the hyperbolic distances between the points. Furthermore, Theorem 5.8 holds for quasiconformal mappings, too, because the sense-preserving K-quasiconformal mappings form a subclass of K-quasiregular mappings [7,  Rmk. 15.30 & (15.6), p. 289], [18,  p. VI] and, for every sense-reversing K-quasiconformal mapping f, the function composition $\sigma \circ f$ of f and any reflection $\sigma$ is a sense-preserving K-quasiconformal mapping and the hyperbolic distances do not change under reflection $\sigma$.

Consequently, Theorem 5.8 can be written as:

Theorem 5.9

Let $G_1$ and $G_2$ be simply-connected domains in $\mathbb {R}^2$ and $f:G_1\rightarrow G_2=f(G_1)$ a $K-$quasiconformal homeomorphism. Then

$$\begin{aligned} \rho _{G_2}(f(x),f(y))\le c(K)\max \{\rho _{G_1}(x,y),\rho _{G_1}(x,y)^{1/K}\} \end{aligned}$$

for all $x,y\in G_1$.

Corollary 5.10

Let $G_1$ and $G_2$ be simply-connected domains in $\mathbb {R}^2$ and $f:G_1\rightarrow G_2=f(G_1)$ a K-quasiconformal homeomorphism. Suppose that there exist $A,B\in (0,\infty )$ so that $As_{G_2}(u,v)\le \mathrm{th}(\rho _{G_2}(u,v)/2)$ for all $u,v\in G_2$ and $\mathrm{th}(\rho _{G_1}(x,y)/2)\le Bs_{G_1}(x,y)$ for all $x,y\in G_1$. Then, for all $x,y\in G_1$,

$$\begin{aligned} s_{G_2}(f(x),f(y))\le \frac{c(K)B^{1/K}}{A}s_{G_1}(x,y)^{1/K}. \end{aligned}$$

Proof

By Theorem 5.9,

$$\begin{aligned} s_{G_2}(f(x),f(y))&\le \frac{1}{A}\text {th}\left( \frac{\rho _{G_2}(f(x),f(y))}{2}\right) \le \frac{1}{A}\text {th}\left( \frac{c(K)}{2}\max \{\rho _{G_1}(x,y),\rho _{G_1}(x,y)^{1/K}\}\right) \\&\le \frac{1}{A}\text {th}\left( \frac{c(K)}{2}\max \{2\text {arth}(Bs_{G_1}(x,y)),(2\text {arth}(Bs_{G_1}(x,y)))^{1/K}\}\right) , \end{aligned}$$

and, applying Theorem 5.3 with $C=c(K)$, we will have

$$\begin{aligned} s_{G_2}(f(x),f(y))\le \frac{1}{A}H(Bs_{G_1}(x,y))\le \frac{c(K)B^{1/K}}{A}s_{G_1}(x,y)^{1/K}. \end{aligned}$$

$\square$

Corollary 5.11

If $\alpha ,\beta \in (0,2\pi )$ and $f:S_\alpha \rightarrow S_\beta =f(S_\alpha )$ is a K-quasiconformal homeomorphism, the following inequalities hold for all $x,y\in S_\alpha$.

$$\begin{aligned}&(1) \quad \frac{\beta }{c(K)^K\pi \sin (\frac{\beta }{2})}s_{S_\alpha }(x,y)^K\le s_{S_\beta }(f(x),f(y))\le c(K)\left( \frac{\pi }{\alpha }\sin \left( \frac{\alpha }{2}\right) \right) ^{1/K}s_{S_\alpha }(x,y)^{1/K}\\&\quad \quad \text {if }\alpha ,\beta \in (0,\pi ],\\&(2) \quad \frac{1}{c(K)^K}s_{S_\alpha }(x,y)^K\le s_{S_\beta }(f(x),f(y))\le \frac{c(K)\beta }{\pi }\left( \frac{\pi }{\alpha }\sin \left( \frac{\alpha }{2}\right) \right) ^{1/K}s_{S_\alpha }(x,y)^{1/K}\\&\quad \quad \text {if }\alpha \in (0,\pi )\text { and }\beta \in (\pi ,2\pi ),\\&(3)\quad \left( \frac{\pi }{c(K)\alpha }\right) ^Ks_{S_\alpha }(x,y)^K\le s_{S_\beta }(f(x),f(y))\le \frac{c(K)\beta }{\pi }s_{S_\alpha }(x,y)^{1/K}\\&\quad \quad \text {if }\alpha ,\beta \in [\pi ,2\pi ). \end{aligned}$$

Proof

Follows from Corollaries 4.9 and 5.10, and the fact that the inverse mapping $f^{-1}$ of a K-quasiconformal mapping f is another K-quasiconformal mapping with the same constant c(K). $\square$

Corollary 5.12

If $f:\mathbb {H}^2\rightarrow \mathbb {H}^2=f(\mathbb {H}^2)$ is a K-quasiconformal homeomorphism,

$$\begin{aligned} \frac{1}{c(K)^K}s_{\mathbb {H}^2}(x,y)^K\le s_{\mathbb {H}^2}(f(x),f(y))\le c(K)s_{\mathbb {H}^2}(x,y)^{1/K}. \end{aligned}$$

Proof

Follows from Corollary 5.11, or directly from Corollary 5.10 and the fact that, in the upper half-plane, th$(\rho _{\mathbb {H}^2}(x,y)/2)=s_{\mathbb {H}^2}(x,y)$. $\square$

Remark 5.13

Note that the inequality in Corollary 5.12 reduces to an identity if $K=1$.

Corollary 5.14

If $\theta \in (0,2\pi )$ and $f:S_0\rightarrow S_\theta =f(S_0)$ is a K-quasiconformal homeomorphism, the following inequalities hold for all $x,y\in S_0$.

$$\begin{aligned}&(1)\quad \frac{\theta }{c(K)^K\pi \sin (\frac{\theta }{2})}s_{S_0}(x,y)^K\le s_{S_\theta }(f(x),f(y))\le c(K)\left( \frac{\pi }{2}\right) ^{1/K}s_{S_0}(x,y)^{1/K}\\&\quad \quad \text {if }\theta \in (0,\pi ],\\&(2)\quad \frac{1}{c(K)^K}s_{S_0}(x,y)^K\le s_{S_\theta }(f(x),f(y))\le \frac{c(K)\theta }{\pi }\left( \frac{\pi }{2}\right) ^{1/K}s_{S_0}(x,y)^{1/K}\text { if }\theta \in [\pi ,2\pi ). \end{aligned}$$

Proof

Follows from Corollary 4.9, Theorem 4.12 and Corollary 5.10. $\square$

Lemma 5.15

If $\alpha ,\beta \in (0,\pi ]$ and $f:S_\alpha \rightarrow S_\beta$, $f(z)=z^{(\beta /\alpha )}$, then for all $x,y\in S_\alpha$

$$\begin{aligned}&s_{S_\alpha }(x,y)\le s_{S_\beta }(f(x),f(y))\le \frac{\beta \sin (\frac{\alpha }{2})}{\alpha \sin (\frac{\beta }{2})}s_{S_\alpha }(x,y)\text { if }\alpha \le \beta ,\\&\frac{\beta \sin (\frac{\alpha }{2})}{\alpha \sin (\frac{\beta }{2})}s_{S_\alpha }(x,y)\le s_{S_\beta }(f(x),f(y))\le s_{S_\alpha }(x,y)\text { otherwise.} \end{aligned}$$

Furthermore, the constants here are sharp.

Proof

By symmetry, we can suppose that $\arg (x)\le \arg (y)$ and $\arg (x)\le \alpha -\arg (y)$. It follows that

$$\begin{aligned}&\inf _{z\in \partial S_\alpha }(|x-z|+|z-y|)=|\overline{x}-y|, \\&\inf _{z\in \partial S_\beta }(|f(x)-z|+|z-f(y)|)=|\overline{f(x)}-f(y)|. \end{aligned}$$

Consider now the quotient

$$\begin{aligned} \frac{s_{S_\beta }(f(x),f(y))}{s_{S_\alpha }(x,y)} =\frac{|f(x)-f(y)||\overline{x}-y|}{|\overline{f(x)}-f(y)||x-y|} =\frac{\text {th}\left( \frac{\rho _{\mathbb {H}^2}(f(x),f(y))}{2}\right) }{\text {th}\left( \frac{\rho _{\mathbb {H}^2}(x,y)}{2}\right) }. \end{aligned}$$

(5.16)

By Lemma 4.5, there exists a conformal mapping $h:S_\alpha \rightarrow S_\alpha$ such that $h(x)=e^{(1-k)\alpha i/2}$ and $h(y)=e^{(1+k)\alpha i/2}$ for some $k\in (0,1)$, and the quotient (5.16) is invariant to this transformation. Thus, we can fix $x=e^{(1-k)\alpha i/2}$ and $y=e^{(1+k)\alpha i/2}$. Now, $f(x)=e^{(1-k)\beta i/2}$ and $f(y)=e^{(1+k)\beta i/2}$, so it follows that the quotient (5.16) is

$$\begin{aligned} Q(k,\alpha ,\beta )\equiv \frac{\sin (\frac{k\beta }{2})\sin \left( \frac{\alpha }{2}\right) }{\sin \left( \frac{k\alpha }{2}\right) \sin \left( \frac{\beta }{2}\right) }. \end{aligned}$$

By differentiation, it can be proved that this quotient is monotonic with respect to k, and its extreme values are therefore

$$\begin{aligned} \lim _{k\rightarrow 0^+}Q(k,\alpha ,\beta )=\frac{\beta \sin (\frac{\alpha }{2})}{\alpha \sin (\frac{\beta }{2})} \quad \text {and}\quad \lim _{k\rightarrow 1^-}Q(k,\alpha ,\beta )=1. \end{aligned}$$

It only depends on whether $\alpha \le \beta$ or not, which one of these extreme values is the minimum and which one the maximum, so our theorem follows. $\square$