1 Introduction

Toxoplasmosis is considered to be a leading cause of death attributed to foodborne illness in the United States (CDC 2022). More than 40 million men, women, and children in the U.S. carry the Toxoplasma parasite and worldwide toxoplasmosis infection has a high prevalence (CDC 2022). Toxoplasma gondii (T. gondii) is a protozoan parasite that is the causative agent of toxoplasmosis (Attias et al. 2020; Dubey 2008). Despite the great majority of the infected people are either asymptomatic or have mild symptoms, some persons suffer from neurologic damage (Attias et al. 2020; Matta et al. 2021). Furthermore, a woman who is newly infected with Toxoplasma during pregnancy can pass the infection to her unborn child and there can be severe consequences for the unborn child, such as fetal death, child disability, diseases of the nervous system and eyes (CDC 2022; Bigna et al. 2020; Robert-Gangneux et al. 2011). Pregnant women can be infected through zoonotic transmission or foodborne transmission (CDC 2022; Dubey 2008; Dubey and Beattie 1988; Dubey 1996).Immunodeficient people can have severe consequences due to toxoplasmosis (CDC 2022; Matta et al. 2021). The life-cycle of T. gondii is complex, with more than one infective form and several transmission pathways (Attias et al. 2020; Dubey 2020).

The protozoan T. gondii is a prevalent parasite in wild and domestic animals worldwide especially in cats (Dubey 2020; Reyes-Lizano et al. 2001; Beaver et al. 1984; Markell et al. 1990). T. gondii parasites in cats have a full life cycle and in most cases do not affect the cat’s life (Attias et al. 2020; Dubey 2008). However, in few cats that are immunosuppressed clinical signs appear and the central nervous system, muscles, lungs and eyes can be affected (Hartmann et al. 2013). Oocysts are the environmentally resistant stage of the protozoan parasite T. gondii (Dubey 1995; Frenkel et al. 1970; Ndao et al. 2020). Cats can pose a risk for humans when they shed oocysts, but this only occurs once in their lifetime (Hartmann et al. 2013). It is important to mention that T. gondii can infect most species of warm-blooded animals (CDC 2022; Dubey 2008, 2020). In South America it has been found a seroprevalence in cats of \(45\%\) (Dubey et al. 2006). Other studies estimated the seroprevalence to be 35% and 59% in domestic cats and wild felids (Montazeri et al. 2020). Cats are crucial in the life cycle of T. gondii because they are the only hosts that can excrete the environmentally-resistant oocysts (Dubey et al. 2006, 2020; Attias et al. 2020). Cats shed unsporulated oocysts in their feces that are not instantaneously infectious (CDC 2022; Dubey et al. 1970; Frenkel et al. 1970; González-Parra et al. 2022). These oocysts spread and contaminate the environment (Aramini et al. 1999; Dumètre and Dardé 2003; Dubey et al. 1998; Trejos and Duarte 2010). Humans can get infected by ingestion of cysts in raw/uncooked meat and drinking contaminated water with oocysts (Aramini et al. 1999).

Intermediate hosts such as rodents become infected after ingesting soil, water or plant material contaminated with oocysts (CDC 2022; Dubey and Frenkel 1976; Dubey 2008). In Vargas-Villavicencio et al. (2016), the congenital transmission using a mouse model was studied. They also determined parasite load and vertical transmission. It has been reported that maternal–fetal transmission of T. gondii occurs in mice (Robert-Gangneux et al. 2011; Shiono et al. 2007; Darcy and Zenner 1993; Pezerico et al. 2009). Vertical transmission has been reported to occur through successive generations in mice (Rejmanek et al. 2010). Current studies suggest that vertical transmission is common in natural populations of mice (Hide 2016; Marshall et al. 2004; Murphy et al. 2008) and that mice are extremely vulnerable to the consequences of infection with T. gondii (Innes 1997).

Mathematical epidemiological models have been designed to investigate many diseases related to viruses and parasites (Bedson et al. 2021; Chowell et al. 2016; Chowell and Hyman 2016; Brauer and Castillo-Chavez 2001; Hethcote 2005) and different mathematical models have been used to investigate the dynamics of toxoplasmosis under different assumptions (Deng et al. 2021). Previous models focused in different populations such as humans, cats and mice (Ferreira et al. 2017; González-Parra et al. 2009; Arenas et al. 2010; Turner et al. 2013; Lélu et al. 2010; Mateus-Pinilla et al. 2002; Marinović et al. 2020; Trejos and Duarte 2005). In addition, few articles have investigated the effect of vaccination of cats (Arenas et al. 2010; González-Parra et al. 2022; Lélu et al. 2010; Mateus-Pinilla et al. 2002; Marinović et al. 2020; Turner et al. 2013). For instance in Mateus-Pinilla et al. (2002) a model that considers vaccination in a population of cats and swine was presented. It has been mentioned that there is a need to develop a safe and effective toxoplasmosis vaccine (Wang et al. 2019). Moreover, successful vaccination of domestic cats is one way to reduce T. gondii transmission to humans and food-producing animals (Wang et al. 2019). In Wang et al. (2019), the authors mentioned that an effective toxoplasmosis vaccine must be able to induce both humoral and cellular immune responses, directed against multiple different proteins, at different stages of the parasites life cycle. In addition, a mathematical model based on delay differential equations, but does not include the mouse population has been developed previously (González-Parra et al. 2022). However, including more hosts makes the analysis more complex.

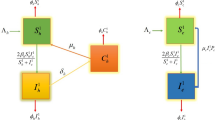
The mathematical model proposed in this work considers the transmission of the T. gondii by an effective contact between oocysts and mice (CDC 2022). In addition, the cats can get infected by contact with oocysts (Arenas et al. 2010; Deng et al. 2021; Lélu et al. 2010). The model includes vertical transmission in both the cat and mouse populations (Hide 2016; Marshall et al. 2004; Murphy et al. 2008) and also includes the vaccination of cats. The constructed model has several additional underlying hypotheses that are mentioned in the next section. The cat population is divided into three subpopulations, susceptibles S(t), infectious I(t) and vaccinated/recovered \(V_{R}(t)\). On the other hand, the mouse population is composed by only two classes; susceptibles \(S_{m}(t)\) and infectious \(I_{m}(t)\). The model does not include a recovered class for the mouse population since in the infected mice the parasite disseminate systemically, reaching tissue sites that support chronic infection including the brain, muscle, and other tissues (Bierly et al. 2008; Melchor and Ewald 2019; Remington and Krahenbuhl 1982). Moreover, for the infected mouse the parasite can remain, potentially for the host’s lifetime (Dubey et al. 1998; Webster 2007). The mathematical model considers the T. gondii oocysts that are the vector that transmits the toxoplasmosis disease. Animals can be infected by eating infected meat, by ingestion of feces from a cat that has itself recently been infected, or by transmission from mother to fetus. Cats have been shown as a major reservoir of this infection (Arenas et al. 2010; Lappin 1999; Torda 2001; Turner et al. 2013). We investigate the local and global stability of the equilibrium points of the system and we compute the basic reproductive number \({\mathcal {R}}_{0}\) to study the stability of the toxoplasmosis-free steady state. Numerical computer simulations are included to get useful insight on the dynamics of toxoplasmosis. Moreover, these simulations allow us to study the effect of control strategies.

The paper is organized as follows: In Sect. 2 we construct the mathematical model. Section 3 is devoted to analyzing the steady states and finding the basic reproduction number \({\mathcal {R}}_{0}\). In addition, we construct a Lypaunov function that allow us to prove the global stability of the disease free steady state. Section 4 contains numerical simulations of different scenarios and in Sect. 5 conclusions are presented.

2 Mathematical model

In this section, we construct the mathematical model for the transmission of toxoplasmosis in cat and mouse populations. The model considers a constant vaccination program for cats (Arenas et al. 2010; Lélu et al. 2010; Mateus-Pinilla et al. 2002; Marinović et al. 2020; Turner et al. 2013). In addition, the model includes the oocyst population since they are primarily responsible for the maintenance of T. gondii in the environment (Lappin 1999). This is crucial since the cats are the only ones known to excrete T. gondii oocysts (Arenas et al. 2010; Lappin 1999). The constructed model considers the direct contact of cats with the oocysts in the environment. Contamination of the environment by oocysts has been well documented (Dubey and Beattie 1988). As expected, the likelihood of acquisition of T. gondii infection depends on the amount of oocysts in the environment (Mateus-Pinilla et al. 2002). There are normally two sources of infection: tissue cysts from prey and oocysts in the environment (Dubey and Beattie 1988). However, infection of prey ultimately is traced indirectly to oocyst shedding by cats. The proposed model considers the assumption that the infection depends on the environmental load of oocysts, which depends on the number of infected cats during previous weeks (Arenas et al. 2010; Hill and Dubey 2002).

The constructed mathematical model is based on a system of ordinary differential equations. The model includes parameters related to vaccination rate and survival time of oocysts. The model assumes lifelong immunity after recovery from infection since even though the cats can be re-infected with Toxoplasma and shed oocysts again but the amount of shedding in future episodes is relatively insignificant (CDC 2022; Dubey 2020). We assume that the vaccine provide complete immunity to vaccinated cats, therefore we have created just one compartment for the vaccinated and the recovered cats. Vertical transmission in the cat population is considered based on several studies (Dubey et al. 1996; Powell and Lappin 2001; Sato et al. 1993) and on the fact that it has been detected lactational transmission with T. gondii (Powell and Lappin 2001; Dubey et al. 1995; Powell et al. 2001). A natural exponential decay is considered for the oocysts. The model does not consider a subpopulation of exposed oocysts, but in future works might be included since after oocysts are shed by the cats, they are not infective for about 24–48 h. Sporulated oocysts survive for long periods under most ordinary environmental conditions (Hill and Dubey 2002). In order to construct the model the following notations and hypothesis are taken:

  • The total population of cats N(t) is divided into three disjoint subpopulations: Cats who may become infected (Susceptible S(t)), cats infected by T. gondii (Infected I(t)), and cats who have been vaccinated or have immunity by recovering (Vaccinated/recovered) \(V_{R}(t)\)).

  • The total population of mice \(N_{m}(t)\) is divided into two disjoint subpopulations: Susceptible \(S_{m}(t)\) and infected \(I_{m}(t)\).

  • Oocysts O(t): Number of oocysts in the environment.

  • The birth rate is assumed equal to the cat natural death rate \(\mu \), thus the total cat population remains constant, i.e. \(\dot{N(t)}=0\).

  • A susceptible cat or mouse transits to the infected subpopulation following an effective contact with oocysts (at rate \(\beta \) and \(\beta _{m}\) respectively).

  • The period from when the oocysts are shed by the cats until they are infective is assumed null.

  • A susceptible cat transits to the vaccinated subpopulation \(V_{R}(t)\) at a rate \(\gamma \). An infected cat transits to the vaccinated/recovered subpopulation \(V_{R}(t)\) at a rate \(\alpha \).

  • The increase of oocysts O(t) at time t is proportional to the number of infected cats I(t).

  • \(\mu _{0}\) is the death or clearance rate of oocysts.

  • Vertical transmission is assumed in the subpopulations I(t) and \(I_{m}(t)\).

  • Cats not vaccinated can be re-infected with Toxoplasma in the future, but do not shed oocysts again (Dubey 2020).

  • The model assumes that the vaccine produces lifelong immunity (Freyre et al. 1993; Frenkel 1990).

  • Homogenous mixing is assumed, i.e, all the susceptible subpopulations S(t) and \(S_{m}(t)\) have the same probability to become infected.

The general developed model is a first order nonlinear system of ordinary differential equations \(SIV_{R}\) (Susceptible, Infected and Vaccinated or Recovered). After considering a constant cat population, a simple linear recruitment rate for the mice population, and vertical transmission in both populations one gets,

$$\begin{aligned} \begin{array}{crl} {\dot{S}}(t)&{}=&{}\mu V_{R}(t)-\beta S(t)O(t) - \gamma S(t),\\ {\dot{I}}(t)&{}=&{}\beta S(t)O(t) -\alpha I(t),\\ {\dot{V}}_{R}(t)&{}=&{}\alpha I(t)+\gamma S(t)-\mu V_{R}(t),\\ {\dot{O}}(t)&{}=&{}k\, I(t)-\mu _{0}O(t),\\ {\dot{S}}_{m}(t)&{}=&{} (b-\mu _{m})S_{m}-\beta _{m}\,S_{m}(t)\, O(t),\\ {\dot{I}}_{m}(t)&{}=&{} (b-\mu _{m})I_{m} +\beta _{m} S_{m}(t)\, O(t),\\ \end{array} \end{aligned}$$
(1)

where \(k>0\) is the rate of appearance of new oocysts in the environment per infected cat. The total population of cats and mice is given by \({N}(t)= S(t)+I(t)+V_{R}(t),\) and \(N_m(t)=S_m(t)+I_m(t)\) respectively. Now, using \(x=S_{m}/N(t)\), \(y=I_{m}/N(t)\), taking into account that \({\dot{S}}_{m}={\dot{x}}N_{m}+x{\dot{N}}_{m}\), \({\dot{I}}_{m}={\dot{y}}N_{m}+y{\dot{N}}_{m}\), and after simplifications replacing again x(t) by S(t) and y(t) by I(t) one gets

$$\begin{aligned} \begin{array}{crl} {\dot{S}}(t)&{}=&{}\mu V_{R}(t)-\beta S(t)O(t) - \gamma S(t),\\ {\dot{I}}(t)&{}=&{}\beta S(t)O(t) -\alpha I(t),\\ {\dot{V}}_{R}(t)&{}=&{}\alpha I(t)+\gamma S(t)-\mu V_{R}(t),\\ {\dot{O}}(t)&{}=&{}k I(t)-\mu _{0}\,O(t),\\ {\dot{S}}_{m}(t)&{}=&{} -\beta _{m}\,S_{m}(t)\, O(t),\\ {\dot{I}}_{m}(t)&{}=&{} \beta _{m}\, S_{m}(t)\, O(t). \end{array} \end{aligned}$$
(2)

Additionally, without loss of generality the total population of cats is assumed to be \({N}(t)= S(t)+I(t)+V_{R}(t)=1,\) i.e., constant and scaled. Notice, that the terms related to births (b) and deaths (\(\mu _m\)) in the mouse population disappear due to the previous scaling of the mouse population. Setting the right hand side to zero we can find the equilibrium points of system (2). Notice, that if \(O(t)=0\) we obtain that the susceptible and infected mouse populations can have any value at the equilibrium point and therefore there are infinitely many equilibrium points (Hethcote 2005). On the other hand, if \(O(t)>0\) then only one endemic equilibrium point exists. Now, taking into account the scaled populations we can reduce the model (2) to a simpler one as follows,

$$\begin{aligned} \begin{array}{crl} {\dot{S}}(t)&{}=&{}\mu (1-I(t))-\beta S(t)O(t) - (\mu +\gamma ) S(t),\\ {\dot{I}}(t)&{}=&{}\beta S(t)O(t) -\alpha I(t),\\ {\dot{O}}(t)&{}=&{}k I(t)-\mu _{0}O(t),\\ {\dot{S}}_{m}(t)&{}=&{} -\beta _{m}\,S_{m}(t)\, O(t), \end{array} \end{aligned}$$
(3)

where \(I_m(t)=1-S_m(t)\) and \(V_{R}(t)=1-S(t)-I(t)\). The initial conditions at time \(t=0\) are given by

$$\begin{aligned} S(0)>0,I(0)\ge 0, O(0) \ge 0, S_m(0)\ge 0. \end{aligned}$$
(4)

The model is depicted graphically in Fig. 1. The next section is devoted to the equilibrium and stability analysis of the mathematical model (3).

Fig. 1
figure 1

Diagram of the mathematical model (2) including cat and mouse populations. In both populations vertical transmission is considered

Full size image

3 Stability analysis of the model

In this section, the mathematical model (3) is analyzed qualitatively in order to investigate the existence and stability of its associated equilibria. First we perform local stability analysis for the disease-free equilibrium and then the global stability analysis. From the analytic theory of ordinary differential equations, it can be proven that for any set of initial data (4), there exists a unique solution, \((S(t),I(t),O(t),S_m(t))\) defined on the maximum open interval \((-T_{c},T_{c})\) with \(T_{c} > 0\) (Hale 1969; Khalil 2002; Lakshmikantham et al. 1989).

It is important from a biological point of view to prove that the solutions are positive for all \(t\ge 0\) and that them are bounded. The next theorem guarantees this fact.

Theorem 1

If the parameters of model (3) are all positive and the initial conditions given by (4) are verified, then the solutions of the model (3) given by

$$\begin{aligned} \Big (S(t),I(t),O(t),S_m(t)\Big ) \end{aligned}$$

remain positive and uniformly bounded in \([0,+\infty )\).

Proof

Since \(N(t)\le 1,\) then from the third equation of system (3), it is clear that

$$\begin{aligned} {\dot{O}}(t)&\le k -\mu _{0}O(t). \end{aligned}$$

Therefore, if \(O(0)\le \dfrac{k}{\mu _{0}}\) then \(O(t)\le \dfrac{k}{\mu _{0}}.\) On the other hand, if \(O(0)>\dfrac{k}{\mu _{0}}\) then \(O(t)<O(0).\) Let \(B_{O}=\max \left\{ \dfrac{k}{\mu _{0}},O(0)\right\} >0.\) Therefore, \(O(t)\le B_{O}\) for all \(t\le 0.\) Now, from first equation of model (3), we have that

$$\begin{aligned} {\dot{S}}(t)>\mu (1-I(t))-\beta S(t)B_{O}- (\mu +\gamma ) S(t), \end{aligned}$$

it implies that

$$\begin{aligned} S(t)\ge S(0)\exp (-B_{T}t)+\exp (-B_{T}t)\displaystyle \int _{0}^{t}\exp (B_{T}s)\mu (1-I(s))ds>0, \end{aligned}$$

for all \(t\ge 0\) and where \(B_{T}=\beta B_{O}+\mu +\gamma .\) Let’s assume that there exists a \(t_0>0\) such that \(I(t_0)=0,\)  \({\dot{I}}(t_0)\le 0\) and \(I(t)>0\) for all \(t\in [0,t_0).\) Then using the second equation of (3) one gets that \(0\ge O(t_0).\) Using again the third equation of system (3) we obtain

$$\begin{aligned} {\dot{O}}(t)>-\mu _{0}O(t), \end{aligned}$$

for all \(t\in [0,t_{0}).\) Thus, since O(t) is continuous one obtains

$$\begin{aligned} O(t_0)\ge O(0)\exp (-\mu _0 t_0)>0. \end{aligned}$$

Then we have a contradiction. Thus, \(I(t)>0\) for all \(t>0.\) Using the third equation of model (3) one gets that \(O(t)\ge 0\) for all \(t\ge 0,\) and in the same way that \(S_{m}(t)\ge 0\) with \(t\ge 0\). In the same way, when \(0<O(t)\le B_{O},\) from the last equation of system (3) we can see that

$$\begin{aligned} S_{m}(t)=S_m(0)\,exp\left( -\beta _{m}\int _{0}^{t}O(s)ds\right) \ge S_m(0)\,exp\left( -\beta _{m}B_{O}t\right) >0. \end{aligned}$$

It is clear that \(S_m(t)\rightarrow 0\) as \(t\rightarrow \infty \). Now, if \(O(t)=0,\) then \(S_m\) is constant. \(\square \)

Next, it is clear that the subpopulation S is bounded by \(\frac{\mu }{\mu +\gamma }.\) Indeed, by the standard comparison theorem (Lakshmikantham et al. 1989) one can obtain that

$$\begin{aligned} S(t)\le S(0)\exp (-(\mu +\gamma )t)+\frac{\mu }{\mu +\gamma }(1-\exp (-(\mu +\gamma )t)). \end{aligned}$$

For th case that \(S(0)\le \frac{\mu }{\mu +\gamma }\), we obtain that \(S(t)\le \frac{\mu }{\mu +\gamma }\). Let us focus on the dynamics of the model (3) in the following restricted region:

$$\begin{aligned} \varOmega _0= & {} \Bigl \{(S,I,O,S_m)\in {\mathbb {R}}_{+}^{4}/0<S\le \frac{\mu }{\mu +\gamma },0\le I\le \dfrac{\beta k\mu }{\mu _{0}\alpha (\mu +\gamma )},S+I<1, 0\\{} & {} \le O\le \frac{k}{\mu _{0}},0\le S_m+I_m\le 1\Bigr \}, \end{aligned}$$

where \({\mathbb {R}}_{+}^{4}\) denotes the nonnegative cone of \({\mathbb {R}}^{4}\). Therefore, \(\varOmega _{0}\) is positively invariant. For the case that \(S(0)>\frac{\mu }{\mu +\gamma }\), then either the solutions enter \(\varOmega _{0}\) in finite time or S(t) approaches \(\frac{\mu }{\mu +\gamma }\) asymptotically (similarly for the oocysts O(t) if \(O(0)>\frac{k}{\mu _{0}}\)). Hence, the region \(\varOmega _{0}\) attracts all solutions in \({\mathbb {R}}_{+}^{4}\). Thus, we arrive to the following result.

Proposition 1

The region \(\varOmega _{0}\) is positively invariant and attracting.

Thus, by proposition (1), it is sufficient to consider the dynamics of the solutions of model (3) in \(\varOmega _{0}\), i.e., system (3) is mathematically well-posed in \(\varOmega _{0}\).

3.1 Disease free equilibrium points

The equilibrium states of the epidemic models are generally important and provide insightful information related to the dynamics of the diseases. Generally, these models have disease free, endemic equilibrium points and periodic solutions. The local and global stability depends on the parameters of the model. One important secondary parameter is the basic reproduction number \({\mathcal {R}}_0\), which determines the number of secondary cases generated by an infectious individual entering a fully susceptible population, measuring the diffusion of the disease (van den Driessche and Watmough 2002; Van den Driessche and Watmough 2008).

The mathematical model (3) has infinitely many toxoplasmosis-free equilibrium points, which are obtained by considering \(I=0\) and \(O=0\). This occurs due to the fact that the variable \(S_m\) is independent of the equations that govern the dynamics of cats (Hethcote 2005). The set formed by all these equilibrium points form an invariant set which is a subset of \(\varOmega _{0}\), where these points have as coordinates: \(\left( \frac{\mu }{\mu +\gamma }, 0, 0,S^{*}_{m}\right) \in \varOmega _{0}\). Notice that we have a total disease free equilibrium point \(F^{*}_{0}=\left( \frac{\mu }{\mu +\gamma }, 0, 0,1\right) \) when we consider that all the subpopulations do not have infected cases. However, since the mice can’t spread the disease under the model (3) we consider that whenever \(I=0\) and \(O=0\), one gets a toxoplasmosis-free steady state. Thus, we can define a toxoplasmosis-free equilibrium set as

$$\begin{aligned} J=\left\{ (S,I,O,S_m): \left( \frac{\mu }{\mu +\gamma }, 0, 0,S^{*}_{m}\right) \in \varOmega _{0}\right\} . \end{aligned}$$
(5)

The stability of this set J can be determined by the LaSalle’s invariance principle (Lakshmikantham et al. 1989; Khalil 2002). In the next subsection, we will propose a V function to prove that when \({\mathcal {R}}_0<1\) all the solutions of the system (3) converge to the toxoplasmosis-free set J.

Let’s study the particular local stability of the total disease free equilibrium point \(F^{*}_{0}=\left( \frac{\mu }{\mu +\gamma }, 0, 0,1\right) \), which is determined by considering the system (2) in steady state and \(I=0\), \(O=0\) and \(I_m=0\). The local stability of \(F^{*}_{0}\) is determined by the eigenvalues of \(J(F^{*}_{0})\). The disease free equilibrium point \(F^{*}_{0}\) is locally asymptotically stable if the real part of the eigenvalues are all negative. Evaluating the Jacobian of the system (3) at \(F^{*}_{0}\) one gets:

$$\begin{aligned} J(F^{*}_{0})= \left( \begin{array}{cccr} -\mu -\gamma \text { }&{}\text { }-\mu &{}\text { }-\frac{\beta \mu }{\mu +\gamma }&{}\text { }0\\ 0 \text { }&{}\text { }-\alpha &{}\text { }\frac{\beta \mu }{\mu +\gamma }&{}\text { }0\\ 0\text { }&{} k\text { }&{}\text { }-\mu _{0}&{}\text { } 0\\ 0\text { }&{} 0\text { }&{}\text { }-\beta _m&{}\text { } 0\\ \end{array} \right) . \end{aligned}$$

Thus, computing the eigenvalues of \(J(F^{*}_{0})\) one gets that \(\lambda _{1}=-\mu - \gamma \), is a eigenvalue. The rest of the eigenvalues are the roots of the polynomial given by

$$\begin{aligned} p(\lambda )=\lambda \,\left( \,(\lambda +\alpha )(\lambda +\mu _{0})-k\beta \dfrac{\mu }{\mu +\gamma }\right) \end{aligned}$$
(6)

However, one gets an eigenvalue \(\lambda =0\) and then we might apply the center manifold theorem (Guckenheimer and Holmes 2013). However, it is clear that whenever \(I\ne 0\) or \(O\ne 0\), then the system is not able to reach the total disease free equilibrium point \(F^{*}_{0}\). Therefore, \(F^{*}_{0}\) is not locally asymptotically stable (las). However, in the next subsection we will use global stability analysis to prove that all the solutions of the system (3) converge to the toxoplasmosis-free set J, which includes the total disease free equilibrium point \(F^{*}_{0}\).

3.2 Global stability of disease-free equilibrium point

Here we will find the conditions for the relative eradication of the disease independently of the initial conditions of the subpopulations.

Let us define the threshold parameter

$$\begin{aligned} {\mathcal {R}}_{0}=\sqrt{{\frac{\mu \,k\beta }{\mu _{0}\, \left( \gamma +\mu \right) \alpha }}}. \end{aligned}$$
(7)

For the global stability analysis, we will show that if \({\mathcal {R}}_0\le 1,\) then regardless of the initial conditions all the trajectories of the solutions X(t) of system (3) converge to the set \(J \in \varOmega _0\). This is proven below.

Theorem 2

All the trajectories of the solutions X(t) of the system (3) converge to the set \(J \in \varOmega _0\) if \( {\mathcal {R}}_0\le 1.\)

Proof

We analyze the global stability by proposing a suitable function \({\mathcal {L}}\) as follows

$$\begin{aligned} {\mathcal {L}}(X(t))=\dfrac{k\,I(t)}{\alpha \,\mu _{0}} + \dfrac{O(t)}{\mu _{0}}. \end{aligned}$$
(8)

where \(X(t)=\left( S(t),I(t),O(t),S_{m}(t) \right) .\) The function \({\mathcal {L}}\) satisfies

$$\begin{aligned}&{\mathcal {L}}(F^{*})=0, \,\,\text { for all } F^{*} \in J,\nonumber \\&{\mathcal {L}}(X(t))>0,\,\,\text { for all } X(t)\ne F^{*},\\&{\mathcal {L}}(X(t))\rightarrow \infty ,\,\,\text { when } \left\| X \right\| \rightarrow \infty .\,\,\text { It follows that } {\mathcal {L}}(X(t))\,\,\text { is radially unbounded.} \nonumber \end{aligned}$$
(9)

Now, taking the time derivative of \({\mathcal {L}}(X(t))\) along the trajectories of system (3), and from the restricted region \(\varOmega _0\) one gets that

$$\begin{aligned} \dfrac{d{\mathcal {L}}(X(t))}{dt}=&\dfrac{k\,{\dot{I}}(t)}{\alpha \,\mu _{0}} + \dfrac{{\dot{O}}(t)}{\mu _{0}}=\dfrac{k\,(\beta \,S(t)\,O(t)-\alpha \,I(t))}{\alpha \,\mu _{0}} + \dfrac{kI(t)-\mu _{0}\,O(t)}{\mu _{0}}\\\\ =&\dfrac{k\,(\beta \,S(t)\,O(t)}{\alpha \,\mu _{0}} - O(t)=\left( \dfrac{k\,\beta \,S(t)}{\alpha \,\mu _{0}}-1\right) \, O(t)\le \left( \dfrac{\mu \,k\,\beta }{\mu _{0}(\mu +\gamma )\alpha }-1\right) \, O(t) \\\\=&\left( {\mathcal {R}}^{2}_0-1\right) \, O(t)=\left( {\mathcal {R}}_0-1\right) \left( {\mathcal {R}}_0+1\right) O(t). \end{aligned}$$

Thus, \(\dfrac{d{\mathcal {L}}(X(t))}{dt}\le 0\) when \({\mathcal {R}}_0\le 1,\) and \(\dfrac{d{\mathcal {L}}(X(t))}{dt}=0\) if and only if \(X(t)=0\) and \(O(t)=0\), or \(O(t)=0\), or \(S(t)=\frac{\alpha \,\mu _{0}}{k\,\beta }\).This implies that the largest time invariant set such that

$$\begin{aligned} {\mathcal {L}}_{ F^{*}}= \left\{ X(t)\in \varOmega _0:\dfrac{d{\mathcal {L}}(X(t))}{dt}=0\right\} \end{aligned}$$

is reduced to the set J. Then, applying LaSalle’s invariance principle (Khalil 2002), one gets that the limit set of each solution is contained in the largest time invariant set \(J\in \varOmega _0\) if \({\mathcal {R}}_0\le 1\). Then every solution starting in \(\varOmega _0\) approaches J as \(t\rightarrow \infty \). \(\square \)

In the numerical simulations section we will see that whenever \({\mathcal {R}}_0\le 1\) the solution approaches J as \(t\rightarrow \infty \) regardless of the initial conditions. Notice that \({\mathcal {R}}_0\) does not depend on the transmission rate \(\beta _{m}\) between the oocysts and the mouse population. This fact can be explained on the basis that mice is an intermediate host and cannot generate oocysts and therefore does not affect the load of oocysts in the environment and therefore can’t spread the disease under the assumptions of model (1).

3.3 Endemic equilibrium point

From Eq. (6) it can be deduced that the total disease free point \(F^{*}_{0}\) is unstable when \({\mathcal {R}}_0>1.\) In a similar way, it can be found that any equilibrium point in the set Jis also unstable whenever \({\mathcal {R}}_0>1.\) Thus, the solutions of the model (3) might converge to endemic points when \({\mathcal {R}}_0>1.\) It is important to determine these endemic points and their stability. For this, we set the left-hand side of the system (3) to zero. We obtain the following

$$\begin{aligned} \begin{array}{crl} 0&{}=&{}\mu (1-I^{*})-\beta S^{*}O^{*} - (\mu +\gamma ) S^{*},\\ 0&{}=&{}\beta S^{*}O^{*} -\alpha I^{*},\\ 0&{}=&{}k I^{*}-\mu _{0}\,O^{*},\\ 0&{}=&{} -\beta _{m}\,S_{m}^{*}\, O^{*}, \end{array} \end{aligned}$$
(10)

Thus, the endemic point will be the positive solutions of nonlinear system (10) denoted by

$$\begin{aligned} E^{*}=\left( S^{*},I^{*},O^{*},S_{m}^{*}\right) . \end{aligned}$$
(11)

Now, if \(I(t)>0\), \(O(t)>0\), then from system (10) one gets that \(S_m^{*}=0.\) Thus, an endemic equilibrium point is

$$\begin{aligned} E^{*}_{0}=(S^*=\dfrac{\alpha \mu _{0}}{\beta k},I^*=\dfrac{\mu \beta k-(\gamma +\mu )\alpha \mu _{0}}{\beta k (\mu +\alpha )},O^*\!=\!\dfrac{\mu \beta k-(\gamma +\mu )\alpha \mu _{0}}{\mu _0 k (\mu +\alpha )},S_m^{*}=0) \in \varOmega _{0}.\nonumber \\ \end{aligned}$$
(12)

This endemic equilibrium is feasible biologically if \(\mu \beta k-(\gamma +\mu )\alpha \mu _{0}>0\), or in terms of the threshold number, if \({\mathcal {R}}_{0}>1\). Evaluating the Jacobian at \(E^{*}_{0}\) one gets the characteristic polynomial:

$$\begin{aligned} P(\lambda )=\left| \begin{array}{cccr} -\beta O^{*}-\mu -\gamma -\lambda \text { }&{}\text { }-\mu &{}\text { }-\beta S^*&{}\text { }0\\ \beta O^* \text { }&{}\text { }-\alpha -\lambda &{}\text { }\beta S^*&{}\text { }0\\ 0\text { }&{} k\text { }&{}\text { }-\mu _{0}-\lambda &{}\text { } 0\\ 0\text { }&{} 0\text { }&{}\text { }0&{}\text { } -\beta _{m} O^*-\lambda \\ \end{array} \right| \end{aligned}$$

Clearly, one gets that one eigenvalue is given by \(\lambda _{1}=-\beta _{m} O^*\), which is negative. The rest of the eigenvalues are the roots of the third degree polynomial given by

$$\begin{aligned} \lambda ^3+(p_0+\alpha +\mu _0)\,\lambda ^2+(p_0\,(\alpha +\mu _0)+\beta O^*\mu )\,\lambda +\beta \, O^*(\mu \, \mu _{0}+\alpha \mu _{0})=0. \end{aligned}$$
(13)

where \(p_0=\beta O^*+\gamma +\mu \). We can rewrite this characteristic equation as:

$$\begin{aligned} \lambda ^3+A\lambda ^2+B\lambda +C=0 \end{aligned}$$
(14)

where

$$\begin{aligned} A&=(\beta O^*+\gamma +\mu )+\alpha +\mu _0,\\ B&=(\beta O^*+\gamma +\mu )\,(\alpha +\mu _0)+\beta \, O^*\mu ,\\ C&=\beta O^*(\mu \, \mu _{0}+\alpha \mu _{0}). \end{aligned}$$

By Routh–Hurwitz theorem (Routh 1877), the roots of Eq. (14) has all roots in the open left half plane if and only if A, C are positive and \(A\,B>C\). It is clear that \(A,B,C>0\) since \(O^{*}>0\). Moreover, the following calculation shows that

$$\begin{aligned} AB-C&=\Bigl (\beta O^*+\gamma +\mu +\alpha +\mu _0\Bigr )\, \Bigl ((\beta O^*+\gamma +\mu )\,(\alpha +\mu _0)+\beta \, O^*\mu \Bigr )\\&\quad -\beta O^*(\mu \, \mu _{0}+\alpha \mu _{0})\\&=\Bigl (\beta O^*+\gamma +\mu +\alpha +\mu _0\Bigr )\, \Bigl [(\beta O^*+\gamma +\mu )\,(\alpha +\mu _0)\Bigr ]\\ {}&\quad +\Bigl (\beta O^*+\gamma +\mu +\alpha +\mu _0\Bigr )\,\beta \, O^*\mu -\beta O^*(\mu \, \mu _{0}+\alpha \mu _{0})\\&=\Bigl (\beta O^*+\gamma +\mu +\mu _0\Bigr )\, \Bigl [(\beta O^*+\gamma +\mu )\,(\alpha +\mu _0)\Bigr ]\\&\quad +\alpha \,\Bigl [(\beta O^*+\gamma +\mu )\,(\alpha +\mu _0)\Bigr ]\\&\quad +\Bigl (\beta O^*+\gamma +\mu +\alpha \Bigr )\,\beta O^*\mu +\beta O^*\mu _0\mu -\beta O^*\mu \, \mu _{0}-\beta O^*\alpha \mu _{0}\\&=\Bigl (\beta O^*+\gamma +\mu +\mu _0\Bigr )\, \Bigl [(\beta O^*+\gamma +\mu )\,(\alpha +\mu _0)\Bigr ]+\alpha ^{2}\,(\beta O^*+\gamma +\mu )\\ {}&\quad +\alpha \mu _0\,(\beta O^*+\gamma +\mu ) +\Bigl (\beta O^*+\gamma +\mu +\alpha \Bigr )\,\beta O^*\mu -\beta O^*\alpha \mu _{0}\\&=\Bigl (\beta O^*+\gamma +\mu +\mu _0\Bigr )\, \Bigl [(\beta O^*+\gamma +\mu )\,(\alpha +\mu _0)\Bigr ]+\alpha ^{2}\,(\beta O^*+\gamma +\mu )\\ {}&\quad +\alpha \mu _0\,(\gamma +\mu ) +\Bigl (\beta O^*+\gamma +\mu +\alpha \Bigr )\,\beta O^*\mu >0, \end{aligned}$$

then by Routh-Hurwitz theorem, the roots of equation (14) all have negative real parts. Thus, we have the following theorem,

Theorem 3

If \({\mathcal {R}}_{0}>1\), then the unique endemic equilibrium point \(E^{*}_{0}\) is locally asymptotically stable.

Now, the analysis of the global stability of the endemic point is given by the following theorem:

Theorem 4

For \({\mathcal {R}}_{0}>1\) the unique endemic equilibrium \(E^{*}_{0}\) of the model (3), is globally asymptotically stable with respect to \(\varOmega _{0}{\setminus } J\) whenever \({\mathcal {R}}_{0}>1\).

Proof

We analyze the global stability at the endemic equilibrium \(E^{*}_{0}\), using the following function \({\mathcal {L}}\),

$$\begin{aligned} {\mathcal {L}}(X(t))=S_m(t) \end{aligned}$$
(15)

The function \({\mathcal {L}}\) satisfies

$$\begin{aligned}&{\mathcal {L}}(E^{*}_{0})=0,\nonumber \\&{\mathcal {L}}(X(t))>0,\,\,\text { for all } X(t)\ne E^{*}_{0} \qquad \text {(positive definite)}\nonumber \\&\Vert (X(t)\Vert \rightarrow \infty \implies {\mathcal {L}}(X(t))\rightarrow \infty . \end{aligned}$$
(16)

The time derivative of \({\mathcal {L}}(X(t))\) along the solutions of (3) is

$$\begin{aligned} \dfrac{d{\mathcal {L}}(X(t))}{dt}= -\beta _{m}\,S_m(t)\,O(t). \end{aligned}$$

Thus, \(\dfrac{d{\mathcal {L}}(X(t))}{dt}\le 0\) and \(\dfrac{d{\mathcal {L}}(X(t))}{dt}=0\) if and only if \(S_m(t)=0\) or \(O(t)=0.\) Then, applying LaSalle’s invariance principle, the endemic equilibrium \(E^{*}_{0}\) is globally asymptotically stable with respect to \(\varOmega _{0}{\setminus } J\) if \({\mathcal {R}}_0>1.\) \(\square \)

Based on the previous results the basic reproduction number \({\mathcal {R}}_{0}\) is a unique threshold parameter that determines the long term qualitative behavior of the system. From to the global stability analysis, we expect that the disease will die out for any initial conditions whenever \({\mathcal {R}}_{0}\le 1\). On the other hand, if \({\mathcal {R}}_{0}>1\), then we expect the disease would become endemic for any initial conditions such that at least one infectious cat or oocysts exists.

4 Numerical simulations

In this section, we will perform some numerical simulations of the mathematical model (3) varying the scenarios related to the toxoplasmosis disease. We consider scenarios with \({\mathcal {R}}_{0}<1\) and \({\mathcal {R}}_{0}>1\) in order to support the theoretical results. Two main public health control interventions that can be done in order to reduce toxoplasmosis prevalence are vaccination and removing oocysts from the environment. Therefore, for the numerical simulation we vary the vaccination rate and the removal rate of oocysts. In addition, we use several values for the transmission rates between oocysts and both populations of cat and mouse. Finally, the vaccination rate \(\gamma \) is varied to obtain different situations related to the vaccination program.

For each numerical simulation we compute the steady states in order to corroborate the global theoretical stability results obtained in the previous section. One important key parameter is the transmissibility of the toxoplasmosis through the oocysts, since it is related to the basic reproduction number \({\mathcal {R}}_{0}\) (Hethcote 2005; van den Driessche and Watmough 2002; Van den Driessche and Watmough 2008). For the initial environment load of oocysts we use an approximation based on an adapted equation from (Mateus-Pinilla et al. 2002).

Most of the numerical simulations are performed using the parameter values given in Table 1, which are approximations of the real world values and some of them have more uncertainty than others. For instance, we use the fact that usually the cats only shed oocysts for 3–10 days after ingestion of tissue cysts (Hartmann et al. 2013). We also use the fact that cats are immune to toxoplasma and can eject more than 20 million oocysts between 4 and 13 days after infection (Dubey 1995). As it has been aforementioned we also consider that in the cats, T. gondii can be passed to the fetus via the placenta (Sibley and Boothroyd 1992). We also take into account that feces of cats shedding T. gondii may contain \(2.5\times 10^{6}\) oocysts/gr and that a single cat may shed as many as 20 million oocysts per day in about 20 g. of feces (Fayer 1981).

Table 1 Model parameters and variables
Full size table

4.1 Disease free scenario (\({\mathcal {R}}_{0}<1\))

First we consider a scenario where \({\mathcal {R}}_{0}<1\) and a vaccination program with a low vaccination rate \(\gamma =0.001\). Figure 2 shows the dynamics of the subpopulations and the caption gives the values of the parameters used. On the left-hand side we can see that the infected cat population becomes extinct when the initial conditions are close to the steady state \(F^{*}_{0}\). The right-hand side simulation just starts with initial conditions far from the steady state \(F^{*}_{0}\). Thus, we can observe that even with a low vaccination rate the disease disappears. These numerical results are in agreement with the theoretical stability analysis.

Fig. 2
figure 2

Dynamics of the different subpopulations when \(\beta =0.15\times 10^{-9}\), \(\gamma =0.001\) and \({\mathcal {R}}_{0}=0.98\). On the left-hand side the initial conditions are close to the steady state \(F^{*}_{0}\) and on the right-hand side the initial conditions are far from \(F^{*}_{0}\)

Full size image

4.2 Endemic scenario (\({\mathcal {R}}_{0}>1\))

Let’s consider a transmission rate \(\beta \) such that \({\mathcal {R}}_{0}>1\). Figure 3, shows that the disease becomes endemic since the infected cats reach a steady state different than zero. Thus, increasing the transmission rate \(\beta \) such that \({\mathcal {R}}_{0}>1\) allows the system to reach the endemic equilibrium point \(E^{*}_{0}\).

Fig. 3
figure 3

Dynamics of the different subpopulations when \(\beta =0.18\times 10^{-9}\), \(\gamma =0.001\) and \({\mathcal {R}}_{0}=1.04\). The initial conditions are far from the endemic steady state \(E^{*}_{0}\)

Full size image

4.3 Efficacy of a cat’s vaccination program

Here we study the effect of a vaccination program on the dynamics of the cat and mouse populations. We consider a scenario with a high infectivity from the oocysts to the cats. Notice that cats get the T. gondii parasite by eating anything contaminated with feces from another cat that is shedding the microscopic parasite in its feces. We set the value of the transmission rate \(\beta \) such that \({\mathcal {R}}_{0}=10.4\) and then increase the vaccination rate to \(\gamma =0.1\) such that the basic reproduction number \({\mathcal {R}}_{0}\) becomes less than one. In addition, we set the initial conditions far from the disease free equilibrium \(F^{*}_{0}\). Figure 4 shows that the the proportion of infected cats and the number of oocysts become extinct, despite the fact that the oocysts present a high infectivity. This particular result shows the effectiveness of a vaccination program for cats in order to eradicate the disease by making the basic reproduction number \({\mathcal {R}}_{0}<1\).

Fig. 4
figure 4

Dynamics of the different subpopulations when \(\beta =0.15\times 10^{-9}\) (high infectivity), \(\gamma =0.1\) and \({\mathcal {R}}_{0}=0.9\). The initial conditions are far from the disease free steady state \(F^{*}_{0}\)

Full size image

4.4 Effect of oocysts clearance in the environment

Now we consider a scenario without vaccination and only a public health program that reduces the amount of oocysts in the environment. We choose a high infectivity from the oocysts to the cats (\({\mathcal {R}}_{0}\approx 13.1\)) and then we set the clearance rate of oocysts in the environment such that \({\mathcal {R}}_{0}<1\). In addition, we set the initial conditions far from the disease free equilibrium \(F^{*}_{0}\) in order to also show the global stability feature of the endemic state \(E^{*}_{0}\). Figure 5 shows that increasing the clearance rate of oocysts from the environment allows the system to approach to the disease free steady state. Thus, we can conclude that it is possible to reduce the prevalence of the toxoplasmosis even without a vaccination program, but this would require an excellent oocysts-environment cleaning program.

Fig. 5
figure 5

Dynamics of the different subpopulations when there is high infectivity (high \(\beta \)), \(\gamma =0.001\), \(\mu _0=14/26\) and \({\mathcal {R}}_{0}=0.9\). The initial conditions are far from the disease free steady state \(F^{*}_{0}\)

Full size image

4.5 Sensitivity analysis for the basic reproduction number \({\mathcal {R}}_0\)

The aim here is to perform sensitivity analysis of the basic reproduction number \({\mathcal {R}}_0\). The idea is to determine how sensitive \({\mathcal {R}}_0\) is to each of the parameters. Sensitivity analysis allow us to estimate or measure the relative importance of the different parameters responsible for the disease transmission related to the basic reproduction number (Castillo-Garsow and Castillo-Chavez 2020; Chitnis et al. 2008; Florian and Vermiglio 2020; Samsuzzoha et al. 2013; van den Driessche and Watmough 2002; Vermiglio and Zamolo 2022).

There are various methods to perform sensitivity analysis (Castillo-Garsow and Castillo-Chavez 2020; Chitnis et al. 2008; Florian and Vermiglio 2020; Samsuzzoha et al. 2013; Vermiglio and Zamolo 2022). These analyses allow us to measure how a change in the values of the parameters impact the dynamical behavior of the system or model. It is important to remark that in the model (3) the long-term behavior is completely determined by the values of \({\mathcal {R}}_0\). Thus, it make sense to perform sensitivity analysis of the basic reproduction number \({\mathcal {R}}_0\). Here the crucial idea of sensitivity analysis is to see how a small change in one parameter modifies the corresponding percentage change in the basic reproduction number \({\mathcal {R}}_0\). Usually, it is better to perform the sensitivity analysis using percentages instead of absolute changes, Thus, the parameters with different units can have a fair comparison. The sensitivity index of \({\mathcal {R}}_0\) with respect to a parameter \(\xi \) is given by

$$\begin{aligned} \phi _{\xi }=\dfrac{\partial {\mathcal {R}}_0}{\partial \xi }\dfrac{\xi }{{\mathcal {R}}_0}. \end{aligned}$$
(17)

Therefore, in order to compute the normalized sensitivity index of \({\mathcal {R}}_0\), we need to compute the partial derivatives of \({\mathcal {R}}_0\) respect to each of the parameters that affect \({\mathcal {R}}_0\). In order to evaluate these partial derivatives it is necessary to use particular or estimated parameter values. In this section, we use the related parameters’ values given in Table 1. Sensitivity indices for the basic reproduction number change with the change in parameter values. However, the parameters of the model (3) that affect \({\mathcal {R}}_0\) are extremely difficult to estimate correctly and vary depending on the region where the toxoplasmosis epidemic is being studied. Even for the very well studied influenza epidemics the estimation of parameters is challenging (Samsuzzoha et al. 2013).

The particular values of the sensitivity indices of \({\mathcal {R}}_0\) are shown in Table 2. The sensitivity indices \(\phi _{\beta }, \phi _{k}\) and \(\phi _{\mu }\) are positive and the indices \(\phi _{\mu _0}, \phi _{\gamma }\) and \(\phi _{\alpha }\) are negative. The indices \(\phi _{\mu }\) and \(\phi _{\nu }\) are functions of \(\mu \) and \(\gamma \) parameters. Therefore, the sensitivity indices will change when the values of these parameters change. The sensitivity index \(\phi _{\beta }\) indicates that in order to decrease 1% the value of \({\mathcal {R}}_0\) a 1% decrease is needed in the value of \(\beta \). In a similar way we can interpret the other indices for each parameter in Table 2. In particular, if we increase the vaccination rate \(\gamma \) in \(1\%\) one gets that \({\mathcal {R}}_0\) would decrease in approximately \(0.79\%\). This means that increasing the vaccination rate has a good effect to reduce the prevalence of toxoplasmosis (recall that the endemic point depends on \({\mathcal {R}}_0\)), but for instance increasing the removal rate of the oocysts in \(1\%\) would reduce \({\mathcal {R}}_0\) in approximately \(1\%\), which seems more effective. However, the public health intervention would depend on how difficult would be to achieve these aforementioned percentage changes on the parameters. It is important to remark that in order to calculate the sensitivity analysis, we have the values of the parameters shown in Table 2.

Table 2 Sensitivity indices of \({\mathcal {R}}_0\)
Full size table

5 Conclusions

In this paper, we proposed an epidemiological type mathematical model to study toxoplasmosis dynamics with multiple hosts and considering vertical transmission in both cat and mouse populations. We investigate under what conditions the T. gondii parasite can be eradicated and the impact of some parameters related to the vaccination rate, clearance of the oocysts in the environment and oocysts’ transmissibility on the dynamics. We include the mouse population as an intermediate host. We prove that the basic reproduction number \({\mathcal {R}}_{0}\) completely determines the global dynamics of the toxoplasmosis and the final outcome of the disease. We found that if \({\mathcal {R}}_{0}\le 1\), then the solutions approach to the set composed by all the disease-free equilibrium points regardless of the initial conditions. Thus, the toxoplasmosis disease would be eradicated from the cat’s population. If \({\mathcal {R}}_{0}>1\), we found that there is only one biological feasible endemic equilibrium and we proved that is globally asymptotically stable. This translates in that under this situation the toxoplasmosis will become endemic for both populations and would persist over the time whenever \({\mathcal {R}}_{0}>1\). Moreover, the larger the basic reproduction number \({\mathcal {R}}_{0}\) the higher toxoplasmosis would be since the endemic point depends on the basic reproduction number \({\mathcal {R}}_{0}\).

We performed numerical simulations that support the theoretical results obtained in this study. We used some parameter values that are not fully well-known and provided in silico simulations that allow to get deeper insight on the toxoplasmosis dynamics. This study provides helpful information to health institutions in order to deal or reduce the burden caused by toxoplasmosis. From the basic reproduction number of the constructed model we can deduce that increasing the vaccination rate reduces the toxoplasmosis prevalence and the parasite T. gondii can disappear. This is analogous to the situation with the clearance rate of oocysts from the environment. Numerical simulations show that vaccination of cats and oocysts removal are efficient ways to reduce the prevalence of toxoplasmosis and therefore useful for the public health. Furthermore, we performed sensitivity analysis and computed the normalized sensitivity indices. This shows what are the impacts of changes of all parameters on changing the basic reproduction number \({\mathcal {R}}_{0}\). The results show that public health interventions such as vaccination or the removal of oocysts for the environment would reduce the basic reproduction number \({\mathcal {R}}_{0}\) and therefore the prevalence of toxoplasmosis.

As any mathematical modeling study of epidemics there are limitations. For instance, reliable estimation of some parameter values are not yet available. Therefore, specific values for the model such that \({\mathcal {R}}_{0}<1\) are not possible in an accurate way. Therefore, we cannot provide these values to health institutions in order to eliminate toxoplasmosis in cat populations. The model also considers a constant population for the cats which might not be realistic in many places. In addition, we used a life expectancy for the cats of five years, but this varies for domestic cats and depends on several factors (Berthier et al. 2000). In both populations of cats and mice the model includes full vertical transmission and a relative proportion might be more accurate, but the models becomes more complex to analyze. Another important limitation of the developed model is that it does not consider other intermediate hosts such as humans, birds, pigs, sheep, etc (Dubey 2020; Dubey et al. 2020; Dubey 1996; Williams et al. 2005). This, could greatly affect the dynamics of toxoplasmosis as well the prey-predator effects.

Finally, from this study we have seen that the health authorities have two clear options to reduce the disease. One is to implement a vaccination program for cats and the other option is to develop cleaning activities regarding the amount of oocysts in the environment. Further, studies related to optimal control are necessary assess which strategy is better taking into account economic and social factors related to both options. Based on the results of those type of studies we can see which strategy is the optimal in terms of economical costs and efficacy related to the vaccines. In addition, the costs of oocysts-environmental removing activities should be taken into account. Future research works can include a variety of models that consider other hosts, different assumptions regarding vertical transmission, different type of vaccination program and prey-predator effects. Also more complex models that integrate between-hosts and within-hots can be studied.