Skip to main content
SpringerLink
Log in

Optimal control of the dynamics of a tumor growth model with Hollings’ type-II functional response

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

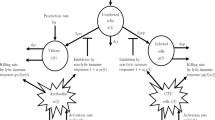
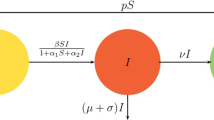
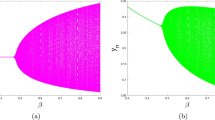
In this paper, a simple predator–prey type model for interaction of immune system (consisting of resting and hunting cells) with tumor cells using Hollings’ type-II functional response is considered. It is found that the model system has no positive equilibrium if the half-saturation population of resting cells is greater than a critical value. In case of violation of this condition, model system mostly has unique positive equilibrium but when the half-saturation population of cancer cells is smaller than one, it may have three positive equilibriums. Local stability of the feasible equilibriums is studied. These results suggest that a positive equilibrium can be locally asymptotically stable or unstable based on the system parameter values. In case of unstable positive equilibrium (equilibriums), long-time sustenance of immune system with tumor in terms of limit cycle through Hopf bifurcation is observed with half-saturation population of resting cells as bifurcation parameter. The necessary optimal control inputs that make the unstable equilibriums of the model system asymptotically stable and minimize the required performance measure are given as nonlinear functions of the system densities.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  • Banerjee S, Sarkar R (2008) Delay-induced model for tumor-immune interaction and control of malignant tumor growth. Biosystems 91:268–288

    Google Scholar 

  • Bellomo N, Delitala M (2008) From the mathematical kinetic, and stochastic game theory for active particles to modelling mutations, onset, progression and immune competition of cancer cells. Phys Life Rev 5:183–206

    Article  Google Scholar 

  • Bellomo N, Li N, Maini P (2008) On the foundations of cancer modeling: selected topics, speculations, and perspectives. Math Models Methods Appl Sci 18(4):593–646

    Article  MathSciNet  MATH  Google Scholar 

  • Bellouquid A, De Angelis E, Knopoff D (2013) From the modeling of the hallmarks of cancer to a black swan in biology. Math Models Methods Appl Sci 23:949–978

    Article  MathSciNet  MATH  Google Scholar 

  • Bodnar M, Foryś U (2007) Three types of simple DDE’s describing tumour growth. J Biol Syst 15:1–19

    Article  Google Scholar 

  • Burden T, Ernstberger J, Fister KR (2004) Optimal control applied to immunotherapy. Discrete Continuous Dyn Syst Ser B 4(1):135–146

    MathSciNet  MATH  Google Scholar 

  • Byrne H, Alarcon T, Owen M, Webb S, Maini P (2006) Modeling aspects of cancer dynamics: a review. Philos Trans R Soc A 364:1563–1578

    Article  MathSciNet  Google Scholar 

  • Castiglione F, Piccoli B (2007) Cancer immunotherapy, mathematical modeling and optimal control. J Theor Biol 247:723–732

    Article  MathSciNet  Google Scholar 

  • Cooper EL (2010) Evolution of immune system from self/not self to danger to artificial immune system. Phys Life Rev 7:55–78

    Article  Google Scholar 

  • d’Onofrio A, Gatti F, Cerrai P, Freschi L (2010) Delay-induced oscillatory dynamics of tumour-immune system interaction. Math Comput Model 51:572–591

    Article  MathSciNet  MATH  Google Scholar 

  • de Pillis LG, Radunskaya AE (2003) The dynamics of an optimally controlled tumor model: a case study. Math Comput Model 37:1221–1244

    Article  MATH  Google Scholar 

  • de Pillis L, Radunskaya A, Wiseman C (2005) A validated mathematical model of cell-mediated immune response to tumor growth. Cancer Res 65(17):7950–7958

    Google Scholar 

  • de Pillis LG, Gu W, Fister KR, Head T, Maples K, Murugan A, Neal T, Yoshida K (2007) Chemotherapy for tumors: an analysis of the dynamics and a study of quadratic and linear optimal controls. Math Biosci 209:292–315

    Article  MathSciNet  MATH  Google Scholar 

  • Efftimie R, Bramson JL, Earn DLD (2011) Interaction between the immune system and cancer: a brief review of non-spatial mathematical models. Bull Math Biol 73:2–32

    Article  MathSciNet  Google Scholar 

  • El-Gohary A (2008) Chaos and optimal control of cancer self-remission and tumor system steady states. Chaos Solitons Fractals 37(5):1305–1316

    Article  MathSciNet  MATH  Google Scholar 

  • Goldstein B, Faeder J, Hlavacek W (2004) Mathematical and computational models of immune receptor signaling. Nat Rev Immunol 4(6):445–456

    Article  Google Scholar 

  • Grivennikov SI, Greten FR, Karin M (2010) Immunity, inflammation, and cancer. Cell 140:883–899

    Article  Google Scholar 

  • Kirschner D, Panetta JC (1998) Modeling immunotherapy of the tumor-immune interaction. J Math Biol 37(3):235–252

    Article  MATH  Google Scholar 

  • Kronik N, Kogan Y, Vainstein V, Agur Z (2008) Improving alloreactive CTL immunotherapy for malignant gliomas using a simulation model of their interactive dynamics. Cancer Immunol Immunother 57:425–439

    Article  Google Scholar 

  • Kuznetsov V, Makalkin I, Taylor M, Perelson A (1994) Nonlinear dynamics of immunogenic tumors: parameter estimation and global bifurcation analysis. Bull Math Biol 56(2):295–321

    Article  MATH  Google Scholar 

  • Martins M Jr, Ferreira SC, Vilela M (2007) Multiscale models for the growth of avascular tumors. Phys Life Rev 4:128–156

    Article  Google Scholar 

  • Menta B, Agarwal M (1980) Cyclic oscillations in leukocyte count in chronic myeloid leukemia. Acta Haematol 63:68–70

    Article  Google Scholar 

  • Merola A, Cosentino C, Amato F (2008) An insight into tumor dormancy equilibrium via the analysis of its domain of attraction. Biomed Sign Process Control 3:212–219

    Article  Google Scholar 

  • Nagy J (2005) The ecology and evolutionary biology of cancer: a review of mathematical models of necrosis and tumor cells diversity. Math Biosci Eng 2(2):381–418

    Article  MathSciNet  Google Scholar 

  • Ogata K (1970) Modern control engineering. Prentice-Hall, Englewood Cliffs

    Google Scholar 

  • Piotrowska MJ (2008) Hopf bifurcation in a solid avascular tumour growth model with two discrete delays, special issue: towards a mathematical description of cancer: analytical, numerical and modelling aspects. Math Comput Model 47:597–603

    Article  MathSciNet  MATH  Google Scholar 

  • Quesnel B (2008) Dormant tumor cells as therapeutic target? Cancer Lett 267:10–17

    Article  Google Scholar 

  • Raza SA, Clifford GM, Frenceschi S (2007) Worldwide variation in the relative importance of hepatitis B and hepatitis C viruses in hepatocellular carcinoma: a systematic review. Br J Cancer 96:1127–1134

    Article  Google Scholar 

  • Sachs R, Hlatky L, Hahnfeldt P (2001) Simple ODE models of tumor growth and anti angiogenic or radiation treatment. Math Comput Model 33:1297–1305

    Article  MathSciNet  MATH  Google Scholar 

  • Saleem M, Agrawal T (2012) Chaos in a tumor growth model with delayed responses of the immune system. J Appl Math 2012:16 Article ID 891095

  • Sarkar R, Banerjee S (2005) Cancer and self remission and tumor stability, a stochastic approach. Math Biosci 169:65–81

    Article  MathSciNet  Google Scholar 

  • Vesely MD, Kershaw MH, Schreiber RD, Smyth MJ (2011) Natural innate and adaptive immunity to cancer. Annu Rev Immunol 29:235–271

    Article  Google Scholar 

  • Weinberg RA (2007) The Biology of Cancer. Garland Sciences, Taylor and Francis, New York

    Google Scholar 

  • Whiteside TL (2006) Immune suppression in cancer: effects on immune cells, mechanisms and future therapeutic intervention. Sem Cancer Biol 16:3–15

    Article  Google Scholar 

  • Zamarron BF, Chen WJ (2011) Dual roles of immune cells and their factors in cancer development and progression. Int J Biol Sci 7:651–658

    Article  Google Scholar 

Download references

Acknowledgments

This work has been supported by the University Grants Commission, New Delhi under the Project No. 37-483/2009 (SR). The authors thank the anonymous referee for valuable comments that certainly guided us to improve this manuscript.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Z.H. College of Engineering and Technology, A.M.U., Aligarh, 202002, India

    Tanuja Agrawal & M. Saleem

  2. Department of Mathematics, Linagaya’s University, Faridabad, Haryana, 121002, India

    S. K. Sahu

Authors
  1. Tanuja Agrawal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Saleem
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. K. Sahu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tanuja Agrawal.

Additional information

Communicated by Enrique Zuazua.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Agrawal, T., Saleem, M. & Sahu, S.K. Optimal control of the dynamics of a tumor growth model with Hollings’ type-II functional response. Comp. Appl. Math. 33, 591–606 (2014). https://doi.org/10.1007/s40314-013-0083-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40314-013-0083-x

Keywords

Mathematics Subject Classification (2010)

Search

Navigation