Graph sampling

Abstract

We synthesise the existing theory of graph sampling. We propose a formal definition of sampling in finite graphs, and provide a classification of potential graph parameters. We develop a general approach of Horvitz–Thompson estimation to T-stage snowball sampling, and present various reformulations of some common network sampling methods in the literature in terms of the outlined graph sampling theory.

1 Introduction

Many technological, social and biological phenomena exhibit a network structure that may be the interest of study; see e.g. Newman [20]. As an example of technological networks, consider the Internet as consisting of routers that are connected to each other via cables. There are two types of objects, namely routers and cables. A router must be connected to a cable to be included in the Internet, and a cable must have two routers at both ends. As another example, consider the social network of kinships. Again, there are two types of objects, namely persons and kinships. Each person must have two or more kinships, and each kinship must represent a connection between two persons. However, while it is obvious that any two routers must be connected by cables to each other either directly or via other routers in the Internet, it is not sure that any two persons can be connected to each other in the network of kinships. The difference can be articulated in terms of some appropriate characterisation of their respective network structures.

Following Frank [11, 12, 14], we refer to network as a valued graph, and graph as the formal structure of a network. The structure of a network, i.e. a graph, is defined as a collection of nodes and edges (between the nodes); measures may be attached to the nodes or the edges or both to form a valued graph, i.e. a network. For a statistical approach to networks one may choose to model the entire population network as a random realisation [16], or to exploit the variation over possible sample networks taken from a given fixed population network. Graph sampling theory deals with the structure of a network under the latter perspective. In comparison, finite-population sampling [3, 21] can mostly be envisaged as sampling in a ‘graph’ with no edges at all. We shall refer to such a setting as list sampling.

Ove Frank has undoubtedly made the most contributions to the existing graph sampling theory. See e.g. Frank [8, 10, 12,13,14] for his own summary. However, the numerous works of Frank scatter over several decades, and are not easily appreciable as a whole. For instance, Frank derives results for different samples of nodes [5, 8, 15], dyads [5,6,7, 10] or triads [5, 10]. But he never proposes a formal definition of the “sample graph” which unifies the different samples. Or, Frank studies various characteristics of a graph, such as order [5, 8, 15], size [5,6,7, 10], degree distribution [5, 11], connectedness [5, 9], etc. But he never provides a structure of possible graph parameters which allows one to classify and contrast the different interests of study. Finally, Frank does not appear to have articulated the role of graph sampling theory in relation to some common “network sampling methods” (e.g. [1, 19, 24]), which “are not explicitly stated as graph problems but which can be given such formulations” [8].

The aim of this paper is to synthesise and extend the existing graph sampling theory, many elements of which are only implicit in Frank’s works. In particular, we propose a definition of sample graph taken from a given population graph, together with the relevant observation procedures that enable sampling in a graph (Sect. 2). In Sect. 3, we provide a structure of graph totals and graph parameters, which reflects the extended scope of investigation that can be difficult or impossible using only a list representation. Next, we develop a general approach to HT-estimation under arbitrary T-stage snowball sampling (Sect. 4). In Sect. 5, we present various graph sampling reformulations of multiplicity sampling [1], indirect sampling [19] and adaptive cluster sampling [24], all of which are referred to as unconventional sampling methods in contrast to the more familiar finite-population sampling methods, such as stratified multi-stage sampling. Finally, some concluding remarks are given in Sect. 6, together with a couple of topics of current research.

2 Sampling on a graph

2.1 Terms and notations

A graph $G=(U, A)$ consists of a set of nodes U and a set of edges A. Define $|U|=N$ and $|A|= R$ as the order and size of G, respectively. Let $A_{ij} \subset A$ be the set of all edges from i to j; let $a_{ij} = |A_{ij}|$ be its size. If $a_{ij} >1$ for some $i,j\in U$, the graph is called a multigraph; it is a simple graph if $a_{ij} = 0, 1$. The edges in $A_{i+}= \bigcup _{j \in U} A_{ij}$ and $A_{+i}=\bigcup _{j \in U} A_{ji}$ are called the outedges and inedges at i, respectively. Let $a_{i+} = |A_{i+}| = \sum _{j\in U} a_{ij}$ and $a_{+i} = |A_{+i}| = \sum _{j\in U} a_{ji}$. The node i is incident to each outedge or inedge at i. The number of edges incident at a node i is called the degree of i, denoted by $d_i = a_{i+} + a_{+i}$. Two nodes i and j are adjacent if there exists at least one edge between them, i.e. $a_{ij} + a_{ji} >1$. For any edge in $A_{ij}$, i is called its initial node and j its terminal node. Let $\alpha _i$ be the successors of i, which are the terminal nodes of outedges at i; let $\beta _i$ be the predecessors of i, which are the initial nodes of inedges at i. For a simple graph, we have $a_{i+} = |\alpha _i|$ and $a_{+i} = |\beta _i|$. A graph is said to be directed (i.e. a digraph) if $A_{i+} \ne A_{+i}$; it is undirected if $A_{i+} = A_{+i}$, in which case there is no distinction between outedge and inedge, so that $d_i = a_{i+} = a_{+i}$, and $\alpha _i = \beta _i$. Finally, an edge $a_{ii}$ connecting the same node i is called a loop, which can sometimes be a useful means of representation. Whether or not loops are included in the definitions of the terms and notations above is purely a matter of convention.

Remark

Adjacency refers to relationship between nodes, as objects of the same kind; incidence refers to relationship between nodes and edges, i.e. objects of different kinds.

Remark

Let the $N\times N$ adjacency matrix $\mathbf{A}$ have elements $a_{ij} = |A_{ij}|$. It is defined to be symmetric for undirected graphs. Put the diagonal degree matrix $\mathbf{D} = \text{ diag }(\mathbf{A} 1_{N \times 1})$. The Laplacian matrix $\mathbf{L} = \mathbf{D} - \mathbf{A}$ sums to 0 by row and column, which is of central interest in Spectral Graph Theory (e.g. [2]).

2.2 Definition of sample graph

Denote by $s_1$ an initial sample of nodes, for $s_1 \subseteq U$. Under a probability design, let $\pi _{i}$ and $\pi _{ij}$ (or $\bar{\pi }_{i}$ and $\bar{\pi }_{ij}$) be the probabilities of inclusion (or exclusion) of respectively a node and a pair of nodes in $s_1$. (The exclusion probability of i is the probability of $i\not \in s_1$, and the exclusion probability of a pair (i, j) is the probability that neither i nor j is in $s_1$.) A defining feature of sampling on graphs is that one makes use of the edges to select the sample graph, denoted by $G_s$. Given $s_1$, the relevant edges are either in $\alpha (s_1) = \bigcup _{i\in s_1} \alpha _i$ or $\beta (s_1) = \bigcup _{i\in s_1} \beta _i$, where $\alpha (s_1) = \beta (s_1)$ for undirected graphs. An observation procedure of the edges needs to be specified, and the observed edges can be given in terms of a reference set of node pairs, denoted by $s_2$ where $s_2 \subseteq U\times U$, under the convention that the set of edges $A_{ij}$ are observed whenever $(ij) \in s_2$. Notice that generally speaking (ij) and (ji) are considered as two distinct elements in $U\times U$. Denote by $\pi _{(ij)}$ (or $\bar{\pi }_{(ij)}$) the corresponding inclusion (or exclusion) probability of $(ij)\in s_2$, and by $\pi _{(ij)(kl)}$ (or $\bar{\pi }_{(ij)(kl)}$) the inclusion (or exclusion) probability of these two pairs in $s_2$. Denote by $A_s = A(s_2)$ the edge set inherent of $s_2$, and $U_s = s_1 \cup \text{ Inc }(A_s)$ the union of $s_1$ and those nodes that are incident to $A_s$. The sample graph is $G_s = \big ( U_s, A_s \big )$.

Example 1

Let $U = \{1, 2, 3\}$, and $a_{12} = 1$. Suppose $s_1 = \{ 1\}$. Provided $s_2 = s_1 \times \alpha (s_1)$, where $\alpha (s_1) =\{ 2\}$ in this case, the sample graph $G_s$ has $A_s = A(s_2) = A_{12}$ and $U_s = \{ 1, 2\}$. The same sample graph can equally be given by $s_2' = s_1\times U$, since $A(s_2') = A_{12} = A(s_2)$.

Observation procedure Frank [8] considers several observation procedures, which can be formalised as follows. First, given $s_1$, a procedure is induced if $A_{ij}$ is observed iff both $i\in s_1$ and $j\in s_1$, or incident reciprocal if $A_{ij}$ and $A_{ji}$ are both observed provided either $i\in s_1$ or $j\in s_1$. Second, for digraphs, an incident non-reciprocal procedure is forward if $A_{ij}$ is observed provided $i\in s_1$, or backward if $A_{ij}$ is observed provided $j\in s_1$. For example, provided $i\in s_1$ and $j\not \in s_1$ and $a_{ij}>0$ and $a_{ji}>0$, we would observe both $A_{ji}$ and $A_{ji}$ given an incident reciprocal procedure; only $A_{ij}$ if it is incident forward; only $A_{ji}$ if it is incident backward; neither $A_{ij}$ nor $A_{ji}$ given an induced procedure from $s_1$.

Initial sampling of edges Sample graph initiated by a sample of edges can be defined analogously. Bernoulli or Poisson sampling can be useful, because it is not required to know all the edges in advance. Notice that when one is interested in the totals or other functions of the edges of a graph, initial Bernoulli or Poisson sampling of edges is meaningful—see e.g. Frank [8, Section 12], whereas initial simple random sampling (of edges) would have been a trivial set-up, because one would need to know all the edges to start with.

2.3 Some graph sampling methods

We describe some sampling methods based on the aforementioned observation procedures. Frank [8] elicited several sampling methods based on the aforementioned observation procedures. We include several alternative specifications which are marked by $\dagger$. By way of introduction, the first- and second-order inclusion probabilities of (ij) in $s_2$ are given in terms of the relevant inclusion probabilities in $s_1$, which facilitates Horvitz–Thompson (HT) estimation of any totals defined on $U\times U$. As will be illustrated, given $s_1$ and the observation procedure, the sample graph can be specified using different reference sets $s_2$, but the inclusion probabilities are more readily obtained for some choices of $s_2$.

• (i) $s_2 = s_1\times s_1$ [Induced]: Both $(ij)\in s_2$ and $(ji)\in s_2$ iff $i\in s_1$ and $j\in s_1$. Then, $\pi _{(ij)} = \pi _{ij}$ and $\pi _{(ij)(kl)} = \pi _{ijkl}$.

• (ii.1) $s_2 = s_1\times s_a$, $s_a = \alpha (s_1) \cup s_1$ [Incident forward]: $(ij)\in s_2$ iff $i\in s_1$ and $j \in s_a$. Let $B_j = \{ j\} \cup \beta _j$, i.e. itself and its predecessors, then $j\in s_a$ iff $B_j \cap s_1 \ne \emptyset$. Thus,

  $$\begin{aligned} \bar{\pi }_{(ij)} = \bar{\pi }_i + \bar{\pi }_{B_j} - \bar{\pi }_{B_j \cup \{ i\}}. \end{aligned}$$

  Similarly, $(ij),(kl)\in s_2$ iff $i,k\in s_1$ and $B_j\cap s_1\ne \emptyset$ and $B_l\cap s_1\ne \emptyset$, so that

  $$\begin{aligned} \bar{\pi }_{(ij)(kl)}&= \bar{\pi }_{ik} + \bar{\pi }_{B_j\cup \{k\}} + \bar{\pi }_{B_l \cup \{ i\}} + \bar{\pi }_{B_j \cup B_l} \\&\quad - \bar{\pi }_{B_j\cup \{i,k\}} - \bar{\pi }_{B_l \cup \{ i,k\}} - \bar{\pi }_{B_j \cup B_l\cup \{i\}} - \bar{\pi }_{B_j \cup B_l\cup \{k\}} + \bar{\pi }_{B_j \cup B_l\cup \{i, k\}}. \end{aligned}$$

• (ii.2) $s_2 = s_1\times U$ [Incident forward]: $(ij) \in s_2$ iff $i \in s_1$. Then, $\pi _{(ij)} = \pi _i$ and $\pi _{(ij)(kl)} = \pi _{ik}$.

Remark

The sample edge set $A(s_2)$ is the same in (ii.2) and (ii.1), because the observation procedure is the same given $s_1$. For the estimation of any total over A, the two reference sets would yield the same HT-estimate: any $(ij) \in s_2$ with $a_{ij}=0$ does not contribute to the estimate, regardless of its $\pi _{(ij)}$; whereas for any $(ij) \in s_2$ with $a_{ij} >0$, we have $\pi _{(ij)} = \pi _i$ given $s_2$ in (ii.2), just as one would have obtained in (ii.1) since $B_j = B_j \cup \{ i\}$ provided $a_{ij} >0$. But it appears easier to arrive at $\pi _{(ij)}$ and the HT-estimator in (ii.2) than (ii.1).

• (ii.3) $^{\dagger }$ $s_2 = s_b \times \alpha (s_1)$, $s_b = s_1 \cap \beta \big ( \alpha (s_1)\big )$ [Incident forward]: This is the smallest Cartesian product that contains the same sample edge set as in (ii.1) and (ii.2).

• (ii.4) $^{\dagger }$ $s_2 = \bigcup \nolimits _{i \in s_1} i \times \alpha _i$, where $i \times \alpha _i =\emptyset$ if $\alpha _i =\emptyset$ [Incident, forward]: Only (ij) with $a_{ij}>0$ is included $s_2$. This is the smallest reference set for the same $G_s$ in (ii.1)–(ii.4).

• (iii) $s_2 = s_a \times s_a$, $s_a = \alpha (s_1) \cup s_1$ [Induced from $s_a$]: $(ij) \in s_2$ even if $i\in s_a {\setminus } s_1$ and $j\in s_a {\setminus } s_1$. Similarly to (ii.1), $(ij)\in s_2$ iff $B_i \cap s_1\ne \emptyset$ and $B_j \cap s_1\ne \emptyset$, and so on. Then,

  $$\begin{aligned} \bar{\pi }_{(ij)}&= \bar{\pi }_{B_i} + \bar{\pi }_{B_j} - \bar{\pi }_{B_i \cup B_j}, \\ \bar{\pi }_{(ij)(kl)}&= \bar{\pi }_{B_i \cup B_k} + \bar{\pi }_{B_i\cup B_l} + \bar{\pi }_{B_j \cup B_k} + \bar{\pi }_{B_j \cup B_l} \\&\quad - \bar{\pi }_{B_i\cup B_k \cup B_l} - \bar{\pi }_{B_j \cup B_k \cup B_l} - \bar{\pi }_{B_i \cup B_j\cup B_k} - \bar{\pi }_{B_i \cup B_j\cup B_l} + \bar{\pi }_{B_i \cup B_j\cup B_k \cup B_l}. \end{aligned}$$

Remark

Observation of the edges between $i\in s_a {\setminus } s_1$ and $j\in s_a {\setminus } s_1$ may be demanding in practice, even when the observation procedure is reciprocal. For example, let the node be email account. Then, by surveying $i\in s_1$ only, it is possible to observe all the email accounts that have exchanges with i due to reciprocality. But one would have to survey the accounts in $\alpha _i {\setminus } s_1$ additionally, in order to satisfy the requirement of (iii).

• (iv.1) $s_2 = s_1\times U \cup U \times s_1$ [Incident reciprocal]: $(ij)\not \in s_2$ iff $i\not \in s_1$ and $j\not \in s_1$. Then, $\pi _{(ij)} =1 - \bar{\pi }_{ij}$ and $\pi _{(ij)(kl)} = 1 - \bar{\pi }_{ij}- \bar{\pi }_{kl} + \bar{\pi }_{ijkl}$.

• (iv.2) $^\dagger$ $s_2 = s_1 \times s_a \cup s_a \times s_1$, $s_a = \alpha (s_1) \cup s_1$ [Incident reciprocal]: We have $s_a\times s_a = s_2 \cup (s_a{\setminus } s_1) \times (s_a{\setminus } s_1)$, where the two sets on the right-hand side are disjoint. The inclusion probabilities can thus be derived from those in (iii) and those of $(s_a{\setminus } s_1) \times (s_a{\setminus } s_1)$. However, the sample edge set $A(s_2)$ is the same as in (iv.1), and it is straightforward to derive the HT-estimator of any total over A based on the reference set $s_2$ specified in (iv.1).

• (iv.3) $^{\dagger }$ $s_2 = \big ( \bigcup \nolimits _{i \in s_1} i\times \alpha _i\big ) \cup \big ( \bigcup \nolimits _{i \in s_1} \beta _i \times i\big )$ [Incident reciprocal]: This is the smallest reference set of the sample edge set in (iv.1)–(iv.3).

Example 2

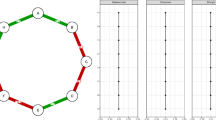
Figure 1 illustrates the four sampling methods (i)–(iv) described above, all of which are based on the same initial sample $s_1= \{3,6,10\}$.

Fig. 1

Population graph (top) and four sample graphs (i)–(iv) based on $s_1 = \{ 3, 6, 10\}$

3 Graph parameter and HT-estimation

Frank [12] reviews some statistical problems based on population graphs. In a list representation, the target population U is a collection of elements, which are associated with certain values of interest. In a graph representation $G = (U, A)$, the elements in U can be the nodes that have relations to each other, which are presented by the edges in A. It becomes feasible to investigate the interactions between the elements, their structural positions, etc. which are difficult or unnatural using a list representation. The extended scope of investigation is above all reflected in the formulation of the target parameter. In this Section, we provide our own classification of the potential target parameters based on a graph in terms of graph totals and graph parameters.

Graph total and graph parameter Let $M_k$ be a subset of U, where $|M_k| = k$. Let $\mathcal {C}_k$ be the set of all possible $M_k$’s, where $|\mathcal {C}_k| = N! [k! (N-k)!]^{-1}$. Let $G(M_k)$ be the subgraph induced by $M_k$. Let $y\big (G(M_k)\big )$, or simply $y(M_k)$, be a function of integer or real value. The corresponding kth order graph total is given by

$$\begin{aligned} \theta = \sum _{M_k \in \mathcal {C}_k} y(M_k). \end{aligned}$$

(1)

We refer to functions of graph totals as graph parameters.

Remark

Network totals can as well be defined by (1), where $y(\cdot )$ can incorporate the values associated with the nodes and edges of the induced subgraph $G(M_k)$.

Motif A subset $M\subset U$ with specific characteristics is said to be a motif, denoted by [M]. For example, denote by $[i: d_i = 3]$ a 1st-order motif, i.e. a node with degree 3. Or, denote by $[i,j : a_{ij} = a_{ji} =1]$ the motif of a pair of nodes with mutual simple relationship, or by $[i,j : a_{ij} = a_{ji} =0]$ the motif of a pair of non-adjacent nodes. A motif may or may not have a specific order, giving rise to graph totals with or without given orders.

3.1 Graph totals of a given order

3.1.1 First-order graph total: $M_1 = \{ i\}$

Each $M_1$ corresponds to a node. In principle any first-order graph total can be dealt with by a list sampling method that does not make use of the edges, against which one can evaluate the efficiency of any graph sampling method. For the two parameters given below, estimation of the order by snowball sampling is considered by Frank [5, 8, 15], and estimation of the degree distribution is considered by Frank [5, 11].

Order (of G) Let $y(i) \equiv 1$, for $i\in U$. Then, $\theta = |U| = N$.

Number of degree- d nodes Let $y(i) = \delta (d_i =d)$ indicate whether or not $d_i$ equals d, for $i\in U$. Then, $\theta$ is the number of nodes with degree d.

3.1.2 Second-order graph total: $M_2 = \{ i, j\}$

An $M_2$ of a pair of nodes is called a dyad, for $M_2 \subset U$ and $|M_2| = 2$. Some dyad totals are considered by Frank [5, 10].

Size (of G) Let $y(M_2) = a_{ij} + a_{ji}$ be the adjacency count between i and j in a digraph, or $y(M_2) = a_{ij}$ for an undirected graph. Then, $\theta = \sum _{M_2\in \mathcal {C}_2} y(M_2) = R$ is the size (of G).

Remark

If there are loops, one can let $y(M_1) = a_{ii}$ for $M_1 = \{ i\}$, and $\theta ' =\sum _{M_1\in \mathcal {C}_1} y(M_1)$. Then, $R = \theta + \theta '$ is a graph parameter based on a 1st- and a 2nd-order graph totals.

Remark

Let $N_d$ be the no. degree-d nodes, which is a 1st-order graph total. Then,

$$\begin{aligned} 2 R = \sum _{i\in U} d_i = \sum _{d=1}^{D} d N_d,\quad \text {where}\quad D = \max _{i\in U} d_i. \end{aligned}$$

This is an example where a higher-order graph total (R) can be ‘reduced’ to lower-order graph parameters ($N_d$). Such reduction can potentially be helpful in practice, e.g. when it is possible to observe the degree of a sample node without identifying its successors.

Number of adjacent pairs Let $y(M_2) = \delta (a_{ij} + a_{ji} >0)$ indicate whether i and j are adjacent. Then, $\theta$ is the total number of adjacent pairs in G. Its ratio to $|\mathcal {C}_2|$ provides a graph parameter, i.e. an index of immediacy in the graph. Minimum immediacy is the case when a graph consists of only isolated nodes, and maximum immediacy if the graph is a clique, where every pair of distinct nodes are adjacent with each other.

Number of mutual relationships Let $y(M_2) = \delta (a_{ij} a_{ji} >0)$ indicate whether i and j have reciprocal edges between them, in which case their relationship is mutual. Then, $\theta$ is the number of mutual relationships in the graph. Goodman [17] studies the estimation of the number of mutual relationships in a special digraph, where $a_{i+} = 1$ for all $i\in U$.

3.1.3 Third-order graph total: $M_3 = \{ i, j, h\}$

An $M_3$ of three nodes is called a triad, for $M_3 \subset U$ and $|M_3| = 3$. Some triad totals are considered by Frank [5,6,7, 10].

Number of triads Let $y(M_3) = \delta (a_{ij} a_{jh} a_{ih} >0)$ indicate whether the three nodes form a triangle in an undirected graph. Then, $\theta ^*$ by (1) is the total number of triangles. Triangles on undirected graphs are intrinsically related to equivalence relationships: for a relationship (represented by an edge) to be transitive, every pair of connected nodes must be adjacent; hence, any three connected nodes must form a triangle. For a simple undirected graph, transitivity is the case iff $\theta ' =0$, when $\theta '$ is given by (1), where

$$\begin{aligned} y(M_3) = a_{ij} a_{jh} (1- a_{hi}) + a_{ih} a_{jh} (1- a_{ij}) + a_{ij} a_{ih} (1- a_{jh}). \end{aligned}$$

Provided this is not the case, one can e.g. still measure the extent of transitivity by

$$\begin{aligned} \tau = \theta ^* / (\theta ^* + \theta '), \end{aligned}$$

i.e. a graph parameter. Next, for digraphs and ordered (jih), let $z(jih) = a_{ji} a_{ih} a_{hj}$ be the count of strongly connected triangles from j via i and h back to j. Let $\widetilde{M}_3$ contain all the possible orderings of $M_3$, i.e. (ijh), (ihj), (jih), (jhi), (hij) and (hji). Then, the number of strongly connected triangles in a digraph is given by (1), where

$$\begin{aligned} y(M_3) = \sum _{(ijh)\in \widetilde{M}_3} z(ijh)/3. \end{aligned}$$

Remark

For undirected simple graphs, Frank [13] shows that there exists an explicit relationship between the mean and variance of the degree distribution and the triads of the graph. Let the numbers of triads of respective size 3, 2 and 1 be given by

$$\begin{aligned} \theta _{3,3}&= \sum _{M_3\in \mathcal {C}_3} a_{ij} a_{jh} a_{ih}, \\ \theta _{3,2}&= \sum _{M_3\in \mathcal {C}_3} a_{ij} a_{ih} (1- a_{jh}) + a_{ij} a_{jh} (1- a_{ih}) + a_{ih} a_{jh} (1- a_{ij}), \\ \theta _{3,1}&= \sum _{M_3\in \mathcal {C}_3} a_{ij} (1-a_{jh}) (1- a_{ih}) + a_{ih} (1- a_{ij}) (1- a_{jh}) + a_{jh} (1- a_{ij}) (1- a_{ih}). \end{aligned}$$

Let $\mu = \sum _{d=1}^N d N_d/N = 2R/N$ and $\sigma ^2 = Q/N - \mu ^2$, where $Q =\sum _{d=1}^N d^2 N_d$. We have

$$\begin{aligned} R = \frac{1}{N-2} \big ( \theta _{3,1} + 2 \theta _{3,2} + 3 \theta _{3,3} \big ), \quad Q = \frac{2}{N-1} \big ( \theta _{3,1} + N \theta _{3,2} + 3(N-1) \theta _{3,3} \big ). \end{aligned}$$

3.2 Graph totals of unspecified order

A motif is sometimes defined in an order-free manner. Insofar as the corresponding total can be given as a function of graph totals of specific orders, it can be considered a graph parameter. Below are some examples that are related to the connectedness of a graph. The number of connected components is considered by Frank [5, 9].

Number of connected components The subgraph induced from $M_k$ is a connected component of order k, provided there exists a path for any $i\ne j\in M_k$ and $a_{ij} = a_{ji} =0$ for any $i\in M_k$ and $j\not \in M_k$, in which case let $y(M_k) =1$ but let $y(M_k) =0$ otherwise. Then, $\theta _k$ given by (1) is the number of connected components of order k. The number of connected components (i.e. as a motif of unspecified order) is the graph parameter given by $\theta = \sum _{k=1}^N \theta _k$. At one end, where $A = \emptyset$, i.e. there are no edges at all in the graph, we have $\theta = N = \theta _1$ and $\theta _k = 0$ for $k> 1$. At the other end, where there exists a path between any two nodes, we have $\theta = \theta _N = 1$ and $\theta _k = 0$ for $k< N$.

Number of trees in a forest In a simple graph, a motif $[M_k]$ is a tree if the number of edges in $G(M_k)$ is $k -1$. As an example where $\theta$ can be reduced to a specific graph total, suppose the undirected graph is a forest, where every connected component is a tree. We have then $\theta = N -R$, where R is the size of the graph, which is a 2nd-order parameter.

Number of cliques A clique is a connected component, where there exists an edge between any two nodes of the component. It is a motif of unspecified order. The subgraph induced by a clique is said to be complete. A clustered population can be represented by a graph, where each cluster of population elements (i.e. nodes) form a clique, and two nodes i and j are adjacent iff the two belong to the same cluster.

Index of demographic mobility Given the population of a region (U), let there be an undirected edge between two persons i and j if their family trees intersect, say, within the last century, i.e. they are relatives of each other within a ‘distance’ of 100 years. Each connected component in this graph G is a clique. The ratio between the number of connected components $\theta$ and N, where N is the maximum possible $\theta$, provides an index of demographic mobility that varies between 1 / N and 1. Alternatively, an index can be given by the ratio between the number of edges R and $|\mathcal {C}_2|$, which varies between 0 and 1, and is a function of a 2nd-order graph total. This is an example where the target parameter can be specified in terms of a lower-order graph total than higher-order totals.

Remark

In the context of estimating the number of connected components, Frank [5] discusses the situation where observation is obtained about whether a pair of sample nodes are connected in the graph, without necessarily including the paths between them in the sample graph. The observation feature is embedded in the definition of the graph here.

Geodesics in a graph Let an undirected graph G be connected, i.e. $U = M_N$ is a connected component. The geodesic between nodes i and j is the shortest path between them, denoted by $[M_k]$, where $M_k$ contains the nodes on the geodesic, including i and j. A geodesic $[M_k]$ is a motif of order k, whereas geodesic is generally a motif of unspecified order. Let $\theta$ be the harmonic mean of the length of the geodesics in G, which is a closeness centrality measure [20]. For instance, it is at its minimum value 1 if G is complete. Alternatively, let $y(M_2) = 1/(k-1)$, provided $[M_k]$ is the geodesic between i and j, so that $\theta$ can equally be given as a 2nd-order graph parameter. Again, this is an example where a lower-order graph parameter can be used as the target parameter instead of alternatives involving higher-order graph totals, provided the required observation.

3.3 HT-estimation

A basic estimation approach in graph sampling is the HT-estimator of a graph total (1). Provided the inclusion probability $\pi _{(M_k)}$ for $M_k \in \mathcal {C}_k$, the HT-estimator is given by

$$\begin{aligned} \hat{\theta } = \sum _{M_k\in \mathcal {C}_k} \delta _{[M_k]} y(M_k)/\pi _{(M_k)}, \end{aligned}$$

(2)

where $\delta _{[M_k]} = 1$ if $[M_k]$ is observed and $\pi _{(M_k)}$ is its inclusion probability. The observation of $[M_k]$ means not only $M_k \subseteq U_s$, but also it is possible to identify whether $M_k$ is a particular motif in order to compute $y(M_k)$. The probability $\pi _{(M_k)}$ is defined with respect to a chosen reference set $s_2$ and the corresponding sample graph $G_s$. It follows that a motif $[M_k]$ is observed in $G_s$ if $M_k \subseteq U_s$ and $M_k \times M_k \subseteq s_2$. More detailed explanation of $\pi _{(M_k)}$ will be given in Sect. 4. The example below illustrates the idea.

Example 3

Consider an undirected simple graph. Let 3-node star be the motif of interest, and $y(M_3) = a_{ij} a_{ih} (1- a_{jh}) + a_{ij} a_{jh} (1- a_{ih}) + a_{ih} a_{jh} (1- a_{ij})$ the corresponding indicator. Suppose incident observation and $s_2 = s_1 \times U$. Consider $M_3 = \{ i, j, h\} \subset U_s$. To be able to identify whether it is the motif of interest, all the three pairs (ij), (ih) and (jh) need to be in $s_2$; accordingly, $\pi _{(M_3)} = \text{ Pr }\big ( (ij)\in s_2, (ih) \in s_2, (jh) \in s_2\big )$. An example where this is not the case is $i\in s_1$ and $j,h\in \alpha (s_1) {\setminus } s_1$, so that the observed part of this triad is a star, but one cannot be sure if $a_{jh} = 0$ in the population graph, because $(jh) \not \in s_2$.

Symmetric designs The inclusion probability $\pi _{(M_k)}$ depends on the sampling design of initial $s_1$. At various places, Frank consider simple random sampling (SRS) without replacement, Bernoulli sampling and Poisson sampling for selecting the initial sample. In particular, a sampling design is symmetric [6] if the inclusion probability $\pi _{M_k} = \text{ Pr }(M_k \in s_1)$ only depends on k but is a constant of $M_k$, for all $1\le k\le N$. SRS with or without replacement and Bernoulli sampling are all symmetric designs. SRS without replacement is the only symmetric design with fixed sample size of distinct elements.

Approximate approach The initial inclusion probability $\pi _{M_k}$ has a simpler expression under Bernoulli sampling than under an SRS design. Provided negligible sampling fraction of $s_1$, many authors use Bernoulli sampling with probability $p = |s_1|/N$ to approximate any symmetric designs. Similarly, initial unequal probability sampling may be approximated by Poisson sampling with the same $\pi _i$, for $i\in U$, provided negligible sampling fraction $|s_1|/N$. Finally, Monte Carlo simulation [4] may be used to approximate the relevant $\pi _{M_k}$ under sampling without replacement.

4 T-stage snowball sampling

An incident observation procedure (Sect. 2.3) provides the means to enlarge a set of sample nodes by their out-of-sample adjacent nodes. It yields a method of 1-stage snowball sampling, which can be extended successively to yield the T-stage snowball sampling. Below we assume that all the successors are included in the sample. But it is possible to take only some of the successors at each stage (e.g. [23]). In particular, taking one successor each time yields a T-stage walk (e.g. [18]). Two different observation procedures will be considered, i.e. incident forward in digraphs and incident reciprocal in directed or undirected graphs. We develop general formulae for inclusion probabilities under T-stage snowball sampling. It is shown that additional observation features are necessary for the HT-estimator based on T-stage snowball sampling, which will be referred to as incident ancestral. Previously, Goodman [17] has studied the estimation of mutual relationships between i and j, where $a_{ij} a_{ji} >0$ for $i\ne j\in U$, based on T-stage snowball sampling in a special digraph with fixed $a_{i+} \equiv 1$; Frank [8] and Frank and Snijders [15] considered explicitly HT-estimation based on 1-stage snowball sampling.

Sample graph $G_s = (U_s, A_s)$ Let $s_{1,0}$ be the initial sample of seeds, and $\alpha (s_{1,0})$ its successors. Let $U_0 \subseteq U$ be the set of possible initial sample nodes. The additional nodes $s_{1,1} = \alpha (s_{1,0}) {\setminus } s_{1,0}$ are called the fist-wave snowball sample, which are the seeds of the second-wave snowball sample, and so on. At the tth stage, let $s_{1,t} = \alpha (s_{1,t-1}) {\setminus } \big ( \bigcup \nolimits _{h=0}^{t-1} s_{1,h} \big )$ be the tth stage seeds, for $t = 1, 2,\ldots , T$. If $s_{1,t} = \emptyset$, set $s_{1,t+1} = \cdots = s_{1,T} = \emptyset$ and terminate, otherwise move to stage $t+1$. Let $s_1 = \bigcup \nolimits _{t=0}^{T-1} s_{1,t}$ be the sample of seeds. This may result in two different sample graphs.

• I Let $s_2 = s_1 \times U$ provided incident forward observation in digraphs, such that the sample graph $G_s$ has edge set $A_s = \bigcup \nolimits _{i\in s_1} \bigcup \nolimits _{j\in \alpha _i} A_{ij}$ and node set $U_s = s_1 \cup \alpha (s_1)$.

• II Let $s_2 = s_1 \times U \cup U\times s_1$ provided incident reciprocal observation, digraphs or not, such that $G_s$ has edge set $A_s = \bigcup \nolimits _{i\in s_1} \bigcup \nolimits _{j\in \alpha _i} (A_{ij}\cup A_{ji})$ and node set $U_s = s_1 \cup \alpha (s_1)$.

Remark

One may disregard any loops in snowball sampling, because they do not affect the propagation of the waves of nodes, but only cause complications to their definition.

4.1 Inclusion probabilities of nodes and edges in $G_s$

Below we develop the inclusion probabilities $\pi _{(i)}$ and $\pi _{(i)(j)}$ of nodes in $U_s$, and $\pi _{(ij)}$ and $\pi _{(ij)(hl)}$ of edges in $A_s$, under T-stage snowball sampling with $s_2$ as specified above.

Forward observation in digraphs The stage-specific seed samples $s_{1,0}, \ldots , s_{1,T-1}$ are disjoint, so that each observed edge, denoted by $\langle ij \rangle \in A_s$, can only be included at a particular stage. For $i\in U$, let $\beta _i^{[0]} =U_0 \cap \{ i\}$; let $\beta _i^{[t]} =U_0 \cap \Big ( \beta (\beta _i^{[t-1]}) {\setminus } \big ( \bigcup \nolimits _{h=0}^{t-1} \beta _i^{[h]}\big ) \Big )$ be its tth generation predecessors, for $t>0$, which consists of the nodes that would lead to i in t-stages from $s_{1,0}$ but not sooner. Notice that $\beta _{i}^{[0]}, \beta _{i}^{[1]}, \beta _{i}^{[2]}, \ldots$ are disjoint. We have

$$\begin{aligned}&\pi _{(i)} = 1 - \bar{\pi }_{B_i} \quad \text {for}\quad B_i = \bigcup _{t=0}^{T} \beta _i^{[t]}, \\&\pi _{(ij)} = 1 - \bar{\pi }_{B_{ij}} \quad \text {for}\quad B_{ij} = \bigcup _{t=0}^{T-1} \beta _i^{[t]}. \end{aligned}$$

The respective joint inclusion probabilities follow as $\pi _{(i)(j)} = 1 - \bar{\pi }_{B_i} - \bar{\pi }_{B_j} + \bar{\pi }_{B_i \cup B_j}$ and $\pi _{(ij)(hl)} = 1 - \bar{\pi }_{B_{ij}} - \bar{\pi }_{B_{hl}} + \bar{\pi }_{B_{ij} \cup B_{hl}}$.

Incident reciprocal observation Each $\langle ij\rangle \in A_s$ can only be included at a particular stage, where either i or j is in the seed sample, regardless if the graph is directed or not. For $i\in U$, let $\eta _i = \{ j\in U; a_{ij} + a_{ji} >0\}$ be the set of its adjacent nodes. Let $\eta _i^{[0]} =U_0 \cap \{ i\}$; let $\eta _i^{[t]} =U_0 \cap \Big ( \eta (\eta _i^{[t-1]}) {\setminus } \big ( \bigcup \nolimits _{h=0}^{t-1} \eta _i^{[h]}\big ) \Big )$ be its tth step neighbours, for $t>0$, which are the nodes that would lead to i in t-stages from $s_{1,0}$ but not sooner. We have

$$\begin{aligned}&\pi _{(i)} = 1 - \bar{\pi }_{R_i } \quad \text {for}\quad R_i = \bigcup _{t=0}^{T} \eta _i^{[t]}, \end{aligned}$$

(3)

$$\begin{aligned}&\pi _{(ij)} = 1 - \bar{\pi }_{R_{ij}} \quad \text {for}\quad R_{ij} = \bigcup _{t=0}^{T-1} \eta _i^{[t]} \cup \eta _j^{[t]}. \end{aligned}$$

(4)

The respective joint inclusion probabilities follow as $\pi _{(i)(j)} = 1 - \bar{\pi }_{R_i} - \bar{\pi }_{R_j} + \bar{\pi }_{R_i \cup R_j}$ and $\pi _{(ij)(hl)} = 1 - \bar{\pi }_{R_{ij}} - \bar{\pi }_{R_{hl}} + \bar{\pi }_{R_{ij} \cup R_{hl}}$.

Incident ancestral observation procedure It is thus clear that additional features of the observation procedure is required in order to calculate $\pi _{(i)}$ and $\pi _{(i)(j)}$ given any $T\ge 1$, or $\pi _{(ij)}$ and $\pi _{(ij)(hl)}$ given any $T\ge 2$. Reciprocal or not, an incident procedure is said to be ancestral in addition, if one is able to observe all the nodes that would lead to the inclusion of a node $i\in U_s$, which will be referred to as its ancestors. These are the predecessors of various generations for forward observation in digraphs, or the neighbours of various steps for reciprocal observation in directed or undirected graphs. Notice that the edges connecting the sample nodes in $U_s$ and their out-of-sample ancestors are not included in the sample graph $G_s$. More comments regarding the connections between snowball sampling and some well-known network sampling methods will be given in Sect. 5.

Remark

Frank [5] defines the reach at i as the order of the connected component containing node i. The requirement of observing the reach, without including the whole connected component in the sample graph, is similar to that of an ancestral observation procedure, even though the two are clearly different.

Example 4

To illustrate the inclusion probabilities (3) and (4), consider the population graph $G = (U, A)$, and a sample graph $G_s = (U_s, A_s)$ by 2-stage snowball sampling, with the initial sample $s_{1,0}=\{3,4\}$ by SRS with sample size 2. The 1st- and 2nd-wave snowball samples are $s_{1,1} = \{ 8,9,10\}$ and $s_{1,2}=\{ 1,5,7\}$, respectively. The sample of seeds is $s_1 = \{ 3,4,8,9,10\}$. Both G and $G_s$ are given in Fig. 2. To the left of Fig. 3, the true node inclusion probabilities $\pi _{(i)}$ are plotted against those given by (3), where there are 5 distinct values; to the right, the true edge inclusion probabilities $\pi _{(ij)}$ are plotted against those given by (4), where there are 4 distinct values. In both cases, the true inclusion probabilities are calculated directly over the 45 possible initial samples of size 2.

Fig. 2

Population graph G with 10 nodes and 11 edges (left), a sample graph $G_s$ by 2-stage snowball sampling starting from $s_{1,0} = \{ 3,4\}$ by simple random sampling (right)

Fig. 3

Inclusion probability $\pi _{(i)}$: true vs. (3), left; $\pi _{(ij)}$: true vs. (4), right

4.2 Arbitrary $M_k$ with $k\ge 2$ and $s_2 = s_1\times U \cup U \times s_1$

To fix the idea, consider incident reciprocal observation in directed or undirected graphs. Notice that one can as well let $s_2 = s_1 \times U$ in the case of undirected graphs.

Definition of $\pi _{(M_k)}$ for $M_k \subset U$ To be clear, write $\{ i_1, i_2, \ldots , i_k \}$ for $M_k\subset U$. Let $M_k^{(h)} = M_k {\setminus } \{ i_h \}$ be the subset obtained by dropping $i_h$ from $M_k$, for $h=1, \ldots , k$. As explained in Sect. 3.3, to be able to identify the motif $[M_k]$, there can be at most one node in $M_k$ that belongs to the last wave of snowball sample ($s_{1,T}$). In other words, at least one of the k subsets $M_k^{(h)}$ must be in the sample of seeds $s_1$. We have

$$\begin{aligned} \pi _{(M_k)}&= \text{ Pr }\Big ( M_k^{(1)} \subseteq s_1 \text { or } M_k^{(2)} \subseteq s_1 \text { or } \cdots \text { or } M_k^{(k)} \subseteq s_1 \text { or } M_k \subseteq s_1 \Big ) \nonumber \\&= \sum _{h=1}^k \text{ Pr }\Big ( M_k^{(h)} \subseteq s_1 \Big ) - (k-1) \text{ Pr }\Big ( M_k \subseteq s_1 \Big ), \end{aligned}$$

(5)

where $\text{ Pr }\big ( M_k \subseteq s_1 \big ) = \pi _{(i_1)(i_2)\cdots (i_k)}$ is joint inclusion probability of the relevant nodes in $s_1$, similarly for $\text{ Pr }\big ( M_k^{(h)} \subseteq s_1 \big )$, where $h=1, \ldots , k$. The expression (5) follows from noting $\{ M_k^{(h)} \subseteq s_1 \} \cap \{ M_k\subseteq s_1\} =\{ M_k\subseteq s_1\}$, and $\{ M_k^{(h)} \subseteq s_1 \} \cap \{ M_k^{(l)}\subseteq s_1\} =\{ M_k\subseteq s_1\}$, and $\Big ( \{ M_k^{(h)} \subseteq s_1 \} {\setminus } \{ M_k\subseteq s_1\} \Big ) \cap \Big ( \{ M_k^{(l)} \subseteq s_1 \} {\setminus } \{ M_k\subseteq s_1\} \Big ) = \emptyset$.

Joint inclusion probability $\pi _{(M_k)(M_k')}$ For $M_k \subset U$ and $M_k' \subset U$, the joint observation of $[M_k]$ and $[M_k']$ requires that (i) at most one node i in $s_{1,T}$, provided $i\in M_k \cap M_k'$, or (ii) at most two nodes i, j in $s_{1,T}$, provided $i\in M_k{\setminus } M_k'$ and $j\in M_k' {\setminus } M_k$. Put $M = M_k \cup M_k'$. The relevant subsets are $M^{(i)}$ for all $i\in M_k\cap M_k'$, and $M^{(ij)}$ for all $i\in M_k{\setminus } M_k'$ and $j\in M_k' {\setminus } M_k$. The joint inclusion probability $\pi _{(M_k)(M_k')}$ follows, similarly as above for $\pi _{(M_k)}$, as the probability that at least one of these subsets is in the sample of seeds $s_1$.

Probability $\pi _{(i_1)(i_2)\cdots (i_k)}$ In the case of $k=2$, $\pi _{(i)(j)}$ is as given earlier in Sect. 4.1. To express $\pi _{(i_1)(i_2)\cdots (i_k)}$ in terms of the probabilities for the initial seed sample $s_{1,0}$, we have

$$\begin{aligned} \pi _{(i_1)(i_2)\cdots (i_k)} = \sum _{L\subseteq M_k} (-1)^{|L|} \bar{\pi }(L), \end{aligned}$$

(6)

where L includes $\emptyset$, and |L| is its cardinality, and $\bar{\pi }(L)$ is the exclusion probability

$$\begin{aligned} \bar{\pi }(L) = \text{ Pr }(L \cap s_1 = \emptyset ) = \text{ Pr }(R_L \cap s_{1,0} = \emptyset ) = \bar{\pi }_{R_L} = \sum _{D\subseteq R_L} (-1)^{|D|} \pi _{D}, \end{aligned}$$

(7)

where $R_L = \bigcup \nolimits _{i\in L} R_i$ and $R_i = \bigcup _{t=0}^{T-1} \eta _i^{[t]}$ is the ancestors of i up to the $T-1$ steps, and $\pi _D$ is joint inclusion probability of the nodes in D in the initial sample of seeds $s_{1,0}$.

4.3 Arbitrary $M_k$ with $k\ge 2$ and $s_2^* = s_1\times s_1$

By dropping the nodes $s_{1,T}$ of the last wave of T-stage snowball sampling, we ensure that the motif of any subset $M_k \in s_1$ is observable. The idea is developed below.

Definition of $\pi _{(M_k)}$ for $M_k \subseteq s_1$ Let $G_s = (U_s, A_s)$ be the sample graph of T-stage snowball sampling, with reference set $s_2 = s_1\times U \cup U \times s_1$. Let $G_s^* = (U_s^*, A_s^*)$ be the reduced sample graph obtained from dropping $s_{1,T}$, with reference set $s_2^* = s_1\times s_1$, where $A_s^* = A_s {\setminus } \{ \langle ij\rangle ; i\in s_1, j\in s_{1,T}\}$ and $U_s^* = U_s {\setminus } s_{1,T} = s_1$. Notice that $A_s^*$ contains all the edges between any $i,j\in s_1$ in the population graph G, and $G_s^*$ is the same sample graph that is obtained from $s_1$ by induced observation directly. It follows that one observes the motif for any $M_k \in s_1$, so that the inclusion probability $\pi _{(M_k)}$ is given by

$$\begin{aligned} \pi _{(M_k)} = \text{ Pr }\big ( M_k \subseteq s_1 \big ) = \pi _{(i_1)(i_2)\cdots (i_k)}, \end{aligned}$$

(8)

where $\pi _{(i_1)(i_2)\cdots (i_k)}$ is given by (6) and (7) as before.

Joint inclusion probability $\pi _{(M_k)(M_k')}$ For $M_k \subset s_1$ and $M_k' \subset s_1$, the joint observation of $[M_k]$ and $[M_k']$ requires simply $M= M_k \cup M_k' \subseteq s_1$. The joint inclusion probability $\pi _{(M_k)(M_k')}$ is therefore given by $\pi _{(M)}$ on replacing $M_k$ by M in (8), (6) and (7).

Other reduced graphs The sample graph $G_s^*$ is obtained from dropping the Tth wave nodes $s_{1,T}$. Rewrite $G_s^*$ as $G_s^{(T-1)}$; it can be reduced to $G_s^{(T-2)}$ by dropping $s_{1,T-1}$ as well. This yields $G_s^{(T-2)}$ as the induced graph among $s_1 {\setminus } s_{1,T-1}$. The inclusion probability $\pi _{(M_k)}$ for $M_k \subset A_s^{(T-2)}$ can be derived similarly as (8). Carrying on like this, one obtains in the end the reduced graph $G_s^{(0)}$, with reference set $s_2 = s_{1,0} \times s_{1,0}$, which is just the induced graph among $s_{1,0}$. The inclusion probability $\pi _{(M_k)}$ for $M_k\in s_{1,0}$ is $\pi _{M_k} = \text{ Pr }\big ( M_k \subseteq s_{1,0} \big )$ directly. Notice that the sample graph $G_s^{(0)}$ under T-stage snowball sampling can equally be obtained as $G_s^{(0)}$ under 1-stage snowball sampling. It follows that the additional $T-1$ wave-samples would simply have been wasted, had one only used $G_s^{(0)}$ for estimation. For the same reason it is equally implausible to use $G_s^{(1)}, \ldots , G_s^{(T-2)}$. However, $G_s^{(T-1)} = G_s^*$ is different because the last wave serves to establish $G_s^*$ as an induced sub-population graph, i.e. with no potentially missing edges among the relevant nodes.

Comparisons between $G_s^*$ and $G_s$ On the one hand, whichever motif of interest, $G_s$ always has a larger or equal number of observations than $G_s^*$. Hence, one may expect a loss of efficiency with $G_s^*$. On the other hand, estimation based on $G_s$ requires more computation than $G_s^*$. Firstly, for any $M_k \subseteq s_1$, it requires about k times extra computation for $\pi _{(M_k)}$ by (5) than by (8). This is due to the need to compute the probability of possibly observing $M_k$ as $M_k^{(h)} \subset s_1$ and $h\in s_{1,T}$, even if $M_k$ is observed as $M_k \subset s_1$, which is unnecessary with respect to $s_2^*$, where the observations are restricted to those among the nodes in $s_1$ without involving $s_{1,T}$. Secondly, corresponding to each $M_k \subseteq s_1$, there are additional observations with respect to $s_2$, which are all the possible $M_k' = \{ M_k^{(h)}, j; h\in M_k, j\not \in s_1\}$, because the motif of such an $M_k'$ can be identified. The motif of any $M_k'$ is unknown, if it differs from any $M_k \subseteq s_1$ by at least two nodes.

Fig. 4

Population graph G with 13 nodes and 19 edges (top); sample graphs $G_s$ (bottom left) and $G_s^*$ (bottom right) by 2-stage snowball sampling with initial $s_{1,0}=\{ 4, 5,10\}$

Example 5

To illustrate the inclusion probabilities (5) and (8), consider the population graph $G=(U,A)$ in Fig. 4, where $|U| = 13$ and $|A|=19$, together with the two 2-stage snowball sample graphs $G_s$ and $G_s^*$, both with $s_{1,0}=\{ 4, 5,10\}$ by SRS of sample size 3. We have $s_{1,1} = \{ 1,2,8,9 \}$, $s_{1,2} = \{ 3, 6,12,13\}$ and $s_1 = \{1,2,4,5,8,9,10\}$. Table 1 lists 6 selected triad ($M_3$) inclusion probabilities given by (5) and (8), respectively, with respect to $s_2 = s_1\times U$ and $s^*_2 = s_1 \times s_1$. These are seen to be equal to the true probabilities calculated directly over all possible initial samples $s_{1,0}$, under SRS of sample size 3. Table 2 shows the estimates of the four 3rd-order graph totals $\hat{\theta }_{3,h}$, for $h=0, 1, 2, 3$, which are as defined in Sect. 3.1.3, based on these two sample graphs $G_s$ and $G^*_s$. The expectation and standard error of each estimators are also given in Table 2, which can be evaluated directly over all the possible initial sample $s_{1,0}$. The true totals in the population graph G are $(\theta _{3,0},\theta _{3,1}, \theta _{3,2},\theta _{3,3}) = (121, 123,40,2)$. Clearly, both HT-estimators are unbiased, and using $G_s^*$ entails a loss of efficiency against $G_s$, as commented earlier.

Table 1 Inclusion probability $\pi _{(M_3)}$ of selected $M_3 = \{ i_1, i_2, i_3\}$

Table 2 Third-order graph total estimate, expectation and standard error

4.4 Proportional representative sampling in graphs

A traditional sampling method is sometimes said to be (proportional) representative if the sample distribution of the survey values of interest is an unbiased estimator of the population distribution directly. This is the case provided equal probability selection. Equipped with the general formulae for $\pi _{(M_k)}$ under T-stage snowball sampling, below we propose and examine a proportional representativeness concept for graph sampling.

Graph proportional representativeness Let $m_k \ne m_k'$ be two distinct motifs of the order k. A graph sampling method is k th order proportionally representative (PR$_k$) if

$$\begin{aligned} E[\theta _s]/\theta = E[\theta '_s]/ \theta ', \end{aligned}$$

(9)

where $\theta$ is the number of $m_k$ in the population graph G, and $\theta _s$ that of the observed $m_k$ in the sample graph $G_s$ with reference set $s_2$, and similarly with $\theta '$ and $\theta _s'$ for $m_k'$. Let $y(M_k) = 1$ if $[M_k] = m_k$ and 0 otherwise. Let $\delta _{[M_k]}$ be the observation indicator with respect to $s_2$. We have $\theta = \sum _{M_k \in \mathcal {C}_k} y(M_k)$ and $\theta _s = \sum _{M_k \in \mathcal {C}_k} \delta _{[M_k]} y(M_k)$. Clearly, a graph sampling method will be PR$_k$ if $\pi _{(M_k)}$ is a constant for different motifs of order k. Under any PR$_k$ design, one may estimate the relative frequency between $m_k$ and $m_k'$ by $\theta _s/\theta _s'$.

Result 1. Induced observation from $s_1$ is $PR_k$ for $k\ge 1$, provided $s_2 = s_1\times s_1$ and symmetric design $p(s_1)$. The result follows since, for any $M_k \subset A_s = s_1$, we have $\pi _{(M_k)} = \pi _{M_k}$, which is a constant of $[M_k]$ by virtue of symmetric design $p(s_1)$.

Result 2. One-stage snowball sampling is $PR_k$ for $k\ge 2$, provided $s_2 = s_1\times U \cup U\times s_1$ and symmetric design $p(s_1)$. Suppose first reciprocal observation. We have $R_i = \{ i\} \cup \eta _i^{[1]}$, whose cardinality varies for different nodes in G. It follows that $\pi _{(M_1)} = \pi _{(i)}$ by (3) is not a constant over U, i.e. the design is not PR$_1$. Next, for $M_k$ with $k\ge 2$, $\pi _{(M_k)}$ by (5) depends on $k+1$ probabilities given by (6) and (7). Each relevant probability $\bar{\pi }(L)$ is only a function of $|R_L|$ provided symmetric design $p(s_1)$, where $R_L = \bigcup \nolimits _{i\in L} R_i = L$ since $R_i = \{ i\}$ given $T=1$. It follows that $|R_L| = |L|$ regardless of the nodes in $M_k$, such that $\pi _{(M_k)}$ is a constant of $M_k$, i.e. PR$_k$. Similarly for forward observation in digraphs.

Remark

Setting $s_2^* = s_1\times s_1$ yields induced sample graph from $s_1$ and Result 1.

Result 3. T -stage snowball sampling is generally not $PR_k$ for $k\ge 1$ and $T\ge 2$, despite symmetric design $p(s_1)$. As under 1-stage snowball sampling, the design is not PR$_1$. Whether by (5) or (8) for $k\ge 2$, $\pi _{(M_k)}$ depends on $\bar{\pi }(L)$ in (6), which is only a function of $|R_L|$ provided symmetric design $p(s_1)$. However, given $T\ge 2$ and |L|, $R_L = \bigcup \nolimits _{i\in L} R_i$ generally varies for different L, so that neither $R_L$ nor $|R_L|$ is a constant of the nodes in $M_k$, i.e. the design is not PR$_k$. Similarly for forward observation in digraphs.

5 Network sampling methods

As prominent examples from the network sampling literature we consider here multiplicity sampling [1], indirect sampling [19] and adaptive cluster sampling [24]. Below we first summarise broadly their characteristics in terms of target parameter, sampling and estimator, and then discuss four salient applications of these methods using the snowball sampling theory developed in Sect. 4.

Target parameter In all the network sampling methods mentioned above, the target parameter is the total of a value associated with each node of the graph, denoted by $y_i$ for $i\in U$, which can be referred to as a 1st-order network total $\theta = \sum _{i\in U} y_i$ in light of (1). This does not differ from that when “conventional” sampling methods are applied for the same purpose, where Sirken [22] uses the term conventional in contrast to network. In other words, these network sampling methods have so far only been applied to overcome either certain deficiency of frame or lack of efficiency of the traditional sampling methods, as discussed below in terms of sampling and estimator, but not in order to study genuine network totals or parameters, which are of orders higher than one.

Sampling Like in the definition of sample graph, these network sampling methods start with an initial sample $s_1$. The sampling frame of $s_1$ can be direct or indirect. In the latter case, the sampling units are not the population elements. This may be necessary because a frame of the population elements is unavailable, such as when siblings are identified by following up kins to the household members of an initial sample of households [22]. Or, a frame of the elements may be available but is unethical to use, such as when children are accessed via a sample of parents [19]. In cases a direct frame of elements is used, the initial sample $s_1$ may be inefficient due to the low prevalence of in-scope target population elements, so that an observation procedure depending on the network relationship (between the elements) is used to increase the effective sample size. This is the case with adaptive cluster sampling (Thompson, 1989).

Estimator For 1-st order network parameters (1), where the population elements are represented as nodes in the population graph $G= (U, A)$, the HT-estimator (2) is defined for the observed nodes in the sample graph $G_s = (U_s, A_s)$. Another approach in the aforementioned methods is the HT-estimator defined for the selected sampling units. Let F be the frame of sampling units, where $l\in F$ has inclusion probability $\pi _l$. We have

$$\begin{aligned} \sum _{l\in F} z_l = \sum _{l\in F} \Big ( \sum _{i\in U} w_{li} y_i \Big ) =\sum _{i\in U} y_i \sum _{l\in F} w_{li} = \sum _{i\in U} y_i = \theta , \end{aligned}$$

where $z_l = \sum _{i\in U} w_{li} y_i$ is a value constructed for the sampling units, based on any chosen weights, provided $\sum _{k\in F} w_{ki} =1$, as noted by Birnbaum and Sirken [1]. The corresponding HT-estimator that is unbiased for $\theta$ can be given by

$$\begin{aligned} \tilde{\theta }_{HT} = \sum _{l\in s_1} z_l/\pi _l = \sum _{l\in F} z_l \delta _l/\pi _l, \end{aligned}$$

(10)

where $\delta _l =1$ if $l\in s_1$ and 0 otherwise. To ensure that $z_l$ can be calculated no matter which actual sample $s_1$, the weights $w_{li}$ must not depend on $s_1$. A common approach is to set $w_{li} = 1/m_i$, where l a sampling unit in $s_1$ which gives rise to i, and $m_i$ is the number of all sampling units in F that could lead to the observation of i, for $i\in U$. The number $m_i$ is referred to as the multiplicity of the element [1]. The observation of $m_i$ for each sample element is the same kind of requirement as the observation of the ancestors of a node in $U_s$ under snowball sampling. The literature is inconclusive on the relative efficiency between the two estimators (2) and (10).

5.1 Sampling patients via hospitals

Birnbaum and Sirken [1] consider this situation, without using graph representation. To fix the idea, suppose a sample of hospitals is selected according to a probability design. From each sample hospital, one observes a number of patients of a given type, who are treated at this hospital. Let the target parameter $\theta$ be the population size of such patients. The complication arises from the fact that a patient may receive treatment at more than one hospital. Sirken [22] refers to conventional sampling where every population element is linked to one and only one sampling unit, whereas in the case of network sampling a population element (i.e. patient of a certain type) can be linked to a varying number of sampling units (i.e. hospitals). Sirken [22] refers to ‘cluster’ as the group of population elements which are linked to the same sampling unit, and ‘network’ the group of sampling units which are linked to the same population element. The distinction between cluster and network here needs to be accounted for in estimation.

(P) Projection graph The HT-estimator (2) can be obtained using the following graph sampling set-up. Denote by H the known set of hospitals and P the unknown set of in-scope patients, where $\theta = |P|$. Let $G = (U,A)$ have $U = H \cup P$. For any $i\in H$ and $j\in P$, $a_{ij} \in A$ iff patient j receives treatment at hospital i. Let the simple graph be undirected. Notice that (H, P) form a bipartition of U, where there are no other edges at all except those that project H onto P. Given $s_1\subset H = U_0$, let $s_2 = s_1\times P$ for 1-stage snowball sampling. The observation procedure must be incident ancestral, so that $m_i$ is observed for $i \in \alpha (s_1)$, without including in the sample graph $G_s$ all the edges that are incident at i but outside of $s_2$. The inclusion probability $\pi _{(i)}$ is given by (3), where we have $\eta _i^{[0]} = \emptyset$ since $U_0 \cap P = \emptyset$, and $\eta _i^{[1]} = \beta _i$, so that $R_i = \beta _i$ and $|R_i| = m_i$. Let $y_i = 1$ for all $i\in P$.

Remark

The HT-estimator (2) and (10) correspond to the first two estimators proposed by Birnbaum and Sirken [1]. Their third estimator is defined for the edges in the projection graph, which however lacks a formulation that allows it to be applied generally.

Two-stage snowball sampling Consider 2-stage snowball sampling in the same graph, under which the observation procedure is incident but needs not be ancestral in addition. Given $s_{1,0} \subset H$, let $s_{1,1} = \alpha (s_{1,0}) \subseteq P$ and $s_{1,2} = \alpha (s_{1,1}) \subseteq H$, i.e. reverse projection. The HT-estimator (2) makes only use of the nodes (i.e. motif of interest) in $s_{1,1}$, where $y_i \equiv 1$, and $\pi _{(i)}$ is given by (3), for which $R_i = \beta _i$ is fully observed due to the addition of $s_{1,2}$.

5.2 Sampling children via parents

Lavalleè [19] considers this situation. Children are the population elements. Suppose a sample of parents is selected according to a probability design. One obtains all the children of each sample parent. Without losing generality, let the target parameter $\theta$ be the number of children who are not orphans. The same complication arises from the fact that a child may be accessed via two parents if they are both in the sampling frame. Clearly, the situation is conceptually the same as sampling patients via hospitals above.

Remark

Lavalleè [19] represents the situation using the same graph (P) above, where $U = P\cup C$, and P consists of the parents and C the children. The HT-estimator (2) based on either 1- or 2-stage snowball sampling formulation is the same as above, with $y_i \equiv 1$ for $i\in C$. Lavalleè [19] considers only the HT-estimator (10).

(M) Multigraph Put $G = (U, A)$ where $U = P$ and $A = C$, i.e. with parents as the nodes and children as the edges. Let $A_{ij}$ represent the $a_{ij}$ children of parents i and j. Let loops $A_{ii}$ at node i represent the $a_{ii}$ children of single-parent i. Given $s_1 = s_{1,0} \subset P = U_0$, let $s_{1,1} = \alpha (s_{1,0}) {\setminus } s_{1,0}$, i.e. 1-stage snowball sampling. The incident observation procedure is ancestral by construction here. Let $s_2 = s_1 \times U$. The inclusion probability $\pi _{(ij)}$ of a child $\langle ij\rangle \in A$ is given by (4), where $\eta _i^{[0]} = \{ i\}$ and $\eta _j^{[0]} = \{j\}$ under 1-stage snowball sampling; whereas $\pi _{(ii)}$ of a child $\langle ii\rangle$ of a single parent is also given by (4), where $\eta _i^{[0]} = \{ i\}$.

Remark

Making population elements the edges of the graph is not convenient for the hospital-patient application, because while each child corresponds to only one edge, each patient may appear as multiple edges incident to different nodes (i.e. hospitals).

5.3 Sampling siblings via households

Sirken [22] discusses this situation, without resorting to explicit graph representation. To fix the idea, suppose a sample of households is selected according to a probability design. For each member of the household, one obtains all the siblings who may or may not live in the same household. The observation elements are siblings, denoted by S, which excludes anyone who has no siblings. Without losing generality, let $\theta$ be the number of siblings.

(2P) Twice projection graph Denote by H the households, P the persons, and S the siblings, where $i\in S$ is considered a different element to $j\in P$, even if i and j refer to the same person in real life. Let $G= (U, A)$, where $U = H \cup P \cup S$ and $A = A^{HP} \cup A^{PS}$. Each $A_{hj} \subset A^{HP}$ is such that $h\in H$ and $j\in P$, i.e. $A^{HP}$ projects H onto P; each $A_{ij}\in A^{PS}$ is such that $i\in P$ and $j\in S$ are siblings, including when the two refer to the same person, i.e. $A^{PS}$ projects P onto S. Let the twice projection graph from H to P to S be undirected. Consider 2-stage snowball sampling starting from $s_{1,0} \subset H = U_0$. Let $s_2 = s_1 \times U$, where $s_1 = s_{1,0} \cup s_{1,1}$ is the sample of seeds. The observation procedure must be incident ancestral, provided which the HT-estimator (2) is only based on $s_{1,2}$. For $i\in S$, we have $y_i = 1$ and $\pi _{(i)}$ given by (3), where $\eta _i^{[0]} = \eta _i^{[1]} = 0$ because it can only be reached from $s_{1,0}$ in exactly two waves, and $\eta _i = \eta _i^{[2]}$ where $|\eta _i| = m_i$ is the number of households that can lead to i from $s_{1,0}$, i.e. its multiplicity according to Birnbaum and Sirken [1].

(PR) Projection relation graph Put $G = (U, A)$, where $U =H \cup P$. Let $a_{ij}\in A$ if (i) person j belongs to household i, or (ii) persons i and j are siblings of each other. The edges of type (i) project H on to P, whereas those of type (ii) are relations within P. Notice that each group of siblings form a clique; a person without siblings is a single-node clique. To ensure ancestral observation, consider 3-stage snowball sampling. Given $s_{1,0} \subset H = U_0$, $s_{1,1}$ consists of the members of the households in $s_{1,0}$, and $s_{1,2}$ the siblings of $s_{1,1}$ which are outside of the initial sample households, and $s_{1,3} \subseteq H$ consists of the households to $s_{1,2}$. Let $s_2 = s_1 \times U$, where $s_1 = s_{1,0} \cup s_{1,1} \cup s_{1,2}$. The HT-estimator (2) makes use of $i\in s_1 \cap S$, with $y_i \equiv 1$. The corresponding $\pi _{(i)}$ is given by (3), where $\eta _i^{[0]} = 0$, and $\eta _i^{[1]}$ is the household of i, and $\eta _i^{[2]}$ contains the households of its out-of-household siblings. In other words, $\eta _i$ contains all the households that can lead to i, where $|\eta _i| = m_i$.

Remark

Sampling in the graphs (2P) and (PR) makes use of relationships among the population elements, unlike sampling of patients or children in the projection graph (P).

(HP) Hypernode projection graph Let each clique in the graph (PR) above be a hypernode—all the nodes of a hypernode are always observed together or not at all. Let $G = (U, A)$, where $U = H \cup \mathcal {P}$, and $\mathcal {P}$ consists of all the hypernodes of P. Let $a_{ij} =1$ iff at least one node in the hypernode j belongs to household i. This yields an undirected simple graph as the hypernode projection graph. Consider 2-stage snowball sampling with $U_0 = H$ as in the projection graph, such that observation is ancestral by construction. Both HT-estimators (2) and (10) follow directly, where $y_i$ is the number of nodes in $i\in \mathcal {P}$.

5.4 Adaptive cluster sampling of rare species

In contrast to conventional sampling, Thompson [24] characterises adaptive sampling designs as those in which the procedure to include units in the sample depends on the values of interest observed during the survey. To fix the idea, suppose an area is divided into (spatial) grids as the units of sampling and observation. Each grid in an initial sample of grids is surveyed for a given species of interest. If it is not found there, one would move on to another grid in the initial sample. However, whenever the species is found in grid i, one would survey each of its neighbour grids in four directions, beyond the initial sample, provided not all of them have been surveyed before. This observation procedure can help to increase the number of in-scope grids, compared to random sampling of the same amount of grids, provided the species is more likely to be found given that it is found in a neighbour grid than otherwise. Once in a new grid, the procedure is repeated and the survey may or may not continue to the neighbour grids, depending on the finding in the current grid. The sampling is finished if no new grids can be added to the sample, or if one has reached a predetermined limit in terms of the number of surveyed grids, time, resource, etc. The observed in-scope grids form sampling as well as observation clusters, in the sense that all the member grids of a cluster are sampled and observed if any one of them is.

(T) Transitive graph Adaptive cluster sampling (ACS) can be represented as 2-stage snowball sampling in a transitive graph as follows. Let $G= (U, A)$, where U contains all the grids in ACS. Let $U_A$ contain all the grids where the rare species is present. Let $U_A^c = U{\setminus } U_A$. Let $a_{ij} =1$ iff $i,j\in U_A$ and i and j belong to the same observation cluster under the ACS. This yields an undirected simple transitive graph, where each $i\in U_A^c$ is an isolated node, and each group of connected nodes in $U_A$ form a clique. Without losing generality, let $\theta = |U_A|$. The snowball sampling starts with $s_{1,0} \subset U = U_0$, i.e. any grid can be selected initially. Let $s_{1,1} = \alpha (s_{1,0})$. Notice that the isolated nodes in $s_{1,0}$ do not lead to any nodes in $s_{1,1}$, while a connected node in $s_{1,0}$ leads to all the nodes in the same observation cluster but none in $U_A^c$, since edges exist only among the nodes in $U_A$. In reality, a neighbour grid of $i\in U_A\cap s_{1,0}$ which belongs to $U_A^c$ is also surveyed, but it will not lead to any additional nodes in the next wave, nor will it be the motif of interest in estimation. It is therefore convenient to represent this adaptive nature of the ACS by not including in $s_{1,1}$ any node from $U_A^c$ at all. The 2nd-wave snowball sample will be empty, i.e. $s_{1,2} = \emptyset$, because all the connected nodes in a clique will already be observed either in $s_{1,0}$ or $s_{1,1}$. But the 2nd-stage is needed to ensure that the observation is ancestral by construction. The HT-estimator (2) uses every node $i\in s_1 = s_{1,0} \cup s_{1,1}$, with $y_i =1$, and $\pi _{(i)}$ is given by (3), where $\eta _i^{[0]} = \{ i\}$, and $\eta _i^{[1]}$ contains all its adjacent nodes.

Remark

The graph (T) is the same as the relation part of the graph (PR) in the case of sampling siblings via households. The projection part is not necessary here because the initial sampling uses a direct frame, unlike the other applications above.

Remark

The ACS can as well be represented by the graph (HP), with the cliques in the graph (T) above as the hypernodes. Both HT-estimators (2) and (10) follow directly.

6 Concluding remarks

In this paper we synthesised the existing graph sampling theory, and made several extensions of our own. We proposed a definition of sample graph, to replace the different samples of nodes, dyads, triads, etc. This provides formally an analogy between sample graph as a sub-population graph and sample as a sub-population. Next, we developed a general approach of HT-estimation based on arbitrary T-stage snowball sampling. It is clarified that design-based estimation based on snowball sampling requires the observation procedure to be ancestral, which can be hard to fulfil in many practical applications of snowball or snowball-like sampling, including the estimation of a clandestine target population size. Without satisfying the ancestral requirement, the estimation will have to be based on an appropriate statistical model instead.

We presented various graph sampling formulations of the existing design-based network sampling methods. It is seen that different graph representations reveal the different estimators more or less readily, so the choice matters in applications. The graph sampling theory provides a more general and flexible framework to study and compare these unconventional methods, and to develop possible alternatives and modifications.

Moreover, it transpires that these existing network sampling methods do not really differ from conventional sampling with respect to the target parameter. We believe that the scope of investigation can be greatly extended if one starts to consider other genuine network parameters, which can only be studied using a graph representation. Two research directions can be identified in this respect. First, we are currently examining the scope of problems that can be studied using the (hypernode) projection graph, and the properties of the design-based estimation methods. Second, it seems intuitive that a lower-order network parameter can be estimated using a ‘smaller’ or more fragmented sample graph than a higher-order parameter. It is therefore interesting to understand better the conditions, by which a high-order network parameter can be expressed as a function of lower-order parameters. Although this is perhaps more of a mathematical than statistical problem, such transformations can potentially be very useful for the applications of the graph sampling theory. Developing a comprehensive finite-graph sampling theory, beyond the established finite-population sampling theory, seems an exciting area for future research.